
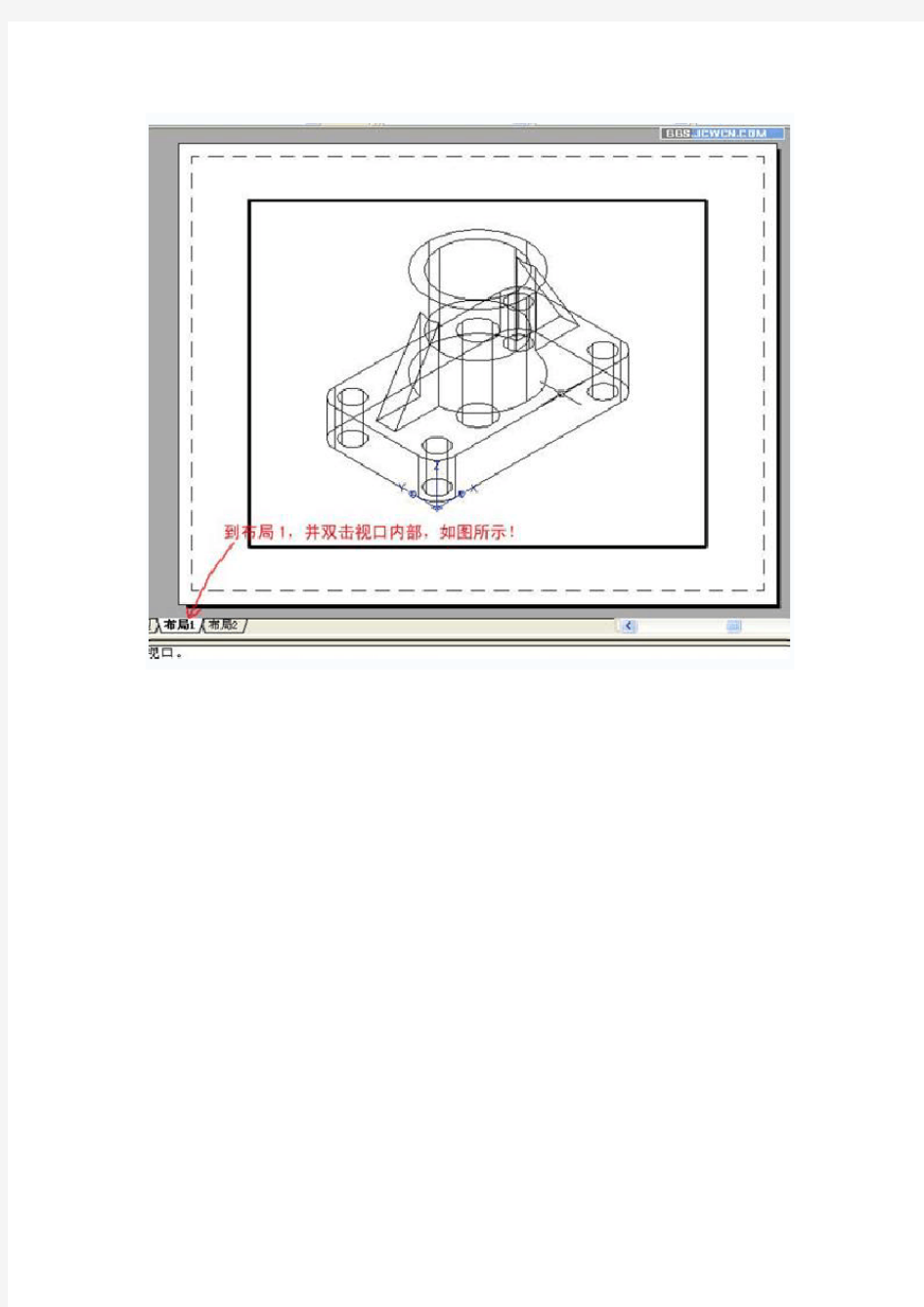
2---3
本文由中国教程网cbxandcbj (烈马不羁) 原创,转载须保留此信息制作完成! 本题主要运用的是设置轮廓命令,将三维模型投影到二维平面!
二维转三维 传统的机械绘图,是想象出零部件的立体形状,然后对立体模型从各个方向上投影,生成各投影面上的二维视图,加以标注尺寸等注释,生成基本的二维的图纸。如下图。 二维的图纸 但是二维图纸的缺点也是明显的,就是略复杂点的就显得不直观,需要人为的正确想象。如果有三维的数模展现,并且能旋转、缩放,就更加直观易懂了。 现在有了三维CAD软件SolidWorks的辅助,实现2D—3D转换,生成一般的三维数模是比较简单的事。对于从AutoCAD到三维软件过渡的设计者来说,SolidWorks的这个功能容易上手,可以帮助你轻松完成从AutoCAD到三维CAD软件的跨越。 从2D-3D的跨越可谓是传统机械绘图的逆向过程(类似图1,但是由投影视图生成立体模型)。输入的2D草图可以是AutoCAD的DWG格式图纸,也可是SolidWorks工程图,或者是SolidWorks的草图。 本文讨论如何从AutoCAD的图纸输入到SolidWorks中实现2D—3D的转换。 原理:很多三维CAD/CAM软件的立体模型的建立,是直接或间接的以草绘(或者称草图)为基础的,这点尤以PRO/E为甚。而三维软件的草绘(草图),与AutoCAD等的二维绘图大同小异(不过不同的就是前者有了参数化的技术)。 在SolidWorks中,就是将AutoCAD的图纸输入,转化为SolidWorks的草图,从而建立三维数模。 基本转换流程: 1.在SolidWorks中,打开AutoCAD格式的文件准备输入。 2.将*DWG,DXF文件输入成SolidWorks的草图。 3.将草图中的各个视图转为前视、上视等。草图会折叠到合适的视角。 4.对齐草图。 5.拉伸基体特征。 6.切除或拉伸其它特征。 在这个转换过程中,主要用2D到3D工具栏,便于将2D图转换到3D 数模。
在射影几何学中,把无穷远点看作是“理想点”。通常的直线再加上一个无穷点就是无穷远直线,如果一个平面内两条直线平行,那么这两条直线就交于这两条直线共有的无穷远点。通过同一无穷远点的所有直线平行。 德国数学家克莱因(图)在爱尔朗根大学提出著名的《爱尔朗根计 划书》中提出用变换群对几何学进行分类 在引入无穷远点和无穷远直线后,原来普通点和普通直线的结合关系依然成立,而过去只有两条直线不平行的时候才能求交点的限制就消失了。 由于经过同一个无穷远点的直线都平行,因此中心射影和平行射影两者就可以统一了。平行射影可以看作是经过无穷远点的中心投影了。这样凡是利用中心投影或者平行投影把一个图形映成另一个图形的映射,就都可以叫做射影变换了。 射影变换有两个重要的性质:首先,射影变换使点列变点列,直线变直线,线束变线束,点和直线的结合性是射影变换的不变性;其次,射影变换下,交比不变。交比是射影几何中重要的概念,用它可以说明两个平面点之间的射影对应。 在射影几何里,把点和直线叫做对偶元素,把“过一点作一直线”和“在一直线上取一点”叫做对偶运算。在两个图形中,它们如果都是由点和直线组成,把其中一图形里的各元素改为它的对偶元素,各运算改为它的对偶运算,结果就得到另一个图形。这两个图形叫做对偶图形。在一个命题中叙述的内容只是关于点、直线和平面的位置,可把各元素改为它的对偶元素,各运算改为它的对偶运算的时候,结果就得到另一个命题。这两个命题叫做对偶命题。这就是射影几何学所特有的对偶原则。在射影平面上,如果一个命题成立,那么它的对偶命题也成立,这叫做平面对偶原则。同样,在射影空间里,如果一个命题成立,那么它的对偶命题也成立,叫做空间对偶原则。研究在射影变换下二次曲线的不变性质,也是射影几何学的一项重要内容。如果就几何学内容的多少来说,射影几何学;仿射几何学;欧氏几何学,这就是说欧氏几何学的内容最丰富,而射影几何学的内容最贫乏。比如在欧氏几何学里可以讨论仿射几何学的对象(如简比、平行性等)和射影几何学的对象(如四点的交比等),反过来,在射影几何学里不能讨论图形的仿射性质,而在仿射几何学里也不能讨论图形的度量性质。
AutoCAD中三维实体转换为二维投影图的方法 唐月撵 辽宁工程技术大学机械工程学院辽宁阜新(123000) E-mail:tangyuenian2008@https://www.doczj.com/doc/9b6386409.html, 摘要:进行三维造型设计、用二维平面投影图来表达空间三维实体形状是工程图学课程的任务。介绍了在AutoCAD软件中进行三维实体造型的过程,在布局空间进行视口设置,利用建立的三维实体模型生成二维投影,在模型空间中进行图形编辑处理,得到二维平面投影图或剖视图的方法。 关键词:工程图学;AutoCAD;三维实体;二维投影图;块 1. 引言 2004年5月年教育部工程图学教学指导委员会推出了最新版的《普通高等院校工程图学课程教学基本要求》,新《教学基本要求》的突出变化是进一步加强对学生计算机绘图能力的培养,首次把三维图形设计能力的培养作为课程任务突显出来。现代工程设计既需要二维图示,也需要三维图示,应用计算机软件可以将两种图样有机地结合起来,进而提高形体的图示表达能力[1]。 随着现代计算机技术和计算机绘图技术的发展,大型三维绘图软件(如UG、 Pro/ENGINEER、AutoCAD等)的出现,三维设计完全成为可能。AutoCAD是应用最广泛的软件之一[2]。本文介绍了在 AutoCAD中绘制与处理三维实体模型,利用建立的三维实体模型转换为二维投影图的方法。 2. 在AutoCAD中绘制三维实体图 图1 形体的三维剖视图 如图1:从该形体的三维剖视图可以看出,此形体左右对称,前后不对称,由底板、肋板、圆柱筒等组成。在AutoCAD软件中绘制该形体的三维实体图主要步骤简要如下:(1)在AutoCAD软件中,调入需要使用的如“绘图”、“修改”、“实体”等工具条。视图选 择俯视图,绘制底板水平投影的外框,定义为面域,通过拉升命令(单击图标)拉升成为柱体,通过拉升命令创建U型槽柱体,选择左视图,创建左右对称两长方体,其长度超 过底板的长度,通过布尔差集运算(图标为)形成底板。 (2)视图选择俯视图投影方向(图标为),在命令行输入cylinder命令或单击图
射影变换 4.1 点列和线束 点列和线束定义. 两个矢量),,(321a a a 和),,(321b b b 表示不同的点当且仅当这两个矢量线性无关. 在两点A ),,(321a a a 与B ),,(321b b b 的连线上任意一点),,(321x x x X 满足 03 2132 13 21=b b b a a a x x x 即,三点A ),,(321a a a ,B ),,(321b b b 与),,(321x x x X 共线的充分必要条件是 03 2132 13 21=b b b a a a x x x 以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλ μ '+=+ =;以m l ,为基线的线束中,任何一直线p 都可以表示为m l p μλ+=,用齐次坐标可以表示为m l m l p λλ μ '+=+=. 练习4-1 1.已知A 和B 的齐次坐标分别为)1,1,5(和)1,0,1(-,求直线AB 上一点C ,使 1)(-=ABC ,若B A C λ+=,求出λ. 解利用非齐次坐标),(y x 与齐次坐标),,(321x x x 之间的关系31x x x = ,3 2x x y =.这时,)1,5(),(=y x A ,)0,1(),(-=y x B ,再利用BC AC ABC = )(. 11 5 -=+-x x ,解得2=x ,
101-=--y y ,解得21=y .即)21,2(=C ,C 点的齐次坐标为)1,2 1 ,2(. 因为B A C 2 1 21+= ,所以 1=λ. 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλ μ '+=+ =. 2.试证明:三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为 03 2 1 3213 21=z z z y y y x x x 证明三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为 λ=--=--=--3 333222 21111y z x z y z x z y z x z 所以 03 32 21 132133221 13 2 1 321321=-------=y z y z y z y y y x z x z x z z z z y y y x x x 4.已知直线0143=++y x 与02=+y x ,求过两直线的交点与点)0,1,2(的直线方程. 解两直线0143=++y x 与02=+y x 的交点为 )5,1,3(1 1 2 1433 21--=x x x 于是点)5,1,3(--与点)0,1,2(的直线方程为 051050 1 2 513321321=+-=--x x x x x x 即05105321=+-x x x .
AutoCAD中由三维模型自动生成二维工程图的研究3 何兵1,2,车林仙1,2 (1.重庆大学机械工程学院,重庆 400044;2.泸州职业技术学院机电工程系,四川泸州 646005) 摘要:基于AutoCAD的二次开发工具VBA语言,给出了AutoCAD中由三维模型自动生成二维工程图(即二维投影图和轴测图)的方法和程序。该方法简单易行,改变了手动操作的繁琐与困难,提高了绘图效率,具有工程应用价值。 关键词:AutoCAD;三维模型;二维工程图;VBA 中图分类号:TP302.4;TP391.72 文献标识码:A 文章编号:1001-2354(2005)09-0010-03 当前,基于特征技术的三维实体造型软件很多,功能强大, 优势明显,如U G2Ⅱ,Pro/Engineer,I2DEAS,SolidWork等。然而,在现阶段,三维实体造型还不能完全取代二维工程图(即二维投影图和轴测图),因为在表达非几何信息(如尺寸、公差、工艺信息等)及合乎工程技术人员的传统习惯方面,二维工程图仍然具有优越性和普遍性。 AutoCAD是目前国内外应用最广泛的PC2CAD软件,它不但具有强大的二维绘图功能,而且还能方便地进行三维实体造型。在AutoCAD中,若先进行三维实体造型,再由该三维模型生成二维投影图,则可以充分发挥三维实体和二维投影图各自的优势,并提高绘图效率。特别是绘制复杂机件的二维工程图时,此方法具有明显优点。文献[1~3]对AutoCAD中由三维模型生成二维工程图的方法进行了深入研究,给出了操作步骤,但其过程较繁琐,在用Solprof,Soldraw,Solview命令时需在模型空间和图纸空间反复切换,技巧性很强,每生成一个图形均需重复这些操作,耗时耗力,且不易被普通用户掌握。有鉴于此,文中改进了文献[1~3]中由三维模型生成二维工程图的方法,并将由三维模型生成二维工程图的过程,编制为VBA (Visual Basic for Application)程序并定义为宏,这样便可一劳永逸,而其后续操作步骤非常简单。先用Lweight设置一个缺省线宽,运行此程序则自动生成二维工程图,然后添加中心线、标注尺寸,即可得到符合国家标准的工程图,大大提高了绘图效率。 1 编程环境 VBA是AutoCAD的内嵌开发工具,与VB类似,采用面向对象技术,具有强大的窗体创建功能,简单实用[4]。因此,选用VBA为二次开发工具。创建VBA工程的方法为:打开Au2 toCAD的菜单“Tools|Macro|Visual Basic Editor”,在“Visu2 al Basic Editor”中创建工程。 2 由三维模型自动生成二维 工程图的方法2.1 用AddPViewport方法在图纸空间创建视口 AutoCAD的三维实体造型环境为模型空间(Model Space),而输出二维图形的环境为图纸空间(Paper Space)[1~4]。由画法几何知,在空间自6个方向观察三维模型,即可得到6个基本视图(二维投影图)。欲同时观察模型的几个方向,则需用Vports命令在模型空间或图纸空间创建多视口,并在不同视口中设置观察方向,从而得到相应的视图。在VBA中,可用AddPViewport方法在图纸空间创建视口,其语法格式如下:’从模型空间切换到图纸空间 ThisDrawing.ActiveSpace=acPaperSpace ThisDrawing.MSpace=False ’定义ProjectViewPort为图纸空间的视口 Dim ProjectViewPort As AcadPViewport ’定义CenPoint数组表示的点为视口中心 Dim CenPoint(0To2)As Double ’Widt h和Height分别为视口的宽和高 Set ProjectViewPort=ThisDrawing.PaperSpace.AddPViewport (CenPoint,Widt h,Height) 2.2 用Direction属性设置观察(投影)方向 在VBA中,可用Direction属性为创建的视口设置观察(投影)方向,其语法格式如下: ’定义ViewDirect数组表示的点为视点,主、俯、左视图的视点可设为(0,-1,0),(0,0,1),(-1,0,0) ’轴测图的视点则根据需要而设置 Dim ViewDirect(0to2)As Double ProjectViewPort.Direction=ViewDirect ’将当前视口设置为活动窗口 ProjectViewPort.Display acOn 2.3 用Solprof命令生成三维模型的轮廓(即二维投影图) 由于VBA没有提供生成三维模型轮廓的函数,因此采用直接调用AutoCAD中Solprof命令的方法,来生成三维模型的轮廓(即二维投影图)。使用该命令时,采用输入“All”来实现全部选中对象,并连续4次输入“Yes”(或直接回车[1])来确认。调用AutoCAD中Solprof命令的格式如下: ’切换到模型空间 第22卷第9期2005年9月 机 械 设 计 J OU RNAL OF MACHIN E DESIGN Vol.22 No.9 Sep. 2005 3收稿日期:2005-01-07;修订日期:2005-04-04 基金项目:中国职业技术教育协会科研规划项目(520123);泸州职业技术学院科研基金资助项目(03B01) 作者简介:何兵(1972-),男,四川泸州人,讲师,重庆大学机械学院在职硕士生,研究方向:机械CAD/CA E及机电控制。
二维射影变换及其性质 王 玮 数学科学学院06050203 摘 要 二维射影变换是射影几何的一个重要分支,重点研究的是点和直线在射影变换下的不变性.本文着重研究了二维射影变换下二重元素的分布状况及其特征性质,从理论上解决了二维射影变换二重元素的结构问题.另外本文对二维射影变换的对合性和变换式的求法进行了探索.二维射影变换式的求法在现行的教科书中涉及较少,本文通过具体例子来说明二维射影变换式的几种求法. 关键词:二维射影变换,对合对应,特征方程,特征根,交比,矩阵 引言 射影几何学是几何学的一个重要分支学科,它是专门研究图形的位置关系的,也是专门用来讨论在把点投影到直线或者平面上的时候,图形的不变性质的科学。在射影几何学中,把无穷远点看作是“理想点”。欧式直线再加上一个无穷点就是射影几何中的直线,如果一个平面内两条直线平行,那么这两条直线就交于这两条直线共有的无穷远点。通过同一无穷远点的所有直线平行。在引入无穷远点和无穷远直线后,原来普通点和普通直线的结合关系依然成立,而过去只有两条直线不平行的时候才能求交点的限制就消失了。 由于经过同一个无穷远点的直线都平行,因此中心射影和平行射影两者就可以统一了。平行射影可以看作是经过无穷远点的中心投影了。这样凡是利用中心投影或者平行投影把一个图形映成另一个图形的映射,就都可以叫做射影变换了。 一、二维射影变换 定义1.1 设,'ππ为两个点场.若:'?ππ→满足 (1)?为双射; (2)?使得共线点变为共线点; (3)?保持四点的交比不变,
则称?为点场π到点场'π的一个二维射影对应。 定义 1.2 若两个平面间的一一对应满足下列条件:(1)保持点和线的结合性;(2)任何共线四点的交比等于对应四点的交比,则此一一对应叫做射影对应. 定义 1.3 设在点场π和'π上咯取定了齐次射影坐标系,则下式所决定的对应 ()111112213322112222333 311322333'',0,0. 'ij x a x a x a x x a x a x a x A a x a x a x a x ρρρρ=++?? =++=≠≠*??=++? 为点场π到'π的一个非奇异线性对应.其中()()123123,,,',','x x x x x x 为对应点的齐次坐标,A 称为这个非奇异线性对应的矩阵.如果'ππ=,且对应点的齐次坐标是关于平面上同一个取定的射影坐标系而论的,则()*为点场π上的一个非奇异线性变换. 定义1.4 两个同底的点场或线场之间的射影对应称为二维射影变换. 显然二维射影变换是特殊的二维射影对应,变换式相对于射影平面上的一个取定的射影坐标系进行的,()*表示了一个点与其像点的坐标之间的关系,二维射影变换具有二维射影对应的全部性质.同时,如果我们将()(12312,,,',',x x x x x )3'x 看成同一个点在平面上不同的射影坐标系下的坐标,则()*式即为射影坐标变换式,于是,射影坐标变换也可以视为射影变换. 二、二维射影变换式的求法 二维射影变换式的求法在现行的射影几何教科书中涉及较少.本节通过具体例子说明二维射影变换式的求法. 定理 2.1在一平面内无三点共线的四点(1,2,3,4)i P i =与另一平面内无三点共线的四点'(1,2,3,4)i P i =唯一确定一个射影对应,使()'1,2,3,4i i P P i →= 定理 2.2设平面π上无三点共线()()()112321233123,,,,,,,,,P a a a P b b b P c c c ()4123,,P d d d 和另外无三点共线的四点()()11232123'',',','',',',P a a a P b b b ()()31234123'',',','',','P c c c P d d d 成射影对应,则存在而且只有一个射影对应?,使
第二章 射影映射 本章将阐明一维射影变换、射影映射和二维射影变换的几何意义;研究它们各有哪些类型;并对其中比较重要的几种特殊类型进行较深入的讨论。 §1透视 透视是一个很简单但又最基本的射影映射。一般非透视的射影变换、射影映射可以用透视来表示。 定义 如果一个点列与一个线束的元素之间建立了一一对应且对应元素是结合的,则这个对应叫做透视对应,点列与线束叫做透视的,或配景。如图2.1记成 (,,,)(,,,,)y z u v a ξηζ?ψ???∧??? 定义 点ξ和ξ’的对应点的连线交于一点s,也就是这两个点列与同一线束s 成透视,则这两个点列叫做透视点列,点s 叫做透视中心,记作 (,,)(,,,)S a b c a b c ξξ∧ ''''??????=或()()a a ξξ''∧,如图2.2 对偶定义: 线束s 和s ’的对应直线的交点在一直线α上,也就是这两个线束与同一点列透视,则这两个线束叫做透视线束。直线α叫做透视轴。记作 (,,,)(,,,)s s αηζ?ηζ?∧ ''''??????=或()()s s α ηη∧ ''=,如图2.3. 两个点列射影的,记作()()a a ξξ''∧;两个线束射影的,记作()()s s ηη''∧ 看图2.2,如果,,,ηζ?ψ是线束s 的四条直线,分别与ξ和ξ’交于a,b,c,d 和a ’,b ’,c ’, d ’,则有 R(a,b ;c,d)=R(,;,ηζ?ψ)=R(a ’,b ’;c ’,d ’) 图2.1 图2.2 图2.3
所以透视对应保持交比不变,又因透视是一一对应,所以透视是射影对应(斯丹纳定义)。显然,透视对应把点ξξ'?映射为自身。 定理1 直线ξ到ξ’的透视是射影对应,它把公共点ξξ'?映射为自身。反过来,又有 定理2 直线ξ到ξ’的一个射影对应,如果把公共点ξξ'?映射为自身,那么这个射影对应是透视。(图2.4) 证明:设ξ到ξ'的射影对应Ф由三对对应点唯一确定: :(,,)(,,)a b y a b y φξξ'''∧且()c c φ'= 令00 ()(),(),(,,) (,,)s a a b b s s c c a b c a b c ξξξ∧ ''''''???=??=∴=记作ψ。 0(,;,)(,;,)(,;,)R a b y c R a b y c R a b y c '''''== 0,c c '∴≡φ与ψ有三对点相同,φψ∴≡φ∴是透视。 'ξ 定理1和定理2的对偶定理请读者自行叙述。由上述定理得结论: 定理3 两个射影点列(线束)成透视的充要条件是它们的公共点(直线)自身对应。 定理4如果(,,)(,,)(,,)a b c a b c a b c ξξξ''''''''''''???∧???∧??? 那么(,,)(,,,)a b c a b c ξξ''''''''???∧??? 定理5 两条不同的直线之间的非透视的射影对应,是两个透视变换的积, 证明:设Ф是直线ξ到'ξ的射影对应, (图 2.5)但不是透视, (,,)(,,)a b c a b c ξξ''''∧ (其中三对对应点中没有任何一点是ξξ'?),在直线a ×a ’上任取二点s 和s ’,作点(s ×b)×(s ’×b ’)~b 0,(s ×c)×(s ’×c ’)~c 0,再作直线ξ0~b 0×c 0, ξ0×(a ×a ’)~a 0,于是有 ' '00(,,)(,,)s s a b c a b c ξξξ∧ ∧ '''=00 (,,)=a b c 图2.4
概述 投影变换完成的是如何将三维模型显示到二维视口上,这是一个三维到二维的过程。你可以将投影变换看作是调整照相机的焦距,它模拟了为照相机选择镜头的过程。投影变换是所有变换中最复杂的一个。 视锥体 视锥体是一个三维体,他的位置和摄像机相关,视锥体的形状决定了模型如何从camera space投影到屏幕上。最常见的投影类型-透视投影,使得离摄像机近的物体投影后较大,而离摄像机较远的物体投影后较小。透视投影使用棱锥作为视锥体,摄像机位于棱锥的椎顶。该棱锥被前后两个平面截断,形成一个棱台,叫做View Frustum,只有位于Frustum内部的模型才是可见的。 透视投影的目的 透视投影的目的就是将上面的棱台转换为一个立方体(cuboid),转换后,棱台的前剪裁平面的右上角点变为立方体的前平面的中心(下图中弧线所示)。由图可知,这个变换的过程是将棱台较小的部分放大,较大的部分缩小,以形成最终的立方体。这就是投影变换会产生近大远小的效果的原因。变换后的x坐标范围是[-1, 1],y坐标范围是[-1, 1],z坐标范围是[0, 1](OpenGL略有不同,z值范围是[-1, 1])。
透视投影矩阵推导 下面来推导一下透视投影矩阵,这样我们就可以自己设置投影矩阵了,就可以模拟神奇的D3DXMatrixPerspectiveLH函数的功能了。那么透视投影到底做了什么工作呢?这一部分算是个难点,无论是DX SDK的帮助文档,还是大多数图形学书籍,对此都是一带而过,很少有详细讨论的,早期的DX SDK文档还讨论的稍微多一些,而新近的文档则完全取消了投影矩阵的推导过程。 我们可以将整个投影过程分为两个部分,第一部分是从Frustum内一点投影到近剪裁平面的过程,第二部分是由近剪裁平面缩放的过程。假设Frustum内一点P(x,y,z)在近剪裁平面上的投影是P'(x',y',z'),而P'经过缩放后的最终坐标设为P''(x",y",z")。假设所求的投影矩阵为M,那么根据矩阵乘法可知,如下等式成立。 PM=P'',即 先看第一部分,为了简化问题,我们考虑YOZ平面上的投影情况,见下图。设P(x, y, z)是Frustum内一点,它在近剪裁平面上的投影是P'(x', y', z')。(注意:D3D以近剪裁平面作为投影平面),设视锥体在Y方向的夹角为Θ。
CAD三维实体转二维投影方法 1、在模型空间打开四个视口,如下图。 2、点击需要投影的一个视口,选择菜单命令:绘图\实体\设置\视图,得到需要投影视口的 一个布局空间,并激活视图命令,如下图。
3、在“绘图\实体\设置\视图”命令输入选项中,选择U+回车,在对下述输入选项默认值< 当前>、视图比例<1>回车确定。在布局图中,在“指定视图中心”选项状态点击布局图中点,进入视图,图形(可能很小)在该视图中心,移开鼠标即可看到,如下图。 4、在视图中,在“指定视图中心”选项状态点击视图的一个位置(可多次更改)+回车, 然后以该位置为中点选定第一点、选定第二点确定视图大小,视图迭放在布局图上,如下图。
5、输入视图名如v1+回车,即结束视图命令操作。命令窗口回到下一视图命令状态。回车, 离开该命令,视图已获得,如下图。 6、这时,打开“格式\图层”菜单命令,可以看到新增图层“v1-DIM、v1-HID、v1-VIS”三个图层。这时视图仍是三维的,通过关闭图层“0”可以证实这一点,在CAD2006帮助菜单命令参考下找到“solview”可以进一步理解。SOLVIEW 在引导用户创建基本视图、辅助视图以及剖视图的过程中计算投影。视图相关的信息随创建的视口一起保存。此信息由SOLDRAW 命令使用,该命令将最终生成图形视图。下面执行“SOLDRAW”命令。 7、选择“绘图\实体\设置\图形”命令,出现选择物体状态,将鼠标方形箭头移到视图边框 上,激活视图边框(边框变为虚线),如下图。
8、按鼠标左键确定+回车,则命令完成。这时视图变为二维投影线,如下图。 9、在模型空间,可以激活对应视口的投影线,说明三维与二维图同时显示在一个视口上, 关闭图层“0”可以只显示二维投影线,如下图。
(0464)《高等几何》复习大纲 仿射坐标与仿射变换 一、要求 1.掌握透视仿射对应概念和性质,以及仿射坐标的定义和性质。熟练掌握单比的定义和坐标表示。2.掌握仿射变换的两种等价定义;熟练掌握仿射变换的代数表示,以及几种特殊的仿射变换的代数表示。3.掌握图形的仿射性质和仿射不变量。 二、考试内容 1.单比的定义和求法。 2.仿射变换的代数表示式,以及图形的仿射性质和仿射不变量。3.仿射变换的不变点和不变直线的求法。 射影平面 一、要求 1.掌握中心射影与无穷远元素的基本概念,理解无穷远元素的引入。 2.熟练掌握笛萨格(Desargues)定理及其逆定理的应用。 3.熟练掌握齐次点坐标的概念及其有关性质。 4.理解线坐标、点方程的概念和有关性质。 5.掌握对偶命题、对偶原则的理论。 二、考核内容 1.中心投影与无穷远元素:中心投影,无穷远元素,图形的射影性质。 2.笛萨格(Desargues)定理:应用笛萨格(Desargues)定理及其逆定理证明有关结论。 3.齐次点坐标:齐次点坐标的计算及其应用。 4.线坐标:线坐标的计算及其应用。 5.对偶原则:作对偶图形,写对偶命题,对偶原则和代数对偶的应用。
射影变换与射影坐标 一、要求 1.熟练掌握共线四点与共点四线的交比与调和比的基本概念、性质和应用。 2.掌握完全四点形与完全四线形的调和性及其应用。 3.掌握一维射影变换的概念、性质,代数表示式和参数表示式。 4.掌握二维射影变换的概念、性质以及代数表示式。 5.理解一维、二维射影坐标的概念以及它们与仿射坐标、笛氏坐标的关系。 二、考试内容 1.交比与调和比:交比的定义、基本性质及其计算方法,调和比的概念及其性质。 2.完全四点形与完全四线形:完全四点形与完全四线形的概念及其调和性。 3.一维基本形的射影对应:一维射影对应的性质,与透视对应的关系,以及代数表示式。。 4.二维射影变换 5.二维射影对应(变换)与非奇线性对应的关系。 6.射影坐标:一维射影坐标、二维射影坐标。 7.一维、二维射影变换的不变元素:求一维射影变换的不变点,二维射影变换的不变点和不变直线。 变换群与几何学
4.3 二维射影对应的坐标表示 定义4.7 设π与'π是两个平面,在其上各建立射影(或笛卡尔)坐标系,平面π的点P(1χ,2χ,3χ)到平面'π的点'P (1'χ,2'χ,3'χ)的一个对应 ?? ? ??++=++=++=333332331332322222123132121111'''χ χχρχχχχρχχχχρχa a a a a a a a a )3,2,1,(0=≠=j i a A ij (4.3) 其中 A= ????? ? ?33 323123 222113 1211a a a a a a a a a , 0≠ρ 这个对应叫做非奇线性对应,A 叫做它的方阵,A 叫做它的行列式,ij a 叫做对应的系数或参数. (4.1)式可简写为 ∑== 3 1 1'j ij a ρχ ()3,2,1=i 若用矩阵写法,则又可写为: ? ??????= ???? ??? 3213 2 1'''χχχχχχρA ()' 1.4 注意 由于点()321',','ρχρχρχ,当ρ取任何不等于零的值时,它表示同一个点的坐标'P ,所以每一个P 点,有唯一一个'P 点与之对应. 如果只讨论两平面上的普通点,则(4.1)式还可以写为非齐次坐标式: ? ? ++++=++++=33 3231232221333231131211''a a a a a a a a a a a a γχγχγγχγχχ (4.2) 容易证明非齐次线性对应是平面π与'π的点之间的一一对应,而且它同时可建立π与'π间线场和线场的非齐次线性对应(证明略).因而非奇线对应保持点与直线的结合性. 下面证明非奇线性对应(4.1)是射影对应.根据定义 4.2只需证明任何共线四点的交比等于其对应四点的交比,为此给出以下引理. 引理 设非齐次线对应(4.1)若使平面π内的点a 与b 顺次对应平面'π内的'a 与'b ,则π内的点b a λ+必与对应'π的点''21b a λρρ+,此处1ρ与2ρ顺次a 对应'a 与b 对应'b 的比例常数ρ的值.(证明略). 定理 4.1 若在两个平面π与'π内各自建立射影(或笛卡尔)坐标系,则这两个平面的点