(03)第3章 用统计量描述数据

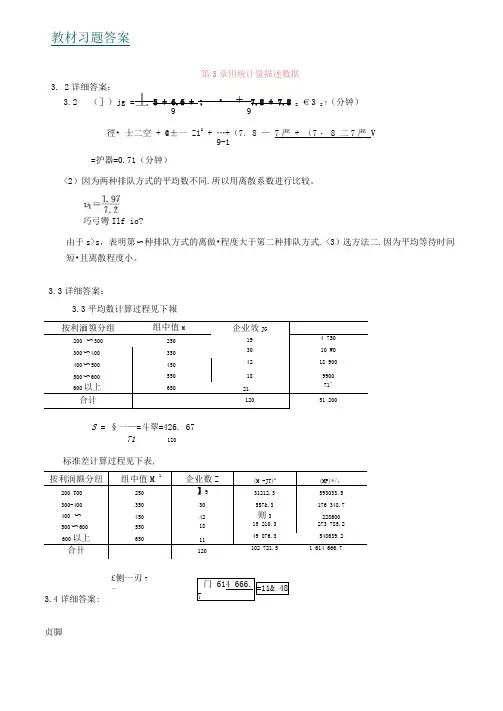
教材习题答案第3章用统计量描述数据3. 2详细答案： 3.2 （］）jg =丄5 + 6.6 + ；・ + 7.8 + 7.8 =€3= ?（分钟）9 9徑• 士二空 + @±一 Z12+ …+（7. 8 — 7严 + （7・ 8 二7严 V 9-1 =护器=0.71（分钟）<2）因为两种排队方式的平均数不同.所以用离散系数进行比较。

巧弓彎Ilf io?由于s>s ，表明第〜种排队方式的离做•程度大于笫二种排队方式. <3）选方法二.因为平均等待时间短•且离散程度小。

3.3详细答案：3.3平均数计算过程见下報 按利湎领分组组中值M企业效JG200 〜300 250 19 4 750 300〜400 350 30 10 WO 400〜500 450 42 18 900 500〜600 550 18 9900 600以上 65021 71" 合计12051 200S = §一—=斗翠=426. 6771 1Z03.4详细答案:贞脚按利润额分纽组中值M 1企业数Z(M -JT)1(MP)*/； 200 TOO 250 】931212.3 593033.5 300-400 350 30 5S7&.3176 348.7 400 〜 450 42 则3228600 500〜600 550 18 15 210.3 273 785.2 600以上65011 49 876.3 548639.2 合卄120102 721.51 614 666.7标准差计算过程见下表, £侧一刃7―门 614 666. 7=11& 48通过计算标准化值来判断，Z ^=1 , Z B = 0-5，说明在A 项测试中该应试者比平均分数高出1 个标准差，而在B 项测试中只高出平均分数0.5个标准差，由于A 项测试的标准化值高于B 项测试, 所以A 项测试比较理想。

3. 5详细答案：3种方法的主要描述统计量如下：(1) 从集中度、离散度和分布的形状三个角度的统计量来评价。

第一章统计和统计数据名词解释1.统计学：收集处理分析解释数据并从数据中得出结论的科学。

2.描述统计：研究数据收集处理汇总图表描述概括与分析等统计方法。

3.推断统计：研究如何利用样本数据来推断总体特征的统计方法。

4.分类数据：只能归于某一类别的非数字型数据。

5.顺序数据：只能归于某一有序类别的非数字型数据。

6.数值型数据：按数字尺度测量的观察值。

7.总体：包含所研究的全部个体（数据）的集合。

8.样本：从总体中抽取的一部分元素的集合。

9.参数：用来描述总体特征的概括性数字度量。

10.变量：说明现象某种特征的概念。

11.分类变量：说明事物类别的一个名称。

12.顺序变量：说明事物有序类别的一个名称。

13.数值型变量：说明事物数字特征的一个名称。

14.概率抽样：随机抽样，遵循随机原则进行的抽样，总体中每个单位都有一定的机会被选入样本。

15.非概率抽样：不随机，根据研究目的对数据的要求，采用某种方式从总体中抽出部分单位对其实施调查。

16.简单随机抽样：从包括总体的N个单位的抽样框中随机，一个个抽取n个单位作为样本，每单位等概论。

17.分层抽样：将抽样单位按某种特征或某种规则划分为不同的层，然后从不同层中独立、随机地抽取样本。

18.整群抽样：总体中若干单位合并为组，群，抽样时直接抽取群，然后对中选群中的所有单位全部实施调查。

19.系统抽样：总体中所有单位按顺序排列，在规定范围内随机抽取一单位作为初始单位，然后按事先规则确定其它样本单位。

20. 抽样误差：由于抽样的随机性引起的样本结果与总体真值之的误差简答题。

1.概率抽样与非概率抽样比较：性质不同，非概不依据随机原则选样本，样本统计量分布不确切，无法使用样本的结果对总体相应参数进行推断。

操作简便，时效快，成本低，专业要求不很高。

概率抽样依据随机原则抽选样本，理论分布存在，对总体有关参数可进行估计，计算估计误差，得到总体参数的置信区间。

提出精度要求。

2.数据收集方法的选择：抽样框中有关信息，目标总体特征，调查问题的内容，有形辅助物的使用，实施调查的资源，管理与控制，质量要求3.误差的控制：抽样误差是抽样随机性带来的，不可避免可以计算，改大样本量。

请举出统计应用的几个例子：1、用统计识别作者：对于存在争议的论文，通过统计量推出作者2、用统计量得到一个重要发现：在不同海域鳗鱼脊椎骨数量变化不大，推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3、挑战者航天飞机失事预测请举出应用统计的几个领域：1、在企业发展战略中的应用2、在产品质量管理中的应用3、在市场研究中的应用④在财务分析中的应用⑤在经济预测中的应用你怎么理解统计的研究内容：1、统计学研究的基本内容包括统计对象、统计方法和统计规律。

2、统计对象就是统计研究的课题，称谓统计总体。

3、统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。

④统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。

举例说明分类变量、顺序变量和数值变量：分类变量：表现为不同类别的变量称为分类变量，如“性别”表现为“男”或“女”，“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等，“学生所在的学院”可能是“商学院”、“法学院”等顺序变量：如果类别有一定的顺序，这样的分类变量称为顺序变量，如考试成绩按等级分为优、良、中、及格、不及格，一个人对事物的态度分为赞成、中立、反对。

这里的“考试成绩等级”、“态度”等就是顺序变量。

数值变量：可以用数字记录其观察结果，这样的变量称为数值变量，如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。

定性数据和定量数据的图示方法各有哪些：1、定性数据的图示：条形图、帕累托图、饼图、环形图2、定量数据的图示：a、分组数据看分布：直方图b、未分组数据看分布：茎叶图、箱线图、垂线图、误差图c、两个变量间的关系：散点图d、比较多个样本的相似性：雷达图和轮廓图直方图与条形图有何区别：1、条形图中的每一个矩形表示一个类别，其宽度没有意义，而直方图的宽度则表示各组的组距。

2、由于分组数据具有连续性，直方图的各矩形通常是连续排列，而条形图则是分开排列。

第3章习题一、选择题1. 一组数据中出现频数最多的变量值称为（）。

A．众数B．中位数C．四分位数D．均值2．一组数据排序后处于中间位置上的变量值称为（）。

A．众数B．中位数C．四分位数D．均值3. n个变量值乘积的n次方根称为（）。

A．众数C4.AC5.AC．极差6.AC．等于7.AC8. 。

A．68%C．99%9.AC10.AC11.200A．C．200 D．理学院12. 对于分类数据，测度其离散程度使用的统计量主要是（）。

A．众数B．异众比率C．标准差D．均值13. 对于右偏分布，均值、中位数和众数之间的关系是（）。

A．均值>中位数>众数B．中位数>均值>众数C．众数>中位数>均值D．众数>均值>中位数14. 在某行业中随即抽取10家企业，第一季度的利润额（单位：万元）分别为72，63.1，54.7，54.3，29，26.9，25，23.9，23，20。

该组数据的极差为（）。

A．22 B．32C．42 D．5215. 某班学生的平均成绩是80分，标准差是10分。

如果已知该班学生的考试分布为对称分布，可以判断成绩在60分~100分之间的学生大约占（）。

A．95%B．89%C．68% D．99%16. 若一组数列为11 2 5 9 13 6 3 ，则该组数据的中位数为（）A.5B.9C.7D.617. 在某公司进行的计算机水平测试中，新员工的平均得分是80分，标准差是5分，中位数是86分，则新员工得分的分布形状是（）。

A．对称的B．左偏的C．右偏的D．无法确定18.差为4A．78C．9119.A．3C．7.120.A．均值C21.A．80C．422.A．均值C23.AC24.AC25.ABC．几何平均数可以用于顺序数据D．均值可以用于分类数据26. 调查了一个企业10名员工上个月的缺勤天数，有3人缺勤0天，2人缺勤2天，4人缺勤3天，1人缺勤4天。

第1章统计和统计数据1统计学的定义:是收集、处理、分析、解释数据并从数据中得出结论的科学描述统计与推断统计的含义、容、目的。

描述统计: 是研究数据收集,处理和描述的统计学方法.其容包括如何取得研究所需要的数据,如何用图表形式对数据进展处理和展示,如何通过对数据的综合,概括与分析,得出所关心的数据特征.推断统计: 是研究如何利用样本数据来推断总体特征的统计学方法,容包括两大类:参数估计: 是利用样本信息推断所关心的总体特征.假设体验:是利用样本信息判断对总体的某个假设是否成立.2、变量与数据：不同数据类型的含义，会判断已有数据的类型.变量:它们的特点是从一次观察到下一次观察会出现不同结果.Ex: 企业销售额, 上涨股票的家数, 生活费支出,投掷一枚骰子观察其出现的点数数据: 把观察到的结果记录下来.总体:包含所研究的全部个体(数据)的集合样本: 从总体中抽取的一局部元素的集合样本量: 构成样本的元素的数目定量变量或数值变量:定量变量的观察结果称为定量数据或数值型数据.可以用阿拉伯数据来记录其观察结果.如“企业销售额〞、“上涨股票的家数〞、“生活费支出〞、“投掷一枚骰子出现的点数〞定性变量:分类变量和顺序变量统称为定性变量分类变量:表现为不同的类别.如“性别〞、“企业所属的行业〞、“学生所在的学院〞等.分类变量的观察结果就是分类数据顺序变量或有序分类变量:具有一定顺序的类别变量. 如考试成绩按等级，一个人对事物的态度.顺序变量的观察结果就是顺序数据或有序分类数据离散型变量: 只能取有限个值得随机变量连续型变量:可以取一个或多个区间中任何值得随机变量3、获得数据的概率抽样方法有哪些？根据一个的概率来抽取样本单位，也称随机抽样-简单随机抽样:从总体N个单位(元素)中随机地抽取n个单位作为样本，使得总体中每一个元素都有一样的时机(概率)被抽中. 抽取元素的具体方法有重复抽样是抽取一个个体记录下数据后，再把这个个体放回到原来的总体中参加下一次抽选。

第3章用统计量描述数据统计学第三版一些人使用统计就像喝醉酒的人使用街灯柱支撑的功能多于照明 Andrew Lang统计名言第3 章用统计量描述数据31 水平的度量32 差异的度量33 分布形状的度量学习目标度量水平的统计量度量差异的统计量度量分布形状的统计量各统计量的的特点及应用场合用Excel和SPSS计算描述统计量哪名运动员的发挥更稳定在奥运会女子10米气手枪比赛中每个运动员首先进行每组10抢共4组的预赛然后根据预赛总成绩确定进入决赛的8名运动员决赛时8名运动员再进行10枪射击再将预赛成绩加上决赛成绩确定最后的名次在2008年8月10日举行的第29届北京奥运会女子10米气手枪决赛中进入决赛的8名运动员的预赛成绩和最后10枪的决赛成绩如下表哪名运动员的发挥更稳定最会的比赛结果是中国运动员郭文珺凭借决赛的稳定发挥以总成绩4923环夺得金牌预赛排在第1名的俄罗斯运动员纳塔利娅·帕杰林娜以总成绩4981环获得银牌预赛排在第4名的格鲁吉亚运动员妮诺·萨卢克瓦泽以总成绩4874环的成绩获得铜牌而预赛排在第3名的蒙古运动员卓格巴德拉赫·蒙赫珠勒仅以4796环的成绩名列第8名由此可见在射击比赛中运动员能否取得好的成绩发挥的稳定性至关重要那么怎样评价一名运动员的发挥是否稳定呢通过本章内容的学习就能很容易回答这样的问题数据分布的特征31 水平的度量 com 平均数 com 中位数和分位数 com 用哪个值代表一组数据第3 章用统计量描述数据com 平均数31 水平的度量平均数mean也称为均值常用的统计量之一消除了观测值的随机波动易受极端值的影响根据总体数据计算的称为平均数记为根据样本数据计算的称为样本平均数记为x简单算数平均Simple mean设一组数据为x1 x2 xn 总体数据xN样本平均数总体平均数加权平均数Weighted mean设各组的组中值为M1 M2 Mk相应的频数为 f1 f2 fk样本加权平均总体加权平均加权平均数例题分析加权平均数权数对均值的影响甲乙两组各有10名学生他们的考试成绩及其分布数据如下甲组考试成绩x 0 20 100人数分布f 1 1 8乙组考试成绩x 0 20 100人数分布f 8 1 1几何平均数geometric meann 个变量值乘积的n 次方根适用于对比率数据的平均主要用于计算平均增长率计算公式为5 可看作是均值的一种变形几何平均数例题分析例某水泥生产企业1999年的水泥产量为100万吨2000年与1999年相比增长率为9[]2001年与2000年相比增长率为16[]2002年与2001年相比增长率为20[]求各年的年平均增长率年平均增长率＝11491[]-11491[]几何平均数例题分析例一位投资者购持有一种股票在200020012002和2003年收益率分别为45[]21[]255[]19[]计算该投资者在这四年内的平均收益率算术平均几何平均com 中位数和分位数31 水平的度量中位数median排序后处于中间位置上的值不受极端值影响中位数的计算数据个数为奇数例 9个家庭的人均月收入数据原始数据 1500 750 780 1080 850 960 2000 1250 1630排序 750 780 850 960 1080 1250 1500 1630 2000位置 1 2 3 4 5 6 7 8 9中位数1080中位数的计算数据个数为偶数例10个家庭的人均月收入数据排序 660 750 780 850 960 1080 1250 1500 1630 2000位置 1 2 3 4 5 6 7 8 9 10四分位数用3个点等分数据quartile排序后处于25[]和75[]位置上的值不受极端值的影响四分位数的计算位置的确定定义算法四分位数的计算位置的确定方法3其中[[] ]表示中位数的位置取整这样计算出的四分位数的位置要么是整数要么在两个数之间05的位置上方法4Excel给出的四分位数位置的确定方法如果位置不是整数则按比例分摊位置两侧数值的差值四分位数的计算数据个数为奇数例9个家庭的人均月收入数据4种方法计算原始数据 1500 750 780 1080 850 960 2000 1250 1630排序 750 780 850 960 1080 1250 1500 1630 2000位置 1 2 3 4 5 6 7 8 9众数mode一组数据中出现次数最多的变量值适合于数据量较多时使用不受极端值的影响一组数据可能没有众数或有几个众数com 用哪个值代表一组数据31 水平的度量众数中位数和平均数的关系众数中位数平均数的特点和应用平均数易受极端值影响数学性质优良实际中最常用数据对称分布或接近对称分布时代表性较好中位数不受极端值影响数据分布偏斜程度较大时代表性接好众数不受极端值影响具有不惟一性数据分布偏斜程度较大且有明显峰值时代表性较好32 差异的度量 com 极差和四分位差 com 方差和标准差com 比较几组数据的离散程度离散系数第3 章用统计量描述数据怎样评价水平代表值假定有两个地区每人的平均收入数据其中甲地区的平均收入为5000元乙地区的平均收入为3000元你如何评价两个地区的收入状况如果平均收入的多少代表了该地区的生活水平你能否认为甲地区的平均生活水平就高于乙地区呢要回答这些问题首先需要搞清楚这里的平均收入是否能代表大多数人的收入水平如果甲地区有少数几个富翁而大多数人的收入都很低虽然平均收入很高但多数人生活水平仍然很低相反乙地区多数人的收入水平都在3000元左右虽然平均收入看上去不如甲地区但多数人的生活水平却比甲地区高原因是甲地区的收入差距大于乙地区怎样评价水平代表值仅仅知道数据的水平是远远不够的还必须考虑数据之间的差距有多大数据之间的差距用统计语言来说就是数据的离散程度数据的离散程度越大各描述统计量对该组数据的代表性就越差离散程度越小其代表性就越甲乙com 极差和四分位差32 差异的度量极差range 一组数据的最大值与最小值之差离散程度的最简单测度值易受极端值影响未考虑数据的分布计算公式为R xi - minxi四分位差quartile deviation也称为内距或四分间距上四分位数与下四分位数之差Qd QU –QL反映了中间50[]数据的离散程度不受极端值的影响用于衡量中位数的代表性25[]75[]com 方差和标准差32 差异的度量方差和标准差variance and standard deviation数据离散程度的最常用测度值反映各变量值与均值的平均差异根据总体数据计算的称为总体方差标准差记为2根据样本数据计算的称为样本方差标准差记为s2s样本方差和标准差sample variance and standard deviation未分组数据组距分组数据未分组数据组距分组数据方差的计算公式标准差的计算公式总体方差和标准差Population variance and Standard deviation 未分组数据组距分组数据未分组数据组距分组数据方差的计算公式标准差的计算公式样本标准差例题分析例计算计算9名员工的月工资收入的方差和标准差 1500 750 780 1080 850 960 2000 1250 1630方差标准差标准分数standard score1 也称标准化值2 对某一个值在一组数据中相对位置的度量3 可用于判断一组数据是否有离群点outlier用于对变量的标准化处理计算公式为标准分数性质1均值等于02 方差等于1标准分数用于数据变换z分数只是将原始数据进行了线性变换它并没有改变一个数据在该组数据中的位置也没有改变该组数分布的形状而只是使该组数据均值为0标准差为1用SPSS对数据进行标准化第1步选择Analyze下拉菜单并选择 Descriptive statistics - Descriptive 选项进入主对话框第2步在主对话框中将变量选入Variables 然后选中Save standardized values as variables点击OKSPSS会将标准化后的变量以Z开头存放在原始变量工作表中标准分数例题分析经验法则经验法则表明当一组数据对称分布时约有68[]的数据在平均数加减1个标准差的范围之内约有95[]的数据在平均数加减2个标准差的范围之内约有99[]的数据在平均数加减3个标准差的范围之内经验法则例题分析9名员工月工资收入的经验法则切比雪夫不等式Chebyshevs inequality 如果一组数据不是对称分布经验法则就不再适用这时可使用切比雪夫不等式它对任何分布形状的数据都适用切比雪夫不等式提供的是下界也就是所占比例至少是多少对于任意分布形态的数据根据切比雪夫不等式至少有1-1k2的数据落在平均数加减k个标准差之内其中k是大于1的任意值但不一定是整数切比雪夫不等式Chebyshevs inequality对于k234该不等式的含义是至少有75[]的数据落在平均数加减2个标准差的范围之内至少有89[]的数据落在平均数加减3个标准差的范围之内至少有94[]的数据落在平均数加减4个标准差的范围之内com 比较几组数据的离散程度----离散系数32 差异的度量离散系数coefficient of variation1 标准差与其相应的均值之比对数据相对离散程度的测度消除了数据水平高低和计量单位的影响4 用于对不同组别数据离散程度的比较5 计算公式为离散系数例题分析例评价哪名运动员的发挥更稳定发挥比较稳定的运动员是塞尔维亚的亚斯娜·舍卡里奇和中国的郭文珺发挥不稳定的运动员蒙古的卓格巴德拉赫·蒙赫珠勒和波兰的莱万多夫斯卡·萨贡33 分布形状的度量偏态与峰态第3 章用统计量描述数据数据分布的形状偏态与峰态偏态峰态偏态skewness统计学家Pearson于1895年首次提出是指数据分布的不对称性测度统计量是偏态系数coefficient of skewness3 偏态系数0为对称分布0为右偏分布0为左偏分布偏态系数大于1或小于-1为高度偏态分布偏态系数在05～1或-1～-05之间为是中等偏态分布偏态系数越接近0偏斜程度就越低计算公式峰态kurtosis统计学家Pearson于1905年首次提出数据分布峰值的高低测度统计量是峰态系数coefficient of kurtosis峰态系数0扁平峰度适中峰态系数 0为尖峰分布计算公式Excel中的统计函数MODE计算众数MEDIAN计算中位数QUARTILE计算四分位数AVERAGE计算平均数HARMEAN计算简单调和平均数GEOMEAN计算几何平均数AVEDEV计算平均差STDEV计算样本标准差STDEVP计算总体标准差SKEW计算偏态系数KURT计算峰态系数TRIMMEAN计算切尾均值用Excel和SPSS计算描述统计量SPSSAnalyzeDescriptive statisticsDescriptivesvariables选入变量Options 选择需要的描述统计量ContinueOK。

第1章统计和统计数据1.1 指出下面的变量类型。

（1）年龄。

（2）性别。

（3）汽车产量。

（4）员工对企业某项改革措施的态度（赞成、中立、反对）。

（5）购买商品时的支付方式（现金、信用卡、支票）。

详细答案：（1）数值变量。

（2）分类变量。

（3）数值变量。

（4）顺序变量。

（5）分类变量。

1.2 一家研究机构从IT从业者中随机抽取1000人作为样本进行调查，其中60%回答他们的月收入在5000元以上，50%的人回答他们的消费支付方式是用信用卡。

（1）这一研究的总体是什么？样本是什么？样本量是多少？（2）“月收入”是分类变量、顺序变量还是数值变量？（3）“消费支付方式”是分类变量、顺序变量还是数值变量？详细答案：（1）总体是“所有IT从业者”，样本是“所抽取的1000名IT从业者”，样本量是1000。

（2）数值变量。

（3）分类变量。

1.3 一项调查表明，消费者每月在网上购物的平均花费是200元，他们选择在网上购物的主要原因是“价格便宜”。

（1）这一研究的总体是什么？（2）“消费者在网上购物的原因”是分类变量、顺序变量还是数值变量？详细答案：（1）总体是“所有的网上购物者”。

（2）分类变量。

1.4 某大学的商学院为了解毕业生的就业倾向，分别在会计专业抽取50人、市场营销专业抽取30、企业管理20人进行调查。

（1）这种抽样方式是分层抽样、系统抽样还是整群抽样？（2）样本量是多少？详细答案：（1）分层抽样。

（2）100。

第3章用统计量描述数据）；）；=426.67；，，第五章1.23.4.5.6.7.5.8 （1）（3.02%，16.98%）。

（2）（1.68%，18.32%）。

5.9 详细答案：（4.06，24.35）。

5.10详细答案： 139。

5.11 详细答案： 57。

5.12 769。

第6章假设检验平看电，绝平，，绝，，绝在，，=100 =50=14.8 =10.4=0.8 =0.6对，，绝。

对设，。

第3章用统计量描述数据教材习题答案3.1随机抽取25个网络用户，得到他们的年19152925242321382218302019191623272234244120311723龄数据如下（单位：周岁）：计算网民年龄的描述统计量，并对网民年龄的分布特征进行综合分析详细答案：网民年龄的描述统计量如下：平均24中位数2325%四分位数1975%四分位数26.5众数19标准差 6.65方差44.25峰度0.77偏度 1.08极差26最小值15最大值41从集中度来看，网民平均年龄为24岁，中位数为23岁。

从离散度来看，标准差在为6.65岁，极差达到26岁，说明离散程度较大。

从分布的形状上看，年龄呈现右偏，而且偏斜程度较大。

3.2某银行为缩短顾客到银行办理业务等待的时间，准备采用两种排队方式进行试验。

一种是所有顾客都进入一个等待队列；另一种是顾客在3个业务窗口处列队3排等待。

为比较哪种排队方式使顾客等待的时间更短，两种排队方式各随机抽取9名顾客，得到第一种排队方式的平均等待时间为7.2分钟，标准差为1.97 分钟，第二种排队方式的等待时间（单位：分钟）如下：5.56.6 6.7 6.87.1 7.3 7.4 7.8 7.8⑴计算第二种排队时间的平均数和标准差。

⑵比两种排队方式等待时间的离散程度。

⑶如果让你选择一种排队方式，你会选择哪一种？试说明理由。

详细答案：（1）兀"（岁）；* OR （岁）。

（2）叫"亦4 ；也=0一102。

第一中排队方式的离散程度大。

（3）选方法二，因为平均等待时间短，且离散程度小。

3.3在某地区随机抽取120家企业，按利润额进行分组后结果如下：按利润额分组（万元）企业数（个）300以下19300〜40030400 ~ 50042500 ~ 60018600以上11合计120计算120家企业利润额的平均数和标准差（注：第一组和最后一组的组距按相邻组计算）。

详细答案：示=426.67 （万元）；2 116朋（万元）。