2016届安徽省马鞍山二中 安师大附中 淮北一中 铜陵一中高三上学期12月四校联考英语试题(Word版)

牛顿第二定律瞬间问题1．如图所示，一木块在光滑水平面上受一恒力F作用而运动，前方固定一个弹簧，当木块接触弹簧后( )A．将立即做变减速运动B．将立即做匀减速运动C．在一段时间内仍然做加速运动，速度继续增大D．在弹簧处于最大压缩量时，物体的加速度为零解析：因为水平面光滑，物块与弹簧接触前，在推力的作用下做加速运动，与弹簧接触后，随着压缩量的增加，弹簧弹力不断变大，弹力小于推力时，物体继续加速，弹力等于推力时，物体的加速度减为零，速度达到最大，弹力大于推力后，物体减速，当压缩量最大时，物块静止．答案：C2．(2017届浏阳一中月考)搬运工人沿粗糙斜面把一个物体拉上卡车，当力沿斜面向上，大小为F时，物体的加速度为a1；若保持力的方向不变，大小变为2F时，物体的加速度为a 2，则( )A．a1＝a2B．a1＜a2＜2a1C．a2＝2a1D．a2＞2a1解析：当力沿斜面向上，大小为F时，物体的加速度为a1，则F－mg sinθ－μmg cosθ＝ma1；保持力的方向不变，大小变为2F时，物体的加速度为a2,2F－mg sinθ－μmg cosθ＝ma2；可见a2＞2a1；综上本题选D.答案：D3．(2017届天津一中月考)如图所示，A、B、C三球质量均为m，轻质弹簧一端固定在斜面顶端、另一端与A球相连，A、B间固定一个轻杆，B、C间由一轻质细线连接．倾角为θ的光滑斜面固定在地面上，弹簧、轻杆与细线均平行于斜面，初始系统处于静止状态，细线被烧断的瞬间，下列说法正确的是( )A．A球的受力情况未变，加速度为零B．C球的加速度沿斜面向下，大小为gC．A、B之间杆的拉力大小为2mg sinθD．A、B两个小球的加速度均沿斜面向上，大小均为12g sinθ解析：细线被烧断的瞬间，以A、B整体为研究对象，弹簧弹力不变，细线拉力突变为0，合力不为0，加速度不为0，故A错误；对球C，由牛顿第二定律得：mg sinθ＝ma，解得：a＝g sinθ，方向向下，故B错误；以A、B、C组成的系统为研究对象，烧断细线前，A、B、C静止，处于平衡状态，合力为零，弹簧的弹力f＝3mg sinθ，烧断细线的瞬间，由于弹簧弹力不能突变，弹簧弹力不变，以A、B为研究对象，由牛顿第二定律得：3mg sinθ－2mg sinθ＝2ma，则B的加速度a＝12g sinθ，故D正确；由D可知，B的加速度为a＝12g sinθ，以B为研究对象，由牛顿第二定律得T－mg sinθ＝ma.解得：T＝32mg sinθ，故C错误；故选D.答案：D9．如图所示，质量分别为m、2m的两物块A、B中间用轻弹簧相连，A、B与水平面间的动摩擦因数均为μ，在水平推力F作用下，A、B一起向右做加速度大小为a的匀加速直线运动。

安徽省马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三第三次联考语文试题何师俭，字桐叔，浙江山阴人。

以纳赀，于康熙六十年选授兵部员外郎。

奉职勤恳，常数月不出署。

雍正元年，迁广西右江道佥事，部请留任一年，世宗命以升衔留任，赐人葠、貂皮。

师俭以执法卻重贿，忤要人，因诬以避瘴故留部。

侍郎李绂昌言曰：“今部曹不名一钱，才者尤劳瘁，苟得郡，争趋之，况监司耶？”期满，复请留，加按察司副使衔。

司疏奏皆出其手，他司事难治者亦时委之。

三年，出为江南驿盐道副使，上召对，勉以操守，复赐人葠、貂皮，许上疏言事。

四年，调广东粮驿道副使。

岁大祲，师俭以存留米五万石给饷，饬所属缓征。

或疑专擅获咎，师俭曰：“请而后行，民已苦箠楚矣！”总督孔毓珣与巡抚杨文乾不相能，以师俭署盐法道，欲引以为助。

文乾疑为毓珣党，令买铜，将以赔累困之。

明年，文乾入觐，上示以毓珣弹事，亦及师俭，乃知师俭非阿毓珣者。

令署按察使，毓珣又疑师俭暱文乾。

及文乾卒，劾师俭违禁开矿，侵蚀铜价。

逾年，署巡抚傅泰会鞫，事始白。

上知其无罪，命往陕西佐治军需。

师俭在兵部，谙悉诸边形势扼塞、战守机宜、刍饷缓急。

至凉州，每集议，指画如素习，总督查郎阿深重之。

署凉庄道参政。

师过凉州，檄至肃州支饷。

两路遥远，师俭即以凉州所蓄给之，师行无乏。

一日羽书数过，师俭策必调取生兵，峙餦以待。

已而果然。

肃州师将行，飞檄令截取公私骡马，官民皇皇。

师俭曰：“在道官商皆赴肃者，若官顿於途，货弃於地，非军前所宜。

进剿未有定期何如听其至肃释所载而后供役军前得人与货亦省刍茭解送之烦是获两利也。

檄虽严，吾自当之。

”於是官商皆安，军事亦无误。

寻调补西安盐驿道副使。

关中旱，诏以湖广米十万石自商州龙驹寨运陕西。

师俭董其役，未半，大雨谿涨，骡马少，不足供转输。

商於山中无顿积所，水次隘，运艘不齐。

师俭以秋穀将登，请止运，民亦不饥。

军中马缺，檄取驿马。

师俭谓：“置邮传命，如人身血脉，不能一日废。

”拒不可，事竟寝。

马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三12月四校联考数 学 试 题（理科）第I 卷（选择题共60分）一、选择题：本大题共1 2小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的。

请把答案填在答题卷的相应位置。

1．集合M= {y| y= lg(x 2 +1)}，N={x|4x<4），则M ∩N 等于( ) A ．[0，+∞） B ．[0，1） C ．（1，+∞） D ．(0，l]2.设复数z l ，z 2在复平面内的对应点关于虚轴对称，z 1 =2+i ，则z 1z 2=( ) A ． -5 B ． 5 C ． - 4+i D ． -4-i 3．角θ的终边与单位圆的交点的横坐标为一12，则tan θ的值为 ( )A ．±1 C 4．若x 、y 满足约束条件且向量a=(3，2)，b=(x ，y),则a ·b 的取值范围是：( )A ．[54，4] B ．[72，5] C.[ 72，4] D ．[54,5] 5．已知函数f (x)=sin2x+2cos 2x-l ，将f(x ）的图像上各点的横坐标缩短为原来的12倍， 纵坐标不变，再将所得图像向右平移4π个单位，得到函数y=g(x)的图像，则函数 y=g(x)的解析式是( )A ．．C ．g （x ）一34π) D ．6．已知各项均为正数的等比数列{a n }中，3a l ，12a 3, 2a 2成等差数列，则= ( )A ．27B ．3C ．一l 或3D ．1或277．在△ABC 中，“AB BC ⋅”是“△ABC 是钝角三角形”的．( )A ．必要不充分条件B ．充分不必要条件C ．充要条件．D ．既不充分也不必要条件8．已知等差数列{a n }和等比数列{b n }各项都是正数，且a 1=b 1,a 11=b 11．那么一定有( ) A. a 6≥ b 6 B. a 6≤b 6 C. a 12≥b 12 D. a 12≤b 129．定义在区间[a,b]（b>a ）上的函数．f(x)= 12sinx 一2cosx 的值域是[一12,1]，则b 一a 的最大值M 和最小值m 分别是 ( ) A ．m=6π,M= 3π B ．m=3π,M= 23π C ．m=43π,M= 2π D ．m=23π,M= 43π10. 函数f(x)=(x 2—2x)e x的图象大致是( )11.如图, 2,2,m ,n ,OC OP AB AC OM OB ON OA ==== ,若m =38, 那么 n = ( ) A.12 B. 23 C. 34 D. 4512.设f(x)的定义域为D ，若f(x)满足下面两个条件，则称f(x)为闭函数，①f(x)在D 内是单调函数；②存在[a ，b] ⊆D ，使f(x)在[a ，b]上的值域为[a ，b].如果f(x)= 为闭函数，那么k 的取值范围是( ) A ．一1<k ≤一12 B ．12≤k<1 C ．k>-1 D ．k<1 第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，满分20分。

第I 卷二、选择题：本题共8小题，每小题6分。

在每小给出的四个选项中，第14—18题只有一项符合题目要求，第19—21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

（本卷中实验题除外，物理计算中210/g m s ）14A 物体从离地面高10m 处做自由落体运动， 1s 后B 物体从离地面高15m 处做自由落体运动，下面物理图像中对A 、B 的运动状态描述合理的是( )【答案】A考点：考查了自由落体运动与速度时间图像【名师点睛】物体AB 都做自由落体运动，根据速度时间公式和位移时间公式判断出v-t 和x-t 的关系即可判断15如图所示，在倾角为θ的固定斜面上有两个靠在一起的物体A 、B ，两物体与斜面的动摩擦因数μ相同，用平行斜面的恒力F 向上推物体A 使两物体沿斜面向上做匀加速运动，且B 对A 的压力平行于斜面，在则下列说法中正确的是：（ ）A ．只减小A 的质量，B 对A 的压力大小不变．B ．只减小B 的质量，B 对A 的压力大小会增大．C ．只减小斜面的倾角，B 对A 的压力大小不变．D ．只减小两物体与斜面的动摩擦因数μ，B 对A 的压力会增大．【答案】C考点：考查了牛顿第二定律的应用【名师点睛】以两物体组成的系统为研究对象，应用牛顿第二定律求出加速度，然后以B 为研究对象，应用牛顿第二定律求出B 与A 间的作用力，然后根据该作用力的表达式分析答题16如图所示，一小球通过不可伸长的轻绳悬于O 点，现从最低点给小球一水平向左的初速度，使小球恰好能在竖直平面内做圆周运动，当小球经过A 点时，其速度为最高点速度的3倍，不计空气阻力，则在A 点轻绳与竖直方向的夹角θ等于（ ）A ．30ºB ．45ºC ．60ºD ．90º【答案】D 【解析】试题分析：因为小球恰好通过最高点，即在最高点绳子的拉力为零，重力完全充当向心力，故有2v mg m L =①，从最低点到最高点过程中，只有重力做功，所以根据动能定理可得2211222B mgL mv mv =-②，从从B到A 的过程，根据机械能守恒定律得：2211 1cos 22A B mv mgL mv θ+-=（）③，因为A v =④，联立可得90θ=︒，D 正确；考点：考查了动能定理，机械能守恒，圆周运动【名师点睛】小球恰好能在竖直平面内做圆周运动时，要最高点由重力提供向心力，由牛顿第二定律求出最高点的临界速度．再由机械能守恒定律分别研究小球从B 到最高点及从B 到A 的过程，联立可求得夹角θ17如图所示，在空间坐标系中存在匀强电场， A 、B 、C 分别是x 、y 、z 轴上到原点距离相等的三个点，P 为AB 连线中点，已知电场线平行于BC 连线，B 点电势为3V ，C 点电势为－3V ，则电荷量为2.0×10-6C 的带正电粒子从O 点运动到P 点，电场力所做的功为（ ）A ．6.0×10-6 JB ．－3.0×10-6 JC ．－2.0×10-6 JD ．1.5×10-6 J【答案】B考点：考查了等势面，电场力做功【名师点睛】本题关键是明确匀强电场的等势面与电场线垂直，且沿着电场线每前进相同距离的电势降落相等，不难先画出等势面，找出等电势点，然后根据W qU =求解电场力做功大小即可18质量相同的A、B两物体分开放在同一水平面上，都受到大小相同的水平力F的作用，从静止开始运动。

安徽省马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三12月四校联考政治试题第I卷选择题本卷共35小题。

每小题4分，共140分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

12.甲乙两种商品关系如图所示，其它因素不变，据此判断A．甲商品为生活必需品 B．乙商品为高档奢侈品C．甲乙商品互为替代品 D．甲乙商品互为互补品13.随着互联网技术的发展，网购渐成常态，据统计，2015年双十一天猫平台总交易额达到912亿元。

这表明A．生产决定消费的对象 B．生产决定消费的方式C．生产决定消费的质量 D．生产为消费创造动力14.根据下表内容，若其他条件不变，2014年甲企业生产M商品的劳动生产率和生产M商品的社会劳动生产率的变化情况分别为A．提高2/3、提高1／3 B．下降2/3、下降l／3C．提高1/2、提高1／5 D．下降1/2、下降1／515.下列表格为我国近3年财政收支情况（单位：万亿）。

据此推断①财政赤字是经济发展过程中的必然现象②国家增加财政支出以抑制经济过热③近三年国家均实施的是积极的财政政策④国家增加财政赤字以刺激社会总需求A．①② B．①④ C．②③ D．③④16. 2015年前三季度，我国国内生产总值比上年增长6.9%，低于7%的目标；服务业增加值比重为51. 4%，比上年提高8.4个百分点；城镇新增就业1066万人。

表明①我国经济结构更加趋于优化②服务业成为我国经济的主导③第三产业吸纳就业的能力强④经济增长主要依靠创新驱动A．①② B．①③ C．②④ D．③④17.全面推动农村经济，实现城乡统筹发展，必须发挥好村官的“领头羊”作用，这是因为A．“村官”是农村基层政权的核心和骨干力量B．广大“村官”是社会主义基层民主制度基础C．“村官”素质事关社会主义新农村建设大局D．“村官”是村民们在民主基础上选举产生的18.十二届全国人大一次会议审议批准了《政府工作报告》，依法选举和决定任命了新一届国家机构领导人员。

安徽省马鞍山二中、安师大附中、淮北一中2016届高三第一学期期中联考语文试题命题人盛庆丰审核人王勇注意事项：1．本试卷分第I卷（阅读题）和第II卷（表达题）两部份，考生务必将自己的姓名、考生号填写在答题卡上。

2．作答时，将答案写在答题卡上。

写在本试卷上无效。

3．考试终止后，将本试卷和答题卡一并交回。

第I卷阅读题（共70分）甲必考题一、现代文阅读（9分，毎小题 3分）阅读下面的文字，完成1~3题舞蹈，这门古老而又充满青春活力的艺术，以人类自身形体动作为媒质的存在方式、呈现方式，决定了它是人类最古老的艺术形式之一。

人类学家常把舞蹈当做一个民族的标记物。

因此了解、熟悉民族舞蹈对熟悉自己民族文化的精粹具有十分重要的意义。

舞蹈与其他不以形体动作为媒质的艺术门类相较较，更富表现性和抒情性，而不擅长具体地描述事物、阐释道理。

它与音乐的特性似乎更为接近，但它所表达的内容往往比音乐更具确信性，它既是时刻艺术，又是空间艺术。

舞蹈的起源与萌芽可远溯至人类进展的洪荒期，很难予以确切考证。

有关舞蹈的起源在古籍、神话中确有一些传奇，不免带有“超人”的梦幻色彩，可考的实证却分明昭示着：舞蹈从原初起就带有很强的维系群体的生存意识和对美好的向往。

原始舞蹈的诸多功能，也增进了人类的自我优化。

现代文明高度进展的现今，舞蹈的呈现仍然须臾难离自身的形体。

高度进化的人体更具智能性、可塑性、自由度。

但现代文明高度进展形成了社会分工的精细化，可能致使脑体劳动失衡，使一部份人显现“大脑发达、四肢萎缩”。

就直观而言，人们可不能把田间插秧看成“插秧舞”，也很容易把生活中的辞别场景与反映离情的舞蹈区别开来。

可是让人准确地回答“舞与非舞”之界定——为舞蹈做出准确的说明和概念，却不大容易。

舞蹈源于生活，却不是生活动作的简单描摹再现。

它基于人的内在精神力量的迸发和情感的升华，作用于人体动作的幅度、力度、速度之呈现，往往超诞生活动作的“常态”、“常量”而具有节拍性、韵律感——形成躯体各部位动静格局的“同一性规律”；删汰了生活动作基于应用性、随意性。

马鞍山二中、安师大附中、淮北一中2016届高三第一学期期中联考英语试题第I卷（共100分）第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What time is it now?A. 6: 40.B. 6: 30.C. 6: 20.2. What does the man mean?A. They have left for the airport.B. They are on the way to the airport.C. They may be late for the plane.3. What kind of music does the woman like?A. Popular music.B. Jazz music.C. Classical music.4. What does the man suggest the woman do?A. Take some medicine.B. Drink more water.C. Go on a diet.5. What does the man tell the woman?A. There is another cat like his.B. He never loses his dog at all.C. She has mistaken it for his dog.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

2016届安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中物理试卷（解析版）一、选择题（共10个小题，1～6题为单选题，7～10题为多选题，多选题少选得2分．每小题4分，共40分）1．分别让一物体按照以下两种情境通过直线上的A、B两点，一种是物体以速度v匀速运动，所用时间为t；另一种是物体从A点由静止出发，先匀加速直线运动（加速度为a1）到某一最大速度v m，立即做匀减速直线运动（加速度大小为a2）至B点速度恰减为0，所用时间仍为t．下列说法正确的是（）A．v m只能为2v，与a1、a2的大小无关B．v m可为许多值，与a1、a2的大小有关C．a1、a2必须是一定的D．a1、a2必须满足=2．设地球是一个密度均匀的球体，已知质量分布均匀的球壳对壳内物体的引力为零，如果沿地球的直径挖一条隧道，将物体从此隧道一端由静止释放刚好运动到另一端（如图所示），不考虑阻力，在此过程中关于物体的运动速度v随时间t变化的关系图象可能是（）A． B． C．D．3．一辆小车沿水平面始终保持做匀变速直线运动．一根细线上端固定在车顶，下端系一个小球M，稳定时，细线的位置如图所示，当时在小车地板上，小球正下方的点是P点．某时刻细线突然断裂，小球落到小车的地板上（该过程小车的运动方向未变，小球没有跟左右两壁相碰，不计空气阻力）．设小球落到小车地板上的点是Q点．则下列说法正确的是（）A．无论小车向左运动还是向右运动，Q点都一定在P点的左侧B．无论小车向左运动还是向右运动，Q点都一定在P点的右侧C．若小车向左运动则Q点一定在P点的左侧，若小车向右运动则Q点一定在P点的右侧D．若小车向左运动则Q点一定在P点的右侧，若小车向右运动则Q点一定在P点的左侧4．如图所示，三角形ABC由三根光滑的杆构成三角形框架，竖直固定放置，∠A=90°，∠B=30°．质量均为m的a、b两个小球分别套在AB、AC杆上，两球间由细线连接，两球静止时，细线与AB 杆成α角．则下列说法中正确的是（）A．30°＜α＜60°B．细线受到的拉力大小为mgC．a、b两小球对杆的压力大小之比为2：D．细线受到的拉力大小为mg5．如图所示，细绳长为L，挂一个质量为m的小球，球离地的高度h=2L，当绳受到大小为2mg的拉力时就会断裂．绳的上端系一质量不计的环，环套在光滑水平杆上，现让环与球一起以速度v=向右运动，在A处环被挡住而立即停止，A离墙的水平距离也为L．球在以后的运动过程中，球第一次碰撞点离墙角B点的距离△H是（不计空气阻力（）A．△H=L B．△H=L C．△H=L D．△H=L6．已知某行星半径为R，以其第一宇宙速度运行的卫星的绕行周期为T，围绕该行星运动的同步卫星运行速率为v．则该行星的自转周期为（）A． B．C．D．7．氢气球下系一小重物G，重物只在重力和绳的拉力作用下做直线运动，重物运动的方向如图中箭头所示虚线方向，图中气球和重物G在运动中所处的位置可能是（）A．B．C．D．8．如图所示，相距l的两小球A、B位于同一高度h（l、h均为定值）．将A向B水平抛出的同时，B自由下落．A、B与地面碰撞前后，水平分速度不变，竖直分速度大小不变、方向相反．不计空气阻力及小球与地面碰撞的时间，则（）A．A、B在第一次落地前能否发生相碰，取决于A的初速度大小B．A、B在第一次落地前若不碰，此后就不会相碰C．A、B不可能运动到最高处相碰D．A、B一定能相碰9．如图所示，花样滑冰双人自由滑比赛时的情形．男运动员以自己为转动轴拉着女运动员做匀速圆周运动．若男运动员转速为30r/min，手臂与竖直方向夹角约为60°，女运动员质量是50kg，她触地冰鞋的线速度为4.7m/s，则下列说法正确的是（）A．女运动员做圆周运动的角速度为πrad/sB．女运动员触地冰鞋做圆周运动的半径约为2mC．男运动员手臂拉力约是850ND．男运动员手臂拉力约是500N10．如图所示，质量为m的物体B叠放在物体A上，A的上表面水平．A、B一起沿着倾角为θ的固定光滑斜面由静止开始下滑，在A、B一起沿光滑斜面下滑的过程中（）A．B受到的支持力为mgsin2θB．B受到的静摩擦力方向水平向左C．A对B的作用力为mgsinθ，方向沿斜面向下D．B物体的机械能守恒二、实验题（共12分）将正确答案填写在答题卡中相应位置上．11．某同学在研究平抛运动时，发现原来的实验方法不容易确定平抛小球在运动中的准确位置．于是，如图所示，在实验中用了一块平木板附上复写纸和白纸，竖直立于正对槽口前某处，使小球从斜槽上滑下，小球撞在木板上留下痕迹A，将木板向后移距离x，再使小球从斜槽上同样高度滑下，小球撞在木板上留下痕迹B，将木板再向后移距离x，小球再从斜槽上同样高度滑下，再得到痕迹C．A、B间距离y1，A、C间距离y2．若测得木板后移距离x=10cm，测得y1=6.0cm，y2=16.0cm．（1）根据以上物理量导出测量小球初速度公式v0=（用题中所给字母表示）．（2）小球初速度值为．（保留2位有效数字，g取9.8m/s2）12．在“探究弹力和弹簧伸长量的关系，并测定弹簧的劲度系数”的实验中，实验装置如图1所示．所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力．实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测出相应的弹簧总长度．（1）有一个同学通过以上实验测量后把6组数据描点在坐标图中（如图2），请作出F﹣L图象．（2）由此图象可得出该弹簧的原长L0=cm，劲度系数k=N/m．（3）试根据以上该同学的实验情况，请你帮助他设计一个记录实验数据的表格（不必填写其实验测得的具体数据）．（4）该同学实验时，把弹簧水平放置与弹簧悬挂放置相比较．优点在于：．缺点在于：．三、计算题（共4个小题，共48分）要求写出必要的文字说明、方程式和演算步骤，只写出最后答案的不能得分，有数值计算的题目必须写出数值和单位．13．在国庆60周年阅兵式中，某直升飞机在地面上空某高度A位置处于静止状态待命，要求该机零时刻由静止状态沿水平方向做匀加速直线运动，经过AB段加速后，进入BC段的匀速受阅区，经过t时间到达C位置，已知：AB段长为L1、BC段长度为L2．求：（1）直升飞机在BC段的速度大小；（2）在AB段做匀加速直线运动时的加速度大小．14．天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星．双星系统在银河系中很普遍．利用双星系统中两颗恒星的运动特征可推算出它们的总质量．已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量．（引力常量为G）15．如图所示，粗细均匀的圆木棒A下端离地面高H，上端套着一个细环B．A和B的质量均为m，A和B间的滑动摩擦力为f，且f＜mg．用手控制A和B使它们从静止开始自由下落．当A与地面碰撞后，A以碰撞地面时的速度大小竖直向上运动，与地面发生碰撞时间极短，空气阻力不计，运动过程中A始终呈竖直状态．求：若A再次着地前B不脱离A，A的长度应满足什么条件？16．如图所示的木板由倾斜部分和水平部分组成，两部分之间由一段圆弧面相连接．在木板的中间有位于竖直面内的光滑圆槽轨道，斜面的倾角为θ．现有10个质量均为m、半径均为r的均匀刚性球，在施加于1号球的水平外力F的作用下均静止，力F与圆槽在同一竖直面内，此时1号球球心距它在水平槽运动时的球心高度差为h．现撤去力F使小球开始运动，直到所有小球均运动到水平槽内．重力加速度为g．求：（1）水平外力F的大小；（2）1号球刚运动到水平槽时的速度；（3）整个运动过程中，2号球对1号球所做的功．2015-2016学年安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中物理试卷参考答案与试题解析一、选择题（共10个小题，1～6题为单选题，7～10题为多选题，多选题少选得2分．每小题4分，共40分）1．分别让一物体按照以下两种情境通过直线上的A、B两点，一种是物体以速度v匀速运动，所用时间为t；另一种是物体从A点由静止出发，先匀加速直线运动（加速度为a1）到某一最大速度v m，立即做匀减速直线运动（加速度大小为a2）至B点速度恰减为0，所用时间仍为t．下列说法正确的是（）A．v m只能为2v，与a1、a2的大小无关B．v m可为许多值，与a1、a2的大小有关C．a1、a2必须是一定的D．a1、a2必须满足=【考点】匀变速直线运动的速度与时间的关系．【专题】直线运动规律专题．【分析】两次运动总位移相等、总时间相等，则平均速度相等，结合匀变速直线运动的推论求解匀加速直线运动的最大速度．【解答】解：两次运动过程平均速度相等，知平均速度的大小为v．根据匀变速直线运动的推论知，，则，与加速度大小无关．故A 正确，B、C、D错误．故选：A．【点评】解决本题的关键掌握匀变速直线运动平均速度的推论，并能灵活运用．2．设地球是一个密度均匀的球体，已知质量分布均匀的球壳对壳内物体的引力为零，如果沿地球的直径挖一条隧道，将物体从此隧道一端由静止释放刚好运动到另一端（如图所示），不考虑阻力，在此过程中关于物体的运动速度v随时间t变化的关系图象可能是（）A． B． C．D．【考点】万有引力定律及其应用；匀变速直线运动的图像．【专题】万有引力定律的应用专题．【分析】根据题意知，地球表面的重力加速度等于半径为R的球体在表面产生的加速度，深度为d 位置的加速度相当于半径为R﹣d的球体在其产生的加速度，根据地球质量分布均匀得到加速度的表达式，再根据半径关系分析加速度的变化求解即可．【解答】解：如果物体在距地心为r处（r≤R），那么这个物体只会受到以地心为球心、以r为半径的那部分球体的万有引力，而距地心为r到R之间的物质对物体作用力的合力为零．物体掉入隧道之后，不是做自由落体运动．设物体的质量为m，地球密度为ρ，以半径为r的那部分球体的质量为M，距地心r处的重力加速度为g，则M=πr3ρ，=mg，得g==πρGr．①由于物体掉入隧道之后，r在变化，由①式可知g也在变化，且离地心越近g越小，在地心处g=0．所以物体不是做自由落体运动．考虑到方向，有g=﹣πρGr，即物体的加速度g与位移r大小成正比、方向相反，所以物体在隧道中的运动是简谐运动．故选C．【点评】解决该题关键要运用万有引力等于重力表示出隧道内的重力加速度的变化情况去分析运动情况．3．一辆小车沿水平面始终保持做匀变速直线运动．一根细线上端固定在车顶，下端系一个小球M，稳定时，细线的位置如图所示，当时在小车地板上，小球正下方的点是P点．某时刻细线突然断裂，小球落到小车的地板上（该过程小车的运动方向未变，小球没有跟左右两壁相碰，不计空气阻力）．设小球落到小车地板上的点是Q点．则下列说法正确的是（）A．无论小车向左运动还是向右运动，Q点都一定在P点的左侧B．无论小车向左运动还是向右运动，Q点都一定在P点的右侧C．若小车向左运动则Q点一定在P点的左侧，若小车向右运动则Q点一定在P点的右侧D．若小车向左运动则Q点一定在P点的右侧，若小车向右运动则Q点一定在P点的左侧【考点】匀变速直线运动的位移与时间的关系．【专题】直线运动规律专题．【分析】细绳断裂后，小球做平抛运动，小车做匀变速直线运动，结合运动学公式，根据两者在水平方向上位移的关系确定落点的位置．【解答】解：细线突然断裂，小球做平抛运动，小车做匀变速直线运动，对小球分析，可知小球的加速度向左，则小车的加速度也向左，若小车向左做匀加速直线运动，设绳子断裂时速度为v，小球经过t时间落到地板上，对小球有：x1=vt，对小车有：，可知，知Q点在P点右侧．若小车向右做匀减速直线运动，对小球有：x1=vt，对小车有：，可知，Q点仍然在P点右侧．故选：B．【点评】解决本题的关键知道小球和小车的运动规律，结合运动学公式分析判断，注意小车可能向左做匀加速直线运动，也可能向右做匀减速直线运动．4．如图所示，三角形ABC由三根光滑的杆构成三角形框架，竖直固定放置，∠A=90°，∠B=30°．质量均为m的a、b两个小球分别套在AB、AC杆上，两球间由细线连接，两球静止时，细线与AB 杆成α角．则下列说法中正确的是（）A．30°＜α＜60°B．细线受到的拉力大小为mgC．a、b两小球对杆的压力大小之比为2：D．细线受到的拉力大小为mg【考点】共点力平衡的条件及其应用；物体的弹性和弹力．【分析】两球均处于静止状态，分别对两球研究，由平衡条件列式，即可求得细线的拉力、杆对球的支持力和α角．【解答】解：根据平衡条件得：对a球有：N1=Tsinα+mgcos30°①Tcosα=mgsin30°②对b球有：N2=Tcosα+mgcos60°③Tsinα=mgsin60°④由③：②得：tanα=，得α=60°由②③解得T=mg由①③得：N1：N2=tanα：1=：1，由牛顿第三定律可得a、b两小球对杆的压力大小之比为：1．故B正确，ACD错误．故选：B【点评】本题是连接体平衡问题，涉及两个物体，运用隔离法，由平衡条件解答．5．如图所示，细绳长为L，挂一个质量为m的小球，球离地的高度h=2L，当绳受到大小为2mg的拉力时就会断裂．绳的上端系一质量不计的环，环套在光滑水平杆上，现让环与球一起以速度v=向右运动，在A处环被挡住而立即停止，A离墙的水平距离也为L．球在以后的运动过程中，球第一次碰撞点离墙角B点的距离△H是（不计空气阻力（）A．△H=L B．△H=L C．△H=L D．△H=L【考点】机械能守恒定律；向心力．【分析】小球先向右做匀速直线运动，环停止后绳断开后做平抛运动，要判断先撞墙还是先落地，根据平抛运动的分位移公式列式求解即可．【解答】解：环被A挡住的瞬间F﹣mg=m，又v=，解得F=2mg，故绳断，之后小球做平抛运动；假设小球直接落地，则h=gt2，球的水平位移x=υt=2L＞L，所以小球先与墙壁碰撞；球平抛运动到墙的时间为t′，则t′==，小球下落高度h′=gt′2=；碰撞点距B的距离△H=2L﹣=L；故选：D【点评】本题关键分析清楚小球的运动规律，然后分段考虑．要注意绳断前瞬间，由重力和绳子的拉力的合力提供小球的向心力．6．已知某行星半径为R，以其第一宇宙速度运行的卫星的绕行周期为T，围绕该行星运动的同步卫星运行速率为v．则该行星的自转周期为（）A． B．C．D．【考点】万有引力定律及其应用．【专题】定量思想；推理法；万有引力定律在天体运动中的应用专题．【分析】第一宇宙速度的轨道半径为R，根据=m R求出GM，再根据万有引力提供向心力=m，求出同步卫星的高度；行星自转周期等于同步卫星的运转周期，根据T=求出自转周期．【解答】解：（1）设同步卫星距地面高度为h，则：=m…①以第一宇宙速度运行的卫星其轨道半径就是R，则：=m R…②由①②得：h=行星自转周期等于同步卫星的运转周期：T==故选：D【点评】解决本题的关键知道第一宇宙速度是卫星贴着行星表面做圆周运动的速度，知道卫星绕行星做圆周运动靠万有引力提供向心力．7．氢气球下系一小重物G，重物只在重力和绳的拉力作用下做直线运动，重物运动的方向如图中箭头所示虚线方向，图中气球和重物G在运动中所处的位置可能是（）A．B．C．D．【考点】牛顿第二定律；力的合成与分解的运用．【专题】牛顿运动定律综合专题．【分析】直线运动的条件是合外力为零或合外力与速度方向共线，重力总是竖直向下，拉力沿着绳子并直线绳子收缩的方向．【解答】解：重物只在重力和绳的拉力作用下做直线运动，故合力为零或者与速度共线；A、可以做匀速直线运动，故A正确；B、可能做匀减速直线运动，故B正确；C、可能做匀加速直线运动，故C正确；D、重力和拉力的合力与速度一定不共线，做曲线运动，故D错误；故选ABC．【点评】本题考查了平衡力的辨别和重力和重力的方向的理解和掌握，重力是一种最常见的力，重力的方向始终是竖直向下的．8．如图所示，相距l的两小球A、B位于同一高度h（l、h均为定值）．将A向B水平抛出的同时，B自由下落．A、B与地面碰撞前后，水平分速度不变，竖直分速度大小不变、方向相反．不计空气阻力及小球与地面碰撞的时间，则（）A．A、B在第一次落地前能否发生相碰，取决于A的初速度大小B．A、B在第一次落地前若不碰，此后就不会相碰C．A、B不可能运动到最高处相碰D．A、B一定能相碰【考点】平抛运动；自由落体运动．【专题】自由落体运动专题．【分析】因为平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据该规律抓住地面碰撞前后，水平分速度不变，竖直分速度大小不变、方向相反与判断两球能否相碰．【解答】解：A、若A球经过水平位移为l时，还未落地，则在B球正下方相碰．可知当A的初速度较大是，A、B在第一次落地前能发生相碰，故A正确．B、若A、B在第一次落地前不碰，由于反弹后水平分速度不变，竖直分速度大小不变、方向相反，则以后一定能碰．故B错误，D正确．C、若A球落地时的水平位移为时，则A、B在最高点相碰．故C错误．故选：AD．【点评】解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，根据该规律进行分析．9．如图所示，花样滑冰双人自由滑比赛时的情形．男运动员以自己为转动轴拉着女运动员做匀速圆周运动．若男运动员转速为30r/min，手臂与竖直方向夹角约为60°，女运动员质量是50kg，她触地冰鞋的线速度为4.7m/s，则下列说法正确的是（）A．女运动员做圆周运动的角速度为πrad/sB．女运动员触地冰鞋做圆周运动的半径约为2mC．男运动员手臂拉力约是850ND．男运动员手臂拉力约是500N【考点】向心力．【分析】根据转速的大小得出圆周运动的角速度，由公式v=ωt求半径．根据拉力沿水平方向上的分力提供向心力，拉力竖直方向上的分力等于女运动员的重力，求出男运动员手臂拉力的大小．【解答】解：A、已知转动转速为：n=30 r/min=0.5 r/s．由公式：ω=2π•n，解得：ω=πrad/s．故A正确．B、由v=ωr得：r==m≈1.5N，故B错误．CD、对女运动研究可知，其在竖直方向上受力平衡，则有Fcos60°=mg得男运动员手臂拉力：F=2mg=1000N．故C、D错误．故选：A【点评】解决本题的关键知道转速与角速度的关系，以及知道女运动员做圆周运动向心力的来源．10．如图所示，质量为m的物体B叠放在物体A上，A的上表面水平．A、B一起沿着倾角为θ的固定光滑斜面由静止开始下滑，在A、B一起沿光滑斜面下滑的过程中（）A．B受到的支持力为mgsin2θB．B受到的静摩擦力方向水平向左C．A对B的作用力为mgsinθ，方向沿斜面向下D．B物体的机械能守恒【考点】机械能守恒定律．【分析】分析B物体的受力情况，由牛顿第二定律求出支持力和摩擦力，再得到A对B的作用力．根据是否只有重力做功，分析B的机械能是否守恒．【解答】解：AB、对于AB组成的整体，整体具有沿斜面向下的加速度，设为a，将a正交分解为竖直方向分量a1，水平分量a2，如图所示，对整体，由牛顿第二定律得（m A+m）gsinθ=（m A+m）a，得a=gsinθ对B，由牛顿第二定律得：竖直方向上：mg﹣N=ma1=mgsinθsinθ水平方向上：f=ma2=mgsinθcosθ则得支持力N=mg﹣mgsin2θ=mgcos2θ，摩擦力大小为f=mgsinθcosθ，方向水平向左．故A错误，B 正确．C、A对B的作用力为F==mgcosθ，方向垂直斜面向上，故C错误．D、由于A对B的作用力垂直于斜面向上，对B不做功，所以B物体的机械能守恒，故D正确．故选：BD．【点评】解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，注意整体法和隔离法的运用．二、实验题（共12分）将正确答案填写在答题卡中相应位置上．11．某同学在研究平抛运动时，发现原来的实验方法不容易确定平抛小球在运动中的准确位置．于是，如图所示，在实验中用了一块平木板附上复写纸和白纸，竖直立于正对槽口前某处，使小球从斜槽上滑下，小球撞在木板上留下痕迹A，将木板向后移距离x，再使小球从斜槽上同样高度滑下，小球撞在木板上留下痕迹B，将木板再向后移距离x，小球再从斜槽上同样高度滑下，再得到痕迹C．A、B间距离y1，A、C间距离y2．若测得木板后移距离x=10cm，测得y1=6.0cm，y2=16.0cm．（1）根据以上物理量导出测量小球初速度公式v0=（用题中所给字母表示）．（2）小球初速度值为 1.6m/s．（保留2位有效数字，g取9.8m/s2）【考点】研究平抛物体的运动．【专题】实验题．【分析】球离开导轨后做平抛运动，将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动．根据匀变速直线运动的推论△x=aT2，由y1、y2求出A到B或B到C的时间，再根据水平方向匀速运动可以求出初速度．【解答】解：（1）平抛物体水平方向匀速运动可知：A到B和B到C的时间相同，设为T，因此根据匀变速直线运动规律有：△h=（y2﹣y1）﹣y1=y2﹣2y1=gT2，得：T=水平方向匀速运动，故有：（2）由题意可知：x=10cm=0.1m，y1=6.0cm=0.06m，y2=16cm=0.16m，代入得：v0==故答案为：，1.6m/s．【点评】解答平抛运动问题的关键是理解其水平方向和竖直方向的运动特点：水平方向匀速运动，竖直方向自由落体运动，同时熟练应用匀变速直线运动的基本规律和推论解答问题．12．在“探究弹力和弹簧伸长量的关系，并测定弹簧的劲度系数”的实验中，实验装置如图1所示．所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力．实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测出相应的弹簧总长度．（1）有一个同学通过以上实验测量后把6组数据描点在坐标图中（如图2），请作出F﹣L图象．（2）由此图象可得出该弹簧的原长L0=5cm，劲度系数k=0N/m．（3）试根据以上该同学的实验情况，请你帮助他设计一个记录实验数据的表格（不必填写其实验测得的具体数据）．（4）该同学实验时，把弹簧水平放置与弹簧悬挂放置相比较．优点在于：避免弹簧自身所受重力对实验的影响．缺点在于：弹簧与桌面及绳子与滑轮间存在的摩擦造成实验的误差．【考点】探究弹力和弹簧伸长的关系．【专题】实验题；学科综合题；定量思想；推理法；弹力的存在及方向的判定专题．【分析】实验中需要测量多组弹力的大小和弹簧的长度，根据要求设计出表格．作出F﹣L的关系图线．当弹簧弹力为零时，弹簧处于原长，结合图线得出弹簧的原长，根据图线的斜率求出劲度系数的大小．误差分析．【解答】解：（1）用平滑的曲线将各点连接起来，如图所示：（2）弹簧的原长L0即为弹力为零时弹簧的长度，由图象可知，L0=5×10﹣2m=5cm．劲度系数为图象直线部分的斜率，k=20N/m．（3）记录数据的表格如下表：（4）优点是：避免弹簧自身所受重力对实验的影响；缺点是：弹簧与桌面及绳子与滑轮间存在的摩擦造成实验的误差．故答案为：（1）如图；（2）5，20；（3）见解析；（4）避免弹簧自身所受重力对实验的影响；弹簧与桌面及绳子与滑轮间存在的摩擦造成实验的误差【点评】本题考查了学生设计的能力和作图的能力，知道F﹣L图线的斜率表示劲度系数．注意掌握分析误差的形成原因．三、计算题（共4个小题，共48分）要求写出必要的文字说明、方程式和演算步骤，只写出最后答案的不能得分，有数值计算的题目必须写出数值和单位．13．在国庆60周年阅兵式中，某直升飞机在地面上空某高度A位置处于静止状态待命，要求该机零时刻由静止状态沿水平方向做匀加速直线运动，经过AB段加速后，进入BC段的匀速受阅区，经过t时间到达C位置，已知：AB段长为L1、BC段长度为L2．求：（1）直升飞机在BC段的速度大小；（2）在AB段做匀加速直线运动时的加速度大小．【考点】匀变速直线运动的位移与时间的关系；匀变速直线运动的速度与时间的关系．【专题】直线运动规律专题．【分析】（1）匀速阶段的时间加上匀加速阶段的时间为总时间，匀速阶段的时间可用位移除以速度表示，匀加速阶段的时间可用位移除以平均速度表示，这样可求出速度．（2）在AB段根据速度与位移的关系公式v2=2ax，就可求解出加速度．。

H θ h F 10 1 2 3 9 4 5 6 7 8 B A H θ h F 10 1 2 3 9 4 5 6 7 8
4．如图所示，三角形ABC由三根光滑的杆构成三角形框架，竖直固定放置，∠A=90°，∠B=30°。质量均为m的a、
b两个小球分别套在AB、AC杆上，两球间由细线连接，两球静止时，细线与AB杆成α角。则下列说法中正确的是
A．30°< α < 60°
B．细线受到的拉力大小为mg
C．a、b两小球对杆的压力大小之比为2:
道一端由静止释放刚好运动到另一端如图所示不考虑阻力，在此过程中关于物体的运动速度v 随时间t 变化的关系图象
可能是
3．一辆小车沿水平面始终保持做匀变速直线运动。一根细线上端固定在车顶，下端系一个小球M，稳定时，细线的
位置如图所示，P点为小球正下方小车地板上的点。某时刻细线突然断裂，小球第一次落到小车的地板上点（点未标出
离x＝10 cm，测得y1＝6.0 cm，y2＝16.0 cm(1)根据以上物理量导出测量小球初速度的公式v0＝________.(用题中所给
字母表示)
()小球初速度值为________．(保留两位有效数字，g取9.8 m/s2)
Ⅱ． (8分)在“探究弹力和弹簧伸长量的关系，并测定弹簧的劲度系数”的实验中，实验装置如图所示所用的每个
劲度系数为图象直线部分的斜率，k＝20 N/m(2分)(3)记录数据的表格如下表(分)
次数123456弹力F/N弹簧的长度L/(×10－2 m)(4)优点是：可以避免弹簧自身重力对实验的影响(1分)
缺点是：弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差(1分)
12．（10分）解析：
将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星双星系统在银河系中很普遍利用双星系统中两颗恒星的运

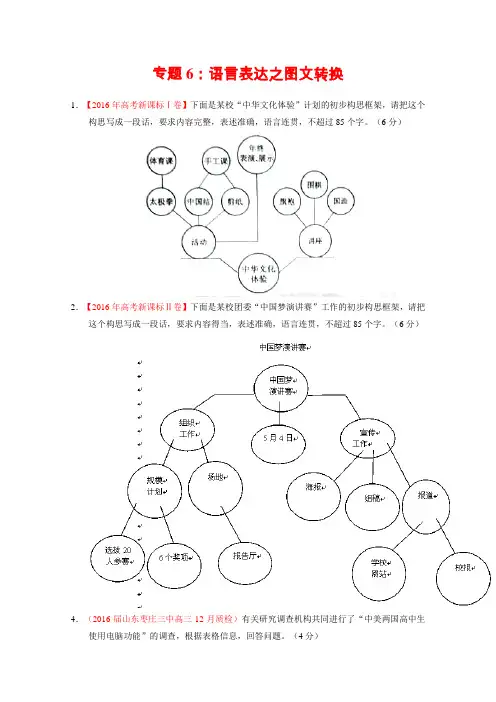
专题6：语言表达之图文转换1．【2016年高考新课标Ⅰ卷】下面是某校“中华文化体验”计划的初步构思框架，请把这个构思写成一段话，要求内容完整，表述准确，语言连贯，不超过85个字。

（6分）2．【2016年高考新课标Ⅱ卷】下面是某校团委“中国梦演讲赛”工作的初步构思框架，请把这个构思写成一段话，要求内容得当，表述准确，语言连贯，不超过85个字。

（6分）4．（2016届山东枣庄三中高三12月质检）有关研究调查机构共同进行了“中美两国高中生使用电脑功能”的调查，根据表格信息，回答问题。

（4分）（1）与美国高中生相比，中国高中生使用电脑的主要情况是什么？请简要分析。

（不得出现具体数字）（2分）（2）根据上表情况，对高中生的网络学习提出一点建议。

（2分）5．（2016届山西平遥中学高三10月考）阅读下面这幅有关生源大战的漫画，用简洁的语言揭示其隐含的意思。

要求：至少运用两种修辞手法，50字以内。

（6分）6．（2016届山西太原五中高三第一次段考）下面是我国颁布的“中国人民抗日战争暨世界反法西斯战争胜利70周年纪念活动标识”，请写出该标识的构图要素及其寓意，要求语意简明，句子通顺，不超过100个字。

（6分）7．（2016届陕西镇安中学高三上第四次月考）下面是2010年广州亚运会志愿者标志，请从构形角度（不包括文字）说明标志的创意，要求语意简明，句子通顺。

（5分）8．（2016届四川成都七中高三1月周练）下面是一个关于我们（人类）身体的某些特别性状出现时间的示意图。

请仔细观察后加以概括，用不超过75个字的一段话把它的大意表述出来。

要求内容完整，表述正确，语言连贯。

（6分）9．（2016届浙江效实中学高三上期中）下面是北京2022年冬奥会申办标识，请从图文特点出发，简要评价它的创意。

（6分）10．（2016届浙江重庆一中高三12月考）下图表示的是人从婴儿期到青年期人际交往发展变化的趋势，据此总结出其发展变化的规律。

带”和“21世纪海上丝绸之路”的战略构想。这一构想的实施
①体现了我国把对外开放作为自己发展的根本基点
②是完善互利共赢、多元平衡开放型经济体系的要求
③标志着我国从“引进来”到“走出去”的战略转变
④是我国顺应经济全球化趋势而作出的重大战略决策
A．①②
B．①③
C．②④
D．③④
18．近年来，我国高铁全方位拓展海外市场，其影响力和发展力不断提升。中国高铁“走出去”
①推进廉政建设的制度保障
②运用新兴技术促进廉政建设
③公民监督政府的主要渠道
④利用社会力量监督公共权力
A．①③
B．①④
C．②③
D．②④
第Ⅱ卷（非选择题 共52分）
25.（21分）阅读材料，完成下列要求。
2015年8月24日， 《中共中央国务院关于深化国有企业改革的指导意见》（简称《指导意见》）印发，开启了国有
B．苹果公司首创了这一商业模式
C．消费者愿意为增加的体验买单
D．程序开发消耗了人的脑力和体力
2．变动情况甲国货币1：6.34甲国货币对人民币汇率升高20%乙国货币1：9.65乙国货币对人民币汇率跌落10%
A．甲国 B．乙国 C．一样D．不确定
4．同样是做帽子，江苏南通富美服饰有限公司因为在帽子中加入文化元素、科技元素、时尚元素，帽子的价格尽
①依托互联网络，提高农业生产科技水平 ②完善分配制度，增加农民的经营性收入
③变革生产关系，促进农村生产力的发展 ④创新土地流转，提高土地资源利用效率
A．①②
B．①③
C．②④
D．③④
11．2015年是全面完成“十二五”规划的收官之年。在我国进入经济发展新常态，经济发展主要受需求不足影响的

说明：1、考试时间：60分钟；本卷满分： 1 0 0 分2、请将答案填写在答案卷上，考试结束后只交答案卷。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Cl35.5 Fe 56 Cu 64Ne 20 Na 23 Mg 24 K 39 Al 27 Ca 40第Ⅰ卷（选择题共42分）一、选择题（本题包括7小题，每小题6分，共42分，每小题只有一个选项符合题意）7．青蒿素是一种高效、速率搞疟药，是中医献给世界的一份礼物。

其结构简式如图所示。

下列有关青蒿素的说法正确的是A．易溶于乙醚等有机溶剂B．分子式为C15H21O5C．能在热的NaOH溶液中存在D．分子结构中只含有极性键【答案】A考点：有机物的结构和性质8．设N A表示阿伏加德罗常数，下列说法正确的是A．1mol丙烯酸含有N A个不饱和键B．标准状况下，11.2L的苯中含有3N A个碳氢键C．0.1mol/L的Na3PO4溶液中含有的阴离子总数大于0.1N AD．1L1.0mol/L的Na2SiO3溶液中含有的氧原子数目大于3N A【答案】D【解析】试题分析：A、丙烯酸中含有碳碳双键和羧基，羧基中碳氧双键，错误，不选A；B、标准状况下苯不是气体，不能使用气体摩尔体积进行计算，错误，不选B；C、磷酸根离子水解，且没有说明溶液的体积，不能计算阴离子总数，错误，不选C；D、1摩尔硅酸钠含有3摩尔氧原子，但水中也有样院子，所以氧原子数大于3摩尔，正确，选D。

考点：阿伏伽德罗常数【名师点睛】阿伏伽德罗常数的考查是考试常见的题型，通常需要注意一下几个方面：1、气体摩尔体积的使用：必须是在标况下，物质为气体，气体摩尔体积才为22.4L/mol。

2、分子中的原子个数，很多的单质分子中含有2个原子，例如氢气，氧气，氮气等，但也有不是2个原子的，例如氦气含有1个原子，臭氧含有3个原子。

当然化合物分子中的原子数也各不相同。

3、有些物质不能用分子一词，例如离子化合物，如氯化钠，过氧化钠等。

安徽省马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三第三次联考语文试题注意事项：1．本试卷分第Ⅰ卷（阅读题）和第Ⅱ卷（表达题）两部分。

2．答题前，考生务必将自己的姓名准考证号填写在试卷相应的位置。

3．全部答案写在答题卡上，写在试卷上无效4．本试卷满分150分，考试时间150分钟，第Ⅰ卷阅读题（70分）甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成后面题目。

中国是一个有着五千年悠久历史的文明古国，在历史发展进程中，茶与中国传统文化表现出了密切的关系，儒释道是中国传统文化的主要的思想来源，中国茶学与儒释道的思想理念有着极深的渊源关系。

陆羽《茶经》是中国最早的的茶学著作，书中也十分鲜明地体现了这种关系。

茶文化与儒家思想中“礼”的关系是相当密切的。

儒家认为礼就是秩序与和谐，“礼”也是一切民俗民风由来的源头。

礼仪的观念深入到社会活动的一切领域，那么在茶文化中，自然也会有所体现。

在古代家庭中的敬神祭祖、宾客相见、婚丧大典、节庆宴饮中都需要用到茶。

晚唐人刘贞亮《茶德》中提出了“十德”说，其中就有“以茶利礼仁，以茶表敬意”二句，这说明最迟在唐代，来客敬茶，以茶为礼，已成为普遍风俗。

而在官场中，茶礼则已经演化为一种区别官阶等级的标志，点茶与点汤成为官场的待下之礼。

“中庸之道”是儒家的核心思想，其哲学思想强调适度原则。

茶文化中体现了这一点，《茶经》中强调选水要选缓流的活水，反对急流之水，也不能用停蓄不流的死水。

在饮茶之中，第一次泡茶之水，仅作“暖盏”之用，并不饮用，第二次的茶汤才是最佳之“至味”，。

饮茶的量也强调适度。

饮茶人通过品茶而悟道，在精神上达到一种“和”的最高境界，这就是茶道。

饮茶的全过程贯穿着儒家的中庸思想，也就是提倡达到通过茶道，营造出社会和谐稳定、人与人之间和睦相处的空间。

唐代诗人们的品茶，已经超越解渴、提神、解乏、保健等生理上的满足，着重从审美的角度来品赏茶汤的色、香、味、形，强调心灵感受，追求达到天人合一的最高境界，通过饮茶与茶道展示，表现出人的精神气度和文化修养，表现人的清高廉洁，节俭朴素的思想品格。

2015-2016学年安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）集合U=R，A={x|x2﹣x﹣2＜0}，B={x|y=ln（1﹣x）}，则图中阴影部分表示的集合是（）A．{x|x≥1}B．{x|1≤x＜2}C．{x|0＜x≤1}D．{x|x≤1}2．（5分）设复数（i为虚数单位）在复平面中对应点A，将OA绕原点O逆时针旋转θ角得到OB，若点B在第二象限，则θ角的可能值是（）A．B．C． D．3．（5分）下列命题中正确的是（）A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题B．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x≠0”C．“”是“”的充分不必要条件D．命题“∀x∈R，2x＞0”的否定是“”4．（5分）已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题：①若α⊥β，m∥α，则m⊥β；②若m⊥α，n⊥β，且m⊥n，则α⊥β；③若m⊥β，m∥α，则α⊥β；④若m∥α，n∥β，且m∥n，则α∥β．其中正确命题的序号是（）A．②③B．①④C．②④D．①③5．（5分）能够把圆O：x2+y2=r2（r＞0）的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”，下列函数不是圆O的“和谐函数”的是（）A．f（x）=4x3+x B．f（x）=ln C．f（x）=tan D．f（x）=e x+e﹣x6．（5分）设f（x）=cosx﹣sinx，把f（x）的图象按向量=（m，0）（m＞0）平移后，图象恰好为函数y=﹣f′（x）的图象，则m的值可以为（）A．B．πC．πD．7．（5分）现有四个函数：①y=xsinx，②y=xcosx，③y=x|cosx|，④y=x•2x的部分图象如下，但顺序被打乱了，则按照从左到右将图象对应的函数序号排列正确的一组是（）A．①②③④B．②①③④C．③①④②D．①④②③8．（5分）数列{a n}满足a n+2=2a n+1﹣a n，且a2014，a2016是函数f（x）=+6x ﹣1的极值点，则log2（a2000+a2012+a2018+a2030）的值是（）A．2 B．3 C．4 D．59．（5分）定义在R上的偶函数f（x）满足：对任意的x1，x2∈（﹣∞，0）（x1≠x2），都有＜0．则下列结论正确的是（）A．f（0.32）＜f（20.3）＜f（log25） B．f（log25）＜f（20.3）＜f（0.32）C．f（log25）＜f（0.32）＜f（20.3） D．f（0.32）＜f（log25）＜f（20.3）10．（5分）已知函数f（x）=cos，根据下列框图，输出S的值为（）A．670 B．670C．671 D．67211．（5分）函数g（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＞0时，xg（x）﹣f（x）＜0，则使得f（x）＜0成立的x的取值范围是（）A．（﹣∞，﹣1）∪（0，1）B．（0，1）∪（1，+∞）C．（﹣∞，﹣1）∪（﹣1，0） D．（﹣1，0）∪（1，+∞）12．（5分）已知函数若关于x的函数y=f2（x）﹣bf（x）+1有8个不同的零点，则实数b的取值范围是（）A．（2，+∞）B．[2，+∞）C．D．二、填空题：（本大题共4小题，每小题5分，共20分．）13．（5分）已知实数1，m，4构成一个等比数列，则圆锥曲线+y2=1的离心率为．14．（5分）已知与的夹角为120°，若（+）⊥（﹣2）且||=2，则在上的投影为．15．（5分）若函数f（x）=x2+ax+2b在区间（0，1），（1，2）内各有一个零点，则的取值范围是．16．（5分）在直角△ABC中，两条直角边分别为a、b，斜边和斜边上的高分别为c、h，则的取值范围是．三.解答题：本大题6小题，满分60分，解答应写出文字说明，证明过程或演算步骤．17．（12分）已知函数f（x）=log3（ax+b）的图象经过点A（2，1）和B（5，2），记a n=3f（n），n∈N*（1）求数列{a n}的通项公式；（2）设b n=，T n=b1+b2+…b n，求证：T n＜3．18．（12分）已知函数f（x）=2的图象与直线y=m（m＞0）相切，并且切点横坐标依次成公差为π的等差数列，且f（x）的最大值为1．（1）x∈[0，π]，求函数f（x）的单调递增区间；（2）将f（x）的图象向左平移个单位，得到函数g（x）的图象，若函数y=g （x）﹣m在上有零点，求实数m的取值范围．19．（12分）在△ABC中，设A、B、C的对边分别为a、b、c，（1）若a=2且（2+b）•（sinA﹣sinB）=（c﹣b）sinC，求△ABC面积S的最大值（2）△ABC为锐角三角形，且B=2C，若=（sinA，cosA），=（cosB，sinB），求|3﹣2|2的取值范围．20．（12分）为了保护环境，某工厂在政府部门的支持下，进行技术改进：把二氧化碳转化为某种化工产品，经测算，该处理成本y（万元）与处理量x（吨）之间的函数关系可近似地表示为：，且每处理一吨二氧化碳可得价值为20万元的某种化工产品．（Ⅰ）当x∈[30，50]时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，则国家至少需要补贴多少万元，该工厂才不亏损？（Ⅱ）当处理量为多少吨时，每吨的平均处理成本最少．21．（12分）已知函数f（x）=lnx﹣ax2+x．（1）若f（1）=0，求函数f（x）的单调减区间；（2）若关于x的不等式f（x）≤ax﹣1恒成立，求整数a的最小值；（3）若a=﹣2，正实数x1，x2满足f（x1）+f（x2）+x1x2=0，证明：x1+x2≥．请考生在第22、23两题中任选一题，如果多做，则按所做的第一题记分.选修4-4：坐标系与参数方程22．（10分）在平面直角坐标系xOy中，直线l的参数方程（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：ρ=4cosθ．（1）把直线l的参数方程化为极坐标方程，把曲线C的极坐标方程化为普通方程；（2）求直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）．选修4-5：不等式选讲23．设函数f（x）=|2x﹣a|+|2x+1|（a＞0），g（x）=x+2．（1）当a=1时，求不等式f（x）≤g（x）的解集；（2）若f（x）≥g（x）恒成立，求实数a的取值范围．2015-2016学年安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）集合U=R，A={x|x2﹣x﹣2＜0}，B={x|y=ln（1﹣x）}，则图中阴影部分表示的集合是（）A．{x|x≥1}B．{x|1≤x＜2}C．{x|0＜x≤1}D．{x|x≤1}【解答】解：由Venn图可知，阴影部分的元素为属于A当不属于B的元素构成，所以用集合表示为A∩（∁U B）．A={x|x2﹣x﹣2＜0}={x|﹣1＜x＜2}，B={x|y=ln（1﹣x）}={x|1﹣x＞0}={x|x＜1}，则∁U B={x|x≥1}，则A∩（∁U B）={x|1≤x＜2}．故选：B．2．（5分）设复数（i为虚数单位）在复平面中对应点A，将OA绕原点O逆时针旋转θ角得到OB，若点B在第二象限，则θ角的可能值是（）A．B．C． D．【解答】解：∵=，∴点A在第一象限，且OA与x轴正半轴所成角小于，∵OA绕原点O逆时针旋转θ角得到OB，点B在第二象限，∴θ角的可能值是．故选：C．3．（5分）下列命题中正确的是（）A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题B．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x≠0”C．“”是“”的充分不必要条件D．命题“∀x∈R，2x＞0”的否定是“”【解答】解：若命题p为真命题，命题q为假命题，则命题“p∧q”为假命题，故A不正确；命题“若xy=0，则x=0”的否命题为：“若xy≠0，则x≠0”，故B不正确；“”⇒“+2kπ，或，k∈Z”，“”⇒“”，故“”是“”的必要不充分条件，故C不正确；命题“∀x∈R，2x＞0”的否定是“”，故D正确．故选：D．4．（5分）已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题：①若α⊥β，m∥α，则m⊥β；②若m⊥α，n⊥β，且m⊥n，则α⊥β；③若m⊥β，m∥α，则α⊥β；④若m∥α，n∥β，且m∥n，则α∥β．其中正确命题的序号是（）A．②③B．①④C．②④D．①③【解答】解：①当α⊥β，m∥α时，m⊥β不一定成立，所以错误；②利用当两个平面的法向量互相垂直时，这两个平面垂直，故成立；③因为m∥α，则一定存在直线n在β，使得m∥n，又m⊥β可得出n⊥β，由面面垂直的判定定理知，α⊥β，故成立；④m∥α，n∥β，且m∥n，α，β也可能相交，如图所示，所以错误，故选：A．5．（5分）能够把圆O：x2+y2=r2（r＞0）的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”，下列函数不是圆O的“和谐函数”的是（）A．f（x）=4x3+x B．f（x）=ln C．f（x）=tan D．f（x）=e x+e﹣x【解答】解：由题意可得，“和谐函数”的图象经过圆心（0，0），结合所给的选项，只有D中的函数f（x）=e x+e﹣x的图象不经过原点，故选：D．6．（5分）设f（x）=cosx﹣sinx，把f（x）的图象按向量=（m，0）（m＞0）平移后，图象恰好为函数y=﹣f′（x）的图象，则m的值可以为（）A．B．πC．πD．【解答】解：函数的导数f′（x）=﹣sinx﹣cosx，则y=﹣f′（x）=sinx+cosx=cos（x﹣），f（x）的图象按向量=（m，0）（m＞0）平移后，得到y=cos（x﹣m）﹣sin（x﹣m）=cos（x﹣m+），则当﹣m+=﹣时，即m=时，满足条件．故选：D．7．（5分）现有四个函数：①y=xsinx，②y=xcosx，③y=x|cosx|，④y=x•2x的部分图象如下，但顺序被打乱了，则按照从左到右将图象对应的函数序号排列正确的一组是（）A．①②③④B．②①③④C．③①④②D．①④②③【解答】解：研究发现①是一个偶函数，其图象关于y轴对称，故它对应第一个图象②③都是奇函数，但②在y轴的右侧图象在x轴上方与下方都存在，而③在y轴右侧图象只存在于x轴上方，故②对应第三个图象，③对应第四个图象，④与第二个图象对应，易判断．故按照从左到右与图象对应的函数序号①④②③故选：D．8．（5分）数列{a n}满足a n+2=2a n+1﹣a n，且a2014，a2016是函数f（x）=+6x ﹣1的极值点，则log2（a2000+a2012+a2018+a2030）的值是（）A．2 B．3 C．4 D．5【解答】解：函数f（x）=+6x﹣1，可得f′（x）=x2﹣8x+6，∵a2014，a2016是函数f（x）=+6x﹣1的极值点，∴a2014，a2016是方程x2﹣8x+6=0的两实数根，则a2014+a2016=8．=2a n+1﹣a n，数列{a n}中，满足a n+2可知{a n}为等差数列，∴a2014+a2016=a2000+a2030，即a2000+a2012+a2018+a2030=16，从而log2（a2000+a2012+a2018+a2030）=log216=4．故选：C．9．（5分）定义在R上的偶函数f（x）满足：对任意的x1，x2∈（﹣∞，0）（x1≠x2），都有＜0．则下列结论正确的是（）A．f（0.32）＜f（20.3）＜f（log25） B．f（log25）＜f（20.3）＜f（0.32）C．f（log25）＜f（0.32）＜f（20.3） D．f（0.32）＜f（log25）＜f（20.3）【解答】解：∵对任意x1，x2∈（﹣∞，0），且x1≠x2，都有＜0，∴f（x）在（﹣∞，0）上是减函数，又∵f（x）是R上的偶函数，∴f（x）在（0，+∞）上是增函数，∵0.32＜20.3＜log25∴f（0.32）＜f（20.3）＜f（log25）．故选：A．10．（5分）已知函数f（x）=cos，根据下列框图，输出S的值为（）A．670 B．670C．671 D．672【解答】解：由程序框图知：第一次运行f（1）=cos=，S=0+．n=1+1=2；第二次运行f（2）=cos=﹣，S=，n=2+1=3，第三次运行f（3）=cosπ=﹣1，S=，n=3+1=4，第四次运行f（4）=cos=﹣，S=，n=4+1=5，第五次运行f（5）=cos=，S=1，n=6，第六次运行f（6）=cos2π=1，S=2，n=7，…直到n=2016时，程序运行终止，∵函数y=cos是以6为周期的周期函数，2015=6×335+5，又f（2016）=cos336π=cos（2π×138）=1，∴若程序运行2016次时，输出S=2×336=672，∴程序运行2015次时，输出S=336×2﹣1=671．故选：C．11．（5分）函数g（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＞0时，xg（x）﹣f（x）＜0，则使得f（x）＜0成立的x的取值范围是（）A．（﹣∞，﹣1）∪（0，1）B．（0，1）∪（1，+∞）C．（﹣∞，﹣1）∪（﹣1，0） D．（﹣1，0）∪（1，+∞）【解答】解：构造函数F（x）=，则F（x）为偶函数且x≠0，求导数可得F′（x）==，∵当x＞0时，xg（x）﹣f（x）＜0，∴F′（x）＜0，∴函数F（x）在（0，+∞）单调递减，由函数为偶函数可得F（x）在（﹣∞，0）单调递增，由f（1）=0可得F（1）=0，∴f（x）＜0等价于xF（x）＜0等价于或，解得x∈（1﹣，0）∪（1，+∞）故选：D．12．（5分）已知函数若关于x的函数y=f2（x）﹣bf（x）+1有8个不同的零点，则实数b的取值范围是（）A．（2，+∞）B．[2，+∞）C．D．【解答】解：∵函数，作出f（x）的简图，如图所示：由图象可得当f（x）在（0，4]上任意取一个值时，都有四个不同的x与f（x）的值对应．再结合题中函数y=f2（x）﹣bf（x）+1 有8个不同的零点，可得关于k的方程k2 ﹣bk+1=0有两个不同的实数根k1、k2，且0＜k1≤4，0＜k2≤4．∴应有，解得2＜b≤，故选：D．二、填空题：（本大题共4小题，每小题5分，共20分．）13．（5分）已知实数1，m，4构成一个等比数列，则圆锥曲线+y2=1的离心率为或．【解答】解：实数1，m，4构成一个等比数列，可得m=±2，m=2时，圆锥曲线+y2=1，它的离心率为：e==．m=﹣2时，圆锥曲线y2﹣=1，它的离心率为：e==．故答案为：或．14．（5分）已知与的夹角为120°，若（+）⊥（﹣2）且||=2，则在上的投影为﹣．【解答】解：∵与的夹角为120°，若（+）⊥（﹣2）且||=2，∴（+）•（﹣2）=0，即﹣﹣22=0，∴4+﹣22=0，解得=，∴在上的投影为cos120°=﹣=﹣×=﹣．故答案为：﹣．15．（5分）若函数f（x）=x2+ax+2b在区间（0，1），（1，2）内各有一个零点，则的取值范围是（3，6）．【解答】解：∵函数f（x）=x2+ax+2b在区间（0，1），（1，2）内各有一个零点，∴，即，画出可行域，如图所示：表示△ABC的内部区域，其中A（﹣3，1），B（﹣2，0），C（﹣1，0）．目标函数z=2+，即2加上点（a，b）与点M（0，4）连线的斜率．数形结合可得，的最小值趋于K AM==1，的最大值趋于K BM==4，故z的最小值趋于2+1=3，最大值趋于2+4=6，故答案为（3，6）．16．（5分）在直角△ABC中，两条直角边分别为a、b，斜边和斜边上的高分别为c、h，则的取值范围是（1，] ．【解答】解：∵直角△ABC中，两条直角边分别为a、b，∴斜边c=，斜边上的高h==，因此，=∵≥=，≤1∴＞1（等号取不到），即又=+•设=t，则=，=可得f（t）=+，（0＜t）∵在区间（0，）上f'（t）＞0，∴f（t）在区间（0，）上是增函数，可得当0＜t时，f（t）的最大值为f （）=综上所述，的取值范围是（1，]故答案为：（1，]三.解答题：本大题6小题，满分60分，解答应写出文字说明，证明过程或演算步骤．17．（12分）已知函数f（x）=log3（ax+b）的图象经过点A（2，1）和B（5，2），记a n=3f（n），n∈N*（1）求数列{a n}的通项公式；（2）设b n=，T n=b1+b2+…b n，求证：T n＜3．【解答】解：（1）∵f（x）=log3（ax+b）的图象经过点A（2，1）和B（5，2），∴，即，得，则f（x）=log3（2x﹣1），则数列{a n}的通项公式a n=3f（n）==2n﹣1，n∈N*；（2）b n==，T n=b1+b2+…b n=+++…+①，T n=+…+++②，①﹣②得T n=+++…+﹣=+（++…+）﹣=﹣﹣，∴T n=3﹣﹣=3﹣＜3．即T n＜3．18．（12分）已知函数f（x）=2的图象与直线y=m（m＞0）相切，并且切点横坐标依次成公差为π的等差数列，且f（x）的最大值为1．（1）x∈[0，π]，求函数f（x）的单调递增区间；（2）将f（x）的图象向左平移个单位，得到函数g（x）的图象，若函数y=g （x）﹣m在上有零点，求实数m的取值范围．【解答】解：（1）函数f（x）=2=sin（2ωx+）+sin2ωx+a=cos2ωx+sin2ωx+a=2sin（2ωx+）+a，它的图象与直线y=m（m＞0）相切，并且切点横坐标依次成公差为π的等差数列，故=π，ω=1．再根据f（x）的最大值为2+a=1，故a=﹣1，f（x）=2sin（2x+）﹣1．令2kπ﹣≤2x+≤2kπ+，求得kπ﹣≤x≤kπ+，k∈Z，可得函数在[0，π]上的增区间为[0，]、[，π]．（2）将f（x）的图象向左平移个单位，得到函数g（x）=2sin[2（x+）+]﹣1=2sin（2x+）﹣1的图象，在上，2x+∈[，]，故当2x+=时，函数g（x）取得最小值为﹣2﹣1=﹣3；当2x+=时，函数g（x）取得最大值为﹣1．若函数y=g（x）﹣m在上有零点，求实数m的取值范围为[﹣3，﹣1]．19．（12分）在△ABC中，设A、B、C的对边分别为a、b、c，（1）若a=2且（2+b）•（sinA﹣sinB）=（c﹣b）sinC，求△ABC面积S的最大值（2）△ABC为锐角三角形，且B=2C，若=（sinA，cosA），=（cosB，sinB），求|3﹣2|2的取值范围．【解答】解：（1）∵（2+b）•（sinA﹣sinB）=（c﹣b）sinC，∴（2+b）•（a﹣b）=（c﹣b）c，∵a=2，∴（a+b）•（a﹣b）=（c﹣b）c，即a2﹣b2=c2﹣bc，∴bc=b2+c2﹣a2．∴cosA==．∴A=．∵a2=b2+c2﹣2bc•cosA=b2+c2﹣bc≥bc，∴bc≤a2=4．∴S=bcsinA=≤．当且仅当b=c时取等号．△ABC∴△ABC的面积最大值为．（2）∵=（sinA，cosA），=（cosB，sinB），∴=1，=1，=sinAcosB+cosAsinB=sin（A+B）=sinC．∴|3﹣2|2=9﹣12+4=13﹣12sinC．∵△ABC为锐角三角形，∴0＜A＜，0＜B＜，0＜C＜．∵B=2C，A+B+C=π，∴C=∴＜C＜．∴＜sinC＜．∴13﹣6＜13﹣12sinC＜7．∴|3﹣2|2的取值范围是（13﹣6，7）．20．（12分）为了保护环境，某工厂在政府部门的支持下，进行技术改进：把二氧化碳转化为某种化工产品，经测算，该处理成本y（万元）与处理量x（吨）之间的函数关系可近似地表示为：，且每处理一吨二氧化碳可得价值为20万元的某种化工产品．（Ⅰ）当x∈[30，50]时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，则国家至少需要补贴多少万元，该工厂才不亏损？（Ⅱ）当处理量为多少吨时，每吨的平均处理成本最少．【解答】解：（Ⅰ）当x∈[30，50]时，设该工厂获利为S，则S=20x﹣（x2﹣40x+1600）=﹣（x﹣30）2﹣700所以当x∈[30，50]时，S＜0，因此，该工厂不会获利，所以国家至少需要补贴700万元，才能使工厂不亏损（Ⅱ）由题意可知，二氧化碳的每吨平均处理成本为：①当x∈[10，30）时，P（x）=，∴P′（x）==∴x∈[10，20）时，P′（x）＜0，P（x）为减函数；x∈（20，30）时，P′（x）＞0，P（x）为增函数，∴x=20时，P（x）取得最小值，即P（20）=48；②当x∈[30，50]时，P（x）=﹣40≥﹣40=40当且仅当x=，即x=40∈[30，50]时，P（x）取得最小值P（40）=40∵48＞40，∴当处理量为40吨时，每吨的平均处理成本最少．21．（12分）已知函数f（x）=lnx﹣ax2+x．（1）若f（1）=0，求函数f（x）的单调减区间；（2）若关于x的不等式f（x）≤ax﹣1恒成立，求整数a的最小值；（3）若a=﹣2，正实数x1，x2满足f（x1）+f（x2）+x1x2=0，证明：x1+x2≥．【解答】解：（1）∵f（x）=lnx﹣ax2+x，f（1）=0，∴a=2，且x＞0．∴f（x）=lnx﹣x2+x，∴=，当f′（x）＜0，即x＞1时，函数f（x）的单调递减，∴函数f（x）的单调减区间（1，+∞）．（2）令F（x）=f（x）﹣ax+1=lnx﹣ax2+（1﹣a）x+1，则F′（x）=﹣ax+1﹣a=﹣=﹣a，当a≤0时，在（0，+∞）上，函数F（x）单调递增，且F（1）=2﹣＞0，不符合题意，当a＞0时，函数F（x）在x=时取最大值，F（）=ln+，令h（a）=ln+=，则根据基本函数性质可知，在a＞0时，h（a）单调递减，又∵h（1）=＞0，h（2）=＜0，∴符合题意的整数a的最小值为2．（3）∵a=﹣2，∴f（x）=lnx+x2+x，∴f（x1）+f（x2）+x1x2=lnx1+x12+x1+lnx2+x22+x1x2+x2=（x1+x2）2+x1+x2+lnx1x2﹣x1x2令g（x）=lnx﹣x，则g′（x）=，∴0＜x＜1时，g′（x）＞0，g（x）单调递增，x＞1时，g′（x）＜0，g（x）单调递减，∴g（x）max=g（1）=﹣1，∴f（x1）+f（x2）+x1x2≤（x1+x2）2+（x1+x2）﹣1，即（x1+x2）2+（x1+x2）﹣1≥0，又∵x1，x2是正实数，∴x1+x2≥．请考生在第22、23两题中任选一题，如果多做，则按所做的第一题记分.选修4-4：坐标系与参数方程22．（10分）在平面直角坐标系xOy中，直线l的参数方程（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：ρ=4cosθ．（1）把直线l的参数方程化为极坐标方程，把曲线C的极坐标方程化为普通方程；（2）求直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）．【解答】解；（1）直线l 的参数方程（t 为参数），消去参数t 化为=0，把代入可得：=0，由曲线C 的极坐标方程为：ρ=4cosθ，变为ρ2=4ρcosθ，化为x 2+y 2﹣4x=0． （2）联立，解得或，∴直线l 与曲线C 交点的极坐标（ρ≥0，0≤θ＜2π）为，．选修4-5：不等式选讲23．设函数f （x ）=|2x ﹣a |+|2x +1|（a ＞0），g （x ）=x +2． （1）当a=1时，求不等式f （x ）≤g （x ）的解集； （2）若f （x ）≥g （x ）恒成立，求实数a 的取值范围．【解答】解：（1）当a=1时，不等式f （x ）≤g （x ）即|2x ﹣1|+|2x +1|≤x +2，等价于①，或②，或③．解①求得 x 无解，解②求得0≤x ＜，解③求得≤x ≤， 综上，不等式的解集为{x |0≤x ≤}．（2）由题意可得|2x ﹣a |+|2x +1|≥x +2恒成立，转化为|2x ﹣a |+|2x +1|﹣x ﹣2≥0 恒成立．令h （x ）=|2x ﹣a |+|2x +1|﹣x ﹣2= （a ＞0），易得h （x ）的最小值为﹣1，令 ﹣1≥0，求得a ≥2．赠送—高中数学知识点【1.3.1】单调性与最大（小）值 （1）函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x =，令()u g x =，若()y fu =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()u g x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减． （2）打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数，分别在[,0)a -、]a 上为减函数．（3）最大（小）值定义①一般地，设函数()y f x =的定义域为I ，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，yxo都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．。

马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三第一学期12月联考数学（文）试题第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数1ii -在复平面上对应的点位于（ ）. A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．设b a 、为两条不同的直线，α为一个平面，下列命题中为真命题的是（ ）. A ．若//,//,a b a α则//b α B ．若,//,a b a α⊥则b α⊥ C ．若//,,a b a α⊥则b α⊥ D ．若,,a b a α⊥⊥则//b α 3．设{}{}2lg(1)A x y B y y x A B ===-⋂=，，则（ ）.A ．(){}11，- B ．(){}01，C ．[]10-，D ．[]10， 4．2:320p x x -+≤成立的一个必要不充分条件是（ ）.A ．1x >B ．1x ≥C ．12x ≤≤D ．12x <<5．设y x 、满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩，则y x -2的最小值是（ ）.A ．4-B ．712C ．0D ．6 6．若先将函数)+cos 66y x x ππ⎛⎫=-- ⎪⎝⎭图象上各点的纵坐标不变，横坐标伸长到原来的 2倍，再将所得图象向左平移6π个单位，所得函数图象的一条对称轴的方程是（ ）. A ．6π=x B ．3π=x C ．2π=x D ．65π=x7．某几何体的三视图如图所示，则它的表面积为（ ）. ABCD8．函数x x x f sin )2()(π-=在[]ππ22，-上的大致图像是（ ）.A B C D9．已知1->a ，2->b ，()()1621=++b a ，则b a +的最小值是（ ）. A ．4 B ．5 C ．6 D ．710．已知8,6,3AB AC BAC π==∠= ，AD DB =，2AE EC = ，线段BE 与线段CD 交于点G ，则AG的值为（ ）.A ．4B ．19C ．52D ．511．已知)1(-x f 是偶函数，且在()∞+，0上单调递增，下列说法正确的是（ ）. A ．⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛81log 8122281f f f B ．⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛81log 2812812f f fC ．⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛22818181log 2f f f D ．⎪⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛>⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛8122281log 81f f f 12．已知数列{}n a 满足121(1,2)(3)n n n n a a a n --=⎧=⎨+≥⎩，则2016a 除以4所得到的余数是（ ）.A ．0B ．1C ．2D ．3第II 卷二、填空题：本大题共4小题，每小题5分。

高中数学学习材料（灿若寒星精心整理制作）2015-2016学年安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数（x∈R）在复平面内对应的点位于以原点O为圆心，以为半径的圆周上，则x的值为（）A．2 B．1+3i C．±2 D．2．设x，y满足约束条件，则目标函数z=的取值范围为（）A．[﹣3，3] B．[﹣2，2] C．[﹣1，1] D．[﹣，]3．在等差数列{a n}中，a1+a2+a3=3，a28+a29+a30=165，则此数列前30项和等于（）A．810 B．840 C．870 D．9004．已知M=，N=，由如右程序框图输出的S为（）A．1 B．ln2 C．D．05．若函数，且f（α）=﹣2，f（β）=0，|α﹣β|的最小值是，则f（x）的单调递增区间是（）A． B．C．D．6．定义在R上的函数f（x）满足f（x+6）=f（x）．当﹣3≤x＜﹣1时，f（x）=﹣（x+2）2，当﹣1≤x＜3时，f（x）=x．则f（1）+f（2）+…+fA．333 B．336 C．1678 D．20157．已知0＜x＜，则﹣＜0是﹣x＞0成立的（）A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件8．，，若A∩B={（cosθ1，sinθ1），（cosθ2，sinθ2）}，则m的取值范围为（）A．[﹣2，2] B．（﹣2，2）C．D．9．若a＞0，，，，则x，y，z的大小顺序为（）A．x＞z＞y B．x＞y＞z C．z＞x＞y D．z＞y＞x10．下列命题中正确的个数是（）①过异面直线a，b外一点P有且只有一个平面与a，b都平行；②异面直线a，b在平面α内的射影相互垂直，则a⊥b；③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；④直线a，b分别在平面α，β内，且a⊥b，则α⊥β．A．0 B．1 C．2 D．311．三角形ABC中，A、B、C所对的边分别为a，b，c；若A=，则=（）A．a+b B．a+c C．b+c D．a+b+c12．已知f（x）=1+x﹣+﹣+…+；g（x）=1﹣x+﹣+﹣…﹣；设函数F（x）=[f（x+3）]•[g（x﹣4）]，且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，则b﹣a的最小值为（）A．8 B．9 C．10 D．11二、填空题：本大题共4小题，每小题5分13．已知||=1，||=2，与的夹角为60°，则+在方向上的投影为______．14．已知a＞b＞0，且a+b=2，则的最小值为______．15．已知α，β为锐角，cosα=，则cosβ=______．16．已知函数f（x）=e ax﹣x﹣1，其中a≠0．若对一切x∈R，f（x）≥0恒成立，则a的取值集合______．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．已知各项均为正数的数列{a n}的前n项和为S，满足=2S n+n+4，且a2﹣1，a3，a7恰为等比数列{b n}的前3项．（1）求数列{a n}，{b n}的通项公式；（2）令c n=﹣，求数列{c n}的前n项和T n．18．已知向量=（cosωx﹣sinωx，sinωx），=（﹣cosωx﹣sinωx，2cosωx），设函数f（x）=•+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）（1）求函数f（x）的最小正周期；（2）若y=f（x）的图象经过点（，0）求函数f（x）在区间[0，]上的取值范围．19．在△ABC中，角A，B，C对应边分别是a，b，c，c=2，sin2A+sin2B﹣sin2C=sinAsinB．（1）若sinC+sin（B﹣A）=2sin2A，求△ABC面积；（2）求AB边上的中线长的取值范围．20．已知a为常数，函数，（1）当a=0时，求函数f（x）的最小值；（2）若f（x）有两个极值点x1，x2（x1＜x2）①求实数a的取值范围；②求证：且x1x2＞1（其中e为自然对数的底）21．已知函数f（x）=e x（2x﹣1），g（x）=ax﹣a（a∈R）．（1）若y=g（x）为曲线y=f（x）的一条切线，求a的值；（2）已知a＜1，若存在唯一的整数x0，使得f（x0）＜g（x0），求a的取值范围．请考生在22、23两题中任选一题作答【选修4-4：坐标系与参数方程】22．在平面直角坐标系xOy中，直线l的参数方程（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：ρ=4cosθ．（1）把直线l的参数方程化为极坐标方程，把曲线C的极坐标方程化为普通方程；（2）求直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）．【选修4-5：不等式选讲】23．设函数f（x）=|2x﹣a|+|2x+1|（a＞0），g（x）=x+2．（1）当a=1时，求不等式f（x）≤g（x）的解集；（2）若f（x）≥g（x）恒成立，求实数a的取值范围．2015-2016学年安徽省马鞍山二中、安师大附中、淮北一中联考高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数（x∈R）在复平面内对应的点位于以原点O为圆心，以为半径的圆周上，则x的值为（）A．2 B．1+3i C．±2 D．【考点】复数代数形式的乘除运算；复数的代数表示法及其几何意义．【分析】利用复数代数形式的乘除运算化简，然后由复数所对应点到原点的距离为列式求得x的值．【解答】解：=，∵复数在复平面内对应的点位于以原点O为圆心，以为半径的圆周上，∴，解得：x=±2．故选：C．2．设x，y满足约束条件，则目标函数z=的取值范围为（）A．[﹣3，3] B．[﹣2，2] C．[﹣1，1] D．[﹣，]【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，进行求解即可．【解答】解：画出满足条件的平面区域，如图示：，目标函数z=几何意义为区域内的点与D （2，0）的斜率，过（﹣1，2）与（2，0）时斜率最小， 过（﹣1，﹣2）与（2，0）时斜率最大，∴Z 最小值==﹣，Z 最大值==，故选：D ．3．在等差数列{a n }中，a 1+a 2+a 3=3，a 28+a 29+a 30=165，则此数列前30项和等于（ ） A ．810 B ．840 C ．870 D ．900 【考点】等差数列的性质．【分析】在等差数列{a n }中，由a 1+a 2+a 3=3，a 28+a 29+a 30=165，知a 1+a 30=56，再由S 30=15（a 1+a 30），能求出此数列前30项和． 【解答】解：在等差数列{a n }中， ∵a 1+a 2+a 3=3，a 28+a 29+a 30=165， ∴3（a 1+a 30）=168， ∴a 1+a 30=56，∴此数列前30项和为S 30=15（a 1+a 30）=15×56=840． 故选：B ．4．已知M=，N=，由如右程序框图输出的S 为（ ）A．1 B．ln2 C．D．0【考点】微积分基本定理；选择结构．【分析】根据积分的定义，分别解出M和N，再判断M与N的大小，代入程序图进行求解；【解答】解：∵M====ln2，N===1，ln2＜1∴M＜N，由程序图可知求两个数的最小值，输出的是最小的一个数，∴S=ln2，故选B；5．若函数，且f（α）=﹣2，f（β）=0，|α﹣β|的最小值是，则f（x）的单调递增区间是（）A． B．C．D．【考点】正弦函数的单调性．【分析】由条件求得ω的值，可得函数的解析式，再根据正弦函数的单调性，求得f（x）的单调递增区间．【解答】解：由题意可得=•=，∴ω=1，f（x）=2sin（x+）．令2kπ﹣≤x+≤2kπ+，k∈z，求得2kπ﹣≤x≤2kπ+，故函数的增区间为2[kπ﹣，2kπ+]，k∈z，故选：D．6．定义在R上的函数f（x）满足f（x+6）=f（x）．当﹣3≤x＜﹣1时，f（x）=﹣（x+2）2，当﹣1≤x＜3时，f（x）=x．则f（1）+f（2）+…+fA．333 B．336 C．1678 D．2015【考点】函数的周期性；函数的值．【分析】由已知得到函数的周期为6，找到与2015函数值相等的（﹣3，3）的自变量，按照周期求值．【解答】解：由已知函数周期为6，并且2015=6×335+5，并且f（1）=1，f（2）=2，f（3）=f（﹣3+6）=f（﹣3）=﹣（﹣3+2）2=﹣1，f（4）=f（﹣2+6）=f（﹣2）=0，f（5）=f（﹣1+6）=f（﹣1）=﹣1，f（6）=f（0）=0，所以f（1）+f（2）+…+f（6）=1，所以f（1）+f（2）+…+f+f（2）+f（3）+f（4）+f（5）=335+1=336；故选B．7．已知0＜x＜，则﹣＜0是﹣x＞0成立的（）A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据三角函数的性质，将不等式进行等价转化，利用充分条件和必要条件的定义进行判断．【解答】解：当0＜x＜，0＜sinx＜1，则不等式﹣＜0等价为＜，即sinx＜1，即x•sin2x＜1，不等式﹣x＞0等价为＞x，即x•sinx＜1，∵0＜sinx＜1，∴若x•sinx＜1，则x•sin2x＜x•sinx＜1，即x•sin2x＜1成立．若xsin2x＜1，不能推出xsinx＜1成立，故充分性不成立．则﹣＜0是﹣x＞0成立的必要不充分条件．故选：C．8．，，若A∩B={（cosθ1，sinθ1），（cosθ2，sinθ2）}，则m的取值范围为（）A．[﹣2，2] B．（﹣2，2）C．D．【考点】交集及其运算．【分析】由题意得到直线y=x+m与圆x2+y2=1（x≠1）交于两点，根据圆心到直线的距离小于半径且+m≠0，即可得到答案．【解答】解：根据题意，直线y=x+m与圆x2+y2=1（x≠1）交于两点，∴＜1且+m≠0，∴﹣2＜m＜2且m≠，故选：D．9．若a＞0，，，，则x，y，z的大小顺序为（）A．x＞z＞y B．x＞y＞z C．z＞x＞y D．z＞y＞x【考点】三角函数中的恒等变换应用．【分析】令a=2，将x，y，z分别化简，比较大小，利用排除法选出答案．【解答】解：令a=2，则x=sin1+cos1，y=1，z=2sin21cos21=≤，∴y＞z，排除A，C，D．故选：B．10．下列命题中正确的个数是（）①过异面直线a，b外一点P有且只有一个平面与a，b都平行；②异面直线a，b在平面α内的射影相互垂直，则a⊥b；③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；④直线a，b分别在平面α，β内，且a⊥b，则α⊥β．A．0 B．1 C．2 D．3【考点】空间中直线与直线之间的位置关系．【分析】列举反例，即可得出结论．【解答】解：①P是异面直线a、b外一点，则过P有一个平面与a、b都平行；此命题不正确，当过点P与两条异面直线中的一条的平面与另一条直线平行时，此时找不到一个过P 的平面与两条异面直线都平行，不正确；②本命题用图形说明，如图：三棱锥P﹣ABC中，侧棱PB垂直于底面，PA，PC两线在底面上的投影垂直，而两线不垂直，不正确；③四边相等的四边形也可以是空间四边形，不正确；④直线a，b分别在平面α，β内，且a⊥b，则α、β不一定垂直，不正确．故选：A．11．三角形ABC中，A、B、C所对的边分别为a，b，c；若A=，则=（）A．a+b B．a+c C．b+c D．a+b+c【考点】余弦定理．【分析】由正弦定理可得：a=2RsinA代入已知式子，由三角函数恒等变换的应用化简即可得解．【解答】解：∵由正弦定理可得：a=2RsinA，∴a（cosC+sinC）=2RsinAcosC+2RsinAsinC=2RsinAcosC+3RsinC=2R（sinAcosC+sinC+sinC）=2R（sinAcosC+cosAsinC+sinC）=2R[sin（A+C）+sinC]=2R（sinB+sinC）=b+c．故选：C．12．已知f（x）=1+x﹣+﹣+…+；g（x）=1﹣x+﹣+﹣…﹣；设函数F（x）=[f（x+3）]•[g（x﹣4）]，且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，则b﹣a的最小值为（）A．8 B．9 C．10 D．11【考点】二分法求方程的近似解．【分析】利用导数分别求出函数f（x）、g（x）的零点所在的区间，然后要求F（x）=f（x+3）•g（x﹣4）的零点所在区间，即求f（x+3）的零点和g（x﹣4）的零点所在区间，根据图象平移即可求得结果【解答】解：∵f（0）=1＞0，f（﹣1）=（1﹣1）+（﹣﹣）+…+（﹣﹣）＜当x∈（﹣1，0）时，f′（x）=＞0，∴函数f（x）在区间（﹣1，0）上单调递增，故函数f（x）有唯一零点x∈（﹣1，0）；∵g（1）=（1﹣1）+（﹣）+…+（﹣）＞0，g（2）=（1﹣2）+（2﹣）+…+（﹣）＜0，当x∈（1，2）时g′（x）=﹣1+x﹣x2+…﹣x2014=﹣＜0∴函数g（x）在区间（1，2）上单调递减，故函数g（x）有唯一零点x∈（1，2）；∵F（x）=f（x+3）•g（x﹣4），且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，∴f（x+3）的零点在（﹣4，﹣3）内，g（x﹣4）的零点在（5，6）内，因此F（x）=f（x+3）•g（x﹣3）的零点均在区间[﹣4，6]内，∴b﹣a的最小值为10．故选C：．二、填空题：本大题共4小题，每小题5分13．已知||=1，||=2，与的夹角为60°，则+在方向上的投影为2．【考点】平面向量数量积的含义与物理意义；数量积表示两个向量的夹角．【分析】根据||=1，||=2，与的夹角为60°，算出|+|=且（+）•=2．再设+与的夹角为θ，结合数量积公式和向量投影的定义，算出|+|cosθ的值，即可得到向量+在方向上的投影值．【解答】解：∵||=1，||=2，与的夹角为60°，∴•=|×||×cos60°=1由此可得（+）2=||2+2•+||2=1+2+4=7∴|+|=．设+与的夹角为θ，则∵（+）•=||2+•=2∴cosθ==，可得向量+在方向上的投影为|+|cosθ=×=2故答案为：214．已知a＞b＞0，且a+b=2，则的最小值为．【考点】基本不等式．【分析】利用“乘1法”与基本不等式的性质即可得出．【解答】解：∵（a+3b）+（a﹣b）=2（a+b）=4，∴ [（a+3b）+（a﹣b）]=1，∴=（）[（a+3b）+（a﹣b）]= [2+++1]≥ [3+2]=，故答案为：．15．已知α，β为锐角，cos α=，则cos β=．【考点】两角和与差的余弦函数．【分析】由条件利用同角三角函数的基本关系求得sin α、cos （α+β）的值，再利用两角差的三角公式求得cos β=cos [（α+β）﹣α]的值．【解答】解：∵α，β为锐角，cos α=＜，∴α＞，sin α=．又 sin （α+β）=，∴α+β 为钝角，∴cos （α+β）=﹣=﹣，∴cos β=cos [（α+β）﹣α]=cos （α+β）cos α+sin （α+β）sin α=﹣•+•=，故答案为：．16．已知函数f （x ）=e ax ﹣x ﹣1，其中a ≠0．若对一切x ∈R ，f （x ）≥0恒成立，则a 的取值集合 {1} ．【考点】利用导数求闭区间上函数的最值．【分析】首先对a 考虑，说明a ＜0不成立，只有a ＞0，求出导数，并求出f （x ）的单调区间，从而求得最小值，令它不小于0，然后构造函数g （t ）=t ﹣tlnt ﹣1，运用导数求出它的最大值，运用两边夹法则即可求出a 的值．【解答】解：若a ＜0，则对一切x ＞0，∵e ax ＜1，∴f （x ）=e ax ﹣x ﹣1＜0，这与题设矛盾．又a ≠0，故a ＞0．而f ′（x ）=ae ax ﹣1，令f ′（x ）=0得x=ln ，当x ＜ln 时，f ′（x ）＜0，f （x ）单调递减；当x ＞ln 时，f ′（x ）＞0，f （x ）单调递增．∴当x=ln ，f （x ）取最小值f （ln ）=﹣ln ﹣1．于是对一切x ∈R ，f （x ）≥0恒成立，当且仅当﹣ln ﹣1≥0．①令g （t ）=t ﹣tlnt ﹣1，（t=）则g ′（t ）=﹣lnt ， 当0＜t ＜1时，g ′（t ）＞0，g （t ）单调递增； 当t ＞1时，g ′（t ）＜0，g （t ）单调递减， ∴当t=1时，g （t ）取最大值g （1）=1﹣1=0．∴当且仅当=1，即a=1时，①式等号成立．综上所述，a 的取值集合为{1}． 故答案为：{1}．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．已知各项均为正数的数列{a n }的前n 项和为S ，满足=2S n +n +4，且a 2﹣1，a 3，a 7恰为等比数列{b n }的前3项．（1）求数列{a n }，{b n }的通项公式；（2）令c n =﹣，求数列{c n }的前n 项和T n ．【考点】数列的求和；数列递推式．【分析】（1）由=2S n +n +4，得到2S n =﹣n ﹣4，当n ≥2时，，两式相减并化简，得数列{a n }为等差数列，再由题目中其他条件结合等差数列和等比数列的性质能计算出{a n }、{b n }的通项公式．（2）由c n =﹣==，利用分组求和法、错位相减法和裂项求和法能求出数列{c n }的前n 项和T n ．【解答】解：（1）∵各项均为正数的数列{a n }的前n 项和为S ，满足=2S n +n +4，∴2S n =﹣n ﹣4，①当n ≥2时，，②①﹣②，得：2a n =﹣1，∴，∵a n ＞0，∴a n +1=a n +1，∵a 2﹣1，a 3，a 7恰为等比数列{b n }的前3项，∴，即（a 1+2）2=（a 1+1﹣1）×（a 1+6），解得a 1=2，∴a n =a 1+（n ﹣1）d=2+（n ﹣1）×1=n +1． b 1=a 2﹣1=（2+1）﹣1=2， b 2=a 3=3+1=4，∴等比数列{b n }的公比q===2，∴b n ==2×2n ﹣1=2n ．（2）∵c n =﹣==，∴数列{c n }的前n 项和：T n =（+…+）﹣（）=（+…+）﹣（），设S n=+…+，③则=，④③﹣④，得==﹣=1﹣﹣．∴T n==．18．已知向量=（cosωx﹣sinωx，sinωx），=（﹣cosωx﹣sinωx，2cosωx），设函数f（x）=•+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）（1）求函数f（x）的最小正周期；（2）若y=f（x）的图象经过点（，0）求函数f（x）在区间[0，]上的取值范围．【考点】三角函数中的恒等变换应用；数量积的坐标表达式；正弦函数的定义域和值域．【分析】（1）先利用向量数量积运算性质，求函数f（x）的解析式，再利用二倍角公式和两角差的余弦公式将函数f（x）化为y=Asin（ωx+φ）+k型函数，最后利用函数的对称性和ω的范围，计算ω的值，从而得函数的最小正周期；（2）先将已知点的坐标代入函数解析式，求得λ的值，再求内层函数的值域，最后将内层函数看做整体，利用正弦函数的图象和性质即可求得函数f（x）的值域．【解答】解：（1）∵f（x）=•+λ=（cosωx﹣sinωx）×（﹣cosωx﹣sinωx）+sinωx×2cosωx+λ=﹣（cos2ωx﹣sin2ωx）+sin2ωx+λ=sin2ωx﹣cos2ωx+λ=2sin（2ωx﹣）+λ∵图象关于直线x=π对称，∴2πω﹣=+kπ，k∈z∴ω=+，又ω∈（，1）∴k=1时，ω=∴函数f（x）的最小正周期为=（2）∵f（）=0∴2sin（2××﹣）+λ=0∴λ=﹣∴f（x）=2sin（x﹣）﹣由x∈[0，]∴x﹣∈[﹣，]∴sin（x﹣）∈[﹣，1]∴2sin（x﹣）﹣=f（x）∈[﹣1﹣，2﹣]故函数f（x）在区间[0，]上的取值范围为[﹣1﹣，2﹣]19．在△ABC中，角A，B，C对应边分别是a，b，c，c=2，sin2A+sin2B﹣sin2C=sinAsinB．（1）若sinC+sin（B﹣A）=2sin2A，求△ABC面积；（2）求AB边上的中线长的取值范围．【考点】余弦定理；正弦定理．【分析】（1）已知等式利用正弦定理化简，再利用余弦定理表示出cosC，将得出关系式代入求出cosC的值，确定出C的度数，sinC+sin（B﹣A）=2sin2A化简后，根据cosA为0与cosA不为0两种情况，分别求出三角形ABC面积即可；（2）根据CD为AB边上的中线，得到=，两边平方并利用平面向量的数量积运算法则变形得到关系式，利用余弦定理列出关系式，将cosC与c的值代入得到关系式，代入计算即可确定出|CD|的范围．【解答】解：（1）由sin2A+sin2B﹣sin2C=sinAsinB，利用正弦定理化简得：a2+b2﹣c2=ab，∴cosC===，即C=，∵sinC+sin（B﹣A）=sin（B+A）+sin（B﹣A）=2sin2A，∴sinBcosA=2sinAcosA，=；当cosA=0，即A=，此时S△ABC=；当cosA≠0，得到sinB=2sinA，利用正弦定理得：b=2a，此时此时S△ABC（2）∵=，∴|CD|2==，∵cosC=，c=2，∴由余弦定理得：c 2=a 2+b 2﹣2abcosC ，即a 2+b 2﹣ab=4，∴|CD |2==＞1，且|CD |2=≤3，则|CD |的范围为（1，]．20．已知a 为常数，函数，（1）当a=0时，求函数f （x ）的最小值； （2）若f （x ）有两个极值点x 1，x 2（x 1＜x 2） ①求实数a 的取值范围；②求证：且x 1x 2＞1（其中e 为自然对数的底）【考点】利用导数求闭区间上函数的最值；利用导数研究函数的极值． 【分析】（1）把a=0代入函数解析式，求得导函数，由导函数的零点得到函数的单调性，由此求得函数的最小值；（2）①由f （x ）有两个极值点，可得导函数有两个不同的零点，进一步转化为有两个不同解，令φ（x ）=，利用导数求其最大值，再结合φ（）=0，可得a ∈（0，1），且x 1∈（）；②由①可得，1+lnx 1=ax 1，f （x 1）=，消去a 可得（x 1lnx 1﹣x 1），x 1∈，构造函数g （x ）=xlnx﹣x ，x ∈（），利用导数求得g （x ）的单调性，即可证得；由①可得lnx 1=ax 1﹣1，lnx 2=ax 2﹣1，联立两式可得=，令t=，构造函数，经过三次求导得答案．【解答】解：（1）当a=0时，f （x ）=xlnx ，f ′（x ）=1+lnx ，当x ∈（0，）时，f ′（x ）＜0，当x ∈（）时，f ′（x ）＞0，∴；（2）①f ′（x ）=1+lnx ﹣ax ，由于f （x ）有两个极值点，可得1+lnx ﹣ax=0有两个不同解，即有两个不同解，令φ（x）=，则φ′（x）=，φ′（1）=0，当x∈（0，1）时，φ′（x）＞0，当x∈（1，+∞）时，φ′（x）＜0，∴φ（x）max=φ（1）=1，且φ（）=0，由数形结合可得a∈（0，1），且x1∈（），②由①可得，1+lnx1=ax1，f（x1）=，消去a可得（x1lnx1﹣x1），x1∈，构造函数g（x）=xlnx﹣x，x∈（），g′（x）=lnx＜0，∴g（x）在（）上单调递减，则，再证x1x2＞1：由①可得lnx1=ax1﹣1，lnx2=ax2﹣1，将两式相加可得lnx1x2=a（x1+x2）﹣2，两式相减可得lnx1﹣lnx2=a（x1﹣x2），即，代入lnx1x2=a（x1+x2）﹣2，可得=，令t=，构造函数，h′（t）=，再令k（t）=t2﹣1﹣2tlnt，t∈（0，1），k′（t）=2（t﹣1﹣lnt），再令g（t）=t﹣1﹣lnt，g′（t）=1﹣，可得g（t）＞g（1）=0，进而k（t）单调递增，可得k（t）＜k（1）=0，∴h（t）单调递增，由洛必达法则，，∴h（t）＞0，lnx1x2＞0，则x1x2＞1．21．已知函数f（x）=e x（2x﹣1），g（x）=ax﹣a（a∈R）．（1）若y=g（x）为曲线y=f（x）的一条切线，求a的值；（2）已知a＜1，若存在唯一的整数x0，使得f（x0）＜g（x0），求a的取值范围．【考点】利用导数研究曲线上某点切线方程．【分析】（1）求出导数，设出切点（m，n），求得切线的斜率，由切线的方程，可得a=e m （2m+1），又n=am﹣a=e m（2m﹣1），解方程可得a的值；（2）函数f（x）=e x（2x﹣1），g（x）=kx﹣k，问题转化为存在唯一的整数x0使得f（x0）在直线y=kx﹣k的下方，求导数可得函数的极值，数形结合可得﹣k＞f（0）=﹣1且f（﹣1）=﹣3e﹣1≥﹣k﹣k，解关于k的不等式组可得．【解答】解：（1）f′（x）=e x（2x﹣1）+2e x=e x（2x+1），设切点为（m，n），由题意可得a=e m（2m+1），又n=am﹣a=e m（2m﹣1），解方程可得，a=1或4；（2）函数f（x）=e x（2x﹣1），g（x）=ax﹣a由题意知存在唯一的整数x0使得f（x0）在直线y=ax﹣a的下方，∵f′（x）=e x（2x﹣1）+2e x=e x（2x+1），∴当x＜﹣时，f′（x）＜0，当x＞﹣时，f′（x）＞0，∴当x=﹣时，f（x）取最小值﹣2，当x=0时，f（0）=﹣1，当x=1时，f（1）=e＞0，直线y=ax﹣a恒过定点（1，0）且斜率为a，故﹣a＞f（0）=﹣1且f（﹣1）=﹣3e﹣1≥﹣a﹣a，解得≤a＜1．请考生在22、23两题中任选一题作答【选修4-4：坐标系与参数方程】22．在平面直角坐标系xOy中，直线l的参数方程（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为：ρ=4cosθ．（1）把直线l的参数方程化为极坐标方程，把曲线C的极坐标方程化为普通方程；（2）求直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（1）直线l的参数方程（t为参数），消去参数t化为=0，把代入即可得出，由曲线C的极坐标方程为：ρ=4cosθ，变为ρ2=4ρcosθ，代入化为直角坐标方程．（2）联立，解出再化为极坐标（ρ≥0，0≤θ＜2π）为．【解答】解；（1）直线l的参数方程（t为参数），消去参数t化为=0，把代入可得：=0，由曲线C的极坐标方程为：ρ=4cosθ，变为ρ2=4ρcosθ，化为x2+y2﹣4x=0．（2）联立，解得或，∴直线l与曲线C交点的极坐标（ρ≥0，0≤θ＜2π）为，．【选修4-5：不等式选讲】23．设函数f（x）=|2x﹣a|+|2x+1|（a＞0），g（x）=x+2．（1）当a=1时，求不等式f（x）≤g（x）的解集；（2）若f（x）≥g（x）恒成立，求实数a的取值范围．【考点】绝对值不等式的解法；函数恒成立问题．【分析】（1）当a=1时，不等式等价于3个不等式组，求出每个不等式组的解集，再取并集，即得所求．（2）由题意可得，|2x﹣a|+|2x+1|﹣x﹣2≥0 恒成立．令h（x）=|2x﹣a|+|2x+1|﹣x﹣2，化简它的解析式，求得它的最小值，再令最小值大于或等于零，求得a的范围．【解答】解：（1）当a=1时，不等式f（x）≤g（x）即|2x﹣1|+|2x+1|≤x+2，等价于①，或②，或③．解①求得x无解，解②求得0≤x＜，解③求得≤x≤，综上，不等式的解集为{x|0≤x≤}．（2）由题意可得|2x﹣a|+|2x+1|≥x+2恒成立，转化为|2x﹣a|+|2x+1|﹣x﹣2≥0 恒成立．令h（x）=|2x﹣a|+|2x+1|﹣x﹣2=（a＞0），易得h（x）的最小值为﹣1，令﹣1≥0，求得a≥2．2016年9月29日。

马鞍山二中、安师大附中、淮北一中、铜陵一中2016届高三第一学期12月联考英语试题满分:150 考试时间：120分钟本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷第一部分听力（共两节，满分30分）第一节（共5个小题：每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从每题所给的A B C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the woman get from the man?A. A book.B. Some flowers.C. Some photos.2. How much was the TV set?A. $30.B. $60.C. $120.3. Who is going for lunch first?A. The man.B. The editor.C. The woman.4. What does the man mean?A. He forgot his office number.B. He will go to the language laboratory.C. He doesn't want to accept the job offer.5. What does the man think of the play?A. It was terrible.B. He liked it very much.C. The actors were enthusiastic.第二节(共15小题；每小题1. 5分，满分22.5分)听下面5段对话。

每段对话后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题给出5秒钟的作答时间。

每段对话读两遍。