
实验题目:人口增长问题与曲线拟合
数学系0901班1号某某某
1.实验问题
英国人口学家马尔萨斯(Malthus)根据百余年的人口统计资料,于1798年提出了著名的人口指数增长模型.这个模型的基本假设是:人口的增长率是常数,或者说,阿单位时间内人口的增长量与当时的人口成正比.
2.实验准备
Clear[ ]清空变量
DSolve[ ]求解微分方程
……
3.实验分析
3.1人口指数增长
如果将人口数量看作离散数据,设今年人口为x
0,k年后人口为x
k
,年增长率
为r,则有x
k =x
(1+r)k.
根据国家统计局的数据,1990年我国人口总数为11.3368亿,2000年人口
总数为12.6583亿,10年人口平均增长率由x
k =x
(1+r)k求得1.096%,以这个
增长率进行计算,可预测2010年、2050年全国人口总数分别为14.1161亿、21.831亿(程序1).80年代我国的人口平均增长率为1.48%,如果按这个增长率计算, 2010年、2050年我国人口总数将分别为15.209、27.373亿(程序1),
r0.01096;
12.65831r^10
12.65831r^50
r0.0148;
11.33681r^20
11.33681r^60
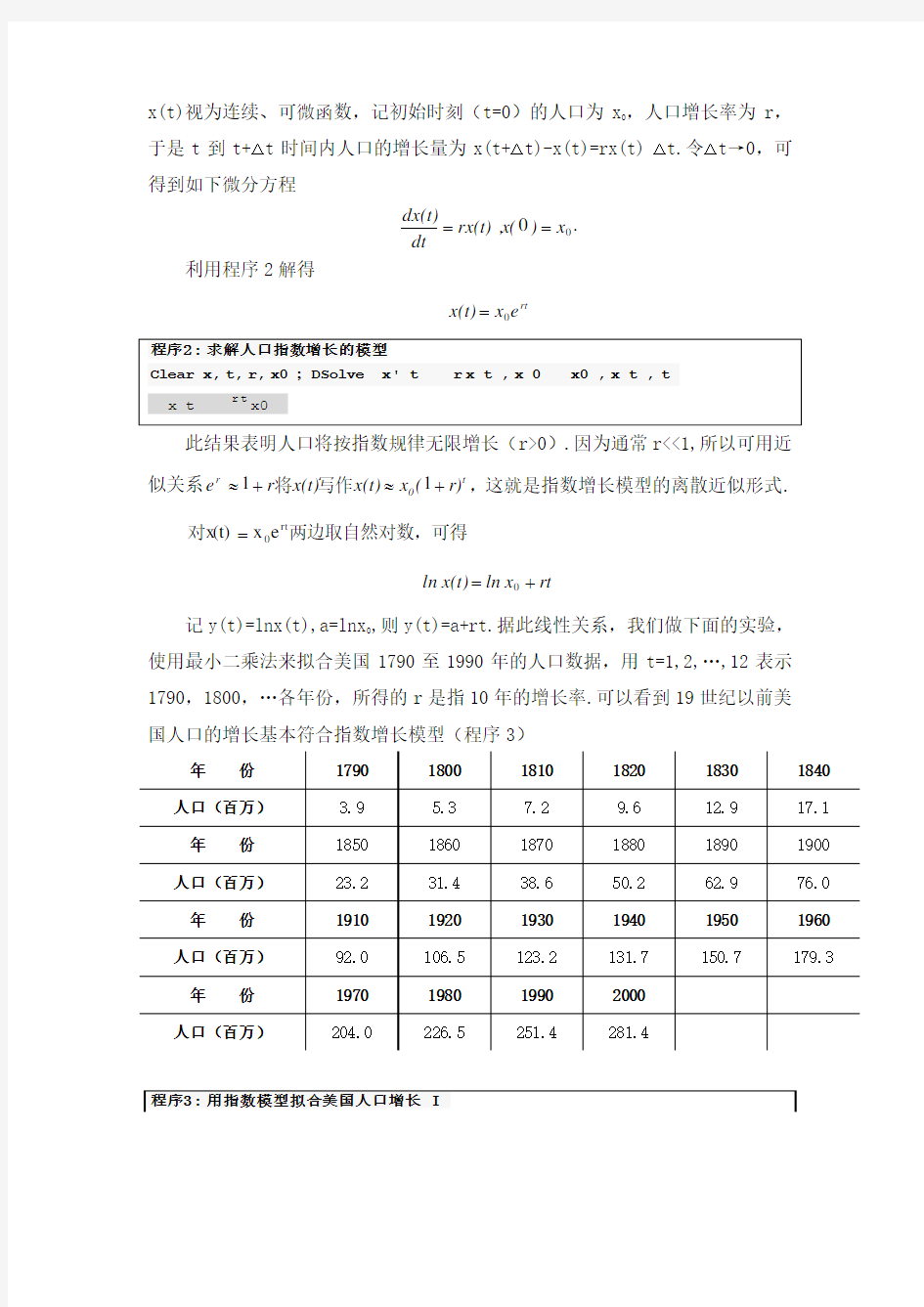
x(t)视为连续、可微函数,记初始时刻(t=0)的人口为x 0,人口增长率为r ,于是t 到t+△t 时间内人口的增长量为x(t+△t)-x(t)=rx(t) △t.令△t →0,可得到如下微分方程
.00x )x( ,rx(t)dt
dx(t)
== 利用程序2解得
rt e x x(t)0=
Clear x,t,r,x0;DSolve x't r x t ,x 0x0,x t ,t
x t
r t
x0
此结果表明人口将按指数规律无限增长(r>0).因为通常r<<1,所以可用近似关系t 0r r)(x x(t)x(t)r e +≈+≈11写作将,这就是指数增长模型的离散近似形式.
两边取自然对数,可得对rt 0e x x (t)=
rt x ln x(t) ln +=0
记y(t)=lnx(t),a=lnx 0,则y(t)=a+rt.据此线性关系,我们做下面的实验,使用最小二乘法来拟合美国1790至1990年的人口数据,用t=1,2,…,12表示1790,1800,…各年份,所得的r 是指10年的增长率.可以看到19世纪以前美国人口的增长基本符合指数增长模型(程序3)
程序3:用指数模型拟合美国人口增长I
Clear h,t,i;stm OpenRead"e:\shuju.txt";
For i1;h,i12,i,
AppendTo h,i,Log Read stm,Number
;
Fit h,1,t,t
1.158010.274324t
x0Exp 1.15801
x t_: 3.18359Exp0.274324t;
stm OpenRead"e:\shuju.txt";
For i1;h,i12,i,
AppendTo h,i,Read stm,Number
;
pic1ListPlot h,PlotStyle PointSize0.02,DisplayFunction Identity; pic2Plot x t,t,1,12,DisplayFunction Identity;
Show pic1,pic2,DisplayFunction$DisplayFunction
Graphics
程序4:用指数模型拟合美国人口增长II
x t_: 3.18359Exp0.274324t;
stm OpenRead"e:\shuju.txt";
For i1;h,i22,i,
AppendTo h,i,Read stm,Number
;
pic1ListPlot h,PlotStyle PointSize0.02,DisplayFunction Identity; pic2Plot x t,t,1,22,DisplayFunction Identity;
Show pic1,pic2,DisplayFunction$DisplayFunction
Graphics
从中可以看出,当用19世纪以后美国的人口统计资料与指数增长模型比较时,出现了相当大的差异.产生上述现象的主要原因是,随着人口的增加,自然资源、环境条件等因素对人口继续增长的阻滞作用越来越显著.如果当人口较少时,相对于资源而言,人口增长率还可以看作常数,当人口增加到一定数量后,增长率就会随着人口的继续增加而逐渐减少.许多国家人口增长的实际情况完全证实了这一点.为了使人口预报特别是长期预报更好地符合实际情况,必须修改指数增长模型关于人口增长率是常数的假设. 3.2 人口阻滞增长
将增长率r 表示为人口x(t)的函数r(x),根据前面的分析,r(x)应是x 的减函数.此时有
00x )x( r(x)x,dt
dx
== 一个最简单的假定是:设r(x)为x 的线性函数r(x)=r-sx,这里r 相当于x=0时的增长率,称为固有增长率.
设自然资源和环境条件所能容纳的最大人口数量为x m ,称为最大人口容量.当x=x m 时增长率应为零,即r(x m )=0,由此确定出s=r/x m .于是
),x x
-r(1r(x)m
= .010x )x( ),x x -rx(dt dx m
==
上式中r 、x m 是根据人口统计数据或经验确定的常数,因子(1-x/x m )体现了资源和环境对人口增长的阻滞作用,求解上述微分方程得(程序5)
rt
-0
m
m
)e 1-x x (1x x(t)+=
Clear x,t,xm,x0;DSolve
x't
r x t
1
x t
xm ,x 0
x0,x t ,t
x t
r t
x0xm x0
r t
x0
xm
上述人口增长模型称为阻滞增长模型,容易知道人口增长率dx/dt 是关于x 的一条开口向下的抛物线,它表明人口增长率随着人口数量x 的增加而先增后减,在x= x m /2处达到最大值.x 是关于t 的一条S 曲线,拐点在x= x m /2处,当t →∞时x →x m ,如下图(为了编程绘图,取x 0=0.1,x m =1,r=0.8,这不会影响x00.1;xm 1;r
0.8;
dx x_:r x 1x xm ;
x t_:
r t
x0xm
x0
r t x0xm ;
Plot dx x ,x,0,1;
Plot x t ,t,0,10;
前面给出的初始微分方程为:
00x )x( r(x)x,dt
dx
== ,其中r(x)=r-sx 将r(x)代入,得dx/dt=(r-sx)x,两端同时除以x 得
m
x r s sx ,-r /x dt dx == 依据此关系,我们做下面的实验(程序7),使用最小二乘法来拟合美国1800年至1990年的人口数据,要先将数据由(t ,x )转换成(dx/dt/x,x ),其中年份t 依然用自然数代替,t 取值为0,1,…,1.实验中用中心差商近似代替微商,即
,hx (a)
2h)
-x (a -h)x (a )/x (a)|dt dx ( ,h 2h)-x (a -h)x (a |dt dx a t a t +=+=== 其中h 取值为1,通过实验拟合可以求得r 、s,再计算x m =r/s, x 0可根据已知数据得到,从而确定了方程x(t).接下来作图观察实验数据与实际数据拟合的For i
0;k ,i 11,i
,AppendTo k,i,h i
10,2;
;
For i
2;l
,i
11,i ,AppendTo l,k
i,2
,k
i
1,2
k
i 1,2
2k
i,2
;
;
Fit l,1,x ,x
0.208360.00047403x
x050.2;
r0.20836;
s0.00047403;
xm r s;
x t
pic1ListPlot k,PlotStyle PointSize0.02,DisplayFunction Identity; pic2Plot x t,t,0,11,DisplayFunction Identity;
Show pic1,pic2,DisplayFunction$DisplayFunction;
22065.40.20836t
389.3550.20.20836t
x12
4.结论
实验表明:20世纪中叶以后,实验数据与实际数据拟合得很好,实验最后,用阻滞模型预测2000年的美国人口数为268.6百万,这与实际人口数相差无几.
教师指导实验7 实验名称:随机变量的概率分布 一、问题:求二项分布、几何分布、正态分布在给定区间上的概率。 二、实验目的: 学会使用Mathematica求二项分布、几何分布、正态分布在给定区间上的概率及期望和方差。 三、预备知识:本实验所用的Mathematica命令提示 1、BinomialDistribution[n,p] 二项分布; GeometricDistribution[p] 几何分布; NormalDistribution[μ,σ] 正态分布; 2、Domain[dist] 求分布dist的定义域; PDF[dist,x] 求点x处的分布dist的密度值; CDF[dist,x] 求点x处的分布dist的函数值; Mean[dist] 求分布dist的期望;Quantile[dist,x] 求x,使CDF[dist,x]=q Variance[dist] 求分布dist的方差;StandardVariance[dist] 求分布dist的标准差; 四、实验的内容和要求: 1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差; 2、对以上数据绘制样本频率分布直方图; 3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。 五、操作提示 1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差; In[1]:=< Mathematica函数大全--运算符及特殊符号一、运算符及特殊符号 Line1;执行Line,不显示结果 Line1,line2顺次执行Line1,2,并显示结果 ?name关于系统变量name的信息 ??name关于系统变量name的全部信息 !command执行Dos命令 n! N的阶乘 !!filename显示文件内容 a-b减 a*b或a b 乘 a/b除 a^b 乘方 base^^num以base为进位的数 lhs&&rhs且 lhs||rhs或 !lha非 ++,-- 自加1,自减1 +=,-=,*=,/= 同C语言 >,<,>=,<=,==,!=逻辑判断(同c) lhs=rhs立即赋值 lhs:=rhs建立动态赋值 lhs:>rhs建立替换规则 expr//funname相当于filename[expr] expr/.rule将规则rule应用于expr expr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式(形式变量)param__名为param的任意多个任意表达式(形式变量) 二、系统常数 Pi 3.1415....的无限精度数值 E 2.17828...的无限精度数值 Catalan 0.915966..卡塔兰常数 EulerGamma 0.5772....高斯常数 GoldenRatio 1.61803...黄金分割数 Degree Pi/180角度弧度换算 I复数单位 Infinity无穷大 50Mathematica线性代数运算命令与例题 第五章 线性代数运算命令与例题 线性代数中常用的工具是矩阵(向量)和行列式。用这些工具可以表示工程技术,经济工作中一些需要用若干个数量从整体上反映其数量关系的问题。用这些工具可以简明凝练而准确地把所要研究的问题描述出来,以提高研究的效率。在线性代数课程中我们看到了用这些工具研究齐次和非齐次线性方程组解的理论和解的结构,矩阵的对角化,二次型化标准形等问题的有力,便捷. 5.1向量与矩阵的定义 数学上矩阵是这样定义的: 由n m ?个数排成m 行n 列的数表 mn m m n n a a a a a a a a a Λ M M M Λ Λ21 2222111211 称为m 行n 列矩阵,特别,当m=1时就是线性代数中的向量。 记作: ????? ?? ?????=mn m m n n a a a a a a a a a A ΛM M M ΛΛ2122221 11211 两个n m ?矩阵称为同型矩阵。 线性代数中的运算对象是向量和矩阵,因此首先介绍向量和矩阵的输入。 5.1.1输入一个矩阵 命令形式1:Table[f[i,j],{i ,m},{j ,n}] 功能: 输入n m ?矩阵,其中f 是关于i 和j 的函数,给出[i , j]项的值. 命令形式2:直接用表的形式来输入 功能:用于矩阵元素表达式规律不易找到的矩阵的输入。 注意: 1.Mathematica 是采用一个二重表的形式来表示矩阵的,即用 {{…},{…},…,{…}} 其中表中的每个表元素都是等长的一维表,第一 个表元素是矩阵的第一行,第二个表元素是矩阵的第二行,一般,第n 个表元素是矩阵的第n 行。要看通常的矩阵形式可以用命令: MatrixForm[%] 2. 对应上述命令形式,输入一个向量的命令为 Table[f[j],{j,n}]或直接输入一个一维表{a1,a2,…,an},这里a1,a2,…,an 是数或字母。 例题 例 1.输入矩阵A=???? ??????---41381639121458561203 12、向量 b={1,4,7,-3}。 解:Mathematica 命令 In[1]:= a={{12,-3,0,2,1},{56,-8,-45,21,91},{3,6,81,13,4}} Out[1]:= {{12,-3,0,2,1},{56,-8,-45,21,91},{3,6,81,13,4}} In[2]:=b={1, 4, 7, -3} Out[2]:= {1, 4, 7, -3} Mathematica的内部常数 Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率π E (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数e I (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位i Infinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞ Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度 Mathematica的常用内部数学函数 指数函数Exp[x]以e为底数 对数函数Log[x]自然对数,即以e为底数的对数 Log[a,x]以a为底数的x的对数 开方函数Sqrt[x]表示x的算术平方根 绝对值函数Abs[x]表示x的绝对值 三角函数 (自变量的单位为弧度)Sin[x]正弦函数 Cos[x]余弦函数 Tan[x]正切函数 Cot[x]余切函数 Sec[x]正割函数 Csc[x]余割函数 反三角函数ArcSin[x]反正弦函数 ArcCos[x]反余弦函数 ArcTan[x]反正切函数 ArcCot[x]反余切函数 ArcSec[x]反正割函数 ArcCsc[x]反余割函数 双曲函数Sinh[x]双曲正弦函数 Cosh[x]双曲余弦函数 Tanh[x]双曲正切函数 Coth[x]双曲余切函数 Sech[x]双曲正割函数 Csch[x]双曲余割函数 反双曲函数ArcSinh[x]反双曲正弦函数 ArcCosh[x]反双曲余弦函数 ArcTanh[x]反双曲正切函数 ArcCoth[x]反双曲余切函数 ArcSech[x]反双曲正割函数 ArcCsch[x]反双曲余割函数 求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度 数论函数GCD[a,b,c,...]最大公约数函数 LCM[a,b,c,...]最小公倍数函数 高等数学实验报告 实验一 一、实验题目 1:作出各种标准二次曲面的图形 ParametricPlot3D Sin u Sin v,Sin u Cos v,Cos u ,u,0,Pi ,v,0,2Pi,P Graphics3D ParametricPlot3D u Sin v,u Cos v,u^2,u,0,2,v,0,2Pi,PlotPoints30 Graphics3D ParametricPlot3D u,v,u^2v^2,u,2,2,v,2,2,PlotPoints30 Graphics3D ParametricPlot3D Sec u Sin v,Sec u Cos v,Tan u,u,Pi4,Pi4,v,0,2 Graphics3D t1ParametricPlot3D u^21Sin v,u^21Cos v,u,u,1,5,v,0,2Pi t2ParametricPlot3D u^21Sin v,u^21Cos v,u,u,5,1,v,0,2 show t1,t2 Graphics3D Graphics3D show Graphics3D,Graphics3D ParametricPlot3D u Cos v,u Sin v,u,u,6,6,v,0,2Pi,PlotPoints60 Graphics3D 2:作出曲面所围的图形 t1ParametricPlot3D Sin u Sin v,Sin u Cos v,Cos u, u,Pi2,pi2,v,0,2Pi,PlotPoints60 t2ParametricPlot3D0.5Cos u12,0.5Sin u, u,0,2Pi,v,0,2Pi,PlotPoints60 t3Plot3D0,PlotPoints60 show t1,t2,t3 Mathematica函数大全一、运算符及特殊符号 Line1; 执行Line,不显示结果 Line1,line2 顺次执行Line1,2,并显示结果 ?name 关于系统变量name的信息 ??name 关于系统变量name的全部信息 !command 执行Dos命令 n! N的阶乘 !!filename 显示文件内容 < >,<,>=,<=,==,!= 逻辑判断(同c) lhs=rhs 立即赋值 lhs:=rhs 建立动态赋值 lhs:>rhs 建立替换规则 lhs->rhs 建立替换规则 expr//funname 相当于filename[expr] expr/.rule 将规则rule应用于expr expr//.rule 将规则rule不断应用于expr知道不变为止 param_ 名为param的一个任意表达式(形式变量) param__ 名为param的任意多个任意表达式(形式变量) 二、系统常数 Pi 3.1415....的无限精度数值 E 2.17828...的无限精度数值 Catalan 0.915966..卡塔兰常数 EulerGamma 0.5772....高斯常数 GoldenRatio 1.61803...黄金分割数 Degree Pi/180角度弧度换算 I 复数单位 Infinity 无穷大 -Infinity 负无穷大 ComplexInfinity 复无穷大 Indeterminate 不定式 三、代数计算 Expand[expr] 展开表达式 Factor[expr] 展开表达式 Simplify[expr] 化简表达式 FullSimplify[expr] 将特殊函数等也进行化简 PowerExpand[expr] 展开所有的幂次形式 ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开 FunctionExpand[expr] 化简expr中的特殊函数 Collect[expr, x] 合并同次项 Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项 Together[expr] 通分 Apart[expr] 部分分式展开 Apart[expr, var] 对var的部分分式展开 Cancel[expr] 约分 ExpandAll[expr] 展开表达式 ExpandAll[expr, patt] 展开表达式 FactorTerms[poly] 提出共有的数字因子 FactorTerms[poly, x] 提出与x无关的数字因子 FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子 Coefficient[expr, form] 多项式expr中form的系数 图3.3里的Mathematica程序(版本8.0) 在Mathematica8.0的命令窗口输入如下命令:Cal[n_,i_]=2i*Binomial[n,i]; Print[ScientificForm[Cal[500,8]*1.0,4]]; Print[ScientificForm[Cal[500,12]*1.0,4]]; Print[ScientificForm[Cal[500,16]*1.0,4]]; Print[ScientificForm[Cal[500,24]*1.0,4]]; Print[ScientificForm[Cal[720,8]*1.0,4]]; Print[ScientificForm[Cal[720,12]*1.0,4]]; Print[ScientificForm[Cal[720,16]*1.0,4]]; Print[ScientificForm[Cal[720,24]*1.0,4]]; 按Shift+Enter组合键,运行可得: 2.344×1019 1.828×1027 3.75×1034 9.199×1047 4.41×1020 1.514×1029 1.381×1037 6.913×1051 图4.3.2.4.1里的Mathematica程序(版本8.0) 在Mathematica8.0的命令窗口输入如下命令:Cal[m_,n_]=Binomial[m,n]; Fun1[B_,m_,n_,ρ_]=((Cal[m,ρ]*Cal[B-m,n-ρ])/Cal[B,n]); X1=i 826Fun1104,26,26,i Cal i,80.267810.267i 8 ; X2=i 1226Fun1104,26,26,i Cal i,120.2671210.267i 12; X3=i 1626Fun1104,26,26,i Cal i,160.2671610.267i 16; X4=i 2426Fun1104,26,26,i Cal i,240.2672410.267i 24; Y1=i 846Fun1248,46,46,i Cal i,80.267810.267i 8; Y2=i 1246Fun1248,46,46,i Cal i,120.2671210.267i 12; Y3=i 1646Fun1248,46,46,i Cal i,160.2671610.267i 16; Y4=i 2446Fun1248,46,46,i Cal i,240.2672410.267i 24; Print[X1 "\n",X2 "\n",X3 "\n",X4 "\n",Y1 "\n",Y2 "\n",Y3 "\n",Y4 "\n"]; 按Shift+Enter 组合键,运行可得: 0.0000951929 3.92256×10-9 5.19076×10-15 7.7419×10-33 0.00104287 5.9339×10-7 3.76588×10-11 3.96973×10-22 数学实验报告 实 验 一 数学与统计学院 信息与计算科学(1)班 郝玉霞 201171020107 数学实验一 一、实验名:微积分基础 二、实验目的:学习使用Mathematica的一些基本功能来验证或观察得出微积分学的几个基本理论。 三、实验环境:学校机房,工具:计算机,软件:Mathematica。 四、实验的基本理论和方法:利用Mathematica作图来验证高中数学知识与大学数学容。 五、实验的容和步骤及结果 容一、验证定积分 dt t s x ?= 1 1 与自然对数 x b ln= 是相等的。 步骤1、作积分 dt t s x ?= 1 1 的图象; 语句:S[x_]:=NIntegrate[1/t,{t,1,x}] Plot[S[x],{x,0.1,10}] 实验结果如下: 图1 dt t s x ?= 1 1 的图象 步骤2、作自然对数 x b ln= 的图象 语句:Plot[Log[x],{x,0.1,10}] 实验结果如下: 2 1 图2 x b ln= 的图象 步骤3、在同一坐标系下作以上两函数的图象 语句:Plot[{Log[x],S[x]},{x,0.1,10}] 实验结果如下: 2 1 图3 dt t s x ?= 1 1 和 x b ln= 的图象 容二、观察级数与无穷乘积的一些基本规律。 (1)在同一坐标系里作出函数和它的Taylor展开式的前几项构成的多项式函数,,的图象,观察这些多项式函数的图象向的图像逼近的情况。 语句1: s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}] Plot[{Sin[x],s[x,2]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下: 642 4 2 图4和它的二阶Taylor展开式的图象 【MATHEMATICA实验报告】 【实验目的】 1.掌握Mathematica软件的启动和退出,以及Mathematica帮助系统。 2.熟悉Mathemaic的计算其功能以及常用的数字函数。 3.掌握变量的定义,变量的操作。 4.掌握函数的定义以及运算。 【实验内容】 1.求下列积分 (1) (4sin()3cos())/(sin()2cos()) x x x x dx ++ ? 输入: y=(4 Sin[x]+3 Cos[x])/(Sin[x]+2Cos[x]); Integrate[y,x] 输出: 2 x-Log[2 Cos[x]+Sin[x]] (2) /2 (cos())^5sin(2) x x dx π ? 输入: y=Cos[x]^5 Sin[2 x] Integrate[y,{x,0,Pi/2}] 输出: Cos x5Sin2x 2 7 (3)1 /(^21)^(3/2) dx x x -+ ? 输入: y=1/(x^2-x+1)^(3/2); Integrate[y,{x,0,1}] 输出: 4 3 2.求积分 1 (1/2)*^(^2/2) e x dx π -∞ - ? 输入:y=E^(-x^2/2)/Sqrt[2*Pi]; NIntegrate[y,{x,Infinity,1}] 输出: -0.158655 3.求y=e^(x^2)在x=0的9阶泰勒公式。 输入: Series[Exp[x^2],{x,0,9}] 输出: 1x 2x 4 2x 66x 824O x 10 4.作出以下参数方程所描述的图形。 (1) 4cos {3sin x t y t ==,(0≤t ≤2π) 输入: ParametricPlot[{4 Cos[t],3 Sin[t]},{t,0,2Pi}] 输出: -4-2 24-3-2 -1 1 2 3 (2)3(cos )^3 {3(sin )^3x t y t -= 输入: ParametricPlot[{3 Cos[t]^3,3 Sin[t]^3},{t,0,2 Pi}] 输出: -3-2-1 123-3-2 -1 12 3 附录B :Mathematica 的基本应用 1. 什么是Mathematica Mathematica 是美国Wolfram Research 公司开发的通用科学计算软件,主要用途是科学研究与工程技术中的计算,这里介绍的是第6版(2008年更新为第7版)。由于它的功能十分强大,使用非常简便,现在已成为大学师生进行教学和科研的有力工具。它的主要特点有: 1)既可以进行程序运行,又可以进行交互式运行。一句简单的Mathematic 命令常常可以完成普通的c 语言几十甚至几百个语句的工作。例如解方程:x 4 + x 3 + 3x -5 = 0只要运行下面的命令: Solve[x^4+x^3+3 x-5 0,x] 。 2) 既可以进行任意高精度的数值计算,又可以进行各种复杂的符号演算,如函数的微分、积分、幂级数展开、矩阵求逆等等。它使许多以前只能靠纸和笔解决的推理工作可以用计算机处理。例如求不定积分:? x 4 e -2x dx 只要运行下面的命令: Integrate[x^4*Exp[2 x],x]。 3) 既可以进行抽象计算,又可以用图形、动画和声音等形式来具体表现,使人能够直观地把握住研究对象的特性。例如绘制函数图形:y = e -x /2 cos x , x ∈ [0, π],只要运行下面的命令: Plot[Exp[x/2]*Cos[x],{x,0,Pi}]。 4) Mathematica 把各种功能有机地结合在一个集成环境里,可以根据需要做不同的操作,给使用者带来极大的方便。 2. Mathematica 的基本功能 2.1 基本运算及其对象 Mathematica 的基本数值运算有加法、减法、乘法、除法和乘(开)方,分别用运算符“+”、“-”、“*”、“/”和“^”来表示(在不引起误解的情况下,乘号可以省略或用空格代替),例 如2.4*3^2 -(5/(6+3))^(1/3)表示3236534.2)(+÷-?。小括号“(”和“)”作为表示运算优先顺 序的符号,用于组合运算;中括号用于命令和函数,大括号用于集合和列表。 Mathematica 的关系运算符有:>、<、>=、<=、!=、== 等,它们的意义与通常的数学语言相同,要注意“!=”表示不等于,双等号“==”表示等于。而单等号“=”和冒号等号“:=”表示定义或赋值,不表示相等。逻辑运算符主要有:!、&&、||,它们的意义与c 语言中相同,分别是“非”、“与”、“或”。 Mathematica 的基本数值运算对象有常数、变数和函数,包含整数,有理数、实数和复数等数值类型。为了方便,Mathematica 预先用符号表示了一些重要常数,如Pi 表示圆周率π,E 表示自然对数的底e = 2.17828…,I 表示虚单位i ,Infinity 表示无穷大∞等。比如说,E^(2*Pi*I)表示i e π2。 Mathematica 还预先定义了大量数学函数以供调用,调用格式为“函数名[自变量]”,预定义的函数名用大写字母开始的标识符表示,常用的有 徐州工程学院数理学院数学应用软件实验报告 课程(实验序号)数学应用软件实验 1 实验地点、日期数学建模机房2011 年 2 月23 日主要仪器设备计算机 使用的软件名称Mathematica 实验类型演示性实验 验证性实验 综合性实验√设计性实验 研究性实验 班级:姓名:孙娅学号:20090402223 一、实验题目名称:函数】变量和表达式 二、实验目的: 理解变量和算式、内核与前端处理器构成的人机对话系统,了解计算的精度问题个Mathematica使用中的几个问题。熟练掌握数的表示和计算、常用数学函数,会绘制简单函数的图形。通过上机初步了解数学应用软件,Mathematica的各种界面。 三、实验内容: 练习题1 1.计算下列各式的数值: (1) Log[2,10] Log[10]/Log[2] (2) Sqrt[Pi^2+1] 1 2 (3) Log[10,3264] Log[3264]/Log[10] (4) E^E ??/2 (5) Cos[135^0] Cos[1] (6) Sin[Pi^2/2] Sin[π2/2] (7) ArcSin[1/2] π/6 (8) 200! 7886578673647905035523632139321850622951359776871732632947425332443594499634033429203042 8401198462390417721213891963883025764279024263710506192662495282993111346285727076331723 7396988943922445621451664240254033291864131227428294853277524242407573903240321257405579 姓名 ### 学院 ###### 班级 ######### 学号 ######### 实验题目 最佳分数值逼近 评分 实验目的: 1、用“连分数展开”的方法计算圆周率π的近似值; 2、通过实验来体会“连分数展开”的方法与其他方法的区别,比较各种方法的优劣; 3、尝试用“连分数展开”的方法对其他的数进行展开。 实验环境: 学校机房,Mathematica4.0软件 实验基本理论和方法: 1、Mathematica 中常用的展开数与多项式的函数的使用; 2、计算圆周率π“连分数展开”方法,并且利用特定的函数来展开其他数。 实验内容和步骤: (一)多项式的展开与化简 多项式是表达式的一种特殊的形式,所以多项式的运算与表达式的运算基本一样,表达式中的各种输出形式也可用于多项式的输出。Mathematica 提供一组按不同形式表示代数式的函数。如: 1、 对12 x 1-进行分解,使用的函数为Factor : 2、 展开多项式 7 x+2()与5 x+y+7(),使用的函数为Expand: 3、 化简(1)^4(2)^(3)x x x +++与(1)^3(2)^4(3)^(1)x x x x +++-,使用的函数为 Pimplify: 4、 连个多项式相除,总能写成一个多项式和一个有理式相加, Mathematic 中提供两个 函数PolynomialQuotient 和PolynomialRemainder 分别返回商式和余式: (二)π的连分数展开 π的求解方法之前我们已经有许多种,但都比较繁琐而且误差较大,如何找到误差较小的π的近似值求解方法,我们在所得整数3的基础上进行分析,有了整数3,则 π=3+1x ,其中10.141592653579...x =是3的误差,101x <<。只要能找到1x 的最佳分数逼近值,再加3就得到π的最佳分数近似值。从而我们使用一种方法“连分数展开“,其原理是: 为了寻找与1x 接近的分数,先找与11 1 7.062513305931...A x = =接近的整数,显然 是7.于是111223377 A π=+ ≈+=,这是祖冲之的效率。 在此基础上,我们可以再用上述方法,要找到比 22 7 误差更小的分数近似值,只需要找到比整数7更接近1A 的分数来作为1A 的近似值。由于127A x =+,其中 200.062513305931...1x <=<。先找22 1 15.996594406685...A x = =的最佳整数近似值,显然是16.于是1211113771616A A =+ ≈+=,从而1 2 111355 3331 1113 7716 A A π=+=+≈+ = + +,这就得到祖冲之的密度。 如果还要进一步提高精确度,就应当在考虑2A 的整数近似值16的误差 32160.003405593314...x A =-=,取33 1 293.6345910144...A x = =的整数近似值294,则可 表达式: Plot[4 x - 9, {x, 0, 9}] f[x_] = x^3 Plot[f[x], {x, 0, 9}] a = Plot[4 x - 9, {x, 0, 9}] b = Plot[x^3, {x, 0, 3}] 两图画在一个坐标系 Show[a, b] a = Plot[4 x - 9, {x, 0, 9}] b = Plot[x^3, {x, 0, 3}] 两图画在一起(一排) c = GraphicsArray[{a, b}] Show[c] a = Plot[4 x - 9, {x, 0, 9}] b = Plot[x^3, {x, 0, 3}] c = GraphicsArray[{a}, {b}] 两图画在一起(两排) Show[c] 二维画图: Automatic 默认值 DisplayFunction -> Identity 不出现图 DisplayFunction -> $DisplayFunction 出现图 PlotRange -> All 画出所有点,指定区域点 PlotStyle -> {RGBColor[1, 0, 0]} 图像颜色 PlotStyle -> {Dashing[{0.01}]} 图像成虚线 PlotStyle -> {Thickness[0.01]} 图像粗细 AxesLabel -> {"x/t", "y/cm"} 坐标标签 PlotLabel -> {"s-t"} 图像标签 Frame -> True 图像边框 Axes -> {True, True} 坐标轴的显示 AxesOrigin -> {0, -5} 设置坐标原点 GridLines -> {{-π, -π/2, 0, π/2, π}, {-1,-0.5,0, 0.5, 1}} 给坐标轴分网格 TextStyle -> {FontSize -> 30} 坐标字体大小AspectRatio -> Automatic 坐标比例一致 Ticks -> {{0, 1, 2, 3}, {0,10,20}} 在坐标轴上显示特定点ParametricPlot[x(t),y(t)},{t,0,6,}] 画参数方程 【Mathematica 简介】 Mathematica 软件是由沃尔夫勒姆研究公司(Wolfram Research Inc.)研发的。Mathematica 版发布于1988年6月23日。发布之后,在科学、技术、媒体等领域引起了一片轰动,被认为是一个革命性的进步。几个月后,Mathematica 就在世界各地拥有了成千上万的用户。今天,Mathematica 已经在世界各地拥有了数以百万计的忠实用户。 Mathematica 已经被工业和教育领域被广泛地采用。实际上,Mathematica 负责将高级的数学和计算引入了传统上非技术的领域,极大的增加了科技软件的市场。一个包含应用、咨询、书籍、和课程软件的行业支持着国际化的 Mathematica 用户群,这个行业还在不断地膨胀。随着沃尔夫勒姆研究公司不断地扩大和 Mathematica 的使用被不断地扩展到不同的领域,将会看到 Mathematica 在全世界范围内对未来产品、重要研究发现、和教学的巨大影响。 数学软件是现在科研工作者的必备的工具,个人比较喜欢用Mathematica,因为它是最接近数学语言的。Mathematica 在15日发布,其最显著的变化是允许自由形式的英文输入,而不再需要严格按照Mathematica语法,这类似于Wolfram|Alpha搜索引擎。Mathematica 8允许用户按照自己习惯的思考过程输入方程式或问题,最令人激动的部分是软件不是逐行执行命令,而是能理解上下文背景。 1. Enter your queries in plain English using new free-form linguistic input 2. Access more than 10 trillion sets of curated, up-to-date, and ready-to-use data 3. Import all your data using a wider array of import/export formats 4. Use the broadest statistics and data visualization capabilities on the market 5. Choose from a full suite of engineering tools, such as wavelets and control systems 6. Use more powerful image processing and analysis capabilities 7. Create interactive tools for rapid exploration of your ideas 8. Develop faster and more powerful applications Wolfram Research 的 CEO 和创立者斯蒂芬·沃尔夫勒姆表示:“传统上,让计算机执行任务必须使用计算机语言或者使用点击式界面:前者要求用户掌握它的语法;而后者则限制了可访问函数的范围。”“自由格式语言学能够理解人类的语言,并将其转化为具有特定语法结构的语言。这是产品适用性上的一个突破。 Mathematica 8 是这种创新思想下的第一个产品,但是它已经能够大幅度提高用户的工作效率。” Mathematica简明教程 第1章Mathematica概述 运行和启动:介绍如何启动Mathematica软件,如何输入并运行命令 第8章Mathematica中的常用函数8.1 运算符及特殊符号 Linel 执行Line,不显示结果 Linel,line2 顺次执行Line1,Line2,并显示结果 ?name 关于系统变量name的信息 ??name 关于系统变量name的全部信息 !command 执行Dos命令 N! N的阶乘 !!filename 显示文件内容 < -Infinity 负无穷大 Complexlnfinity 复无穷大 Indeterminate 不定式 8.3 代数计算 Expand[expr] 展开表达式 Factor[expr] 展开表达式 Simplify[expr] 化简表达式 FullSimplify[expr] 将特殊函数也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2…}] 按复数实部虚部展开FunctionExpand[expr] 化简表达式中的特殊函数 Collect[expr,x] 合并同次项 Collect[expr,{x1,x2,…}] 合并x1,x2,...的同次项 Together[expr] 通分 Apart[expr] 部分分式展开 Apart[expr,var] 对var的部分分式展开 Cancel[expr] 约分 ExpandAll[expr] 展开表达式 ExpandAll[expr,patt] 展开表达式 FactorTermsrpoly] 提出共有的数字因子 FactorTerms[poly,x] 提出与x无关的数字因子 FactorTerms[poly,(x1,x2…)] 提出与xi无关的数字因子 Coefficient[expr,form] 多项式expr中form的系数 Coefficient[expr,form,n] 多项式expr中form^n的系数 Exponent[expr,form] 表达式expr中form的最高指数 Numerator[expr] 表达式expr的分子 Denominator[expr] 表达式expr的分母 ExpandNumerator[expr] 展开expr的分子部分 8.4 解方程 Solve[eqns,vats] 从方程组eqns中解出Vats Solve[eqns,vats,elims] 从方程组eqns中削去变量elims,解出vats DSolve[eqn,y,x] 解微分方程,其中、y是x的函数 DSolve[{eqnl,eqn2,…},{y1,y2…},] 解微分方程组,其中yi是x的函数DSolve[eqn,y,{x1,x2…}]解偏微分方程 Eliminate[eqns,Vats] 把方程组eqns中变量vars约去SolveAlways[eqns,vars] 给出等式成立的所有参数满足的条件Reduce[eqns,Vats] 化简并给出所有可能解的条件LogicalExpand[expr] 用&&和,,将逻辑表达式展开InverseFunction[f] 求函数f的反函数 Root[f,k] 求多项式函数的第k个根 Mathematica for Windows 常用用法 一、Mathematica 的主要功能 Mathematica 是美国Wolfram 公司开发的一个功能强大的计算机数学系统,提供了范围广泛的数学计算功能,主要包括三个方面:符号演算、数值计算、图形。例如:多项式的四则运算、展开、因式分解,有理式的各种计算,有理方程、超越方程的解,向量和矩阵的各种计算,求极限、导数、极值、不定积分、定积分、幂级数展开式,求解微分方程,作一元、二元函数的图形等等。 二、Mathematica 的基本知识 1.输入表达式:直接输入一个表达式(包括算式和命令,长表达式用“Enter ”换行)后,按“Shift+Enter ”执行,执行后以“Out[命令序号]= ……”形式输出执行结果,输出的结果可在后续的表达式中使用。 若命令后有分号,则不输出执行结果(图形输出与Print 命令除外)。 “%”表示上一个输出,“%%”表示倒数第2个输出,“%i”表示第i个 命令的输出。 2.运算符:+、-、*、/、^ ,“*”可用空格代替,“^”表示乘方。 如:In[1]:=2^10,输出为“Out[1]= 1024”,其中“In[1]:=”不需要输入。 In[2]:=3+5,Out[2]= 8;In[3]:=%-2,Out[3]= 6; In[4]:=%2+4,Out[4]= 12; In[5]:=1/3-1/4,Out[5]=12 1 ;In[6]:=N[%],Out[6]= 0.0833333; In[7]:=N[%5+12,10],Out[7]= 12.08333333(注意字母的大小写) 3.变量赋值:变量=表达式,“x=.”或Clear[x] 表示清除对x 的赋值。 表达式/.t ->c ,将表达式中的t 全替换成c 。?x ,查x 信息。 4.常用的数学常数:Pi (π)、E(e)、Infinity (∞)、I (1-) 5.常用的数学函数:Abs, Sin, Cos, Tan, Cot, ArcSin, Log (自然对数), Sqrt, Exp 如:In[1]:=Sqrt[2]+1;In[2]:=Sin[2]+ArcSin[1];In[3]:=Exp[2]+% (自变量用[ ]括,区分大小写,首字母大写) 三、常用运算 1.多项式运算:In[1]:= (2+4*x^2)*(1-x)^3 或 In[1]:= t = (2+4*x^2)*(1-x)^3 (将右端表达式赋值给t ); In[2]:=a=t/.x->4 (计算表达式t 当x=4时的值,并赋值给变量a ) In[3]:=a=. (清除变量a ) In[3]:=Expand[t](展开);In[4]:=Factor[%](把上一个结果因式分解) 2.解方程:In[1]:=Solve[x^2+3*x = = 2];In[2]:=N[%]; In[3]:=Solve[a*x-b= = 0, x]; In[4]:=NSolve[{x-2*y= =0,x^2-y= =1},{x,y}](解方程组并得到数值解) 3.自定义函数:In[1]:= f [x_ ]:=x^2+2*x ; In[2]:=f[5]+7; In[3]:=f[a+b] 4.求极限:In[1]:=Limit[Sin[x]/x, x ->0]; In[2]:=Limit[(1+1/n)^n, n->Infinity],Out[2]=E 5.求(偏)导数:In[1]:=D[a*x^2+3, x];In[2]:=D[x^2+y^3-Sin[2*y], y](对y 的偏导数); In[3]:=D[Log[x], {x,2}] (求对x 的二阶导数); In[4]:=D[Sin[x+y]*Exp[z*y^2],x,y] (求对x 、y 的二阶混合偏导数); In[5]:=Simplify[%] (对前一结果化简); In[6]:=D[Sin[x+y]*Exp[z*y^2],{x,2},{y,3}] 6.求不定积分:In[1]:=Integrate[x^2,x];In[2]:=Integrate[1/(x^2+a^2),x] 7.定积分:In[1]:=Integrate[x^2, {x,0,1}];In[2]:=Integrate[x^2,{x,a,b}]; In[3]:=Integrate[x^2+y^2, {x,0,a},{y,0,b}];(求矩形域上的二重积分) In[4]:=Integrate[1, {x,-1,1},{y,-Sqrt[1-x^2],Sqrt[1-x^2]}];Out[4]=Pi (圆面积) 8.幂级数展开:In[1]:=Series[Exp[x],{x,0,4}](在x=0处展开到x 的四次幂) 9.矩阵的输入和输出:In[1]:= a ={{1,2},{3,4}}(定义一个2x2的矩阵a ,按 行写); In[2]:=MatrixForm[a](输出为矩阵形式);In[3]:=Transpose[a](a 的转置); In[4]:=a[[2]](a 的第2行);In[5]:=Tanspose[a][[2]](a 的第2列); In[6]:=Inverse[a](求a 的逆矩阵);In[7]:=Det[a](矩阵的行列式); In[8]:=Eigenvalues[a](求特征值);In[9]:=Eigenvectors[a](求特征向量); In[10]:=RowReduce[a](把a 化为阶梯形,可用于求矩阵的秩、判断线性相关性); In[11]:= b ={{5,6,7},{8,9,10}};In[12]:= a .b (矩阵a 与b 的乘积) 10.解线性方程组: In[1]:= a ={{3,4,5,6},{6,8,10,12},{4,5,6,7},{5,6,7,8}};(a 的秩为2) In[2]:= b ={1,2,3,5}(列向量);(增广矩阵的秩也为2) In[3]:=LinearSolve[a,b](求线性方程组ax=b 的一个特解); In[4]:=NullSpace[a](求线性方程组ax=0的一个基础解系); In[5]:= x =k1%4[[1]]+k2%4[[2]]+%3(ax=b 的全部解,k1、k2为任意常数) 11.求和:In[1]:=NSum[Sin[n]/n^3,{n,1,Infinity}](求级数∑ ∞=13sin n n n 的和) 12.求极小值:In[1]:=FindMinimum[Sin[x]*Cos[x],{x,0.5}](求函数在0.5附 近的极小值); In[2]:=FindMinimum[Sin[x*y]*Exp[x^2],{x,0.2}, {y,0.3}](求多元函数极小值) 13.求解线性规划问题:Min cx ,mx ≥b ,x ≥0,求向量x 。 In[1]:= c ={2,-3}(列向量);In[2]:= m ={{-1,-1},{1,-1},{1,0}}; In[3]:= b ={-10,2,1}; In[4]:=LinearProgramming[c,m,b] 14.数据拟合:In[1]:= d ={{1,2.18},{1.2,2.56},{1.6,3.0},{1.8,2.66}}; In[2]:= f =Fit[d,{1, x, x^2}, x](求和上面4个点吻合最好的二次多项式f ); 检验效果:In[3]:=ListPlot[d](画d 中4个点的图); In[4]:=Plot[f,{x,0.8,2.0}](画多项式f 在x 从0.8到2.0之间的图); In[5]:=Show[%3, %4](把上面两个图画在一起) 注:函数集{1, x, x^2}可以是更高次的或其它函数集,如三角函数集等。 15.一元函数作图:In[1]:=Plot[Exp[-x^2]*Sin[6*x],{x,-2,2}](如图1) 参数方程作图:In[2]:=ParametricPlot[{Sin[t]^3,Cos[t]^3},{t,0,2*Pi}] 16.二元函数作图:In[1]:=Plot3D[Sin[x*y],{x,-Pi, Pi},{y,-Pi, Pi}];(如图2) In[2]:=Plot3D[Sin[x*y],{x,-Pi, Pi},{y,-Pi, Pi},PlotPoints->40, ViewPoint->{2,-3,2}] In[3]:=ParametricPlot3D[{Cos[u]*Cos[v],Sin[u]*Cos[v],Sin[v]},{u,0,2*P i},{v,-Pi/2,Pi/2}] 17.数据画图:In[1]:= d ={{1,2},{3,4},{7,6}};In[2]:=ListPlot[d]; In[3]:=ListPlot[d, PlotStyle->{RGBColor[1,0,0], PointSize[0.02]}](红色 的大点); 或直接用 In[4]:=ListPlot[{1,2},{3,4},{7,6}] 代替“In[2]:=”。 18.作图范围:In[1]:=Plot[x-x^3/6,{x,-4,4}]; In[2]:=Plot[x-x^3/6,{x,-4,4},PlotRange->{-5,2}](限定纵坐标(函数值)范围) 19.图形组合:In[1]:=Plot[{Sin[x],Cos[x]},{x,0,2*Pi}];或 In[2]:= g1=Plot[Sin[x],{x,0,2*Pi}, PlotStyle->{RGBColor[1,0,0]}]; In[3]:= g2=Plot[Cos[x],{x,0,2*Pi}, PlotStyle->{RGBColor[0,0,1]}]; In[4]:=Show[g1,g2](把g1、g2画在一起) 20.文件的使用:In[1]:= y =25;In[2]:= a ={{1,4},{2,6}};In[3]:= f [x_ ]:=x^2 ; In[4]:= g =Plot[Sin[x],{x,0,2*Pi}, PlotStyle->{RGBColor[1,0,0]}]; In[5]:=Save[“abc .m”,a,y,f,g](将a, y, f, g 保存在文件“abc .m ”中,扩 展名为m ); In[6]:=!!abc .m (显示文件内容); In[1]:=<Mathematica函数大全(内置)
50Mathematica线性代数运算命令与例题
Mathematica的常用函数
mathematica数学实验报告
Mathematica函数大全
Mathematica程序举例1
mathematica 数学实验报告材料 实验一
MATHEMATICA实验报告
附录B:Mathematica的基本应用b
数学应用软件实验报告(mathematica实验程序)1
最佳分数值逼近(mathematica数学实验报告)
Mathematica常用指令
Mathematica使用教程
Mathematica中的常用函数命令
Mathematical常用功能大全-精简版