
第十一章全等三角形综合复习
切记:“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
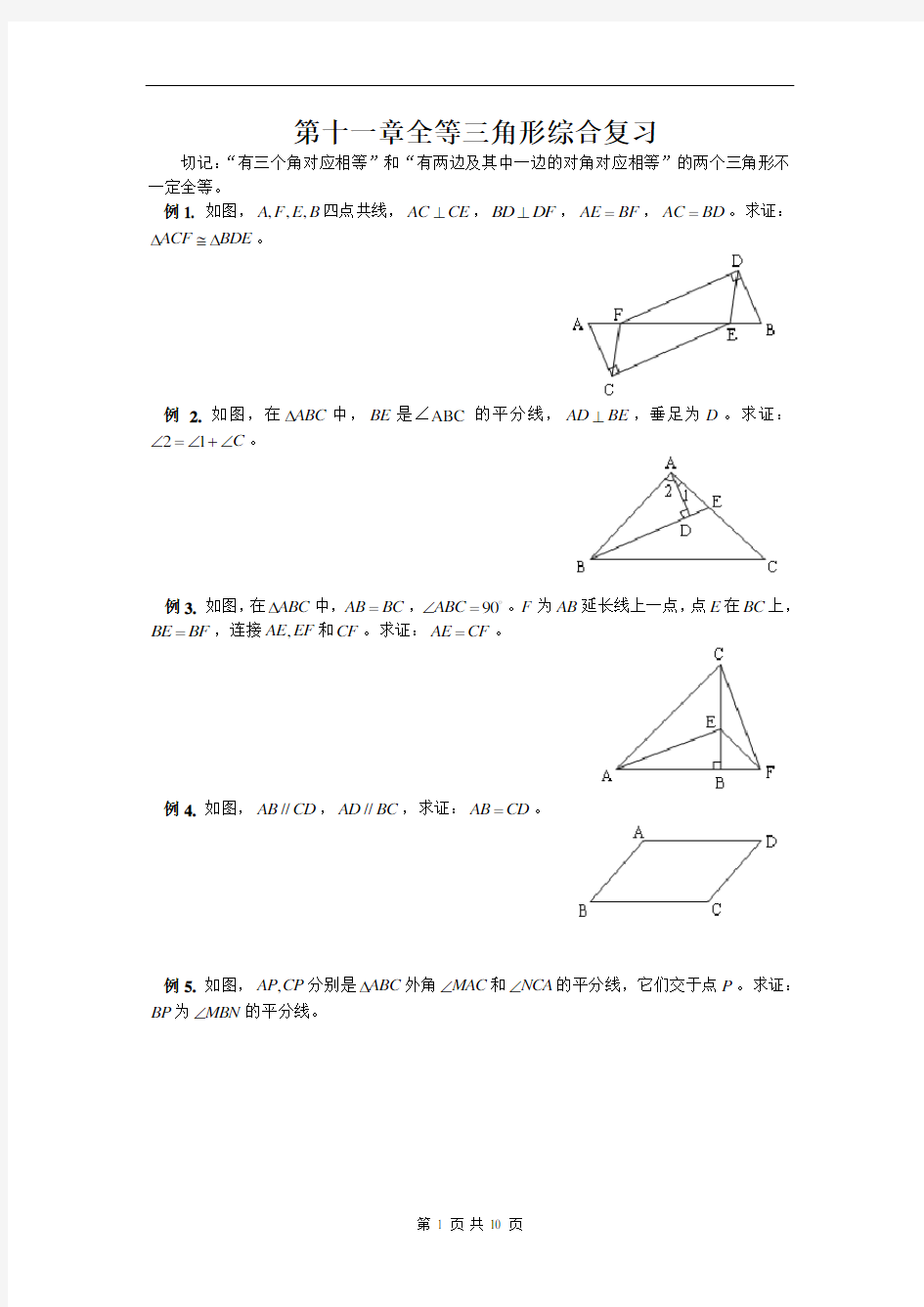
例1. 如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。求证:
ACF BDE ???。
例 2. 如图,在ABC ?中,BE 是∠ABC 的平分线,AD BE ⊥,垂足为D 。求证:21C ∠=∠+∠。
例3. 如图,在ABC ?中,AB BC =,90ABC ∠=o 。F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。求证:AE CF =。
例4. 如图,AB //CD ,AD //BC ,求证:AB CD =。
例5. 如图,,AP CP 分别是ABC ?外角MAC ∠和NCA ∠的平分线,它们交于点P 。求证:
BP 为MBN ∠的平分线。
例6. 如图,D 是ABC ?的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ?的中线。求证:2AC AE =。
例7. 如图,在ABC ?中,AB AC >,12∠=∠,P 为AD 上任意一点。求证:AB AC PB PC ->-。
同步练习
一、选择题:
1. 能使两个直角三角形全等的条件是( ) A. 两直角边对应相等 B. 一锐角对应相等 C. 两锐角对应相等
D. 斜边相等
2. 根据下列条件,能画出唯一ABC ?的是( ) A. 3AB =,4BC =,8CA =
B. 4AB =,3BC =,30A ∠=o
C. 60C ∠=o
,45B ∠=o
,4AB =
D. 90C ∠=o
,6AB =
3. 如图,已知12∠=∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D ∠=∠;④B E ∠=∠。其中能使ABC AED ???的条件有( )
A. 4个
B. 3个
C. 2个
D. 1个
4. 如图,12∠=∠,C D ∠=∠,,AC BD 交于E 点,下列不正确的是( ) A. DAE CBE ∠=∠
B. CE DE =
C. DEA ?不全等于CBE ?
D. EAB ?是等腰三角形
5. 如图,已知AB CD =,BC AD =,23B ∠=o
,则D ∠等于( )
A. 67o
B. 46o
C. 23o
D. 无法确定
二、填空题:
6. 如图,在ABC ?中,90C ∠=o
,ABC ∠的平分线BD 交AC 于点D ,且:2:3CD AD =,10AC cm =,则点D 到AB 的距离等于__________cm ;
7. 如图,已知AB DC =,AD BC =,,E F 是BD 上的两点,且BE DF =,若
100AEB ∠=o ,30ADB ∠=o ,则BCF ∠=____________;
8. 将一张正方形纸片按如图的方式折叠,,BC BD 为折痕,则CBD ∠的大小为_________;
9. 如图,在等腰Rt ABC ?中,90C ∠=o
,AC BC =,AD 平分BAC ∠交BC 于D ,
DE AB ⊥于E ,若10AB =,则BDE ?的周长等于____________;
10. 如图,点,,,D E F B 在同一条直线上,AB //CD ,AE //CF ,且AE CF =,若
10BD =,2BF =,则EF =___________;
三、解答题: 11. 如图,ABC ?为等边三角形,点,M N 分别在,BC AC 上,且BM CN =,AM 与BN 交于Q 点。求AQN ∠的度数。
12. 如图,90ACB ∠=o
,AC BC =,D 为AB 上一点,AE CD ⊥,BF CD ⊥,交CD 延长线于F 点。求证:BF CE =。
答案
例1. 思路分析:从结论ACF BDE ???入手,全等条件只有AC BD =;由AE BF =两边同时减去EF 得到AF BE =,又得到一个全等条件。还缺少一个全等条件,可以是CF DE =,也可以是A B ∠=∠。
由条件AC CE ⊥,BD DF ⊥可得90ACE BDF ∠=∠=o
,再加上AE BF =,AC BD =,可以证明ACE BDF ???,从而得到A B ∠=∠。
解答过程:Q AC CE ⊥,BD DF ⊥ ∴90ACE BDF ∠=∠=o 在Rt ACE ?与Rt BDF ?中 Q AE BF AC BD =??=? ∴Rt ACE Rt BDF ???(HL) ∴A B ∠=∠
Q AE BF =
∴AE EF BF EF -=-,即AF BE =
在ACF ?与BDE ?中 Q AF BE A B AC BD =??
∠=∠??=? ∴ACF BDE ???(SAS)
解题后的思考:本题的分析方法实际上是“两头凑”的思想方法:一方面从问题或结论入手,看还需要什么条件;另一方面从条件入手,看可以得出什么结论。再对比“所需条件”和“得出结论”之间是否吻合或具有明显的联系,从而得出解题思路。
小结:本题不仅告诉我们如何去寻找全等三角形及其全等条件,而且告诉我们如何去分析一个题目,得出解题思路。
例2. 思路分析:直接证明21C ∠=∠+∠比较困难,我们可以间接证明,即找到α∠,证明2α∠=∠且1C α∠=∠+∠。也可以看成将2∠“转移”到α∠。
那么α∠在哪里呢?角的对称性提示我们将AD 延长交BC 于F ,则构造了△FBD ,可以通过证明三角形全等来证明∠2=∠DFB ,可以由三角形外角定理得∠DFB=∠1+∠C 。
解答过程:延长AD 交BC 于F 在ABD ?与FBD ?中
Q 90
ABD FBD BD BD ADB FDB ?∠=∠?
=??∠=∠=?o ∴ABD FBD ???(ASA ∴2DFB ∠=∠
又Q 1DFB C ∠=∠+∠ ∴21C ∠=∠+∠。
解题后的思考:由于角是轴对称图形,所以我们可以利用翻折来构造或发现全等三角形。
例3. 思路分析:可以利用全等三角形来证明这两条线段相等,关键是要找到这两个三角形。以线段AE 为边的ABE ?绕点B 顺时针旋转90o
到CBF ?的位置,而线段CF 正好是
CBF ?的边,故只要证明它们全等即可。
解答过程:Q 90ABC ∠=o ,F 为AB 延长线上一点 ∴90ABC CBF ∠=∠=o 在ABE ?与CBF ?中 Q AB BC ABC CBF BE BF =??
∠=∠??=? ∴ABE CBF ???(SAS) ∴AE CF =。
解题后的思考:利用旋转的观点,不但有利于寻找全等三角形,而且有利于找对应边和对应角。
小结:利用三角形全等证明线段或角相等是重要的方法,但有时不容易找到需证明的三角形。这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。
例4. 思路分析:关于四边形我们知之甚少,通过连接四边形的对角线,可以把原问题转化为全等三角形的问题。
解答过程:连接AC Q AB //CD ,AD //BC ∴12∠=∠,34∠=∠
在ABC ?与CDA ?中 Q 1243AC CA ∠=∠??
=??∠=∠? ∴ABC CDA ???(ASA) ∴AB CD =。
解题后的思考:连接四边形的对角线,是构造全等三角形的常用方法。 例5. 思路分析:要证明“BP 为MBN ∠的平分线”,可以利用点P 到,BM BN 的距离相等来证明,故应过点P 向,BM BN 作垂线;另一方面,为了利用已知条件“,AP CP 分别是MAC ∠和NCA ∠的平分线”
,也需要作出点P 到两外角两边的距离。 解答过程:过P 作PD BM ⊥于D ,PE AC ⊥于E ,PF BN ⊥于F
Q AP 平分MAC ∠,PD BM ⊥于D ,PE AC ⊥于E ∴PD PE =
Q CP 平分NCA ∠,PE AC ⊥于E ,PF BN ⊥于F ∴PE PF =
Q PD PE =,PE PF =
∴PD PF =
Q PD PF =,且PD BM ⊥于D ,PF BN ⊥于F ∴BP 为MBN ∠的平分线。
解题后的思考:题目已知中有角平分线的条件,或者有要证明角平分线的结论时,常过角平分线上的一点向角的两边作垂线,利用角平分线的性质或判定来解答问题。
例6. 思路分析:要证明“2AC AE =”,不妨构造出一条等于2AE 的线段,然后证其等于
AC 。因此,延长AE 至F ,使EF AE =。
解答过程:延长AE 至点F ,使EF AE =,连接DF 在ABE ?与FDE ?中
Q AE FE AEB FED BE DE =??
∠=∠??=? ∴ABE FDE ???(SAS)
∴B EDF ∠=∠
Q ADF ADB EDF ∠=∠+∠,ADC BAD B ∠=∠+∠
又Q ADB BAD ∠=∠ ∴ADF ADC ∠=∠ Q AB DF =,AB CD = ∴DF DC =
在ADF ?与ADC ?中 Q AD AD ADF ADC DF DC =??
∠=∠??=? ∴ADF ADC ???(SAS) ∴AF AC =
又Q 2AF AE = ∴2AC AE =。
解题后的思考:三角形中倍长中线,可以构造全等三角形,继而得出一些线段和角相等,甚至可以证明两条直线平行。
例7. 思路分析:欲证AB AC PB PC ->-,不难想到利用三角形中三边的不等关系来证明。由于结论中是差,故用两边之差小于第三边来证明,从而想到构造线段AB AC -。而构造AB AC -可以采用“截长”和“补短”两种方法。
解答过程:法一:
在AB 上截取AN AC =,连接PN 在APN ?与APC ?中 Q 12AN AC AP AP =??
∠=∠??=? ∴APN APC ???(SAS) ∴PN PC =
Q 在BPN ?中,PB PN BN -<
∴-<-PB PC AB AC ,即AB -AC>PB -PC 。
法二:
延长AC 至M ,使AM AB =,连接PM 在ABP ?与AMP ?中 Q 12AB AM AP AP =??
∠=∠??=? ∴ABP AMP ???(SAS)
∴PB PM =
Q 在PCM ?中,CM PM PC >- ∴AB AC PB PC ->-。
解题后的思考:当已知或求证中涉及线段的和或差时,一般采用“截长补短”法。具体作法是:在较长的线段上截取一条线段等于一条较短线段,再设法证明较长线段的剩余线段等于另外的较短线段,称为“截长”;或者将一条较短线段延长,使其等于另外的较短线段,然后证明这两条线段之和等于较长线段,称为“补短”。
小结:本题组总结了本章中常用辅助线的作法,以后随着学习的深入还要继续总结。我们不光要总结辅助线的作法,还要知道辅助线为什么要这样作,这样作有什么用处。
同步练习的答案
一、选择题: 1. A
2. C
3. B
4. C
5. C
二、填空题: 6. 4
7. 70o
8. 90o
9. 10 10. 6
三、解答题:
11. 解:Q ABC ?为等边三角形
∴AB BC =,60ABC C ∠=∠=o
在ABM ?与BCN ?中 Q AB BC ABC C BM CN =??
∠=∠??=?
∴ABM BCN ???(SAS) ∴NBC BAM ∠=∠
∴60AQN ABQ BAM ABQ NBC ∠=∠+∠=∠+∠=o 。
12. 证明:Q AE CD ⊥,BF CD ⊥ ∴90F AEC ∠=∠=o
∴90ACE CAE ∠+∠=o Q 90ACB ∠=o
∴90ACE BCF ∠+∠=o ∴CAE BCF ∠=∠ 在ACE ?与CBF ?中 Q F AEC CAE BCF AC BC ∠=∠??
∠=∠??=?
∴ACE CBF ???(AAS) ∴BF CE =。