
附录Ⅰ 截面的几何性质
§I ?1 截面的静矩和形心位置
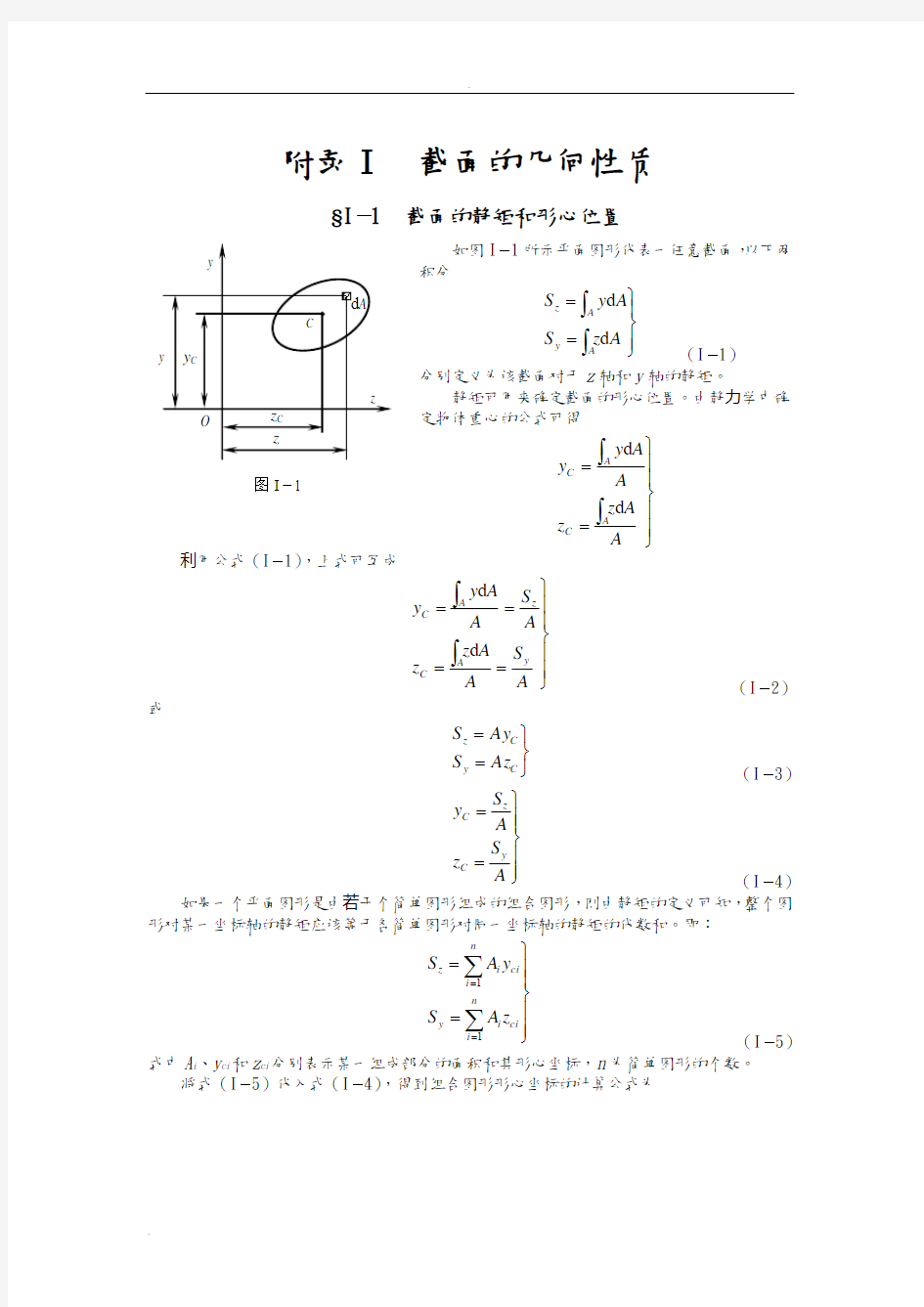
如图I ?1所示平面图形代表一任意截面,以下两积分
?
???
?==??A z S A y S A y A
z d d (I ?1) 分别定义为该截面对于z 轴和y 轴的静矩。
静矩可用来确定截面的形心位置。由静力学中确定物体重心的公式可得
?
???
???
==
??A A z z A A y y A
C A C
d d
利用公式(I ?1),上式可写成
?
???
?
?
?
====
??A S A A z z A S A A
y y y A
C z A
C d d (I ?2) 或
?
?
?
==C y C z Az S Ay S (I ?3)
?
??????
==
A S z A S y y C z C (I ?4)
如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。即:
??
???
??
==∑∑==n
i ci i y n
i ci i z z A S y A S 11
(I ?5)
式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I ?5)代入式(I ?4),得到组合图形形心坐标的计算公式为
图I ?1
???
?
???????
??==∑∑∑∑====n i i n
i ci i c n
i i n
i ci i c A z A z A y A y 111
1 (I ?6) 例题I ?1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。将截面分成Ⅰ、Ⅱ两个矩形,则
A Ⅰ=0.072m 2,A Ⅱ=0.08m 2 y Ⅰ=0.46m ,y Ⅱ=0.2m m
323.008.0072.02
.008.046.0072.0II
I II
II I I 1
1
=+?+?=
++=
=
∑∑==A A y A y A A
y
A y n
i i
n
i ci
i c
§I ?2 惯性矩、惯性积和极惯性矩
如图I ?2所示平面图形代表一任意截面,在图形平面内建立直角坐标系
zOy 。现在图形内取微面积d A ,d A 的形心在坐标系zOy 中的坐标为y 和z ,
到坐标原点的距离为ρ。现定义y 2d A 和z 2
d A 为微面积d A 对z 轴和y 轴的惯
性矩,ρ2
d A 为微面积d A 对坐标原点的极惯性矩,而以下三个积分
?
???
?
?
?===???A ρI A z I A y I A A
y A z d d d 2
P 22 (I ?7) 分别定义为该截面对于z 轴和y 轴的惯性矩以及对坐标原点的极惯性矩。
由图(I ?2)可见,222z y +=ρ,所以有
??+=+==A
y
z A
I I A z y A ρI )d (d 222P (I ?8)
即任意截面对一点的极惯性矩,等于截面对以该点为原点的两任意正交坐标轴的惯性矩之和。
另外,微面积d A 与它到两轴距离的乘积zy d A 称为微面积d A 对y 、z 轴的惯性积,而积分
A
zyd I A
yz ?=
(I ?9)
定义为该截面对于y 、z 轴的惯性积。
例题I ?1图
图I ?2
从上述定义可见,同一截面对于不同坐标轴的惯性矩和惯性积一般是不同的。惯性矩的数值恒为正值,而惯性积则可能为正,可能为负,也可能等于零。惯性矩和惯性积的常用单
位是m 4或mm 4
。
§I ?3 惯性矩、惯性积的平行移轴和转轴公式
一、惯性矩、惯性积的平行移轴公式
图I ?3所示为一任意截面,z 、y 为通过截面形心的一对正交轴,z 1、y 1为与z 、y 平行的坐标轴,截面形心C 在坐标系z 1O y 1中的坐标为(b ,a ),已知截面对z 、y 轴惯性矩和惯性积为I z 、I y 、I yz ,下面求截面对z 1、y 1轴惯性矩和惯性积I z 1、I y 1、I y 1z 1。
A
a I I z z 21+=
(I ?10)
同理可得
A
b I I y y 21+=
(I ?11)
式(I ?10)、(I ?11)称为惯性矩的平行移轴公式。
下面求截面对y 1、z 1轴的惯性积
1
1z y I 。根据定义
??++==A
A
z y A
a y
b z A y z I )d )((d 1111
????+++=A
A
A
A
A
ab A y b A z a A zy d d d d
abA bS aS I
z
y yz +++= 由于z 、y 轴是截面的形心轴,所以S z =S y =0,即
abA
I I
yz z y +=1
1 (I ?12)
式(I ?12)称为惯性积的平行移轴公式。
二、惯性矩、惯性积的转轴公式
图(I ?4)所示为一任意截面,z 、y 为过任一点O 的一对正交轴,截面对z 、y 轴惯性
矩I z 、I y 和惯性积I yz 已知。现将z 、y 轴绕O 点旋转α角(以逆时针方向为正)得到另一对正交轴z 1、y 1轴,下面求截面对z 1、y 1轴惯性矩和惯性积1z I
、
1
y I 、
1
1z y I 。
图I ?3
α
α2sin 2cos 221yz y
z y
z z I I I I I I --+
+=
(I ?13)
同理可得
α
α2sin 2cos 2
2
1yz y
z y
z y I I I I I I +--
+=
(I ?14)
α
α2cos 2sin 211yz y
z z y I I I I +-=
(I ?15)
式(I ?13)、(I ?14)称为惯性矩的转轴公式,式(I ?15)称为惯性积的转轴公式。
§I ?4 形心主轴和形心主惯性矩
一、主惯性轴、主惯性矩
由式(I ?15)可以发现,当α=0o
,即两坐标轴互相重合时,
yz
z y I I =11;当α=90
o
时,yz z y I
I -=11,因此必定有这样的一对坐标轴,使截面对它的惯性积为零。通常把这样的一对坐标轴称为截面的主惯性轴,简称主轴,截面对主轴的惯性矩叫做主惯性矩。
假设将z 、y 轴绕O 点旋转α0角得到主轴z 0、y 0,由主轴的定义
2cos 2sin 2
0000=+-=
ααyz y
z z y I I I I
从而得
y z yz I
I I α--=
22tan 0 (I ?16)
上式就是确定主轴的公式,式中负号放在分子上,为的是和下面两式相符。这样确定的α0
角就使得0z I
等于m ax I
。
由式(I ?16)及三角公式可得
2
204)(2cos yz
y z y
z I I I I I +--=
α
2
204)(22sin yz
y z yz
I I I I +--=
α
将此二式代入到式(I ?13)、(I ?14)便可得到截面对主轴z 0、y 0的主惯性矩
??????
?+--+=+-+
+=22224)(2124)(2
120
0yz
y z y z y yz
y z y
z z I I I I I I I I I I I I (I ?17)
二、形心主轴、形心主惯性矩
通过截面上的任何一点均可找到一对主轴。通过截面形心的主轴叫做形心主轴,截面对形心主轴的惯性矩叫做形心主惯性矩。
例题I ?5 求例I ?1中截面的形心主惯性矩。 解:在例题I ?1中已求出形心位置为
=C z ,m
323.0=C y
过形心的主轴z 0、y 0如图所示,z 0轴到两个矩形形心的距离分别为
m 137.0I =a ,m 123.0II =a
截面对z 0轴的惯性矩为两个矩形对z 0轴的惯性矩之和,即
2
II
II II 2I I I I
I I 0a A I a A I I z z z +++=
2
323
123.04.02.0124.02.0137.012.06.01212.06.0??+?+??+?=
4
2m 1037.0-?=
截面对y 0轴惯性矩为
4
233II I m 10242.0122.04.0126.012.00
0-?=?+?=+=y y y I
I
I
第六章 梁的应力
§6?1 梁的正应力
一、纯弯曲与平面假设
本节将推导梁弯曲时横截面上正应力的计算公式。 为了方便,我们先研究梁横截面上只有弯矩的情况,这种情况称为“纯弯曲”。如图6?1所示的梁,在如图所示荷载作用下,中间CD 段就属于这种情况,由其剪力图和弯矩图可以看到,在CD 段内的弯矩M =Fa =常数,而剪力F S 等于零。
我们先作如下的实验,观察到如下的一些现象:
(1)变形前,梁侧面上与纵向直线垂直的横向线在变形后仍为直线,并且仍然与变形
后的梁轴线(简称挠曲线)保持垂直,但相对转过一个角度。
(2)变形前互相平行的纵向直线,变形后均变为圆弧线,并且上部的纵线缩短,下部的纵线伸长。在梁中一定有一层上的纤维既不伸长也不缩短,此层称为中性层。中性层与梁横截面的交线称为中性轴。
根据这些实验现象,我们对纯弯曲情况下作出如下假设: 1.平面假设:梁的横截面在梁弯曲后仍然保持为平面,并且仍然与变形后的梁轴线保持垂直。
2.单向受力假设:梁的纵向纤维处于单向受力状态,且纵向纤维之间的相互作用可忽略不计。
二、正应力公式的推导
1
相应的纵向线应变为
ρρ
εy x x
y x =
=d d (6?1) M 图
图6?1 (a) (b)
(c)
(b) 图6?2 图6?3
中性层
中性轴
(b)
a
b
O 1 O
2
m
n
p q
(a)
m
n p q
(c)
2
式(6?1)表明:梁的纵向纤维的应变与纤维距中性层的距离成正比,离中性层愈远,纤维的线应变愈大。
2.物理方面
在弹性范围内正应力与线应变的关系为
εE σ=
将式(6?1)代入,得
ρy
E
σ= (6?2)
3.静力学方面
由图6?4可以看出,梁横截面上各微面积上的微内力d F N =σd A 构成了空间平行力系,它们向截面形心简化的结果应为以下三个内力分量
?=A A
σF d N ,?=A y A σz M d ,?=A z A
σy M d
由截面法可求得该截面上只有弯矩M ,即上式中F N ,M y 均等于零,所以有
d N ==?A A σF (d ) 0
d ==?A
y A σz M (e )
M
A σy M A
z ==?d
(f )
由式(d )得
d d N ===?
?A A
ρA
Ey A σF
因E 、ρ为常量,所以有
d ==?
z A
S A y (g )
即梁横截面对中性轴(z 轴)的静矩等于零。由此可知,中性轴通过横截面的形心,于是就确定了中性轴的位置。
由式(e )可得
0d d d ====??
?A
A A
y A zy ρE
A ρEzy A σz M
因此
d ==?
yz A
I A zy (h )
即梁横截面对y 、z 轴的惯性积等于零,说明y 、z 轴应为横截面的主轴,又y 、z 轴过横截面的形心,所以其应为横截面的形心主轴。
最后由式(f )可得
M
A σy M A
z ==?d
即
A 图6?4
ρρ
ρ
σz
A
A
A
EI A y E
A Ey A y M =
=
==?
?
?d d d 22
式中
?=A
z A
y I d 2是梁横截面对中性轴的惯性矩。将上式整理可得
z EI M
=
ρ
1
(6?3)
由式(6?3)可知:曲率与弯矩M 成正比,与EI z 成反比。在相同弯矩下,EI z 值越大,梁的弯曲变形就越小。EI z 表明梁抵抗弯曲变形的能力,称为梁的弯曲刚度。
将式(6?3)代入式(6?2),可得
z I My
σ=
(6?4)
这就是梁在纯弯曲时横截面上任一点的正应力的计算公式。
例题6?1 长为l 的矩形截面梁,在自由端作用一集中力F ,已知h =0.18m ,b =0.12m ,y =0.06m ,a =2m ,F =1.5kN ,求C 截面上K 点的正应力。
解:先求出C 截面上弯矩
m
N 1032105133??-=??-=-=.Fa M C
截面对中性轴的惯性矩
4
43
3m 1058301218012012-?=?==...bh I z
将M C 、I z 、y 代入正应力计算公式,则有
MPa 09.3Pa 1009.3)06.0(10583.0103σ6
4
3=?=-???-==-y I M z C K
K 点的正应力为正值,表明其应为拉应力。
§6?2 梁的正应力强度条件及其应用
一、梁的正应力强度条件
最大正应力发生在距中性轴最远的位置,此时
max max y I M
σz
=
而对整个等截面梁来讲,最大正应力应发生在弯矩最大的横截面上,距中性轴最远的位
置,即
max
max
max y I M σz
=
引用符号
m ax
y I W z z =
,则上式可改写成
z
W M σmax max =
(6?5)
/2 /2
例题6?1图
8 例式中的W z 叫做弯曲截面系数(或抗弯截面系数),它与梁的截面形状和尺寸有关。
对矩形截面
62122
3bh h bh W z =
= 对圆形截面
322
64
3
4d d d W z ππ=
=
正应力强度条件为
[]σW M σz
≤=
m ax
m ax (6?6)
二、三种强度问题的计算
根据式(6?6)可以求解与梁强度有关的三种问题。
(1)强度校核
(2)选择截面 此时应将式(10?6)改写为
[]σM W z max
≥
(3)确定许用荷载 此时应将式(10?6)改写为
[]
σW M z ≤max
例题6?2 已知l =4m ,b =140mm ,h =210mm ,q =2kN/m ,,校核该梁的强度。
解:先画梁的弯矩图(图b )。由梁的弯矩图可以看出,梁中最大弯矩应发生在跨中截面上,其值为
N.m
104410281
813232max ?=???==ql M
弯曲截面系数为
3
222m 10103.021.014.061
6-?=??==bh W z
由于最大正应力应发生在最大弯矩所在截面上,所以有
][3.88MPa Pa 1088.310103.01046
2
3max max σσ<=?=??==-z W M
所以满足正应力强度要求。
§6?3 梁横截面上的切应力·梁的切应力强度条件
一、矩形截面梁的切应力
矩形截面梁的切应力公式的推导,采用了下面的两条假设: (1)横截面上各点切应力均与侧边平行。
(2)切应力沿截面宽度均匀分布,即距中性轴等距离各点的切应力相等。
b I S F τz z *
S =
(6?8)
式(6?8)即为矩形截面梁横截面任一点的切应力计算公式。式中:F S 为横截面上的剪力;S z *为面积A 1对中性轴的静矩;I z 横截面对中性轴的惯性矩;b 为截面的宽度。
对于矩形截面梁,由图6?7a 可知
)
4(2)2(21)2(22
y h
b y h y y h b S *
z
-=??????-+-= (e) 将其代入式(6?8),可得
)
4(222
y h I F τz S -= (f)
此式表明矩形截面梁横截面上切应力沿梁高按二次抛物
线形规律分布。在截面上、下边缘(
2h y ±
=)处,τ=0,
而在中性轴上(y =0)的切应力有最大值,如图10?7b 。即
A F bh F I h F τz 23238S
S 2S max =
== (g)
例题6?5 一矩形截面的简支梁如图所示。已知:l =3m ,h =160mm ,b =100mm ,y =40mm ,
F =3kN ,求m ?m 截面上K 点的切应力。
解:先求出
m ?m 截面上的剪力为3kN ,截面对中性轴的惯性矩为 4
43
3m 10341.01216.01.012
-?=?==bh I z
面积A *
对中性轴的静矩为
33**m 1024.006.004.01.0-?=??==y A
S z
习题6?5图
* 图6?7
τmax
(b)
(a)
图6?5
h
则K 点的切应力为
Mpa 21.0Pa 1021.01.010341.01024.0103I 64
33S =?=?????==--b S F τz z
二、工字形截面梁的切应力 1.腹板上的切应力
1*
S b I S F τz z =
式中:F S 为横截面上的剪力;S z *
为欲求应力点到截面边缘间的面积对中性轴的静矩;I z
为横截面对中性轴的惯性矩;b 1为腹板的厚度。
切应力沿腹板高度的分布规律如图6?8a 所示,仍是按抛物线规律分布,最大切应力τmax
仍发生在截面的中性轴上。 2.翼缘上的切应力 翼缘上的水平切应力可认为沿翼缘厚度是均匀分布的,其计算公式仍与矩形截面的切应力的形式相同,即
δI S F τz z
*S =
式中F S 为横截面上的剪力;S z *
为欲求应力点到翼缘边缘间的面积对中性轴的静矩;I z
横截面对中性轴的惯性矩;δ为翼缘的厚度。
三、T 字型截面梁的切应力
T 字型截面可以看成是由两个矩形组成,下面的狭长矩形与工字形截面的腹板相似,该部分上的切应力仍用下式计算:
1*S b I S F τz z =
最大切应力仍然发生在截面的中性轴上。
四、圆形及环形截面梁的切应力
圆形及薄壁环形截面其最大竖向切应力也都发生在中性轴上,并沿中性轴均匀分布,计算公式分别为
圆形截面
A F τS max 34?=
式中F S 为横截面上的剪力,A 为圆形截面的面积。 薄壁环型截面 A F
τS
max 2?= 式中F S 为横截面上的剪力,A 为薄壁环型截面的面
积。
五、梁的切应力强度条件
图6?8
(b)
(c)
(a)
[]
τb
I S F τz z ≤=
*
max
,max S,max (6?9)
此式即为切应力的强度条件。
例题6?6 一外伸工字型钢梁如图a 所示。工字钢的型号为22a ,已知:l =6m ,F =30kN ,
q =6kN/m ,材料的许用应力[σ]=170MPa ,[τ]=100MPa,试校核梁的强度。 解:(1)校核最大正应力 弯矩图如图c 所示,最大正应力
应发生在最大弯矩的截面上。查型钢
表可知
333m 10309.0cm 309-?==z W 则最大正应力 ]
[MPa 126Pa 1012610
309.0103963
3
max max σσ<=?=??==-z
W M (2)校核最大切应力
剪力图如图b 所示,最大切应力
应发生在最大剪力的截面上。查型钢表可知
0.189m
cm 9.18max
,==z z S I
m 0075.0m m 5.71===d b
则最大切应力
][MPa 12Pa 10120075.0189.0101763
1
max
,max S,max ττ<=?=??==
b I S F z z
所以此梁安全。
§6?4 梁的合理截面形状及变截面梁
一、梁的合理截面形式
由梁的强度条件公式(6?6)可知,梁的抗弯能力直接取决于其弯曲截面系数W z 的大小。
所以梁的合理截面形式就是截面面积相同的条件下具有较大的弯曲截面系数。
W z 值与截面的高度及截面的面积分布有关。截面的高度愈大,面积分布得离中性轴愈远,W z 值就愈大;反之,截面的高度愈小,面积分布得离中性轴愈近,W z 值就愈小。所以,选择合理截面的基本原则是尽可能地增大截面的高度,并使大部分的面积布置在距中性轴较远的地方。这个原则的合理性也可从梁横截面上的正应力的分布规律来说明。因此,在工程实际中,经常采用工字形、环形、箱形等截面形式(如图10?10)。
二、变截面梁
横截面沿着梁轴线变化的梁,称为变截面梁。最理想的变截面梁,是使梁的各个截面上
(a) D
(b) F 例题6?6图
(c) M
图6?10
的最大正应力同时达到材料的许用应力。即
[]σx W x M σz ==
)()
(max
得
[]σx M x W z )
()(=
(6?10)
式中,M (x )为任一横截面上的弯矩,W z (x )为该截面的弯曲截面系数。截面按式(6?10)而变化的梁称为等强度梁。
下面我们来讲一下预制梁的横向力分布系数计算 从上面我能看出常见的预制梁包括板梁、小箱梁、T梁 跨中横向力分布系数: 对于板梁和小箱梁由于横向联系比较薄弱,所以采用铰接板梁法 对于T梁有横隔板比较多,认为是刚接,所以采用刚接板梁法 梁端横向力分布系数: 通常采用杠杆法 下面就讲一下30米简支转连续T梁横向力分布系数计算: 主梁横断面见附件 桥博计算横向力分布系数计算需要输入的数据见附件 包括主梁宽、抗弯、抗扭、左板长、左板惯矩、右板长、右板惯矩、主梁跨度 G/E等 首先计算主梁的抗弯抗扭惯矩(中梁、边梁断面尺寸见附件,梁高200cm) 中梁: ==================================================== = MIDAS SPC TEXT OUTPUT FILE = = (Tue Jun 17 20:45:16 2008) = = - - = ==================================================== ==================================================== UNIT: KN . M ==================================================== ==================================================== * Section-P1 (PLANE) ==================================================== * A : * Asx : * Asy : * Ixx : 抗弯惯矩 * Iyy : 0. * Ixy : * J : 抗扭惯矩---------------------------------------------------- * (+)Cx : * (-)Cx : * (+)Cy :
15-1(I-8) 试求图示三角形截面对通过顶点A并平行于底边BC的轴的惯性矩。 解:已知三角形截面对以BC边为轴的惯性矩是,利用平行轴定理,可求得截面对形心轴的惯性矩 所以 再次应用平行轴定理,得 返回 15-2(I-9) 试求图示的半圆形截面对于轴的惯性矩,其中轴与半圆形 的底边平行,相距1 m。 解:知半圆形截面对其底边的惯性矩是,用 平行轴定理得截面对形心轴的惯性矩
再用平行轴定理,得截面对轴的惯性矩 返回 15-3(I-10) 试求图示组合截面对于形心轴的惯性矩。 解:由于三圆直径相等,并两两相切。它们的圆心构成一个边长为的等边三角形。该等边三角形的形心就是组合截面的形心,因此下面两个圆的圆心,到形心轴的距离是 上面一个圆的圆心到轴的距离是。 利用平行轴定理,得组合截面对轴的惯性矩如下: 返回 15-4(I-11) 试求图示各组合截面对其对称轴的惯性矩。
解:(a)22a号工字钢对其对称轴的惯性矩是。 利用平行轴定理得组合截面对轴的惯性矩 (b)等边角钢的截面积是,其形心距外边缘的距离是28.4 mm,求得组合截面对轴的惯性矩如下: 返回 15-5(I-12) 试求习题I-3a图所示截面对其水平形心轴的惯性矩。关于形心位置,可利用该题的结果。 解:形心轴位置及几何尺寸如图 所示。惯性矩计算如下: 返回 15-6(I-14) 在直径的圆截面中,开了一个的矩形孔,如图所示, 试求截面对其水平形心轴和竖直形心轴的惯性矩和 。
解:先求形心主轴的位置 即 返回 15-7(I-16) 图示由两个20a号槽钢组成的组合截面,若欲使截面对两对称轴的惯性矩和相等,则两槽钢的间距应为多少? 解:20a号槽钢截面对其自身的形心轴、的惯性矩是,;横截面积为;槽钢背到其形心轴的距离是。 根据惯性矩定义和平行轴定理,组合截面对, 轴的惯性矩分别是 ; 若 即
Harbin Institute of Technology 材料力学电算大作业 课程名称:材料力学 设计题目:组合截面几何性质计算 作者院系: 作者班级: 作者姓名: 作者学号: 指导教师: 完成时间:
一、软件主要功能 X4,X5,X6分别是n1个圆形截面,n2个圆环形截面,n3个矩形截面的形心位置X与面积的乘积 Y4,Y5,Y6分别是n1个圆形截面,n2个圆环形截面,n3个矩形截面的形心位置Y与面积的乘积 Xc,Yc是总截面的形心坐标 Ix1,Ix2,Ix3分别是n1个圆形截面,n2个圆环形截面,n3个矩形截面对通过形心且与x轴平行的轴的惯性矩 Iy1,Iy2,Iy3分别是n1个圆形截面,n2个圆环形截面,n3个矩形截面对通过形心且与y轴平行的轴的惯性矩 Ixy1,Ixy2,Ixy3分别是n1个圆形截面,n2个圆环形截面,n3个矩形截面对通过形心且与x,y轴平行的两轴的惯性积 a是通过形心的主轴与x轴的夹角 Imax,Imin分别是截面对形心主轴的主惯性矩 软件截图: 二、程序源代码 Dim n1 As Double Dim d1(10) As Double Dim X1(10) As Double Dim Y1(10) As Double Dim n2 As Double Dim d2(10) As Double
Dim d3(10) As Double Dim X2(10) As Double Dim Y2(10) As Double Dim n3 As Double Dim h(10) As Double Dim d(10) As Double Dim X3(10) As Double Dim Y3(10) As Double Dim S1 As Double, S2 As Double, S3 As Double Dim X4 As Double, Y4 As Double, X5 As Double, Y5 As Double, X6 As Double, Y6 As Double Dim Xc As Double, Yc As Double Dim Ix1 As Double, Iy1 As Double, Ix2 As Double, Iy2 As Double, Ix3 As Double, Iy3 As Double, Imax As Double, Imin As Double Dim Ixy1 As Double, Ixy2 As Double, Ixy3 As Double Dim a As Double Private Sub Text1_Change() n1 = Val(Text1.Text) For i = 1 To n1 d1(i) = Val(InputBox("输入第" & (i) & "个圆的直径")) X1(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的x坐标值")) Y1(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的y坐标值")) Next i For i = 1 To n1 S1 = S1 + 3.14159 * d1(i) * d1(i) / 4 X4 = X4 + X1(i) * 3.14159 * d1(i) * d1(i) / 4 Y4 = Y4 + Y1(i) * 3.14159 * d1(i) * d1(i) / 4 Next i End Sub Private Sub Text2_Change() n2 = Val(Text2.Text) For i = 1 To n2 d2(i) = Val(InputBox("输入第" & (i) & "个圆环的外径")) d3(i) = Val(InputBox("输入第" & (i) & "个圆环的内径")) X2(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的x坐标值")) Y2(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的y坐标值")) Next i For i = 1 To n2 S2 = S2 + 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4 X5 = X5 + X2(i) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4 Y5 = Y5 + Y2(i) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4 Next i End Sub Private Sub Text3_Change()
~ 15-1(I-8) 试求图示三角形截面对通过顶点A并平行于底边BC的轴的惯性矩。 解:已知三角形截面对以BC边为轴的惯性矩是,利用平行轴定理,可求得截面对形心轴的惯性矩 所以 再次应用平行轴定理,得 返回 ) 15-2(I-9) 试求图示的半圆形截面对于轴的惯性矩,其中轴与半圆形的底边平行,相距1 m。
解:知半圆形截面对其底边的惯性矩是,用 平行轴定理得截面对形心轴的惯性矩 再用平行轴定理,得截面对轴的惯性矩 / 返回 15-3(I-10) 试求图示组合截面对于形心轴的惯性矩。 解:由于三圆直径相等,并两两相切。它们的圆心构成一个边长为的等边三角形。该等边三角形的形心就是组合截面的形心,因此下面两个圆的圆心,到形心轴的距离是 上面一个圆的圆心到轴的距离是。 利用平行轴定理,得组合截面对轴的惯性矩如下: {
返回 15-4(I-11) 试求图示各组合截面对其对称轴的惯性矩。 解:(a)22a号工字钢对其对称轴的惯性矩是。 利用平行轴定理得组合截面对轴的惯性矩 (b)等边角钢的截面积是,其形心距外边缘的距离是 mm,求得组合截面对轴的惯性矩如下: : 返回 15-5(I-12) 试求习题I-3a图所示截面对其水平形心轴的惯性矩。关于形心位置,可利用该题的结果。 解:形心轴位置及几何尺寸如图 所示。惯性矩计算如下:
返回 15-6(I-14) 在直径的圆截面中,开了一个的矩形孔,如图所 示,试求截面对其水平形心轴和竖直形心轴的惯性矩 和。 解:先求形心主轴的位置 ! 即 返回 15-7(I-16) 图示由两个20a号槽钢组成的组合截面,若欲使截面对两对称轴的惯性矩和相等,则两槽钢的间距应为多少 ( 解:20a号槽钢截面对其自身的形心轴、的惯性矩是,;横截面积为;槽钢背到其形心轴的距离是。
看大家对横向力分布系数计算疑惑颇多,特在这里做一期横向力分布系数计算教程(本教程讲的比较粗浅,适用于新手)。 总的来说,横向力分布系数计算归结为两大类(对于新手能够遇到的): 1、预制梁(板梁、T梁、箱梁) 这一类也可分为简支梁和简支转连续 2、现浇梁(主要是箱梁) 首先我们来讲一下现浇箱梁(上次lee_2007兄弟问了,所以先讲这个吧) 在计算之前,请大家先看一下截面 这是一个单箱三室跨径27+34+27米的连续梁,梁高1.55米,桥宽12.95米!! 支点采用计算方法为为偏压法(刚性横梁法) mi=P/n±P×e×ai/(∑ai x ai) 跨中采用计算方法为修正偏压法(大家注意两者的公式,只不过多了一个β) mi=P/n±P×e×ai×β/(∑ai x ai) β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii) 其中:∑It---全截面抗扭惯距 Ii ---主梁抗弯惯距Ii=K Ii` K为抗弯刚度修正系数,见后 L---计算跨径 G---剪切模量G=0.4E 旧规范为0.43E P---外荷载之合力 e---P对桥轴线的偏心距 ai--主梁I至桥轴线的距离 在计算β值的时候,用到了上次课程https://www.doczj.com/doc/7213781008.html,/thread-54712-1-1.html 我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩,可以采用midas计算抗弯和抗扭,也可以采用桥博计算抗弯, 或者采用简化截面计算界面的抗扭,下面就介绍一下这种大箱梁是如何简化截面的: 简化后箱梁高度按边肋中线处截面高度(1.55m)计算,悬臂比拟为等厚度板。 ①矩形部分(不计中肋): 计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2) 其中:t,t1,t2为各板厚度
第七章 截面几何性质 基本要求与重点 1.形心与重心 (1)理解重心与形心,熟知常见规则图形形心的位置。 (2)记住以下常见规则几何图形的形心位置:圆及圆环、矩形、三角形。 (3)能熟练计算,由规则图形构成的组合图形的形心位置。 2.面积静矩(又称静矩或面矩) (1)了解面积静矩的积分定义,掌握其有限式定义。 (2)能熟练计算组合图形的静矩。 (3)熟知面积静矩的重要性质。 3.惯性矩与极惯性矩。 (1)理解惯性矩与极惯性矩 (2)了解惯性矩与极惯性矩的定义 (3)掌握惯性矩与极惯性矩之间的关系 (4)掌握平行轴定理及组合图形惯性矩的计算方法。 (5)记住圆及圆环对圆心的极惯性矩 (6)记住矩形截面对其对称轴的惯性矩。 4.了解惯性积、形心主轴的概念 主要内容 1.形心与重心 (1)概念与性质 重心是物体的重力中心,形心是几何体的形状中心。对均质物体,重心与形心位置重合。 若存在几何对称同,则形心必在对称轴上。 (2)计算 形心位置的计算公式分积分式与代数式两种。其中,常用的是代数形式的计算公式: 11n n ic i ic i i i c c x A y A x y A A ==????==∑∑, 2.面积静矩(又称静矩或面矩) (1)定义:分为代数式和积分式两种形式 有限式:几何图形的面积乘以形心到某轴的距离的坐标值,称为该图形对该轴的静矩。 积分式:几何图形的元面积乘以点到某轴的距离的坐标值,称为该元面积对该轴的静矩;所有点的元面积静矩之和,为几何图形的对该轴的静矩。 (2)面积静矩的重要性质:若图形对某轴的面积静矩为零,则该轴过这一图形的形心;反之亦然。也就是说,静矩为零与轴过形心互为充要条件。
附录I 截面的几何性质 习题解 [习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。 (a ) 解:)(24000)1020()2040(3 mm y A S c x =+??=?= (b ) 解:)(422502 65 )6520(3mm y A S c x =??=?= (c ) 解:)(280000)10150()20100(3 mm y A S c x =-??=?= (d ) 解:)(520000)20150()40100(3 mm y A S c x =-??=?= [习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。 解:用两条半径线和两个同心圆截出一微分面积如图所示。 dx xd dA ?=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ?=??=??=?=sin sin )(2 半圆对x 轴的静矩为:
3 2)]0cos (cos [3]cos []3[sin 3300300 2 r r x d dx x S r r x =--?=-?=?=?? πθθθπ π 因为c x y A S ?=,所以c y r r ??=232132π π 34r y c = [习题I-3] 试确定图示各图形的形心位置。 (a ) 解: 习题I-3(a): 求门形截面的形心位置 矩形 L i B i Ai Y ci AiYci Yc 离顶边 上 400 2 8000 160 1280000 左 150 2 3000 7 5 225000 右 150 2 0 3000 7 5 225000 14000 1730000 Ai=Li*Bi Yc=∑AiYci/∑Ai (b) 解: 习题I-3(b): 求L 形截面的形心位置 矩形 L i B i Ai Y ci AiYc i Y c X ci AiX ci X c 下 1 60 10 160 5 8000 8 128 000
截面几何性质计算 计算过上部的人都知道,在计算横向力分布系数和冲击系数的时候都需要计算截面的抗弯惯距和抗扭惯距,下面就介绍几种方法来计算抗弯惯距和抗扭惯距(本教程拿30米简支转连续箱梁截面做样例): 一、在AUTOCAD中有一个命令massprop可以计算截面的面积、周长、质心、惯性矩 操作简介: 1、首先在CAD中画出如下图的图形; 2、用region命令将图形转化成内外两个区域; 3、用subtract命令求内外区域的差集; 4、用move命令将图形移动至(0,0,0),用scale命令将图形单位调整为米; 5、用massprop命令计算截面性质(可惜这个命令不能计算抗扭惯距) Command: mas MASSPROP Select objects: 1 found Select objects: ---------------- REGIONS ---------------- Area(面积): 1.2739 Perimeter(周长): 13.7034 Bounding box(边缘): X: -1.7000 -- 1.7000 Y: 0.0000 -- 1.6000 Centroid(质心): X: 0.0000 Y: 1.0458 Moments of inertia: X: 1.7883 Y: 0.7922 Product of inertia: XY: 0.0000 Radii of gyration: X: 1.1848 Y: 0.7886 Principal moments and X-Y directions about centroid: I: 0.3950 along [1.0000 0.0000]这就是惯距 J: 0.7922 along [0.0000 1.0000] 2008-6-6 23:10
附录Ⅰ 截面的几何性质 §I ?1 截面的静矩和形心位置 如图I ?1所示平面图形代表一任意截面,以下两积分 ? ??? ?==??A z S A y S A y A z d d (I ?1) 分别定义为该截面对于z 轴和y 轴的静矩。 静矩可用来确定截面的形心位置。由静力学中确定物体重心的公式可得 ? ??? ??? == ??A A z z A A y y A C A C d d 利用公式(I ?1),上式可写成 ? ??? ? ? ?==== ??A S A A z z A S A A y y y A C z A C d d (I ?2) 或 ? ? ? ==C y C z Az S Ay S (I ?3) ? ??????== A S z A S y y C z C (I ?4) 如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。即: ?? ??? ?? ==∑∑==n i ci i y n i ci i z z A S y A S 11 (I ?5) 式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。 将式(I ?5)代入式(I ?4),得到组合图形形心坐标的计算公式为 图I ?1
??? ? ?????????==∑∑∑∑====n i i n i ci i c n i i n i ci i c A z A z A y A y 111 1 (I ?6) 例题I ?1 图a 所示为对称T 型截面,求该截面的形心位置。 解:建立直角坐标系zOy ,其中y 为截面的对称轴。因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2 y Ⅰ=0.46m ,y Ⅱ=0.2m m 323.008.0072.02 .008.046.0072.0II I II II I I 1 1 =+?+?= ++= = ∑∑==A A y A y A A y A y n i i n i ci i c §I ?2 惯性矩、惯性积和极惯性矩 如图I ?2所示平面图形代表一任意截面,在图形平面内建立直角坐标系 zOy 。现在图形内取微面积d A ,d A 的形心在坐标系zOy 中的坐标为y 和z ,到坐标原点的距离为ρ。现定义y 2d A 和z 2d A 为微面积d A 对z 轴和y 轴的惯性矩,ρ2d A 为微面积d A 对坐标原点的极惯性矩,而以下三个积分 ? ??? ? ? ?===???A ρI A z I A y I A A y A z d d d 2 P 22 (I ?7) 分别定义为该截面对于z 轴和y 轴的惯性矩以及对坐标原点的极惯性矩。 由图(I ?2)可见,222z y +=ρ,所以有 ??+=+==A y z A I I A z y A ρI )d (d 222P (I ?8) 即任意截面对一点的极惯性矩,等于截面对以该点为原点的两任意正交坐标轴的惯性矩之和。 另外,微面积d A 与它到两轴距离的乘积zy d A 称为微面积d A 对y 、z 轴的惯性积,而积分 A zyd I A yz ?= (I ?9) 例题I ?1图 图I ?2
习题 I ?1 试求平面图形的形心位置。 [ 解:由对称 m 3.0c =z m 357.02 .04.04.02.02.06.07 .02.04.04.04.02.01.02.06.0c =?+?+???+??+??=y 解:m 093.04 .01.01.03.005 .04.01.015.01.03.0c =?+???+??= z 、 m 193.04 .01.01.03.03 .04.01.005.01.03.0c =?+???+??= y I ?2 试求平面图形的形心坐标。 " O (c) (a) z y — (b)
解: l n n dz z zdz z z l n l n 2 1 0c ++= = ?? ()2 c += -=??n l dz z ydy y l y n l n l n n · 解:由对称 r z =c πππ342 322223 20 2 2c r r r r ydy y r y r ==-= ? I ?3 试求图示截面的阴影线面积对z 轴的静矩。(图中C 为截面形心) — 解:3 c **mm 24000302040=??==y A S z z O (d) (a)
解:3 c **mm 422505.322065=??==y A S z ( I ?4 求以下截面对z 轴的惯性矩。(z 轴通过截面形心) ) 解:() 64 64 64 42414 24 1d d d d I z -= - = πππ 【 解:12 12124 2 414241a a a a I z -=-= I ?5 试求图示三角形截面对通过顶点A 并平行于底边BC 的z 轴的惯性矩。 解: (a) [ (b) |
15-1(I-8)? 试求图示三角形截面对通过顶点A并平行于底边BC的轴的惯性矩。解:已知三角形截面对以BC边为轴的惯性矩是,利用平行轴定理,可求得截面对形心轴的惯性矩 ????????????? 所以?????? ?????? 再次应用平行轴定理,得 ????????????? 返回 15-2(I-9)? 试求图示的半圆形截面对于轴的惯性矩,其中轴与半圆形的底边平行,相距 1 m。 ? 解:知半圆形截面对其底边的惯性矩是,用平行轴定理得截面对形心轴的惯性矩 ????????????? ??? 再用平行轴定理,得截面对轴的惯性矩 ????????????? ???????????????????? 返回 15-3(I-10)? 试求图示组合截面对于形心轴的惯性矩。 解:由于三圆直径相等,并两两相切。它们的圆心构成一个边长为的等边三角形。该等边三角形的形心就是组合截面的形心,因此下面两个圆的圆心,到形心轴的距离是
上面一个圆的圆心到轴的距离是。 ??? 利用平行轴定理,得组合截面对轴的惯性矩如下: ????????????? 返回 15-4(I-11)? 试求图示各组合截面对其对称轴的惯性矩。 解:(a)22a号工字钢对其对称轴的惯性矩是。 利用平行轴定理得组合截面对轴的惯性矩 ?????? ?????? (b)等边角钢的截面积是,其形心距外边缘的距离是 mm,求得组合截面对轴的惯性矩如下: ??????? 返回 15-5(I-12) 试求习题I-3a图所示截面对其水平形心轴的惯性矩。关于形心位置,可利用该题的结果。 解:形心轴位置及几何尺寸如图所示。惯性矩计算如下: ?????? 返回 15-6(I-14)? 在直径的圆截面中,开了一个的矩形孔,如图所示,试求截面对其水平形心轴和竖直形心轴的惯性矩和。 解:先求形心主轴的位置 即 ?????? ??????
截面几性质计算 计算过上部的人都知道,在计算横向力分布系数和冲击系数的时候都需要计算截面的抗弯惯距和抗扭惯距,下面就介绍几种法来计算抗弯惯距和抗扭惯距(本教程拿30米简支转连续箱梁截面做样例): 一、在AUTOCAD中有一个命令massprop可以计算截面的面积、长、质心、惯性矩 操作简介: 1、首先在CAD中画出如下图的图形; 2、用region命令将图形转化成外两个区域; 3、用subtract命令求外区域的差集; 4、用move命令将图形移动至(0,0,0),用scale命令将图形单位调整为米; 5、用massprop命令计算截面性质(可惜这个命令不能计算抗扭惯距) Command: mas MASSPROP Select objects: 1 found Select objects: ----------------REGIONS---------------- Area(面积): 1.2739 Perimeter(长):13.7034 Bounding box(边缘):X: -1.7000-- 1.7000 Y: 0.0000-- 1.6000 Centroid(质心):X: 0.0000 Y: 1.0458 Moments of inertia:X: 1.7883 Y: 0.7922 Product of inertia:XY: 0.0000 Radii of gyration:X: 1.1848 Y: 0.7886 Principal moments and X-Y directions about centroid: I: 0.3950 along [1.0000 0.0000]这就是惯距 J: 0.7922 along [0.0000 1.0000] 2008-6-6 23:10
习题 I ?1 试求平面图形的形心位置。 解:由对称 m 3.0c =z m 357.02 .04.04.02.02.06.07 .02.04.04.04.02.01.02.06.0c =?+?+???+??+??=y 解:m 093.04.01.01.03.005 .04.01.015.01.03.0c =?+???+??=z m 193.04 .01.01.03.03 .04.01.005.01.03.0c =?+???+??= y I ?2 试求平面图形的形心坐标。 解: O (c (a z y O (b
l n n dz z zdz z z l n l n 2 10 0c ++==?? ()2 c += -=??n l dz z ydy y l y n l n l n n 解:由对称 r z =c πππ342 322223 2 2 2c r r r r ydy y r y r ==-=? I ?3 试求图示截面的阴影线面积对z 轴的静矩。(图中C 为截面形心) 解:3 c **mm 24000302040=??==y A S z z O (d (a) (b)
解:3 c **mm 422505.322065=??==y A S z I ?4 求以下截面对z 轴的惯性矩。(z 轴通过截面形心) 解:() 64 64 64 42414 24 1d d d d I z -= - =πππ 解:12 12124 2 414241a a a a I z -=-= I ?5 试求图示三角形截面对通过顶点A 并平行于底边BC 的z 轴的惯性矩。 解: 4302bh y bdy h y I h z =?? ? ???=? I ?6 试求图示r =1m 半圆形截面对于z 轴的惯性矩。其中z 轴与半圆形的底边平行,相距1m 。 (a) a (b) C d
附录I 截面的几何性质 习题解 [习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。 (a ) 解:)(24000)1020()2040(3 mm y A S c x =+??=?= (b ) 解:)(422502 65 )6520(3mm y A S c x =??=?= (c ) 解:)(280000)10150()20100(3 mm y A S c x =-??=?= (d ) 解:)(520000)20150()40100(3 mm y A S c x =-??=?= [习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。 解:用两条半径线和两个同心圆截出一微分面积如图所示。 dx xd dA ?=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ?=??=??=?=sin sin )(2 半圆对x 轴的静矩为:
3 2)]0cos (cos [3]cos []3[sin 3300300 2 r r x d dx x S r r x =--?=-?=?=?? πθθθπ π 因为c x y A S ?=,所以c y r r ??=232132π π 34r y c = [习题I-3] 试确定图示各图形的形心位置。 (a ) 解: 习题I-3(a): 求门形截面的形心位置 矩形 Li Bi Ai Yci AiYci Yc 离顶边 上 400 20 8000 160 1280000 左 150 20 3000 75 225000 右 150 20 3000 75 225000 14000 1730000 123.6 46.4 Ai=Li*Bi Yc=∑AiYci/∑Ai 解: 习题I-3(b): 求L 形截面的形心位置 矩形 Li Bi Ai Yci AiYci Yc Xci AiXci Xc 下 160 10 1600 5 8000 80 128000 左 90 10 900 55 49500 5 4500 2500 57500 23 132500 53 Ai=Li*Bi Yc=∑AiYci/∑Ai Xc=∑AiXci/∑Ai (c)
附录I 截面的几何性质 习题解 [习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。 (a ) 解:)(24000)1020()2040(3 mm y A S c x =+??=?= (b ) 解:)(422502 65 )6520(3mm y A S c x =??=?= (c ) 解:)(280000)10150()20100(3 mm y A S c x =-??=?= (d ) 解:)(520000)20150()40100(3 mm y A S c x =-??=?= [习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。 解:用两条半径线和两个同心圆截出一微分面积如图所示。 dx xd dA ?=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ?=??=??=?=sin sin )(2
半圆对x 轴的静矩为: 3 2)]0cos (cos [3]cos []3[sin 3300300 2 r r x d dx x S r r x =--?=-?=?=?? πθθθπ π 因为c x y A S ?=,所以c y r r ??=232132π π 34r y c = [习题I-3] 试确定图示各图形的形心位置。 (a ) 习题I-3(a): 求门形截面的形心位置 矩形 L i B i Ai Y ci AiYci Yc 离顶边 上 400 2 8000 160 1280000 左 150 2 3000 7 5 225000 右 150 2 0 3000 7 5 225000 14000 1730000 Ai=Li*Bi Yc=∑AiYci/∑Ai (b) 解: 习题I-3(b): 求L 形截面的形心位置 矩形 L i B i Ai Y ci AiYc i Y c X ci AiX ci X c 下 1 1 160 5 8000 8 128