
常微分方程组边值问题解法
打靶法Shooti ng Method (shoot in g.m )
% 丁靶法求常微分方程的边值问题
function [x,a,b ,n]=shooti ng(fu n, xO,x n, eps) if nargin<3
eps=1e-3;
end
x1=x0+ra nd;
[a,b]=ode45(fu n, [0,10],[0,x0]');
c0=b(le ngth(b),1);
[a,b]=ode45(fu n, [0,10],[0,x1]');
c1=b(le ngth(b),1);
x2=x1-(c1-x n)*(x1-x0)/(c1-c0);
n=1;
while (no rm(c1-x n)>=eps & no rm(x2-x1)>=eps) x0=x1;x 仁x2;
[a,b]=ode45(fu n,[ 0,10],[0,x0]');
cO=b(le ngth(b),1);
[a,b]=ode45(fu n,[ 0,10],[0,x1]');
c1= b(le ngth(b),1)
x2=x1-(c1-x n)*(x1-x0)/(c1-c0);
n=n+1;
end
x=x2;
应用打靶法求解下列边值问题:
y 10 0 解:将其转化为常微分方程组的初值问题
命令:
xO=[O:O.1:1O];
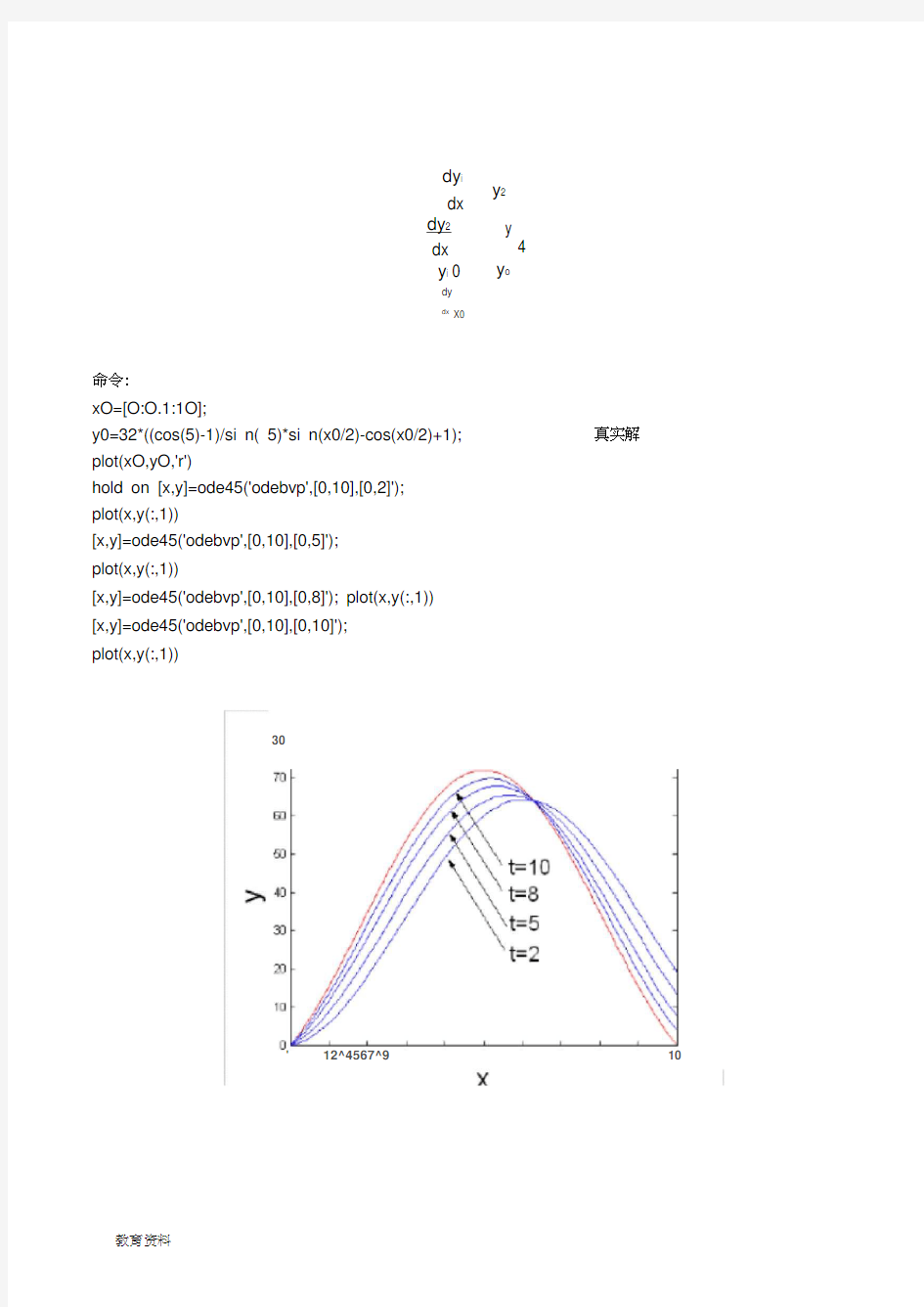
y0=32*((cos(5)-1)/si n( 5)*si n(x0/2)-cos(x0/2)+1); plot(xO,yO,'r')
hold on [x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1))
[x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1))
[x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1))
dy i dx y 2 dy 2 dx y i 0
y 4 y o
dy
dx X0
真实解
30
'
12^4567^9 10
函数:(odebvp.m)
泌值常微分方程(组)函数
function f=odebvp(x,y)
f(1)=y(2);
f(2)=8-y(1)/4;
f=[f(1);f(2)];
命令:
[t,x,y, n]=shoot in g('odebvp',10,0,1e-3)
计算结果:(eps=0.001 )
t=11.9524
plot(x,y(:,1))
x0=[0:1:10];
y0=32*((cos(5)-1)/si n( 5)*si n(x0/2)-cos(x0/2)+1); hold on
plot(xO,yO, ' o')
有限差分法 Finite Differenee Methods FDM
同上例:
Y i i
2
Y i y i i
h 2 2 ——
1
4
函数:(differe nce.m )
%有限差分法求常微分方程的边值问题 function [x,y]=differe nce(xO,x n,yO,yn,n) h=(x n-xO)/n;
a=eye( n-1)*(-(2-h A 2/4)); for i=1: n-2 a(i,i+1)=1; a(i+1,i)=1; end
b=o nes( n-1,1)*8*hA2; b(1)=b(1)-0; b(n-1)=b( n-1)-0; yy=a\b;
x(1)=x0;y(1)=y0; for i=2: n x(i)=x0+(i-1)*h;
Y i i 2
若划分为10个区间,则:
h- Y i Y i 1 8h 2
4
(differe nce.m )
1
h 2 2 4
1
1
Y 1 Y 2
8h 2
8h 2
0 h 2
Y n 2 8h 2
2
4 1
Y n 1
8h 2 0
.2
h 1
2
4
y(i)=yy(i-i);
end
x(n)=xn;y(n)=yn;
命令:
[x,y]=differe nce(0,10,0,0,100);
计算结果:
xO=[O:O.1:1O];
y0=32*((cos(5)-1)/si n( 5)*si n(x0/2)-cos(x0/2)+1);
plot(xO,yO,'r')
hold on
[x,y]=differe nce(0,10,0,0,5);
plot(x,y,'.')
[x,y]=differe nce(0,10,0,0,10);
plot(x,y,'--')
[x,y]=differe nce(0,10,0,0,50);
plot(x,y,'-.')
正交配置法Orthogonal Collocatioin Methods CM
构造正交矩阵函数(collmatrix.m )
%E交配置矩阵(均用矩阵法求对称性与非对称性正交配置矩阵) function [am,bm,wm,an,bn,wn]=collmatrix(a,m,fm,n,fn) 真实解
的
3 4 6 7 9 9 1D
X
xO=symm(a,m,fm); %a为形状因子;m为零点数;fm为对称的权函数(0为权函数1,非0为权
函数1-x A2)
for i=1:m
xm(i)=x0(m+1-i);
end
xm(m+1)=1;
for j=1:m+1
for i=1:m+1
qm(j,i)=xm(j)A(2*i-2);
cm(j,i)=(2*i-2)*xm(j)A(2*i-3);
dm(j,i)=(2*i-2)*(2*i-3+(a-1))*xm(j)A(2*i-3+(a-1)-1-(a-1));
end
fmm(j)=1/(2*j-2+a);
end
am=cm*i nv(qm);
bm=dm*i nv(qm);
wm=fmm*i nv(qm);
x1=unsymm(n,fn); %n 为零点数;fn为非对称的权函数(0为权函数1,非0为权函数1-x) xn (1)=0; for i=2: n+1
xn( i)=x1( n+2-i);
end
xn(n+2)=1;
for j=1: n+2
for i=1: n+2
qn (j,i)=x n(j)A(i-1);
if j==0 | i==1
cn (j,i)=0;
else
cn (j,i)=(i-1)*x n(j)A(i-2);
end
if j==0 | i==1 | i==2
dn (j,i)=O;
else
dn (j,i)=(i-2)*(i-1)*x n(jF(i-3);
end
end
fnn (j)=1/j;
end
an=cn *i nv(qn);
bn=dn *i nv(qn); wn=fnn*inv(qn); %E交多项式求根(适用于对称问题)
fun ctio n p=symm(a,m,fm) %a for i=1:m
c1=1;
c2=1;
c3=1;
c4=1;
for j=0:i-1
c1= c1*(-m+j);
if fm==0
c2=c2*(m+a/2+j);% else
c2=c2*(m+a/2+j+1);% end
c3=c3*(a/2+j);
c4=c4*(1+j);
end
p(m+1-i)=c1*c2/c4/c3;
end
p(m+1)=1;%为多项式系数向量p=sqrt(roots(p)); 为形状因子,m为配置点数,fm为权函数
权函数为1
权函数为1-x A2
,求出根后对对称问题还应开方才是零点
%E交多项式求根(适用于非对称性问题)
目录 引言 (1) 1预备知识 (2) 定义1.1(奇异Sturm-Liouville边值问题的正解) (2) 引理1.1.1 (2) 定义1.2(凸集的概念) (3) 定义1.3锥的定义 (3) 定义1.4(全连续算子的概念) (3) 1.5 (常微分边值问题的定义) (4) 定义1.6混合单调算子得定义) (4) 2 常微分方程边值问题正解得存在性 (5) 2.1 奇异Sturm-Liouville常微分边值问题的正解存在在 (5) 子 (8) 2.2 一类二阶边值问题的存在性 (9) 3一类混合单调算子应用 (11) 3.1一类混合单调算子的存在唯一性?........................ 错误!未定义书签。 3.2 求常微分边值问题的例题 (13) 结束语 (15) 参考文献 (15) 致 (16)
常微分方程边值问题与不动点定 (数学与统计学院 11级数学与应用数学2班)指导教师:攀峰 引言 从历史上看在有了微积分这个概念以后,紧接着出现了常微分方程。发展初期是属于“求通解”得时代,当人们从初期的热潮中结束要从维尔证明了卡帝方程中是一定不会存在一般性的初等解的时候开始的,并且柯西紧接着又提出了初值问题,常微分方程开始从重视“求通解”转向重视“求定解”的历史时代。 大学我们都学习了常微分方程这门学科,如果要研究它的定解问题,我们首先就会知道是常微分方程的初值问题。然而,在科学技术、生产实际问题中,我们还是提出了另一类定解问题-边值问题。对于常微分方程边值问题,伟大的科学家最早在解决二阶线性微分方程时,提出了分离变量法。[]1.在牛顿时期,科学家们已经提出过常微分的边值问题,牛顿也对常微分边值问题进行过研究,并且在1666年10月牛顿已经在这个领域取得了很大的成就,但是由于种种原因当时并没有整理成论文,所以没有及时出版。但在1687年他终于把在常微分方程上研究的成果发表了,虽然不是在数学著作中,却是他的一本力学著作中(《自然哲学的数学原理》)。 在微积分刚创立时期,雅克.伯努利来自瑞士的科学家提出了远著文明的问题-悬链线问题,紧着的地二年著名数学家莱布尼兹就给出了正确的解答,通过对绳子上个点受力分析,建立了以下方程 这个方程满足的定解条件是y(a)=α;y(b)=β.这是一个典型的常微分方程的边值问题。从这开始,常微分边值问题已经是科学家研究微分方程是不可或缺的工具,我就简单列举几个例子:(比如种族的生态系统;梁的非线性震动)等。对于怎么研究它,
微分方程公式运用表 一、 一阶微分方程 判断特征: (,)dy f x y dx = 类型一:()()dy g x h y dx =(可分离变量的方程) 解法(分离变量法): ()()dy g x dx h y =,然后两边同时积分。 类型二:()()dy P x y Q x dx +=(一阶线性方程) 解法(常数变易法):()()(())P x dx P x dx y e C Q x e dx -??=+? 类型三: (,)(,)dy f x y f tx ty dx ==(一阶齐次性方程) 解法(换元法):y u x =?令类型一 类型四:P()y=Q(x)y n dy x dx +(伯努利方程) 解法(同除法):1()()n n dy y P x y Q x dx --+=?类型二 二、 可降阶的高阶微分方程 类型一:()()n y f x = 解法(多次积分法):(1)()()n du u y f x f x dx -=? =?令多次积分求 类型二:''(,')y f x y = 解法:'(,)dp p y f x p dx =?=?令一阶微分方程 类型三:''(,')y f y y = 解法:'(,)dp dp dy dp p y p f y p dx dy dx dy =?==??令类型二 三、线性微分方程 类型一:''()'()0y P x y Q x y ++=(二阶线性齐次微分方程) 解法:找出方程的两个任意线性不相关特解:12(),()y x y x
则:1122()()()y x c y x c y x =+ 类型二:''()'()()y P x y Q x y f x ++=(二阶线性非齐次微分方程) 解法:先找出对应的齐次微分方程的通解:31122()()()y x c y x c y x =+ 再找出非齐次方程的任意特解()p y x ,则:1122()()()()p y x y x c y x c y x =++ 类型三:'''0y py q ++=(二阶线性常系数齐次微分方程) 解法(特征方程法):2 1,20p q λλλ++=?= (一)122121240x x p q y c e c e λλλλ?=->?≠?=+ (二)12120()x y c c x e λλλλ?=?==?=+ (三)12120,(cos sin )x i i y e c x c x αλαβλαβββ?
利用MATLAB求解常微分方程数值解
目录 1. 内容简介 (1) 2. Euler Method(欧拉法)求解 (1) 2.1. 显式Euler法和隐式Euler法 (2) 2.2. 梯形公式和改进Euler法 (3) 2.3. Euler法实用性 (4) 3. Runge-Kutta Method(龙格库塔法)求解 (5) 3.1. Runge-Kutta基本原理 (5) 3.2. MATLAB中使用Runge-Kutta法的函数 (7) 4. 使用MATLAB求解常微分方程 (7) 4.1. 使用ode45函数求解非刚性常微分方程 (8) 4.2. 刚性常微分方程 (9) 5. 总结 (9) 参考文献 (11) 附录 (12) 1. 显式Euler法数值求解 (12) 2. 改进Euler法数值求解 (12) 3. 四阶四级Runge-Kutta法数值求解 (13) 4.使用ode45求解 (14)
1.内容简介 把《高等工程数学》看了一遍,增加对数学内容的了解,对其中数值解法比较感兴趣,这大概是因为在其它各方面的学习和研究中经常会遇到数值解法的问题。理解模型然后列出微分方程,却对着方程无从下手,无法得出精确结果实在是让人难受的一件事情。 实际问题中更多遇到的是利用数值法求解偏微分方程问题,但考虑到先从常微分方程下手更为简单有效率,所以本文只研究常微分方程的数值解法。把一个工程实际问题弄出精确结果远比弄清楚各种细枝末节更有意思,因此文章中不追求非常严格地证明,而是偏向如何利用工具实际求解出常微分方程的数值解,力求将课程上所学的知识真正地运用到实际方程的求解中去,在以后遇到微分方程的时候能够熟练运用MATLAB得到能够在工程上运用的结果。 文中求解过程中用到MATLAB进行数值求解,主要目的是弄清楚各个函数本质上是如何对常微分方程进行求解的,对各种方法进行MATLAB编程求解,并将求得的数值解与精确解对比,其中源程序在附录中。最后考察MATLAB中各个函数的适用范围,当遇到实际工程问题时能够正确地得到问题的数值解。 2.Euler Method(欧拉法)求解 Euler法求解常微分方程主要包括3种形式,即显式Euler法、隐式Euler法、梯形公式法,本节内容分别介绍这3种方法的具体内容,并在最后对3种方法精度进行对比,讨论Euler法的实用性。 本节考虑实际初值问题 使用解析法,对方程两边同乘以得到下式
第8章 常微分方程边值问题的数值解法 引 言 第7章介绍了求解常微分方程初值问题的常用的数值方法;本章将介绍常微分方程的边值问题的数值方法。 只含边界条件(boundary-value condition)作为定解条件的常微分方程求解问题称为常微分方程的边值问题(boundary-value problem). 为简明起见,我们以二阶边值问题为 则边值问题(8.1.1)有唯一解。 推论 若线性边值问题 ()()()()()(),, (),()y x p x y x q x y x f x a x b y a y b αβ'''=++≤≤?? ==? (8.1.2) 满足 (1) (),()p x q x 和()f x 在[,]a b 上连续; (2) 在[,]a b 上, ()0q x >, 则边值问题(8.1.1)有唯一解。 求边值问题的近似解,有三类基本方法: (1) 差分法(difference method),也就是用差商代替微分方程及边界条件中的导数,最终化为代数方程求解; (2) 有限元法(finite element method);
(3) 把边值问题转化为初值问题,然后用求初值问题的方法求解。 差分法 8.2.1 一类特殊类型二阶线性常微分方程的边值问题的差分法 设二阶线性常微分方程的边值问题为 (8.2.1)(8.2.2) ()()()(),,(),(), y x q x y x f x a x b y a y b αβ''-=<
第四章常微分方程数值解 [课时安排]6学时 [教学课型]理论课 [教学目的和要求] 了解常微分方程初值问题数值解法的一些基本概念,如单步法和多步法,显式和隐式,方法的阶数,整体截断误差和局部截断误差的区别和关系等;掌握一阶常微分方程初值问题的一些常用的数值计算方法,例如欧拉(Euler)方法、改进的欧拉方法、龙贝-库塔(Runge-Kutta)方法、阿达姆斯(Adams)方法等,要注意各方法的特点及有关的理论分析;掌握构造常微分方程数值解的数值积分的构造方法和泰勒展开的构造方法的基本思想,并能具体应用它们导出一些常用的数值计算公式及评估截断误差;熟练掌握龙格-库塔(R-K)方法的基本思想,公式的推导,R-K公式中系数的确定,特别是能应用“标准四阶R-K公式”解题;掌握数值方法的收敛性和稳定性的概念,并能确定给定方法的绝对稳定性区域。[教学重点与难点] 重点:欧拉方法,改进的欧拉方法,龙贝-库塔方法。 难点:R—K方法,预估-校正公式。 [教学内容与过程] 4.1 引言 本章讨论常微分方程初值问题 (4.1.1) 的数值解法,这也是科学与工程计算经常遇到的问题,由于只有很特殊的方程能用解析方法求解,而用计算机求解常微分方程的初值问题都要采用数值方法.通常我们假定(4.1.1)中 f(x,y)对y满足Lipschitz条件,即存在常数L>0,使对,有 (4.1.2) 则初值问题(4.1.1)的解存在唯一. 假定(4.1.1)的精确解为,求它的数值解就是要在区间上的一组离散点 上求的近似.通常取 ,h称为步长,求(4.1.1)的数值解是按节点的顺序逐步 推进求得.首先,要对方程做离散逼近,求出数值解的公式,再研究公式的局部截
常微分方程组边值问题解法 打靶法Shooting Method (shooting.m ) %打靶法求常微分方程的边值问题 function [x,a,b,n]=shooting(fun,x0,xn,eps) if nargin<3 eps=1e-3; end x1=x0+rand; [a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1); [a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1); x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=1; while (norm(c1-xn)>=eps & norm(x2-x1)>=eps) x0=x1;x1=x2; [a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1); [a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1) x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=n+1; end x=x2; 应用打靶法求解下列边值问题: ()()??? ????==- =010004822y y y dx y d 解:将其转化为常微分方程组的初值问题
()????? ? ?????==-==t dx dy y y y dx dy y dx dy x 0011221 048 命令: x0=[0:0.1:10]; y0=32*((cos(5)-1)/sin(5)*sin(x0/2)-cos(x0/2)+1); 真实解 plot(x0,y0,'r') hold on [x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1))
第九章 微分方程 一、教学目标及基本要求 (1) 了解微分方程及其解、通解、初始条件和特解的概念。 (2) 掌握变量可分离的方程和一阶线性方程的解法,会解齐次方程。 (3) 会用降阶法解下列方程:),(),,(),()(y y f y y x f y x f y n '='''=''=。 (4) 理解二阶线性微分方程解的性质以及解的结构定理。 (5) 掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程。 (6) 会求自由项多项式、指数函数、正弦函数、余弦函数,以及它们的和与二阶常系数非齐次线性微分方程的 特解和通解。 (7) 会用微分方程解决一些简单的应用问题。 二、本章教学内容的重点和难点 1、理解和熟悉微分方程的一些基本概念; 2、掌握一阶和高阶微分方程的各种初等积分法; 3、熟悉线性方程的基础理论,掌握常系数二阶线性齐次与非齐次方程的解法; 4、会列微分方程及其始值问题去解决实际问题。 三、本章教学内容的深化和拓宽: 1、分离变量法的理论根据; 2、常用的变量代换; 3、怎样列微分方程解应用题; 4、黎卡提方程; 5、全微分方程的推广; 6、二阶齐次方程; 7、高阶微分方程的补充; 8、求线性齐次方程的另一个线性无关的解; 9、求线性非齐次方程的一个特解; 10、常数变易法。 本章的思考题和习题 解下列方程(第1-6题) 1、2)0(,)1(==+'+y x y y x 2、()[]f dx x f e e x f x x x ,)(02?+=可微 3、212 22sin 22sin 1X e y x y y x ++='?+ 4、0)3(24=+-xydx dy x y 5、21)0(,1)0(,022- ='=='+''y y y x y 6、2y y y x y '-'+'= 7、已知可微函数)(x f 满足 ?-=+x x f f x f x x f dx x f 12)()1(,1)()()(和求; 8、已知)(,,1)(2 1)(10x f f x f da ax f 求可微+= ?; 9、求与曲线族C y x =+2232相交成ο45角的曲线; 10、一容器的容积为100L ,盛满盐水,含10kg 的盐,现以每分钟3L 的速度向容器内注入淡水冲淡盐水,又以同样的速度将盐水抽入原先盛满淡水的同样大小的另一容器内,多余的水便从容器内流出,问经过多少时间,两容器内的含盐量相等?
第十一章 常微分方程边值问题的数值解法 工程技术与科学实验中提出的大量问题是常微分方程边值问题.本章将研究常微分方程边值问题的数值求解方法.主要介绍三种边界条件下的定解问题和两大类求解边值问题的数值方法,打靶法算法和有限差分方法. 11.1 引言 在很多实际问题中都会遇到求解常微分方程边值问题. 考虑如下形式的二阶常微分方程 ),,(y y x f y '='', b x a <<, (11.1.1) 在如下三种边界条件下的定解问题: 第一种边界条件: α=)(a y , β=)(b y (11.1.2) 第二种边界条件: α=')(a y , β=')(b y (11.1.2) 第三种边界条件: ? ? ?=-'=-'101 0)()()()(b b y b y a a y a y βα, (11.1.13) 其中0 0, ,00000>+≥≥b a b a . 常微分方程边值问题有很多不同解法, 本书仅介绍打靶方法和有限差分方法. 11.2 打靶法 对于二阶非线性边值问题 ()()().,,βα==≤≤'=''b y a y b x a y y x f y ,,, (11.2.1) 打靶法近似于使用初值求解的情况. 我们需要利用一个如下形式问题初值解的序列: ()()v a w a w b x a w w x f w ='=≤≤'='')(,,,,,α, (11.2.2) 引进参数v 以近似原边界值问题的解.选择参数k v v =,以使: ()()β==∞ →b y v b w k k ,lim , (11.2.3)
其中),(k v x w 定义为初值问题(11.2.2)在k v v =时的解,同时()x y 定义为边值问题(11.2.1)的解. 首先定义参数0v ,沿着如下初值问题解的曲线,可以求出点),(αa 对应的初始正视图 ()()v a w a w b x a w w x f w ='=≤≤'='')(,,,,,α. (11.2.4) 如果),(0v b w 不严格收敛于β,那么我们选择1v 等值以修正近似值,直到),(0v b w 严格逼近β. 为了取得合适的参数k v ,现在假定边值问题(11.2.1)有唯一解,如果),(v x w 定义为初始问题(11.2.2)的解,那么v 可由下式确定: 0),(=-βv b w . (11.2.5) 由于这是一个非线性方程,我们可以利用Newton 法求解.首先选择初始值0v ,然后由下式生成序列 ),)(()),((111----- =k k k k v b dv dw v b w v v β,此处),(),)(( 11--=k k v b dv dw v b dv dw , (11.2.6) 同时要求求得),)(( 1-k v b dv dw ,因为),(v b w 的表达式未知,所以求解这个有一点难度;我们只能得到这么一系列的值。 ,,,),(),(),(),(1210-??k v b w v b w v b w v b w 假如我们如下改写初值问题(11.2.2),使其强调解对x 和v 的依赖性 ()()v v a w v a w b x a v x w v x w x f w ='=≤≤'=''),(,),(),,(,,,,α,(11.2.7) 保留初始记号以显式与x 的微分相关.既然要求当k v v =时),)((v b dv dw 的值,那么我们需要求出表达式(11.2.7)关于v 的偏导数.过程如下: )),(),,(,(),(v x w v x w x v f v x v w '??=?''? ),()),(),,(,()),(),,(,(v x v w v x w v x w x w f v x v x w v x w x x f ??'??+??'??= ) ,()),(),,(,(v x v w v x w v x w x w f ?'?''??+ 又因为x 跟v 相互独立,所以当b x a ≤≤上式如下;
实验八 常微分初值问题的数值解法 8.1实验目的 ① 掌握常微分方程数值解的常用算法; ② 培养编程与上机调试能力. 8.2算法描述 8.2.1改进欧拉法 求解 '0 ()(,)()()y x f x y a x b y a y ?=≤≤?=? 对给定的(,)f x y ,用改进的欧拉公式 1111()[()()]2 n n n n n n n n n n y y hf x y h y y f x y f x y ++++=++???=++++??求解常微分方程初值问题的解. 8.2.2四阶龙格-库塔法 对上述给定的(,)f x y ,用四阶龙格-库塔法求解常微分方程初值问题 112341213243(22)6(,) 11(,)2211(,)22(,)n n n n n n n n n n h y y k k k k k f x y k f x h y hk k f x h y hk k f x h y hk +?=++++??=???=++???=++??=++?? 8.3实验题目 (1) 用改进的欧拉公式,求解常微分方程初值问题的解 20.10.4(0)1 dy y x dx y ?=?≤≤??=? (2) 用四阶龙格-库塔公式解初值问题: / 2.0 2.6,0.2(2.0)1dy x y x h dx y ?=?≤≤=??=?
8.4实验要求 (1)选择一种计算机语言设计出改进欧拉法和四阶龙格-库塔法方法求解常微分方程初值问题的程序,观察运行结果. (2)利用Matlab求解常微分方程初值问题 函数dsolve()用于求解微分方程.Dy表示:dy/dt(t 为缺省的自变量),Dny表示y对t 的n阶导数. Matlab6.1环境下操作如下: >> y=dsolve('Dy=y*y','y(0)=1') %求解题目1 >> y=dsolve('Dy=y/t','y(2.0)=1') %求解题目2 (3)利用最小二乘法拟合通过改进欧拉法求出微分方程的一系列数值解的近似函数方程.并利用Matlab的绘图功能画出函数的曲线 8.5思考 一阶微分方程初值问题有哪些数值解法?比较各种方法的优缺点并举具体例子说明之?
常微分方程组边值问题解法 打靶法Shooti ng Method (shoot in g.m ) % 丁靶法求常微分方程的边值问题 function [x,a,b ,n]=shooti ng(fu n, xO,x n, eps) if nargin<3 eps=1e-3; end x1=x0+ra nd; [a,b]=ode45(fu n, [0,10],[0,x0]'); c0=b(le ngth(b),1); [a,b]=ode45(fu n, [0,10],[0,x1]'); c1=b(le ngth(b),1); x2=x1-(c1-x n)*(x1-x0)/(c1-c0); n=1; while (no rm(c1-x n)>=eps & no rm(x2-x1)>=eps) x0=x1;x 仁x2; [a,b]=ode45(fu n,[ 0,10],[0,x0]'); cO=b(le ngth(b),1); [a,b]=ode45(fu n,[ 0,10],[0,x1]'); c1= b(le ngth(b),1) x2=x1-(c1-x n)*(x1-x0)/(c1-c0); n=n+1; end x=x2; 应用打靶法求解下列边值问题: y 10 0 解:将其转化为常微分方程组的初值问题
命令: xO=[O:O.1:1O]; y0=32*((cos(5)-1)/si n( 5)*si n(x0/2)-cos(x0/2)+1); plot(xO,yO,'r') hold on [x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1)) dy i dx y 2 dy 2 dx y i 0 y 4 y o dy dx X0 真实解 30 ' 12^4567^9 10
下载的,感觉不错,共享一下 常微分方程和常微分方程组的求解 一、实验目的: 熟悉Matlab 软件中关于求解常微分方程和常微分方程组的各种命令,掌握利用Matlab 软件进行常微分方程和常微分方程组的求解。 二、相关知识 在MATLAB 中,由函数dsolve()解决常微分方程(组)的求解问题,其具体格式如下: X=dsolve(‘eqn1’,’eqn2’,…) 函数dsolve 用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解。 例1:求解常微分方程1dy dx x y = +的MATLAB 程序为:dsolve('Dy=1/(x+y)','x'), 注意,系统缺省的自变量为t ,因此这里要把自变量写明。 结果为:-lambertw(-C1*exp(-x-1))-x-1 其中:Y=lambertw(X)表示函数关系Y*exp(Y)=X 。 例2:求解常微分方程2 '''0yy y -=的MATLAB 程序为: Y2=dsolve('y*D2y-Dy^2=0’,’x’) 结果为: Y2 =[ exp((x+C2)/C1)] [ C2] 我们看到有两个解,其中一个是常数。 例3:求常微分方程组253t t dx x y e dt dy x y e dt ?++=??? ?--=??通解的MATLAB 程序为: [X,Y]=dsolve('Dx+5*x+y=exp(t),Dy-x-3*y=exp(2*t)','t') 例4:求常微分方程组020 210cos ,224,0 t t t dx dy x t x dt dt dx dy y e y dt dt =-=?+-==??? ?++==??通解的MATLAB 程序为: [X,Y]=dsolve('Dx+2*x-Dy=10*cos(t),Dx+Dy+2*y=4*exp(-2*t)','x(0)=2','y(0)=0')
微分方程求解是系统仿真、数学模型实现以及很多工程问题求解的核心部分,应用MATLAB可以方便地对一阶常微分方程组进行求解,这里将对其基本方法进行介绍。值得注意的是,高阶微分方程组可以通过引进参变量化为一阶常微分方程组,也可以同样方便解决。 若有一个微分方程(组)的参变量为列向量,即,且它参变量随时间变化的微分方程可以有以下方程描述: 这里的f函数是一个列向量,即, i=1,2,3…,n,它可以是任意非线性函数。 则一般微分方程可以如此求解: [t,x]=ode45(f,timespan,x0) 对于刚性方程,即一些解变化缓慢,一些解变化剧烈,且两者相差较为悬殊的这种方程,通常调用ode15s而非o de45进行求解。 例1: 解:编写function或者用匿名函数 表达f=y-2*x/y即可; function dy=f(t,y) dy=y-2*t/y; end 命令: t=[0,1];%y0=1; [x,y]=ode45('f',t,1);%注意 这里的x相当于自变量t plot(x,y,x,sqrt(1+2*x)),legend('数值解','解析解');
可见求解效果不错。 例2、 解:编写function function dx=f(t,x)%返回值是列向量 dx=[-x(2)-x(3); x(1)+0.2*x(2); 0.2+(x(1)-5.7)*x(3)]; end 命令: t=[0,100]; y0=[0 0 0]';%注意是列向量 [x,y]=ode45('f',t,y0); plot(x,y); 例3、 这是一个二阶微分方程组,可以引进变量,由此ODE可以化成如下形式 可以采用和例2相同的方法求解: function dx=f(t,x) dx=[x(2); -(x(1)^2-1)*x(2)-x(1)]; End
二阶常微分方程边值问题的数值解法 摘要 求解微分方程数值解的方法是多种多样的,它本身已形成一个独立的研究方向,其要点是对微分方程定解问题进行离散化.本文以研究二阶常微分方程边值问题的数值解法为目标,综合所学相关知识和二阶常微分方程的相关理论,通过对此类方程的数值解法的研究,系统的复习并进一步加深对二阶常微分方成的数值解法的理解,为下一步更加深入的学习和研究奠定基础. 对于二阶常微分方程的边值问题,我们总结了两种常用的数值方法:打靶法和有限差分法.在本文中我们主要探讨关于有限差分法的数值解法.构造差分格式主要有两种途径:基于数值积分的构造方法和基于Taylor展开的构造方法.后一种更为灵活,它在构造差分格式的同时还可以得到关于截断误差的估计.在本文中对差分方法列出了详细的计算步骤和Matlab
程序代码,通过具体的算例对这种方法的优缺点进行了细致的比较.在第一章中,本文将系统地介绍二阶常微分方程和差分法的一些背景材料.在第二章中,本文将通过Taylor展开分别求得二阶常微分方程边值问题数值解的差分格式.在第三章中,在第二章的基础上利用Matlab求解具体算例,并进行误差分析. 关键词:常微分方程,边值问题,差分法,Taylor展开,数值解
The Numerical Solutions of Second-Order Ordinary Differential Equations with the Boundary Value Problems ABSTRACT The numerical solutions for solving differential equations are various. It formed an independent research branch. The key point is the discretization of the definite solution problems of differential equations. The goal of this paper is the numerical methods for solving second-order ordinary differential equations with the boundary value problems. This paper introduces the mathematics knowledge with the theory of finite difference. Through solving the problems, reviewing what have been learned systematically and understanding the ideas and methods of the finite difference method in a deeper layer, we can establish a foundation for the future learning.
第八章 常微分方程的数值解法 一.内容要点 考虑一阶常微分方程初值问题:?????==0 0)() ,(y x y y x f dx dy 微分方程的数值解:设微分方程的解y (x )的存在区间是[a,b ],在[a,b ]内取一系列节 点a= x 0< x 1<…< x n =b ,其中h k =x k+1-x k ;(一般采用等距节点,h=(b-a)/n 称为步长)。在每个节点x k 求解函数y(x)的近似值:y k ≈y(x k ),这样y 0 , y 1 ,...,y n 称为微分方程的数值解。 用数值方法,求得f(x k )的近似值y k ,再用插值或拟合方法就求得y(x)的近似函数。 (一)常微分方程处置问题解得存在唯一性定理 对于常微分方程初值问题:?????==0 0)() ,(y x y y x f dx dy 如果: (1) 在B y y A x x 00≤-≤≤,的矩形内),(y x f 是一个二元连续函数。 (2) ),(y x f 对于y 满足利普希茨条件,即 2121y y L y x f y x f -≤-),(),(则在C x x 0≤≤上方程?????==0 0)() ,(y x y y x f dx dy 的解存在且唯一,这里C=min((A-x 0),x 0+B/L),L 是利普希茨常数。 定义:任何一个一步方法可以写为),,(h y x h y y k k k 1k Φ+=+,其中),,(h y x k k Φ称为算法的增量函数。 收敛性定理:若一步方法满足: (1)是p 解的. (2) 增量函数),,(h y x k k Φ对于y 满足利普希茨条件. (3) 初始值y 0是精确的。则),()()(p h O x y kh y =-kh =x -x 0,也就是有 0x y y lim k x x kh 0h 0 =--=→)( (一)、主要算法 1.局部截断误差 局部截断误差:当y(x k )是精确解时,由y(x k )按照数值方法计算出来的1~ +k y 的误差y (x k+1)- 1~ +k y 称为局部截断误差。 注意:y k+1和1~ +k y 的区别。因而局部截断误差与误差e k +1=y (x k +1) -y k +1不同。 如果局部截断误差是O (h p+1),我们就说该数值方法具有p 阶精度。
Matlab 求解常微分方程边值问题的方法:bvp4c 函数 常微分方程的边值问题,即boundary value problems ,简称BVP 问题,是指表达形式为 (,)((),())0'=??=?y f x y g y a y b 或(,,)((),(),)0'=??=? y f x y p g y a y b p 的方程组(p 是未知参数),在MA TLAB 中使用积分器bvp4c 来求解。 [命令函数] bvp4c [调用格式] sol=bvp4c(odefun,bcfun,solinit,options,p1,p2,…) sol 为一结构体,sol.x 、sol.y 、sol.yp 分别是所选择的网格点及其对应的y(x)与y'(x)数值; bvp4c 为带边值条件常微分方程积分器的函数命令;odefun 为描述微分方程组的函数文件;bcfun 为计算边界条件g(f(a),f(b),p)=0的函数文件;solinit 为一结构体,solinit.x 与solinit.y 分别是初始网格的有序节点与初始估计值,边界值条件分别对应a=solinit.x(l)和b=solinit.x(end); options 为bvpset 命令设定的可选函数,可采用系统默认值;p1, p2…为未知参数。 例 求常微分方程0''+=y y 在(0)2=y 与(4)2=-y 时的数值解。 [解题过程] 仍使用常用方法改变方程的形式: 令1=y y ,21'=y y ,则原方程等价于标准形式的方程组1221 ?'=??'=-??y y y y ; 将其写为函数文件twoode.m ; 同时写出边界条件函数对应文件twobc.m ; 分别使用结构solinit 和命令bvp4c 确定y-x 的关系; 作出y-x 的关系曲线图。 [算例代码] solinit =bvpinit(linspace(0,4,5),[1 0]); % linspace(0,4,5)为初始网格,[1,0]为初始估计值 sol=bvp4c(@twoode,@twobc,solinit); % twoode 与twobc 分别为微分方程与边界条件的函数,solinit 为结构 x=linspace(0,4); %确定x 范围 y=deval(sol,x); %确定y 范围 plot(x,y(1,:)); %画出y-x 的图形 %定义twoode 函数(下述代码另存为工作目录下的twoode.m 文件) function dydx= twoode(x,y) %微分方程函数的定义 dydx =[y(2) -abs(y(1))]; %定义twobc 函数(下述代码另存为工作目录下的twobc.m 文件) function res= twobc(ya,yb); %边界条件函数的定义 res=[ya(1);yb(1)+2];
常微分方程和常微分方程组的求解 一、实验目的: 熟悉Matlab 软件中关于求解常微分方程和常微分方程组的各种命令,掌握利用Matlab 软件进行常微分方程和常微分方程组的求解。 二、相关知识 在MATLAB 中,由函数dsolve()解决常微分方程(组)的求解问题,其具体格式如下: X=dsolve(‘eqn1’,’eqn2’,…) 函数dsolve 用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解。 例1:求解常微分方程1dy dx x y = +的MATLAB 程序为:dsolve('Dy=1/(x+y)','x'), 注意,系统缺省的自变量为t ,因此这里要把自变量写明。 结果为:-lambertw(-C1*exp(-x-1))-x-1 其中:Y=lambertw(X)表示函数关系Y*exp(Y)=X 。 例2:求解常微分方程 2 '''0yy y -=的MATLAB 程序为:Y2=dsolve('y*D2y-Dy^2=0’,’x’) 结果为: Y2 =[ exp((x+C2)/C1)] [ C2] 我们看到有两个解,其中一个是常数。 例3:求常微分方程组253t t dx x y e dt dy x y e dt ?++=??? ?--=??通解的MATLAB 程序为: [X,Y]=dsolve('Dx+5*x+y=exp(t),Dy-x-3*y=exp(2*t)','t') 例4:求常微分方程组020 210cos ,224,0 t t t dx dy x t x dt dt dx dy y e y dt dt =-=?+-==??? ?++==??通解的MATLAB 程序 为:
第一章绪论 1.1 引言 常微分方程是现代数学的一个重要分支,是人们解决各种实际问题的有效工具。微分方程的理论和方法从17世纪末开始发展起来,很快成了研究自然现象的强有力工具,在17到18世纪,在力学、天文、科学技术、物理中,就已借助微分方程取得了巨大的成就。1864年Leverrer根据这个方程预见了海王星的存在,并确定出海王星在天空中的位置。现在,常微分方程在许多方面获得了日新月异的应用。这些应用也为常微分方程的进一步发展提供了新的问题,促使人们对微分方程进行更深入的研究,以便适应科学技术飞速发展的需要。 研究常微分方程常用数值解是数学工作者的一项基本的且重要的工作。在国内外众多数学家的不懈努力,使此学科基本上形成了一套完美的体系。微分方程的首要问题是如何求一个给定方程的通解或特解。到目前为止,人们已经对许多微分方程得出了求解的一般方法。由于在生产实际和科学研究中所遇到的微分方程问题比较复杂,使这些问题的解即使能求出解析表达式,也往往因计算量太大而难于求出,而对于一些典型的微分方程则可以运用基本方法求出其解析解,并可以根据初值问题的条件把其中的任意常数确定下来。 由于求通解存在许多困难,人们就开始研究带某种定解条件的特解。首先是Cauchy对微分方程初始解的存在惟一性进行了研究。目前解的存在惟一性、延拓性、大范围的存在性以及解对初始解和参数的延续性和可微性等理论问题都已发展成熟。与此同时,人们开始采取各种近似方法来求微分方程的特解,例如求微分方程数值解的Euler折线法、Runge-Kutta法等,可以求得若干个点上微分方程的近似解。最后,由于当代高科技的发展为数学的广泛应用和深入研究提供了更好的手段。用计算机结合Matlab软件求方程的精确解、近似解,对解的性态进行图示和定性、稳定性研究都十分方便有效。 本章先介绍常微分的一般概念、导出微分方程的一些典型例子及求解微分方程的思路分析。从而得到常微分方程的常用数值解法。