当前位置：文档之家› 高考数学二轮复习专题六立体几何

高考数学二轮复习专题六立体几何

高考数学二轮复习

专题六立体几何

【重点知识回顾】

稳定中有所创新,由知识立意转为能力立意

（1）考查重点及难点稳定：高考始终把空间直线与直线、直线与平面、平面与平面的平行与垂直的性质与判定,以及求线面角、二面角等知识都是重点考查的内容，其中线线角、线面角、二面角的求解更是重中之重在难度上平稳过渡，始终以中等偏难为主。实行新课程的高考，命题者在求稳的同时注重创新高考创新，主要体现在命题的立意和思路上注重对学生能力的考查

（2）空间几何体中的三视图仍是高考的一个重要知识点解答题的考查形式仍要注重在一个具体立体几何模型中考查线面的关系

（3）使用，“向量”仍将会成为高考命题的热点，一般选择题、填空题重在考查向量的概念、数量积及其运算律在有些立体几何的解答题中，建立空间直角坐标系，以向量为工具，利用空间向量的坐标和数量积解决直线、平面问题的位置关系、角度、长度等问题，比用传统立体几何的方法简便快捷，空间向量的数量积及坐标运算仍是2019年高考命题的重点（4）支持新课改，在重叠部分做文章,在知识交汇点处命题立体几何中平行、垂直关系证明的思路清楚吗？平行垂直的证明主要利用线面关系的转化：

线∥线线∥面面∥面

判定线⊥线线⊥面面⊥面性质

线∥线线⊥面面∥面

←→?←→??→??←→?←→?←?

??←→?←→?

线面平行的判定：

a b b a a ∥，面，∥面???ααα

线面平行的性质：

αααβαβ∥面，面，∥?=? b a b 三垂线定理（及逆定理）：

PA AO PO ⊥面，为在内射影，面，则αααa ? a OA a PO a PO a AO ⊥⊥；⊥⊥??

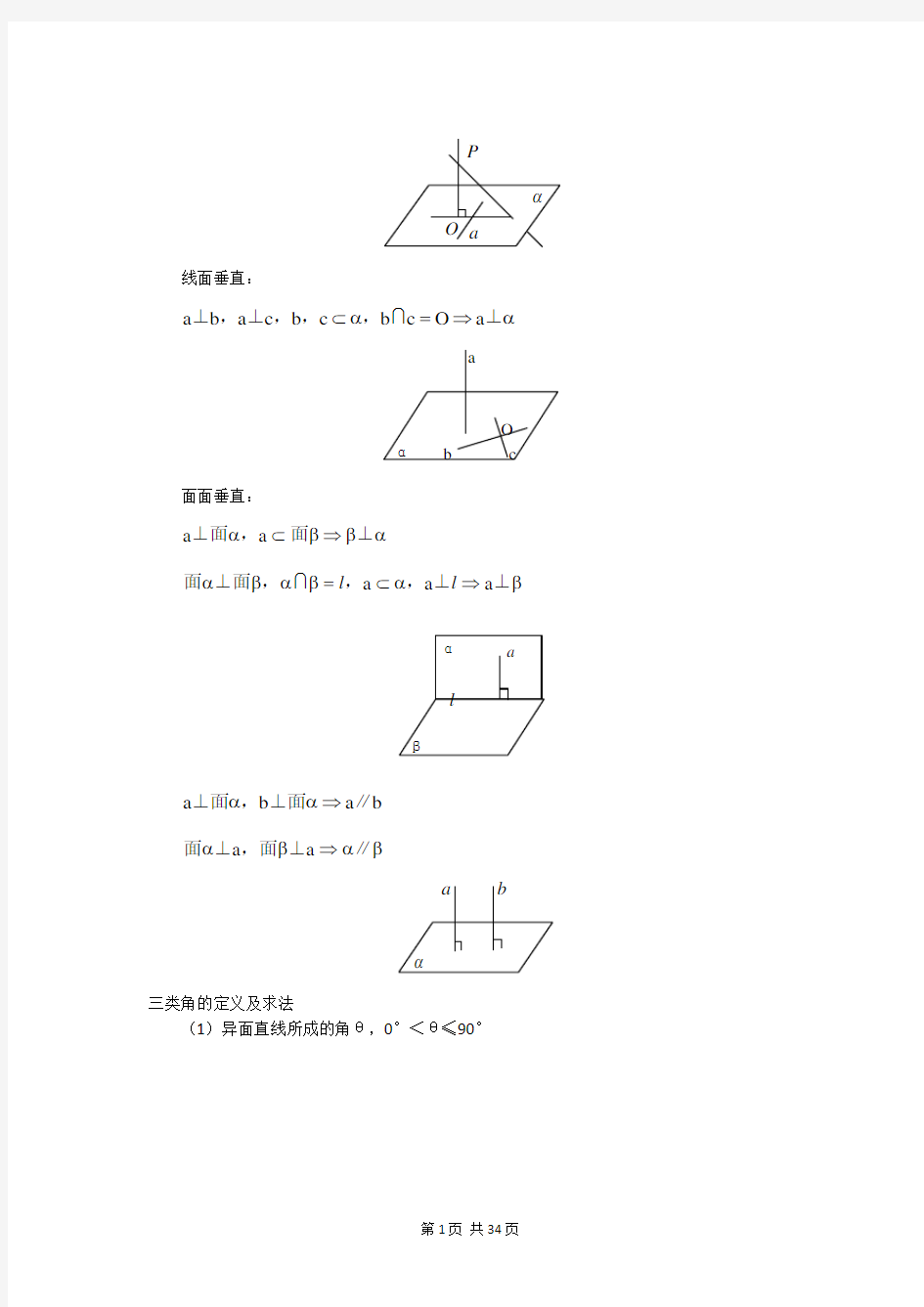
线面垂直：

a b a c b c b c O a ⊥，⊥，，，⊥?=?αα

O α b c

面面垂直：

a a ⊥面，面⊥αββα??

面⊥面，，，⊥⊥αβαβαβ =??l l a a a

α a

a b a b ⊥面，⊥面∥αα? 面⊥，面⊥∥αβαβa a ?

a b

三类角的定义及求法

（1）异面直线所成的角θ，0°＜θ≤90°

（2）直线与平面所成的角θ，0°≤θ≤90° θαα＝时，∥或0b o

b ?

（）二面角：二面角的平面角，30180αβθθ--<≤l o

（三垂线定理法：A ∈α作或证AB ⊥β于B ，作BO ⊥棱于O ，连AO ，则AO ⊥棱l ，∴∠AOB 为所求。）三类角的求法：

①找出或作出有关的角。

②证明其符合定义，并指出所求作的角。 ③计算大小（解直角三角形，或用余弦定理）。

点与点，点与线，点与面，线与线，线与面，面与面间距离。将空间距离转化为两点的距离，构造三角形，解三角形求线段的长（如：三垂线定理法，或者用等积转化法）。

如：正方形ABCD —A 1B 1C 1D 1中，棱长为a ，则：（1）点C 到面AB 1C 1的距离为___________；（2）点B 到面ACB 1的距离为____________；

（3）直线A 1D 1到面AB 1C 1的距离为____________；（4）面AB 1C 与面A 1DC 1的距离为____________；

（5）点B 到直线A 1C 1的距离为_____________。

D C

A B

D 1 C 1

A 1

B 1

你是否准确理解正棱柱、正棱锥的定义并掌握它们的性质？正棱柱——底面为正多边形的直棱柱

正棱锥——底面是正多边形，顶点在底面的射影是底面的中心。

正棱锥的计算集中在四个直角三角形中： Rt SOB Rt SOE Rt BOE Rt SBE ????，，和它们各包含哪些元素？

S C h C h 正棱锥侧·（——底面周长，为斜高）=1

2''

V 锥底面积×高=

球有哪些性质？

（）球心和截面圆心的连线垂直于截面122

r R d =-

（2）球面上两点的距离是经过这两点的大圆的劣弧长。为此，要找球心角！（3）如图，θ为纬度角，它是线面成角；α为经度角，它是面面成角。

（），球球444323S R V R ==

ππ

（5）球内接长方体的对角线是球的直径。正四面体的外接球半径R 与内切球半径r 之比为R ：r ＝3：1。

【典型例题】

1，空间几何体及三视图

例1．用一些棱长为1cm的小正方体码放成一个几何体，图1为其俯视图，图2为其主视图则这个几何体的体积最大是 7 cm3．

图1（俯视图）图2（主视图）

例2.一个多面体的直观图及三视图如图所示，则多面体A CDEF

-的体积为▲．

例4.右图是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体共有▲ 个．5 例5．如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是2

20+ 2

cm。

例 6.矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一

主视图

俯视图

左视图

俯视图

左视图

个直二面角B －AC －D ，则四面体ABCD 的外接球的体积为

π6

125

例7.一个几何体的三视图中，正视图和侧视图都是矩形，俯视图是等腰直角三角形（如图），根据图中标注的长度，可以计算出该几何体的表面积是 12+42 ． 2.平行与垂直

例8.已知：正方体1111ABCD-A B C D ，1AA =2，E 为棱1CC 的中点． ⑴求证：11B D AE ⊥；

⑵求证：//AC 平面1B DE ；⑶求三棱锥1B ADE -的体积

证明：连结BD ，则BD //11B D ， ∵ABCD 是正方形，∴

AC BD ⊥．

∵CE ⊥面ABCD ，∴CE BD ⊥．又C =AC CE ，∴BD ⊥面ACE ．

∵AE ?面ACE ，∴BD AE ⊥， ∴11B D AE ⊥．

⑵证明：作1BB 的中点F ，连结AF CF EF 、、． ∵E F 、是1BB 1CC 、的中点，∴CE

1B F ，

∴四边形1B FCE 是平行四边形，∴ 1CF// B E ． ∵,E F 是1BB 1CC 、的中点，∴//EF BC ，又//BC AD ，∴//EF AD ．

∴四边形ADEF 是平行四边形，AF ∴//ED ， ∵AF CF C =，1B E ED E =， ∴平面//ACF 面1B DE ．又AC ?平面ACF ，∴//AC 面1B DE

例9. 多面体ABCDE 中，1====AE AC BC AB ，2=CD ，ABC AE 面⊥，

CD AE //。

（1）求证：BCD AE 面//；

（2）求证：BCD BED 面面⊥ 证明：（1）∵CD AE //

BCD AE 面?

∴BCD AE 面//

（2）令BC 中点为N ，BD 中点为M ，连结MN 、EN ∵MN 是BCD ?的中位线

∴CD MN //

又∵CD AE // ∴MN AE //

∴ABC MN 面⊥ ∴AN MN ⊥ ∵ABC ?为正?

∴BC AN ⊥ ∴BCD AN 面⊥

又∵1==MN AE ，MN AE //

∴四边形ANME 为平行四边形

∴BCD EN 面⊥

∴BCD BED 面面⊥

例10．如图四边形ABCD 是菱形，PA ⊥平面ABCD ， Q 为PA 的中点. 求证： ⑴ PC ∥平面QBD ； ⑵ 平面QBD ⊥平面PAC .

解：证：设 ?AC BD=0,连OQ ⑴ ∵ABCD 为菱形， ∴ O 为AC 中点，又Q 为PA 中点。

∴OQ ∥PC

又?PC 平面QBD ,

?OQ 平面QBD ∴PC ∥平面QBD

⑵ ∵ABCD 为菱形， ∴⊥BD AC ,

又∵⊥PA 平面ABCD ， ?BD 平面ABCD ∴⊥PA BD 又 PA AC D ?= ∴BD P ⊥平面AC 又?BD 平面QBD ∴P ⊥平面QBD 平面AC 3.距离与角

例11．已知DBC ??和ABC 所在的平面互相垂直，且ＡＢ＝ＢＣ＝ＢＤ，

120=∠=∠DBC CBA ，求：

⑴．直线AD 与平面BCD 所成角的大小；

⑵．直线AD 与直线BC 所成角的大小；

P Q O

⑶．二面角A-BD-C 的余弦值．

⑴如图，在平面ABC 内，过A 作AH ⊥BC ，垂足为H ，

则AH ⊥平面DBC ，∴∠ADH 即为直线AD 与平面BCD 所成的角

由题设知△AHB ≌△AHD ，则DH ⊥BH ，AH =DH ，∴∠ADH =45° ⑵∵BC ⊥DH ，且DH 为AD 在平面BCD 上的射影，

∴BC ⊥AD ，故AD 与BC 所成的角为90°

⑶过H 作HR ⊥BD ，垂足为R ，连结AR ，则由三垂线定理知，AR ⊥BD ，故∠

ARH 为二面角A —BD —C 的平面角的补角设BC =a ,则由题设知，AH =DH =

2,23a BH a =,在△HDB 中，HR =

a ，∴tan ARH =HR

AH =2 故二面角A —BD —C 的余弦值的大小为5

【点评】:本题着眼于让学生掌握通性通法。几何法在书写上体现：“作出来、证出来、指出来、算出来、答出来”五步。斜线和平面所成的角是一个直角三角形所成的锐角，它的三条边分别是平面的垂线段、斜线段及斜线段在平面内的射影。因此求直线和平面所成的角，几何法一般先定斜足、再作垂线找射影、通过解直角三角形求解；向量法则利用斜线和射影的夹角或考虑法向量，设 θ为直线与平面α所成的角，?为直线的方向向量v 与平面α的法向量之间的夹角，则有θπ

?-=

或θπ

?+=

（如图）

特别地 0=?时，2

θ=

，α⊥l ；2

时， 0=θ，α?l 或α//l 。

⑴用两面垂直的性质作垂线，找垂足的位置作出线面角，⑵利用三垂线定理证，

ωα

⑴. PD ⊥平面BCD ，∴BD 是PB 在平面BCD 内的射影， ∴∠PBD 为PB 与平面BCD 所成角,BD ⊥BC ，由三垂线定理得BC ⊥BD ，∴BP=CD ，设BC=a ，则BD=a ，BP=CD=2a ∴在Rt △BPD 中， cos ∠DBP=

∴∠DBP=45°, 即PB 与平面BCD 所成角为45°． ⑵.过B 作BE ⊥CD 于E ，连结PE ，PD ⊥平面BCD 得PD ⊥BE ，∴BE ⊥平面PCD ， ∴∠BPE 为BP 与平面PCD 所成的角,在Rt △BEP 中，BE=2

a, BP=2a,∴∠BPE=30° 即BP 与平面PCD 所成角为30°

例12.在四棱锥P-ABCD 中，已知ABCD 为矩形，PA ⊥平面ABCD ，设PA=AB=a ，BC=2a ，求二面角B-PC-D 的大小

解析1.定义法过D 作DE ⊥PC 于E ，过E 作EF ⊥PC 于F ，连接FD ，由二面角的平面角的定义可知DEF ∠是所求二面角B-PC-D 的平面角。求解二面角B-PC-D 的大小只需解△DEF 即可

【解法一】过D 作DE ⊥PC 于E ，过E 作EF ⊥PC 于F ，连接FD ，由二面角的平面角的定义可知DEF ∠是所求二面角B-PC-D 的平面角

在四棱锥P-ABCD 中， PA ⊥平面ABCD 且ABCD 为矩形，∵AD ⊥DC ∴PD ⊥DC ∵

PA=a

，

AD=BC=2a

，

∴

PD=a 5,PC=a 6,DE=630a PC DC PD =?,CE=662a

CP CD = 同理在Rt △PBC 中，

a BC PB EC EF EC EF BC PB 6

=?==，在Rt △EFC 中,FC=a 2

, 在Rt △DFC 中,DF=a 25, 在△DEF 中由余弦定理cos DEF ∠=510

2222-=?-+ED EF DF ED EF

所求二面角B-PC-D 的余弦值为5

解析2.垂面法易证面PAB ⊥面PBC ，过A 作AM ⊥BP 于M ，显然AM ⊥

解析一

Ｅ

Ｆ B

A 解析三

解析二

面PBC ，从而有AM ⊥PC ，同法可得AN ⊥PC ，再由AM 与AN 相交与A 得PC ⊥面AMN 。设面AMN 交PC 于Q ，则MQN ∠为二面角B-PC-D 的平面角；再利用三面角公式可解【解法二】略

解析3.利用三垂线求解把四棱锥P-ABCD 补成如图的直三棱柱PAB-EDC ，显然二面角E-PC-D 与二面角D-PC-B 互补，转化为求二面角E-PC-D 。易证面PEDA ⊥PDC ，过E 作EF ⊥ PD 于F ，显然PF ⊥面PDC ，在面PCE 内，过E 作EG ⊥PC 于G ，连接GF ，由三垂线得GF ⊥ PC 即EGF ∠为二面角E-PC-D 的平面角，只需解△EFG 即可

解析4.在面PDC 内，分别过D 、B 作DE ⊥PC 于E ，

BF ⊥PC 于F ，连接EF 即可。利用平面知识求BF 、EF 、DE 的长度，再利用空间余弦定理求出θ 即可

【点评】.用几何法求二面角的方法比较多，常见的有：（1）定义法, 在棱上的点分别作棱的垂线，如解析１（2）三垂线求解 ,在棱上的点分别作棱的垂线，如解析２

（3）垂面法, 在棱上的点分别作棱的垂线，如解析３

用几何法将二面角转化为其平面角，要掌握以下三种基本做法：①直接利用定义，图(1).②利用三垂线定理及其逆定理，图 (2).最常用。③作棱的垂面，图(3).

4.空间几何中的向量方法

例13. 如下图，直棱柱ABC —A 1B 1C 1的底面△ABC 中，CA =CB =1，∠BCA =90°，棱AA 1=2，M 、N 分别是A 1B 1、A 1A 的中点.

D P

解析四

Ｅ

Ｆ

α β

O P A B O P α

β (1)

(2)

(3)

（1）求BN 的长；

（2）求异面直线B A 与1C B 1的余弦值；

（3）求证：A 1B ⊥C 1M . 【解法】：∵AC ⊥BC,CC 1⊥面ABC ，

∴可以建立如图所示的坐标系

（1）依题意得B （0， 1，0），N （1，0，1）， ∴｜BN ｜=222)01()10()01(-+-+-=3.

（2）A 1（1，0，2），B （0，1，0），C （0，0，0），B 1（0，1，2）， ∴1BA =(1,-1,2)，1CB =（0，1，2），1BA ·1CB =3，｜1BA ｜=6，｜1CB ｜=5.

∴cos 〈1BA ，1CB 〉11CB BA ?=

. 所以，异面直线B A 与1C B 1的余弦值为

（3）证明：C 1（0，0，2），M （21

，2

1，2），

B A 1=(-1,1,-2)，M

C 1=（2

1，2

1，0），∴B A 1·M C 1=0，∴A 1B ⊥C 1M .

【点评】底面有直角的直棱柱适合建立坐标系的条件，可以用两点间的距离公式，数量积的夹角公式，用坐标法求点点距、向量夹角。特别注意异面直线角的范围(0,

],而向量角的范围为[0,π] 【变式与拓展】在三棱锥S —ABC 中，∠SAB =∠SAC =∠ACB =90°，AC =2，

BC =13，SB =29. （1）求证：SC ⊥BC ；

（2）求SC 与AB 所成角的余弦值.

【解法一】：如下图，取A 为原点，AB 、AS 分别为y 、z 轴建立空间直角坐标系，则有AC =2，BC =13，SB =29，得B （0，17，0）、S （0，0，23）、C （2

，17

4，0），SC =（2

1713，174，－23），CB =（－21713，17

，0）

. （1）∵SC ·CB =0，∴SC ⊥BC .

（2）设SC 与AB 所成的角为α，∵AB =（0，17，0），SC ·AB =4，|SC ||

|=417，∴cos α=

，即为所求. 【解法二】：（1）∵SA ⊥面ABC ，AC ⊥BC ，AC 是斜线SC 在平面ABC 内的射

影，∴SC ⊥B C.

（2）如下图，过点C 作CD ∥AB ，过点A 作AD ∥BC 交CD 于点D ，连结SD 、SC ，则∠SCD 为异面直线SC 与AB 所成的角.∵四边形ABCD 是平行四边形，CD =17，SA =23，

SD =22AD SA +=1312+=5，∴在△SDC 中，由余弦定理得cos ∠SCD =

，即为所求.

例14.如图，在四棱锥ABCD P -中，底面ABCD 是正方形，侧棱⊥PD 底面ABCD ，

DC PD =，E 是PC 的中点，作PB EF ⊥交PB 于点F.

（1）证明 ∥PA 平面EDB ；（2）证明⊥PB 平面EFD ；（3）求二面角D -PB -C 的大小．

【解法】：如图所示建立空间直角坐标系，D 为坐标原点.设.DC a =

⑴证明：连结AC ，AC 交BD 于G.连结EG.

依题意得(,0,0),(0,0,),(0,,)22

a a

A a P a E

底面ABCD 是正方形， G ∴是此正方形的中心，

故点G 的坐标为(,,0)22a a

且(,0,),(,0,).22

a a PA a a EG =-=-

2PA EG ∴=. 这表明EG PA ∥.

而EG ?平面EDB 且PA ?平面EDB ，PA ∴∥平面EDB 。

A B

y z

D P

⑵证明：依题意得(,,0),(,,)B a a PB a a a =-。又(0,,),22

a a

DE =

故02

202

2=-+=?a a DE PB

PB DE ∴⊥, 由已知EF PB ⊥，且,EF DE E =所以PB ⊥平面EFD.

(3)解：设点F 的坐标为000(,,),,x y z PF PB λ=则000(,,)(,,)x y z a a a a λ-=- 从而000,,(1).x a y a z a λλλ===-所以00011(,,)(,(),()).2

a a FE x y z a a a λλλ=---=---

由条件EF PB ⊥知，0=?PB PE 即22211()()0,22

a a a λλλ-+---= 解得 1

3λ=

∴点F 的坐标为2(,,),333a a a 且2(,,),(,,).366333

a a a a a a FE FD =--=---

2332

22=+--=?a a a FD PB ,即PB FD ⊥，

故EFD ∠是二面角C PB D --的平面角.

∵6

91892

222a a a a FD PE =

+-=?且

a a a a FD a a a a PE 3

9499,6636369222222=++==++=

6cos .2

||||

66.a FE FD EFD FE FD a a ∴==

=3EFD π∴∠=,

所以，二面角C —PC —D 的大小为.3

【点评】考查空间向量数量积及其坐标表示，运用向量数量积判断向量的共线与垂直，用向量证明线线、线面、面面的垂直与平行关系。

【变式与拓展】如图，已知矩形ABCD 所在平面外一点P ，PA ⊥平面ABCD ， E 、F 分别是AB 、PC 的中点．（1）求证：EF ∥平面PAD ；（2）求证：EF ⊥CD ；

（3）若∠PDA ＝45?，求EF 与平面ABCD 所成的角．证明：如图，建立空间直角坐标系A －xyz ，

设AB ＝2a ，BC ＝2b ，PA ＝2c ，则：A (0, 0, 0)，

B (2a , 0, 0)，

C (2a , 2b , 0)，

D (0, 2b , 0)， P (0, 0, 2c )∵

E 为AB 的中点，

F 为PC 的中点

∴ E (a , 0, 0)，F (a , b , c )

(1)∵EF ＝(0, b , c )，AP ＝(0, 0, 2c )，AD ＝(0, 2b , 0) ∴EF ＝12

(→ AP ＋→

AD ) ∴EF 与AP 、AD 共面

又∵ E ? 平面PAD ∴ EF ∥平面PAD ．

(2)∵ →

CD ＝(-2a , 0, 0 )

∴→CD ·→

EF ＝(-2a , 0, 0)·(0, b , c )＝0 ∴ CD ⊥EF ．

(3)若∠PDA ＝45?，则有2b ＝2c ，即 b ＝c ，∴ →

EF ＝(0, b , b )，

→ AP ＝(0, 0, 2b ) ∴ cos ?→ EF ，→ AP ?＝2b 22b ·

＝

∴ ?→ EF ，→

AP ?＝ 45?

∵ → AP ⊥平面AC ，∴ →

AP 是平面AC 的法向量

∴ EF 与平面AC 所成的角为：90?－?→ EF ，→

AP ?＝ 45?．

例15.如图，在正四棱柱1111D C B A ABCD -中，已知2=AB ，,51=AA E 、F 分别为D D 1、B B 1上的点，且.11==F B DE

（Ⅰ）求证：⊥BE 平面ACF ；（Ⅱ）求点E 到平面ACF 的距离.

解：(Ⅰ)以D 为原点，以、、D 1的正向分别为x 轴、y 轴、z 轴建立空间直角坐标系，则

).4,2,2(),1,0,0(),5,0,0(),0,2,0(),0,2,2(),0,0,2(),0,0,0(1F E D C B A D

于是).1,2,2(),4,2,0(),0,2,2(--==-=

,,,0,0AF BE AC BE ⊥⊥∴=?=? 且,A AF AC = ∴⊥BE 平面ACF

（Ⅱ）由(Ⅰ)知，为平面ACF 的一个法向量，

∴向量AE 在BE 上的射影长即为E 到平面ACF 的距离，设为d ，于是

51)2()2(|

)1,2,2()1,0,2(||||,cos |||222=+-+---?-=

故点E 到平面ACF 的距离为.3

图9

A B

A 1

B 1

C 1

例16.如图，在四棱锥P —ABCD 中，底面ABCD 为矩形，侧棱PA ⊥底面ABCD ，AB =3，

BC =1，PA =2，E 为PD 的中点．

（Ⅰ）求直线AC 与PB 所成角的余弦值；

（Ⅱ）在侧面PAB 内找一点N ，使NE ⊥面PAC ，并求出N 点到AB 和AP 的距离．

解：方法一、（1）设AC ∩BD=O ，连OE ，则OE//PB ，

∴∠EOA 即为AC 与PB 所成的角或其补角.

在△AOE 中，AO=1，OE=,27

21=

PB ,2

21==

PD AE ∴.14731

245

471cos =??-

EOA 即AC 与PB 所成角的余弦值为

3. （2）在面ABCD 内过D 作AC 的垂线交AB 于F ，则6

=∠ADF .

连PF ，则在Rt △ADF 中.3

tan ,332cos ====

ADF AD AF ADF AD DF

设N 为PF 的中点，连NE ，则NE//DF ，

∵DF ⊥AC ，DF ⊥PA ，∴DF ⊥面PAC ，从而NE ⊥面PAC. ∴N 点到AB 的距离12

AP ，N 点到AP 的距离.6321=

=AF 方法二、（Ⅰ）建立如图所示的空间直角坐标系，

则A 、B 、C 、D 、P 、E 的坐标为A （0，0，0）、 B （3，0，0）、C （3，1，0）、D （0，1，0）、

P （0，0，2）、E （0，2

，1），

从而).2,0,3(),0,1,3(-==PB AC

设PB AC 与的夹角为θ，则

,14

3723

||||cos ==?=PB AC PB AC θ

D E

∴AC 与PB 所成角的余弦值为

3. （Ⅱ）由于N 点在侧面PAB 内，故可设N 点坐标为（x ，O ，z ），

则)1,2

,(z x NE --=，

由NE ⊥面PAC 可得，

?????=+-=-?

????=?--=?--?????=?=?.021

3,01.0)0,1,3()1,2

1,(,0)2,0,0()1,21,(.0,0x z z x z x AC NE AP NE 化简得即 ∴?????==163z x 即N 点的坐标为)1,0,63(

，从而N 点到AB 、AP 的距离分别为1，6

【模拟演练】

一、选择

1．已知正方体外接球的体积是

324

π，那么正方体的棱长为（） A ．23 B ．33 C ．3 D ．3

2．一个几何体的三视图如图所示，已知侧视图是一个等腰三角形, 根据图中尺寸(单位:cm ),可知这个几何体的体积是（）

5俯视图

侧视图

正视图

A.360 cm

B.350 cm

C.330 cm

D.3

30 3 cm

4．已知、m 是不重合的直线，α、β、γ是两两不重合的平面，给出下列命题：①若

,,,,l m l a m a αα??⊥⊥则a α⊥；②若l m //，,α⊥m 则α⊥l ;③若βα⊥，

βα⊥?l l 则,；④若.//,//,,l m l m 则βαγβγα== 其中真命题的序号为

（）

A ①②

B ①③

C ①④

D ②④

5. 在正三棱锥A BCD -中，,E F 分别为AB 、CD 的中点，若EF 与BD 所成的角为6

π，则

EF 与AC 所成的角为（） A.

6π B. 4π C. 3π D. 2

7．已知直三棱柱ABC －A 1B 1C 1中，AC =BC ，M 、N 分别是A 1B 1，AB 的中点，P 点在线段1AC 上，则MP 与平面1B CN 的位置关系是（）

A ．垂直

B ．平行

C ．相交但不垂直

D ．要依P 点的位置而定

C 1

B 1

A 1

11. 如图所示，设地球半径为R ，点,A B 在赤道上，O 为地心，点C 在北纬30°的纬线

（O '为其圆心）上，且点,,A C D ，O '，O 共面，点D 、O '、O 共线若 90=∠AOB ，则异面直线AB 与CD 所成角的正弦值为

（）

B. 46-

104

D. 104

立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系 (1)如图所示，在正方体ABCD－A 1B 1 C 1 D 1 中，M，N分别是C 1 C， B 1C 1 的中点．求证：MN∥平面A 1 BD. (2)在正方体AC 1 中，M，N，E，F分别是A 1 B 1 ，A 1 D 1 ，B 1 C 1 ，C 1 D 1 的中点，求证：平面AMN∥平面EFDB. 思考题1 (1)如图所示，平面PAD⊥平面ABCD，ABCD为正方形，△PAD 是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点，求证：平面EFG∥平面PBC. (2)如图，在四面体A－BCD中，AD⊥平面BCD，BC⊥CD，AD＝2，BD ＝22，M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ＝3QC. 求证：PQ∥平面BCD. 题型二证明垂直关系(微专题) 微专题1：证明线线垂直 (1)已知空间四边形OABC中，M为BC中点，N为AC中点，P为OA中点，Q为OB中点，若AB＝OC.求证：PM⊥QN. (2)(2019·山西太原检测)如图，直三棱柱ABC－A 1B 1 C 1 中，AA 1 ＝AB ＝AC＝1，E，F分别是CC 1，BC的中点，AE⊥A 1 B 1 ，D为棱A 1 B 1 上的点，求证：DF⊥AE. 微专题2：证明线面垂直 (3)在正方体ABCD－A 1B 1 C 1 D 1 中，求证：BD 1 ⊥平面ACB 1 . (4)(2019·河南六市一模)在如图所示的几何体中，ABC－A 1B 1 C 1 为三棱柱，且AA 1 ⊥平面ABC，四边形ABCD为平行四边形，AD＝2CD，∠ADC＝60°. 若AA 1＝AC，求证：AC 1 ⊥平面A 1 B 1 CD. 微专题3：证明面面垂直 (5)已知正方体ABCD－A 1B 1 C 1 D 1 中，E，F分别是BB 1 ，CD的中点，求证：平面DEA⊥平面A 1FD 1 .

近五年高考数学(理科)立体几何题目汇总

高考真题集锦（立体几何部分） 1.(2016.理1）如图是由圆柱和圆锥组合而成的几何体的三视图，则该几何体的表面积是（） A 20π B24π C28π D.32π 2. βα，是两个平面，m,n 是两条直线，有下列四个命题：（1）如果m ⊥n,m ⊥α，n ∥β，那么βα⊥；（2）如果m ⊥α，n ∥α，那么m ⊥n. （3）如果αβα?m ，∥那么m ∥β。（4）如果m ∥n,βα∥，那么m 与α所成的角和n 与β所成的角相等。其中正确的命题有___________ 3.（2016年理1）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是π328，则它的表面积是 A 17π B.18π C.20π D.28π 4.平面α过正方体1111D C B A ABCD -的顶点A ，α//平面11D CB ，?α平面ABCD =m ， ?α平面11A ABB =n,则m,n 所成角的正弦值为（） A.23 B.22 C.33 D.3 1 5.（2016年理1）如图，在以A,B,C,D,E,F 为顶点的五面体中，面ABEF 为正方形，AF=2FD ，∠AFD=90°，且二面角D-AF-E 与二面角C-BE-F 都是60° .（12分）（Ⅰ）证明：平面ABEF ⊥平面EFDC ；（Ⅱ）求二面角E-BC-A 的余弦值.

6. (2015年理1）圆柱被一个平面截取一部分后与半球（半径为r ）组成一个几何体，该几何体三视图的正视图和俯视图如图所示，若该几何体的表面积是16+20π，则r=（） A.1 B.2 C.7 D.8 7.如图，四边形ABCD 为菱形，∠ABC=120°，E,F 是平面ABCD 同一侧的亮点，BE ⊥平面ABCD,DF ⊥平面ABCD,BE=2DF,AE ⊥EC. (1) 证明：平面AEC ⊥平面AFC; (2) 求直线AE 与直线CF 所成角的余弦值。 8.一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截取部分体积和剩余部分体积的比值为（） 9.如图，长方体1111D C B A ABCD -中，AB = 16，BC = 10，AA1 = 8，点E ，F 分别在1111C D B A ，上，411==F D E A ，过点E,F 的平面α与此长方体的面相交，交线围成一个正方形。（1）在图中画出这个正方形（不必说明画法和理由）；（2）求直线AF 与平面α所成的角的正弦值 10.如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB=5，AC=6，点E,F 分别在AD,CD 上，AE=CF=45 ，EF 交BD 于点H.将△DEF 沿EF 折到△DEF 的位置，OD ’=10 （1）证明：D ’H ⊥平面ABCD （2）求二面角B-D ’A-C 的正弦值

[数学]数学高考压轴题大全

1、（本小题满分14分）已知函数．（1）当时，如果函数仅有一个零点，求实数的取值范围；（2）当时，试比较与的大小；（3）求证：（）． 2、设函数，其中为常数．（Ⅰ）当时，判断函数在定义域上的单调性；（Ⅱ）若函数的有极值点，求的取值范围及的极值点；（Ⅲ）当且时，求证：． 3、在平面直角坐标系中，已知椭圆.如图所示，斜率为且不过原点的直线交椭圆于，两点，线段的中点为，射线交椭圆于点，交直线于点. （Ⅰ）求的最小值；（Ⅱ）若?，（i）求证：直线过定点；

（ii ）试问点，能否关于轴对称？若能，求出此时的外接圆方程；若不能，请说明理由. 二、计算题（每空？分，共？分） 4 、设函数的图象在点处的切线的斜率为，且函数为偶函数．若函数满足下列条件：①；② 对一切实数，不等式恒成立．（Ⅰ）求函数的表达式；（Ⅱ）求证：． 5 、已知函数：（1 ）讨论函数的单调性；（2）若函数的图像在点处的切线的倾斜角为，问：在什么范围取值时，函数在区间上总存在极值？ (3)求证：．

6、已知函数=，. (Ⅰ)求函数在区间上的值域；（Ⅱ）是否存在实数，对任意给定的，在区间上都存在两个不同的，使得成立.若存在，求出的取值范围；若不存在，请说明理由；（Ⅲ）给出如下定义：对于函数图象上任意不同的两点，如果对于函数图象上的点（其中总能使得成立，则称函数具备性质“”，试判断函数是不是具备性质“”，并说明理由. 7、已知函数（Ⅰ）若函数是定义域上的单调函数，求实数的最小值；（Ⅱ）方程有两个不同的实数解，求实数的取值范围；（Ⅲ）在函数的图象上是否存在不同两点，线段的中点的横坐标为，有成立？若存在，请求出的值；若不存在，请说明理由． 8、已知函数： ⑴讨论函数的单调性；

2018年高考数学立体几何试题汇编

2018年全国一卷（文科）：9．某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为 A ．217 B ．25 C ．3 D ．2 18．如图，在平行四边形ABCM 中，3AB AC ==，90ACM =?∠，以AC 为折痕将△ACM 折起，使点M 到达点 D 的位置，且AB DA ⊥．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且2 3 BP DQ DA == ，求三棱锥Q ABP -的体积．全国1卷理科理科第7小题同文科第9小题 18. 如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点 P 的位置，且PF BF ⊥. （1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值. 全国2卷理科： 9．在长方体1111ABCD A B C D -中，1AB BC ==，13AA =，则异面直线1AD 与1DB 所成角的余弦值为 A ．15 B ． 5 C ． 5 D ． 2 20．如图，在三棱锥P ABC -中，22AB BC ==，4PA PB PC AC ====，O 为AC 的中点．

（1）证明：PO⊥平面ABC； --为30?，求PC与平面PAM所成角的正弦值．（2）若点M在棱BC上，且二面角M PA C 全国3卷理科 3．中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是 19．（12分）如图，边长为2的正方形ABCD所在的平面与半圆弧?CD所在平面垂直，M是?CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱锥M ABC -体积最大时，求面MAB与面MCD所成二面角的正弦值． 2018年江苏理科： 10．如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为▲ ．

2020高考数学专题复习----立体几何专题

空间图形的计算与证明一、近几年高考试卷部分立几试题 1、（全国 8）正六棱柱 ABCDEF －A 1B 1C 1D 1E 1F 1 底面边长为 1，侧棱长为 2 ，则这个棱柱的侧面对角线 E 1D 与 BC 1 所成的角是（） A 、90° B 、60° C 、45° D 、30° [评注]主要考查正六棱柱的性质，以及异面直线所成角的求法。 2、（全国 18）如图，正方形ABCD 、ABEF 的边长都是 1，而且平面 ABCD 、ABEF 互相垂直，点 M 在 AC 上移动，点 N 在 BF C 上移动，若 CM=NB=a(0

的底面是边长为a的正方形，PB⊥面ABCD。（1）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；（2）证明无论四棱锥的高怎样变化，面PAD与面 PCD所成的二面角恒大于90°。 [评注]考查线面关系和二面角概念，以及空间想象力和逻辑推理能力。 4、（02全国文22）（一）给出两块面积相同的正三角形纸片，要求用其中一块剪拼成一个正三棱锥模型，使它们的全面积都与原三角形面积相等，请设计一种剪拼法，分别用虚线标示在图（1）（2）中，并作简要说明。 (3) (1)(2) （二）试比较你剪拼的正三棱锥与正三棱柱的体积的大小。（三）如果给出的是一块任意三角形的纸片，如图（3）要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形面积相等，请设计一种剪拼方法，用虚线标出在图3中，并作简要说明。

立体几何专题训练(附答案)

立体几何 G5 空间中的垂直关系 18．、[2014·广东卷] 如图1-4，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E. (1)证明：CF⊥平面ADF； (2)求二面角D- AF- E的余弦值．图1-4 19．、[2014·湖南卷] 如图1-6所示，四棱柱ABCD-A1B1C1D1的所有棱长都相等，AC∩BD ＝O，A1C1∩B1D1＝O1，四边形ACC1A1和四边形BDD1B1均为矩形． (1)证明：O1O⊥底面ABCD； (2)若∠CBA＝60°，求二面角C1-OB1-D的余弦值． 19．解：(1)如图(a)，因为四边形ACC1A1为矩形，所以CC1⊥AC.同理DD1⊥BD. 因为CC1∥DD1，所以CC1⊥BD.而AC∩BD＝O，因此CC1⊥底面ABCD. 由题设知，O1O∥C1C.故O1O⊥底面ABCD. (2)方法一：如图(a)，过O1作O1H⊥OB1于H，连接HC1. 由(1)知，O1O⊥底面ABCD O1O⊥A1C1. 又因为四棱柱ABCD-A1B1C1D1的所有棱长都相等，所以四边形A1B1C1D1是菱形，因此A1C1⊥B1D1，从而A1C1⊥平面BDD1B1，所以A1C1⊥OB1，于是OB1⊥平面O1HC1. 进而OB1⊥C1H.故∠C1HO1是二面角C1-OB1-D的平面角．

不妨设AB ＝2.因为∠CBA ＝60°，所以OB ＝3，OC ＝1，OB 1＝7. 在Rt △OO 1B 1中，易知O 1H ＝OO 1·O 1B 1OB 1＝237.而O 1C 1＝1，于是C 1H ＝O 1C 21＋O 1H 2 ＝ 1＋12 7 ＝ 197 . 故cos ∠C 1HO 1＝O 1H C 1H ＝ 23 7197 ＝25719. 即二面角C 1-OB 1-D 的余弦值为257 19 . 方法二：因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，所以四边形ABCD 是菱形，因此AC ⊥BD .又O 1O ⊥底面ABCD ，从而OB ，OC ，OO 1两两垂直．如图(b)，以O 为坐标原点，OB ，OC ，OO 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O -xyz ，不妨设AB ＝2.因为∠CBA ＝60°，所以OB ＝3，OC ＝1，于是相关各点的坐标为O (0，0，0)， B 1(3，0，2)， C 1(0，1，2)．易知，n 1＝(0，1，0)是平面BDD 1B 1的一个法向量．设n 2＝(x ，y ，z )是平面OB 1C 1的一个法向量，则?????n 2·OB →1＝0，n 2·OC →1＝0，即???3x ＋2z ＝0， y ＋2z ＝0. 取z ＝－3，则x ＝2，y ＝23，所以n 2＝(2，23，－3)．设二面角C 1-OB 1-D 的大小为θ，易知θ是锐角，于是 cos θ＝|cos 〈，〉|＝??????n 1·n 2|n 1|·|n 2|＝2319＝25719. 故二面角C 1-OB 1-D 的余弦值为25719 . 19．、、[2014·江西卷] 如图1-6，四棱锥P - ABCD 中，ABCD 为矩形，平面PAD ⊥平面ABCD . 图1-6 (1)求证：AB ⊥PD .

高三立体几何专题复习

高三立体几何专题复习 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

高考立体几何专题复习一．考试要求：（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图，能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。（2）了解空两条直线的位置关系，掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念（对于异面直线的距离，只要求会计算已给出公垂线时的距离）。（3）了解空间直线和平面的位置关系，掌握直线和平面平行的判定定理和性质定理，理解直线和平面垂直的判定定理和性质定理，掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念，了解三垂线定理及其逆定理。（4）了解平面与平面的位置关系，掌握两个平面平行的判定定理和性质定理。掌握二面角、二面角的平面角、两个平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理。（5）会用反证法证明简单的问题。（6）了解多面体的概念，了解凸多面体的概念。（7）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图。（8）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图。（9）了解正多面体的概念，了解多面体的欧拉公式。（10）了解球的概念，掌握球的性质，掌握球的表面积、体积公式。二．复习目标： 1．在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上，研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用；在有关问题的解决过程中，进一步了解和掌握相关公理、定理的内容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用． 2．在掌握空间角(两条异面直线所成的角，平面的斜线与平面所成的角及二面角)概念的基础上，掌握它们的求法(其基本方法是分别作出这些角，并将它们置于某个三角形内通过计算求出它们的大小)；在解决有关空间角的问题的过程中，进一步巩固关于直线和平面的平行垂直的性质与判定的应用，掌握作平行线(面)和垂直线(面)的技能；通过有关空间角的问题的解决，进一步提高学生的空间想象能力、逻辑推理能力及运算能力． 3．通过复习，使学生更好地掌握多面体与旋转体的有关概念、性质，并能够灵活运用到解题过程中．通过教学使学生掌握基本的立体几何解题方法和常用解题技巧，发掘不同问题之间的内在联系，提高解题能力． 4．在学生解答问题的过程中，注意培养他们的语言表述能力和“说话要有根据”的逻辑思维的习惯、提高思维品质．使学生掌握化归思想，特别是将立体几何问题转化为平面几何问题的思想意识和方法，并提高空间想象能力、推理能力和计算能力． 5．使学生更好地理解多面体与旋转体的体积及其计算方法，能够熟练地使用分割与补形求体积，提高空间想象能力、推理能力和计算能力．三．教学过程：（Ⅰ）基础知识详析重庆高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立

2015年高考理科数学试题汇编(含答案)：立体几何-小题

（新课标1）（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（） A.14斛 B.22斛 C.36斛 D.66斛【答案】B 考点：圆锥的体积公式（新课标1）（9）已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为A．36π B.64π C.144π D.256π 【答案】C

试题分析：因为α，β是两个不同的平面，m是直线且mα?．若“mβ∥”，则平面、 αβ可能相交也可能平行，不能推出// αβ， αβ，反过来若// mα ?，则有mβ∥，则“mβ∥”是“αβ∥”的必要而不充分条件. 考点：1.空间直线与平面的位置关系；2.充要条件. （福建）7．若,l m是两条不同的直线，m垂直于平面α，则“l m⊥”是“//lα的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件【答案】B 考点：空间直线和平面、直线和直线的位置关系．（湖南）10.某工件的三视图如图3所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用

2021高考数学立体几何专题

专题09立体几何与空间向量选择填空题历年考题细目表题型年份考点试题位置单选题2019 表面积与体积2019年新课标1理科12 单选题2018 几何体的结构特征2018年新课标1理科07 单选题2018 表面积与体积2018年新课标1理科12 单选题2017 三视图与直观图2017年新课标1理科07 单选题2016 三视图与直观图2016年新课标1理科06 单选题2016 空间向量在立体几何中的应用2016年新课标1理科11 单选题2015 表面积与体积2015年新课标1理科06 单选题2015 三视图与直观图2015年新课标1理科11 单选题2014 三视图与直观图2014年新课标1理科12 单选题2013 表面积与体积2013年新课标1理科06 单选题2013 三视图与直观图2013年新课标1理科08 单选题2012 三视图与直观图2012年新课标1理科07 单选题2012 表面积与体积2012年新课标1理科11 单选题2011 三视图与直观图2011年新课标1理科06 单选题2010 表面积与体积2010年新课标1理科10 填空题2017 表面积与体积2017年新课标1理科16 填空题2011 表面积与体积2011年新课标1理科15 填空题2010 三视图与直观图2010年新课标1理科14 历年高考真题汇编 1．【2019年新课标1理科12】已知三棱锥P﹣ABC的四个顶点在球O的球面上，P A＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是P A，AB的中点，∠CEF＝90°，则球O的体积为（） A．8πB．4πC．2πD．π 2．【2018年新课标1理科07】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）

历年高考数学压轴题集锦

高考数学压轴题集锦 1．椭圆的中心是原点O ，它的短轴长为(,)0F c （0>c ）的准线l 与x 轴相交于点A ，2OF FA =，过点A 的直线与椭圆相交于P 、Q 两点。（1）求椭圆的方程及离心率；（2）若0OP OQ ?=，求直线PQ 的方程；（3）设AP AQ λ=（1λ>），过点P 且平行于准线l 的直线与椭圆相交于另一点M ，证明FM FQ λ=-. (14分) 2．已知函数)(x f 对任意实数x 都有1)()1(=++x f x f ，且当]2,0[∈x 时，|1|)(-=x x f 。（1） )](22,2[Z k k k x ∈+∈时，求)(x f 的表达式。（2）证明)(x f 是偶函数。（3）试问方程01 log )(4=+x x f 是否有实数根？若有实数根，指出实数根的个数；若没有实数根，请说明理由。 3．（本题满分12分）如图，已知点F （0，1），直线L ：y=-2，及圆C ：1)3(2 2 =-+y x 。（1）若动点M 到点F 的距离比它到直线L 的距离小1，求动点M 的轨迹E 的方程；（2）过点F 的直线g （3）过轨迹E 上一点P 点P 的坐标及S

4.以椭圆2 22y a x +＝1（a ＞1）短轴一端点为直角顶点，作椭圆内接等腰直角三角形，试判断并推证能作出多少个符合条件的三角形. 5 已知，二次函数f （x ）＝ax 2 ＋bx ＋c 及一次函数g （x ）＝－bx ，其中a 、b 、c ∈R ，a ＞b ＞c ，a ＋b ＋c ＝0. （Ⅰ）求证：f （x ）及g （x ）两函数图象相交于相异两点；（Ⅱ）设f （x ）、g （x ）两图象交于A 、B 两点，当AB 线段在x 轴上射影为A 1B 1时，试求|A 1B 1|的取值范围. 6 已知过函数f （x ）=12 3++ax x 的图象上一点B （1，b ）的切线的斜率为－3。（1）求a 、b 的值；（2）求A 的取值范围，使不等式f （x ）≤A －1987对于x ∈[－1，4]恒成立；（3）令()()132 ++--=tx x x f x g 。是否存在一个实数t ，使得当]1,0(∈x 时，g （x ）有最大值1？ 7 已知两点M （－2，0），N （2，0），动点P 在y 轴上的射影为H ，︱PH ︱是2和→ → ?PN PM 的等比中项。（1）求动点P 的轨迹方程，并指出方程所表示的曲线；（2）若以点M 、N 为焦点的双曲线C 过直线x+y=1上的点Q ，求实轴最长的双曲线C 的方程。 8．已知数列{a n }满足a a a a b a a a a a a a n n n n n n +-=+=>=+设,2),0(322 11 （1）求数列{b n }的通项公式；（2）设数列{b n }的前项和为S n ，试比较S n 与 8 7 的大小，并证明你的结论. 9．已知焦点在x 轴上的双曲线C 的两条渐近线过坐标原点，且两条渐近线与以点)2,0(A 为圆心，1为半径的圆相切，又知C 的一个焦点与A 关于直线x y =对称．（Ⅰ）求双曲线C 的方程；（Ⅱ）设直线1+=mx y 与双曲线C 的左支交于A ，B 两点，另一直线l 经过M （-2，0）及AB 的中点，求直线l 在y 轴上的截距b 的取值范围；（Ⅲ）若Q 是双曲线C 上的任一点，21F F 为双曲线C 的左，右两个焦点，从1F 引21QF F ∠的平分线的垂线，垂足为N ，试求点N 的轨迹方程． 10. )(x f 对任意R x ∈都有.2 1)1()(= -+x f x f

高中数学立体几何专题

高中课程复习专题——数学立体几何一空间几何体㈠空间几何体的类型 1 多面体：由若干个平面多边形围成的几何体。围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点。 2 旋转体：把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。其中，这条直线称为旋转体的轴。㈡几种空间几何体的结构特征 1 棱柱的结构特征棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。棱柱的分类棱柱的性质 ⑴侧棱都相等，侧面是平行四边形； ⑵两个底面与平行于底面的截面是全等的多边形； ⑶过不相邻的两条侧棱的截面是平行四边形； ⑷直棱柱的侧棱长与高相等，侧面的对角面是矩形。长方体的性质 ⑴长方体的一条对角线的长的平方等于一个顶点上三条棱的平方和：AC12 = AB2 + AC2 + AA12 ⑵长方体的一条对角线AC1与过定点A的三条棱所成图1-2 长方体

的角分别是α、β、γ，那么： cos2α + cos2β + cos2γ = 1 sin2α + sin2β + sin2γ = 2 ⑶ 长方体的一条对角线AC1与过定点A的相邻三个面所组成的角分别为α、β、γ，则： cos2α + cos2β + cos2γ = 2 sin2α + sin2β + sin2γ = 1 棱柱的侧面展开图：正n棱柱的侧面展开图是由n个全等矩形组成的以底面周长和侧棱为邻边的矩形。棱柱的面积和体积公式 S直棱柱侧面 = c·h (c为底面周长，h为棱柱的高) S直棱柱全 = c·h+ 2S底 V棱柱 = S底·h 2 圆柱的结构特征 2-1 圆柱的定义：以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆柱。图1-3 圆柱 2-2 圆柱的性质 ⑴上、下底及平行于底面的截面都是等圆； ⑵过轴的截面(轴截面)是全等的矩形。 2-3 圆柱的侧面展开图：圆柱的侧面展开图是以底面周长和母线长为邻边的矩形。 2-4 圆柱的面积和体积公式 S圆柱侧面= 2π·r·h (r为底面半径，h为圆柱的高) S圆柱全= 2π r h + 2π r2 V圆柱 = S底h = πr2h 3 棱锥的结构特征 3-1 棱锥的定义 ⑴棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

高考中常见的立体几何题型和解题方法

高考中常见的立体几何题型和解题方法黔江中学高三数学教师：付超高考立体几何试题一般共有2——3道(选择、填空题1——2道, 解答题1道), 共计总分18——23分左右,考查的知识点在20个以内. 选择填空题考核立几中的逻辑推理型问题, 而解答题着重考查立几中的计算型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的方向发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合 1．有关平行与垂直(线线、线面及面面)的问题，是在解决立体几何问题的过程中，大量的、反复遇到的，而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容，因此在主体几何的总复习中，首先应从解决“平行与垂直”的有关问题着手，通过较为基本问题，熟悉公理、定理的内容和功能，通过对问题的分析与概括，掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想，以提高逻辑思维能力和空间想象能力． 2．判定两个平面平行的方法：（1）根据定义——证明两平面没有公共点；（2）判定定理——证明一个平面内的两条相交直线都平行于另一个平面；（3）证明两平面同垂直于一条直线。 3．两个平面平行的主要性质： ⑴由定义知：“两平行平面没有公共点”。 ⑵由定义推得：“两个平面平行，其中一个平面内的直线必平行于另一个平面。 ⑶两个平面平行的性质定理：“如果两个平行平面同时和第三个平面相交，那么它们的交线平行”。 ⑷一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。 ⑸夹在两个平行平面间的平行线段相等。 ⑹经过平面外一点只有一个平面和已知平面平行。以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”，但在解题过程中均可直接作为性质定理引用。 4．空间角和距离是空间图形中最基本的数量关系，空间角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等．解这类问题的基本思路是把空间问题转化为平面问题去解决．空间角，是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念，由它们的定义，可得其取值范围，如两异面直线所成的角θ∈(0，2π]，直线与平面所成的角θ∈0,2π?????? ，二面角的大小，可用它们的平面角来度量，其平面角θ∈[0，π]．对于空间角的计算，总是通过一定的手段将其转化为一个平面内的角，并把它置于一个平面图形，而且是一个三

高考数学压轴题汇编

高考数学压轴题汇编 1．〔本小题满分12分〕设函数在上是增函数.求正实数的取值范围；设，求证：1 ,0>>a b .ln 1b b a b b a b a +<+<+ 高考数学压轴题练习2 2．已知椭圆C 的一个顶点为，焦点在x 轴上，右焦点到直线(0,1)A -10x y -+= 〔1〕求椭圆C 的方程；〔2〕过点F 〔1，0〕作直线l 与椭圆C 交于不同的两点A 、B ，设，若的取值范围. 高考数学压轴题练习2 2．已知椭圆C 的一个顶点为，焦点在x 轴上，右焦点到直线(0,1)A -10x y -+= 〔1〕求椭圆C 的方程；〔2〕过点F 〔1，0〕作直线l 与椭圆C 交于不同的两点A 、B ，设，若的取值范围. 高考数学压轴题练习4 4．设函数3 2 2 ()f x x ax a x m =+-+(0)a > 〔1〕若时函数有三个互不相同的零点，求的范围；〔2〕若函数在内没有极值点，求的范围；〔3〕若对任意的，不等式在上恒成立，求实数的取值范围．高考数学压轴题练习5 5．〔本题满分14分〕已知椭圆的离心率为，直线与以原点为圆心、以椭圆的短半轴长为半径的圆相切. 〔Ⅰ〕求椭圆的方程；〔Ⅱ〕设椭圆的左焦点为F1，右焦点为F2，直线过点F1，且垂直于椭圆的长轴，动直线垂直于点P ，线段 PF2的垂直平分线交于点M ，求点M 的轨迹C2的方程；〔Ⅲ〕若AC 、BD 为椭圆C1的两条相互垂直的弦，垂足为右焦点F2，求四边形ABCD 的面积的最小值．高考数学压轴题练习6 6．〔本小题满分14分〕已知椭圆＋＝1〔a>b>0〕的左．右焦点分别为F1．F2，离心率e ＝，右准线方程为x ＝2．〔1〕求椭圆的标准方程；〔2〕过点F1的直线l 与该椭圆相交于M ．N 两点，且|＋|＝，求直线l 的方程．高考数学压轴题练习7 7.〔本小题满分12分〕已知，函数，〔其中为自然对数的底数〕．〔1〕判断函数在区间上的单调性；〔2〕是否存在实数，使曲线在点处的切线与轴垂直? 若存在，求出的值；若不存在，请说明理由．

2010年高考立体几何专题复习-6

2010年高考立体几何专题复习岱山中学孙珊瑚鲁纪伟高考立体几何试题一般有选择、填空题, 解答题,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合 1．有关平行与垂直(线线、线面及面面)的问题，是在解决立体几何问题的过程中，大量的、反复遇到的，而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容，因此在主体几何的总复习中，首先应从解决“平行与垂直”的有关问题着手，通过较为基本问题，熟悉公理、定理的内容和功能，通过对问题的分析与概括，掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想，以提高逻辑思维能力和空间想象能力． 2.判定两个平面平行的方法：（1）根据定义——证明两平面没有公共点；（2）判定定理——证明一个平面内的两条相交直线都平行于另一个平面；（3）证明两平面同垂直于一条直线。 3.两个平面平行的主要性质： ⑴由定义知：“两平行平面没有公共点”。 ⑵由定义推得：“两个平面平行，其中一个平面内的直线必平行于另一个平面。 ⑶两个平面平行的性质定理：“如果两个平行平面同时和第三个平面相交，那么它们的交线平行”。 ⑷一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。 ⑸夹在两个平行平面间的平行线段相等。 ⑹经过平面外一点只有一个平面和已知平面平行。以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”，但在解题过程中均可直接作为性质定理引用。 4.空间的角和距离是空间图形中最基本的数量关系，空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等．解这类问题的基本思路是把空间问题转化为平面问题去解决．空间的角，是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念，由它们的定义，可得其取值范围，如两异面直线所成的角θ∈(0，2π]，直线与平面所成的角θ∈0,2π?? ???? ，二面角的大小，可用它们的平面角来度量，其平面角θ∈[0，π]．对于空间角的计算，总是通过一定的手段将其转化为一个平面内的角，并把它置于一个平面图形，而且是一个三角形的内角来解决，而这种转化就是利用直线与平面的平行与垂直来实现的，因此求这些角的过程也是直线、平面的平行与垂直的重要应用．通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力．如求异面直线所成的角常用平移法（转化为相交直线）与向量法；求直线与平面所成的角常利用射影转化为相交直线所成的角；而求二面角－l －的平面角（记作）通常有以下几种方法： (1) 根据定义； (2) 过棱l 上任一点O 作棱l 的垂面，设∩＝OA ，∩＝OB ，则∠AOB ＝； (3) 利用三垂线定理或逆定理，过一个半平面内一点A ，分别作另一个平面的垂线AB (垂足为B ),或棱l 的垂线AC (垂足为C )，连结AC ，则∠ACB ＝或∠ACB ＝－； (4) 设A 为平面外任一点，AB ⊥，垂足为B ，AC ⊥，垂足为C ，则∠BAC ＝或∠BAC ＝－； (5) 利用面积射影定理，设平面内的平面图形F 的面积为S ，F 在平面内的射影图形的面积为S ，则cos ＝S S ' . 5.空间的距离问题，主要是求空间两点之间、点到直线、点到平面、两条异面直线之间（限于给出公垂线

高考数学15立体几何小题.docx

立体几何 1、平面βα⊥，直线α?b ，m β?，且b m ⊥，则b 与β( ) A ．b β⊥ B ．b 与β斜交 C ．b //β D ．位置关系不确定 2、过三棱柱111ABC A B C -的任意两条棱的中点作直线，其中与平面11ABB A 平行的直线共有( )条 A ．2 B ．4 C ．6 D ．8 3、一条直线与一个平面所成的角等于3π，另一直线与这个平面所成的角是6 π 。则这两条直线的位置关系( ) A ．必定相交 B ．平行 C ．必定异面 D ．不可能平行 4、在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1:3，则锥体被截面所分成的两部分的体积之比为( ) A ． B ．1:9 C ．1: D ．1:1) 5、正方体1111ABCD A B C D -中，,,P Q R 分别是11,,AB AD B C 的中点．那么，正方体的过,,P Q R 的截面图形是( ) A ．三角形 B ．四边形 C ．五边形 D ．六边形 6、正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为( ) A ．75° B ．60° C ．45° D ．30° 7、已知平面α与β所成的二面角为80°，P 为,αβ外一定点，过点P 的一条直线与,αβ所成的角都是30°，则这样的直线有且仅有( ) A ．1条 B ．2条 C ．3条 D ．4条 8、如图所示，PAB ?所在的平面α和四边形ABCD 所在的平面β互相垂直，且AD α⊥，BC α⊥，4AD =， 8BC =，6AB =。若tan 2tan 1ADP BCP ∠-∠=，则动点P 在平面α内的轨迹是( ) A ．椭圆的一部分 B ．线段 C ．双曲线的一部分 D ．以上都不是 9、如图所示，已知球O 为棱长为1的正方体1111ABCD A B C D -的内切球，则平面1ACD 截球O 的截面面积为( ) A ． 6 π B ． 3 π C D

高考数学压轴题精编精解100题

个个高考数学压轴题精编精解精选100题，精心解答{完整版} 1．设函数()1,12 1,23x f x x x ≤≤?=?-<≤? ，()()[],1,3g x f x ax x =-∈，其中a R ∈，记函数()g x 的最大值与最小值的差为()h a 。（I ）求函数()h a 的解析式；（II ）画出函数()y h x =的图象并指出()h x 的最小值。 2．已知函数()()ln 1f x x x =-+,数列{}n a 满足101a <<, ()1n n a f a +=; 数列{}n b 满足1111 ,(1)22 n n b b n b +=≥+, *n N ∈.求证: （Ⅰ）101;n n a a +<<<（Ⅱ）21;2 n n a a +< （Ⅲ）若12 ,2a =则当n ≥2时,!n n b a n >?. 3．已知定义在R 上的函数f (x ) 同时满足：（1）2 1212122()()2()cos24sin f x x f x x f x x a x ++-=+（12,x x ∈R ，a 为常数）；（2）(0)()14f f π==；（3）当0, 4x π ∈［］时，()f x ≤2 求：（Ⅰ）函数()f x 的解析式；（Ⅱ）常数a 的取值范围． 4．设)0(1),(),,(22 222211>>=+b a b x x y y x B y x A 是椭圆上的两点，满足0),(),( 2211=?a y b x a y b x ，椭圆的离心率,23 =e 短轴长为2，0为坐标原点. （1）求椭圆的方程；（2）若直线AB 过椭圆的焦点F （0，c ），（c 为半焦距），求直线AB 的斜率k 的值；（3）试问：△AOB 的面积是否为定值？如果是，请给予证明；如果不是，请说明理由. 5．已知数列{}n a 中各项为： 12、1122、111222、 (111) ??????14243222n ??????14243 …… （1）证明这个数列中的每一项都是两个相邻整数的积. （2）求这个数列前n 项之和S n .

(完整版)非常好高考立体几何专题复习

立体几何综合习题一、考点分析 1．棱柱——有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。 ①? ? ??????→?? ?????→? ? ?? L 底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 ★ 底面为矩形底面为正方形侧棱与底面边长相等 2. 棱锥棱锥——有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。 ★正棱锥——如果有一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥。 3 ．球球的性质： ①球心与截面圆心的连线垂直于截面； ★②r（其中，球心到截面的距离为 d、球的半径为R、截面的半径为r） ★球与多面体的组合体：球与正四面体，球与长方体，球与正方体等的内接与外切. 注：球的有关问题转化为圆的问题解决. B

1．求异面直线所成的角(]0,90θ∈??：解题步骤：一找（作）：利用平移法找出异面直线所成的角；（1）可固定一条直线平移另一条与其相交；（2）可将两条一面直线同时平移至某一特殊位置。常用中位线平移法二证：证明所找（作）的角就是异面直线所成的角（或其补角）。常需要证明线线平行；三计算：通过解三角形，求出异面直线所成的角； 2求直线与平面所成的角[]0,90θ∈??：关键找“两足”：垂足与斜足解题步骤：一找：找（作）出斜线与其在平面内的射影的夹角（注意三垂线定理的应用）；二证：证明所找（作）的角就是直线与平面所成的角（或其补角）（常需证明线面垂直）；三计算：常通过解直角三角形，求出线面角。 3求二面角的平面角[]0,θπ∈ 解题步骤：一找：根据二面角的平面角的定义，找（作）出二面角的平面角；二证：证明所找（作）的平面角就是二面角的平面角（常用定义法，三垂线法，垂面法）；三计算：通过解三角形，求出二面角的平面角。

文档之家

高考数学二轮复习专题六 立体几何