
学科教师辅导讲义
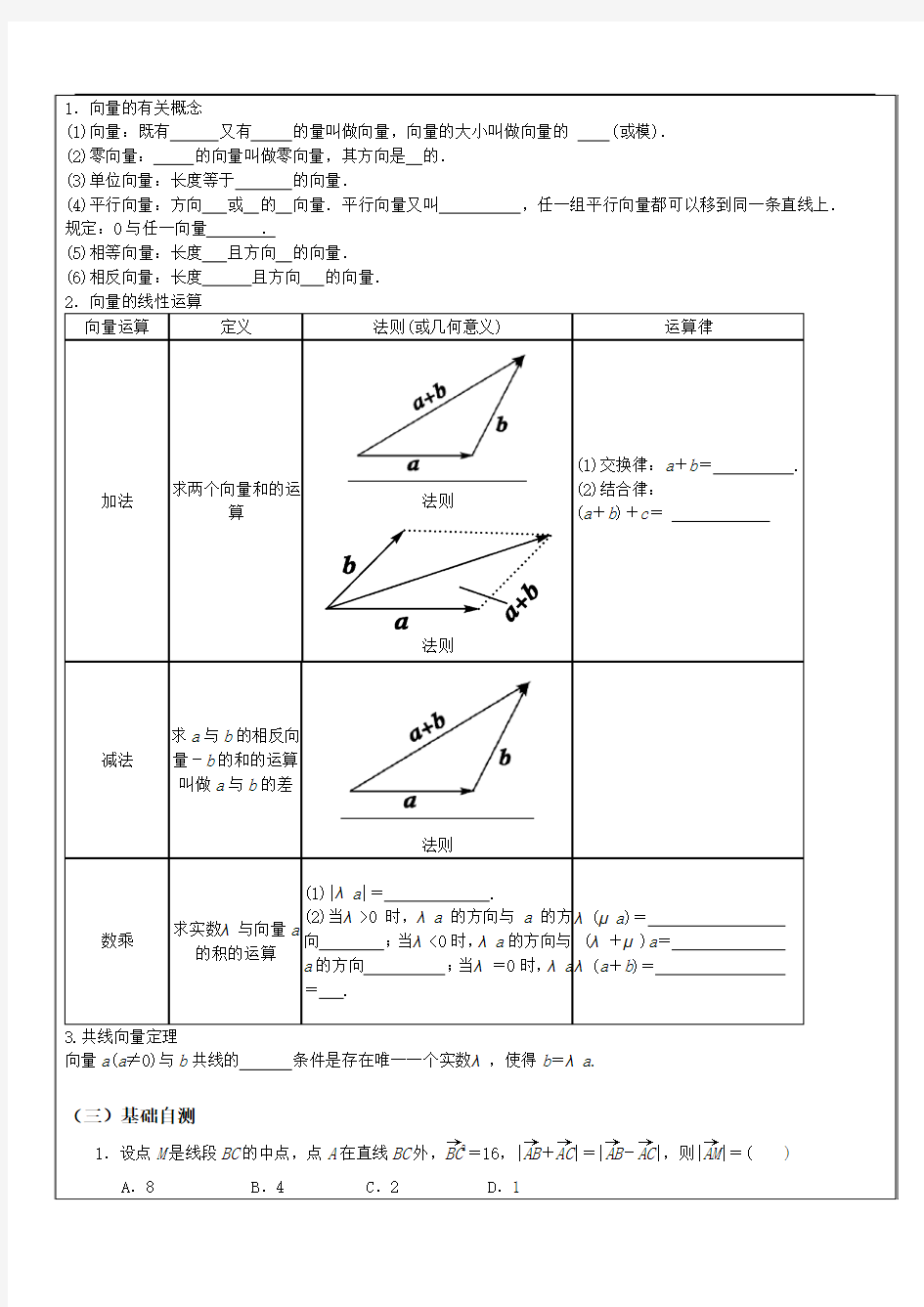
法则
4.设P 是△ABC 所在平面内的一点,A.PA →+PB →
=0
B.PB →+[答案] C
[答案] b -1
2
a
[解析] 设F 是AB 的中点,连接
6.将4(3a +2b )-2(b -2a )化简成最简式为[答案] 16a +6b
[解析] 4(3a +2b )-2(b -2a )=127.如图,AM →=13AB →,AN =13AC →.
[证明] MN →=AN →-AM →=13AC →-13
(四)典型例题
1.命题方向:向量的有关概念
[例1] 给出下列六个命题:①若两个向量相等,则它们的起点相同,终点相同;②若|a |=|b |,则a =b ;
跟踪练习2:
如图,D 、E 、F 分别为△ABC
[分析] 在三角形中其他向量最好向三条边上的向量靠拢,即用[证明] 因为AD →=AC →+CD →,所以2AD →=AC →+AB →+CD →+即2AD →=AC →+AB →.
同理2BE →=BA →+BC →,2CF →所以2(AD →+BE →+CF →)=AC →故AD →+BE →+CF →
=0.
3.命题方向:向量共线问题[例3] 已知非零向量e 1和(1)如果AB →=e 1+e 2,BC →(2)欲使ke 1+e 2和e 1+[分析] 对于(1),要证明共线,则一定存在λ,使ke →
AB→-AC→)+1
3 BC→
运用三角形法则求和向量时,应“始终相接,始指向终”;求差向量时,应“同始连终,指向被减”.
=0.
、FP .
-12b =-12
(a +b ).
AB →=2e 1+ke 2,CB →=e 1+3e 2,
=ha +hb ,BF →=BA →+AF →
=-a +=-ka +k 4b ,
.
[分析] 先用平面向量基本定理设出[解析] 设OM →
=ma +nb (m 则AM →=OM →-OA →
=(m -1)a +AD →
=OD →-OA →=1
2b -a =-a 因为A ,M ,D 三点共线,所以
而CM →=OM →-OC →
=(m -14
)a +CB →=OB →-OC →
=b -14a =-14
[解析] ∵G 是△ABO 的重心,∴OG →=23OC →=13(OA →+OB →)=∴GP →=OP →-OG →=ma -13(a +GQ →=OQ →-OG →
=nb -13(a +b 又GP →∥GQ →,∴? ????m -13? ?n -13∴13(m +n )=mn ,即1m +1
n =2.命题方向:平面向量的坐标运算[例2] 已知点A (-1,2)[分析] 根据题意可设出点[解析] 设点C 、D 的坐标分别为-y 2),BA →
=(-3,-6).
因为AC →=13AB →,DA →
=-13
BA →
设向量p=(a+c,b),q=(b c+2d
数学思维与训练 高中(三) ------------向量复习专题 向量思想方法和平面向量问题是新考试大纲考查的重要部分,是新高考的热点问题。题型多为选择或填空题,向量作为中学数学中的一个重要工具在三角、函数、解几、立几等问题解决中处处闪光。最近几年的考试中向量均出现在解析几何题中,在解析几何的框架中考查向量的概念和方法、考查向量的运算性质、考查向量几何意义的应用,并直接与距离问题、角度问题、轨迹问题等相联系。 附Ⅰ、平面向量知识结构表 1. 考查平面向量的基本概念和运算律 此类题经常出现在选择题与填空题中,主要考查平面向量的有关概念与性质,要求考生深刻理解平面向量的相关概念,能熟练进行向量的各种运算,熟悉常用公式及结论,理解并掌握两向量共线、垂直的充要条件。 1.(北京卷) | a |=1,| b |=2,c = a + b ,且c ⊥a ,则向量a 与b 的夹角为 ( ) A .30° B .60° C .120° D .150° 2.(江西卷·理6文6) 已知向量 ( ) A .30° B .60° C .120° D .150° 3.(重庆卷·理4)已知A (3,1),B (6,1),C (4,3),D 为线段BC 的中点,则向 量与 的夹角为 ( C ) A . B . C . D .- 4.(浙江卷)已知向量≠,||=1,对任意t ∈R ,恒有| -t |≥| -|,则 ( ) 向量 向量的概念 向量的运算 向量的运用 向量的加、减法 实数与向量的积 向量的数量积 两个向量平行的充要条件两个向量垂直的充要条件 定比分点公式 平移公式 在物理学中的应用 在几何中的应用
平面向量练习题集答案 典例精析 题型一向量的有关概念 【例1】下列命题: ①向量AB的长度与BA的长度相等; ②向量a与向量b平行,则a与b的方向相同或相反; ③两个有共同起点的单位向量,其终点必相同; ④向量AB与向量CD是共线向量,则A、B、C、D必在同一直线上. 其中真命题的序号是. 【解析】①对;零向量与任一向量是平行向量,但零向量的方向任意,故②错;③显然错;AB与CD 是共线向量,则A、B、C、D可在同一直线上,也可共面但不在同一直线上,故④错.故是真命题的只有①. 【点拨】正确理解向量的有关概念是解决本题的关键,注意到特殊情况,否定某个命题只要举出一个反例即可. 【变式训练1】下列各式: a?; ①|a|=a ②(a?b) ?c=a?(b?c); ③OA-OB=BA; ④在任意四边形ABCD中,M为AD的中点,N为BC的中点,则AB+DC=2MN; ⑤a=(cos α,sin α),b=(cos β,sin β),且a与b不共线,则(a+b)⊥(a-b). 其中正确的个数为() A.1 B.2 C.3 D.4 a?正确;(a?b) ?c≠a?(b?c);OA-OB=BA正确;如下图所示,【解析】选D.| a|=a MN=MD+DC+CN且MN=MA+AB+BN, 两式相加可得2MN=AB+DC,即命题④正确; 因为a,b不共线,且|a|=|b|=1,所以a+b,a-b为菱形的两条对角线, 即得(a+b)⊥(a-b). 所以命题①③④⑤正确.
题型二 与向量线性运算有关的问题 【例2】如图,ABCD 是平行四边形,AC 、BD 交于点O ,点M 在线段DO 上,且DM = DO 31,点N 在线段OC 上,且ON =OC 3 1 ,设AB =a , AD =b ,试用a 、b 表示AM ,AN ,MN . 【解析】在?ABCD 中,AC ,BD 交于点O , 所以DO =12DB =12(AB -AD )=1 2 (a -b ), AO =OC =12AC =12(AB +AD )=1 2(a +b ). 又DM =13DO , ON =1 3OC , 所以AM =AD +DM =b +1 3DO =b +13×12(a -b )=16a +56 b , AN =AO +ON =OC +1 3OC =43OC =43×12(a +b )=2 3(a +b ). 所以MN =AN -AM =23(a +b )-(16a +56b )=12a -16 b . 【点拨】向量的线性运算的一个重要作用就是可以将平面内任一向量由平面内两个不共线的向量表示,即平面向量基本定理的应用,在运用向量解决问题时,经常需要进行这样的变形. 【变式训练2】O 是平面α上一点,A 、B 、C 是平面α上不共线的三点,平面α内的动点P 满足OP =OA +λ(AB +AC ),若λ=1 2 时,则PA ?(PB +PC )的值为 . 【解析】由已知得OP -OA =λ(AB +AC ), 即AP =λ(AB +AC ),当λ=12时,得AP =1 2(AB +AC ), 所以2AP =AB +AC ,即AP -AB =AC -AP , 所以BP =PC , 所以PB +PC =PB +BP =0, 所以PA ? (PB +PC )=PA ?0=0,故填0.
一、选择题【共12道小题】 1、下列说法中正确的是( ) A.两个单位向量的数量积为1 B.若a··c且a≠0,则 C. D.若b⊥c,则()··b 参考答案与解析:解析:A中两向量的夹角不确定中若a⊥⊥与c反方向则不成立中应为中b⊥·0,所以()····b. 答案:D 主要考察知识点:向量、向量的运算 2、设e是单位向量222,则四边形是( ) A.梯形 B.菱形 C.矩形 D.正方形参考答案与解析:解析:,所以,且∥,所以四边形是平行四边形.又因为2,所以四边形是菱形. 答案:B 主要考察知识点:向量、向量的运算 3、已知1,a与b的夹角为90°,且2a3b,4b,若c⊥d,则实数k的值为( ) A.6 6 C.3 3 参考答案与解析:解析:∵c⊥d,∴c·(23b)·(4b)=0,即212=0,∴6. 答案:A 主要考察知识点:向量、向量的运算 4、设0≤θ<2π,已知两个向量=(θ,θ)(2θ,2θ),则向量长度的最大值是( )
A. B. C. D. 参考答案与解析:解析:=(2θθ,2θθ), 所以≤=. 答案:C 主要考察知识点:向量与向量运算的坐标表示 5、设向量(13),(-2,4),(-12),若表示向量4a、4b-2c、2()、d的有向线段首尾相接能构成四边形,则向量d为( ) A.(2,6) B.(-2,6) C.(26) D.(-26) 参考答案与解析:解析:依题意,4422()0,所以644(-2,-6). 答案:D 主要考察知识点:向量与向量运算的坐标表示 6、已知向量(3,4),(-3,1),a与b的夹角为θ,则θ等于( ) A. C.3 3 参考答案与解析:解析:由已知得a·3×(-3)+4×15,5,, 所以θ=. 由于θ∈[0,π], 所以θ=. 所以θ 3. 答案:D 主要考察知识点:向量与向量运算的坐标表示
第一部分:平面向量的概念及线性运算 欧阳光明(2021.03.07) 一.基础知识自主学习 1.向量的有关概念 名称定义备注 向量既有又有的量;向量的大小叫做向量 的(或称) 平面向量是自由向量 零向量长度为的向量;其方向是任意的记作0 单位向量长度等于的 向量 非零向量a的单位向量为± a |a| 平行向量方向或的非零向量 0与任一向量或共线共线向量的非零向量又叫做共线向量 相等向量长度且方向的向量两向量只有相等或不等,不能比 较大小 相反向量长度且方向的向量0的相反向量为0 2.向量的线性运算 向量运算定义法则(或几何 意义) 运算律 加法求两个向量和的运算(1)交换律: a+b=b+a. (2)结合律: (a+b)+c=a+(b+c). 减法求a与b的相反向量-b 的和的运算叫做a与b 的差 法则 a-b=a+(-b) 数乘求实数λ与向量a的积的 运算 (1)|λa|=|λ||a|. (2)当λ>0时,λa的方向与a的方向; 当λ<0时,λa的方向与a的方向;当λ =0时,λa=0. λ(μa)=λμa; (λ+μ)a=λa+μa; λ(a+b)=λa+λb. 向量a(a≠0)与b共线的条件是存在唯一一个实数λ,使得b=λa. 二.难点正本疑点清源 1.向量的两要素 向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系.同向且等长的有向线
段都表示同一向量.或者说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说,即向量不能比较大小. 2.向量平行与直线平行的区别 向量平行包括向量共线(或重合)的情况,而直线平行不包括共线的情况.因而要利用向量平行证明向量所在直线平行,必须说明这两条直线不重合. 三.基础自测 1.化简OP →-QP →+MS →-MQ → 的结果等于________. 2.下列命题:①平行向量一定相等;②不相等的向量一定不平行;③平行于同一个向量的两个向量是共线向量; ④相等向量一定共线.其中不正确命题的序号是_______. 3.在△ABC 中,AB →=c ,AC →=b.若点D 满足BD →=2DC →,则AD → =________(用b 、c 表示). 4.如图,向量a -b 等于() A .-4e1-2e2 B .-2e1-4e2 C .e1-3e2 D .3e1-e2 5.已知向量a ,b ,且AB →=a +2b ,BC →=-5a +6b ,CD → =7a -2b ,则一定共线的三点是 () A .A 、B 、DB .A 、B 、C C .B 、C 、DD .A 、C 、D 四.题型分类深度剖析 题型一 平面向量的有关概念 例1 给出下列命题: ①若|a|=|b|,则a =b ;②若A ,B ,C ,D 是不共线的四点,则AB →=DC → 是四边形ABCD 为平行四边形的充要条件;③若a =b ,b =c ,则a =c ;④a =b 的充要条件是|a|=|b|且a ∥b ;⑤若a ∥b ,b ∥c ,则a ∥c.其中正确的序号是________. 变式训练1 判断下列命题是否正确,不正确的请说明理由. (1)若向量a 与b 同向,且|a|=|b|,则a>b ; (2)若|a|=|b|,则a 与b 的长度相等且方向相同或相反; (3)若|a|=|b|,且a 与b 方向相同,则a =b ; (4)由于零向量的方向不确定,故零向量不与任意向量平行; (5)若向量a 与向量b 平行,则向量a 与b 的方向相同或相反; (6)若向量AB →与向量CD → 是共线向量,则A ,B ,C ,D 四点在一条直线上; (7)起点不同,但方向相同且模相等的几个向量是相等向量; (8)任一向量与它的相反向量不相等 题型二 平面向量的线性运算 例2 如图,以向量OA →=a ,OB →=b 为边作?OADB ,BM →=13BC →,CN →=13 CD →,用a 、b 表示OM →、ON →、MN → . 变式训练2 △ABC 中,AD →=23 AB →,DE ∥BC 交AC 于E ,BC 边上的中线AM 交DE 于N.设AB →=a ,AC → =b ,用a 、b 表示向 量AE →、BC →、DE →、DN →、AM →、AN →. 题型三 平面向量的共线问题 例3 设e1,e2是两个不共线向量,已知AB →=2e1-8e2,CB →=e1+3e2,CD → =2e1-e2. (1)求证:A 、B 、D 三点共线; (2)若BF → =3e1-ke2,且B 、D 、F 三点共线,求k 的值.
平面向量练习题 一.填空题。 1. BA CD DB AC +++等于________. 2.若向量=(3,2),=(0,-1),则向量2-的坐标是________. 3.平面上有三个点A (1,3),B (2,2),C (7,x ),若∠ABC =90°,则x 的值为________. 4.向量a 、b 满足|a |=1,|b |=2,(a +b )⊥(2a -b ),则向量a 与b 的夹角为________. 5.已知向量a =(1,2),b =(3,1),那么向量2a -21b 的坐标是_________. 6.已知A (-1,2),B (2,4),C (4,-3),D (x ,1),若与CD 共线,则|BD |的值等于________. 7.将点A (2,4)按向量=(-5,-2)平移后,所得到的对应点A ′的坐标是______. 8. 已知a=(1,-2),b=(1,x),若a ⊥b,则x 等于______ 9. 已知向量a,b 的夹角为ο120,且|a|=2,|b|=5,则(2a-b )·a=______ 10. 设a=(2,-3),b=(x,2x),且3a ·b=4,则x 等于_____ 11. 已知y x 且),3,2(),,(),1,6(--===∥,则x+2y 的值为_____ 12. 已知向量a+3b,a-4b 分别与7a-5b,7a-2b 垂直,且|a|≠0,|b|≠0,则a 与b 的夹角为____ 13. 在△ABC 中,O 为中线AM 上的一个动点,若AM=2,则()OA OB OC +u u u r u u u r u u u r 的最小值是 . 14.将圆22 2=+y x 按向量v =(2,1)平移后,与直线0=++λy x 相切,则λ的值为 . 二.解答题。 1.设平面三点A (1,0),B (0,1),C (2,5). (1)试求向量2+的模; (2)试求向量与的夹角;
平面向量专题
向量专题 ☆零向量:长度为0的向量,记为0 ,其方向是任意的, 与任意向量平行 ☆单位向量:模为1个单位长度的向量 向量0 a 为单位 向量?|0 a |=1 ☆平行向量(共线向量):方向相同或相反的非零向量平 行向量也称为共线向量 ☆向量加法AB BC +=AC 向量加法有“三角形法则”与“平 行四边形法则”:AB BC CD PQ QR AR +++++=,但这时必须“首 尾相连”. ☆实数与向量的积: ①实数λ与向量a 的积是一个向量,记作λa ,它的长 度与方向规定如下: (Ⅰ)a a ?=λλ; (Ⅱ)当0>λ时,λa 的方向与a 的方向相同;当0<λ时, λa 的方向与a 的方向相反;当0=λ时,0 =a λ,方向是任意 的 ☆两个向量共线定理: 向量b 与非零向量a 共线?有且只有一个实数λ,使得b =a λ ☆平面向量的基本定理: 如果2 1 ,e e 是一个平面内的两个不共线向量,那么对这
一平面内的任一向量a ,有且只有一对实数2 1 ,λλ使: 2211e e a λλ+=,其中不共线的向量2 1 ,e e 叫做表示这一平面内所有向量的一组基底 ☆平面向量的坐标运算: (1) 若()()1 1 2 2 ,,,a x y b x y ==,则()1212,a b x x y y ±=±±,12 12 a b x x y y ?=?+? (2) 若()()2 2 1 1 ,,,y x B y x A ,则() 2 121,AB x x y y =-- (3) 若a =(x,y),则λa =(λx, λy) (4) 若()()1 1 2 2 ,,,a x y b x y ==,则12 21//0 a b x y x y ?-= (5) 若()()1 1 2 2 ,,,a x y b x y ==,则a b ⊥,0 212 1 =?+?y y x x ☆向量的运算向量的加减法,数与向量的乘积,向量的数量(内积)及其各运算的坐标表示和性质 ☆两个向量的数量积: 已知两个非零向量a 与b ,它们的夹角为θ,则a · b =︱a ︱·︱b ︱cos θ 叫做a 与b 的数量积(或内积) 规定00a ?= ☆向量的投影:︱b ︱cos θ=|| a b a ?∈R ,称为向量 b 在a 方向上的投影投影的绝对值称为射影 ☆数量积的几何意义: a · b 等于a 的长度与b 在a 方向上的投影的乘积 ☆向量的模与平方的关系:2 2 ||a a a a ?== ☆乘法公式成立: ()()2 2 22 a b a b a b a b +?-=-=-;
试卷第1页,总5页 一、选择题 1.已知三点)143()152()314(--,,、,,、,,λC B A 满足⊥,则λ的值 ( ) 2.已知)2 , 1(-=,52||=,且//,则=( ) 5.已知1,2,()0a b a b a ==+= ,则向量b 与a 的夹角为( ) 6.设向量(0,2),==r r a b ,则, a b 的夹角等于( ) 7.若向量()x x a 2,3+=和向量()1,1-=→b 平行,则 =+→→b a ( ) 8.已知()()0,1,2,3-=-=b a ,向量b a +λ与b a 2-垂直,则实数λ的值为( ). 9.设平面向量(1,2)a = ,(2,)b y =- ,若向量,a b 共线,则3a b + =( ) 10.平面向量a 与b 的夹角为60 ,(2,0)a = ,1b = ,则2a b + = 11.已知向量()1,2=,()1,4+=x ,若//,则实数x 的值为 12.设向量)2,1(=→a ,)1,(x b =→,当向量→→+b a 2与→→-b a 2平行时,则→→?b a 等于 13.若1,2,,a b c a b c a ===+⊥ 且,则向量a b 与的夹角为( ) 142= ,2||= 且(b a -)⊥a ,则a 与b 的夹角是 ( ) 15.已知向量AB =(cos120°,sin120°),AC =(cos30°,sin30°),则△ABC 的形状为 A .直角三角形 B .钝角三角形 C .锐角三角形 D .等边三角形 17.下列向量中,与(3,2)垂直的向量是( ). A .(3,2)- B .(2,3) C .(4,6)- D .(3,2)- 18.设平面向量(3,5),(2,1),2a b b ==--= 则a ( ) 19.已知向量)1,1(=a ,),2(n =b ,若b a ⊥,则n 等于 20. 已知向量,a b 满足0,1,2,a b a b ?=== 则2a b -= ( ) 21.设向量a =(1.cos θ)与b =(-1, 2cos θ)垂直,则cos 2θ等于 ( ) 23.化简AC - BD + CD - AB = 25.如图,正方形ABCD 中,点E ,F 分别是DC ,BC 的中点,那么=EF ( )
专题:平面向量的概念 知识梳理 1.向量的定义:既有大小又有方向的量叫做向量.例如:力,速度。 2.表示方法:用有向线段来表示向量.有向线段的长度表示向量的大小,用箭头所指的方向表示向量 的方向.用小写字母a ,b …或用AB ,BC ,…表示. 注意:我们用有向线段表示向量,而不能认为向量就是一个有向线段. 3.模:向量的长度叫向量的模,记作a 或AB .向量不能比较大小,但向量的模可以比较大小. 4.零向量:长度为零的向量叫做零向量,记作0 ;零向量的方向不确定. 注意:0和0 是不同,0是一个数字,0 代表一个向量,不要弄混. 5.单位向量:长度为1个长度单位的向量叫做单位向量.a a a =0 注意:单位向量不是只有一个,有无数多个,如果把它们的起始点重合,终止点刚好可以构成一个单位圆。 6.共线向量:方向相同或相反的向量叫共线向量,规定零向量与任何向量共线. 注意:由于向量可以进行任意的平移,平行向量总可以平移到同一直线上,故平行向量也称为共线向 量平行向量和共线向量是一个意思,对于两个非零向量b a ,,若存在非零常数λ使b a λ=是b a ∥的充 要条件. 7.相等的向量:长度相等且方向相同的向量叫相等的向量. 练习:★判断下列命题的真假 1、平行向量的方向一定相同的. ( × ) 解:有可能方向相反. 2、与零向量相等的向量必定是零向量. ( √ ) 3、零向量与任意的向量方向都相同。 ( √ ) 4、向量就是一条有向的线段。 ( × ) 5、若m n =,n k =,则m k =. ( √ ) 6、若,b a =,则.0=-b a (× ) 解:注意区分0和零向量.
第一部分:平面向量的概念及线性运算 一.基础知识自主学习 1.向量的有关概念 名称定义备注 向量既有又有的量;向量的大小叫做向量 平面向量是自由向量的(或称) 零向量长度为的向量;其方向是任意的记作 0 单位向量长度等于的非零向量 a 的单位向量为± a 向量|a| 平行向量方向或的非零向量 0 与任一向量或共线共线向量的非零向量又叫做共线向量 相等向量长度且方向的向量两向量只有相等或不等,不能比 较大小 相反向量长度且方向的向量0 的相反向量为 0 2.向量的线性运算 向量运算定义法则 (或几何 运算律意义 ) 加法求两个向量和的运算 求 a 与 b 的相反向量- b 减法的和的运算叫做 a 与 b 的差 (1)交换律: a+ b= b+ a. (2)结合律: (a+ b)+ c= a+ (b+c). a- b= a+ (- b) 法则 求实数λ与向量 a 的积的(1)|λa|= |λ||a|. ;λ(μa)=λμa; 数乘 (2)当λ>0 时,λa 的方向与 a 的方向 运算当λ<0 时,λa 的方向与 a 的方向;当λ (λ+μ)a=λa+μa; =0 时,λa= 0. λ(a+ b)=λa+λb. 3.共线向量定理 向量 a(a≠0)与 b 共线的条件是存在唯一一个实数λ,使得 b=λa. 二.难点正本疑点清源 1.向量的两要素 向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系.同向且等长的有向线段都表示同一向量.或者说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说, 即向量不能比较大小. 2.向量平行与直线平行的区别 向量平行包括向量共线 (或重合 )的情况,而直线平行不包括共线的情况.因而要利用向量平行证明向量所在直线平行,必须说明这两条直线不重合.
山东省高考数学一轮基础复习:专题 12 平面向量
姓名:________
班级:________
成绩:________
一、 单选题 (共 12 题;共 24 分)
1. (2 分) (2016 高一下·黑龙江期中) 已知△ABC 中,D 是 BC 边的中点,过点 D 的直线分别交直线 AB、AC 于点 E、F,若 =λ , =μ ,其中 λ>0,μ>0,则 λμ 的最小值是( )
A.1
B.
C.
D.
2. (2 分) (2019 高一下·湖州月考) 与向量
方向相反的单位向量是( )
A.
B.
C.
D.
或
3. (2 分) 如图所示,M,N 是函数
上运动,当△MPN 面积最大时
, 则 ω=
(ω>0)图像与 x 轴的交点,点 P 在 M,N 之间的图像 ()
第 1 页 共 18 页
A.
B.
C.
D.8
4. (2 分) (2018 高一下·集宁期末) 如图所示,点 , , 是圆 上的三点,线段
交于圈内一点 ,若
,
,则 ( )
与线段
A. B. C. D. 5. (2 分) 如图,△ABC 中,∠C =90°,且 AC=BC=4,点 M 满足
,则
=( )
A.2
第 2 页 共 18 页
B.3 C.4 D.6 6. (2 分) (2017 高二上·驻马店期末) 若 0<x<1,则 A.2 B . 1+2 C . 2+2 D . 3+2
的最小值为( )
7. (2 分) (2018 高二上·鄂尔多斯月考) 双曲线
的面积为 ,则
等于( )
A.2
B.3
C.4
D.5
的两个焦点为
,点 P 在双曲线上,
8. (2 分) 已知 D 为
的边 BC 的中点,
所在平面内有一点 P,满足,
设
则 的值为
()
A.1
B. C.2
D.
第 3 页 共 18 页
A C 平面向量 一.选择题: 1. 在平面上,已知点A(2,1),B(0,2),C(-2,1),O(0,0).给出下面的结论: ①= -②= +③2 - = 其中正确 ..结论的个数是() A.1个B.2个C.3个D.0个 2.下列命题正确的是() A.向量的长度与向量的长度相等B.两个有共同起点且相等的向量,其终点可能不同C.若非零向量与CD是共线向量,则A、B、C、D四点共线D.若 → a → b → c,则 → a → c 3. 若向量= (1,1), = (1,-1), =(-1,2),则等于( ) A.+ B. C. D.+ 4.若,且与也互相垂直,则实数的值为( ) A. B.6 C. D.3 5.已知=(2,3) , =(,7) ,则在上的正射影的数量为()A. B. C. D. 6.己知(2,-1) .(0,5) 且点P在的延长线上,, 则P点坐标为( ) A.(-2,11) B.( C.(,3) D.(2,-7) 7.设, a b是非零向量,若函数()()() f x x x =+- a b a b的图象是一条直线,则必有() A.⊥ a b B.∥ a b C.|||| = a b D.|||| ≠ a b 8.已知D点与ABC三点构成平行四边形,且A(-2,1),B(-1,3),C(3,4),则D点坐标为() A.(2,2) B.(4,6) C. (-6,0) D.(2,2)或(-6,0)或(4,6) 9.在直角ABC ?中,CD是斜边AB上的高,则下列等式不成立的是 (A) 2 AC AC AB =?(B)2 BC BA BC =? (C) 2 AB AC CD =?(D)2 2 ()() AC AB BA BC CD AB ??? = 10.设两个向量22 (2,cos) aλλα =+-和(,sin), 2 m b mα =+其中,,m λα为实数.若2, a b =则 m λ 的取值范围是 ( ) A.[6,1] - B.[4,8] C.(,1] -∞ D.[1,6] - 10.已知P={a|a=(1,0)+m(0,1),m∈R},Q={b|b=(1,1)+n(-1,1),n∈R}是两个向量集合,则P∩Q等于()A.{(1,1)} B.{(-1,1)} C.{(1,0)} D.{(0,1)} 二. 填空题:11.若向量a b ,的夹角为 60,1 a b ==,则() a a b -=. 12.向量2411 ()() ,,, a=b=.若向量() λ ⊥ b a+b,则实数λ
高中平面向量经典练习题 【编著】黄勇权 一、填空题 1、向量a=(2,4),b=(-1,-3),则向量3a-2b的坐标是。 2、已知向量a与b的夹角为60°,a=(3,4),|b | =1,则|a+5b | = 。 3、已知点A(1,2),B(2,1),若→ AP=(3,4),则 → BP= 。 4、已知A(-1,2),B(1,3),C(2,0),D(x,1),若AB与CD共线,则|BD|的值等于________。 5、向量a、b满足|a|=1,|b|= 2 ,(a+b)⊥(2a-b),则向量a与b的夹角为________。 6、设向量a,b满足|a+b|= 10,|a-b|= 6 ,则a·b=。 7、已知a、b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是。 8、在△ABC中,D为AB边上一点,→ AD = 1 2 → DB, → CD = 2 3 → CA + m → CB,则 m= 。 9、已知非零向量a,b满足|b|=4|a|,a⊥(2a+b),则a与b的夹角是。 10、在三角形ABC中,已知A(-3,1),B(4,-2),点P(1,-1)在中线AD 上,且→ AP= 2 → PD,则点C的坐标是()。 二、选择题 1、设向量→ OA=(6,2),→ OB=(-2,4),向量→ OC垂直于向量→ OB,向量 → BC平行于 →OA,若→ OD + → OA= → OC,则 → OD坐标=()。 A、(11,6) B、(22,12) C、(28,14) D、(14,7) 2、把A(3,4)按向量a(1,-2)平移到A',则点A'的坐标() A、(4 , 2) B、(3,1) C、(2,1) D、(1,0) 3、已知向量a,b,若a为单位向量, 且 | a| = | 2b| ,则(2a+ b)⊥(a-2b),则向量a与b的夹角是()。 A、90° B、60° C、30° D、0° 4、已知向量ab的夹角60°,| a|= 2,b=(-1,0),则| 2a-3b|=()
专题十二 平面向量的坐标运算 (一)知识梳理: 1、平面向量的基本定理:如果21,e e 是同一平面内的两个不共线的向量,那么,对于平面内的任一向量,_______________一对实数21,λλ,使得=_____________。 其中21,e e 叫做这一平面内所有向量的一组.. _______。 2、平面向量的坐标运算: (1)平面向量的坐标表示:在直角坐标系中,分别取与x 轴、y 轴方向相同的两个单位向量j i ,作为基底,则对平面内任一向量a ,由平面向量的基本定理得,___________ 一对实数x 、y ,使得a =_____________,我们把(___,___)叫做向量a 的坐标,记 作___________。显然,______i =,______=,______=。 (2)平面向量的坐标运算: ①向量坐标的加减、数乘运算: 设),(),,(2211y x b y x a ==则=±(_______,_______),λ=(____,____). ②向量坐标与向量起点、终点的关系: 若O (0,0),A (x ,y ),则=(___,___).知,从原点..出发.. 的向量,向量 的坐标等于_____________。 若),(),,(2211y x B y x A ==,则=(_______,______).知,一个向量的坐标 等于____________________________。 (3)向量平行的坐标表示:设),(),,(2211y x b y x a ==,则?// _______________ 3、线段的中点坐标公式:设),(),,(2211y x B y x A ==,C 是线段AB 的中点, 则点C=(_______,________) (二)例题讲解: 考点1:平面向量的基本定理 例1(a 级)、已知12,e e 是两个不共线的向量,则下列几组向量中,可以作为基底的是( ) A.113,2e b e a -== B. 0a =,1b e = C.121212,2a e e b e e =-=-+ D. 2121,e e e e +=-= 易错笔记: 例2(a 级)、实数x,y 满足3(10)(47)2xa y b y a xb +-=++,求x,y 的值. 易错笔记: 考点2:平面向量的坐标运算 例3(a 级)、若向量(1,1)a =,(1,1)b =-,(1,2)c =-,则c 等于 ( ) A 、1322a b -+ B 、1322a b - C 、3122a b - D 、3122 a b -+
A 平面向量 一.选择题: 1. 在平面上,已知点A (2,1),B (0,2),C (-2,1),O (0,0).给出下面的结论: ①BC CA AB =- ②OB OC OA =+ ③OA OB AC 2-= 其中正确..结论的个数是 ( )A .1个 B .2个 C .3个 D .0个 2. 下列命题正确的是 ( ) A .向量A B 的长度与向量BA 的长度相等 B .两个有共同起点且相等的向量,其终点可能不同 C .若非零向量AB 与C D 是共线向量,则A 、B 、C 、D 四点共线 D .若→ a → b → c ,则→ a → c 3. 若向量= (1,1), = (1,-1), =(-1,2),则 等于( ) A.+ B. C. D.+ 4. 若 ,且与也互相垂直,则实数的值为( ) A . C. 5.已知=(2,3) , =(,7) ,则在上的正射影的数量为( )A. B. C. D. 6. 己知 (2,-1) . (0,5) 且点P 在 的延长线上, , 则P 点坐标为( ) A.(-2,11) B.( C.( ,3) D.(2,-7) 7.设,a b 是非零向量,若函数()()()f x x x =+-a b a b 的图象是一条直线,则必有( ) A .⊥a b B .∥a b C .||||=a b D .||||≠a b 8.已知D 点与ABC 三点构成平行四边形,且A (-2,1),B (-1,3),C (3,4),则D 点坐标为( ) A.(2,2) B.(4,6) C. (-6,0) D.(2,2)或(-6,0)或(4,6) 9.在直角ABC ?中,CD 是斜边AB 上的高,则下列等式不成立的是 (A )2AC AC AB =? (B ) 2 BC BA BC =? (C )2 AB AC CD =? (D ) 2 2 ()() AC AB BA BC CD AB ???= 10. 设两个向量22 (2,cos )a λλα=+-和(, sin ),2m b m α=+其中,,m λα为实数.若2,a b =则m λ 的取值范围是 ( ) A.[6,1]- B.[4,8] C.(,1]-∞ D.[1,6]- 10.已知P ={a |a =(1,0)+m (0,1),m ∈R },Q ={b |b =(1,1)+n (-1,1),n ∈R }是两个向量集合,则P ∩Q 等于( )A .{(1,1)} B .{(-1,1)} C .{(1,0)} D .{(0,1)} 二. 填空题:11.若向量a b , 的夹角为 60,1a b ==,则() a a b -= .
高中数学平面向量专题训练 一、选择题: 1、若向量方程23(2)0x x a --=r r r r ,则向量x r 等于 A 、65 a r B 、6a -r C 、6a r D 、65 a -r 2、两列火车从同一站台沿相反方向开去,走了相同的路程,设两列火车的位移向量分别为a r 和b r ,那么下列命题中错误的一个是 A 、a r 与b r 为平行向量 B 、a r 与b r 为模相等的向量 C 、a r 与b r 为共线向量 D 、a r 与b r 为相等的向量 3、AB BC AD +-=u u u r u u u r u u u r A 、AD u u u r B 、CD uuu r C 、DB u u u r D 、DC u u u r 4、下列各组的两个向量,平行的是 A 、(2,3)a =-r ,(4,6)b =r B 、(1,2)a =-r ,(7,14)b =r C 、(2,3)a =r ,(3,2)b =r D 、(3,2)a =-r ,(6,4)b =-r 5、若P 分AB u u u r 所成的比为4 3 ,则A 分BP u u u r 所成的比为 A 、7 3 - B 、3 7 - C 、73 D 、 3 7 6、已知(6,0)a =r ,(5,5)b =-r ,则a r 与b r 的夹角为 A 、045 B 、060 C 、0135 D 、0120 7、已知i r ,j r 都是单位向量,则下列结论正确的是 A 、1i j ?=r r B 、22 i j =r r C 、i r ∥j i j ?=r r r D 、0i j ?=r r 8、如图,在四边形ABCD 中,设AB a =u u u r r ,AD b =u u u r r , BC c =u u u r r ,则DC =u u u r A 、a b c -+r r r B 、()b a c -+r r r C 、a b c ++r r r D 、b a c -+r r r 9、点),0(m A )0(≠m ,按向量a r 平移后的对应点的坐标是)0,(m ,则向量a r 是 C B A D
专题12 平面向量 考纲解读明方向 掌握平行四边形法则与三角形法则.3.向量共线的条件要结合向量数乘的意义去理解,并能灵活应用.4.向量的概念与运算是必考内容.5.本节在高考中主要考查平面向量的线性运算及其几何意义,分值约为5分, 分析解读1.理解平面向量基本定理的实质,理解基底的概念,会用给定的基底表示向量.2.掌握求向量坐标的方法,掌握平面向量的坐标运算.3.能够根据平面向量的坐标运算解决向量的共线、解三角形等有关问题.4.用坐标表示的平面向量共线的条件是高考考查的重点,分值约为5分,属中低档题.
量积的应用几何问题; ②会用向量方法解决简单的力学问题 与其他一些实际问题2016山东,8; 2015重庆,6;2014重庆,4 分析解读1.理解数量积的定义、几何意义及其应用.2.掌握向量数量积的性质及运算律;掌握求向量长度的方法.3.会用向量数量积的运算求向量夹角,判断或证明向量垂直.4.利用数形结合的方法和函数的思想解决最值等综合问题. 2018年高考全景展示 1.【2018年浙江卷】已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2?4e·b+3=0,则|a?b|的最小值是 A. ?1 B. +1 C. 2 D. 2? 【答案】A 【解析】分析:先确定向量所表示的点的轨迹,一个为直线,一个为圆,再根据直线与圆的位置关系求最小值. 详解:设,则由得, 由得因此的最小值为圆心到直线
的距离减去半径1,为选A. 点睛:以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算,将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系,是解决这类问题的一般方法. 2.【2018年理数天津卷】如图,在平面四边形ABCD中,,,,. 若点E为边CD上的动点,则的最小值为 A. B. C. D. 【答案】A 【解析】分析:由题意建立平面直角坐标系,然后结合点的坐标得到数量积的坐标表示,最后结合二次函数的性质整理计算即可求得最终结果. 详解:建立如图所示的平面直角坐标系,则,,,, 点在上,则,设,则:,即,据此可得:,且:,,由数量积的坐标运算法则可 得:,整理可得:, 结合二次函数的性质可知,当时,取得最小值.本题选择A选项.
一、多选题 1.若a →,b →,c → 是任意的非零向量,则下列叙述正确的是( ) A .若a b →→ =,则a b →→ = B .若a c b c →→→→?=?,则a b →→ = C .若//a b →→,//b c →→,则//a c →→ D .若a b a b → → → → +=-,则a b →→ ⊥ 2.下列说法中正确的是( ) A .对于向量,,a b c ,有()() a b c a b c ??=?? B .向量()11,2e =-,()25,7e =能作为所在平面内的一组基底 C .设m ,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0m n ?<”的充分而不必要条件 D .在ABC 中,设D 是BC 边上一点,且满足2CD DB =,CD AB AC λμ=+,则 0λμ+= 3.已知在平面直角坐标系中,点()10,1P ,()24,4P .当P 是线段12PP 的一个三等分点时,点P 的坐标为( ) A .4,23?? ??? B .4,33?? ??? C .()2,3 D .8 ,33?? ??? 4.在ABC ?中,内角,,A B C 的对边分别为,,,a b c 若,2,6 A a c π ===则角C 的大小 是( ) A . 6 π B . 3 π C . 56 π D . 23 π 5.已知点()4,6A ,33,2B ??- ??? ,与向量AB 平行的向量的坐标可以是( ) A .14,33?? ??? B .97,2?? ??? C .14,33?? - - ??? D .(7,9) 6.在RtABC 中,BD 为斜边AC 上的高,下列结论中正确的是( )
平面向量专题讲解 向量是数学中的重要概念,以向量为工具可以把几何问题(平面、空间)转化为简单的向量运算,变抽象的逻辑推理为具体的向量运算,实现形与数的结合. 题型一:考查与向量概念有关的问题 ⑴向量不同于数量,数量是只有大小的量(称标量),而向量既有大小又有方向;数量可以比较大小,而向量不能比较大小,只有它的模才能比较大小.记号“a >b ”错了,而|a |>|b |才有意义. ⑵有些向量与起点有关,有些向量与起点无关.由于一切向量有其共性(力和方向),故我们只研究与起点无关的向量(既自由向量).当遇到与起点有关向量时,可平移向量. ⑶平行向量(既共线向量)不一定相等,但相等向量一定是平行向量,既向量平行是向量相等的必要条件. ⑷单位向量是模为1的向量,其坐标表示为(,),其中x 、y 满足 +2x 2y =1(可用(cos θ,sin θ)(0≤θ≤2π)表示). ⑸零向量0的长度为0,是有方向的,并且方向是任意的,实数0仅仅是一个无方向的实数. ⑹有向线段是向量的一种表示方法,并不是说向量就是有向线段. 题型二:与向量运算有关的问题 ⑴向量与向量相加,其和仍是一个向量(对应坐标相加). ①当两个向量和不共线时,+的方向与、都不相同,且|+|<||+|b |; ②当两个向量和共线且同向时,+、、的方向都相同,且=+||||||+; ③当向量和反向时,若||>||,+与 方向相同 , 且|+|=||-||;
若|a |<|b |时,b a +与b 方向相同,且|a +b |=|b |-|a |. ⑵向量与向量相减,其差仍是一个向量.向量减法的实质是加法的逆运算. ⑶围成一周首尾相接的向量(有向线段表示)的和为零向量. 如,+AB +BC 0=CA ,(在△ABC 中) +++=.(□ABCD 中) ⑷判定两向量共线的注意事项 如果两个非零向量,,使=λb (λ∈R ),那么∥; 反之,如∥,且≠0,那么=λ. 这里在“反之”中,没有指出是非零向量,其原因为=0时,与λ的方向规定为平行. ⑸数量积的8个重要性质 ①两向量的夹角为0≤θ≤π.由于向量数量积的几何意义是一个向量的长度乘以另一向量在其上的射影值,其射影值可正、可负、可以为零,故向量的数量积是一个实数. ②设、都是非零向量,是单位向量,θ是与的夹角,则 ③?⊥)1|.(cos ||==?=?e a θ0=?(∵θ=90°,)0cos =θ ④在实数运算中ab =0a ?=0或b=0.而在向量运算中b a ?=0a ?=0或b =0是错误的,故0=a 或0=b 是b a ?=0的充分而不必要条件. ⑤当a 与b 同向时b a ?=||||b a ?(θ=0,cos θ=1); 当a 与b 反向时,b a ?=-||||b a ?(θ=π,cos θ=-1),即a ∥b 的另一个充要条件是||||b a ?=?. 特殊情况有2=?=2 |a .