
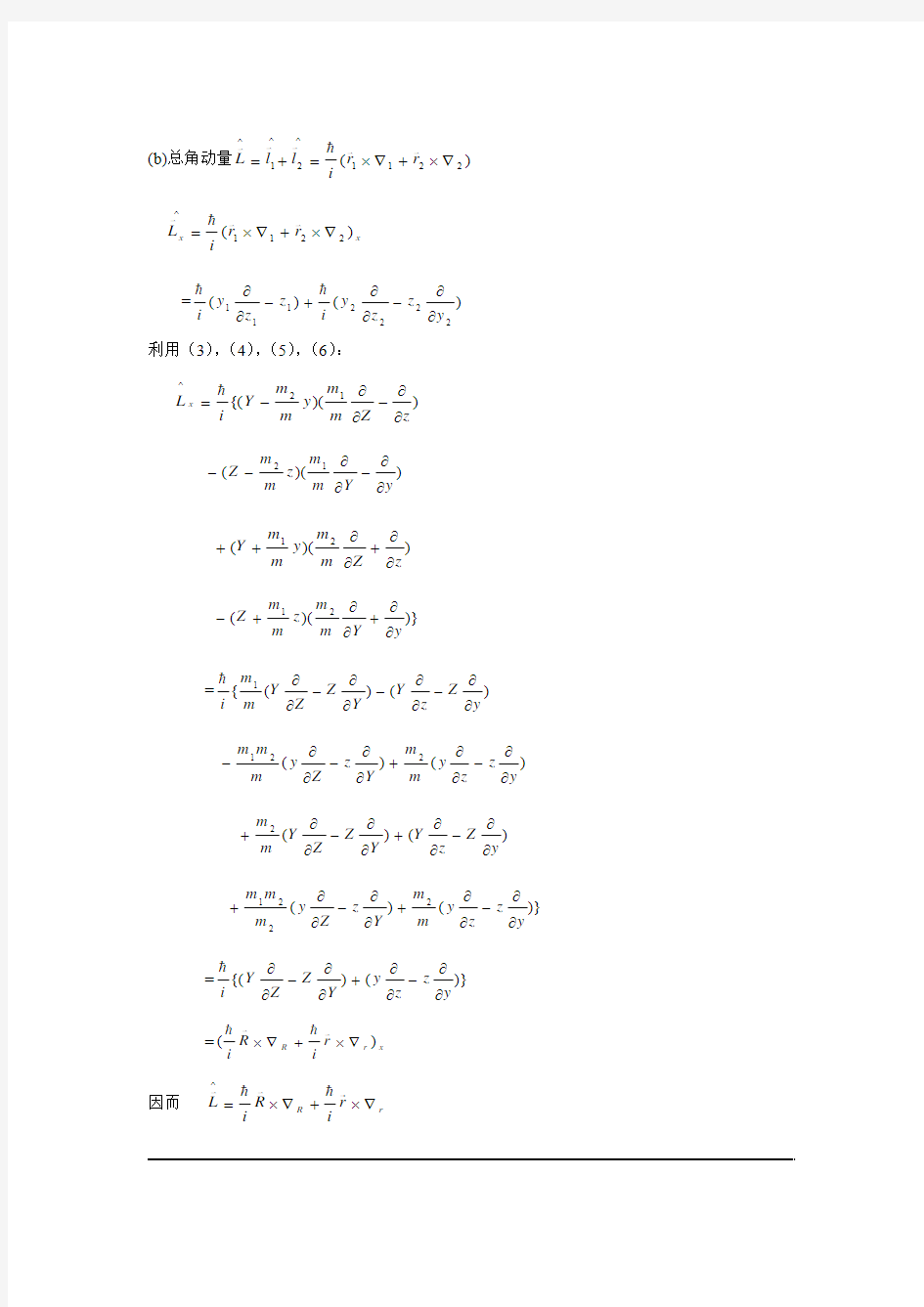
第六章:中心力场
[1]质量分别为 m 1,m 2的两个粒子组成的体系,质心座标及相对座R 标r
为:
R =
2
12
211m m r m r m ++ (1) r 12r r r
-= (2)
试求总动量21p p P
+=及总角动量21l l L +=在R ,
r
表象中的
算符表示。
1. [解] (a )合动量算符21p p P
+=。根据假设可以解出1r ,2
r
令21m m m +≡ : r m m R r
1
21-= (3)
r m m R r
2
12+=
(4)
设各个矢量的分量是),,(1111z y x r
,),(22,22z y x r
,
)
,,(z y x r
和),,(Z Y X R 。为了计算动量的变换式先求对x ,
2x 等的偏导数:
x
X
m m x x x X x X x ??-
??=
????+
??
??=
??1111
(5)
x
X
m m x
x x X x X
x ??+
??=
??
??+??
??=
??2222
(6)
关于1
y ??,
2
y ??,
1
z ??,2
z ?? 可以写出与(5)(6)类似的式子,因而:
)()(212^
1^^
2^1^
x x i p p p p P x x x x ??+??=+=+=
=
X
i x X m m x X m m i ??
=??+??+??-?? )(21
R
i
Z i k Y i j X i i P ?=??+??+??= ^
(b)总角动量)(2211^2^1^
??+??=+=r r i
l l L
x x r r i
L )(2211^??+??=
=
)()(2
2
2
2
11
1
y z z y i
z z y i
??-??+
-??
利用(3),(4),(5),(6):
))(
{(12^
z
Z
m m y m
m Y i
L x ??-
??-
=
))(
(12y
Y
m m z m
m Z ??-
??-
-
))(
(21z
Z
m m y m
m Y ??+
??+
+
)})((21y
Y
m m z m
m Z ??+??+-
=
)()({1y Z z Y Y Z Z Y m m i ??
-??-??-?? )()(22
1y
z z
y m
m Y z Z y m m m ??-??+??-??-
)()(2y
Z
z
Y
Y
Z Z
Y m
m ??-??+??-??+
)}()(22
21y
z
z
y
m
m Y
z
Z
y
m m m ??-??+
??-??+
=
)}(){(y
z
z
y
Y
Z
Z
Y
i
??-??+??-??
=x r R r i
R i )(
??+??
因而 r R r i
R i L ??+??=
^
[2]证明r
r r ??+
=
?1],[2
12 ,?=?],[2
1
2r
(证明)第一式
ψ)(2
12
2?-?r r
=
))((21
2
222
22
22
2ψz y x z
y
x ++??
+
??
+
??
)(
2
12
2
2
2
2
2
2
2
2
z
y
x
z y
x ??+
??+
??++-ψψψ
但
x
z
y x z
y x x z y x x ??+++++=
++??ψψψ2
222
2
2
2
22
)(
2
2
2
2
222
2
(
)(z
y x x x
z y x x
++??=
++??
ψψ
+)2
22x
z
y x ??++ψ
=
232222
2
2
2
)())((z y x x x
x
z y x ++-+??++ψ
ψψ
+2
2
2
222
3222)
(x
z
y x z y x x x
??+++++??ψψ
即
2
2
2
222
222
2x
z
y x z y x x
??++-
++??
ψψ
=
2
32
2
2
2
2
2
2
)
(2z y x x z
y x x
x ++-
+++??ψψ
ψ
同样写出关于y,z 的式子,相加得:
2
2
2
2
2222{
2
1)(2
1z
y x z
z
y
y
x
x r r ++??+??+??=
?-?ψψψψ
+
}32
22z
y x ++-ψ
ψ
=
r
z
r z y
r y x
r x ψψψψ+
??+
??+
??
=ψ)1(
r
r +
??
因ψ是任意函数,因而第一式得证。
第二式的证明:该式是矢量的恒等式,取等式左方一式的x 分量
并蒋它运算于任何函数ψ,要注意2? 标量算符而 r
是矢量算符:
)(2
1],[21
2
22ψψψ?-?=?x x r x =))({(
2
12
22
22
2ψx z
y
x
??
+
??
+
??
)(
2
2
2
2
2
2
z
y
x
x ??+
??+
??-ψψψ}
=
)2
(2
12
2
2
2
2
2z
x
y
x
x x
x
??+??+??+??ψψψψ
x
z
x
y
x x
x
?ψ?=
??-??-??-}2
2
22
2
2ψψψ
因此在出写出关于y,z 的式子后有
?=??+??+??=?z
k y j x i r
],[21
2
[3]中心力场)(r V 中的经典粒子的哈密顿量是
)(222
2r V mr
l m p
H r
++
=
其中p r r
p r
?=
1^
。当过渡到量子力学时,r p 要换为 )1(]1
1[21^
r
r i r r p p r r p r +??-=?+?=
问p r r
r i
?=??-1是否厄米算符?r p ^
是否厄米算符。 (解)对第一个算符取厄米共轭算符,加以变换,看其是否与原 算符相等,为此利用乘积的厄米算符公式
(^
A ^
B ^
C )+
=^^^+
+
+
A B C
若p r r
p r
?=
1^
,则 +++++??=??=)1()1(^^
^^r
r p p r r p r
因为^
p ,r ,r
1
等自身是厄米的,因而有
)1( ^
^^r
r p p r
?=
要看出^+r
p ,r p ^
的关系将r p ^
作用于任意函数ψ:
ψψψψr
z p r y p r x p r r p z y x 111)1(^
^++=?
=)}()()({ψψψr z
z r y y r x x i ??+??+??
=}2)(1{r
z z y y x x r i ψ
ψψψ+??+??+??
=ψ)21(^^r
p r r +?
即 r
p p
r
2^^
+=+
,因而r p ^
不是厄米算符。因为^^+
≠r r p p
利用以上结果,或者直接对^
r p 取厄米共轭式,都证明+
=r r p p ^
因此可认为r p ^
是厄米的,证明在后面,但是关于这问题学术上有争论, 因为它还需要满足另一些条件(Liboff)。
C ?f ?R ?L ?Liboff: American Journal of Physics 976(1973)
++
?+?=]11[21)
(^
^^^^
r
r p p r r p r
=^^^
^^
^
)1()1((21+
++++
++??p r r
r r p
=^
^^^^]11[21r p p r r
r r p =?+?
C ?f ?A ?Messian:Quantum Mecnanics P ?346(1961)
[4]经典力学中
22222
)()(p r p r p r l
?-?=?=
在量子力学中此式是否成立?在什么条件下此式成立?
(解))()()(^^^^2
^^p r p r p r ???=?
=)()(^
^^^^^^^y x y x p z p y p z p y --
+)()(^
^^
^
^
^^
^
x x x x p x p z p x p z --
+)()(^
^
^
^
^
^
^
^x y x y p y y x p y p x --
=)(^2
^2
^
^
^
^^
^^
^
^2^2
y z y y x x
p z p y p z p z p y p y +--
+)(^
2^2
^
^^^^^^^^2^2
z x z z x x
p x p z p x p x p z p z +--
+)(^
2
^2
^
^
^
^
^
^
^
^
^2^
2
x y x z y
y
p y
p x p y p y p
x p x
+--
=)(^2
^2
^2^2
^2^2
^2^2
^2^2
^2^2
x y
z
x
y
x
p y p x p x p z p z p y +++++
x y y x p i
p y z p i
p z y ^
^
^^^^
^)()( +
-+
-
~206~
物83—309蒋
x y z x p i p y x p i p x z ^
^
^^^^
^^
)()( +
-+
-
y y y x p i
p y x p i
p x y ^
^
^
^
^
^
^^
)()( +-+-
最后一式加上下述这个等于零的式子:
^
2
^2
^2^2
^2^2
^2
^2^2
^2^2
z y
x
y
x
p z
p y
p x z p y
p x ---++
得:^^2
^^2^2^2^^2)()()()(p r i p r p r p r ?+?-=?
因此经典角动量平方公式与量子力学的不相同,只有 =0才相同。
[5]求出氢原子基态波函数在动量表象中的表示式。利用所得结
果,计算2x p 。用x 表象中的氢原子波函数计算2
x ,并验证测不准关
系式。
(解)本题是三维问题,氢原子基态波函数用座标表象时写作:
a
r e
a
r -
=
2
3
1
),,(π?θψ (1)
但2
2e
a μ
≡
是玻尔半径,将(1)代入三维的座标,动量波函数变换式,
此式是:
x d e
r p h
r p i 3
^)()
2(1)(2
3 ?-???=
τ
ψπ? (2)
为使计算简单,可选择z 轴与动量p
的瞬时方向重合,这样
θc o s pr r p =?
~207
将(2)中的)(r ψ用(1)式代入,进行积分,积分的次序是?,θ,r :
???--=
r
i p r a r e
a p ?θθ
π?
cos 2
2
3
)
2(1
)(
?θθd d r d
r s i n 2
=
??
--r
ipr a r dr r d e a θθ
θθπ2
cos )sin ()
2(1
2
3
=
rdr e
e
ipr
a ipr a
r ipr a
r r
π
π0)()
2(1
2
3
-
-+
-
-?
=
rdr e
e
ip a ipr a
r ipr a
r )()
2(1
2
3
-
-
+
-
-?π
=
})
(1)
(1{
)
2(1
2
2
2
3
ip a r ip a r ip a --
---?π
=
2
222)
()2(23
+p a a π (3)
其次为了验证氢原子的测不准关系,需要计算座标动量的平均值,计 算与座标有关的平均值时,用)(r
ψ为波函数,反之计算动量平 均值时,可用动量波函数)(p
?:测不准关系的验证,是通过一个指 定方向(如x 轴)的分量间关系: ??????-
=
=θ?
τ
πψr a
r e
a
r xd r x 22
22
1
)(
0s i n )c o s s i n (2
=??θθ?θd d r d r r
~208~ 物83 –309蒋
???
???=
=
θ?
τ
πψr a
r d x r x
2
2
22
2
1
)(
?
θθ?θd drd r r e
a
r sin cos sin 2
2222?-
=
???===-
π?
π
θ??θ
θπ20
2
3
4
22
cos sin 1
d d dr r e
a
r a
r
=
θθθππ
θd dr r e
a
r a
r )sin 4
3
43sin (
1
4
23
?
?==-
+?
??π?
d )2c o s 2
12
1(
20
?=+
?
=
2
53
6
8)2(!41
a a
a
=??
?
ππ (4)
在计算动量有关平均值时,可采用动量相空间的球面极座标参考系, 设动量相空间直角坐标为x p ,y p ,z p 则球面极座标用l l l r ?θ,,表 示,p r l =
l
l x p p ?θc o s s i n = l
l y p p ?θs i n s i n =
l z p p θc o s =
2
5
32
)2()(π
?
a r p p p l
x x =
=
???
l
l l l l r d d p d p p a
p
l
l
l ?θθ?θψ
?
θs i n c o s s i n )(22
22
?+?
???
=
?
∞
=+0
4
222
3
2
5
3)
()2(r p a dp p a
π
?
?=?π
?π
θ
??θθ20
2
c o s s i n l
l
d d l
l
(5)
~209~
l
x x r d p p p 322
2
)(???
=
?
=
?
∞
=+0
4
222
4
2
5
3
)
()2(r p a dp p a
π
l
l
l
d d ??==?
π?
π
θ
??θ
θ20
20
3
c o s s i n (6)
与p 有关的积分可用替代ξtg ap =入(6)式的第一道积分,得:
??
∞
=∞
=
+2
2
4
3
5
4
222
4
cos sin
1)
(πξ
ξξd a p a dp p
=
?=+--
2
3
5
)2
6cos 4cos 2
2cos 1(161π
ξ
ξξξξd a
=
3
5
1
64
a π 代入(6)得: ?=-?
?
=
π
θ
θθθπ
π0
2
5
3
3
5
2)3sin sin 3(4
181
64l
l l x
d a p
l
l
l
d ??π
?
?=-?
20
)2c o s 1(21
=
2
20
2
2
33cos 3
1cos 332a
a l l
=
?+
-?πθ
θπ
π
代入测不准关系式:
2
22
2)()(x x x p p x x p x -?
-=
?δδ 2
3
3 >=?=a
a
[6]在动量表象中写出氢原子的能量本征方程式,并证明角动 量的各个分量均为守恒量。
(解)(一)建立动量表象的能量本征方程式,势能r
e
r V 2
)(-
=
为此先写下座标表象的薛氏方程式(直角坐标还是球面极座标不分):
)()()(22
2
2r E r r
e r
ψψψμ=-?- 遍乘
r p i e
?-2
3)
2(1π,并对座标积分:
x d r e
r p i 32
2
)()2()
2(12
3
ψμ
πτ
?-
????-
x d r e
r
r p i 3
)(1
)2(12
3
ψπτ
????--
x d r e
E r p i 3
)()
2(23
ψπτ
????-=
(1)
等号左方第一积分用二次分部积分中的)(r
ψ加以下述 福里哀变换,就得到动量表象的能量本征方程:
l
p
r p i p d p e
r 3)()
2(1)(2
3
?πψ???
?-=
(2)
得:
)()(),()(232
p E p d p p p G p p
l l p
l
???μ
=+
???
(3)
式中 x d e
r
e
p p G r p p i l l 3
)(2
21
)
2(),(????--=
τ
π
(4)
(二)核),(l p p G
的计算:
先作(4)式类似的计算,假设r
e
2
-
是个座标表象的波函数,它的
~211~
相应的动量表象函数是)(p G
,则正逆两种变换是: x d e
r e
p G r p i 3
2
21
)
2()(????-=
τ
π
(5)
p d e p G r
e
p
r p i 3
2
)()
2(12
3????=
-
π (6) 将拉普拉斯算符 2
22
22
22
z
y
x
??
+
??
+
??
=
?
作用于两边,得:
???-
=
p
p G r e )()1()
2(1)(42
2
πδπ
p d p e
r p i 32
??
(7)
根据(7)式写出它的逆变换式,并且与(5)式对比,有: x d e r e c p r p i 3
22
2)(4)
2(12
3???
?-=
-
τ
δππ
=
2
3
2
e
π
2
2
12)(p
e
p G π
-
= (8)
将(4)(5)二式比较知道),(l p p G 只需在)(p G 中作置换l p p p
-→, 再乘
2
3)
2(1 π
2
2
2
21
),(l
l
p p e
p p G --=
π (9)
因此我们最后得到动量表象的三维能量本征方程式,专用于库仑场。
???-+
p l
l p d p p
p e
p p
3
2
22
2
)(2)(2 ?π?μ
= )(p E
? (10) (三)动量表象中,角动量分量守恒的证明。
有两面种方法,或用直角坐标表示角动量算符,或用球面极座标表 示,用前者较为简单,要证明角动量分量(例如x l
)是守恒量,其必
要条件是它可以和哈密顿H
?算符对易,即: []
0?,?=H L x
(11) 这里,用动量表象书写时,可以用直角坐标表标表象的式子加以适宜
的置换来得到这种置换是:
x
p i
x ??→ y
p i
y ??→ z
p i
z ??→
因而得到
=x l ?)(y z
z y p p p p i ??
-?? (12) 至于y l ?,z l ?的动量表象依类似方法。(10)式中的哈氏算符可从(10)看 出:
()
???--
≡p
l l
p d p
p p
d e
p H
3
2
32
2222??
πμ
(13)
右方第二项是“积分算符”,当它运算于)(p Φ时,就相当于将)(l
p Φ 填入括号( )。设想对易算符[]
H L x
?,?作用在一个任意的动量表象的 波函数)(l
p Φ上面:
)(]?,?[p H l I x Φ≡ (14)
假使能证明I=0,则因为)(p Φ任意,我们便证明了(11),将(13) 代入(14)
}22?{?????2
322
2???-Φ-Φ=Φ-Φ=p l l
x x x p
p p
d e p l l H H l I
πμ
}?2?2?{32
2
2
2l
l
x x p d p
p l e l p ???
-Φ-Φ-
πμ =
}????{2122Φ-Φx x l p p l μ
}??{232
32
2
2l
l x l
l x p d p
p l p d p
p l e
???
???
-Φ
--Φ
-
π
(15)
分别计算动能与势能这两部分的对易算符,先计算动能部分的:
}????{2122Φ-Φx x l p p
l μ
=
Φ++??+
??)???)({(
222
2z y x y z
z y
p
p p p p p p i μ
})??)(???(22
2Φ??-??++-y z
z y
z y x p
p p
p p p p
=
Φ++??
)?????({
23
22z y z x z y
p p p p p p i
μ
Φ++??-
)?????(232z y y
x y z
p p p p p p
~214~ 物83—309蒋
}?)???()???(22
2222z
y z y x y
z z y x p p p
p p p p p
p p ?Φ?+++?Φ?++-
=
y
z y x z p p
p p p i ?Φ?++)???({222
2μ
+z
z y x y y z p p
p p p p p ?Φ?++-Φ)???(???222
2
y
z z y x p p p p p
?Φ?++-?)???(222
0}?)???(??22
222=?Φ?+++Φ-p
p p
p p p p y z y x z y (16)
这证明了动能部份,是和角动量分量相能相对易的。
其次计算(15)式中与势能有关部分的对易式,即(15)式第二个
大括号内一式,能够证明,括号内两项相抵消,为此从第二项开始 变形:
???
???
-?
Φ=
-?
Φl
l
p
l
l x p
l l x p d p
p l p
p p d l 32
2
3)1(?))?(
???
Φ--
l
p
l
l x
p d p
p l 32
)1(
=l
l l
y z
l l
z y
l p d p
p p p
p p
i 32
)1)((
-?
Φ??-
?????
l
l l
y z
l l z y
l p d p
p p p
p p
i 32
]1)
(
[Φ-??-
??-
???
=l
z l y l x p p p l z
z l y
y l x
x l
z l
y l
x l z y
l dp dp dp p p p p p p p p p p p
i z
y x ???
-+-+-Φ??2
2
2
)
()()()
,,(
~215~
l
z l y l x p p p l
z z l
y y l
x x l
z l y l x l y z dp dp dp p p p p p p p p p p p i
z
y x ???
-+-+-Φ??
-2
2
2
)
()()()
( 2
1[l
l y
l
z
l z l y l x p
p p
p i dp dp dp -??-?????
l
z l y l x l l
z
l
y
dp dp dp p
p p p Φ-??-]12
(17)
前一式的第一二个积分分别为对分动量y p 和z p 进行积分后,分别代入 积分限),(∞-∞y p ,),(∞-∞z p ,如果)(z y x p p p Φ是个三维 的平方可积函数,即当±∞→z y x p p p ,,时0→Φ,则在代入分限 后被积函数也趋于零,只剩下三个积分:
???-?Φl
p
l l x
p
p p d l
2
3)?(
=l
p
l z l y l x l l
z z l
y l
y y l
z p d p p p p
p p p p p p p i l
34
)()
()(2???Φ----?
--
=l
p
l z l y l x l l
z l y z l
y l
y l
z y l z p d p p p p
p p p p p p p p p i l
34
)()
2???
Φ----
=l
l z l y l x l z y z l
y y z y l
z p d p p p p
p p p p p p p p p i 34
)()
2???
Φ-+--
=l
p
l z l y l x l l
y y z l
z z y p d p p p p
p p p p p p p i l
34
)()
()(2???
Φ--+--
=l
p
l z l y l x l y
z
z
y
p d p p p p
p p p p p i l
32
)(1)
(???Φ-??-??
~216~ 物83—309蒋
= l
p
l z l y l x l y
z
z
y
p d p p p p
p p p p p i l
32
)(1)(???
Φ-??-??
= l
p
l x p d p
p l l
32
1
????
Φ- (18)
(18)式最前一式和最一式的关系相当于(15)式第二部分为零。 0)(]?,?[=Φ=p H l I x
因为)(p Φ是任意函数,因而0]?,?[=H l x 说明x
l ?是守恒量。同理 可以证明y l ?,z l ?在动量表象的有心力问题中也是守恒的。
[7]设氢原子处于基态,求电子处于经典力学不允许区(E —V =T 〈0 〉的几率。 (解)在经典力学中,当总能量一定时,轨道半径r 受到限制, 设玻耳半径a ,则总能量
a
e
E 22
-
=
粒子的势能则随着到核的距离r 而变,表示作r
e
2
-
,动能是一者的
差数:(从理论上讲,距离r 可以扩展到无限远处。)
r
e
a
e
r T 2
2
2)(+
-
= (1)
使T(r)>0,r<2a,在量子力学中,电子可以在离核任何距 离r 处出现,它在经典力学中不允许范围中出现的几率是:
??
?∞
====
2
020r d τψ
ωπθπ
?
=
??
?∞===0
2
20203
sin )(1
r a
r d d dr r e
a
?θθππ
θπ?
=
?
∞
=a
r a
r
dr r e
a 22
23
4ππ
=
??∞=-
∞=-
=
a
r a
r a
r a
r a
r e
d r e
a a
dr r e
a
222
23
22
23
)()
2
(44
=?
∞
∞
-
+
-
a
a
r
a
a
r dr e
r e
r a
22822
2
22
=??
∞
∞
-
-+
-
+
a
a
r
a
a
r dr e
a
e
r e a
e
22222
4
2
)2
(48
=4413)128(--=++e e
[8]证明,对于库仑场E V 2=,E T -=(V T E ==是 总能量)
(证明)对于库仑场中的束缚电子,在基态以外的情形r
1的计
算比较专门。(参看Landau-Lifsshitz Quantum Mechauics 1958?Appendicos&f ) 它的公式是: a
n Z r 2
)1
(=
(Z 原子序,a 波尔半径,n 主量子数)。
先计算(n,T.m )在任意的势能平均值。
???-
=
τψ
ψ
d r
Ze V nlm
nlm
)(2
*
=???-
-τψ
ψ
d r
Ze
nlm
nlm
)1(*2
=____
2
)1(r Ze --=a n e
Z 22
2
又因为类氢原子的能级是:
a
n e
Z n
e Z E
n 2
2
22
242
22-
=-=/ μ
因而 E V 2=
总能量E ,动能T ,势能V 的关系是: E=T+V 取平均值 V T E E n +==
a
n e
Z a
n e
Z a
n e
Z V E T n 2
2
22
2
22
2
222=
+
-
=-=
E T -=
(9)对于氢原子的,计算
?+=
dr r R r
r nl 2
2
]()[λλ 2,1±±=λ
(解)第一法:本题公式是由氢原子的正交归一化波函数 ),()(),,(?θ?θψ
lm nl nlm
Y r R r =
来计算λr 的平均值的公式 简化而成,但),(),(?θlm nl Y r R 假定 ~219~。 已归一化。Kramers 导得有关λ
r
,
1
-λr
,
2
-λr
,三者的递推式如下:
0]
)12[(4
1
)
12(1
2
2
2
2
2
2=-++
-+-+-λλλ
λλλ
λr
a ar r n l (1)
它的证明根据有关r 的微分方程式[从略],在运用此式时,可先令λ=1代入(1)式得:
0)1(323
2
2=++--r
a
l l r
a
r n
(2)
式中
2
-r
是与电子势能平均值成正比的[仅相差系数e 2
?
-
=
dr r r
e
r R v r
2
2
2
].)[(
根据维里定理,在库仑场情形 V T 2
1-=
和能量世关系式:En=V
T +
a
n e
a
n e
En V 2
2
2
2)2(22-
=-
?==
a
n r
2
11
-
=- (3)
又径波函数归一化条件相当于
r
的情形,因而
10
=r
(4)
(3)和(4)代入(2),得:
})1(3{}12)1(3{2
2
2
2
2
2
n
l l a
n a l l a r a n n
++
=
?
++=
将λ=2代入(1):
)
344(2
53
2
2
2
2
=-++
-r
l l a
r
a
r n
(5)
将
r
和
r
=1代(5)得:
(6)
2
-r
的表示式不能由(1)求得,用直接积分可有:
)
21(13
2
2
+
=
l n a r
(C.f.A.Messiah:Quantum Mechanics V ol I.p.431.Ex.1.)
第二法:利用Laguerre 函数,氢原子的径向波函数可表示为:
???)(2
E Nnl r Rnl -
= 但ξna
r 2≡ (7)
????(ξ)是自变量ξ的缔合(或名连带)Laguerre 函数,它的定义是:
),1,()}({)(ξξξ
ξ
ξ+-=∈
=
-h k h F e
d d
e d d L E
k h
k h
h h
k
波函数(7)中的121
++l n L (ξ)满足以下微分方程式。(课本ξ 6.3式17,217)
0]1[]
22[2
2
2
=-+--++L n l d dL d L d l
ξ
ξξ
ξ
题给的
λ
r 的公式,可以通过式(7)转变为ξ的积分如下:
ξξξ
λλ
λ
d L
na N
r l n
l l E e E nl
2
12220
2)}({3)2
(
++++-=?
?
+=
但
3
4
2]
1)[(1)1(4a l n l n n
N
nl
+--?
=
E.schrodinger 导得了一个和前式相似的积分求值式,使用它可以解决所需的平均值。此式是:
]}
21)1(1[32{242
2
2
n
l l a
n r +
+-
+=
)!
8()!8()!8()!8()!
8()!
(!!)1()(1
1
1
!
01
1
11
1
1+---+---+?
-+
-=-=
∑
?=k p h k k p h k p h p k k d E pe s s k k h h p kk hh
L
I
σ
ξξξ
8的取值应使各阶乘数是正的,在此式中令 2
2
1
11
8221
???21
1
]
)!82][()81[(!)
822()!1(2])![(:
.,22,1,12+++----+++?
++=++=+==+==∑
--=++++λλλλλn l l n s l l n p n k k h h n l n l l
l
I
得 (9)
从此式看出,8的取值应满足:
1--l n ≥8≥2---λl n
例如当λ=1时,可取决8=3,2,1------l n l n l n 三个值所相当的三项,当λ=1时,取8=1--l n 的一项,详细的计算从略。 C.f.Mott.Sneddon:Wave Mechanics and its Applica tions.p.380-381。 #
[10]根据氢原子光谱理论,讨论(1)“电子偶素”(指e +—e -的束缚态)的能级。(2)
μ介原子的能谱。(3)μ介子素(指μ+-e -束缚态)的能谱。
[解]
(1) 电子偶素(氩positronium )指低温时超导现象中的导电媒介,即正负电子对,
按类氢原子理论,氢的能级是由折合质量计算的,在正常氢原子情形,设质子质量m ,则折合质量μ
μM
m mM +=
但
m
n a
e n
e E c
me M c me m n 9995.0),3,2,1(22/3.938,/51.02
2
2
2
2
==-=
-
===μσ
υσν
在电子偶素情形,可用正电子代替氢核的质子,折合质量
μ=
2
2
m m
m m
=
÷
)3,2,1(22
2
411 =-
=n n
e
E
n
μ
μ5.05.01
==m
En E
n
5.01=
(2) μ介原于是被氢核荐的μ-
介子构成的原子,这种原子的折合质量是
2
/7.105c me m M
m M m υμμμμ
=+=
''但
μμm 9.0='' μμ207=n
量子力学习题及解答 第一章 量子理论基础 1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即 m λ T=b (常量); 并近似计算b 的数值,准确到二位有效数字。 解 根据普朗克的黑体辐射公式 dv e c hv d kT hv v v 1 1 833 -? =πρ, (1) 以及 c v =λ, (2) λρρd dv v v -=, (3) 有 ,1 18)()(5-?=?=?? ? ??-=-=kT hc v v e hc c d c d d dv λλλ πλλρλλ λρλρ ρ 这里的λρ的物理意义是黑体波长介于λ与λ+d λ之间的辐射能量密度。 本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下: 011511 86 ' =???? ? ?? -?+--?= -kT hc kT hc e kT hc e hc λλλλλ πρ
? 0115=-?+ -- kT hc e kT hc λλ ? kT hc e kT hc λλ= -- )1(5 如果令x= kT hc λ ,则上述方程为 x e x =--)1(5 这是一个超越方程。首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有 xk hc T m =λ 把x 以及三个物理常量代入到上式便知 K m T m ??=-3109.2λ 这便是维恩位移定律。据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。 1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。 解 根据德布罗意波粒二象性的关系,可知 E=h v , λ h P = 如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么 e p E μ22 = 如果我们考察的是相对性的光子,那么 E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0?,因此利用非相对论性的电子的能量——动量关系式,这样,便有 p h = λ
第一章量子力学作业习题 [1] 在宏观世界里,量子现象常常可以忽略.对下列诸情况,在数值上加以证明: ( l )长l=lm ,质量M=1kg 的单摆的零点振荡的振幅; ( 2 )质量M=5g ,以速度10cm/s 向一刚性障碍物(高5cm ,宽1cm )运动的子弹的透射率; ( 3 )质量M= 0.1kg ,以速度0.5m/s 运动的钢球被尺寸为1×1.5m2时的窗子所衍射. [2] 用h,e,c,m(电子质量), M (质子质量)表示下列每个量,给出粗略的数值估计: ( 1 )玻尔半径(cm ) ; ( 2 )氢原子结合能(eV ) ; ( 3 )玻尔磁子;( 4 )电子的康普顿波长(cm ) ; ( 5 ) 经典电子半径(cm ) ; ( 6 )电子静止能量(MeV ) ; ( 7 )质子静止能量( MeV ) ; ( 8 )精细结构常数;( 9 )典型的氢原子精细结构分裂 [3]导出、估计、猜测或背出下列数值,精确到一个数量级范围内, ( 1 )电子的汤姆逊截面;( 2 )氢原子的电离能;( 3 )氢原子中基态能级的超精细分裂能量;( 4 )37Li ( z=3 )核的磁偶极矩;( 5 )质子和中子质量差;( 6 )4He 核的束缚能;( 7 )最大稳定核的半径;( 8 )Π0 介子的寿命;( 9 )Π-介子的寿命;( 10 )自由中子的寿命. [4]指出下列实验中,哪些实验表明了辐射场的粒子性?哪些实验主要证明能量交换的量子性?哪些实验主要表明物质粒子的波动性?简述理由. ( 1 )光电效应;( 2 )黑体辐射谱;( 3 ) Franck – Hertz实验;( 4 ) Davisson -Ger - mer 实验;散射. [5]考虑如下实验:一束电子射向刻有A 、B 两缝的平板,板外是一装有检测器阵列的屏幕,利用检测器 能定出电子撞击屏幕的位置.在下列各种情形下,画出入射电子强度随屏幕位置变化的草图,给出简单解释. ( 1 ) A 缝开启,B缝关闭; ( 2 ) B 缝开启,A 缝关闭; ( 3 )两缝均开启. [6]验算三个系数数值:(1 2 ;(3)hc
1、以下说法是否正确: (1)量子力学适用于微观体系,而经典力学适用于宏观体系; (2)量子力学适用于η不能忽略的体系,而经典力学适用于η可以忽略的体系。 解答:(1)量子力学是比经典力学更为普遍的理论体系,它可以包容整个经典力学体系。 (2)对于宏观体系或η可以忽略的体系,并非量子力学不能适用,而是量子力学实际上已 经过渡到经典力学,二者相吻合了。 2、微观粒子的状态用波函数完全描述,这里“完全”的含义是什么? 解答:按着波函数的统计解释,波函数统计性的描述了体系的量子态。如已知单粒子(不考虑自旋)波函数)(r ? ψ,则不仅可以确定粒子的位置概率分布,而且如粒子的动量、能量等其他力学量的概率分布也均可通过)(r ? ψ而完全确定。由于量子理论和经典理论不同,它一般只能预言测量的统计结果,而只要已知体系的波函数,便可由它获得该体系的一切可能物理信息。从这个意义上说,有关体系的全部信息显然已包含在波函数中,所以说微观粒子的状态用波函数完全描述,并把波函数称为态函数。 3、以微观粒子的双缝干涉实验为例,说明态的叠加原理。 解答:设1ψ和2ψ是分别打开左边和右边狭缝时的波函数,当两个缝同时打开时,实验说明到达屏上粒子的波函数由1ψ和2ψ的线性叠加2211ψψψc c +=来表示,可见态的叠加不是概率相加,而是波函数的叠加,屏上粒子位置的概率分布由222112 ψψψ c c +=确定,2 ψ中 出现有1ψ和2ψ的干涉项]Re[2* 21* 21ψψc c ,1c 和2c 的模对相对相位对概率分布具有重要作用。 4、量子态的叠加原理常被表述为:“如果1ψ和2ψ是体系的可能态,则它们的线性叠加 2211ψψψc c +=也是体系的一个可能态”。 (1)是否可能出现)()()()(),(2211x t c x t c t x ψψψ+=; (2)对其中的1c 与2c 是任意与r ? 无关的复数,但可能是时间t 的函数。这种理解正确吗? 解答:(1)可能,这时)(1t c 与)(2t c 按薛定谔方程的要求随时间变化。
1. 你认为Bohr 的量子理论有哪些成功之处?有哪些不成功的地方?试举一例说明。 (简述波尔的原子理论,为什么说玻尔的原子理论是半经典半量子的?) 答:Bohr 理论中核心的思想有两条:一是原子具有能量不连续的定态的概念;二是两个定态之间的量子跃迁的概念及频率条件。首先,Bohr 的量子理论虽然能成功的说明氢原子光谱的规律性,但对于复杂原子光谱,甚至对于氦原子光谱,Bohr 理论就遇到了极大的困难(这里有些困难是人们尚未认识到电子的自旋问题),对于光谱学中的谱线的相对强度这个问题,在Bohr 理论中虽然借助于对应原理得到了一些有价值的结果,但不能提供系统解决它的办法;其次,Bohr 理论只能处理简单的周期运动,而不能处理非束缚态问题,例如:散射;再其次,从理论体系上来看,Bohr 理论提出的原子能量不连续概念和角动量量子化条件等,与经典力学不相容的,多少带有人为的性质,并未从根本上解决不连续性的本质。 2. 什么是光电效应?光电效应有什么规律?爱因斯坦是如何解释光电效应的? 答:当一定频率的光照射到金属上时,有大量电子从金属表面逸出的现象称为光电效应;光电效应的规律:a.对于一定的金属材料做成的电极,有一个确定的临界频率0υ,当照射光频率0υυ<时,无论光的强度有多大,不会观测到光电子从电极上逸出;b.每个光电子的能量只与照射光的频率有关,而与光强无关;c.当入射光频率0υυ>时,不管光多微弱,只要光一照,几乎立刻910s -≈观测到光电子。爱因斯坦认为:(1)电磁波能量被集中在光子身上,而不是象波那样散布在空间中,所以电子可以集中地、一次性地吸收光子能量,所以对应弛豫时间应很短,是瞬间完 成的。(2)所有同频率光子具有相同能量,光强则对应于光子的数目,光强越大,光子数目越多,所以遏止电压与光强无关,饱和电流与光强成正比。(3)光子能量与其频率成正比,频率越高,对应光子能量越大,所以光电效应也容易发生,光子能量小于逸出功时,则无法激发光电子。 3.简述量子力学中的态叠加原理,它反映了什么? 答:对于一般情况,如果1ψ和2ψ是体系的可能状态,那么它们的线性叠加:1122c c ψψψ=+(12c c ,是复数)也是这个体系的一个可能状态。这就是量子力学中的态叠加原理。态叠加原理的含义表示当粒子处于态1ψ和2ψ的线性叠加态ψ时,粒子是既处于态1ψ,又处于态2ψ。它反映了微观粒子的波粒二象性矛盾的统一。量子力学中这种态的叠加导致在叠加态下观测结果的不确定性。 4. 什么是定态?定态有什么性质? 答:体系处于某个波函数()()[]exp r t r iEt ψψ=-,所描写的状态时,能量具有确定值。这种状态称为定态。定态的性质:(1)粒子在空间中的概率密度及概率流密度不随时间变化;(2)任何力学量(不显含时间)的平均值不随时间变化;(3)任何力学量(不显含时间)取各种可能测量值的概率分布也不随时间变化。 5. 简述力学量与力学量算符的关系? 答:算符是指作用在一个波函数上得出另一个函数的运算符号。量子力学中采用算符来表示微观粒子的力学量。如果量子力学中的力学量F 在经典力学中有相应的力学量,则表示这个力学量的算符?F 由经典表示式F (r,p )中将p 换为算符?p 而得出的,即:
09光信息量子力学习题集 一、填空题 1. 设电子能量为4电子伏,其德布罗意波长为( 6.125ο A )。 2. 索末菲的量子化条件为=nh pdq ),应用这量子化条件求得一维谐振 子的能级=n E ( ηωn )。 3. 德布罗意假说的正确性,在1927年为戴维孙和革末所做的( 电 )子衍 射实验所证实,德布罗意关系(公式)为( ηω=E )和( k p ρηρ = )。 4. 三维空间自由粒子的归一化波函数为()r p ρ ρψ=( r p i e ρ ρη η?2 /3) 2(1π ), () ()=? +∞ ∞ -*'τψψd r r p p ρρρρ( )(p p ρ ρ-'δ )。 5. 动量算符的归一化本征态=)(r p ρ ρψ( r p i e ρ ρηη?2/3)2(1π ),=' ∞ ?τψψd r r p p )()(*ρρρρ( )(p p ρ ρ-'δ )。 6. t=0时体系的状态为()()()x x x 2020,ψψψ+=,其中()x n ψ为一维线性谐振子的定态波函数,则()=t x ,ψ( t i t i e x e x ωωψψ2 522 0)(2)(--+ )。 7. 按照量子力学理论,微观粒子的几率密度w =2 ),几率流密度= ( () ** 2ψ?ψ-ψ?ψμ ηi )。 8. 设)(r ρψ描写粒子的状态,2)(r ρψ是( 粒子的几率密度 ),在)(r ρψ中F ?的平均值为F =( ??dx dx F ψψψψ* *? ) 。 9. 波函数ψ和ψc 是描写( 同一 )状态,δψi e 中的δi e 称为( 相因子 ), δi e 不影响波函数ψ1=δi )。 10. 定态是指( 能量具有确定值 )的状态,束缚态是指(无穷远处波函数为 零)的状态。 11. )i exp()()i exp()(),(2211t E x t E x t x η η-+-=ψψψ是定态的条件是 ( 21E E = ),这时几率密度和( 几率密度 )都与时间无关。 12. ( 粒子在能量小于势垒高度时仍能贯穿势垒的现象 )称为隧道效应。 13. ( 无穷远处波函数为零 )的状态称为束缚态,其能量一般为( 分立 )谱。 14. 3.t=0时体系的状态为()()()x x x 300,ψψψ+=,其中()x n ψ为一维线性谐振子的定态波函数,则()=t x ,ψ( t i t i e x e x ωωψψ2 732 0)()(--+ )。 15. 粒子处在a x ≤≤0的一维无限深势阱中,第一激发态的能量为
曾谨言《量子力学》(卷I )第四版(科学出版社)2007年1月摘录 第三版序言 我认为一个好的高校教师,不应只满足于传授知识,而应着重培养学生如何思考问题、提出问题和解决问题。 这里涉及到科学上的继承和创新的关系。“继往”中是一种手段,而目的只能是“开来”。 讲课虽不必要完全按照历史的发展线索讲,但有必要充分展开这种矛盾,让学生自己去思考,自己去设想一个解决矛盾的方案。 要真正贯彻启发式教学,教师有必要进行教学与科学研究。而教学研究既有教学法的研究,便更实质性的是教学内容的研究。从教学法来讲,教师讲述一个新概念和新原理时,应力求符合初学者的认识过程。在教学内容上,至少对于像量子力学这样的现代物理课程来讲,我信为还有很多问题并未搞得很清楚,很值得研究。 量子力学涉及物质运动形式和规律的根本变革.20世纪前的经典物理学(经典力学、电动力学、热力学与统计物理学等),只适用于描述一般宏观 从物质波的驻波条件自然得出角动量量子化的条件及自然理解为什么束缚态的能量是量子化的:P17~18; 人类对光的认识的发展历史把原来人们长期把物质粒子看作经典粒子而没有发现错误的启发作用:P18; 康普顿实验对玻尔电子轨道概念的否定及得出“无限精确地跟踪一个电子是不可能的”:P21; 在矩阵力学的建立过程中,玻尔的对应原理思想起了重要的作用;波动力学严于德布罗意物质波的思想:P21; 微观粒子波粒二象性的准确含义:P29; 电子的双缝衍射实验对理解电子波为几率波的作用:P31 在非相对论条件下(没有粒子的产生与湮灭),概率波正确地把物质粒子的波动性与粒子性联系起来,也是在此条件下,有波函数的归一化及归一化不随时间变化的结果:P32; 经典波没有归一化的要领,这也是概率波与经典波的区别之一:P32; 波函数归一化不影响概率分布:P32 多粒子体系波函数的物理意义表明:物质粒子的波动性并不是在三维空间中某种实在的物理量的波动现象,而一般说来是多维的位形空间中的概率波。例如,两个粒子的体系,波函数刻画的是六维位形空间中的概率波。这个六维空间,只不过是标志一个具有6个自由度体系的坐标的抽象空间而已。 动量分布概率: 1 波包的频谱分析 具有一定波长的平面波可表示为: ()e x p ()k x i k x ψ= (A1.1) 波长2/k λπ=,其特点是是波幅(或强度)为常数.严格的平面波是不存在的,实际问题中碰到的都是波包,它们的强度只在空间有限区域不为0.例如,高斯波包 221()exp()2x a x ψ=- (A1.2) 其强度分布222()exp()x a x ψ=-,如图A.1所示.可以看出,波包主要集中在1 x a < 区域中. 所以波包宽度可近似估计为:
量子力学习题集及解答
目录 第一章量子理论基础 (1) 第二章波函数和薛定谔方程 (5) 第三章力学量的算符表示 (28) 第四章表象理论 (48) 第五章近似方法 (60) 第六章碰撞理论 (94) 第七章自旋和角动量 (102) 第八章多体问题 (116) 第九章相对论波动方程 (128)
第一章 量子理论基础 1.设一电子为电势差V 所加速,最后打在靶上,若电子的动能转化为一个光子,求当这光子相应的光波波长分别为5000 A (可见光),1 A (x 射线)以及0.001 A (γ射线)时,加速电子所需的电势差是多少? [解] 电子在电势差V 加速下,得到的能量是eV m =22 1 υ这个能量全部转化为一个光子的能量,即 λ νυhc h eV m ===221 ) (1024.1106.11031063.64 19834 A e hc V λλλ?=?????==∴--(伏) 当 A 50001=λ时, 48.21=V (伏) A 12=λ时 421024.1?=V (伏) A 001.03=λ时 731024.1?=V (伏) 2.利用普朗克的能量分布函数证明辐射的总能量和绝对温度的四次方成正比,并求比例系数。 [解] 普朗克公式为 1 8/33-?=kT hv v e dv c hv d πνρ 单位体积辐射的总能量为 ? ?∞∞-==0 0/331 3T hv v e dv v c h dv U κπρ 令kT hv y = ,则 4 40333418T T e dy y c h k U y σπ=? ??? ??-=?∞ (★) 其中 ?∞-=033341 8y e dy y c h k πσ (★★) (★)式表明,辐射的总能量U 和绝对温度T 的四次方成正比。这个公式就是斯忒蕃——玻耳兹曼公式。其中σ是比例常数,可求出如下: 因为 )1()1(1 121 +++=-=-------y y y y y y e e e e e e
第七章:粒子在电磁场中的运动 P367——7.1,7.2 证明在磁场B 中,带电粒子的速度算符的各分量,满足下述的对易关系: [] z y x c q i v v B ?,2μ = (1) [] x z y c q i v v B ?,2μ = (2) []y x z c q i v v B ? ,2 μ = (3) [证明]根据正则方程组: x x p H x v ??== ? ,Φ+?? ? ??-=q A c q p H 2 21? μ ? ? ? ?? -=x x x A c q p v ??1?μ 同理 ? ? ? ? ?-=y y y A c q p v ??1?μ ()z y x p p p p ?,?,?? 是正则动量,不等于机械动量,将所得结果代入(1)的等号左方: [] ? ? ????--=y y x x y x A c q p A c q p v v ??,??1,2μ ] [] y x A A c q ?,?2 2 μ+ (4) [] 0?,?=y x p p 又A ? [] z x y y x B c y x i c v v 22 ,μμ = ??? ??-?? = (因A B ??=??) 其余二式依轮换对称写出。 P368证明在规范变换下 ψψρ* = (1) [ ]ψψμψψψψμ * * *- -=A c q p p j ??21 (2)
??? ? ?-=A c q p v ?μ (机械动量的平均值)都不变 (3) (证明)如课本证明,要规范变换下,若将体系的波函数作以下变换(P368 20式) ψψc iqf e → (4) 则薛定谔方程形式不变,将(4)代入(1)式等号右方,设变换后几率密度: ρ ρψ ψψψψψ ρ='=?=??? ? ? ???? ? ? ?='* * -* c iqf c iqf c iqf c iqf e e e e 又设变换后几率流密度是j ',将(4)代入(2)式右方,同时又代入 ()t r f A A , ?+→ ψψψψμc iqf c iqf c iqf c iqf e P e e p e j * - * -????? ?-='21 (5) 注意到算符的对易关系 推广到三维:() )(F )(F ,?r i r p ??=? 6) 令c iqf e r =)(F 则有: c iqf e p -=e p c iqf (7) =-e p c iqf (8) 将(7)(5)式成为: ()() j A c q p p f A c q f c q p e e f c q p e e j c iqf c iqf c iqf c iqf =--=?+-????????? ???--??? ???+=* ***-*-ψψμψψψψμψψμψψψψμ2121 (9) 在证明第3式时,设变换后的v 是v ' 。写出右方平均值的显式,用(4)的波数变换,和)4('的矢势的变换式:
第一章 ⒈玻尔的量子化条件,索末菲的量子化条件。 ⒉黑体:能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。 ⒎普朗克量子假说: 表述1:对于一定频率ν的辐射,物体只能以hν为能量单位吸收或发射电磁辐射。 表述2:物体吸收或发射电磁辐射时,只能以量子的方式进行,每个量子的能量为:ε=h ν。 表述3:物体吸收或发射电磁辐射时,只能以能量ε的整数倍来实现,即ε,2ε,3ε,…。 ⒏光电效应:光照射到金属上,有电子从金属上逸出的现象。这种电子称之为光电子。 ⒐光电效应有两个突出的特点: ①存在临界频率ν0:只有当光的频率大于一定值v0 时,才有光电子发射出来。若光频率小于该值时,则不论光强度多大,照射时间多长,都没有光电子产生。 ②光电子的能量只与光的频率有关,与光的强度无关。光的强度只决定光电子数目的多少。⒑爱因斯坦光量子假说: 光(电磁辐射)不仅在发射和吸收时以能量E= hν的微粒形式出现,而且以这种形式在空间以光速C 传播,这种粒子叫做光量子,或光子。爱因斯坦方程 ⒒光电效应机理: 当光射到金属表面上时,能量为E= hν的光子立刻被电子所吸收,电子把这能量的一部分用来克服金属表面对它的吸引,另一部分就是电子离开金属表面后的动能。 ⒓解释光电效应的两个典型特点: ①存在临界频率v0:由上式明显看出,当hν- W0≤0时,即ν≤ν0 = W0 / h时,电子不能脱出金属表面,从而没有光电子产生。 ②光电子动能只决定于光子的频率:上式表明光电子的能量只与光的频率ν有关,而与光的强度无关。 ⒔康普顿效应:高频率的X射线被轻元素如白蜡、石墨中的电子散射后出现的效应。 ⒕康普顿效应的实验规律: ①散射光中,除了原来X光的波长λ外,增加了一个新的波长为λ'的X光,且λ' >λ; ②波长增量Δλ=λ-λ随散射角增大而增大。 ⒖量子现象凡是普朗克常数h在其中起重要作用的现象 ⒗光具有微粒和波动的双重性质,这种性质称为光的波粒二象性
结构化学练习之量子力学基础习题附参考答案
量子力学基础习题 一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。 1104、测不准关系是_____________________,它说明了_____________________。 1105、一组正交、归一的波函数ψ1,ψ2,ψ3,…。 正交性的数学表达式为,归一性的表达式为。1106、│ψ(x1,y1,z1,x2,y2,z2)│2
代表______________________。 1107、物理量xp y- yp x的量子力学算符在直角坐标系中的表达式是_____。 1108、质量为m的一个粒子在长为l的一维势箱中运动, (1)体系哈密顿算符的本征函数集为_______________________________ ; (2)体系的本征值谱为____________________,最低能量为____________ ; (3)体系处于基态时,粒子出现在0 ─l/2间的概率为_______________ ; (4)势箱越长,其电子从基态向激发态跃迁时吸收光谱波长__________ ; (5)若该粒子在长l、宽为2l的长方形势箱
中运动, 则其本征函数集为____________,本征 值 谱 为 _______________________________。 1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。波函数ψ 211(x ,y ,z )= _________________________;当粒子处于状态 ψ 211 时,概率密度最大处坐标是 _______________________;若体系的能量为 2 247ma h ,其简并度是_______________。 1110、在边长为a 的正方体箱中运动的粒子,其能级E = 2 243ma h 的简并度是_____,E '= 2 2827ma h 的简 并度是______________。 1111、双原子分子的振动,可近似看作是质量为μ= 2 121m m m m +的一维谐振子,其势能为V =kx 2/2,它 的 薛 定 谔 方 程 是
7.1.证明:i z y x =σσσ ??? 证:由对易关系 z x y y x i σσσσσ ?2????=- 及 反对易关系 0????=+x y y x σσσσ , 得 z y x i σσσ ???= 上式两边乘z σ ?,得 2????z z y x i σσσσ= ∵ 1?2=z σ ∴ i z y x =σσσ ??? 7.2 求在自旋态)(2 1z S χ中,x S ?和y S ?的测不准关系: ?)()(22=y x S S ?? 解:在z S ?表象中)(2 1z S χ、x S ?、y S ?的矩阵表示分别为 ???? ??=01)(21z S χ ???? ??=01102? x S ???? ??-=002?i i S y ∴ 在)(2 1z S χ态中 00101102)0 1(2121=??? ? ?????? ??==+ χχx x S S 4010110201102)0 1(?2 22 2 121 =???? ?????? ?????? ??==+ χχx x S S 4 )(22 22 =-=?x x x S S S 001002)0 1(?212 1=??? ? ?????? ??-==+i i S S y y χχ 401002002)0 1(?222 2 121 =??? ? ?????? ??-???? ??-==+ i i i i S S y y χχ 4 )(22 22 =-=?y y y S S S
16 )()(4 2 2 =??y x S S ① 讨论:由x S ?、y S ?的对易关系 [x S ?,y S ?]z S i ? = 要求 4 )()(2 2 2 2z y x S S S ≥?? 在)(2 1z S χ态中,2 = z S ∴ 16 )()(4 2 2 ≥y x S S ?? 可见①式符合上式的要求。 7.3.求??? ? ??--=???? ??=002?01102?i i S S y x 及的本征值和所属的本征函数。 解:x S ?的本征方程为01102a a b b λ??????= ??? ? ?????? 移项得: 20 2 a b λ λ? ? - ???= ? ? ???- ??? x S ?的久期方程为 02 2=--λ λ 可得 20)2(22 ±=?=-λλ ∴ x S ?的本征值为2 ±。 设对应于本征值2 的本征函数为 ???? ??=112/1b a χ 由本征方程 2 /12/12 ?χχ =x S ,得
量子力学思考题 1、以下说法是否正确: (1)量子力学适用于微观体系,而经典力学适用于宏观体系; (2)量子力学适用于 不能忽略的体系,而经典力学适用于 可以忽略的体系。 解答:(1)量子力学是比经典力学更为普遍的理论体系,它可以包容整个经典力学体系。 (2)对于宏观体系或 可以忽略的体系,并非量子力学不能适用,而是量子力学实际上已 经过渡到经典力学,二者相吻合了。 2、微观粒子的状态用波函数完全描述,这里“完全”的含义是什么? 解答:按着波函数的统计解释,波函数统计性的描述了体系的量子态。如已知单粒子(不考虑自旋)波函数)(r ψ,则不仅可以确定粒子的位置概率分布,而且如粒子的动量、能量等其他力学量的概率分布也均可通过)(r ψ而完全确定。由于量子理论和经典理论不同,它一般只能预言测量的统计结果,而只要已知体系的波函数,便可由它获得该体系的一切可能物理信息。从这个意义上说,有关体系的全部信息显然已包含在波函数中,所以说微观粒子的状态用波函数完全描述,并把波函数称为态函数。 3、以微观粒子的双缝干涉实验为例,说明态的叠加原理。 解答:设1ψ和2ψ是分别打开左边和右边狭缝时的波函数,当两个缝同时打开时,实验说明到达屏上粒子的波函数由1ψ和2ψ的线性叠加2211ψψψc c +=来表示,可见态的叠加不是概率相加,而是波函数的叠加,屏上粒子位置的概率分布由222112 ψψψ c c +=确定,2 ψ中 出现有1ψ和2ψ的干涉项]Re[2* 21* 21ψψc c ,1c 和2c 的模对相对相位对概率分布具有重要作用。 4、量子态的叠加原理常被表述为:“如果1ψ和2ψ是体系的可能态,则它们的线性叠加 2211ψψψc c +=也是体系的一个可能态”。 (1)是否可能出现)()()()(),(2211x t c x t c t x ψψψ+=; (2)对其中的1c 与2c 是任意与r 无关的复数,但可能是时间t 的函数。这种理解正确吗? 解答:(1)可能,这时)(1t c 与)(2t c 按薛定谔方程的要求随时间变化。 (2)如按这种理解 ),()(),()(),(2211t x t c t x t c t x ψψψ+=
浅谈多媒体课件制作与中学物理教学 计算机技术的普及和发展,冲击着教育观念的改变和教学手段的提高。也成为新贯彻新课改的有力工具。为教育的现代化改革开拓了一个广阔的前景与空间,给优化课堂教学,构建新型的教学模式,提供了丰富的土壤。多媒体集文字、图形、图象、声音、动画、影视等各种信息传输手段为一体,具有很强的真实感和表现力,可以激发学生学习兴趣,可以动态地、对比地演示一些物理现象,极大地提高教与学的效率,达到最佳的教学效果。 随着计算机技术的迅猛发展及计算机的大量普及,很多中学配备了微机室、专用多媒体教室,建立电教中心,为计算机辅助教学(CAI)打下了硬件基础。CAI在现代教学中有着重要的地位,如何充分发挥CAI在中学教学中的作用,是摆在广大中学教育工作者面前的一个重要课题。笔者就CAI在中学物理教学中的应用以及对中学物理教学中的影响谈几点拙见。 一个优秀的CAI课件应充分地发挥计算机多媒体的特点,在制作过程中应注重视听教学的特征,突出启发教学,还应注重教学过程的科学性和合理性,应做到构图合理、美观,画面清晰、稳定,色彩分明、色调悦目,动画流畅,真实感强,解说清晰动听,功能丰富,演播运行安全可靠。 一.在制作多媒体CAI课件时应具备以下几点: ⒈加强课前研究,建立素材资源库 课前研究是教学的准备,只有课前进行充分的研究,才能取得理想的教学效果。在备课过程中,走素材资源库和制作平台相结合的思路。物理教师应根据教学实际,充分利用现有条件下的网络信息资源素材库和教学软件,以及相关的CD、VCD资源,选取适合教学需要的内容来制作自己的课件,从而适应不同教学情境的需要。同时,教师可在Internet上建立自己的网站,把以网页浏览形式制作的CAI课件、教案、论文等放在该网站中,并把在教学过程中制作的每一个课件链接起来,从而逐步建立一个完整的教学课件体系。 2.选择合适的制作工具 为了创作出一个成功的多媒体CAI课件,工具选择得好可以大大地加快开发进程,节省开发人力和资金,有利于将主要精力投入到脚本和软件的设计中去。选择多媒体制作工具,主要应从以下几个方面综合考虑:编程环境、超级链接能力、媒体集成能力、动画创作能力、易学习性、易使用性、文档是否丰富等 3.应充分发挥交互作用
第七章习题 1. 有一平凹氦氖激光器,腔长m 5.0,凹镜曲率半径为m 2,现欲用小孔光阑选出 00TEM 模,试求光阑放于紧靠平面镜和紧靠凹面镜处两种情况下小孔直径各为多少?(对于氦氖激光器,当小孔光阑的直径约等于基模半径的3.3倍时,可选出基横模。) 解:由R L g -=1,可计算出75.01=g ,0.12=g ,满足1021
量子力学习题(三年级用) 北京大学物理学院 二O O三年
第一章 绪论 1、计算下列情况的Broglie d e -波长,指出那种情况要用量子力学处理: (1)能量为eV .0250的慢中子 () 克2410671-?=μ .n ;被铀吸收; (2)能量为a MeV 的5粒子穿过原子克2410646-?=μ.a ; (3)飞行速度为100米/秒,质量为40克的子弹。 2、两个光子在一定条件下可以转化为正、负电子对,如果两光子的能量相等,问要实现这种转化,光子的波长最大是多少? 3、利用Broglie d e -关系,及园形轨道为各波长的整数倍,给出氢原子能量 可能值。
第二章 波函数与波动力学 1、设()() 为常数a Ae x x a 222 1 -= ? (1)求归一化常数 (2).?p ?,x x == 2、求ikr ikr e r e r -=?=?1121和的几率流密度。 3、若() ,Be e A kx kx -+=? 求其几率流密度,你从结果中能得到什么样的结 论?(其中k 为实数) 4、一维运动的粒子处于 ()? ? ?<>=?λ-0 00x x Axe x x 的状态,其中,0>λ求归一化系数A 和粒子动量的几率分布函数。 5、证明:从单粒子的薛定谔方程得出的粒子的速度场是非旋的,即求证 0=υ?? 其中ρ= υ/j 6、一维自由运动粒子,在0=t 时,波函数为 ()()x ,x δ=?0 求: ?)t ,x (=?2
第三章 一维定态问题 1、粒子处于位场 ()00 0000 ??? ?≥?=V x V x V 中,求:E >0V 时的透射系数和反射系数(粒子由右向左运动) 2、一粒子在一维势场 ?? ???>∞≤≤<∞=0 000x a x x V ) x ( 中运动。 (1)求粒子的能级和对应的波函数; (2)若粒子处于)x (n ?态,证明:,/a x 2= () .n a x x ?? ? ??π-=-2222 6112 3、若在x 轴的有限区域,有一位势,在区域外的波函数为 如 D S A S B D S A S C 22211211+=+= 这即“出射”波和“入射”波之间的关系,
量子力学习题及解答 第一章 量子理论基础 1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即 m λ T=b (常量); 并近似计算b 的数值,准确到二位有效数字。 解 根据普朗克的黑体辐射公式 dv e c hv d kT hv v v 1 1 833 -? =πρ, (1) 以及 c v =λ, (2) λρρd dv v v -=, (3) 有 这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。 本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下: 如果令x= kT hc λ ,则上述方程为 这是一个超越方程。首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=,经过验证,此解正是所要求的,这样则有 把x 以及三个物理常量代入到上式便知 这便是维恩位移定律。据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。 1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。 解 根据德布罗意波粒二象性的关系,可知 E=hv , 如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么 如果我们考察的是相对性的光子,那么 E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 6 1051.0?, 因此利用非相对论性的电子的能量——动量关系式,这样,便有 在这里,利用了 以及 最后,对
第六章:中心力场 [1]质量分别为m, ,m 2的两个粒子组成的体系,质心座标R及相对座标r为: m" m zD “、 R = 一一⑴ m, m2 rr 二O -「1 ⑵ 试求总动量P = p,亠p2及总角动量L = h亠丨2在R,r表象中的 算符表示。 1.[解](a)合动量算符p = P1 ? P2。根据假设可以解出r i,r2 - - m2 令 m 三m ,亠口2: 「=R_ ----- r (3) m 1 m1 r2= R ? r (4) m2 设各个矢量的分量是r1(x1, y1, z1) , r2 (x2, y 2, z2), r(x, y,z)和R(X,Y,Z)。为了计算动量的变换式先求对x , X2等的偏导数: L、L、# L、r L、L、L、 X x m1 ' ' ' '' 1(5) :x1;:x1;:X ;:x1;:x m ;:X ;:x jx2cX cx2 L、rx x ;X ;x2 a m2 e jx m ;X :x (6) 关于 L、L、 d d-可以写出与( 5) (6) 类似的式子,因而-71 -7 2 .z1.z2 A A A A A d e P - (P1 ■P2)x 二P 1x p2x -( - -) i ;x1;x2 L、L、*-?.L、
m1m2 =_(」2): i m ;X :x m ;:X ;:x i ;X --h d P 二i ' i _:X r d j i ;: Y -h k —
A " ■ ■ /t ■ ■ (b)总角动量 L = l i ?丨2 =— (「1 ::甘 1 ?「2 ::詁 2) i L x — (「i J j J)x i m 2 -(Z -z)(- m cY ^(yi--z) i Z -(y 2- i :z 利用(3), (4), ( 5), (6): L x {(丫一匹 i m m-:: y)(- m cZ m —-—) :-y m 1 (Y -y)( m m 2 m ;Z -) m i _(Z ? — z)( m m E -—)} :-y -f Z i m ;Z c c )-(丫 一 -Z —) ;z .y m 1m 2 (y 「 z jz m 2 —(Y m -(Y - 'z -Z mm m 2 .L 、 ,l~. G C (y z ) :z :丫 (y — :z -z :)} :y h d =— c c -Z ) (y — Y 'z -z^)} -y h - = (—R I R i h _ ■ -r J)x i
2002级量子力学期末考试试题和答案 B 卷 一、(共25分) 1、厄密算符的本征值和本征矢有什么特点?(4分) 2、什么样的状态是束缚态、简并态和偶宇称态?(6分) 3、全同玻色子的波函数有什么特点?并写出两个玻色子组成的全同粒子体系的波函数。(4分) 4、在一维情况下,求宇称算符P ?和坐标x 的共同本征函数。(6分) 5、简述测不准关系的主要内容,并写出时间t 和能量E 的测不准关系。(5分) 二、(15分)已知厄密算符B A ?,?,满足1??22==B A ,且0????=+A B B A ,求 1、在A 表象中算符A ?、B ?的矩阵表示; 2、在A 表象中算符B ?的本征值和本征函数; 3、从A 表象到B 表象的幺正变换矩阵S 。 三、(15分)线性谐振子在0=t 时处于状态 )21exp(3231)0,(2 2x x x ααπαψ-??????-=,其中 ημω α=,求 1、在0=t 时体系能量的取值几率和平均值。 2、0>t 时体系波函数和体系能量 的取值几率及平均值 四、(15分)当λ为一小量时,利用微扰论求矩阵
??? ?? ? ?++λλλλλλ23303220 21的本征值至λ的二次项,本征矢至λ的一次项。 五、(10分)一体系由三个全同的玻色子组成, 玻色子之间无相互作用. 玻色子只有两个可能的单粒子态. 问体系可能的状态有几个? 它们的波函数怎样用单粒子波函数构成? 一、1、厄密算符的本征值是实数,本征矢是正交、归一和完备的。 2、在无穷远处为零的状态为束缚态;简并态是指一个本征值对应一个以上本征函数的情况;将波函数中坐标变量改变符号,若得到的新函数与原来的波函数相同,则称该波函数具有偶宇称。 3、全同玻色子的波函数是对称波函数。两个玻色子组成的全同粒子体系的波函数为: [])()()()(21 12212211q q q q S ????φ+= 4、宇称算符P ?和坐标x 的对易关系是:P x x P ?2],?[-=,将其代入测不准关系知,只有当0?=P x 时的状态才可能使P ?和x 同时具有确定值,由)()(x x -=δδ知,波函数)(x δ满足上述要求,所以)(x δ是算符P ?和x 的共同本征函数。 5、设F ?和G ?的对易关系k ?i F ?G ?G ?F ?=-,k 是一个算符或普通的数。以F 、G 和k 依次表示F ?、G ?和k 在态ψ中的平均值,令 F F ?F ?-=?,G G ?G ?-=?, 则有 42 2 2 k )G ?()F ?(≥???,这个关系式称为测不准关系。 时间t 和能量E 之间的测不准关系为: 2η ≥ ???E t 二、1、由于1?2=A ,所以算符A ?的本征值是1±,因为在A 表象中,算符A ?的矩阵是对角矩阵,所以,在A 表象中算符A ?的矩阵是:???? ??-=1001)(?A A