有限单元法试卷

1、有限元法是近似求解（连续）场问题的数值方法。

2、有限元法将连续的求解域（离散），得到有限个单元，单元与单元之间用（节点）相连。

3、从选择未知量的角度看，有限元法可分为三类（位移法力法混合法）。

4、以（节点位移）为基本未知量的求解方法称为位移量。

5、以（节点力）为基本未知量的求解方法称为力法。

7、直梁在外力作用下，横截面上的内力有（剪力）和（弯矩）两个。

8、平面刚架结构在外力作用下，横截面上的内力有（剪力）、（弯矩）、（轴力）。

9、进行直梁有限元分析，节点位移有（转角）、（挠度）。

10、平面刚架有限元分析，节点位移有（转角）、（挠度）、（？？？）。

11、在弹性和小变形下，节点力和节点位移关系是（）。

12、弹性力学问题的方程个数有（15）个，未知量个数有(15)个。

13、弹性力学平面问题方程个数有（8），未知数（8）个。

15h、几何方程是研究（应变）和（位移）关系的方程。

16、物理方程描述（应力）和（应变）关系的方程。

17、平衡方程反映（应力）和（位移）关系的方程。

18、把进过物体内任意一点各个（截面）上的应力状况叫做（该点）的应力状态。

19、形函数在单元节点上的值，具有本点为（1），他点为零的性质，并在三角形单元的后一节点上，三个形函数之和为（1）。

20、形函数是（三角形）单元内部坐标的（线性位移）函数，它反映了单元的（位移）状态。

21、节点编号时，同一单元相邻节点的（编号）尽量小。

25、单元刚度矩阵描述了（节点力）和（节点位移）之间的关系。

矩形单元边界上位移是（线性）变化的。

从选择未知量的角度来看，有限元法可分为三类，下面那种方法不属于其中（C）。

力法B、位移法C、应变法D、混合法下面对有限元法特点的叙述中，哪种说法是错误的（D）。

可以模拟各种几何形状负责的结构，得出其近似值。

解题步骤可以系统化，标准化。

容易处理非均匀连续介质，可以求解非线性问题。

需要适用于整个结构的插值函数。

几何方程研究的是（A）之间关系的方程式。

岩土工程数值分析试题一、简答题（40分）1．简述梁单元、杆单元、连续梁单元、平面三角形常量单元和四边形等参单元的特点（10分）。

答：1）梁单元是由两个节点组成，每一个节点都具有三个方向的线性移动位移和三个方向的旋转位移，因而每个节点具有6个自由度，梁单元具有拉，压，剪，弯，扭的变形刚度。

计算理论成熟，建模方便,计算量小，在工程结构有限元分析中得到广泛的应用，适用于各种截面形式的杆件分析。

2）由有限个构件以一定方式连接起来所形成的结构，在同一平面内的杆系结构，其所受的外力作用线位于该平面内，在杆系中，每一个杆件可视为一个单元，每个单元的端点成为结点。

3）对于每跨各自等截面的连续梁，以每跨为一个单元。

结点编号和单元编号一般是从连续梁的左端顺序编到右端。

由于连续梁各单元的轴线方向一致，各单元坐标系与结构坐标系的方向相同，因此在矩阵位移法的计算过程中无须进行坐标变换，在单元坐标系和结构坐标系中单元刚度矩阵的表达式是相同的。

4) 平面三角形单元具有适应性强的优点，较容易进行网络划分和逼近边界形状，应用比较灵活。

其缺点是它的位移模式是线性函数，单元应力和应变都是常数，精度不够理想。

5) 四边形等参单元能更好地反映物体内的应力变化，适应曲线边界，常使用于弹性力学平平面问题的分析。

八结点单元一共有16个已知的结点位移分量。

2．除有限单元法外，岩土工程常用到哪些数值方法，并对比其优缺点(10分)。

答：岩土工程常用的数值方法包括：有限差分法、边界元法、离散元法、颗粒元法、不连续变形分析法、流形元法、模糊数学方法、概率论与可靠度分析方法、灰色系统理论、人工智能与专家系统、神经网络方法、时间序列分析法。

有限单元法的优缺点：有限单元法的理论基础是虚功原理和基于最小势能的变分原理，它将研究域离散化，对位移场和应力场的连续性进行物理近似。

有限单元法适用性广泛，从理论上讲对任何问题都适用，但计算速度相对较慢。

即，物理概念清晰、灵活、通用、计算速度叫慢。

山东科技大学2012—2013学年第一学期《有限元方法》考试试卷（A卷）班级姓名学号一、选择题（每题1分，共10分）1、弹性力学与材料力学的主要不同之处在于C。

A. 任务；B. 研究对象；C. 研究方法；D. 基本假设。

σ是 C 。

2、在轴对称问题中，径向应力分量rA. 恒为零；B. 与r无关；C. 与θ无关；D. 恒为常数。

3、利用ANSYS进行结构分析时，结果文件为。

A. jobname.rst；B. jobname.rth；C. jobname.rfl；D. jobname.rmg。

4、在ANSYS的单元库中，PLANE42单元属于。

A. 结构梁单元；B. 结构壳单元；C. 结构线单元；D. 结构实体单元。

5、在一个分析中，可能有多个材料特性组，ANSYS通过独特的来识别每个材料特性组。

A. 特性；B. 说明；C. 参考号；D.方法。

6、ANSYS与Pro/E的接口文件类型是。

A..x_t；B. .prt；C. .sat；D. .model。

7、载荷包括所有边界条件以及外部或内部作用效应，下列不属于ANSYS 载荷的是。

A. DOF约束；B. 力；C. 体载荷；D.应力。

8、要求面或者体有规则的形状，即必须满足一定的准则。

A.自由网格；B. 映射网格；C. Sweep分网；D. 其他。

9、独立于有限元网格，即可以改变单元网格而不影响施加的载荷。

A.阶跃载荷；B. 有限元模型载荷；C. 实体模型载荷；D. 斜坡载荷。

10、有限元法首先求出的解是，单元应力和应变可由它求得。

A.节点坐标；B.节点自由度；C. 节点载荷；D. 节点位移。

二、填空题（每空1分，共20分）1、在整个有限元分析的过程中，是分析的基础。

2、平面应力问题与薄板弯曲问题的弹性体几何形状都是，但前者受力特点是，变形发生在板面内；后者受力特点是的力的作用，板将变成有弯有扭的曲面。

3、典型的ANSYS文件包括、、。

4、平面应力问题与平面应变问题都具有个独立的应力分量，个独立的应变分量，但对应的弹性体几何形状前者为，后者为。

专升本《深基坑工程技术》一、 (共75题,共150分）1. 当基坑开挖深度( ）时，通常可采用明沟排水。

（2分）A.小于2m B。

大于2m C。

大于3m D.小于3m标准答案:D2. 下面哪种土压力为集中荷载作用下产生的侧压力（）（2分）A。

B。

C。

D。

标准答案：A3. 下列哪种稳定性分析不用考虑嵌固深度的影响（ ) （2分）A.整体稳定性分析B。

基坑底部土体突涌稳定性分析C。

基坑底部土体抗隆起稳定性分析D。

基坑渗流稳定性分析标准答案:B4。

近年来采用有限单元法，根据比较符合实际情况的弹塑性应力应变关系,分析土坡的变形和稳定，一般称为（）. （2分）A。

极限分析法 B。

Bishop法 C.极限平衡法 D。

Taylor法。

标准答案：A5. 当基坑开挖较浅,还未设支撑时，不论对刚性墙体还是柔性墙体，均表现为（）。

(2分）A。

墙顶位移最大，向基坑方向水平位移B.墙顶位移最大，向基坑方向竖直位移C。

墙顶位移向基坑方向水平位移D.墙顶位移向基坑方向竖直位移。

标准答案：A6。

对于假想铰法求多支撑挡土结构内力时其关键问题是( ）（2分）A.假想铰点的位置B.土压力的分布假设C。

对支撑结构的静定与超静定分析D。

解决变形协调问题。

标准答案：A7. 层间水就是夹于两不透水层之间含水层中所含的水,如果水充满此含水层，水带有压力，这种水称之为（ ) （2分）A.无压层间水B.潜水 C。

层间水 D.承压层间水标准答案：D8。

单撑（单锚)板桩入土深度较浅时，板桩上端为简支,下端为( ）（2分）A.固定支承 B。

铰接 C。

简支 D.自由支承标准答案：D9。

基底的隆起验算时,验算地基强度采用( ) (2分)A.反分析法B.稳定安全系数法C.Terzaghi-Peck法D.圆弧法。

标准答案：C10. 在基坑工程中应用的最大的地下连续墙形式为（）（2分）A。

T形及II形地下连续墙 B。

格形地下连续墙C。

壁板式 D。

预应力U形折板地下连续墙。

有限元法理论及应用大作业1、试简要阐述有限元理论分析的基本步骤主要有哪些？答：有限元分析的主要步骤主要有：（1）结构的离散化，即单元的划分；（2）单元分析，包括选择位移模式、根据几何方程建立应变与位移的关系、根据虚功原理建立节点力与节点位移的关系，最后得到单元刚度方程；（3）等效节点载荷计算；（4）整体分析，建立整体刚度方程；（5）引入约束，求解整体平衡方程。

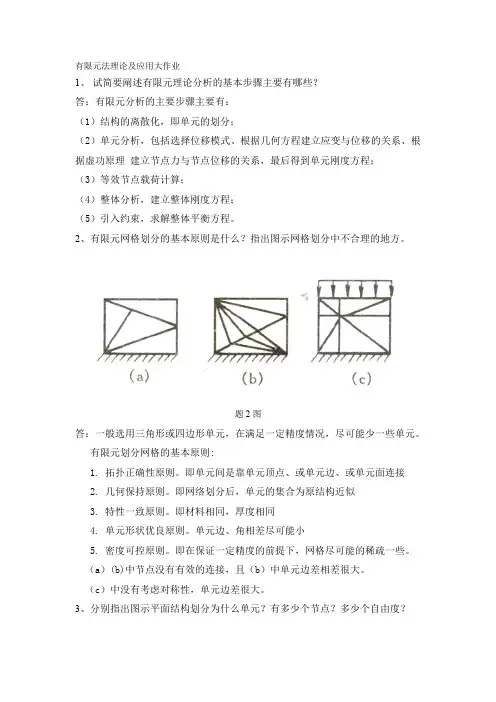
2、有限元网格划分的基本原则是什么？指出图示网格划分中不合理的地方。

题2图答：一般选用三角形或四边形单元，在满足一定精度情况，尽可能少一些单元。

有限元划分网格的基本原则:1.拓扑正确性原则。

即单元间是靠单元顶点、或单元边、或单元面连接2.几何保持原则。

即网络划分后，单元的集合为原结构近似3.特性一致原则。

即材料相同，厚度相同4.单元形状优良原则。

单元边、角相差尽可能小5.密度可控原则。

即在保证一定精度的前提下，网格尽可能的稀疏一些。

（a）(b)中节点没有有效的连接，且（b）中单元边差相差很大。

（c）中没有考虑对称性，单元边差很大。

3、分别指出图示平面结构划分为什么单元？有多少个节点？多少个自由度？题3图答：（a ）划分为杆单元， 8个节点，12个自由度。

（b ）划分为平面梁单元，8个节点，15个自由度。

（c ）平面四节点四边形单元，8个节点，13个自由度。

（d ）平面三角形单元，29个节点，38个自由度。

4、什么是等参数单元？。

答：如果坐标变换和位移插值采用相同的节点，并且单元的形状变换函数与位移插值的形函数一样，则称这种变换为等参变换，这样的单元称为等参单元。

5、在平面三节点三角形单元中，能否选取如下的位移模式，为什么？(1).⎪⎩⎪⎨⎧++=++=26543221),(),(y x y x v yx y x u αααααα (2). ⎪⎩⎪⎨⎧++=++=2652423221),(),(yxy x y x v yxy x y x u αααααα 答：（1）不能，因为位移函数要满足几何各向同性，即单元的位移分布不应与人为选取的 坐标方位有关，即位移函数中的坐标x,y 应该是能够互换的。

2024版《工贸企业有限空间作业安全规定》法规考试卷姓名：部门：得分：一、单选题。

（1.5分*16题，共24分）1.《工贸企业有限空间作业安全规定》已经2023年11月6日应急管理部第28次部务会议审议通过，现予公布，自 A 起施行。

A.2024.1.1B.2024.3.1C.2024.1.3 C.2024.1.312.《工贸企业有限空间作业安全规定》所称的有限空间作业，是指人员进入 A 实施的作业。

A.有限空间B.封闭C.部分封闭D.未被设计为固定工作场所3.工贸企业 D 是有限空间作业安全第一责任人。

A.安全管理人员B.法人C.总经理D.主要负责人4.有限空间作业监护人员应当具备与监督有限空间作业相适应的 C ，能够正确使用气体检测、机械通风、呼吸防护、应急救援等用品、装备。

A.安全知识B.应急处置能力C.安全知识和应急处置能力D. 安全知识或应急处置能力5.工贸企业应当对有限空间进行 B ，建立有限空间管理台账，明确有限空间数量、位置以及危险因素等信息，并及时更新。

鼓励工贸企业采用信息化、数字化和智能化技术，提升有限空间作业安全风险管控水平。

A.管理B.辨识C.标识D.安全防护6.工贸企业应当根据有限空间作业 A ，明确审批要求。

A.安全风险大小B.面积C.人数D.面积和人数7.工贸企业有限空间作业，存在 D 等中毒和窒息等风险。

A.硫化氢B.一氧化碳C.二氧化碳D.A+B+C8.工贸企业有限空间作业，应当由工贸企业主要负责人或者其书面委托的人员进行审批，委托进行审批的，相关责任由工贸企业 B 承担。

A.作业人员B.主要负责人C.委外方D.安全管理人员9.未经工贸企业确定的作业审批人批准， C 实施有限空间作业。

A.可以B.先作业后报批C.不得D.口头报批后可以10.工贸企业应当每年至少组织 A 次有限空间作业专题安全培训，对作业审批人、监护人员、作业人员和应急救援人员培训有限空间作业安全知识和技能，并如实记录。

有限元试题及答案一、选择题1. 有限元法是一种数值方法，主要用于求解什么类型的数学问题？A. 线性代数方程B. 微分方程C. 积分方程D. 偏微分方程答案：D2. 在有限元分析中，以下哪项不是网格划分的基本原则？A. 网格应尽量均匀B. 网格应避免交叉C. 网格应尽量小D. 网格应适应几何形状答案：C3. 有限元方法中，单元的局部刚度矩阵可以通过以下哪种方式获得？A. 直接积分B. 矩阵乘法C. 线性插值D. 经验公式答案：A二、填空题1. 有限元方法中，______ 是指将连续的域离散化成有限数量的小单元。

答案：离散化2. 在进行有限元分析时，______ 是指在单元内部使用插值函数来近似求解场变量。

答案：近似3. 有限元法中，______ 是指在单元边界上满足的连续性条件。

答案：边界条件三、简答题1. 简述有限元法的基本步骤。

答案：有限元法的基本步骤包括：（1）定义问题域；（2）离散化问题域，生成网格；（3）为每个单元定义局部坐标系和形状函数；（4）组装全局刚度矩阵和载荷向量；（5）施加边界条件；（6）求解线性代数方程；（7）提取结果并进行后处理。

2. 描述有限元分析中的单元类型有哪些，并简述每种单元的特点。

答案：常见的单元类型包括：（1）一维单元，如杆单元和梁单元，特点是沿一个方向传递力；（2）二维单元，如三角形和四边形单元，特点是在平面内传递力；（3）三维单元，如四面体和六面体单元，特点是在空间内传递力。

每种单元都有其特定的形状函数和刚度矩阵。

四、计算题1. 给定一个简单的一维弹性杆问题，其长度为L，两端固定，中间施加集中力P。

使用有限元法求解该杆的位移和应力分布。

答案：首先，将杆离散化为一个单元。

使用一维杆单元的局部刚度矩阵和形状函数，可以推导出全局刚度矩阵。

然后，施加边界条件，即杆的两端位移为零。

最后，将集中力P转换为等效节点载荷，求解线性代数方程，得到节点位移。

应力可以通过位移和杆的截面特性计算得出。

地大《计算结构力学》在线作业二
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1.下述对有限元法特点的描述中，哪种说法是错误的（）。

A.需要适用于整个结构的插值函数
B.解题步骤可以系统化、标准化
C.容易处理非均匀连续介质，可以求解非线性问题
D.可以模拟各种几何形状复杂的结构，得出其近似解
答案:A
2.平衡方程研究的是（）之间关系的方程式。

A.应变和位移
B.应力和应变
C.应力和体力
D.应力和位移
答案:C
3.等参变换是指单元坐标变换和函数插值采用（）的结点和（）的插值函数。

A.相同，相同
B.相同，不相同
C.不相同，相同
D.不相同，不相同
答案:A
4.弹性力学平面问题的方程个数有（）个。

A.以上都不是
B.9
C.8
D.15
答案:C
5.下面关于有限元分析法的描述中，那种说法是错误的（）
A.应力变化梯度较大的部位划分的单元可小一些
B.单元各边的长度以及各内角不应相差太大。

C.单元之间通过其边界连接成组合体
D.分布载荷与自由边界的分界点、支撑点等应取为节点
答案:C
6.下面四种假设中，那种不属于分析弹性力学的基本假设（）
A.有限变形假设
B.无初应力假设
C.小变形假设
D.各向同性假设
答案:B。