
高三数学函数与导数专题试卷 说明:1.本卷分第Ⅰ卷(选择题),第Ⅱ卷(填空题与解答题),第ⅠⅡ卷的答案写在答题卷的答案纸上,学生只要交答题卷. 第Ⅰ卷 一.选择题(10小题,每小题5分,共50分) (4)()f x f x +=,当(0,2)x ∈时,()2f x x =+,则(7)f =( ) A . 3 B . 3- C . D . 1- 2.设A ={x ||x |≤3},B ={y |y =-x 2+t },若A ∩B =?,则实数t 的取值范围是( ) A .t <-3 B .t ≤-3 C .t >3 D .t ≥3 3.设0.3222,0.3,log (0.3)(1)x a b c x x ===+>,则,,a b c 的大小关系是 ( ) A .a b c << B .b a c << C .c b a << D .b c a << 4.函数x x f +=11)(的图像大致是( ) 5.已知直线ln y kx y x ==是的切线,则k 的值为( ) A. e B. e - C. 1e D. 1e - 6.已知条件p :x 2+x-2>0,条件q :a x >,若q 是p 的充分不必要条件,则a 的取值范围可以是( ) A .1≥a B .1≤a C .1-≥a D.3-≤a 7.函数3()2f x x ax =+-在区间(1,)+∞上是增函数,则a 的取值范围是( ) A. [3,)+∞ B. [3,)-+∞ C. (3,)-+∞ D. (,3)-∞- 8. 已知函数f (x )=log 2(x 2-2x -3),则使f (x )为减函数的区间是( ) A .(-∞,-1) B .(-1,0) C .(1,2) D .(-3,-1)
高考数学二轮复习专题 02:函数与导数
姓名:________
班级:________
成绩:________
一、 单选题 (共 17 题;共 34 分)
1. (2 分) (2016 高一上·厦门期中) 已知函数 f(x)=xln(x﹣1)﹣a,下列说法正确的是( )
A . 当 a=0 时,f(x)没有零点
B . 当 a<0 时,f(x)有零点 x0 , 且 x0∈(2,+∞)
C . 当 a>0 时,f(x)有零点 x0 , 且 x0∈(1,2)
D . 当 a>0 时,f(x)有零点 x0 , 且 x0∈(2,+∞)
2. (2 分) (2018 高二下·沈阳期中) 函数 A. B. C. D.
恰有一个零点,则实数 的值为( )
3. (2 分) 已知函数 f(x)= -cosx,若 A . f(a)>f(b) B . f(a)
, 则( )
4. ( 2 分 ) (2019 高 二 上 · 浙 江 期 中 ) 已 知
的两个相邻的零点,且
,则
,且
,
,
是函数
的值为( )
第 1 页 共 12 页
A. B. C. D.
5. (2 分) 定义在 R 上的奇函数 f(x),当 x≥0 时,f(x)= =f(x)﹣a(0<a<1)的所有零点之和为( )
A . 3a﹣1 B . 1﹣3a C . 3﹣a﹣1 D . 1﹣3﹣a
, 则关于 x 的函数 F(x)
6. (2 分) 已知函数 取值范围是( )
A. B.
的图像为曲线 C,若曲线 C 存在与直线
垂直的切线,则实数 m 的
C.
D.
7. (2 分) (2016 高一上·沈阳期中) 已知函数 f(x)满足:当 f(x)= ()
A.
第 2 页 共 12 页
,则 f(2+log23)=
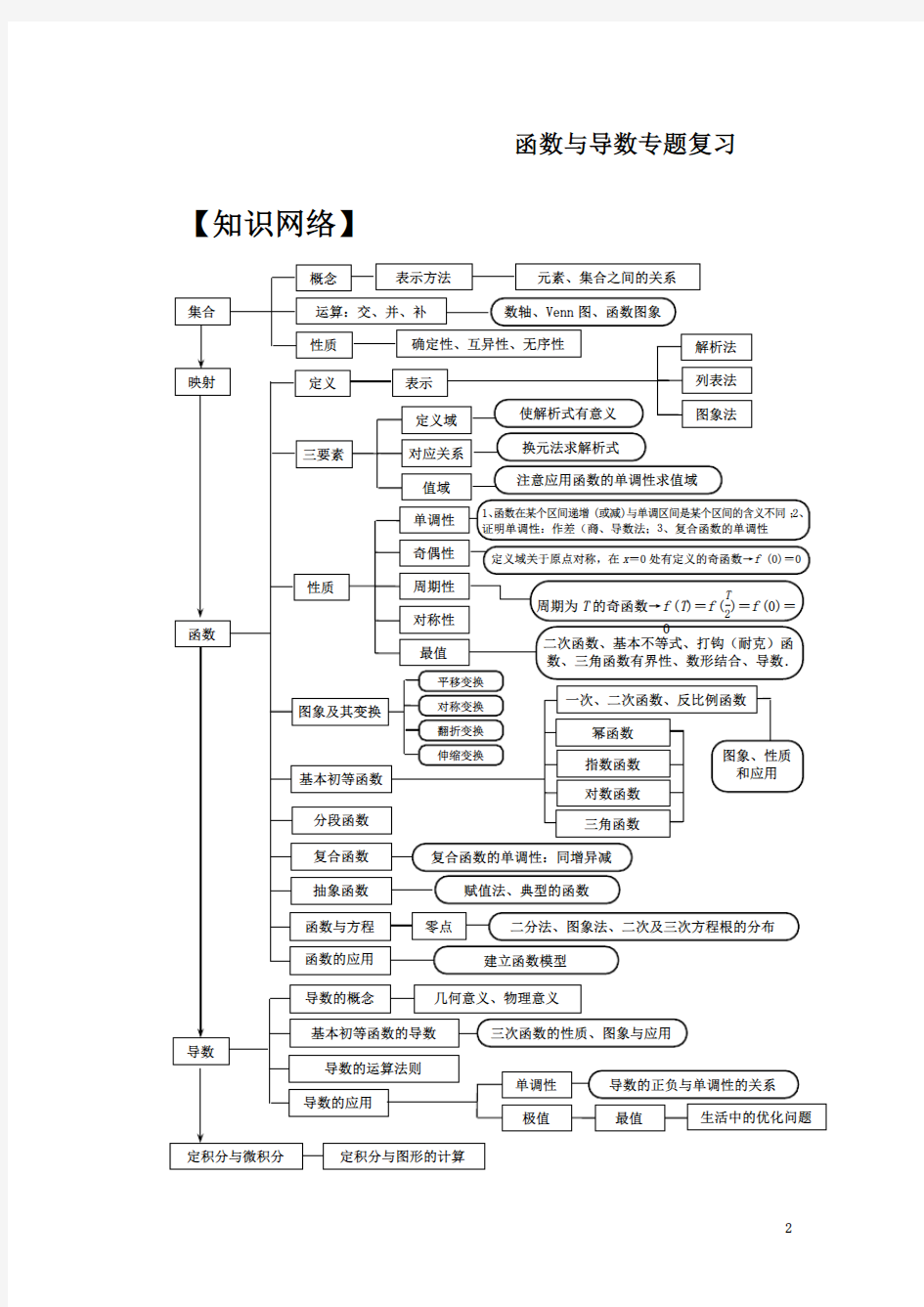
函数与导数专题1.在解题中常用的有关结论(需要熟记):
考点一:导数几何意义: 角度一 求切线方程 1.(2014·洛阳统考)已知函数f (x )=3x +cos 2x +sin 2x ,a =f ′? ?? ?? π4,f ′(x )是f (x ) 的导函数,则过曲线y =x 3上一点P (a ,b )的切线方程为( ) A .3x -y -2=0 B .4x -3y +1=0 C .3x -y -2=0或3x -4y +1=0 D .3x -y -2=0或4x -3y +1=0 解析:选A 由f (x )=3x +cos 2x +sin 2x 得f ′(x )=3-2sin 2x +2cos 2x ,则a = f ′? ?? ??π4=3-2sin π2+2cos π2=1.由y =x 3得y ′=3x 2,过曲线y =x 3上一点P (a ,b )的切线的斜率k =3a 2=3×12=3.又b =a 3,则b =1,所以切点P 的坐标为(1,1),故过曲线y =x 3上的点P 的切线方程为y -1=3(x -1),即3x -y -2=0. 角度二 求切点坐标 2.(2013·辽宁五校第二次联考)曲线y =3ln x +x +2在点P 0处的切线方程为4x -y -1=0,则点P 0的坐标是( ) A .(0,1) B .(1,-1) C .(1,3) D .(1,0) 解析:选C 由题意知y ′=3 x +1=4,解得x =1,此时4×1-y -1=0,解得y =3,∴点P 0的坐标是(1,3). 角度三 求参数的值 3.已知f (x )=ln x ,g (x )=12x 2+mx +7 2(m <0),直线l 与函数f (x ),g (x )的图像都相切,且与f (x )图像的切点为(1,f (1)),则m 等于( )
第三课时函数与导数的应用 1.若函数f (x )=ax 4+bx 2+c 满足f ′(1)=2,则f ′(-1)=( ) A .-1 B .-2 C .2 D .0 2.已知某生产厂家的年利润y (单位:万元)与年产量x (单位:万件)的函数关系 式为y =-13 x 3 +81x -234,则使该生产厂家获取最大的年利润的年产量为( ) A .13万件 B .11万件 C .9万件 D .7万件 3:由直线x =-π3,x =π 3 ,y =0与曲线y =cos x 所围成的封闭图形的面积为( ) A.12 B .1 C.3 2 D.3 4.若函数 y =f (x )在R 上可导,且满足不等式xf ′(x )>-f (x )恒成 立,且常数a ,b 满足a >b ,则下列不等式一定成立的是( ) A .af (a )>bf (b ) B .af (a )
函数与导数专题复习 类型一 导数的定义 运算及几何意义 例1:已知函数)(x f 的导函数为)('x f ,且满足x xf x f ln )1(2)(' +=,则=)1('f ( ) A .-e B.-1 C.1 D.e 解:x f x f 1)1(2)(''+=,1)1(1)1(2)1('''-=∴+=f f f 【评析与探究】求值常用方程思想,利用求导寻求)('x f 的方程是求解本题的关键。 变式训练1 曲线33+-=x x y 在点(1,3)处的切线方程为 类型二 利用导数求解函数的单调性 例2:d cx bx x x f +++= 233 1)(何时有两个极值,何时无极值?)(x f 恒增的条件是什么? 解:,2)(2'c bx x x f ++=当0442>-=?c b 时, 即c b >2时,0)('=x f 有两个异根2,1x x ,由)('x f y =的图像知,在2,1x x 的左右两侧)('x f 异号,故2,1x x 是极值点,此时)(x f 有两个极值。 当c b =2时,0)('=x f 有实数根0x ,由)('x f y =的图像知,在0x 左右两侧)(' x f 同号,故0x 不是)(x f 的极值点 当c b <2时,0)(' =x f 无根,当然无极值点 综上所述,当时c b ≤2,)(x f 恒增。 【评析与探究】①此题恒增条件c b ≤2易掉“=”号,②c b =2 时,根0x 不是极值点也易错。 变式训练2 已知函数b x x g ax x x f +=+=232)(,)(,它们的图像在1=x 处有相同的切线 ⑴求函数)(x f 和)(x g 的解析式;
2015专题五:函数与导数 在解题中常用的有关结论(需要熟记): (1)曲线()y f x =在0x x =处的切线的斜率等于0()f x ',切线方程为000()()()y f x x x f x '=-+ (2)若可导函数()y f x =在0x x =处取得极值,则0()0f x '=。反之,不成立。 (3)对于可导函数()f x ,不等式()f x '0>0<()的解集决定函数()f x 的递增(减)区间。 (4)函数()f x 在区间I 上递增(减)的充要条件是:x I ?∈()f x '0≥(0)≤恒成立 (5)函数()f x 在区间I 上不单调等价于()f x 在区间I 上有极值,则可等价转化为方程 ()0f x '=在区间I 上有实根且为非二重根。 (若()f x '为二次函数且I=R ,则有0?>)。 (6)()f x 在区间I 上无极值等价于()f x 在区间在上是单调函数,进而得到()f x '0≥或 ()f x '0≤在I 上恒成立 (7)若x I ?∈,()f x 0>恒成立,则min ()f x 0>; 若x I ?∈,()f x 0<恒成立,则max ()f x 0< (8)若0x I ?∈,使得0()f x 0>,则max ()f x 0>;若0x I ?∈,使得0()f x 0<,则min ()f x 0<. (9)设()f x 与()g x 的定义域的交集为D 若x ?∈D ()()f x g x >恒成立则有[]min ()()0f x g x -> (10)若对11x I ?∈、22x I ∈,12()()f x g x >恒成立,则min max ()()f x g x >. 若对11x I ?∈,22x I ?∈,使得12()()f x g x >,则min min ()()f x g x >. 若对11x I ?∈,22x I ?∈,使得12()()f x g x <,则max max ()()f x g x <. (11)已知()f x 在区间1I 上的值域为A,,()g x 在区间2I 上值域为B , 若对11x I ?∈,22x I ?∈,使得1()f x =2()g x 成立,则A B ?。 (12)若三次函数f(x)有三个零点,则方程()0f x '=有两个不等实根12x x 、,且极大值大 于0,极小值小于0. (13)证题中常用的不等式: ① ln 1(0)x x x ≤->② ln +1(1)x x x ≤>-()③ 1x e x ≥+ ④ 1x e x -≥-⑤ ln 1 (1)12 x x x x -<>+⑥ 22 ln 11(0)22x x x x <->
函数与导数问题解题方法探寻及典例剖析【考情分析】 【常见题型及解法】 1. 常见题型 2. 在解题中常用的有关结论(需要熟记):
【基本练习题讲练】 【例1】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发 现乌龟快到终点了,于是急忙追赶,但为时已晚 乌龟还是先到达了终点……用S1、S2分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是( ) 【答案】 B 【解析】在选项B 中,乌龟到达终点时,兔子在同一时间的路程比乌龟短.【点评】函数图象是近年高考的热点的试题,考查函数图象的实际应用,考查学生解决问题、分析问题的能力, 在复习时应引起重视. 【例2】(山东高考题)已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若 方程 ()(0 f x m m =>在区间 [8,8 -上有四个不同的根 123,,,x x x x ,则 1234 _________.x x x x +++= A B C D
【例3】若1x 是方程lg 3x x +=的解,2x 是310=+x x 的解,则21x x +的值为( ) A . 2 3错误!未指定书签。 B . 3 2 C .3 D . 31 【例4】若函数 ()(01)x f x a x a a a =-->≠且有两个零点,则实数a 的取值范围是 . 【例 5】已知偶函数()f x 在区间[0,)+∞单调递增,则满足(21)f x -<1 ()3 f 的x 取值范围是( ) (A )( 1,2) (B) [1,2) (C)(1,2) (D) [1,2)
函数与导数 1.求函数的定义域,关键是依据含自变量x 的代数式有意义来列出相应的不等式(组)求解,如开偶次方根、被开方数一定是非负数;对数式中的真数是正数;列不等式时,应列出所有的不等式,不应遗漏. 对抽象函数,只要对应关系相同,括号里整体的取值范围就完全相同. [问题1] 函数y 的定义域是________. 答案 ??? ?0,14 2.用换元法求解析式时,要注意新元的取值范围,即函数的定义域问题. [问题2] 已知f (cos x )=sin 2x ,则f (x )=________. 答案 1-x 2(x ∈[-1,1]) 3.分段函数是在其定义域的不同子集上,分别用不同的式子来表示对应关系的函数,它是一个函数,而不是几个函数. [问题3] 已知函数f (x )=????? e x ,x <0,ln x ,x >0, 则f ????f ????1e =________. 答案 1e 4.判断函数的奇偶性,要注意定义域必须关于原点对称,有时还要对函数式化简整理,但必须注意使定义域不受影响. [问题4] f (x )=lg (1-x 2) |x -2|-2是________函数(填“奇”“偶”或“非奇非偶”). 答案 奇
解析 由? ???? 1-x 2>0, |x -2|-2≠0得定义域为(-1,0)∪(0,1), f (x )=l g (1-x 2) -(x -2)-2=lg (1-x 2) -x . ∴f (-x )=-f (x ),f (x )为奇函数. 5.弄清函数奇偶性的性质 (1)奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反. (2)若f (x )为偶函数,则f (-x )=f (x )=f (|x |). (3)若奇函数f (x )的定义域中含有0,则必有f (0)=0. 故“f (0)=0”是“f (x )为奇函数”的既不充分也不必要条件. [问题5] 设f (x )=lg ????21-x +a 是奇函数,且在x =0处有意义,则该函数为( ) A .(-∞,+∞)上的减函数 B .(-∞,+∞)上的增函数 C .(-1,1)上的减函数 D .(-1,1)上的增函数 答案 D 解析 由题意可知f (0)=0,即lg(2+a )=0, 解得a =-1, 故f (x )=lg 1+x 1-x ,函数f (x )的定义域是(-1,1), 在此定义域内f (x )=lg 1+x 1-x =lg(1+x )-lg(1-x ), 函数y 1=lg(1+x )是增函数,函数y 2=lg(1-x )是减函数,故f (x )=y 1-y 2是增函数.选D. 6.求函数单调区间时,多个单调区间之间不能用符号“∪”和“或”连接,可用“及”连接,或用“,”隔开.单调区间必须是“区间”,而不能用集合或不等式代替. [问题6] 函数f (x )=1 x 的减区间为________. 答案 (-∞,0),(0,+∞) 7.求函数最值(值域)常用的方法: (1)单调性法:适合于已知或能判断单调性的函数.
函数与导数二轮复习建议 金陵中学 朱骏 函数是高中数学的核心内容,因而在历年的江苏高考中,函数一直是考查的重点和热点.高考既注重单独考查函数的基础知识,也会突出考查函数与其它知识的综合应用;既考查具体函数的图象与性质,也考查函数思想方法的应用. 下表列出的是《考试说明》对函数部分具体考查要求及2019年~2019年四年江苏高考 基本题型一:函数性质的研究 例1(2019年江西理改)若f (x )= 1log(2x +1) ,则f (x )的定义域为____________. 【解析】由???2x +1>0log(2x +1)>0 ,解得?????x >-12x <0 ,故-12<x <0,答案为(-1 2,0). 说明:以函数定义域为载体,考查对数函数的图象与性质. 例2(2019年江苏)设函数f (x )=x (e x +a e -x )(x ∈R )是偶函数,则实数a =_______. 【解析】 由g (x )=e x +a e -x 为奇函数,得g (0)=0,解得a =-1;也可以由奇函数的定义解得. 说明:1.函数奇偶性的定义中应关注两点:①定义域关于数0对称是函数具有奇偶性的必要条件;②f (0)=0是定义域包含0的函数f (x )是奇函数的必要条件.2.利用特殊与一般的关系解题是一种非常重要的方法. 变式:若函数f (x )=k -2x 1+k ·2 x (k 为常数)在定义域上为奇函数,则k 的值是_______. 答案:±1.
例3 设a (0<a <1)是给定的常数,f (x )是R 上的奇函数,且在(0,+∞)上是增函数,若f (1 2 )=0,f (log a t )>0,则t 的取值范围是________. 【解析】 因为f (x )是R 上的奇函数,且在(0,+∞)上是增函数,故f (x )在区间(-∞,0)上也是增函数.画出函数f (x )的草图. 由图得-12<log a t <0或log a t >12,解得t (0,a ) ∪(1,a a ). 说明:1.单调性是函数的局部性质,奇偶性是函数的整体 性质,单调性和奇偶性常常结合到一起考查. 2.函数图象是函数性质的直观载体,“以形辅数”是数形结合思想的重要体现. 例4(2019年江苏卷)已知函数f (x )=???x 2 +1,x ≥0,1, x <0,则满足不等式f (1-x 2 )>f (2x ) 的x 的范围是 . 【解析】画出函数f (x )的图象,根据单调性,得???1-x 2 >2x , 1-x 2 >0. ,解得 x ∈(-1,2-1). 说明:1.函数单调性是比较大小和解不等式的重要依据,如果把式f (1-x 2 )>f (2x )具体化,需要分类,情形比较复杂,本题对能力要求较高.2.分段函数是高考常考的内容之一,解决相关问题时,应注意数形结合、分类讨论思想的运用. 变式:设偶函数f (x )=log a |x -b |在(-∞,0)上单调递增,则f (a +1)与f (b +2)的大小关系为________________________. 答案:f (a +1)>f (b +2). 例5(2019年江苏)设a 为实数,函数f (x )=2x 2 +(x -a )|x -a |.(1)若f (0)≥1,求a 的取值范围;(2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a , +∞),直接写出....(不需给出演算步骤)不等式h (x )≥1的解集.【解析】(1)因为f (0)=-a |-a |≥1,所以,-a >0,即a <0.由a 2 ≥1,得a ≤-1. (2)记f (x )的最小值为g (a ), f (x )=2x 2 +(x -a )|x -a |=? ????3(x - a 3)2+2a 2 3,x >a , ①(x +a )2-2a 2 , x ≤a , ② (ⅰ)当a ≥0时,f (-a )=-2a 2 ,由①②知f (x )≥-2a 2 ,此时,g (a )=-2a 2 . (ⅱ)当a <0时,f (a 3)=23a 2.若x >a ,则由①知f (x )≥23 a 2 ;若x ≤a ,则x +a ≤2a <0,由②知f (x )≥2a 2 >23a 2.此时,g (a )=23 a 2.
专题04 函数与导数之零点问题 一.考情分析 零点问题涉及到函数与方程,但函数与方程是两个不同的概念,但它们之间有着密切的联系,方程f (x )=0的解就是函数y =f (x )的图像与x 轴的交点的横坐标,函数y =f (x )也可以看作二元方程f (x )-y =0通过方程进行研究.就中学数学而言,函数思想在解题中的应用主要表现在两个方面: ①是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题:②是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性 质,达到化难为易,化繁为简的目的. 许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决.函数与方程的思想是中学数学的基本思想,也是各地模考和历年高考的重点. 二.经验分享 1.确定函数f (x )零点个数(方程f (x )=0的实根个数)的方法: (1)判断二次函数f (x )在R 上的零点个数,一般由对应的二次方程f (x )=0的判别式Δ>0,Δ=0,Δ<0来完成;对于一些不便用判别式判断零点个数的二次函数,则要结合二次函数的图象进行判断. (2)对于一般函数零点个数的判断,不仅要用到零点存在性定理,还必须结合函数的图象和性质才能确定,如三次函数的零点个数问题. (3)若函数f (x )在[a ,b ]上的图象是连续不断的一条曲线,且是单调函数,又f (a )·f (b )<0,则y =f (x )在区间(a ,b )内有唯一零点. 2.导数研究函数图象交点及零点问题 利用导数来探讨函数)(x f y =的图象与函数)(x g y =的图象的交点问题,有以下几个步骤: ①构造函数)()()(x g x f x h -=; ②求导)('x h ;
【最新】《函数与导数》专题 一、选择题 1.三个数0.20.4 0.44,3,log 0.5的大小顺序是 ( ) A .0.40.2 0.43<4log 0.5< B .0.40.2 0.43
函数与导数小题专题训练 班级 姓名 1.对二次函数2 ()f x ax bx c =++(a 为非零常数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是( ) A .1-是()f x 的零点 B .1是()f x 的极值点 C .3是()f x 的极值 D. 点(2,8)在曲线()y f x =上 2.下列关于函数()sin f x x x =+图象的描述错误的是( ) A.图象关于原点对称 B.图象有无数个对称中心 C.图象有无数条对称轴 D.图象与x 轴只有一个交点 3.设二次函数2()f x x bx c =++,{|(),}A x f x x x R ==∈, {|(()),}B x f f x x x R ==∈, 如果A 中只含有1个元素,则( ) .A A B ? .B B A ? .C A B = .D A B ?=Φ 4.已知,x y ∈R ,若y x y x cos cos ->+,则下面式子一定成立的是( ) A .0x y +< B .0>+y x C .0>-y x D .0x y -< 5. 设函数()f x 在R 上的导函数为()'f x ,且()()22'f x xf x x +>, 下面的不等式在R 上恒成立的是 ( ) A.()0f x > B.()0f x < C. ()f x x > D.()f x x < 6.设函数()f x 的定义域为R,00(0)x x ≠是()f x 的极大值点,以下结论一定正确的( ) A .0,()()x R f x f x ?∈≤ B .0x -是()f x -的极小值点 C . 0x -是()f x -的极小值点 D .0x -是()f x --的极小值点 7. 已知函数()f x 与()f x '的图像如下图所示, 则函数()()x f x g x e =的递减区间为( ) A .()0,4 B .()4,1,,43??-∞ ??? C .40,3?? ??? D .()()0,1,4,+∞
专题03 函数与导数 1.(2020?北京卷)已知函数()21x f x x =--,则不等式()0f x >的解集是( ). A . (1,1)- B . (,1)(1,)-∞-+∞ C . (0,1) D . (,0)(1,)-∞?+∞ 【答案】D 【解析】作出函数2x y =和1y x =+的图象,观察图象可得结果. 【详解】因为()21x f x x =--,所以()0f x >等价于21x x >+, 在同一直角坐标系中作出2x y =和1y x =+的图象如图: 两函数图象的交点坐标为(0,1),(1,2),不等式21x x >+的解为0x <或1x >. 所以不等式()0f x >的解集为:()(),01,-∞?+∞.故选:D. 【点睛】本题考查了图象法解不等式,属于基础题. 2.(2020?北京卷)函数1 ()ln 1 f x x x =++的定义域是____________. 【答案】(0,)+∞ 【解析】根据分母不为零、真数大于零列不等式组,解得结果. 【详解】由题意得0 10 x x >?? +≠?,0x ∴>故答案为:(0,)+∞ 【点睛】本题考查函数定义域,考查基本分析求解能力,属基础题. 3.(2020?北京卷)已知函数2 ()12f x x =-. (Ⅰ)求曲线()y f x =的斜率等于2-的切线方程; (Ⅱ)设曲线()y f x =在点(,())t f t 处的切线与坐标轴围成的三角形的面积为()S t ,求()S t 的最小值. 【答案】(Ⅰ)2130x y +-=,(Ⅱ)32.
【解析】(Ⅰ)根据导数的几何意义可得切点的坐标,然后由点斜式可得结果; (Ⅱ)根据导数的几何意义求出切线方程,再得到切线在坐标轴上的截距,进一步得到三角形的面积,最后利用导数可求得最值. 【详解】(Ⅰ)因为()212f x x =-,所以()2f x x '=-, 设切点为()00,12x x -,则022x -=-,即01x =,所以切点为()1,11, 由点斜式可得切线方程:()1121y x -=--,即2130x y +-=. (Ⅱ)显然0t ≠, 因为()y f x =在点( )2 ,12t t -处的切线方程为:()()2 122y t t x t --=--, 令0x =,得2 12y t =+,令0y =,得2122t x t +=,所以()S t =()221121222||t t t +?+?, 不妨设0t >(0t <时,结果一样),则()423241441144 (24)44t t S t t t t t ++==++, 所以()S t '=422 2211443(848)(324)44t t t t t +-+-=222 22 3(4)(12)3(2)(2)(12)44t t t t t t t -+-++== , 由()0S t '>,得2t >,由()0S t '<,得02t <<, 所以()S t 在()0,2上递减,在()2,+∞上递增,所以2t =时,()S t 取得极小值, 也是最小值为()1616 2328 S ?= =. 【点睛】本题考查了利用导数的几何意义求切线方程,考查了利用导数求函数的最值,属于中档题. 4.(2020?全国1卷)函数43()2f x x x =-的图像在点(1 (1))f ,处的切线方程为( ) A. 21y x =-- B. 21y x =-+ C. 23y x =- D. 21y x =+ 【答案】B 【解析】求得函数()y f x =的导数()f x ',计算出()1f 和()1f '的值,可得出所求切线的点斜式方程,化简即可. 【详解】 ()432f x x x =-,()3246f x x x '∴=-,()11f ∴=-,()12f '=-,
专题强化训练(十五) 函数与导数 一、选择题 1.[2019·全国卷Ⅱ]若a >b ,则( ) A .ln(a -b )>0 B .3a <3b C .a 3 -b 3 >0 D .|a |>|b | 解析:通解:由函数y =ln x 的图象(图略)知,当0<a -b <1时,ln(a -b )<0,故A 不正确;因为函数y =3x 在R 上单调递增,所以当a >b 时,3a >3b ,故B 不正确;因为函数 y =x 3在R 上单调递增,所以当a >b 时,a 3>b 3,即a 3-b 3>0,故C 正确;当b <a <0时, |a |<|b |,故D 不正确.故选C. 优解:当a =0.3,b =-0.4时,ln(a -b )<0,3a >3b ,|a |<|b |,故排除A ,B ,D ,故选C. 答案:C 2.[2019·唐山模拟]设函数f (x )=x (e x +e -x ),则f (x )( ) A .是奇函数,且在(0,+∞)上是增函数 B .是偶函数,且在(0,+∞)上是增函数 C .是奇函数,且在(0,+∞)上是减函数 D .是偶函数,且在(0,+∞)上是减函数 解析:通解:由条件可知,f (-x )=(-x )(e -x +e x )=-x (e x +e -x )=-f (x ),故f (x )为奇函数.f ′(x )=e x +e -x +x (e x -e -x ),当x >0时,e x >e -x ,所以x (e x -e -x )>0,又e x +e -x >0,所以f ′(x )>0,所以f (x )在(0,+∞)上是增函数,故选A. 优解:根据题意知f (-1)=-f (1),所以函数f (x )为奇函数.又f (1) 函数与导数二轮复习建议 金陵中学 朱骏 函数是高中数学的核心内容,因而在历年的江苏高考中,函数一直是考查的重点和热点.高考既注重单独考查函数的基础知识,也会突出考查函数与其它知识的综合应用;既考查具体函数的图象与性质,也考查函数思想方法的应用. 下表列出的是《考试说明》对函数部分具体考查要求及2019年~2019年四年江苏高考 基本题型一:函数性质的研究 例1(2019年江西理改)若f (x )= 1 log(2x +1) ,则f (x )的定义域为____________. ' 【解析】由???2x +1>0log(2x +1)>0 ,解得?????x >-1 2x <0 ,故-12<x <0,答案为(-1 2,0). 说明:以函数定义域为载体,考查对数函数的图象与性质. 例2(2019年江苏)设函数f (x )=x (e x +a e -x )(x ∈R )是偶函数,则实数a =_______. 【解析】 由g (x )=e x +a e -x 为奇函数,得g (0)=0,解得a =-1;也可以由奇函数的定义解得. 说明:1.函数奇偶性的定义中应关注两点:①定义域关于数0对称是函数具有奇偶性的必要条件;②f (0)=0是定义域包含0的函数f (x )是奇函数的必要条件.2.利用特殊与一般的关系解题是一种非常重要的方法. 变式:若函数f (x )=k -2x 1+k ·2 x (k 为常数)在定义域上为奇函数,则k 的值是_______. 答案:±1. > 例3 设a (0<a <1)是给定的常数,f (x )是R 上的奇函数,且在(0,+∞)上是增函数,若f (1 2 )=0,f (log a t )>0,则t 的取值范围是________. 【解析】 因为f (x )是R 上的奇函数,且在(0,+∞)上是增函数,故f (x )在区间(-∞,0)上也是增函数.画出函数f (x )的草图. 由图得-12<log a t <0或log a t >12,解得t (0,a ) ∪(1,a a ). 说明:1.单调性是函数的局部性质,奇偶性是函数的整体 性质,单调性和奇偶性常常结合到一起考查. 2.函数图象是函数性质的直观载体,“以形辅数”是数形结合思想的重要体现. 例4(2019年江苏卷)已知函数f (x )=???x 2 +1,x ≥0,1, x <0,则满足不等式f (1-x 2 )>f (2x ) 的x 的范围是 . ¥ 【解析】画出函数f (x )的图象,根据单调性,得???1-x 2 >2x , 1-x 2 >0. ,解得 x ∈(-1,2-1). 说明:1.函数单调性是比较大小和解不等式的重要依据,如果把式f (1-x 2 )>f (2x )具体化,需要分类,情形比较复杂,本题对能力要求较高.2.分段函数是高考常考的内容之一,解决相关问题时,应注意数形结合、分类讨论思想的运用. 变式:设偶函数f (x )=log a |x -b |在(-∞,0)上单调递增,则f (a +1)与f (b +2)的大小关系为________________________. 答案:f (a +1)>f (b +2). 例5(2019年江苏)设a 为实数,函数f (x )=2x 2 +(x -a )|x -a |.(1)若f (0)≥1,求a 的取值范围;(2)求f (x )的最小值;@ (3)设函数h (x )=f (x ),x ∈(a , +∞),直接写出.... (不需给出演算步骤)不等式h (x )≥1的解集. 函数导数与不等式专题 2 函数导数与不等式专题 一.利用切线与导数之间的联系解决不等式有关问题 1.(2013年高考四川)已知函数 22,0()ln ,0 x x a x f x x x ?++<=?>?,其中a 是实数. 设11(,())A x f x ,22(,())B x f x 为该函数图象上的两点,且12 x x <. (1)指出函数()f x 的单调区间; (2)若函数()f x 的图象在点,A B 处的切线互相垂直,且20x <,证明:211x x -≥; (3)若函数()f x 的图象在点,A B 处的切线重合,求a 的取值范围. 2.(2014届江西省新余)已知函数x (=, f ln ) x b x ax g. x =a R) ( ) (2∈ - (1)若曲线)(x f与)(x g在公共点)0,1(A处有相同的切线,求实数a、b的值; (2)当1=b时,若曲线)(x f与)(x g在公共点P处有相同的切线,求证:点P唯一; (3)若0>a,1=b,且曲线)(x f与)(x g总存在公切线,求正实数a的最小值. 3 4 二.利用函数的单调性、极值与导数的联系解决有关不等式问题 3.(2014届云南省师大附中)已知函数2()f x x ax =-,()ln g x x =. (1)若()()f x g x ≥对于定义域内的x 恒成立,求实数a 的取值范围; (2)设()()()h x f x g x =+有两个极值点12,x x ,且110,2x ??∈ ??? ,求证:12 3()()ln 24h x h x ->-; 高考数学二轮复习 专题2 函数与导数 教案 文 专题二 函数与导数 【重点知识回顾】 1.函数是高考数学的重点内容之一,函数的观点和思想方法是高中数学的一条重要的主线,选择、填空、解答三种题型每年都有,函数题的身影频现,而且常考常新.以基本函数为背景的综合题和应用题是近几年的高考命题的新趋势.函数的图象也是高考命题的热点之一.近几年来考查导数的综合题基本已经定位到压轴题的位置了. 2.对于函数部分考查的重点为:函数的定义域、值域、单调性、奇偶性、周期性对称性和函数的图象;指数函数、对数函数的概念、图象和性质;应用函数知识解决一些实际问题;导数的基本公式,复合函数的求导法则;可导函数的单调性与其导数的关系,求一些实际问题(一般指单峰函数)的最大值和最小值. 【典型例题】 1.函数的性质与图象 函数的性质是高考考查的重点内容.根据函数单调性和奇偶性的定义,能判断函数的奇偶性,以及函数在某一区间的单调性,从数形结合的角度认识函数的单调性和奇偶性,掌握求函数最大值和最小值的常用方法.函数的图象是函数性质的直观载体,能够利用函数的图象归纳函数的性质.对于抽象函数一类,也要尽量画出函数的大致图象,利用数形结合讨论函数的性质. 例1.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用S1、S2分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是( ) 答案: B A B C D 解析:在选项B 中,乌龟到达终点时,兔子在同一时间的路程比乌龟短. 点评:函数图象是近年高考的热点的试题,考查函数图象的实际应用,考查学生解决问题、分析问题的能力,在复习时应引起重视. 例2.已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,则 1234_________.x x x x +++= 答案:-8 解析:因为定义在R 上的奇函数,满足(4)()f x f x -=-,所以 (4)()f x f x -=-,所以, 由) (x f 为奇函数,所以函数图象关于直线 2x =对称且(0)0f =,由(4)()f x f x -=-知(8)()f x f x -=,所以函数是以8为周期的 周期函数,又因为)(x f 在区间[0,2]上是增函数,所以)(x f 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,不妨设 1234 x x x x <<<, 由对称性知 1212 x x +=-, 344 x x +=. 所以 12341248 x x x x +++=-+=-. 点评:本题综合考查了函数的奇偶性,单调性,对称性,周期性,以及由函数图象解答方程问题,运用数形结合的思想和函数与方程的思想解答问题. 2.函数与解方程、不等式的综合问题 函数与方程、不等式、数列是密切相关的几个部分,通过建立函数模型来解决有关他们的综合问题是高考的考查方向之一,解决该类问题要善于运用转化的思想方法,将问题进行不断转化,构建模型来解决问题. 例2.x 为何值时,不等式()23log log 2 - 专题一高考函数与导数命题动向 高考命题分析 函数是数学永恒的主题,是中学数学最重要的主干知识之一;导数是研究函数的有力工具,函数与导数不仅是高中数学的核心内容,还是学习高等数学的基础,而且函数的观点及其思想方法贯穿于整个高中数学教学的全过程,高考对函数的考查更多的是与导数的结合,发挥导数的工具性作用,应用导数研究函数的性质、证明不等式问题等,体现出高考的综合热点.所以在高考中函数知识占有极其重要的地位,是高考考查数学思想、数学方法、能力和素质的主要阵地. 高考命题特点 函数与导数在高考试卷中形式新颖且呈现出多样性,既有选择题、填空题,又有解答题.其命题特点如下: (1)全方位:近年新课标的高考题中,函数的知识点基本都有所涉及,虽然高考不强调知识点的覆盖率,但函数知识点的覆盖率依然没有减小. (2)多层次:在近年新课标的高考题中,低档、中档、高档难度的函数题都有,且题型齐全.低档难度题一般仅涉及函数本身的内容,诸如定义域、值域、单调性、周期性、图象等,且对能力的要求不高;中、高档难度题多为综合程度较高的试题,或者函数与其他知识结合,或者是多种方法的渗透. (3)巧综合:为了突出函数在中学数学中的主体地位,近年高考强化了函数与其他知识的渗透,加大了以函数为载体的多种方法、多种能力(甚至包括阅读能力、理解能力、表述能力、信息处理能力)的综合程度. (4)变角度:出于“立意”和创设情景的需要,函数试题设置问题的角度和方式也不断创新,重视函数思想的考查,加大了函数应用题、探索题、开放题和信息题的考查力度,从而使函数考题显得新颖、生动、灵活. (5)重能力:以导数为背景与其他知识(如函数、方程、不等式、数列等)交汇命题.利用导数解决相关问题,是命题的热点,而且不断丰富创新.解决该类问题要注意函数与方程、转化与化归、分类讨论等数学思想的应用.综合考查学生分析问题、解决问题的能力和数学素养.函数与导数二轮复习建议
函数导数与不等式专题
高考数学二轮复习 专题2 函数与导数 教案 文
专题一 高考函数与导数命题动向