分布列概念

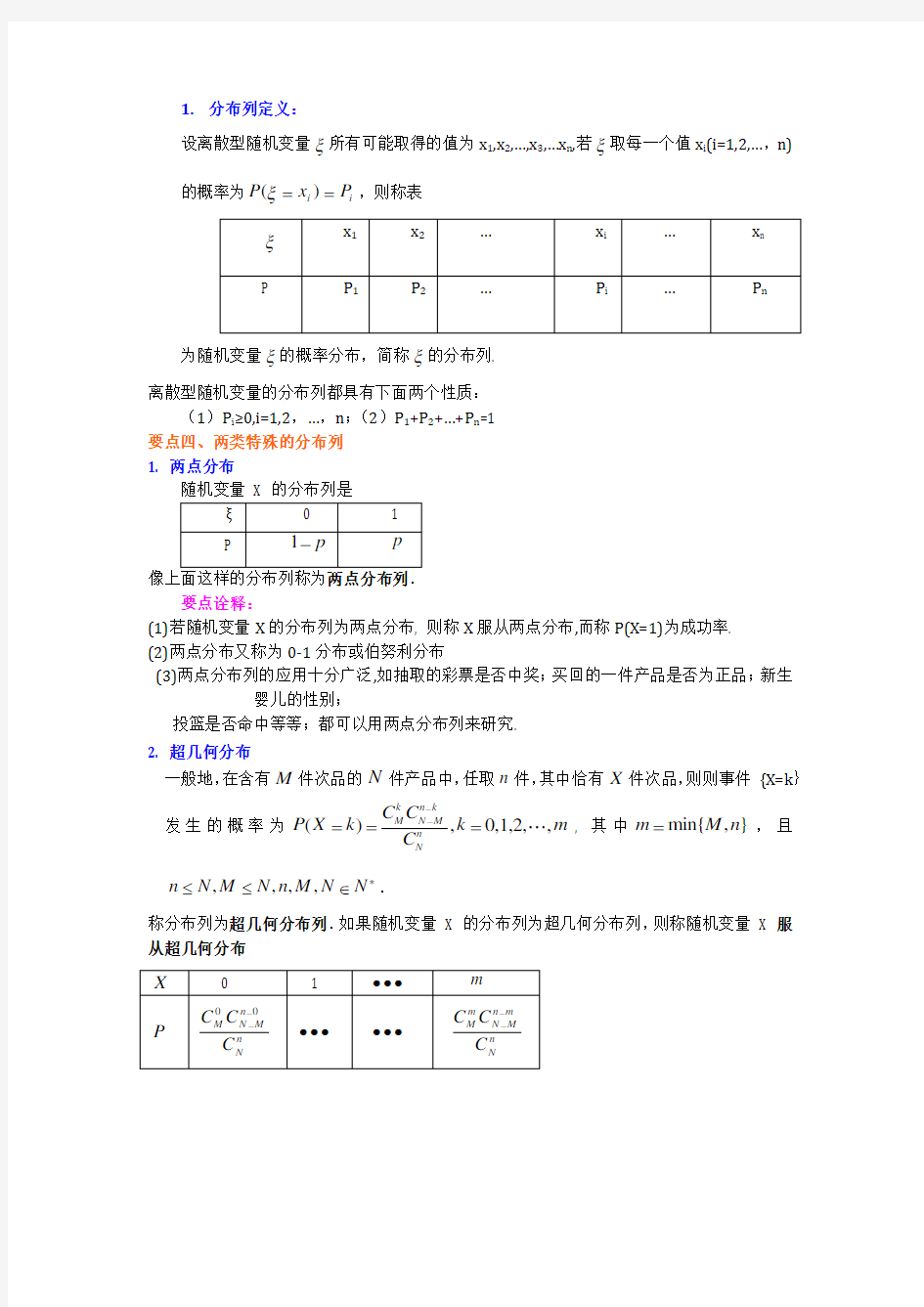
1. 分布列定义：

设离散型随机变量所有可能取得的值为x 1,x 2,…,x 3,…x n ,若取每一个值x i (i=1,2,…，n)的概率为，则称表

为随机变量的概率分布，简称的分布列. 离散型随机变量的分布列都具有下面两个性质：

（1）P i ≥0,i=1,2，…，n ；（2）P 1+P 2+…+P n =1 要点四、两类特殊的分布列 1. 两点分布

像上面这样的分布列称为两点分布列． 要点诠释：

(1)若随机变量X 的分布列为两点分布, 则称X 服从两点分布,而称P(X=1)为成功率. (2)两点分布又称为0-1分布或伯努利分布

(3)两点分布列的应用十分广泛,如抽取的彩票是否中奖；买回的一件产品是否为正品；新生

婴儿的性别；

投篮是否命中等等；都可以用两点分布列来研究. 2. 超几何分布

一般地，在含有件次品的件产品中，任取件，其中恰有件次品，则则事件 {X=k ｝

发生的概率为, 其中，且

．

称分布列为超几何分布列．如果随机变量 X 的分布列为超几何分布列，则称随机变量 X 服从超几何分布

ξξi i P x P ==)(ξξξM N n X (),0,1,2,,k n k

M N M

n

N

C C P X k k m C --===min{,}m

M n =,,,,n N M N n M N N *≤≤∈

要点一、条件概率的概念 1.定义

设、为两个事件，且，在已知事件发生的条件下，事件B 发生的概率叫做条件概率。用符号表示。

读作：发生的条件下B 发生的概率。

要点诠释

在条件概率的定义中，事件A 在“事件B 已发生”这个附加条件下的概率与没有这个附加条件的概率是不同的，应该说，每一个随机试验都是在一定条件下进行的．而这里所说的条件概率，则是当试验结果的一部分信息已知，求另一事件在此条件下发生的概率．

2．P （A ｜B ）、P （AB ）、P （B ）的区别

P （A ｜B ）是在事件B 发生的条件下，事件A 发生的概率。 P （AB ）是事件A 与事件B 同时发生的概率，无附加条件。 P （B ）是事件B 发生的概率，无附加条件． 它们的联系是：． 要点诠释

一般说来，对于概率P(A|B)与概率P(A)，它们都以基本事件空间Ω为总样本，但它们取概率的前提是不相同的。概率P(A)是指在整个基本事件空间Ω的条件下事件A 发生的可能性大小，而条件概率P(A|B)是指在事件B 发生的条件下，事件A 发生的可能性大小。

例如，盒中球的个数如下表。从中任取一球，记A=“取得蓝球”，B=“取得玻璃球”。基本事件空间Ω包含的样本点总数为16，事件A 包含的样本点总数为11，故。

如果已知取得玻璃球的条件下取得蓝球的概率就是事件B 发生的条件下事件A 发生的条件概率，那么在事件B 发生的条件下可能取得的样本点总数应为“玻璃球的总数”，即把样本空间压缩到玻璃球全体。而在事件B 发生的条件下事件A 包含的样本点数为蓝玻璃球数，故。 要点二、条件概率的公式

A B ()0P A >A (|)P B A (|)P B A A ()

(|)()

P AB P A B P B =11()16

P A =

42(|)63

P A B =

=

1．计算事件B 发生的条件下事件A 发生的条件概率，常有以下两种方式： ①利用定义计算．

先分别计算概率P （AB ）及P （B ），然后借助于条件概率公式求解． ②利用缩小样本空间的观点计算．

在这里，原来的样本空间缩小为已知的条件事件B ，原来的事件A 缩小为事件AB ，从而，即：，此法常应用于古

典概型中的条件概率求解． 要点诠释

概率P(B|A)与P(AB)的联系与区别： 联系：事件A ，B 都发生了。 区别：

①在P(B|A)中，事件A ，B 发生有时间上的差异，事件A 先发生事件B 后发生；在P(AB)中，事件A ，B 同时发生；

②基本事件空间不同在P(B|A)中，事件A 成为基本事件空间；在P(AB)中，基本事件空间仍为原基本事件空间。 2．条件概率公式的变形． 公式揭示了P （B ）、P （A ｜B ）、P （AB ）的关系，常常用于知二求一，即要熟练应用它的变形公式如，若P （B ）＞0，则P （AB ）=P （B ）·P （A ｜B ），该式称为概率的乘法公式． 要点诠释

条件概率也是概率，所以条件概率具有概率的性质．如： ①任何事件的条件概率取值在0到1之间；

②必然事件的条件概率为1，不可能事件的条件概率为0； ③条件概率也有加法公式：

P （B ∪C ｜A ）=P （B ｜A ）+P （C ｜A ），

其中B 和C 是两个互斥事件． 要点三、相互独立事件 1.定义：

事件（或）是否发生对事件（或）发生的概率没有影响，即，这样的两个事件叫做相互独立事件。

()

(|)()

P AB P A B P B =(|)AB P A B B =

包含的基本事件数包含的基本事件数()

(|)()

n AB P B A n A =()

(|)()

P AB P A B P B =

A B B A (|)()P B A P B =

若与是相互独立事件，则与，与，与也相互独立。 2．相互独立事件同时发生的概率公式：

对于事件A 和事件B ，用表示事件A 、B 同时发生。 （1）若与是相互独立事件，则； （2）若事件相互独立，那么这个事件同时发生的概率，等于每个事件

发生的概率的积，

即：。

要点诠释

（1）P （AB ）=P （A ）P （B ）使用的前提是A 、B 为相互独立事件，也就是说，只有相互独立的两个事件同时发生的概率，才等于每个事件发生的概率的积．

（2）两个事件、相互独立事件的充要条件是。 3．相互独立事件与互斥事件的比较

互斥事件与相互独立事件是两个不同的概念，它们之间没有直接关系。

互斥事件是指两个事件不可能同时发生，而相互独立事件是指一个事件是否发生对另一个事件发生的概率没有影响。

一般地，两个事件不可能既互斥又相互独立，因为互斥事件是不可能同时发生的，而相互独立事件是以它们能够同时发生为前提的。相互独立事件同时发生的概率等于每个事件发生的概率的积,这一点与互斥事件的概率和也是不同的。 4. 几种事件的概率公式的比较

已知两个事件A ，B ，它们发生的概率为P （A ），P （B ），将A ，B 中至少有一个发生记为事件A+B ，都发生记为事件A·B ，都不发生记为事件A B ?，恰有一个发生记为事件，至多有一个发生记为事件，则它们的概率间的关系如下表所示：

要点二、独立重复试验的概率公式

A B A B A B A B A B ?A B ()()()P A B P A P B ?=?12,,,n A A A n 1212()()()()n n P A A A P A P A P A ???=???A B ()()()P A B P A P B ?=?A B A B ?+?A B A B A B ?+?+?

1.定义

如果事件A 在一次试验中发生的概率为P ，那么n 次独立重复试验中，事件A 恰好发生k 次的概率为：

（k=0，1，2，…，n ）． 令得，在n 次独立重复试验中，事件A 没有发生的概率为．．．．．．．．

令得，在n 次独立重复试验中，事件A 全部发生的概率为．．．．．．．．

。

要点诠释：

1. 在公式中，n 是独立重复试验的次数，p 是一次试验中某事件A 发生的概率，k 是在n 次独立重复试验中事件A 恰好发生的次数，只有弄清公式中n ，p ，k 的意义，才能正确地运用公式．

2. 独立重复试验是相互独立事件的特例，就像对立事件是互斥事件的特例一样，只是有“恰好”字样的用独立重复试验的概率公式计算更方便．

要点三、n 次独立重复试验常见实例：

1.反复抛掷一枚均匀硬币

2.已知产品率的抽样

3.有放回的抽样

4.射手射击目标命中率已知的若干次射击 要点诠释：

抽样问题中的独立重复试验模型：

①从产品中有放回地抽样是独立事件，可按独立重复试验来处理； ②从小数量的产品中无放回地抽样不是独立事件，只能用等可能事件计算；

③从大批量的产品中无放回地抽样，每次得到某种事件的概率是不一样的，但由于差别太小，相当于是独立事件，所以一般情况下仍按独立重复试验来处理。

要点四、离散型随机变量的二项分布 1. 定义：

在一次随机试验中，事件A 可能发生也可能不发生，在次独立重复试验中事件A 发生的次数是一个离散型随机变量．如果在一次试验中事件A 发生的概率是，则此事件不发生的概率为，那么在

次独立重复试验中事件A 恰好发生次的概率是

，（）． ()(1)

k k n k

n n P k C p p -=-0k =00(0)(1)(1)n n

n n P C p p p =-=-k n =0()(1)n n n n n P n C p p p =-=n ξp 1q p =-n k ()()k k n k

n n n P k P k C p q

-===ξ0,1,2,...,k n =

于是得到离散型随机变量的概率分布如下：

由于表中第二行恰好是二项展开式

中各对应项的值，

所以称这样的随机变量服从参数为

，的二项分布，记作．

要点诠释：

判断一个随机变量是否服从二项分布，关键有三： 其一是独立性。即每次试验的结果是相互独立的； 其二是重复性。即试验独立重复地进行了n 次；

其三是试验的结果的独特性。即一次试验中，事件发生与不发生，二者必居其一。 2．如何求有关的二项分布

（1）分清楚在n 次独立重复试验中，共进行了多少次重复试验，即先确定n 的值，然后确定在一次试验中某事件A 发生的概率是多少，即确定p 的值，最后再确定某事件A 恰好发生了多少次，即确定k 的值；

（2）准确算出每一种情况下，某事件A 发生的概率；

（3）用表格形式列出随机变量的分布列。 要点一、离散型随机变量的期望 1.定义：

一般地，若离散型随机变量的概率分布为

则称…… 为的均值或数学期望，简称期望． 要点诠释：

（1）均值（期望）是随机变量的一个重要特征数，它反映或刻画的是随机变量取值的平均水平．

（2）一般地，在有限取值离散型随机变量的概率分布中，令…，则有…，…，所以的数学期望又称为平均数、均值。

（3）随机变量的均值与随机变量本身具有相同的单位．

ξ0

11100)(q p C q p C q p C q p C p q n n n k n k k n n n n n n +++++=+-- ξn p ~(,)B n p ξξ=ξE +11p x +22p x ++n n p x ξξ=1p =2p n p ==

1p =2p n p n 1=

==ξE +1(x +2x n

x n 1

)?+ξ

2．性质：

①；

②若(a 、b 是常数)，是随机变量，则也是随机变量，有

；

的推导过程如下：：

的分布列为

于是……

＝……)……)＝ ∴。

要点二：离散型随机变量的方差与标准差 1.一组数据的方差的概念：

已知一组数据，，…，，它们的平均值为，那么各数据与的差的平方的平均数

＋＋…＋叫做这组数据的方差。 2.离散型随机变量的方差：

一般地，若离散型随机变量的概率分布为

则称＝＋＋…＋＋…称为随机变量的方差，式中的是随机变量的期望．

的算术平方根叫做随机变量的标准差，记作．

()E E E ξηξη+=+b a +=ξηξηb aE b a E +=+ξξ)(b aE b a E +=+ξξ)(η=ηE ++11)(p b ax ++22)(p b ax ()i i ax b p ++++11(p x a +22p x i i x p ++++1(p b +2p i p ++b aE +ξb aE b a E +=+ξξ)(1x 2x n x x x [1

2n

S =

21)(x x -22)(x x -])(2x x n -ξξD 12

1)(p E x ?-ξ22

2)(p E x ?-ξ2()n i x E p ξ-?ξξE ξξD ξD ξσξ

要点诠释：

⑴随机变量的方差的定义与一组数据的方差的定义式是相同的；

⑵随机变量的方差、标准差也是随机变量ξ的特征数，它们都反映了随机变量取值的稳定与波动、集中与离散的程度；方差（标准差）越小，随机变量的取值就越稳定（越靠近平均值）．

⑶标准差与随机变量本身有相同的单位，所以在实际问题中应用更广泛。 3.期望和方差的关系：

4.方差的性质：

若(a 、b 是常数)，是随机变量，则也是随机变量，

；

要点三：常见分布的期望与方差 1、二点分布：

若离散型随机变量服从参数为的二点分布，则 期望 方差

证明：∵,,, ∴

2、二项分布：

若离散型随机变量服从参数为的二项分布，即则 期望 方差 期望公式证明：

∵，

∴

ξξ22()()D E E ξξξ=-b a +=ξηξη2()D D a b a D ηξξ=+=ξp E p ξ=(1).D p p ξ=-(0)P q ξ==(1)P p ξ==01p <<1p q +=01E q p p ξ=?+?=22(0)(1)(1).D p q p p p p ξ=-?+-?=-ξ,n p ~(),B n P ξ，E nP ξ=(1-)D np p ξ=k

n k k n k n k k n q p C p p C k P --=-==)1()(ξ

，

又∵，

∴＋＋…＋＋…＋ ．

3、几何分布：

独立重复试验中，若事件在每一次试验中发生的概率都为，事件第一次发生时所做的试验次数是随机变量，且，，称离散

型随机变量服从几何分布，记作：。

若离散型随机变量服从几何分布，且则 期望 方差 要点诠释：随机变量是否服从二项分布或者几何分布，要从取值和相应概率两个角度去验证。

4、超几何分布：

若离散型随机变量服从参数为的超几何分布，则 期望 要点四：离散型随机变量的期望与方差的求法及应用 1、求离散型随机变量的期望、方差、标准差的基本步骤： ①理解的意义，写出可能取的全部值； ②求取各个值的概率，写出分布列；

001112220

012......n n n k k n k n n n n n n n E C p q C p q C p q k C p q n C p q ξ---=?+?+?++?++?1

1)]!

1()1[()!1()!1()!(!!--=-----?=-?

=k n k

n nC k n k n n k n k n k kC =ξE (np 0011n n C p q

--2111--n n q p C )1()1(111------k n k k n q p C )0

111q p C n n n ---np q p np n =+=-1)(A p A ξ1()(1)k P k p p -ξ==-0,1,2,3,,,

k n =ξ~()()P k k P ξξ==g ，ξ~()()P k k P ξξ==g ，，1

.E p

ξ=

21-p

D p

ξ=

ξ,,N M n ()nM

E N

ξ=

ξξξξ

③根据分布列，由期望、方差的定义求出、、：

.

注意：常见分布列的期望和方差，不必写出分布列，直接用公式计算即可． 2.离散型随机变量的期望与方差的实际意义及应用

① 离散型随机变量的期望，反映了随机变量取值的平均水平；

② 随机变量的方差与标准差都反映了随机变量取值的稳定与波动、集中与离散的程度。方差越大数据波动越大。

③对于两个随机变量和，当需要了解他们的平均水平时，可比较和的大小。 ④和相等或很接近，当需要进一步了解他们的稳定性或者集中程度时，比较和

，方差值大时，则表明ξ比较离散，反之，则表明ξ比较集中．品种的优劣、仪器的

好坏、预报的准确与否、武器的性能等很多指标都与这两个特征数（数学期望、方差）有关． 【典型例题】

正态分布

编稿：赵雷 审稿：李霞

【学习目标】

1. 了解正态分布曲线的特点及曲线所表示的意义。

2. 了解正态曲线与正态分布的性质。 【要点梳理】

要点诠释：

要点一、概率密度曲线与概率密度函数

1．概念：

对于连续型随机变量，位于轴上方，落在任一区间（a ，b]内的概率等于它与轴、直线

与直线所围成的曲边梯形的面积（如图阴影部分）

，这条概率曲线叫做的概率密度曲线，以其作为图象的函数叫做的概率密度函数。

E ξD ξσξ1122n n E x p x p x p ξ=++

++

()()()2

2

2

1122n n D x E p x E p x E p ξ=-ξ+-ξ++-ξ

+

σξ=1ξ2ξ1ξE 2ξE 1ξE 2ξE 1ξD 2ξD X x X x

x a =x b =X ()f x X

2、性质：

①概率密度函数所取的每个值均是非负的。 ②夹于概率密度的曲线与

轴之间的“平面图形”的面积为1

③的值等于由直线，与概率密度曲线、轴所围成的“平面

图形”的面积。 要点二、正态分布

1.正态变量的概率密度函数

正态变量的概率密度函数表达式为：，

（）

其中x 是随机变量的取值；μ为正态变量的期望；是正态变量的标准差. 2．正态分布 （1）定义

如果对于任何实数随机变量满足：，

则称随机变量服从正态分布。记为。

（2）正态分布的期望与方差 若，则的期望与方差分别为：，。

要点诠释：

（1）正态分布由参数和确定。

参数是均值，它是反映随机变量取值的平均水平的特征数，可用样本的均值去估计。是

标准差，它是衡量随机变量总体波动大小的特征数，可以用样本的标准差去估计。 （2）经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用

结果之和，它就服从或近似服从正态分布．

在现实生活中，很多随机变量都服从或近似地服从正态分布．例如长度测量误差；某一地区同年龄人群的身高、体重、肺活量等；一定条件下生长的小麦的株高、穗长、单位面积产量等；正常生产条件下各种产品的质量指标（如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等）

；某地每年七月份的平均气温、

x ()P a X b <

x 22

()2,()(R)

x x x μσμσ?--=∈0,σμ>-∞<<+∞σ,()a b a b

a P a X

b x dx μσ?<≤=?X 2(,)X N μσ2(,)X

N μσX EX μ=2DX σ=μσμσ

平均湿度、降雨量等；一般都服从正态分布．

要点三、正态曲线及其性质：

1. 正态曲线

如果随机变量X 的概率密度函数为，其中实数和为

参数（），则称函数的图象为正态分布密度曲线，简称正态曲线。

2．正态曲线的性质： ①曲线位于

轴上方，与轴不相交；

②曲线是单峰的，它关于直线对称； ③曲线在

； ④当时，曲线上升；当时，曲线下降.并且当曲线向左、右两边无限延伸时，以x 轴为渐近线，向它无限靠近.

⑤曲线与

轴之间的面积为1；

⑥决定曲线的位置和对称性；

当一定时，曲线的对称轴位置由确定；如下图所示，曲线随着的变化而沿轴

平移。

⑦确定曲线的形状；

当一定时，曲线的形状由确定。越小，曲线越“高瘦”，表示总体的分布越集中；

22

()2()(R)x f x x μσ--=∈μσ0,σμ>-∞<<+∞()f x x x x μ=μ=x μx x μσμμx σμσσ

越大，曲线越“矮胖”，表示总体的分布越分散。如下图所示。

要点诠释：

性质①说明了函数具有值域（函数值为正）及函数的渐近线（x 轴）．性质②并且说明了函数具有对称性；性质③说明了函数在x=时取最值；性质⑦说明越大，总体分布越分散，越小，总体分布越集中． 要点四、求正态分布在给定区间上的概率 1. 随机变量取值的概率与面积的关系

若随机变量ξ服从正态分布，那么对于任意实数a 、b （a ＜b ），当随机变量ξ在区间（a ，b]上取值时，其取值的概率与正态曲线与直线x=a ，x=b 以及x 轴所围成的图形的面积相等．如图（1）中的阴影部分的面积就是随机变量孝在区间（a ，b]上取值的概率．

一般地，当随机变量在区间（－∞，a ）上取值时，其取值的概率是正态曲线在x=a 左侧以及x 轴围成图形的面积，如图（2）．随机变量在（a ，+∞）上取值的概率是正态曲线在x=a 右侧以及x 轴围成图形的面积，如图（3）．

根据以上概率与面积的关系，在有关概率的计算中，可借助与面积的关系进行求解．

2、正态分布在三个特殊区间的概率值：

； ； 。

上述结果可用下图表示：

σμσσ2(,)N μ

σ()0.683P X μσμσ-<≤+=(22)0.954P X μσμσ-<<+=(33)0.997P X μσμσ-<≤+=

要点诠释：

若随机变量服从正态分布，则落在内的概率约为

0.997，落在之外的概率约为0.003，一般称后者为小概率事件，并认为在一次试验中，小概率事件几乎不可能发生。

一般的，服从于正态分布的随机变量通常只取之间的值，简称为原则。

3、求正态分布在给定区间上的概率方法 （1）数形结合，利用正态曲线的对称性及曲线与

轴之间面积为1。

①正态曲线关于直线对称，与对称的区间上的概率相等。 例如； ②； ③若，则。

(2)利用正态分布在三个特殊区间内取值的概率： ①； ②； ③。 【典型例题】

X 2

(,)N μσX (3,3)μσμσ-+(3,3)μσμσ-+2(,)N μσX (3,3)μσμσ-+3σx x μ=x μ=()()P X P X μσμσ<-=>+()1()P X a P X a <=-≥b μ<1()

()2

P b X b P X b μμ--<<+<=

()0.6826P X μσμσ-<≤+=(22)0.9544P X μσμσ-<<+=(33)0.9974P X μσμσ-<≤+=

正态分布的性质及实际应用举例

华北水利水电学院 正态分布的性质及实际应用举例 课程名称：概率论与数理统计 专业班级：电气工程及其自动化091班 成员组成：姓名：邓旗学号： 2 姓名：王宇翔学号：1 姓名：陈涵学号：2 联系方式： 2012年5月24日

1 引言：正态分布（normal distribution）又名高斯分布（Gaussian distribution），是一个在数学、物理及工程等领域都非常重要的概率分布，在 统计学的许多方面有着重大的影响力。本文就从正态分布的实际性质应用举例等各个方面进行简单阐述并进行探讨，使同学们能够对所掌握的知识有更清楚地认识。 2 研究问题及成果： 正态分布性质； 3原则及标准正态分布； 实际应用举例说明 摘要：正态分布是最重要的一种概率分布。正态分布概念是由德国数学家与天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学研究，故此正态分布又称高斯分布。在许多实际问题中遇到的随机变量都服从或近似服从正态分布：在生产中，产品的质量指标，如电子管的使用寿命，电容器的电容量，零件的尺寸。铁水含磷量，纺织品的纤度和强度等一般都服从正态分布。在测量中，如大地测量，天平称量物体，化学分析某物之中某元素的含量等，测量结果一般服从正态分布。在生物学中，同一群体的某种特性指标，如某地同龄儿童的身高，体重，肺活量，在一定条件下生长的农作物的产量等一般服从正态分布。在气象学中，某地每年7月份的平均气温，平均温度以及降水量等一般也服从正态分布。总之。正态分布广泛存在于自然现象，社会现象以及生产，科学技术的各个领域中。本文就从正态分布的实际性质应用举例等各个方面进行简单阐述并进行探讨，使同学们能够对所掌握的知识有更清楚地认识。 关键词：正态分布 The nature of the normal distribution and the example of practical application

二项分布概念与图表和查表方法

二项分布概念及图表 二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。 目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例

）。如果进行次伯努利试验，取得成功次数为的概率可用下面的二项分布概率公式来描述： 二项分布公式 二项分布公式 P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。

二项分布

以用于可靠性试验。可靠性试验常常是投入n个相同的式样进行试验T小时，而只允许k个式样失败，应用二项分布可以得到通过试验的概率。

正面向上的平均次数为5次(μ= np=)，正面向上的散布程度为√10×（1/2）×（1/2)= 1.58(次)，这是根据理论的计算，而在实际试验中，有的人可得10个正面向上，有人得9个、8个……，人数越多，正面向上的平均数越接近5，分散程度越接近1.58。 图形特点 （1）当（n+1）p不为整数时，二项概率P{X=k}在k=[(n+1)p]时达到最大值； （2）当（n+1）p为整数时，二项概率P{X=k}在k=(n+1)p和k=(n+1)p-1时达到最大值。 注：[x]为不超过x的最大整数。 应用条件 1．各观察单位只能具有相互对立的一种结果，如阳性或阴性，生存或死亡等，属于两分类资料。 2．已知发生某一结果（阳性）的概率为π，其对立结果的概率为1-π，实际工作中要求π是从大量观察中获得比较稳定的数值。 二项分布公式 3．n次试验在相同条件下进行，且各个观察单位的观察结果相互独立，即每个观察单位的观察结果不会影响到其他观察单位的结果。如要求疾病无传染性、无家族性等。 应用实例 二项分布在心理与教育研究中，主要用于解决含有机遇性质的问题。所谓机遇问题，即指在实验或调查中，实验结果可能是由猜测而造成的。比如，选择题目的回答，划对划错，可能完全由猜测造成。凡此类问题，欲区分由猜测而造成的结果与真实的结果之间的界限，就要应用二项分布来解决。下面给出一个例子。 已知有正误题10题，问答题者答对几题才能认为他是真会，或者说答对几题，才能认为不是出于猜测因素?

正态分布的概念

1. 正态分布的概念 随机变量X 的概率密度2()2(),()x f x x μσ--=-∞<<+∞， 称X 服从正态分布， 记作),(~2σμN X 。 标准正态分布(0,1)N ，其概率密度22 (),()x x x ?- =-∞<<+∞，分布函数 为 2 2 ()t x x e dt φ- -∞ = 。 2. 设 ) ,(~2σμN X ， 则 {}x P X x μφσ-?? ≤= ? ?? ， {}b a P a X b μμφφσσ--???? <≤=- ? ????? ，()x φ的数值有表可查，特别有 (0)0.5,()1,()1()x x φφφφ=+∞=-=-。 3. 设),(~2σμN X ，则2(),()E X D X μσ==。 4. 设),(~2σμN X ，则),(~22σμb b a N bX a Y ++=)0(≠b 。 若),(~211σμN X ，),(~2 22σμN Y ，X 与Y 相互独立，则 ),(~2 22121σσμμ+++N Y X 。 若12,,,n X X X 相互独立，),,2,1)(,(~2n i N X i i i =σμ，则 ∑∑∑===n i n i n i i i i n i i i c c c c c N X c 1 1 21221 )(,(~为常数） ，，， σμ 5. 二维随机变量(,)X Y 服从二维正态分布，记作 ），，，，（），（γσσμμ222121~N Y X ，其中12(),() E X E Y μμ==， 2212(),()D X D Y σσ==，(,)r R X Y =。 设(,)X Y 服从二维正态分布，则X 与Y 相互独立的充分必要条件是0r =。 6. 当n 充分大时，独立同分布的随机变量12,,,n X X X 的和1n i i X =∑近似服从正态 分布2(,)N n n μσ。 特别是当n 充分大时，若相互独立的随机变量12,,,n X X X 都服从“0-1”分

二项分布

【模块标题】二项分布 【模块目标】★★★★★☆ 迁移 【模块讲解】 知识回顾： 1.定义：在n 次独立重复试验中，事件A 发生的次数ξ是一个随机变量，其所有可能取的值为0,1,2,,n ???， 并且()() 1n k k k n P k C p p ξ?==?（其中0,1,2,,k n =???），即分布列为 ()n p B ，2.二项分布的期望与方差：若()n p B ξ ，，则()=E np ξ，()()1D np p ξ=? 【教材内容1】利用二项分布的计算式求解问题(3星) <讲解指南> 一.题型分类： 1.二项分布基本概念题型； 2.根据二项分布求某一事件的概率；

3.根据二项分布求某一范围的概率； 4.根据二项分布求EX 、DX 及其变形； 5.根据EX 求概率 p 及某一事件的概率 6.根据EX 和DX 求np 二.方法步骤： 1.根据条件判断是否服从二项分布； 2.根据二项分布的性质列出相应的分布列 3. 根据二项分布的公式求解数学期望及方差； 三.难点： 本节的难点在于根据二项分布的公式进行某一事件或某一范围求概率的题型，需要教会学生求解二项分布里面的参数，然后套用公式进行求解。 <题目讲解> 例1. 下列随机变量ξ服从二项分布的是（ ）。 （1）随机变量ξ表示重复抛掷一枚骰子n 次中出现点数是3的倍数的次数； （2）某射手击中目标的概率为0.9，从开始射击到击中目标所需的射击次数ξ； （3）有一批产品共有N 件，其中M 件为次品，采用有放回抽取方法，ξ表示n 次抽取中出现次品的件数 ()M N ＜； （4）有一批产品共有N 件，其中M 件为次品，采用不放回抽取方法，ξ表示n 次抽取中出现次品的件数()M N ＜ A. ()2 ()3 B. ()1 ()4 C. ()3 ()4 D. ()1 ()3 练1. 下面随机变量 X 的分布列不属于二项分布的是（ ） A 、据中央电视台新闻联播报道，一周内在某网站下载一次数据，电脑被感染某种病毒的概率是0.65，设 在这一周内，某电脑从该网站下载数据n 次中被感染这种病毒的次数为 X B 、某射手射击击中目标的概率为p ，设每次射击是相互独立的，从开始射击到击中目标所需要的射击次

正态分布的概念和特征

第一节正态分布的概念和特征 一、正态分布的概念 由表1.1的频数表资料所绘制的直方图，图3.1（1）可以看出，高峰位于中部，左右两侧大致对称。我们设想，如果观察例数逐渐增多，组段不断分细，直方图顶端的连线就会逐渐形成一条高峰位于中央（均数所在处），两侧逐渐降低且左右对称，不与横轴相交的光滑曲线图3.1（3）。这条曲线称为频数曲线或频率曲线，近似于数学上的正态分布（normal distribution）。由于频率的总和为100%或1，故该曲线下横轴上的面积为100%或1。 图3.1频数分布逐渐接近正态分布示意图 为了应用方便，常对正态分布变量X作变量变换。 （3.1） 该变换使原来的正态分布转化为标准正态分布 (standard normal distribution)，亦称u分布。u被称为标准正态变量或标准正态离差（standard normal deviate）。 二、正态分布的特征： 1．正态曲线（normal curve）在横轴上方均数处最高。

2．正态分布以均数为中心，左右对称。 3．正态分布有两个参数，即均数和标准差。是位置参数，当固定不变时，越大，曲线沿横轴越向右移动；反之，越小，则曲线沿横轴越向左移动。 是形状参数，当固定不变时，越大，曲线越平阔；越小，曲线越尖峭。 通常用表示均数为，方差为的正态分布。用N（0，1）表示标准正态分布。 4．正态曲线下面积的分布有一定规律。 实际工作中，常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数，以便估计该区间的例数占总例数的百分数（频数分布）或观察值落在该区间的概率。正态曲线下一定区间的面积可以通过附表1求得。对于正态或近似正态分布的资料，已知均数和标准差，就可对其频数分布作出概约估计。 查附表1应注意：①表中曲线下面积为-∞到u的左侧累计面积；②当已知μ、σ和X时先按式（3.1）求得u值，再查表，当μ、σ未知且样本含量n足够大时，可用样本均数和标准差S分别代替μ和σ，按式求得u 值，再查表；③曲线下对称于0的区间面积相等，如区间（-∞，-1.96）与区间（1.96，∞）的面积相等，④曲线下横轴上的总面积为100%或1。 正态分布曲线下有三个区间的面积应用较多，应熟记：①标准正态分布时区间（-1,1）或正态分布时区间（μ-1σ,μ+1σ）的面积占总面积的68.27%；②标准正态分布时区间（-1.96,1.96）或正态分布时区间（μ-1.96σ,μ+1.96σ）的面积占总面积的95%；③标准正态分布时区间（-2.58,2.58）或正态分布时区间（μ-2.58σ,μ+2.58σ）的面积占总面积的99%。如图3.2所示。 图3.2 正态曲线与标准正态曲线的面积分布

数字地图制图复习

简述数字地图、电子地图、模拟地图的基本概念与差别？数字地图是在一定坐标系统内具有确定坐标和属性标志的制图要素和离散数据在计算机可识别的存储介质上概括而有序的集合。具有计算机可识别性、可量算性、可分析性、可传输性及数字与模拟地图的互转性，是生产电子地图和纸质地图的基础。电子地图：是数字地图在计算机屏幕上的符号化显示，是计算机条件下的空间信息可视化，是人眼直接可视的，包括二维、三维电子地图。模拟地图：传统地图一般绘制印刷在布匹、木板、石板铜板和纸张等介质上，这种地图称为模拟地图。 数字地图的特性：可识别性：指计算机可识别，而目视一般不可识别；可量算：计算可进行几何度量，长度、面积、方位等；可分析性：分析的深度取决于数据结构和数据模型；可转化性：是数字地图与模拟地图之间能够相互转化；可传输性：可借助于当代通讯技术进行远程或近距离传输；存储与显示分离：存储与其显示是分离的； 地图数据的几何变换有哪些类型，各自有什么特征？缩放（比例）、对称、旋转、平移、投影、错切、二维组合等各种变换。平移变换用于移动坐标系的原点变换前后的坐标必须满足，。旋转变换指图形的放置围绕原点旋转θ角，且逆时针为正，顺时针为负。平移和旋转变换都保持二维空间上目标变换时的距离及大小不变，但缩放变换会改变坐标系的单位长度（距离）。 顺序存储、随机存储、链式存储的比较链式存储在某些特定操作上具有比顺序存储和随机存储更多的优点。它能很容易地处理因节点的绝对位置改变带来的变化。尽管一个节点在表中的绝对位置改变了，但它的物理存储位置可以保持不变，只是节点的属性值即地址要改变。随机存储也允许节点的存储位置保持不变，但要改变其指向存储位置的指针。在不改变表中任何节点的绝对位置时，顺序存储和随机存储要优于链式存储。在顺序或随机存储中，可以很容易地访问第j个节点。 DCEL模型的原理? 1.假设C的方向从pN到sN，则与其相邻的多边形RP位于右边，LP位于左边。弧段C是由围绕点sN处的下一个逆时针弧段RC和围绕点pN的下一个逆时针弧段LC界定的边界之内。 2.所谓下一弧段表示了在终结点sN关联的弧段中，该弧段逆时针方向的第一条弧段RC，而所谓上一弧段则表示了在始结点pN关联的弧段中，该弧段逆时针方向的第一条弧段LC。 3.如果沿着多边形RP顺时针移动，那么弧段RC紧位于C后， 4.如果沿着多边形LP顺时针移动，那么LC紧位于C后 路径拓扑模型有哪些，网络拓扑模型有哪些，各自的基本原理?路径拓扑模型有面条模型（面状单元间的边界作为坐标记录下来，没有关于坐标串与单个多边形间关系的相应信息；地理底图的轮廓线可以从这种数据模型中轻易获取）、多边形模型（记录和存储了每个多边形的外轮廓线；很容易标识每个多边形实体，但其存储空间却迅速扩大,因为多边形间的公共边被存储两次）、点位字典模型（该模型是对多边形模型的一个改进，它记录的是各多边形边界上各点的编码ID并构成循环表，同时以数据字典方式记录下各点的坐标值，利用字典就可通过点的编码找到其相应的坐标）、弧段/点位字典模型（表达了多边形与弧段，以及弧段与点的构成和组成关系；在该模型中，每个多边形由弧段的循环表组成，而每条弧段又由一列点组成）。网络拓扑模型有DIME模型（1.要找出所有的DIME段及其左右多边形。 2.这些段按以下顺序排列：第一段的止点是后一段的起点，最后一个段的止点是第一个段的起点，这样便形成了一个循环表。在这个过程中，起、止点是可以按需切换的，以使多边形始终位于每个段的右边。）、POLYVRT模型（将弧段的关系按DIME段给出，弧段的端点被称为结点而不是点）、结点模型（用结点结构来组织这些关系，根据任何一个结点都具有且仅有三个相邻结点，每个结点都具有且仅有三条相关链和与这三条相关链相关的右多边形(按右手法则确定)，在拓扑文件中记录下各结点的三个相邻结点、三条相关链和三个右多边形，以此来实现数据处理时对多边形的操作与检索）、扩展弧段模型（弧段的邻域可加以扩展，从而包含围绕某一结点的下一逆时针弧段的ID。当沿着某一多边形轮廓顺时针方向前进时，这些弧段将依顺序成为下一条弧段。每一弧段的邻域关系包括了第一和最后一个结点，左、右多边形以及相应的左、右弧段(LC和RC)。右弧段依顺序是右多边形的下一条弧段，左弧段依顺序是左多边形的下一条弧段）。 4叉树的基本原理?四叉树分割的基本思想是首先把一幅图像或一幅栅格地图等分成四部分，逐块检查其格网值。四个等分区称为四个子象限，按顺序为左上（NW）、右上（NE）、左下（SW）、右下（SE），可以用树结构表示。如果某个子区的所有格网都含有相同的值，则这个子区就不再往下分割；否则，把这个区域再分割成四个子区，这样递归地分割，直到每个子块都只含有相同的灰度或属性值为止。这就是常规四叉树的建立过程。 数字地图数据采集的方式有哪些？比较各自的优缺点和实用范围?数字遥感数据获取、数字化、野外测量等。数字化具有简便，效率较高，但是精度比野外测量差。 数据测量的尺度有哪4种，各自的特征？定名尺度，顺序尺度，间隔尺度还有比例尺度什么是地图综合，它与数据压缩、比例尺缩放的差别？空间信息数量庞大，类型复杂，因此，在有限的计算机存贮空间与地图的图面上要反映这些庞大而复杂的空间信息，就不得不反映其主要的、本质性的方面，舍弃次要的、非本质性的方面，以确保地图的易读性,满足空间数据库的多尺度表达和GIS的多层次规划、管理与分析决策的需要，这个过程就是地图与GIS综合。数据压缩是指在不丢失信息的前提下，缩减数据量以减少存储空间，提高其传输、存储和处理效率的一种技术方法。或按照一定的算法对数据进行重新组织，减少数据的冗余和存储的空间。比例尺缩放只是指一幅地图的比例尺变大或者缩小，地图的所包含的信息数据并没有变。地图综合与数据压缩都导致信息量的减少，都是为了缩小存储空间和节省计算处理时间而去掉繁杂细节。但数据压缩一般是在无损图解精度的前提下去掉“贡献”小而用插值方法可近似恢复的数据元素，即数据压缩可用数据的插值加密手段进行逆处理，而制图综合不受图解精度约束，被删除或被派生的信息不可逆。 地图综合的过程分为几个阶段？分为三个阶段：综合规则的制定，综合过程的控制，综合结果的评测。 线状要素的综合算法有哪些？各自的基本原理和优缺点？独立算法（它不顾及相邻点之间的几何关系。如选取每第k点法，去掉其它点。还有随机取点法。很难捕捉到特征点，会引起曲线的变形。这种方法只能用于简单的数据压缩，而不能用于真正的地理信息综合。）、局部处理算法（该方法在对顶点选择时顾及到直接相邻诸顶点的特征。算法所产生的变形比独立点算法小。但比后继方法差。）、约束扩展局部处理算法（在线的某段周围定义一个搜索域，并利用距离、角度或点数来搜索更多的相邻点。）、无约束扩展局部处理算法（利用线的复杂度，坐标点的密度、开始点的定位等来搜索相邻的点。）、全局算法（它考虑到整条线或特定线段的特征）、基于自然法则的化简算法（对于任何特定的地图比例尺，就必然有其上地图目标的一个极小尺寸SVO ，在这个尺寸内，所有的细部信息都会丢失）。 可视化和符号化的概念？可视化：是指在人脑中形成对事物的图像,是一个心理处理过程，促使对事物的观察力及建立概念等。科学计算可视化：是通过研制计算机工具、技术和系统，把实验或数值计算获得的大量抽象数据转换为人的视觉可以直接感受的计算机图形图像，从而可进行数据探索和分析。地学相关的可视化：测绘学家的地形图测绘编制，地理学家、地质学家使用的图解，地图学家专题、综合制图等，都是用图形(地图)来表达对地理世界现象与规律的认识和理解。包括地图可视化、地理信息系统(GIS)可视化及其在专业应用领域的可视化。符号化是指将专题数字信息转化为模拟的制图符号。 数据增强的手段？数据增强（给线、面状要素增加细节以改进显示效果或者为没有数据采样的地方进行估值。近似地看作为数据选取和其它综合操作的逆过程）有线性插值，分段拟合（用一段一段的曲线来代替每条线段，而且只在每条线段的端点处才相交。使用分段多项式函数能产生理想的结果），曲线拟合，空间插值。 多边形晕线填充的原理？多边形的晕线填充算法要求代表某值的晕线与起点对齐。相邻区域如果属性值相同，这两个区域的晕线则完全对齐。方法：通过固定晕线位置，使之同X 轴平行就可以保持这种特性。 首先将坐标轴按晕线的方向角旋转。然后在旋转后的坐标空间中找到多边形的最大Y坐标(YMAX)。穿过多边形的晕线中最顶端的那条Y坐标可以根据下式计算：Y*=INT [YMAX / DELTA ] × DELTA （其中INT是最大取整函数；DELTA是晕线间的垂直距离。）取得多边形晕线中的最高一条的Y坐标后，其他各晕线的Y坐标可以通过将Y*依次递减DELTA值来得到，这个过程直到该多边形中再没有晕线经过时停止。基本方法有：单线法（首先将多边形先旋转一个方向角，然后依序每次一条晕线地分别处理各线。下一步检查多边形轮廓的每一段，判断其是否与所处理的晕线相交，保存交点并按X坐标排序。这种排序是为了通过一系列（移动，绘制）对操作来保证恰当地绘出晕线。最后所有的交点旋转回原始多边形空间显示），绕行法（原理是环绕多边形一周以计算所有晕线与多边形的交点）。 网格法追踪原则和鞍部处理？通过网格追踪等值线方法的优点，在于网格可以按照行列编号隐式地建立起邻域间的位置关系。步骤：1.一条等高线从网格单元(i,j)的四个邻接单元(i-1,j),(i+1,j),(i,j-1),(i,j+1)之一进入，应退出该单元并继续往其余三个网格单元追踪。2.确定当前单元的哪条边作为退出边时，要看该边两端点的z值范围是否包含了zi值。 3.等值线在退出边上的准确位置通常使用内插方法确定， 4.该内插是在网格单元的边上进行的。在得到等值线与网格的交点以后可以按顺序直接绘出。“鞍点”现象：一个网格单元内可能会出现多于一条的有相同z值的等值线段。出现“鞍点”时的追踪：基于四个端点的z值内插出网格单元的中心点的z值，然后把单元分成四个三角形(图6－36d)。对于每个三角形来说，由于其只有三边，就不存在难以确定追踪方向的。问题：如果一条等值线从三角形的一边进入的话，只可能从另外两边的一边中出去。网格中心点的z值为53，所以应该把S1与S2，S3与S4相连 位-平面方法裁剪线段的算法（分区裁剪）？1.窗口把这个平面分成九个区域。2.点的x,y 坐标如果都位于四个角区域中的任一个，那么该点位于窗口外。3.如果点的x或y坐标位于四个边区域的任一个，那么这个点也在窗口外。4.除了角区域和边区域，就是剪裁窗口了。5.如果一条线段的端点都位于窗口的内部，那么这条线段就全部显示出来。6.而两端点都位于窗口的同一条边界外，这条线段就要全部剪裁掉。7.只有当端点一个位于窗口外，一个在窗口内，或者两端点都在窗口外但是线段穿过不同的窗口边界时才需要进一步处理。

概率论的基本概念

第一章概率论的基本概念 第一节随机事件、频率与概率 一、教学目的： 1.通过本节起始课序言简介,使学生初步了解概率论简史、特色，从 而引导学生了解本课程概况及学习本课程的思想方法 2.通过本次课教学，使学生理解随机事件概念、频率与概率的概念， 了解随机试验、样本空间的概念，掌握事件的关系和运算，掌握 概率的基本性质及其运算 二、教学重点：概率的概念 三、教学难点：事件关系的分析与运算 四、教学内容： 1.序言：⑴简史⑵学法 2.§1.随机试验: ⑴实例⑵确定性现象⑶随机现象 3.§2.样本空间、随机事件: ⑴样本空间⑵随机事件⑶事件关系 与运算 4.§3. 频率与概率⑴频率定义、性质⑵概率定义、性质 五、小结： 六、布置作业： 标准化作业第一章题目 第二节古典概型、条件概率 一、教学目的： 通过本节教学使学生了解古典概型的定义，理解条件概率的概念，并能够解决一些古典概型、条件概率的有关实际问题． 二、教学重点：古典概率、条件概率计算 三、教学难点：古典概型与条件概率分析与建模 四、教学内容： 1.§４.古典概型 2.§５.条件概率（一） 五、小结： 六、布置作业： 标准化作业第一章题目 第三节乘法公式、全概率公式、Bayes公式、独立性 一、教学目的： 1.通过本节教学使学生在理解条件概率概念的基础上,掌握乘法公

式、全概率公式、Bayes公式以及能够运用这些公式进行概率计算。 2.理解事件独立性概念，掌握用独立性概念进行计算． 二、教学重点： 1.乘法公式及其使用 2.独立性概念及其应用 三、教学难点：应用公式分析与建模 四、教学内容： １.§５.条件概率（二、三）２.§６.独立性 五、小结： 六、布置作业： 标准化作业第一章题目 第四节习题课 一、教学目的： 通过本习题课教学使学生全面系统对概率论的基本概念进一步深化，同时熟练掌握本章习题类型，从而提高学生的分析问题与解决问题的能力． 二、教学重点： 1.知识内容系统化 2.几类问题解决方法 三、教学难点：实际问题转化为相应的数学模型 四、教学内容： 1.本章知识内容体系归纳 2.习题类型： ⑴古典概型计算 ⑵事件关系与运算 ⑶条件概率计算 ⑷乘法公式、全概率公式、Bayes公式使用与计算． ⑸独立性问题的计算 五、讲练习题 第二章随机变量及其分布 第一节随机变量、离散型随机变量的概率分布 一、教学目的： 通过本节教学使学生理解随机变量的概念，理解离散型随机变量的分布及其性质，掌握二项分布、泊松分布，并会计算有关事件的概率及其分布．

正态分布定义 (2)

正态分布 科技名词定义 中文名称：正态分布 英文名称：normal distribution 定义1：概率论中最重要的一种分布，也是自然界最常见的一种分布。该分布由两个参数——平均值和方差决定。概率密度函数曲线以均值为对称中线,方差越小，分布越集中在均值附近。 所属学科：生态学（一级学科）；数学生态学（二级学科） 定义2：一种最常见的连续性随机变量的概率分布。 所属学科：遗传学（一级学科）；群体、数量遗传学（二级学科） 本内容由全国科学技术名词审定委员会审定公布 百科名片

编辑本段 正态分布的由来 normal distribution 正态分布 一种概率分布。正态分布是具有两个参数μ和σ2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ，σ2 )。服从正态分布的随机变量的概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。它的形状是中间高两边低，图像是一条位于x轴上方的钟形曲线。当μ＝0，σ2 ＝1时，称为标准正态分布，记为N（0，1）。μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。 正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。 生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中

二项分布概念及图表和查表方法

目录 1定义 ?统计学定义 ?医学定义 2概念 3性质 4图形特点 5应用条件 6应用实例 定义 统计学定义 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当 时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。

考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。如果进行次伯努利试验，取得成功次数为 的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 式中的n为独立的伯努利试验次数，π为成功的概率，（1-π）为失败的概率，X为在n次伯努里试验中出现成功的次数，表示在n次试验中出现X的各种组合情况，在此称为二项系数（binomial coefficient）。 所以的含义为：含量为n的样本中，恰好有X例阳性数的概率。 概念 二项分布（Binomial Distribution），即重复n次的伯努利试验（Bernoulli Experiment），用ξ表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望：Eξ=np； 方差：Dξ=npq； 其中q=1-p 证明：由二项式分布的定义知，随机变量X是n重伯努利实验中事件A发生的次数，且在每次试验中A发生的概率为p。因此，可以将二项式分布分解成n个相互独立且以p为参数的（0-1）分布随机变量之和。 设随机变量X（k）(k=1,2,3...n)服从（0-1）分布，则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立，所以期望：

电子地图 4D技术

电子地图4D技术 电子地图可理解为数字地图。数字地图是存储在计算机的硬盘、软盘、光盘或磁带等介质上的数字化地图，地图的内容是通过数字来表示的，它需要通过专用的计算机软件对这些数字进行显示、读取、检索、分析、修改、喷绘等等。在数字地图上可以表示的内容和信息量远远大于普通的常规地图。 数字地图是一种"活"的地图。数字地图可以非常方便的将各种或一种普通地图或专业（专题）地图的内容进行任意形式的要素分层组合、拼接、增加、删减等，形成新的实用地图。可以对数字地图进行任意比例尺、任意范围的放大、缩小、裁切和绘图输出等。数字地图绘制图时间较常规制图方法可以大规模缩短。数字地图可以十分方便的与卫星遥感影像、航空照片、其它电子地图和其它信息数据库进行整合、拟合、挂接显示等，生成各种类别的新型地图。数字地图（电子地图）与传统纸介质地图相比，还具有如下优点： １、制作工艺先进、成本低、速度快、效益高； ２、数字化存储、信息量大、可以网上传输，体积小，便于携带； ３、保存时间长，不易损坏和变形，节省档案保存空间； ４、制图精度高、无介质变形，可接受多种投影变换； ５、数字信息可与多种空间信息拟合，便于更新、修编、组合，生成各种图； ６、输出绘制方便、出版方便、复制方便、使用方便； ７、数字地球、数字城市、数字政府、数字商务、数字化可视管理必需的基础工作。 数字地图种类很多，如数字（线划）地图（DLG）、数字栅格地图（DRG）、数字遥感（正射）影像图（DOM）、数字（地面）高程模型图（DEM）和各种数字专题（专业或非专业）地图等。 所谓＂4D＂技术是指数字正射影像图（DOM）、数字地面高程模型（DEM）、数字栅格地图（DRG）、数字线划地图（DLG）四种技术的集合，是用以解决电子地图及数字地图的主要手段，下面介绍各种技术的应用方法及相应的概念，供您参考。 1．数字高程模型（Digital Elevation Model 简称DEM） 1.1 基本概念 DEM是在特定投影平面上规则的空间水平间隔的高程值矩阵。DEM的水平间隔应随地貌类型的不同而改变。为控制地表形态，可配套提供离散高程点数据。换句话说，即为具有不同坐标的不同地面分布点上的不同高度数据，组织集合构成对地表形态变化的控制。 DEM应用可转换为等高线图、透视图、断面图以及专题图等各种图解产品，或者按照用户的需求计算出体积、空间距离、表面覆盖面积等工程数据和统计数据。 1.2 生产技术 1.2.1原始资料 卫片航片：最好是近期采集的高分辨率卫星遥感像片数据或近期新拍摄的航空像片。（有关采集问题请查询本网站"数据增值服务"有关部分。） 地形图：最好采用最近一次更新测量的地形图，其中等高线必须由解析测图仪或精测仪测绘。 1.2.2 DEM的生产及技术要求 DEM的获取方法有以下几种：

正态分布的概念及表和查表方法

正态分布概念及图表 正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A·棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P·S·拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。 正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。 若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ= 0,σ= 1时的正态分布是标准正态分布。 目录 1历史发展 2定理 3定义 ?一维正态分布 ?标准正态分布 4性质 5分布曲线 ?图形特征 ?参数含义 6研究过程 7曲线应用 ?综述 ?频数分布 ?综合素质研究 ?医学参考值

历史发展 正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（G.Hagen）在一篇论文中正式提出了这个学说。 其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差”之和，每只取两值，其概率都是1/2，由此出发，按狄莫佛的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差的正态性）为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。 定理 由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x 的概率。只要会用它求正态总体在某个特定区间的概率即可。 为了便于描述和应用，常将正态变量作数据转换。将一般正态分布转化成标准正态分布。 若 服从标准正态分布，通过查标准正态分布表就可以直接计算出原正态分布的概率值。故该变换被称为标准化变换（标准正态分布表：标准正态分布表中列出了标准正态曲线下从-∞到X（当前值）范围内的面积比例）。

地图学复习

地图学复习 第四章 1，地图符号的概念 地图符号：表示地图信息各要素空间位置、大小和数量质量特征，由形状不同、大小不一、色彩有别的图形和文字组成，是地图的语言，具有形象直观，一目了然的特点。 2，地图符号的概念 地图符号是符号的子集，它具有可视性（指实地图）。它用一种物质的对象来代替一个抽象的概念，以一种易为心灵了解和便于记忆的形式，把制图对象的抽象概念呈现在地图上，从而使人们产生深刻的印象。 3，地图符号的功用 1）地图语言：地图符号具有别的符号所有的基本属性——约定俗成。 2）综合概括：通过对地理事物的归纳、分类分级而制订的抽象的概念化的地图符号，实质上就是对地理事物进行了一次重要的制图综合。 3）空间模型：可建立地理事物的空间模型，以再现或塑造无法观测的地理现象，以供量算和比较，进行各种分析和研究。 4，地图符号的分类 （1）按空间分布状态 点状线状面状体状 （2）按比例关系分类 依比例符号——用轮廓线（实线、点线或虚线）表示真实位置和形状，在轮廓线内填绘其它符号、注记或颜色，以表明该地物的质量与数量特征， 不依比例符号如点状符号 半依比例符号如线状符号 按符号结构变化特征划分，可分为组合结构与扩张结构两种符号类型。 5，地图符号的基本变量P154 静态符号的基本视觉变量

1）形状变量 2）尺寸变量 3）方向变量 4）颜色变量 5）密度变量 6，视觉变量的感受效果 1）整体感 2）等级感 3）数量感 4）质量感 5）动态感 6）立体感 7，地图符号的量表系统 1）定名量表：只处理空间信息或数据的定性关系而不处理其定量关系的量表系统。 2）顺序量表：是将客观存在的物体或现象按某一标志排成序列，表现为一个相对等级的量表系统。 3）间隔量表：利用某种统计单位对顺序量表排序的量表系统。 4）比率量表：是以数据起始点为基础，按某种比率关系排序且能反应比率变化的量表。 8，地图注记的概念 地图上的文字与数字总称地图注记。它是地图的基本内容之一，与地图符号相配合完成地图的信息传输功能与作用。注记本身在某种程度上还具有符号的作用，它不仅丰富了地图的内容，而且在一定程度上还补充了符号的不足。 9，地图注记的种类 1)名称注记。用于注释地物名称的文字。（点状注记线状注记面状注记） 2)说明注记。用于补充说明符号含义不足的简要文字。

二项分布概念及图表和查表方法

目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例 定义 统计学定义 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当 时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。

考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。如果进行次伯努利试验，取得成功次数为的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望：Eξ=np； 方差：Dξ=npq； 其中q=1-p 证明：由二项式分布的定义知，随机变量X是n重伯努利实验中事件A发生的次数，且在每次试验中A发生的概率为p。因此，可以将二项式分布分解成n个相互独立且以p为参数的（0-1）分布随机变量之和。 设随机变量X（k）(k=1,2,3...n)服从（0-1）分布，则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立，所以期望：

论正态分布的重要地位和应用2要点

学部：工学部 学生姓名：王梅影 学号：2011070102021 年级：2011级 专业班级：信息与计算科学 指导教师：赵姣珍职称：讲师完成时间：2015/5/15 中国·贵州·贵阳

成果声明 本人的毕业论文是在贵州民族大学人文科技学院赵姣珍老师的指导下独立撰写并完成的。毕业论文没有剽窃、抄袭、造假等违反学术道德、学术规范和侵权行为，除文中已经注明引用的内容外，本论文不含任何其他个人或集体已经发表或撰写过的作品或成果。对本文的研究做出重要贡献的个人和集体，均已在文中以明确方式标明。本声明的法律结果由本人承担。 论文作者签名： 日期年月日

目录 摘要 (1) Abstract (2) 1绪论 (3) 1.1研究背景 (3) 1.2研究目的 (3) 1.3研究现状 (4) 1.4研究意义 (4) 2 正态分布相关知识介绍 (5) 2.1正态分布的概念 (5) 2.2正态分布曲线特性 (5) 2.3 标准正态分布 (8) 3 正态分布的应用 (9) 3.1 正态分布应用实例 (9) 3.1.1 正态分布在生产中的应用 (9) 3.1.2正态分布在日常生活中的应用 (10) 3.1.3正态分布在销售分类中的应用 (11) 3.1.4正态分布在工作学习中的应用 (12) 3.1.5 正态分布在仪器测量中的应用 (12) 3.2 正态分布的应用价值 (14) 总结 (15) 参考文献 (16) 致谢 (17)

摘要：正态分布是一种最常见的连续型随机变量的分布,是概率论中最重要的一中分布.在理论上和实际生活中正态分布具有重要地位，数理统计中的正态分布是很多重要问题的解决的基础，在理论研究中占有举足轻重的地位.本文首先针对正态分布这一理论研究与实际应用都占有重要地位的概率分布展开分析研究，从其基本概念出发，然后分析其特性以及各种应用价值，最后通过一系列研究给出正态分布具有重大作用的理论依据. 关键词：正态分布标准正态分布方差标准差

分布列概念

1. 分布列定义： 设离散型随机变量所有可能取得的值为x 1,x 2,…,x 3,…x n ,若取每一个值x i (i=1,2,…，n)的概率为，则称表 为随机变量的概率分布，简称的分布列. 离散型随机变量的分布列都具有下面两个性质： （1）P i ≥0,i=1,2，…，n ；（2）P 1+P 2+…+P n =1 要点四、两类特殊的分布列 1. 两点分布 像上面这样的分布列称为两点分布列． 要点诠释： (1)若随机变量X 的分布列为两点分布, 则称X 服从两点分布,而称P(X=1)为成功率. (2)两点分布又称为0-1分布或伯努利分布 (3)两点分布列的应用十分广泛,如抽取的彩票是否中奖；买回的一件产品是否为正品；新生 婴儿的性别； 投篮是否命中等等；都可以用两点分布列来研究. 2. 超几何分布 一般地，在含有件次品的件产品中，任取件，其中恰有件次品，则则事件 {X=k ｝ 发生的概率为, 其中，且 ． 称分布列为超几何分布列．如果随机变量 X 的分布列为超几何分布列，则称随机变量 X 服从超几何分布 ξξi i P x P ==)(ξξξM N n X (),0,1,2,,k n k M N M n N C C P X k k m C --===min{,}m M n =,,,,n N M N n M N N *≤≤∈

要点一、条件概率的概念 1.定义 设、为两个事件，且，在已知事件发生的条件下，事件B 发生的概率叫做条件概率。用符号表示。 读作：发生的条件下B 发生的概率。 要点诠释 在条件概率的定义中，事件A 在“事件B 已发生”这个附加条件下的概率与没有这个附加条件的概率是不同的，应该说，每一个随机试验都是在一定条件下进行的．而这里所说的条件概率，则是当试验结果的一部分信息已知，求另一事件在此条件下发生的概率． 2．P （A ｜B ）、P （AB ）、P （B ）的区别 P （A ｜B ）是在事件B 发生的条件下，事件A 发生的概率。 P （AB ）是事件A 与事件B 同时发生的概率，无附加条件。 P （B ）是事件B 发生的概率，无附加条件． 它们的联系是：． 要点诠释 一般说来，对于概率P(A|B)与概率P(A)，它们都以基本事件空间Ω为总样本，但它们取概率的前提是不相同的。概率P(A)是指在整个基本事件空间Ω的条件下事件A 发生的可能性大小，而条件概率P(A|B)是指在事件B 发生的条件下，事件A 发生的可能性大小。 例如，盒中球的个数如下表。从中任取一球，记A=“取得蓝球”，B=“取得玻璃球”。基本事件空间Ω包含的样本点总数为16，事件A 包含的样本点总数为11，故。 如果已知取得玻璃球的条件下取得蓝球的概率就是事件B 发生的条件下事件A 发生的条件概率，那么在事件B 发生的条件下可能取得的样本点总数应为“玻璃球的总数”，即把样本空间压缩到玻璃球全体。而在事件B 发生的条件下事件A 包含的样本点数为蓝玻璃球数，故。 要点二、条件概率的公式 A B ()0P A >A (|)P B A (|)P B A A () (|)() P AB P A B P B =11()16 P A = 42(|)63 P A B = =