
沙漏模型
【1】在正方形ABCD中,DE=CE,BF:FD=2:3,那么,
CG:GF= AC:FM=
【2】在正方形ABCD中,DG:GC=2:1,BE:EC=1:3,那么,
AD:EF= AD:CF= DH:HE=
【3】在正方形ABCD中,DM:MC=1:2,BF:FC=1:2,AE=ED,那么,EM:MN= ED:CN= DG:GF= ED:FN=
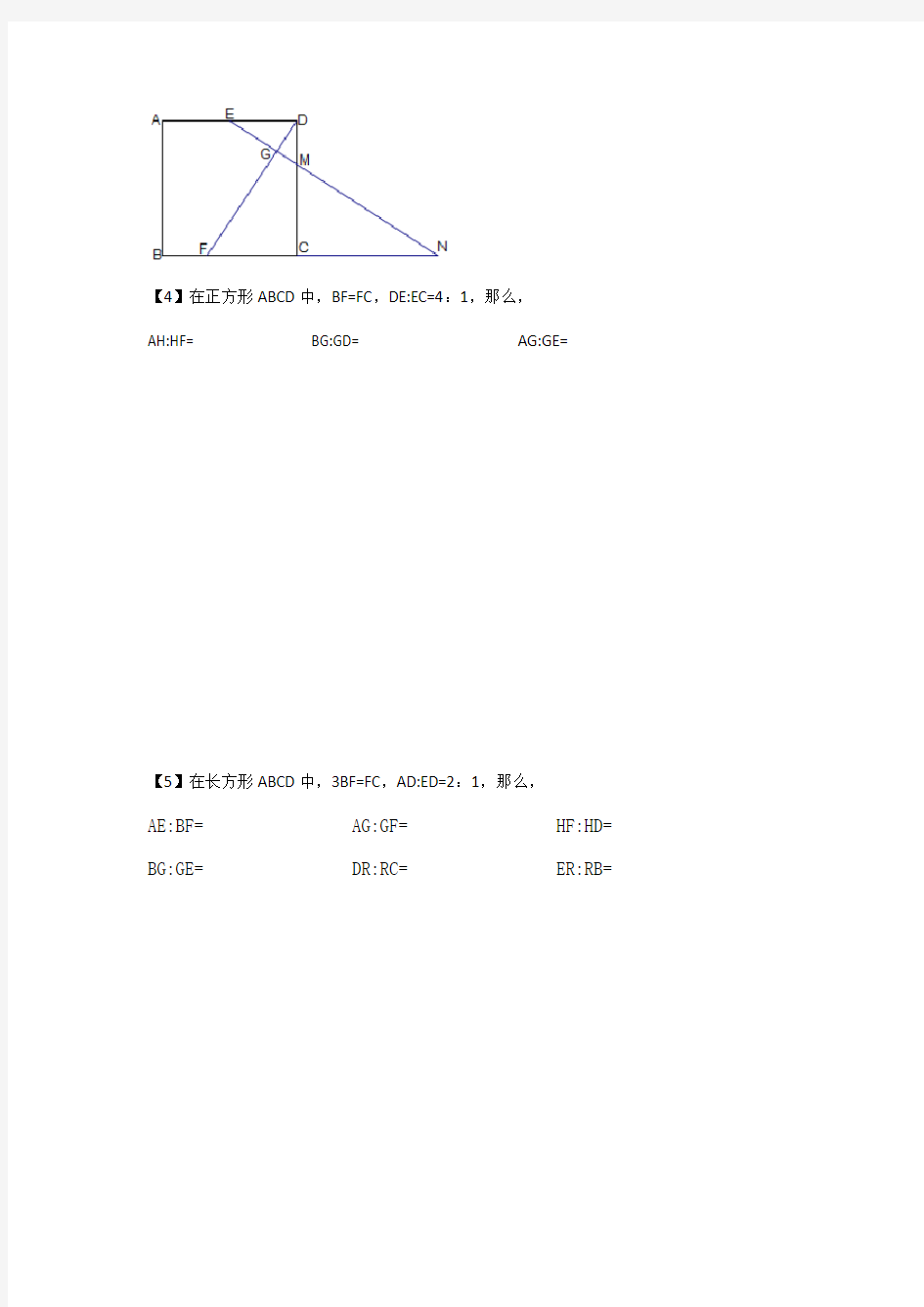
【4】在正方形ABCD中,BF=FC,DE:EC=4:1,那么,
AH:HF= BG:GD= AG:GE=
【5】在长方形ABCD中,3BF=FC,AD:ED=2:1,那么,
AE:BF= AG:GF= HF:HD= BG:GE= DR:RC= ER:RB=
【6】正方形ABCD的边长为4,正方形CEFH的边长为6,那么
BN:NF= HM:ME= FM:MB=
【7】在长方形ABCD中,△EFD的面积为15,△DFC的面积为35,那么ED:BC= DF:FB= △ABE的面积=
【8】已知长方形ABCD的面积为120,且△ABF的面积是30,△ADE的面积是40,那么,BF:FC= DE:EC=
【9】如图,边长为1正方形ABCD中,BE=2EC,CF=FD,求三角形AEG的面积。(07年人大附考题)
第一步:求阴影部分面积,利用()转化为求线段比:()第二步:用()求线段比。
模型四 相似三角形模型 (一)金字塔模型 (二) 沙漏模型 ①AD AE DE AF AB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:。 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线。 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。 【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长 度是多少? 【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD , 所以::4:161:4BF FC BE CD ===,所以4 10814 FC =?=+. 【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份。 如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大? 【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米。 【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________。 【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=, 22:2:54:25ADE ABC S S ==△△, 任意四边形、梯形与相似模型
金字塔模型与沙漏模型 ADAE DEAF ①AB=AC=BC=AG 2 2 ②S△ADE:S△ABC=AF:AG 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变他们都相似),与相似三角形相关,常用的性质及定理如下: (1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似 比; (2)相似三角形面积的比等于它们相似比的平方; (3)连接三角形两边中点的线段我们叫做三角形的中位线; 三角形中位线定理:三角形的中位线长等于他所对应的底边长的一半。 相似三角形 对应角相等、对应边成比例的两个三角形叫做相似三角形。如果三边分别对应A,B,C 和a,b,c:那么:A/a=B/b=C/c,即三边边长对应比例相同。 判定方法 定义 对应角相等,对应边成比例的两个三角形叫做相似三角形。 预备定理 平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似。(这 是相似三角形判定的定理,是以下判定方法证明的基础。这个引理的证明方法需要平行线与 线段成比例的证明) 1判定定理 常用的判定定理有以下6条: 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个 三角形相似。(简叙为:两角对应相等,两个三角形相似。)(AA) 判定定理2:如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两 个三角形相似。(简叙为:两边对应成比例且夹角相等,两个三角形相似。)(SAS)判定定理3:如果两个三角形的三组对应边成比例,那么这两个三角形相似。(简叙为:三边对应成比例,两个三角形相似。)(SSS)
判定定理4:两个三角形三边对应平行,则个两三角形相似。(简叙为:三边对应平行, 两个三角形相似。) 判定定理5:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条 直角边对应成比例,那么这两个直角三角形相似。(简叙为:斜边与直角边对应成比例,两个 直角三角形相似。)(HL) 判定定理6:如果两个三角形全等,那么这两个三角形相似(相似比为1:1)(简叙为:全等三角形相似)。 相似的判定定理与全等三角形基本相等,因为全等三角形是特殊的相似三角形。 一定相似 符合下面的情况中的任何一种的两个(或多个)三角形一定相似: 1.两个全等的三角形 全等三角形是特殊的相似三角形,相似比为1:1。 补充:如果△ABC∽△A‘B’C‘,∴AB/A’B‘=AC/A’C‘=BC/B'C’ =K 当K=1时,这两个三角形全等。(K为它们的比值)2.任意 一个顶角或底角相等的两个等腰三角形 两个等腰三角形,如果其中的任意一个顶角或底角相等,那么这两个等腰三 角形相似。 3.两个等边三角形 两个等边三角形,三个内角都是60度,且边边相等,所以相似。 4.直角三角形被斜边上的高分成的两个直角三角形和原三角形 由于斜边的高形成两个直角,再加上一个公共的角,所以相似。 2性质定理 (1)相似三角形的对应角相等。 (2)相似三角形的对应边成比例。 (3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。 (4)相似三角形的周长比等于相似比。 (5)相似三角形的面积比等于相似比的平方。[1] 由(5)可得:相似比等于面积比的算术平方根。 3定理推论 推论一:顶角或底角相等的两个等腰三角形相似。 推论二:腰和底对应成比例的两个等腰三角形相似。 推论三:有一个锐角相等的两个直角三角形相似。 推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。 推论五:如果一个三角形的两边和三角形任意一边上的中线与另一个三角形的对应部 分成比例,那么这两个三角形相似。 性质
金字塔模型与沙漏模型 ① AD AB =AE AC =DE BC =AF AG ② S △ADE :S △ABC =AF 2:AG 2 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变他们都相似),与相似三角形相关,常用的性质及定理如下: (1) 相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2) 相似三角形面积的比等于它们相似比的平方; (3) 连接三角形两边中点的线段我们叫做三角形的中位线; 三角形中位线定理:三角形的中位线长等于他所对应的底边长的一半。 相似三角形 对应角相等、对应边成比例的两个三角形叫做相似三角形。如果三边分别对应A,B,C 和a ,b ,c :那么:A/a=B/b=C/c ,即三边边长对应比例相同。 判定方法 定义 对应角相等,对应边成比例的两个三角形叫做相似三角形。 预备定理 平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似。(这是相似三角形判定的定理,是以下判定方法证明的基础。这个引理的证明方法需要平行线与线段成比例的证明) 1判定定理 常用的判定定理有以下6条: 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。(简叙为:两角对应相等,两个三角形相似。)(AA ) 判定定理2:如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似。(简叙为:两边对应成比例且夹角相等,两个三角形相似。)(SAS ) 判定定理3:如果两个三角形的三组对应边成比例,那么这两个三角形相似。(简叙为:三边对应成比例,两个三角形相似。)(SSS )
蝴蝶模型&沙漏模型训练题参考答案 1、 已知四边形ABCD 和CEFG 都是正方形,且正方形ABCD 的边长为10厘米,那么图中阴影 三角形BFD 的面积为多少平方厘米 ? 【分析】 连接FC ,有FC 平行BD ,设BF 与DC 连接于O ,那么在梯形蝴蝶中有 1 ===50 2 DFO BCO DCB ABCD S S S S S ???=阴影 2、图中的四边形土地总面积为52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。那么最大的一个三角形的面积是多少公顷? 7 6 【分析】 7 6E D C B A 在图形中标A 、B 、C 、D 、E 有 :6:7:5213391821 ABE BCE ADE DCE ADE DCE ADE DCE S S S S S S S S ????????==+=-===, 最大的三角形面积是21公顷 3、如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是多少平方厘米?
H F G E D C B A 【分析】延长EB 到K ,使BK=CD 。 三角形EGK 与三角形DGC 成比例,DC :EK=2:3,所以DG :GK=2:3,由于三角形DEK=90,所以EGK=90÷3/5=54,所以四边形EBFG=EGK-BKF=24。同理,EB :DC=1:2,所以BH :HC=1:2,所以三角形EBH=1/3EBD=10所以,四边形BGHF 的面积是24-10=14平方厘米 H K F G E D C B A 4、如图,ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为边AB 、BC 的中点.则图形中阴影部分的面积为多少平方厘米? 【分析】连接EC ,因为AE 平行于DC ,所以四边形AECD 为梯形,有AE:DC=1:2,所以 :1:4AEG DCG S S ??=, AGD ECG AEG DCG S S S S ?????=?,且有AGD ECG S S ??=,所以:1:2AEG ADG S S ??=,而这两个 三角形高相同,面积比为底的比,即EG :GD=1:2,同理FH :HD=1:2. 有AED AEG AGD S S S ???=+,而111822 AED ABCD S S ?= ??=(平方厘米)有 EG:GD= :AEG AGB S S ??,所以 1 612 AEG AED S S ??= ?=+(平方厘米)
Ian Foster于2001年提出了网格计算协议体系结构,认为网格建设的核心是标准化的协议与服务,并与Internet网络协议进行类比。该结构主要包括以下五个层次。 ?构造层(Fabric): ?连接层(Connectivity): ?资源层(Resource): ?汇集层(Collective): ?应用层(Application): 构造层(Fabric):控制局部的资源。由物理或逻辑实体组成,目的是为上层提供共享的资源。常用的物理资源包括计算资源、存储系统、目录、网络资源等;逻辑资源包括分布式文件系统、分布计算池、计算机群等。构造层组件的功能受高层需求影响,基本功能包括资源查询和资源管理的QoS(Qualities of Service服务质量)保证。 连接层(Connectivity):支持便利安全的通信。该层定义了网格中安全通信与认证授权控制的核心协议。资源间的数据交换和授权认证、安全控制都在这一层控制实现。该层组件提供单点登录、代理委托、同本地安全策略的整合和基于用户的信任策略等功能。 资源层(Resource):共享单一资源。该层建立在连接层的通信和认证协议之上,满足安全会话、资源初始化、资源运行状况监测、资源使用状况统计等需求,通过调用构造层函数来访问和控制局部资源。 汇集层(Collective):协调各种资源。该层将资源层提交的受控资
源汇集在一起,供虚拟组织的应用程序共享和调用。该层组件可以实现各种共享行为,包括目录服务、资源协同、资源监测诊断、数据复制、负荷控制、账户管理等功能。 应用层(Application):为网格上用户的应用程序层。应用层是在虚拟组织环境中存在的。应用程序通过各层的应用程序编程接口(API)调用相应的服务,再通过服务调动网格上的资源来完成任务。为便于网格应用程序的开发,需要构建支持网格计算的大型函数库。五层沙漏结构是目前学术界公认的网格基本体系结构,该结构主要侧重于定性的描述而不是具体的协议定义,因而很容易从整体对网格进行理解。五层沙漏模型以“协议”为中心,强调服务、API和SDK 的重要性,但是并不提供严格的规范,也不提供对全部所需协议的完整罗列,而是对该结构中各部分组件的通用要求进行定义,并且将这些组件形成一定的层次关系,每一层的组件具有相同的特征,上层组件可以在任何一个低层组件的基础之上进行建造。五层沙漏结构根据该结构中各组成部分与共享资源的距离,将对共享资源进行操作、管理和使用的功能分散在五个不同的层次,越往下层就越接近于物理的共享资源,因此该层与特定资源相关的成分就比较多;越往上层就越感觉不到共享资源的细节特征,也就是说上层是更加抽象的共享资源表示,因此就不需要关心与底层资源相关的具体实现问题
金字塔模型与沙漏模型 ①AD AB = AE AC = DE BC = AF AG ② S△ADE:S△ABC =AF2:AG2 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变他们都相似),与相似三角形相关,常用的性质及定理如下:(1) 相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2) 相似三角形面积的比等于它们相似比的平方; (3) 连接三角形两边中点的线段我们叫做三角形的中位线; 三角形中位线定理:三角形的中位线长等于他所对应的底边长的一半。 相似三角形 对应角相等、对应边成比例的两个三角形叫做相似三角形。如果三边分别对应A,B,C和a,b,c:那么:A/a=B/b=C/c,即三边边长对应比例相同。 判定方法 定义 对应角相等,对应边成比例的两个三角形叫做相似三角形。 预备定理 平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似。(这是相似三角形判定的定理,是以下判定方法证明的基础。这个引理的证明方法需要平行线与线段成比例的证明) 1判定定理 常用的判定定理有以下6条: 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。(简叙为:两角对应相等,两个三角形相似。)(AA)判定定理2:如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似。(简叙为:两边对应成比例且夹角相等,两个三角形相似。)(SAS) 判定定理3:如果两个三角形的三组对应边成比例,那么这两个三角形相似。(简叙为:三边对应成比例,两个三角形相似。)(SSS)
模型四 相似三角形模型 (一)金字塔模型 (二) 沙漏模型 G F E A B C D A B C D E F G ①AD AE DE AF AB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:。 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线。 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。 【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长 度是多少? F E D C B A 【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD , 所以::4:161:4BF FC BE CD ===,所以4 10814FC =?=+. 任意四边形、梯形与相似模型
【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份。 如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大? 60 5040 30 2010 E A D C B 【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米。 【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________。 A E D C B 【解析】 根据金字塔模型 :::2:(23)2:5AD AB AE AC DE BC ===+=, 22:2:54:25ADE ABC S S ==△△, 设4ADE S =△份,则25ABC S =△份,255315BEC S =÷?=△份,所以 :4:15ADE ECB S S =△△。 【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==, 则::ADE DEGF FGCB S S S =△四边形四边形 。 E G F A D C B 【解析】 设1ADE S =△份,根据面积比等于相似比的平方, 所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△,因此 4AFG S =△份,9ABC S =△份, 进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形
第九讲 六年级奥数——沙漏模型(教师版) 一、知识储备 沙漏模型 AB ∶CD =AO S △AOB ∶S △COD 根据沙漏模型可得, 二、例题讲解 1、如图,在平行四边形ABCD 中,AB=16厘米,AD=10厘米,BE=4厘米,那么FC 的长度是多少? 8
2、直角三角形ABC 中,AB 平行于DE ,AB=4厘米,BC=6厘米。又知BE:EC=1:3,求三角形CDE 的面积。 6.75 3、如图,ABC ? 中,DE ,FG ,BC 互相平行,FB DF AD ==, 则FGCB DEGF ADE S S S 四边形四边形::?=? 1:3:5 4、如图,边长为8厘米和12厘米的两个正方形并排放在一起,求图中三角形EOF 和三角形GHO 的面积。 16.2 E G F A D C B
5、如图,DE 平行BC ,若3:2:=DB AD ,那么ECB ADE S S ??:=? 4:15 6、如图,梯形ABCD 的面积是36平方厘米,下底长是上底长的2倍,阴影三角形的面积是多少? 16 7、如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知△AOB 与△BOC 的面积分别为25平方厘米与35平方厘米,那么梯形ABCD 的面积是多少平方厘米? 144 35 25O A B C D A E D C B
8、如图,梯形ABCD 中,△AOB 、△COD 的面积分别为1.2和2.7,求梯形ABCD 的面积。 7.5 9、如图,三角形ABC 中,AB=4AE ,AC=4AD ,ED 与BC 平行,三角形EOD 的面积是1平方厘米.那么三角形AED 的面积是多少平方厘米? 35 10、如图,DEFG 均为各边上的三等分点,线段EG 和DF 把三角形ABC 分成四部分,如果四边形FOGC 的面积是24平方厘米,求三角形ABC 的面积。 281 O D C B A A C D E O
沙漏与金字塔模型 例1 如图所示,梯形ABCD的面积是36,下底长是上底长的2倍,阴影部分三角形的面积是多少? 练习1 如图所示,梯形的面积是48平方厘米,下底长是上底长的3倍,求阴影部分图形的面积。 例2 如图,平行四边形ABCD的面积是90。已知E点是AB上靠近A点的三等分点,求阴影部分图形的面积。 练习2 如图,正方形ABCD的边长是6,E点时BC的中点,求△AOD的面积。 例3 如图所示,边长为8厘米和12厘米的两个正方形并排放在一起,求图中阴影部分图形的面积。
练习3 如图所示,图中的两个正方形的边长分别是10和6,那么图中阴影部分图形的面积是多少? 例4 如图,直角三角形ABC中,AB=4,BC=6.又知BE:EC=1:3。求△CDE的面积。 练习4 如图,EF与BC平行,AF:FB=1:2。已知AE=2,EF=3,那么CE的长度是多少?AC 的长度是多少?BC 的长度是多少? 例5 如图所示,在正方形ABCD中,E、F分别是BC、CD的中点,已知正方形ABCD的面积为60平方厘米,求阴影部分图形的面积。 例6 已知三角形ADE的面积为3平方厘米,D是AB边的三等分点(靠近A点),且DE与BC平行,请求出三角形OBC的面积是多少平方厘米?
作业 1、如图1所示,AB与CD平行,已知AB:CD=3:4,AO=6,那么OC等于多少? 2、如图2所示,AC与BD平行,交点为O,已知AO=2,OB=4,则△OBD的面积是△AOC 面积的几倍? 3、如图3所示,BC与DE平行,已知AD=4厘米,BD=5厘米,DE=16厘米,则BC是多少厘米? 4、如图4所示,BC与DE平行,已知AD=4厘米,BD=5厘米,△ADE的面积为32平方厘米,则四边形DECB面积是多少平方厘米? 5、如图5所示,梯形ABCD的面积是50,下底长是上底长的1.5倍,阴影部分三角形的面积是多少? 6、如图6所示,正方形ABCD的边长是6,E点是BC上靠近B点的三等分点,求△AOD的面积。