
第五章 定积分
内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。 要求:理解定积分的概念和性质。掌握牛顿-莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。
重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。 难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。
§1.定积分的概念
一、实例分析
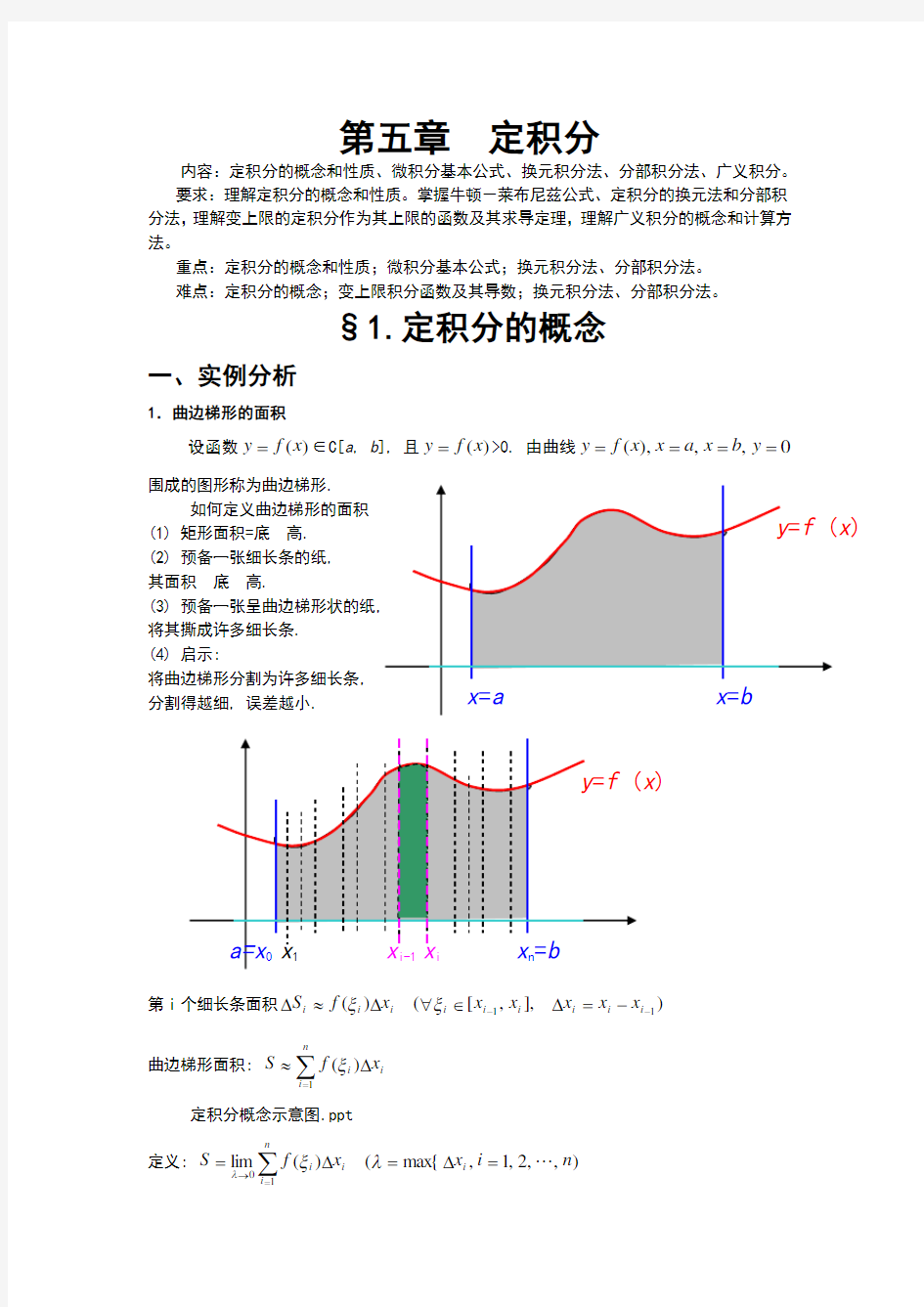
1.曲边梯形的面积
设函数)(x f y =∈C[a , b ], 且)(x f y =>0. 由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形.
如何定义曲边梯形的面积 (1) 矩形面积=底高. (2) 预备一张细长条的纸, 其面积底高.
(3) 预备一张呈曲边梯形状的纸, 将其撕成许多细长条. (4) 启示:
将曲边梯形分割为许多细长条,
分割得越细, 误差越小.
第i 个细长条面积)],,[()(11---=?∈??≈?i i i i i i i i i x x x x x x f S ξξ
曲边梯形面积: ∑=?≈
n
i i
i
x
f S 1
)(ξ
定积分概念示意图.ppt
定义: ),,2,1,max {()(lim
1
n i x x
f S i n
i i
i
Λ=?=?=∑=→λξλ
y =f (x )
x =a x =b y =f (x )
a=x 0 x 1 x i-1 x i x n =b
抛开上述过程的几何意义,将其数学过程定义为定积分. 二、定积分的定义 1. 定义
设)(x f y =在[a , b ]有定义, 且有界.
(1) 分割: 用分点b x x x a n =<<<=Λ10把[a , b ]分割成n 个小区间:
}
,,2,1,max{,,,2,1],,[11n i x x x x n
i x x i i i i i i ΛΛ=?=-=?=--λ记
(2) 取点: 在每个小区间],[1i i x x -上任取一点i
, 做乘积: i i x f ?)(ξ.
(3) 求和:
∑=?n
i i
i
x
f 1
)(ξ
(4) 取极限: ∑=→?n
i i
i
x
f 1
)(lim
ξλ
若极限存在, 则其为)(x f 在[a , b ]上的定积分, 记作:
?
b
a
dx x f )(. 即:
∑?
=→?=n
i i i b
a
x f dx x f 1
)(lim )(ξλ
[a , b ]: 积分区间;a :积分下限;b :积分上限;
∑=?n
i i
i
x
f 1
)(ξ积分和式.
问题: 定积分是极限值, 在求极限的过程中, 谁是常量, 谁是变量 注: (1) ∑
=?n
i i i x f 1
)(ξ与区间的分割法x i 和取点法
i
有关; 而
?
b
a
dx x f )(与x i 和
i
无
关.
(2)
?
b
a
dx x f )(与a 、b 、f 有关,与x 无关,即:
[][]????
===b
a
b a
b a
b
a
d f du u f dt t f dx x f )()()()(
2.定积分存在定理
定理 若)(x f 在[a , b ]上有界且只有有限个间断点,则)(x f 在[a , b ]上可积. 推论 若)(x f 在[a , b ]上连续,则)(x f 在[a , b ]上可积.
例1. 求
?1
xdx
解: x x f =)(在[0, 1]连续, 积分存在.
∑?=→?=n
i i
i x xdx 1
1
lim ξλ
与[0, 1]的分割法和
i
的取法无关. 选取特殊的分割法和取点法, 可使计算简便.
(1) 将[0, 1]n 等分, n
x n i x i i 1
,=?= (2) 取点
i
=2)(,
n
i
x f x i i i i =?=ξξ
(3) 求和
2)1(1)(2
1
21
+==?∑
∑
==n n n
n i x f n
i n
i i i ξ (4) 取极限212)1(lim
)(lim 20
=+=?∞→→n
n n x f n i i ξλ 故
2
1
1
=
?
xdx 3. 定积分的几何意义
若)(x f 在[a , b ]上非负, 则?b
a dx x f )(=曲边梯形面积; 若)(x f 在[a ,
b ]?
b
a
?
b a
dx x f )(的几何意义是由曲线0,,),(====y b x a x x f y 围成曲边梯形面积的代
数和.
例2. a b dx xdx dx x b
a
-===
-?
??
-;0sin ;
122
1
2
π
ππ
.
S +
S +
S -
三、定积分的性质 1.规定
??
?-==a
b b
a
a
a
dx
x f dx x f dx x f )()()
2(0
)()1(
2.性质
????????+=±=±=b
c
c a
b a
b
a
b a
b a
b
a
b
a
dx
x f x f dx x f dx x g dx x f dx x g x f dx
x f k x kf )()()()3()()()]()([)2()()()1(
????????+=-=?+=b
c
c
a
c
a
c
b
b
a
b a
c
b
c a
dx
x f dx x f dx x f dx x f dx x f dx
x f dx x f dx x f )()()()()()()()(
(4) 若在[a , b ]上有)(0)(b a x f <≥,则0)(≥?b
a
dx x f
推论1 若)()()(b a x g x f <≥,则??
≥b
a
b a
dx x g dx x f )()(
推论2
?
?
≥
b
a
b
a
dx x f dx x f )()(
(5) 设M 、m 分别为)(x f 在[a , b ]上的最大、最小值)(b a <,则
)()()(a b M dx x f a b m b
a
-≤≤-?
(6) (积分中值定理) 设],[)(b a C x f ∈, 则),(b a ∈?ξ, 使得
))(()(a b f dx x f b
a
-=?
ξ
y =f (ξ)
将中值定理变形得:
a
b dx x f f b
a
-=
?)()(ξ
称为)(x f 在[a , b ]上的平均值.
§2. 微积分基本公式
一、变速直线运动中的位置函数与速度函数之间的关系(略)
二、积分上限的函数及其导数
设)(x f 在[a , b ]上连续, 则x [a , b ], 有)(x f 在[a , x ]上连续. 从而?
x
a
dx x f )(存
在.
在这里, 积分上限x 与被积变量x 的性质是不同的. ?
b
a
dx x f )(与a 、b 、f 有关,与x
无关.
??
=x
a
x
a
dt t f dx x f )()(与a 、x 、f 有关.
对于[a , b ]上的任一点x , ?
x
a
dt t f )(有一个确定的对应值, 故?x
a
dt t f )(是x 的函数,
记作(x ), 即:
)(,)()()(b x a dt t f dx x f x x
a
x
a
≤≤==Φ??
称为积分上限的函数.
定理 若)(x f 在[a , b ]上连续, 则积分上限的函数
?=Φx
a
dt t f x )()(
在[a , b ]上可导, 且
)()()(x f dt t f x x
a ='??
? ??=Φ'? 证明: ??+→?=Φ-?+Φ=???='x x x x dt t f x x x y x
y
y )()()(,lim 0
)()(lim )(lim )(lim
)(000
x f f x
x
f x dt t f x x x x
x x
x ==??=?=Φ'→?→??+→??
ξξ积分中值定理
.
注: 若)(x f 在[a , b ]上不连续, 则最后一个等式不成立. 此定理说明, ?
=
Φx
a
dt t f x )()(是)(x f 的一个原函数.
例1. 202sin sin x dt t x
='??
? ???
例2. ?
=
x t dt e x G 1
)(, 求)(x G '
例3. 求极限x
dt
e x
t x sin lim 0
?
→.
三、牛顿—莱布尼茨公式
定理 若)(x f 在[a , b ]上连续, )(x F 是)(x f 的一个原函数,则
)()()(a F b F dx x f b
a
-=?
证明:)(x F 是)(x f 的一个原函数, ?
=
Φx
a
dt t f x )()(也是)(x f 的一个原函数, 同
一个函数的两个原函数之间相关一个常数, 于是有:
)
()()()(0)()()()()()()()(a F b F dx x f a F C C a F dx x f C b F dx x f C
x F dx x f C x F dt t f b
a a a
b a x
a
x
a
-=??????-=?=+=+=?+=?=-?????
[]b
a
b a
b
a
dx
x f x F a F b F dx x f ??
=
=-=)()()()()(记作
记作
例1.
?
9
4
dx x
例2.
?
-214
1)
1(1dx x x
[]
3
)124(2arcsin 212)
1(1214
1214
1214
1π
ππ=-==-=-?
?
x
x
x d dx x x
例3.
?--1
21
dx x
[]2ln ln 11
2
1
2-==----?x dx x 例4.
?
-3
2
2dx x
[]
[]
942)(2230
2
02
2
3
2
3
2
+=+-=+-=---???
x x xdx dx x dx x
例5.
{}
?
2
2,max dx x x
{
}
3
8
21,max 2
210
2
2
+=
+=???
dx x xdx dx x x 例6.
?
-π
3sin sin dx x x
()()3
4sin 32sin 32)cos (sin cos sin cos sin sin sin 2
23202
3
2
20
3
=???
???-??????=-+?==-???
?
π
ππ
π
ππ
π
π
x x dx x x xdx x dx
x x dx x x
注:在数学计算过程中, 要对结论(答案)作合理性检验.
§3. 定积分的换元法和分部积分法
一、定积分的换元法
定理 若)(],
,[)(t x b a C x f ?=∈满足如下条件:
(1) )(t ?是[α,β](或[β,α])上单值单调函数; (2) )(t ?在[α,β](或[β,α])有连续导数; (3) b a ==)(,)(β?α? 则:
??
'=β
α
??dt t t f dx x f b
a
)()]([)(.
例1.
dx x x ?
++4
1
22
令2
1
,122-==+t x t x . 当x =0时, t =1; 当x =4时, t =3.
322
332123221
1223
1
33123124
=
+?=+=?+-=++???
t dt t tdt t t dx x x (若不定积分掌握得很好得话, 可以直接凑微分:
40404
12132122112221)12(21122?????
?+++=++-+=++????
dx x dx x dx x x dx x x ) 与不定积分换元法相比较, 有两点不同:
(1) 积分变量由x 变为t 时, 积分的上下限也要随之改变; (2) 求出关于t 的原函数后无须回代成x 的函数. 例2.
dx x x ?
---2
2
2
1
1
12)1(tan sec sec 1
1433
243321
cos sec 2
2
2
ππ
πππ-=-==
-??
?
=
=--dt dt t t t dx
x x x t t
x
注:换元积分公式,满足)(t ?所要求的条件很重要,如:
I dt t
dt t t dx x I t x -=+-=-
?+=
+=?
??
--=
-1
1
11222
11
12
11
)1(11111
而事实上,[]2
arctan 1
1π
=
=-x I ,其原因在于)(t ?在t=0不可导.
例3. 证明: (1) 若)(x f 是[-a , a ]上的偶函数, 则??
=-a
a
a
dx x f dx x f 0
)(2)(
(2) 若证明)(x f 是[-a , a ]上的奇函数, 则0)(=?
-a
a
dx x f
证明:
???
+=--a
a
a
a
dx x f dx x f dx x f 0
0)()()(
????
???
?+-=+-=-=-=--=
--=-a
a
a a
a
a
a a
t
x a dt
x f x f dx x f dx x f dx x f dx
x f dt t f t d t f dx x f 0
)]()([)()()()()()()()(
此例提示我们, 在计算定积分时, 看到对称的积分限, 要保持敏感. 例
?
-=+1
1
5340)(cos x x x .
例4. ]1,0[)(C x f ∈, 证明:
?
???=
=π
π
π
π
π
20
20
)(sin 2)(sin )2()(cos )(sin )1(dx
x f dx x xf dx x f dx x f
并计算
?
+π
2
cos 1sin dx x
x
x ?????????=?-=--=
=-=
-=-=π
π
π
ππππ
π
π
π
π
πππ0
20
22
20
)(sin )(sin 2)(sin )(sin )()(sin )()(sin )2()(cos )()(cos )(sin )1(dx
x f dx x xf dt t tf dx x f t d t f t dx x xf dx
x f t d t f dx x f t
x t x
[][]4
)arctan(cos 2
)arctan(cos 2
cos cos 11
2cos 1sin 2cos 1sin 2
02020
2π
π
π
πππ
ππππ
=
=
-
=+-=+=+???
x x x d x
dx x x dx x x x
二、定积分的分部积分法
????'-=-=='dx u v uv vdu uv udv dx v u
[]?
??'-=='b
a
b a
b a
b a
dx u v uv udv dx v u
定积分的分部积分法适用的函数类型与不定积分的分部积分法相同. 例1. ?
--1
2dx xe x
例2.
12ln 23ln 3ln 3
2
--=?dx
例3. )(cos 20
N n xdx I n n ∈=
?
π
[
]
()??????
???-?--??-?--====
=??????
??-?--?-?--=--?-=-=
-=?-=?--=--=--=-=-===????????-----------为奇数为偶数为奇数
为偶数n n n n n n n n n n I xdx I dx x I n I n n n n n I n n n n I n n n n I n n I I n
n I I n nI I I n dx
x x n xdx
x n xdx x n x
xd x x x xd xdx I n n n n n n n n n n n n n n n n n n
n 13
5)2(24)3)(1(224)2(13)3)(1(1
cos 2
cos 35)2(24)3)(1(24)2(1
3)3)(1(23
111
)1())(1(]cos [cos )1(cos )cos 1()1(cos
sin )1(cos sin sin cos
sin cos
cos 20
120
01
04222220
220
2220
2
220
1201
20
1
20
ΛΛΛΛΛΛΛΛπ
ππ
π
π
π
π
π
ππ
π
积分公式:????????-?-==??为奇数为偶数n n n n n n xdx xdx n
n 1!
!!)!1(2!!!)!1(cos sin 20
20π
ππ
例4.
16
322413cos 2
4π
ππ
=???=
?
xdx
§4. 反常积分(广义积分)
定义定积分
?
b
a
dx x f )(需满足如下条件: (1) )(x f 有界 (2) )(x f 只有有限个间断
点 (3) a , b 为确定的数值, 即积分限是有限值. 反常积分是对无穷积分限和无界函数定义的积分.
一、无穷限的反常积分
定义 设),[)(∞+∈a C x f , 取t >a , 若极限
?
+∞→t
a
t dx x f )(lim
存在, 则称此极限为),[)(∞+a x f 在上的反常积分, 记作
?
+∞
a
dx x f )(, 即:
?
?
+∞→+∞
=t
a
t a
dx x f dx x f )(lim
)(
?
+∞→t
a
t dx x f )(lim
存在, 也称为?
+∞
a
dx x f )(收敛;
若?
+∞→t
a
t dx x f )(lim
不存在, 则称?
+∞a
dx x f )(发散.
类似地, 定义:
))
,()(()()()(])
,()(()(lim
)(∞+-∞∈+=-∞∈=?
??
?
?∞
+∞
-∞
+∞
--∞→∞-C x f dx x f dx x f dx x f b C x f dx x f dx x f c
c b
t
t b
注:
都收敛收敛?
??
+∞
∞
-+∞
∞
-?c
c dx x f dx x f dx x f )(,)()(
[]∞+∞
++∞
→='∞
+='??
?=
=-=
-=a
a
t x f x F a
x f x F t
a
dx
x f x F a F t F dx
x f a F t F dx
x f )()()()(lim )()
()()()
()()
()(记作
记作
例1. 2arctan 110
02π==+∞
+∞
+?
x dx x
例2.
?
∞
-0
dx xe x
[][]1
lim lim ][lim lim
lim
-=---=-===-∞
→-∞
→-∞
→-∞→-∞→∞
-??
?
?
t
t t
t t
x
t
x
t t
x t t
x t x
e e te dx e xe xde dx
xe dx xe 例3.
?∞
+∞-+dx x x
21
)()1ln(2111110
22
02022发散+∞=+=++++=+?
???∞
+∞
+∞+∞-∞
+∞-x dx x x dx x x dx x x dx x x
故
?∞
+∞-+dx x x
21发散.
二、无界函数的反常积分
定义 设∞=∈+→)(lim ],,()(x f b a C x f a
x , 取b >t >a , 若极限
?+→b
t
a
t dx x f )(lim
存在, 则称此极限为],()(b a x f 在上的反常积分, 仍记作
?
b
a
dx x f )(, 即:
??
+→=b
t
a
t b
a
dx x f dx x f )(lim )(
亦称为
?
b
a
dx x f )(收敛; 否则,称?b
a
dx x f )(发散.
类似地, 定义:
?????+=∞
=-∞=+?∈=∞
=-∈-→b c
c
a
b
a
t
a
b
t b a
dx
x f dx x f dx x f c f c f b c c a C x f dx x f dx x f b f b a C x f )()()(:)0()0(]},
,)(),{[)()(lim )(:)0(),
,[)(定义或若定义若
注:
都收敛收敛??
?
?
b
c
c
a
b
a
dx x f dx x f dx x f )(,)()(
例4.
?
-1
2
1dx x
x
11221lim 1lim 11lim
0210
21
1
2
2
1=??????-?-=-=-∞
=---→→→?
?
t
t t
t x x dx x
x
dx x x x x
例5.
?10
ln xdx
[]1ln lim ln lim ln 1
1
1
-=-==++→→??
t t t
t x x x xdx xdx
例6.
?
-2
2
)
1(1
dx x
发散1
11
022121022022111lim )1(1)1(1
)1(1)1(1)1(1
lim
??????-=--+-=-∞
=--→→????x dx x dx x dx x dx x x t x 故
?
-2
2
)
1(1
dx x 发散. 注: 计算
?
b
a
dx x f )(前, 首先判断)(x f 在[a , b ]上是否有无穷点.
定积分小结
一、基本概念 1.定积分
∑?
=→?=n
i i i b
a
x f dx x f 1
)(lim )(ξλ
2.变上限积分函数
?=Φx
a
dt t f x )()(
3.广义积分 (1)无穷积分限 (2)无穷间断点 二、定积分的性质
1.定积分与被积分字母无关
[][]????
===b
a
b a
b a
b
a
d f du u f dt t f dx x f )()()()(
2.积分限的分割
???
+=b
c
c a
b
a
dx x f x f dx x f )()()(
3.积分中值定理
设],[)(b a C x f ∈, 则),(b a ∈?ξ, 使得))(()(a b f dx x f b
a
-=?
ξ
4.对称函数在对称区间上的积分
???
??=??
-为偶函数为奇函数)()(2)(0)(0
x f dx x f x f dx x f a
a
a
三、定积分的计算
1.牛——莱公式 2.换元积分法 3.分部积分法
四、积分上限函数求导
)()]([)()()()()
(x u x u f dt t f x f dt t f x x u a x
a '?='??
? ??='??
? ??=Φ'??
【第五部分】不定积分 1.书本知识(包含一些补充知识) (1)原函数:F ’(x )=f (x ),x ∈I ,则称F (x )是f (x )的一个“原函数”。 (2)若F (x )是f (x )在区间上的一个原函数,则f (x )在区间上的全体函数为F (x )+c (其中c 为常数) (3)基本积分表 c x dx x +?+?=?+???11 1(α≠1,α为常数) (4)零函数的所有原函数都是c (5)C 代表所有的常数函数 (6)运算法则 []??????±?=?±??=??dx x g dx x f dx x g x f dx x f a dx x f a )()()()()()(②① (7)[][]c x F dx x x f +=??)()(')(???复合函数的积分: c b x F dx b x f c b ax F a b ax d b ax f a dx b ax f ++=?+++?=+?+?=?+???)()()(1)()(1)(一般地, (9)连续函数一定有原函数,但是有原函数的函数不一定连续,没有原函数的函数一定不连续。 (10)不定积分的计算方法 ①凑微分法(第一换元法),利用复合函数的求导法则 ②变量代换法(第二换元法),利用一阶微分形式不变性 ③分部积分法: 【解释:一阶微分形式不变性】 数乘运算 加减运线性运 (8
释义:函数 对应:y=f(u) 说明: (11)c x dx a x a x ++??++?22ln 1 22 (12)分段函数的积分 例题说明:{} dx x ??2,1max (13)在做不定积分问题时,若遇到求三角函数奇次方的积分,最好的方法是将其中的一 (16)隐函数求不定积分 例题说明: (17)三角有理函数积分的万能变换公式 (18)某些无理函数的不定积分 ②欧拉变换 (19)其他形式的不定积分 2.补充知识(课外补充) ☆【例谈不定积分的计算方法】☆ 1、不定积分的定义及一般积分方法 2、特殊类型不定积分求解方法汇总 1、不定积分的定义及一般积分方法 (1)定义:若函数f(x)在区间I 上连续,则f(x)在区间I 上存在原函数。其中Φ(x)=F(x)+c 0,(c 0为某个常数),则Φ(x)=F(x)+c 0属于函数族F(x)+c (2)一般积分方法 值得注意的问题:
2018考研高数重点复习定积分与不定积 分定理总结 在暑期完成第一轮基础考点的复习之后,9月份开始需要对考研数学所考的定理定义进行必要的汇总。本文为同学们整理了高数部分的定积分与不定积分定理定义汇总。 ?不定积分 1、原函数存在定理 ●定理如果函数f(x)在区间I上连续,那么在区间I上存在可导函数F(x),使对任一x ∈I都有F’(x)=f(x);简单的说连续函数一定有原函数。 ●分部积分法 如果被积函数是幂函数和正余弦或幂函数和指数函数的乘积,就可以考虑用分部积分法,并设幂函数和指数函数为u,这样用一次分部积分法就可以使幂函数的幂降低一次。如果被积函数是幂函数和对数函数或幂函数和反三角函数的乘积,就可设对数和反三角函数为u。 2、对于初等函数来说,在其定义区间上,它的原函数一定存在,但原函数不一定都是初等函数。 ?定积分 1、定积分解决的典型问题 (1)曲边梯形的面积(2)变速直线运动的路程 2、函数可积的充分条件 ●定理设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积,即连续=>可积。 ●定理设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积。 3、定积分的若干重要性质 ●性质如果在区间[a,b]上f(x)≥0则∫abf(x)dx≥0。 ●推论如果在区间[a,b]上f(x)≤g(x)则∫abf(x)dx≤∫abg(x)dx。
●推论|∫abf(x)dx|≤∫ab|f(x)|dx。 ●性质设M及m分别是函数f(x)在区间[a,b]上的最大值和最小值,则m(b-a)≤∫abf(x)dx ≤M(b-a),该性质说明由被积函数在积分区间上的最大值及最小值可以估计积分值的大致范围。 ●性质(定积分中值定理)如果函数f(x)在区间[a,b]上连续,则在积分区间[a,b]上至少存在一个点ξ,使下式成立:∫abf(x)dx=f(ξ)(b-a)。 4、关于广义积分 设函数f(x)在区间[a,b]上除点c(a ?定积分的应用 1、求平面图形的面积(曲线围成的面积) ●直角坐标系下(含参数与不含参数) ●极坐标系下(r,θ,x=rcosθ,y=rsinθ)(扇形面积公式S=R2θ/2) ●旋转体体积(由连续曲线、直线及坐标轴所围成的面积绕坐标轴旋转而成)(且体积V=∫abπ[f(x)]2dx,其中f(x)指曲线的方程) ●平行截面面积为已知的立体体积(V=∫abA(x)dx,其中A(x)为截面面积) ●功、水压力、引力 ●函数的平均值(平均值y=1/(b-a)*∫abf(x)dx)
第五章 不定积分习题答案 练习5.1 1. 是 2. 不是,2 13 x c +为2 x 的全部原函数 3. 22,xdx x c =+?,曲线为2 x c +,c 为常数 4. 2 1(2)22 x dx x x c += ++?,由已知 ,当2x =时 1.4452 c ++= 得1c =-,所以函数为2 1212 y x x =+- 练习5.2 1.3 4 1(1)4 x x x c -=- +?,c 为任意常数 2. 原式=1 1 3 1 3 7 222 2444()()7 x x dx x dx x dx x c === +?? 3. 4. 2 2 2 222 cos 1sin 1cot ( 1)sin sin sin cot x x xdx dx dx dx x x x x x c -= = = -=--+??? ? 练习5.3 1.3332 1 2 22(3)33ln x x x dx d x c = = +?? 2.23 3 33 1 1 1(1)ln(1)1313 x dx d x x c x x = +=++++? ? 3.cos cos sin x x x x x e e dx e de e c ==+?? 4. 3 2 2 sin 1tan tan (sec 1)tan (tan )tan ln cos cos 2 x xdx x x dx xd x dx x x c x = -= - =++???? 5.令 4 4 2 3 2 2 2 1111[(1)]tan 1 1 1 3 x x dx dx x dx x x x c x x x -+= =-+ = -+++++?? ?
不定积分
一、原函数 定义1 如果对任一I x ∈,都有 )()(x f x F =' 或 dx x f x dF )()(= 则称)(x F 为)(x f 在区间I 上的原函数。 例如:x x cos )(sin =',即x sin 是x cos 的原函数。 2 211)1ln([x x x +='++,即)1ln(2x x ++是 2 11x +的原函数。 原函数存在定理:如果函数)(x f 在区间I 上连续,则)(x f 在区间I 上一定有原函数,即存在区间I 上的可导函数)(x F ,使得对任一I x ∈,有)()(x f x F ='。 注1:如果)(x f 有一个原函数,则)(x f 就有无穷多个原函数。 设)(x F 是)(x f 的原函数,则)(])([x f C x F ='+,即C x F +)(也为)(x f 的原函数,其中C 为任意常数。 注2:如果)(x F 与)(x G 都为)(x f 在区间I 上的原函数,则)(x F 与)(x G 之差为常数,即C x G x F =-)()((C 为常数) 注3:如果)(x F 为)(x f 在区间I 上的一个原函数,则C x F +)((C 为任意常数)可表达)(x f 的任意一个原函数。 二、不定积分 定义2 在区间I 上,)(x f 的带有任意常数项的原函数,成为)(x f 在区间I 上的不定积分,记为?dx x f )(。 如果)(x F 为)(x f 的一个原函数,则 C x F dx x f +=?)()(,(C 为任意常数)
x y o )(x F y = C x F y +=)( 三、不定积分的几何意义 不定积分的几何意义如图5—1所示: 图 5—1 设)(x F 是)(x f 的一个原函数,则)(x F y =在平面上表示一条曲线,称它为 )(x f 的一条积分曲线.于是)(x f 的不定积分表示一族积分曲线,它们是由) (x f 的某一条积分曲线沿着y 轴方向作任意平行移动而产生的所有积分曲线组成的.显然,族中的每一条积分曲线在具有同一横坐标x 的点处有互相平行的切线,其斜率都等于)(x f . 在求原函数的具体问题中,往往先求出原函数的一般表达式C x F y +=)(,再从中确定一个满足条件 00)(y x y = (称为初始条件)的原函数)(x y y =.从几何上讲,就是从积分曲线族中找出一条通过点),(00y x 的积分曲线. 四、不定积分的性质(线性性质) [()()]()()f x g x dx f x dx g x dx ±=±??? ()() kf x dx k f x dx =??k ( 为非零常数)
第四章 不 定 积 分 § 4 – 1 不定积分的概念与性质 一.填空题 1.若在区间上)()(x f x F =',则F(x)叫做)(x f 在该区间上的一个 , )(x f 的 所有原函数叫做)(x f 在该区间上的__________。 2.F(x)是)(x f 的一个原函数,则y=F(x)的图形为?(x)的一条_________. 3.因为 dx x x d 2 11)(arcsin -= ,所以arcsinx 是______的一个原函数。 4.若曲线y=?(x)上点(x,y)的切线斜率与3 x 成正比例,并且通过点A(1,6)和B(2,-9),则该 曲线方程为__________?。 二.是非判断题 1. 若f ()x 的某个原函数为常数,则f ()x ≡0. [ ] 2. 一切初等函数在其定义区间上都有原函数. [ ] 3. ()()()??'='dx x f dx x f . [ ] 4. 若f ()x 在某一区间内不连续,则在这个区间内f ()x 必无原函数. [ ] 5. =y ()ax ln 与x y ln =是同一函数的原函数. [ ] 三.单项选择题 1.c 为任意常数,且)('x F =f(x),下式成立的有 。 (A )?=dx x F )('f(x)+c; (B )?dx x f )(=F(x)+c; (C )? =dx x F )()('x F +c; (D) ?dx x f )('=F(x)+c. 2. F(x)和G(x)是函数f(x)的任意两个原函数,f(x)≠0,则下式成立的有 。 (A )F(x)=cG(x); (B )F(x)= G(x)+c; (C )F(x)+G(x)=c; (D) )()(x G x F ?=c. 3.下列各式中 是| |sin )(x x f =的原函数。 (A) ||cos x y -= ; (B) y=-|cosx|; (c)y={ ;0,2cos , 0,cos <-≥-x x x x (D) y={ . 0,cos ,0,cos 21<+≥+-x c x x c x 1c 、2c 任意常数。 4.)()(x f x F =',f(x) 为可导函数,且f(0)=1,又2 )()(x x xf x F +=,则f(x)=______.
42 / 9 第五章 定积分 第一节 定积分的概念与性质 一、填空题: 在 ? +10 3 1dx x 与? +1 41dx x 中值比较大的是 . 二、选择题(单选): 1.积分中值定理 ? -=b a a b f dx x f ))(()(ξ,其中: (A) ξ是[]b a ,上任一点; (B) ξ是[]b a ,上必定存在的某一点; (C) ξ是[]b a ,唯一的某点; (D) ξ是[]b a ,的中点. 答:( ) 2.曲线x e y =与该曲线过原点的切线及y 轴所围成图形的面积值为: (A) ?-10)(dx ex e x ; (B) ?-e dy y y y 1 )ln (ln ; (C) ? -e x x dx xe e 1 )(; (D) ?-1 )ln (ln dy y y y . 答:( ) 第二节 微积分基本公式 一、填空题: 1.=-? -212 12 11dx x . 2. 0)32(0 2=-? k dx x x )0(>k ,则=k . 二、选择题(单选): 若)(x f 为可导函数,且已知0)0(=f ,2)0(='f ,则 2 )(lim x dt t f x x ?→ (A)0; (B)1; (C)2; (D)不存在. 答:( ) 三、试解下列各题: 1.设??? ??>≤+=1,2 11 ,1)(32x x x x x f ,求?20 )(dx x f .
43 / 9 2.设?? ???><≤≤=ππ x x x x x f ,0,00,sin 21 )(,求?=x dt t f x 0 )()(?在),(∞+-∞上的表达式. 四、设)(x f 在],[b a 上连续,且0)(>x f ,? ? += x a x b t f dt dt t f x F ) ()()(.证明: (1)2)('≥x F ; (2)方程0)(=x f 在),(b a 内有且仅有一个根. 第三节 定积分的换元法和分部积分法
关于高等数学不定积分例题思路和答案超全 Last revision on 21 December 2020
第4章 不定积分 习题4-1 1.求下列不定积分: 知识点:直接积分法的练习——求不定积分的基本方法。 思路分析:利用不定积分的运算性质和基本积分公式,直接求出不定积分! ★(1) 思路: 被积函数52 x - =,由积分表中的公式(2)可解。 解:53 2 2 23x dx x C - -==-+?
★(2) dx - ? 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:1 14111 33322 23 ()2 4dx x x dx x dx x dx x x C - - =-=-=-+???? ★(3)22 x x dx +? () 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:2 2 3 2122ln 23 x x x x dx dx x dx x C +=+=++? ??() ★(4) 3)x dx - 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:315 3 2 2 222 3)325 x dx x dx x dx x x C -=-=-+?? ★★(5)4223311x x dx x +++? 思路:观察到422 22 3311311x x x x x ++=+++后,根据不定积分的线性性质,将被积函数分项,分别积分。 解:422 32233113arctan 11x x dx x dx dx x x C x x ++=+=++++??? ★★(6)2 21x dx x +? 思路:注意到 22222 111 1111x x x x x +-==-+++,根据不定积分的线性性质,将被积函数分项,分别积分。 解:2221arctan .11x dx dx dx x x C x x =-=-+++??? 注:容易看出(5)(6)两题的解题思路是一致的。一般地,如果被积函数为一个有理的假分式,通常先将其分解为一个 整式加上或减去一个真分式的形式,再分项积分。 ★(7)x dx x x x ?34134 (-+-) 2 思路:分项积分。 解:3411342x dx xdx dx x dx x dx x x x x --=-+-? ????34134(-+-)2
不定积分内容概要
课后习题全解 习题4-1 1.求下列不定积分: 知识点:直接积分法的练习——求不定积分的基本方法。 思路分析:利用不定积分的运算性质和基本积分公式,直接求出不定积分!★(1) 思路: 被积函数 5 2 x- =,由积分表中的公式(2)可解。 解:53 22 2 3 x dx x C -- ==-+ ? ★ (2)dx - ? 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:114 111 333 222 3 ()2 4 dx x x dx x dx x dx x x C -- -=-=-=-+ ???? ★(3)2 2x x dx + ?() 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:223 21 22 ln23 x x x x dx dx x dx x C +=+=++ ??? ( ) ★(4)3) x dx - 思路:根据不定积分的线性性质,将被积函数分为两项,分别积分。 解:3153 2222 2 3)32 5 x dx x dx x dx x x C -=-=-+ ??
★★(5)4223311 x x dx x +++? 思路:观察到422223311311 x x x x x ++=+++后,根据不定积分的线性性质,将被积函数分项,分别积分。 解:42232233113arctan 11x x dx x dx dx x x C x x ++=+=++++??? ★★(6)2 21x dx x +? 思路:注意到222221111111x x x x x +-==-+++,根据不定积分的线性性质,将被积函数分项, 分别积分。 解:2221arctan .11x dx dx dx x x C x x =-=-+++??? 注:容易看出(5)(6)两题的解题思路是一致的。一般地,如果被积函数为一个有理的假分式,通常先将其分解为一个整式加上或减去一个真分式的形式,再分项积分。 ★(7)x dx x x x ?34134(-+-)2 思路:分项积分。 解:3411342x dx xdx dx x dx x dx x x x x --=-+-?? ???34134(-+-)2 223134ln ||.423 x x x x C --=--++ ★(8) 23(1dx x -+? 思路:分项积分。 解: 2231(323arctan 2arcsin .11dx dx x x C x x -=-=-+++?? ★★(9) 思路=11172488x x ++==,直接积分。 解:715888.15 x dx x C ==+? ★★(10)221(1)dx x x +? 思路:裂项分项积分。
第五章定积分 教学目的: 1、理解定积分的概念。 2、掌握定积分的性质及定积分中值定理,掌握定积分的换元积分法与分部积分法。 3、理解变上限定积分定义的函数,及其求导数定理,掌握牛顿—莱布尼茨公式。 4、了解广义积分的概念并会计算广义积分。 教学重点: 1、定积分的性质及定积分中值定理 2、定积分的换元积分法与分部积分法。 3、牛顿—莱布尼茨公式。 教学难点: 1、定积分的概念 2、积分中值定理 3、定积分的换元积分法分部积分法。 4、变上限函数的导数。 §5. 1 定积分概念与性质 一、定积分问题举例 1.曲边梯形的面积 曲边梯形:设函数y=f(x)在区间[a,b]上非负、连续.由直线x=a、x=b、y=0及曲线y=f (x)所围成的图形称为曲边梯形,其中曲线弧称为曲边. 求曲边梯形的面积的近似值: 将曲边梯形分割成一些小的曲边梯形,每个小曲边梯形都用一个等宽的小矩形代替,每个小曲边梯形的面积都近似地等于小矩形的面积,则所有小矩形面积的和就是曲边梯形面积的近似值.具体方法是:在区间[a,b]中任意插入若干个分点 a=x0 高等数学之不定积分的计算方法总结不定积分中有关有理函数、三角函数有理式、简单无理函数的求法,是考研中重点考察的内容,也是考研中的难点。不定积分是计算定积分和求解一阶线性微分方程的基础,所以拿握不定积分的计算方法很重要。不定积分考查的函数特点是三角函数、简单无理函数、有理函数综合考查,考查方法是换元积分法、分部积分法的综合应用。不定积分的求法的理解和应用要多做习题,尤其是综合性的习题,才能真正掌握知识点,并应用于考研。 不定积分的计算方法主要有以下三种: (1)第一换元积分法,即不定积分的凑微分求积分法; (2)第二换元积分法 (3)分部积分法常见的几种典型类型的换元法: 樂,Q? o 金J犷- / .乍治阳必厶二如皿盒.「宀丄" 名% =a仏 找.』x二a沁沁r 年”十I '九久二严詈严妬5inx八ic5兄厶 整 I—炉 叶严 山二启虫? 常见的几种典型类型的换元法 题型一:利用第一换元积分法求不定积分 分析: 1-3 ? - IK )-忑.旦r x 二)祝成);网><可久切 二2氐化如(長)寸 a 花不直押、朱 J 、 解: 2少弋協“尤十C__ -辿迪牆H JS m 弟 R Eff 洱 ->1和弟r 直 - —7朮呻' g 丄 U P A J 齐—系卩£.§计 一 H a8~t ' J 乂 u D y " ?朮? p o r t v 卩 J (r 4 5*〉J" 卩?对渎 t-k )+c p T + T d ? g T + c m -辿」 当积分j/O心(X)不好计算容易计算时[使用分部私jf(A-)Jg(.v)二f(x)g(x)- J g(x)df(x).常见能使用分部积分法的类型: ⑴卩"“dx J x n srn xdx J尢"cos皿等,方法是把。',sin-t, cosx 稽是降低X的次数 是化夫In 尢9 arcsine arctanx. 例11: J (1 + 6-r )arctanAz/.r :解:arctan f xdx等,方法是把疋; Jx" arcsm11xdx 第五章不定积分 第一节不定积分的概念与性质 一、原函数 在微分学中,导数是作为函数的变化率引进的,例如,已知变速直线运动物体的路程函数s=s(t),则物体在时刻t的瞬时速度v(t)=s′(t),它的反问题是:已知物体在时刻t的瞬时速度v=v(t),求路程函数s(t),也就是说,已知一个函数的导数,要求原来的函数.这就引出了原函数的概念. 定义1 设f(x)是定义在区间I上的已知函数,如果存在函数F(x),使对任意x∈I都有 F′(x)=f(x),或d F(x)=f(x)d x,(5-1-1)则称F(x)为f(x)在区间I上的一个原函数. 例如在(1,+∞)内 , [ln(x)]′ (1,+∞)内的一个原函数.显然,ln(x)+2, 故ln(x ln(x) 的原函数.一般地,对任意常数C,ln(x)+C 由此可知,当一个函数具有原函数时,它的原函数不止一个. 关于原函数,我们首先要问:一个函数具备什么条件,能保证它的原函数一定存在?这个问题将在下一章中讨论,这里先介绍一个结论. 定理1(原函数存在性定理) 如果函数f(x)在区间I上连续,则在区间I上存在可导函数F(x),使对任意x∈I,都有 F′(x)=f(x). 这个结论告诉我们连续函数一定有原函数. 我们已经知道:一个函数如果存在原函数,那么原函数不止一个,这些原函数之间的关系有如下定理: 定理2 如果F(x)是f(x)在区间I上的一个原函数,则在区间I上f(x)的所有原函数都可以表示成形如F(x)+C(C为任意常数)的形式. 定理需要证明两个结论: (1) F(x)+C是f(x)的原函数; (2) f(x)的任一原函数都可以表示成F(x)+C的形式. 第五章 定积分 内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。 要求:理解定积分的概念和性质。掌握牛顿-莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。 重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。 难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。 §1.定积分的概念 一、实例分析 1.曲边梯形的面积 设函数)(x f y =∈C[a , b ], 且)(x f y =>0. 由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形. 如何定义曲边梯形的面积 (1) 矩形面积=底高. (2) 预备一张细长条的纸, 其面积底高. (3) 预备一张呈曲边梯形状的纸, 将其撕成许多细长条. (4) 启示: 将曲边梯形分割为许多细长条, 分割得越细, 误差越小. 第i 个细长条面积)],,[()(11---=?∈??≈?i i i i i i i i i x x x x x x f S ξξ 曲边梯形面积: ∑=?≈ n i i i x f S 1 )(ξ 定积分概念示意图.ppt 定义: ),,2,1,max {()(lim 1 n i x x f S i n i i i Λ=?=?=∑=→λξλ y =f (x ) x =a x =b y =f (x ) a=x 0 x 1 x i-1 x i x n =b 抛开上述过程的几何意义,将其数学过程定义为定积分. 二、定积分的定义 1. 定义 设)(x f y =在[a , b ]有定义, 且有界. (1) 分割: 用分点b x x x a n =<<<=Λ10把[a , b ]分割成n 个小区间: } ,,2,1,max{,,,2,1],,[11n i x x x x n i x x i i i i i i ΛΛ=?=-=?=--λ记 (2) 取点: 在每个小区间],[1i i x x -上任取一点i , 做乘积: i i x f ?)(ξ. (3) 求和: ∑=?n i i i x f 1 )(ξ (4) 取极限: ∑=→?n i i i x f 1 )(lim ξλ 若极限存在, 则其为)(x f 在[a , b ]上的定积分, 记作: ? b a dx x f )(. 即: ∑? =→?=n i i i b a x f dx x f 1 )(lim )(ξλ [a , b ]: 积分区间;a :积分下限;b :积分上限; ∑=?n i i i x f 1 )(ξ积分和式. 问题: 定积分是极限值, 在求极限的过程中, 谁是常量, 谁是变量 注: (1) ∑ =?n i i i x f 1 )(ξ与区间的分割法x i 和取点法 i 有关; 而 ? b a dx x f )(与x i 和 i 无 关. (2) ? b a dx x f )(与a 、b 、f 有关,与x 无关,即: [][]???? ===b a b a b a b a d f du u f dt t f dx x f )()()()( 2.定积分存在定理 定理 若)(x f 在[a , b ]上有界且只有有限个间断点,则)(x f 在[a , b ]上可积. 推论 若)(x f 在[a , b ]上连续,则)(x f 在[a , b ]上可积. 例1. 求 ?1 xdx 第四章不定积分 前面讨论了一元函数微分学,从本章开始我们将讨论高等数学中的第二个核心内容:一元函数积分学.本章主要介绍不定积分的概念与性质以及基本的积分方法. 第1节不定积分的概念与性质 不定积分的概念 在微分学中,我们讨论了求一个已知函数的导数(或微分)的问题,例如,变速直线运动中已知位移函数为 =, s s t () 则质点在时刻t的瞬时速度表示为 =. () v s t' 实际上,在运动学中常常遇到相反的问题,即已知变速直线运动的质点在时刻t的瞬时速度 v v t =, () 求出质点的位移函数 =. s s t () 即已知函数的导数,求原来的函数.这种问题在自然科学和工程技术问题中普遍存在.为了便于研究,我们引入以下概念. 1.1.1原函数 定义 1 如果在区间I 上,可导函数()F x 的导函数为()f x ,即对任一x I ∈,都有 ()()F x f x '= 或 d ()()d F x f x x =, 那么函数()F x 就称为()f x 在区间I 上的原函数. 例如,在变速直线运动中,()()s t v t '=,所以位移函数()s t 是速度函数()v t 的原函数; 再如,(sin )'cos x x =,所以 sin x 是 cos x 在 (,) -∞+∞上的一个原函 数.1 (ln )'(0),x x x =>所以ln x 是1x 在(0,)+∞的一个原函数. 一个函数具备什么样的条件,就一定存在原函数呢这里我们给出一个充分条件. 定理1 如果函数()f x 在区间I 上连续,那么在区间I 上一定存在可导函数()F x ,使对任一∈x I 都有 ()()'=F x f x . 简言之,连续函数一定有原函数.由于初等函数在其定义区间上都是连续函数,所以初等函数在其定义区间上都有原函数. 定理1的证明,将在后面章节给出. 关于原函数,不难得到下面的结论: 第五章定积分综合练习题 一、填空: 1、函数)(x f 在],[b a 上有界是 )(x f 在],[b a 上可积的 条件,而) (x f 在],[b a 上连续是)(x f 在],[b a 上可积的 条件; 2、由定积分的几何意义,则 ? -1 21dx x = ; 3、设 ,18)(31 1 =? -dx x f ,4)(3 1 =?-dx x f 则=?3 1 )(dx x f ; 4、正弦曲线 x y sin =在 ],0[π上与x 轴所围成的平面图形的面积 是 ; 5、某汽车开始刹车,其运动规律为,510)(t t v -=问从刹车开始到停车,汽车驶过的距离是 ; 6、?=x tdt y 02sin ,则4 π= 'x y = ; 7、估计定积分? +4 /54 /2)sin 1(ππdx x 的值的范围是: ; 8、比较下列两个积分值的大小:? 2 1 ln xdx ?2 1 2)(ln dx x ; 9、)(x f ''在],[b a 上连续,则=''? b a dx x f x )( ; 10、无穷积分? +∞ 1 dx x p 收敛,则p 的取值范围是 . 二、计算下列各导数. 1、 ?+2 211x x dt t dx d 2、?? ???==??t t udu y udu x 00sin cos ,求dx dy . 三、计算下列各定积分. 1、 dx x x )1(2 1 +? 2、dx x ?+3 31211 3、dx x ?--2121211 4、 dx x ? 40 2 tan π 5、dx x x x ?-+++0 122 41133 6、dx x ?π20sin 四、求极限 2 )sin(0 2lim x tdt x x ?→. 五、用换元积分法求下列定积分: 1、?-+1 12 ) 511(1 dx x 2、?2 /6 /2 cos ππ udu 3、?+2 1 ln 1e x x dx 4、 ? -π θθ0 3 )sin 1(d 5、? -2 2 2dx x 6、? +41 1x dx 六、用分部积分法求下列定积分: 1、 ? e xdx x 1 ln 2、? 2 /30 arcsin xdx 3、?-1 dt te t 七、求定积分 ?10 dx e x 八、求定积分 ?2 /0 cos πxdx e x 九、求定积分 ? π 3cos 2sin xdx x . 十、求定积分 ? 4 /0 4tan πxdx . 十一、设 ,0 ,0,1)(2???≥<+=-x e x x x f x 求?-2 )1(dx x f . 十二证明:若函数)(x f 在],[a a -上连续,则?-=--a a dx x f x f 0)]()([. 十三证明:??+=+1 1 12211x x t dt t dt . 十四、判定无穷积分 ? +∞ 1 41 dx x 的收敛性,如果收敛,计算其值. 由十个例题掌握有理分式定积解法 【摘要】 当被积函数为两多项式的商 () () P x Q x 的有理函数时,解法各种各样、不易掌握,在此由易到难将其解法进行整理、总结 【关键词】 有理分式 真分式 假分式 多项式除法 拆项法 凑微分法 定积分 两个多项式的商 () () P x Q x 称为有理函数,又称为有理分式,我们总假定分子多项式()P x 与分母多项式()Q x 之间无公因式,当分子多项式()P x 的次数小与分母多项式()Q x ,称有理式为真分式,否则称为假分式. 1.对于假分式的积分:利用多项式除法,总可将其化为一个多项式与一个真分式之和的形式. 例1.2 422 23 1 x x dx x +++? ()222 2 2131 x x x dx x ++-=+? 解 原式 2 2 2212311 x x dx dx dx x x =+-++??? ()42 2222 2 22 222223321.11 311 31 13111 31 arctan x x dx x x x x dx x x x dx dx x x dx dx x x dx dx dx x x x x C +++-=+=-+? ?=-- ?+?? =-++=--+?????????例 解 原式 3 24arctan 3 x x x C = +-+ 总结:解被积函数为假分式的有理函数时,用多项式出发将其化简为多项式和真分式之和的形式,然后进行积分.对于一些常见函数积分进行记忆,有助于提高解题速度,例如: 2221111x dx dx x x ? ?=- ?++?? ?? 对于真分式 () () P x Q x ,若分母可分解为两个多项式乘积()Q x =()()12Q x Q x ,且()1Q x ,()2Q x 无公因式,则可拆分成两个真分式之和: ()()P x Q x ()()()() 1 212P x P x Q x Q x =+,上述过程称为 把真分式化为两个部分分式之和.若()1Q x 或()2Q x 再分解为两个没有公因式的多项式乘积,则最后有理函数分解式中出现多项式、() () 1k P x x a -、 () () 22 l P x x px q ++等三类函数,则多项 式的积分容易求的 2.先举例,有类型一、类型二、类型三,以此为基础求解较复杂的真分式积分 2.1 类型一 ()m k ax b dx cx +? 例2.1.1 () 3 2 1x dx x -? 322 331 =x x x dx x -+-?解 原式 211 =33xdx dx dx dx x x -+-???? 211 =332x x In x C x -+++ 总结:当被积函数多项式与单项式相乘的形式,将其进行化简,使被积函数为简单幂函数, 然后利用常见积分公式进行运算 2.2 类型二 () k m cx dx ax b +? 第五章 定积分 【考试要求】 1.理解定积分的概念和几何意义,了解可积的条件. 2.掌握定积分的基本性质. 3.理解变上限的定积分是变上限的函数,掌握变上限定积分求导数的方法. 4.掌握牛顿——莱布尼茨公式. 5.掌握定积分的换元积分法与分部积分法. 6.理解无穷区间广义积分的概念,掌握其计算方法. 7.掌握直角坐标系下用定积分计算平面图形的面积. 【考试内容】 一、定积分的相关概念 1.定积分的定义 设函数 ()f x 在[,]a b 上有界,在[,]a b 中任意插入若干个分点 0121n n a x x x x x b -=<<<<<=, 把区间[,]a b 分成n 个小区间01[,]x x ,12[,]x x ,,1[,]n n x x -, 各个小区间的长度依次为1 10x x x ?=-,221x x x ?=-,,1n n n x x x -?=-.在 每个小区间1[,]i i x x -上任取一点i ξ (1i i i x x ξ-≤≤) ,作函数值()i f ξ与小区间长度i x ?的乘积()i i f x ξ? (1,2, ,i n =),并作出和1 ()n i i i S f x ξ==?∑. 记 12max{,,,}n x x x λ=???,如果不论对[,]a b 怎样划分,也不论在小区间 1[,]i i x x -上点i ξ怎样选取,只要当0λ→时,和S 总趋于确定的极限I ,那么称这个极 限I 为函数 ()f x 在区间[,]a b 上的定积分(简称积分),记作 ()b a f x dx ?,即 1 ()lim ()n b i i a i f x dx I f x λξ→===?∑? , 其中 ()f x 叫做被积函数,()f x dx 叫做被积表达式,x 叫做积分变量,a 叫做积分下限, b 叫做积分上限,[,]a b 叫做积分区间. 说明:定积分的值只与被积函数及积分区间有关,而与积分变量的记法无关,也就是说 ()()()b b b a a a f x dx f t dt f u du ==? ??. 2.定积分存在的充分条件(可积的条件) (1)设 ()f x 在区间[,]a b 上连续,则()f x 在[,]a b 上可积. (2)设 ()f x 在区间[,]a b 上有界,且只有有限个间断点,则()f x 在区间[,]a b 上可积. 说明:由以上两个充分条件可知,函数()f x 在区间[,]a b 上连续,则()f x 在[,]a b 上 一定可积;若 ()f x 在[,]a b 上可积,则()f x 在区间[,]a b 上不一定连续,故函数() f x 在区间[,]a b 上连续是 ()f x 在[,]a b 上可积的充分非必要条件. 3.定积分的几何意义 在区间[,]a b 上函数 ()0f x ≥时,定积分()b a f x dx ?在几何上表示由曲线 ()y f x =、两条直线x a =、x b =与x 轴所围成的曲边梯形的面积. 在区间[,]a b 上 ()0f x ≤时,由曲线()y f x =、两条直线x a =、x b =与x 轴 所围成的曲边梯形位于x 轴的下方,定积分()b a f x dx ? 在几何上表示上述曲边梯形面积的 负值. 在区间[,]a b 上 ()f x 既取得正值又取得负值时,函数()f x 的图形某些部分在x 轴 的上方,而其他部分在x 轴的下方,此时定积分 ()b a f x dx ? 表示x 轴上方图形的面积减去 x 轴下方面积所得之差. 二、定积分的性质 《高等数学》不定积分课后习题详解 篇一:高等数学第四章不定积分习题 第四章不 定 积 分 4 – 1 不定积分的概念与性质 一.填空题 1.若在区间上 F?(x)?f(x),则 F(x)叫做 f(x)在该区间上的一个 f(x)的 所有原函数叫做 f(x) 在该区间上的__________。 2.F(x)是 f(x)的一个原函数,则 y=F(x)的图形为?(x)的一条_________. 3.因为 d(arcsinx)? 1?x2 dx ,所以 arcsinx 是______的一个原函数。 4.若曲线 y=?(x)上点(x,y)的切线斜率与 x 成正比例,并且通过点 A(1,6)和 B(2,-9),则该曲线 方程为__________ 。 二.是非判断题 1. 若 f?x?的某个原函数为常数,则 f?x??0.[ ] 2. 一切初等函数在其定义区间上都有原 函数.[ ] 3. 3 ??f?x?dx???f??x?dx.[ ] ? 4. 若 f?x?在某一区间内不连续,则在这个区间内 f?x?必无原函数. [ ] 5.y?ln?ax?与 y?lnx 是同一函数的原函数.[ ] 三.单项选择题 1.c 为任意常数,且 F'(x)=f(x),下式成立的有 。(A)?F'(x)dx?f(x)+c;(B)?f(x)dx=F(x)+c; (C)?F(x)dx?F'(x)+c;(D) ?f'(x)dx=F(x)+c. 2. F(x)和 G(x)是函数 f(x)的任意两个原函数,f(x)?0,则下式成立的有 。(A)F(x)=cG(x); (B)F(x)= G(x)+c;(C)F(x)+G(x)=c;(D) F(x)?G(x)=c.3.下列各式中是 f(x)?sin|x|的原函数。(A) y??cos|x| ;(B) y=-|cosx|;(c)y=? ?cosx,x?0,cosx?2,x?0; (D) y=? ?cosx?c1,x?0,cosx?c2,x?0. c1、c2 任意常数。 4.F?(x)?f(x),f(x) 为可导函数,且 f(0)=1,又 F(x)?xf(x)?x2,则 f(x)=______.(A) ?2x?1 (B)?x?1 (C)?2x?1(D)?x?1 5.设 f?(sin2x)?cos2x,则 f(x)=________. 1 (A)sinx?sin2x?c;(B)x?1x2?c; (C)sin2x?1sin4x?c;(D)x2?1x4?c; 1 / 30 第五章 不定积分 前面,我们讨论了如何求一个函数的导函数的问题,本章即将讨论它的反问题,即要求一个可导函数,使得它的导函数等于已知函数。这就是积分学的基本问题之一——不定积分。 §5.1 不定积分的概念与性质 5.1.1原函数 如果已知物体的运动方程)(t f s =,则此物体的速度是距离s 对时间t 的导数.反过来,如果已知物体的运动速度v 是时间t 的函数)(t v v =,求物体运动方程 )(t f s =,使得它的导数)(t f '等于已知函数)(t v .这就是求导运算的逆运算。 一般地,我们给出下面的定义: 定义 5.1.1 设)(x f 是定义在某个区间上的函数,如果存在函数)(x F 对该区间上的每一点都有: )()(x f x F =' 或 dx x f x dF )()(= . 则称函数)(x F 是已知函数)(x f 在此区间上的一个原函数。 例如,在()+∞∞-,内,x x cos )(sin =',故x sin 是x cos 在()+∞∞-,内的一个原函数。 5.1.2不定积分的概念 由求导公式和求导法则,可以得出: )(2'x =x 2 , )1(2'+x =x 2 , )1000(2'+x =x 2 , )(2'+c x =x 2 (c 为任意常数). 显然, 2x ,12+x ,10002+x ,c x +2等都是x 2的原函数.即x 2的原函数不唯一,且有无穷多个。 一般而言,如果)(x F 为)(x f 的一个原函数,则c x F +)((c 为任意常数)也满足 []'+c x F )(=)(x f ,所以c x F +)(都是)(x f 的原函数.此外,由拉格朗日中值定理[全]高等数学之不定积分的计算方法总结[下载全]
微积分李建平第五章+不定积分
高等数学第五章定积分总结
同济大学(高等数学)_第四章_不定积分
第五章定积分综合练习题
高等数学中有理分式定积分解法总结
专升本高等数学 第五章定积分及其应用
《高等数学》不定积分课后习题详解
第五章不定积分