实验一 常微分方程解析

实验一 常微分方程

1. 分别用Euler 法和ode45解下列常微分方程并与解析解比较： (1) ,(0)1,03y x y y x '=+=<<

解析法：

y=dsolve('Dy=x+y','y(0)=1','x') y = 2*exp(x) - x - 1 Euler:

function [x,y]=euler(od efun,xspan,y0,h) x=xspan(1):h:xspan(2); y(1)=y0;

for i=1:length(x)-1

y(k+1)=y(i)+h*feval(od efun,x(i),y(i)); end x=x' ;

y=y' ; end od e45:

od efun=inline('x+y','x','y'); xspan=[0,3]; y0=1; h=0.1;

[x1,y1]=euler(od efun,xspan,y0,h); [x2,y2]=od e45(od efun,xspan,y0); x3=0:0.1:3;

y3=2*exp(x3)-x3-1;

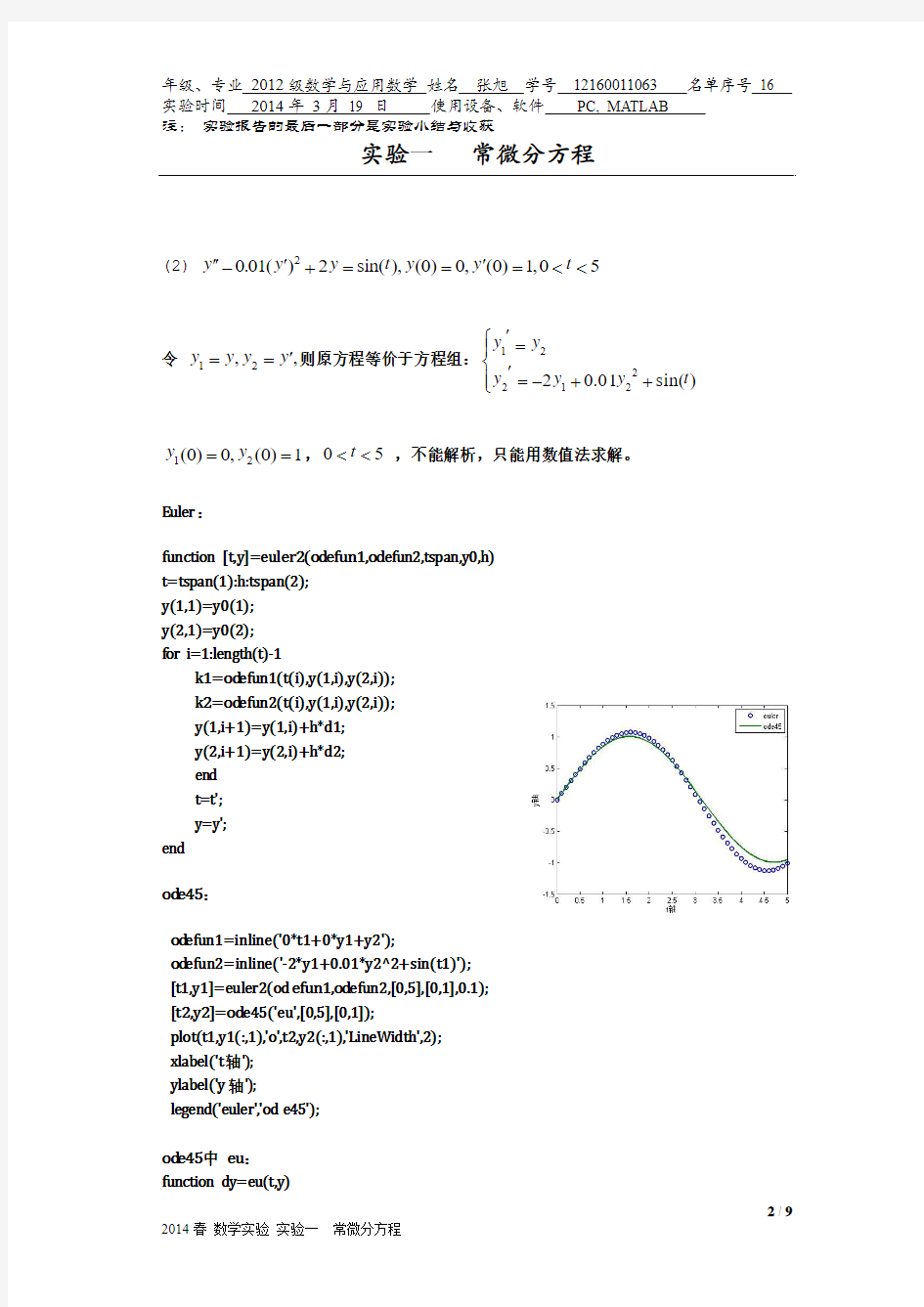
plot(x1,y1,'k',x2,y2,'ko',x3,y3,'k*'); xlabel('x 轴'); ylabel('y 轴');

legend('euler','od e45','dsolve');

od e45求得的结果与用解析法求得的结果更接近，故od e45的精度较高， Euler 法求得的结果精度较低。

实验一 常微分方程

(2) 20.01()2sin(),(0)0,(0)1,05y y y t y y t ''''-+===<<

令 ,,21y y y y '==则原方程等价于方程组：?????++-='=')

sin(01.0222122

1t y y y y y

1)0(,0)0(21==y y ，50<

Euler ：

function [t,y]=eul er2(od efun1,od efun2,tspan,y0,h)

t=tspan(1):h:tspan(2); y(1,1)=y0(1); y(2,1)=y0(2); for i=1:length(t)-1

k1=od efun1(t(i),y(1,i),y(2,i)); k2=od efun2(t(i),y(1,i),y(2,i)); y(1,i+1)=y(1,i)+h*d1; y(2,i+1)=y(2,i)+h*d2; end t=t'; y=y'; end od e45：

od efun1=inline('0*t1+0*y1+y2');

od efun2=inline('-2*y1+0.01*y2^2+sin(t1)'); [t1,y1]=euler2(od efun1,od efun2,[0,5],[0,1],0.1); [t2,y2]=od e45('eu',[0,5],[0,1]);

plot(t1,y1(:,1),'o',t2,y2(:,1),'LineWidth',2); xlabel('t 轴'); ylabel('y 轴');

legend('euler','od e45');

od e45中 eu ：

function dy=eu(t,y)

实验一 常微分方程

dy=zeros(2,1); dy(1)=y(2);

dy(2)=-2*y(1)+0.01*y(2)^2+sin(t);

od e45求得的结果精度较高，euler 法求得的结果在准确值上下波动。

2. 一通过原点的曲线，它在(,)x y 处的切线斜率等于22,0 1.57.x y x +<<若x 上限增为1.58，1.60会发生什么？

等价于求解2

2y x y +=' ，,0)0(y =且57.10<

解析法：

y=dsolve('Dy=2*x+y^2','y(0)=0','x')

y =(2^(1/3)*airy(3,-2^(1/3)*x)+2^(1/3)*3^(1/2)*airy(1,-2^(1/3)*x))/(3^(1/2)*airy(0, -2^(1/3)*x) + airy(2, -2^(1/3)*x)) od e45：

od efun=inline('2*x+y^2');

subplot(1,3,1);od e45(od efun,[0,1.57],0);title('0

曲线单调递增，且在x>1.5之后的斜率增长速度很快，若x 上限增为1.58，1.60，则相应的y 将会出现更大的增长。

实验一 常微分方程

3. 求解刚性方程组：

11212

1211000.25999.750.5,(0)1,050.

999.751000.250.5,(0)1,y y y y x y y y y '=-++=?<

'=-+=-?

function dy=fun(t,y) dy=zeros(2,1);

dy(1)=-1000.25*y(1)+999.75*y(2)+0.5; dy(2)=999.75*y(1)-1000.25*y(2)+0.5; od e45：

[t,y]=od e15s('fun',[0,50],[1,-1]);

plot(t,y(:,1),'o',t,y(:,2),'k-','LineWidth',2);

legend('y1','y2');

4. (温度过程)夏天把开有空调的室内一支读数为20℃ 的温度计放到户外，10分钟后读2

5.2℃ , 再过10分钟后读数28.32℃ 。建立一个较合理的模型来推算户外温度。 由题意可知由于随着时间的增加，温度增长越来越慢，户外温度与温度计示数之差也越来越小，且温差为零时温度的增长率也为零，故可以认为温度的增长率与温差成正比，设户外温度为m ，温度计的示数为y ，比例系数为k ，则可建立模型 20)0(),(=-='y y m k y

解析法：

y=dsolve('Dy=k*(c-y)','y(0)=20','t')

实验一 常微分方程

y = m - (m - 20)/exp(k*t)

由y （10）=25.2,y(20)=28.32建立方程组???

????=--=--32.28202.25202010k k

e m m e m m ，消去k ，得： （m-20）

（m-28.32）=（m-25.2）（m-25.2） 解得：m=33 所以户外温度约为33℃ 。

5. (广告效应)某公司生产一种耐用消费品，市场占有率为5%时开始做广告，一段时间

的市场跟踪调查后，该公司发现：单位时间内购买人口百分比的相对增长率与当时还没有买的百分比成正比，且估得此比例系数为0.5。

(1) 建立该问题的数学模型，并求其数值解与模拟结果作以比较； 设t 时刻该消费品的市场占有率为y ，建立方程：

%5)0(),1(*5.0=-='y y y

解析解：

y=dsolve('Dy=0.5-0.5*y','y(0)=0.05') y = 1 - (19*exp(-t/2))/20 数值解：

od efun=inline('0.5-0.5*y','t','y'); [t1,y1]=od e45(od efun,[0,10],0.05); t2=0:0.1:10;

y2=1-(19*exp(-t2/2))/20; plot(t1,y1,'o',t2,y2,'k'); legend('od e','dsolve');

实验一 常微分方程

(2) 厂家问：要做多少时间广告，可使市场购买率达到80%？ 由解析解可列出方程 1 - (19*exp(-t/2))/20=0.8，所以19

4ln 2-=t 解得t=3.1163

6. (肿瘤生长) 肿瘤大小V 生长的速率与V 的a 次方成正比，其中a 为形状参数，0≤a ≤1;而其比例系数K 随时间减小，减小速率又与当时的K 值成正比，比例系数为环境参数b 。设某肿瘤参数a=1, b=0.1, K 的初始值为2，V 的初始值为1。问 (1)此肿瘤生长不会超过多大？

由已知列出方程组???='-='a

kv

v bk k ，代入具体数值，得???='-='kv v k

k 1.0 ， 1)0(,2)0(==v k ，的函数）

都是关于时间（t v k , 解析法：

[k,v]=dsolve('Dk=-0.1*k','Dv=k*v','k(0)=2','v(0)=1','t') k =2*exp(-t/10)

v =exp(20)*exp(-20*exp(-t/10)) t=0:0.1:100;

v=exp(20)*exp(-20*exp(-t/10)); plot(t,v,'LineWidth',2); xlabel('t 轴'); ylabel('v 轴');

因肿瘤不断长大，故t 趋于无穷时，该肿瘤达到最大，此时极限为exp(20)=4.8517*10^8，故此肿瘤生长不会超过4.8517*10^8 。

实验一 常微分方程

(2)过多长时间肿瘤大小翻一倍？

令exp(20)*exp(-20*exp(-t/10))=2，解得t=-10*ln(1-1/20*ln2)=0.3527, (3)何时肿瘤生长速率由递增转为递减？

由已求得的结果可得v '与t 的关系为v '=2*exp(20-t/10)*exp(-20*exp(-t/10))， t1=0:0.1:100;

v1=2*exp(20-t1/10).*exp(-20*exp(-t1/10)); plot(t1,v1,'LineWidth',2); xlabel('t 轴'); ylabel('v 轴');

显然，最大值处对应的t 即为所求： t2=0:0.01:100;

v2=2*exp(20-t1/10).*exp(-20*exp(-t1/10)); [m,n]=max(v2); t=t2(n) 得到t = 29.96 (4)若参数a=2/3呢？

1、建立方程组???

??='-='32

1.0kv

v k k ，1)0(,2)0(==v k 解析法：

[k,v]=dsolve('Dk=-0.1*k','Dv=k*v^(2/3)','k(0)=2','v(0)=1','t') k = 2*exp(-t/10) 2*exp(-t/10) 2*exp(-t/10)

v = -(20*exp(-t/10) - 23)^3/27

实验一常微分方程

(37/2 + (3^(1/2)*3*i)/2 - 20*exp(-t/10))^3/27

-(20*exp(-t/10) + (3^(1/2)*3*i)/2 - 37/2)^3/27

取实解k = 2*exp(-t/10) v=-(20*exp(-t/10) - 23)^3/27

并画出v-t图像：

t=0:0.1:100;

v=-(20*exp(-t/10) - 23).^3/27;

plot(t,v,'LineWidth',2);

xlabel('t轴');

ylabel('v轴');

显然，当t趋于无穷时，该肿瘤达到最大，此时极限为-(- 23)^3/27=450.6296，故此肿瘤生长不会超过450.6296 。

2、令-(20*exp(-t/10) - 23)^3/27=2，解得t=0.3977,

3、由已求得的结果可得v'与t的关系为

v'=2*exp(-t/10)*(20*exp(-t/10) - 23)^2/9，

t1=0:0.1:100;

v1=2*exp(-t1/10).*(20*exp(-t1/10) - 23).^2/9;

plot(t1,v1,'LineWidth',2);

xlabel('t轴');

ylabel('v轴');

显然，最大值处对应的t即为所求，：

t2=0:0.01:100;

v2=2*exp(-t2/10).*(20*exp(-t2/10) - 23).^2/9;

[m,n]=max(v2);

t=t2(n)

t = 9.5900

选做题：

1.(生态系统的振荡现象)第一次世界大战中，因为战争很少捕鱼，按理战后应能捕到更

实验一 常微分方程

多的鱼才是。可是大战后，在地中海却捕不到鲨鱼，因而渔民大惑不解。

令x 1为鱼饵的数量，x 2为鲨鱼的数量，t 为时间。微分方程为

式中a 1, a 2, b 1, b 2都是正常数。第一式鱼饵x 1的增长速度大体上与x 1成正比，即按a 1x 1比率增加, 而被鲨鱼吃掉的部分按b 1x 1x 2的比率减少；第二式中鲨鱼的增长速度由于生存竞争的自然死亡或互相咬食按a 2x 2的比率减少，但又根据鱼饵的量的变化按b 2x 1x 2的比率增加。对a 1=3, b 1=2, a 2=2.5, b 2=1, x 1(0)=x 2(0)=1求解。画出解曲线图和相轨线图，可以观察到鱼饵和鲨鱼数量的周期振荡现象。

代入具体数值后，原方程组变为：?????+-='-='2

1222

1115.223x x x x x x x x ，x 1(0)=x 2(0)=1

od e45：

[t,x]=od e45('oscar',[0,10],[1,1]);

plot(t,x(:,1),'o-',t,x(:,2)); xlabel('t 轴'); ylabel('x 轴'); legend('x1','x2'); oscar:

function dx=myfun2(t,x) dx=zeros(2,1);

dx(1)=3*x(1)-2*x(1)*x(2); dx(2)=-2.5*x(2)+x(1)*x(2);

常微分方程练习题及答案复习题)

常微分方程练习试卷 一、 填空题。 1. 方程23 2 10d x x dt +=是 阶 （线性、非线性）微分方程. 2. 方程 ()x dy f xy y dx =经变换_______，可以化为变量分离方程 . 3. 微分方程 3230d y y x dx --=满足条件(0)1,(0)2y y '==的解有 个. 4. 设常系数方程 x y y y e αβγ'''++=的一个特解*2()x x x y x e e xe =++，则此方程的系数α= ，β= ，γ= . 5. 朗斯基行列式 ()0W t ≡是函数组12(),(),,()n x t x t x t 在a x b ≤≤上线性相关的 条件. 6. 方程 22(2320)0xydx x y dy ++-=的只与y 有关的积分因子为 . 7. 已知 ()X A t X '=的基解矩阵为()t Φ的，则()A t = . 8. 方程组 20'05??=???? x x 的基解矩阵为 ． 9.可用变换 将伯努利方程 化为线性方程. 10 .是满足方程 251y y y y ''''''+++= 和初始条件 的唯一解. 11.方程 的待定特解可取 的形式: 12. 三阶常系数齐线性方程 20y y y '''''-+=的特征根是 二、 计算题 1.求平面上过原点的曲线方程, 该曲线上任一点处的切线与切点和点(1,0)的连线相互垂直. 2．求解方程13 dy x y dx x y +-=-+. 3. 求解方程 222()0d x dx x dt dt += 。 4．用比较系数法解方程. . 5．求方程 sin y y x '=+的通解. 6．验证微分方程 22(cos sin )(1)0x x xy dx y x dy -+-=是恰当方程，并求出它的通解.

2016春作业实验(1)常微分方程

1. 分别用Euler 法和ode45解下列常微分方程并与解析解比较： (1) ,(0)1, 03y x y y x '=+=<< function [ t,y ] = euler(f,ts,y0,h) t=ts(1):h:ts(2); y(1)=y0; for i=1:length(t)-1 y(i+1)=y(i)+h*f(t(i),y(i)); end t=t'; y=y'; end f=(t,y)t+y; [t1,y1]=euler(f,[0,3],1,0.05); [t2,y2]=ode45(f,[0,3],1); plot(t1,y1,'.-',t2,y2,'ro') hold on y3=dsolve('Dy=x+y','y(0)=1','x') ezplot(y3,[0,3]) hold off legend('euler','ode45','解析解');

（2）22()5()3()45,(0)2,(0)1, 02t x t x t x t e x x t ''''--===<< f=(t,x)[2*x(2);5*x(2)+3*x(1)+45*exp(2*t)]; [t1,y1]=ode45(f,[0,2],[2,1]); plot(t1,y1)

2. 求一通过原点的曲线，它在(,)x y 处的切线斜率等于2 2,0 1.57.x y x +<<若x 上限增为1.58，1.60会发生什么？ function dy = odefun_2(x,y) dy=2*x+y^2; dy=dy(:); end

[t1,y]=ode45('odefun_2',[0,1.58],0) plot(t1,y); [t2,y]=ode45('odefun_2',[0,1.60],0) plot(t2,y);

一阶常微分方程解法总结

页脚内容1 第 一 章 一阶微分方程的解法的小结 ⑴、可分离变量的方程： ①、形如 )()(y g x f dx dy = 当0)(≠y g 时，得到 dx x f y g dy )()(=，两边积分即可得到结果； 当0)(0=ηg 时，则0)(η=x y 也是方程的解。 例1.1、xy dx dy = 解：当0≠y 时，有xdx y dy =，两边积分得到)(2ln 2为常数C C x y += 所以)(11212 C x e C C e C y ±==为非零常数且 0=y 显然是原方程的解； 综上所述，原方程的解为)(1212 为常数C e C y x = ②、形如0)()()()(=+dy y Q x P dx y N x M 当0)()(≠y N x P 时，可有dy y N y Q dx x P x M ) ()()()(=，两边积分可得结果； 当0)(0=y N 时，0y y =为原方程的解，当0(0=） x P 时，0x x =为原方程的解。 例1.2、0)1()1(22=-+-dy x y dx y x

页脚内容2 解：当0)1)(1(22≠--y x 时，有dx x x dy y y 1 122-=-两边积分得到 )0(ln 1ln 1ln 22≠=-+-C C y x ，所以有)0()1)(1(22≠=--C C y x ； 当0)1)(1(22=--y x 时，也是原方程的解； 综上所述，原方程的解为)()1)(1(22为常数C C y x =--。 ⑵可化为变量可分离方程的方程： ①、形如)(x y g dx dy = 解法：令x y u = ，则udx xdu dy +=，代入得到)(u g u dx du x =+为变量可分离方程，得到)(0),,(为常数C C x u f =再把u 代入得到)(0),,(为常数C C x x y f =。 ②、形如)0(),(≠+=ab by ax G dx dy 解法：令by ax u +=，则b du adx dy +=，代入得到)(1u G b a dx du b =+为变量可分离方程，得到)(0),,(为常数C C x u f =再把u 代入得到)(0),,(为常数C C x by ax f =+。 ③、形如 )(222111c y b x a c y b x a f dx dy ++++= 解法：01、02211 =b a b a ，转化为)(by ax G dx dy +=，下同①； 02、0221 1 ≠b a b a ，???=++=++00222111c y b x a c y b x a 的解为),(00y x ，令???-=-=00y y v x x u

常微分方程期末试题B答案

2005——2006学年第二学期 常微分方程课程试卷（B） 一、填空题（每空2 分，共16分）。 1．李普希滋条件是初值问题存在唯一解的充分条件． 2. 一阶微分方程的一个特解的图像是二 维空间上的一条曲线． 3．线性齐次微分方程组Y A Y ) ( d d x x =的一个基本解组的个数不能多于n个，其中R ∈ x，n R Y∈． 4．二阶线性齐次微分方程的两个解) ( 1 x y? =,) ( 2 x y? =成为其基本解组的充要条件是线性无关． 5．方程2 sin() y xy y '' =+的通解是 6．变量可分离方程()()()()0= +dy y q x p dx y N x M的积分因子是()() x P y N 1 7．性齐次微分方程组的解组) ( , ), ( ), ( 2 1 x x x n Y Y Y 为基本解组的充分必要条件是它们的朗斯基行列式0 ) (≠ x W． 8．方程540 y y y ''' ++=的基本解组是x x e e4 ,- - 二、选择题（每小题3 分，共15分）。 9．两个不同的线性齐次微分方程组（ D ）的基本解组． (A) 一定有相同(B) 可能有相同 (C) 一定有相似(D) 没有相同 10．方程组 ? ? ? ?? ? ? + = + = y x t y y x t x 4 3 d d 2 d d 的奇点)0,0(的类型是（D ）． （A）稳定焦点（B）不稳定焦点（C）鞍点（D）不稳定结点11．方程x(y2－1)d x+y(x2－1)d y=0的所有常数解是（ C ）． (A) 1± = x(B)1± = y

(C )1±=y , 1±=x (D )1=y , 1=x 12．n 阶线性非齐次微分方程的所有解（ D ）． （A ）构成一个线性空间 （B ）构成一个1-n 维线性空间 （C ）构成一个1+n 维线性空间 （D ）不能构成一个线性空间 13．方程4d d +-=x y x y （ A ）奇解． (A) 无 (B) 有一个 (C) 有两个 (D) 可能有 三、计算题（每小题8分，共48分） 。 14．求方程 x y x y x y tan d d +=的通解 解：令x y u =，则u x u y '+='， u x u x tan d d = 当0tan ≠u 时，等号两边积分 1d tan d C x x u u +=?? C x u ln ln sin ln += 0≠C Cx x y =sin 15．求方程0d d )1(2=+--y x x y x 的通解 解：积分因子21)(x x =μ， 则 0d 1d 122=+--y x x x y x 为全微分方程．取10=x ，00=y ，于是通积分为 1012 2d d 1C y x x y x y x =+--?? 即 C x x x y =++1 16．求方程2221)(x y x y y + '-'=的通解 解:令 p y ='，得到2 2 2x xp p y +-= （*） ，两端同时关于求导，

(整理)实验五用matlab求解常微分方程.

实验五 用matlab 求解常微分方程 1．微分方程的概念 未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。如果未知函数是一元函数，称为常微分方程。常微分方程的一般形式为 0),,",',,()(=n y y y y t F 如果未知函数是多元函数，成为偏微分方程。联系一些未知函数的一组微分方程组称为微分方程组。微分方程中出现的未知函数的导数的最高阶解数称为微分方程的阶。若方程中未知函数及其各阶导数都是一次的，称为线性常微分方程，一般表示为 ) ()(')()(1)1(1)(t b y t a y t a y t a y n n n n =++++-- 若上式中的系数 n i t a i ,,2,1),( =均与t 无关，称之为常系数。 2．常微分方程的解析解 有些微分方程可直接通过积分求解.例如,一解常系数常微分方程1 +=y dt dy 可化为 dt y dy =+1,两边积分可得通解为 1-=t ce y .其中c 为任意常数.有些常微分方程可用一些技巧,如分离变量法,积分因子法,常数变异法,降阶法等可化为可积分的方程而求得解析解. 线性常微分方程的解满足叠加原理,从而他们的求解可归结为求一个特解和相应齐次微分方程的通解.一阶变系数线性微分方程总可用这一思路求得显式解。高阶线性常系数微分方程可用特征根法求得相应齐次微分方程的基本解，再用常数变异法求特解。 一阶常微分方程与高阶微分方程可以互化，已给一个n 阶方程 ),,",',()1()(-=n n y y y t f y 设 ) 1(21,,',-===n n y y y y y y ，可将上式化为一阶方程组 ?????????====-),,,,(''''2113221n n n n y y y t f y y y y y y y 反过来，在许多情况下，一阶微分方程组也可化为高阶方程。所以一阶微分方程组与高阶常微分方程的理论与方法在许多方面是相通的，一阶常系数线性微分方程组也可用特征根法求解。 3．微分方程的数值解法 除常系数线性微分方程可用特征根法求解，少数特殊方程可用初等积分法求解外，大部分微分方程无限世界，应用中主要依靠数值解法。考虑一阶常微分方程初值问题 ?? ?=<<=000)()),(,()('y t y t t t t y t f t y f

(整理)常微分方程试题及参考答案

常微分方程试题 一、填空题(每小题3分，共39分) 1.常微分方程中的自变量个数是________. 2.路程函数S(t)的加速度是常数a，则此路程函数S(t)的一般形式是________. 3.微分方程=g( )中g(u)为u的连续函数，作变量变换________，方程可化为变 量分离方程. 4.微分方程F(x,y′)=0中令P=y′,若x、P平面上的曲线F(x,P)=0的参数形式 为x= (t),P=ψ(t),t为参数，则方程参数形式的通解为________. 5.方程=(x+1)3的通解为________. 6.如果函数f(x,y)连续，y= (x)是方程=f(x,y)的定义于区间x0≤x≤x0+h上，满 足初始条件 (x0)=y0的解.则y= (x)是积分方程________定义于x0≤x≤x0+h 上的连续解. 7.方程=x2+xy，满足初始条件y(0)=0的第二次近似解是________. 8.方程+a1(t) +…+a n-1(t) +a n(t)x=0 中a i(t) i=1,2,…，n是〔a,b〕上的连续函数，又x1(t),x2(t),…，x n(t)为方程n 个线性无关的解，则其伏朗斯基行列式W(t) 应具有的性质是：________. 9.常系数线性方程x(4)(t)-2x″(t)+x(t)=0的通解为________. 10.设A(t)是区间a≤t≤b上的连续n×n矩阵，x1(t),x2(t),…，x n(t)是方程组 x′=A(t)x的n个线性无关的解向量.则方程组的任一解向量x(t)均可表示为：x(t)=________的形式. 11.初值问题(t)+2x″(t)-tx′(t)+3x(t)=e-t,x(1)=1,x′(1)=2,x″(1)=3 可化为与之 等价的一阶方程组________. 12.如果A是3×3的常数矩阵，-2为A的三重特征值，则方程组x′=Ax的基 解矩阵exp A t=________. 13.方程组 的奇点类型是________. 二、计算题(共45分) 1.(6分)解方程 = . 2.(6分)解方程 x″(t)+ =0. 3.(6分)解方程 (y-1-xy)dx+xdy=0. 4.(6分)解方程

常微分方程的初等解法与求解技巧

师大学本科毕业论文（设计） 常微分方程的初等解法与求解技巧 姓名娟 院系数学与计算机科学学院 专业信息与计算科学 班级12510201 学号1251020126 指导教师王晓锋 答辩日期 成绩

常微分方程的初等解法与求解技巧 容摘要 常微分方程在数学中发挥着举足轻重的作用，同时它的应用在日常生活里随处可见，因此掌握常微分方程的初等解法与求解技巧是非常必要的.本论文主要论述了其发展、初等解法与求解技巧，前者主要有变量分离、积分因子、一阶隐式微分方程的参数表示，通过举例从中总结出其求解技巧，目的是掌握其求解技巧. 【关键词】变量分离一阶隐式微分方程积分因子求解技巧

Elementary Solution and Solving Skills of Ordinary Differential Equation Abstract Ordinary differential equations take up significant position in mathematics, and at the same time, the application of it can be seen everywhere in our daily life, therefore, it’s necessary to grasp the elementary solution of ordinary differential equations and solving skills. This paper mainly introduced the definition of ordinary differential equations, elementary solution method and solving skills, the former mainly included the separation of variables, integral factor, a parameter-order differential equations implicit representation, by way of examples to sum up their solving skills, the purpose is to master the skills to solve. 【Key Words】the separation of variables the first order implicit differential equation integrating factor solution techniques

实验七 常微分方程

实验七 常微分方程 【实验目的】 1． 了解常微分方程的基本概念。 2． 了解常微分方程的解析解。 3． 了解常微分方程的数值解。 4． 学习掌握MATLAB 软件有关的命令。 【实验内容】 如右图所示，一根长l 的无弹性细线，一段固定，另一端悬挂一个 质量为m 的小球，在重力的作用下小球处于垂直的平衡位置。若使小球 偏离平衡位置一个角度θ，让它自由，它就会沿圆弧摆动。在不考虑空气 阻力的情况下，小球会做一定周期的简谐运动。利用牛顿第二定律得到如 下的微分方程 0)0(',)0(,sin "0===θθθθθmg ml 问该微分方程是线性的还是非线性的？是否存在解析解？如果不存在解析解，能否求出其近似解？ 【实验准备】 1．微分方程的概念 未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。如果未知函数是一元函数，称为常微分方程。常微分方程的一般形式为 0),,",',,()(=n y y y y t F 如果未知函数是多元函数，成为偏微分方程。联系一些未知函数的一组微分方程组称为微分方程组。微分方程中出现的未知函数的导数的最高阶解数称为微分方程的阶。若方程中未知函数及其各阶导数都是一次的，称为线性常微分方程，一般表示为 )()(')()(1)1(1)(t b y t a y t a y t a y n n n n =++++-- 若上式中的系数n i t a i ,,2,1),( =均与t 无关，称之为常系数或定常、自治、时不变的。 2．常微分方程的解析解 有些微分方程可直接通过积分求解.例如,一解常系数常微分方程 1+=y dt dy 可化为dt y dy =+1 ,两边积分可得通解为1-=t ce y .其中c 为任意常数.有些常微分方程可用一些技巧,如分离变量法,积分因子法,常数变异法,降阶法等可化为可积分的方程而求得解析解(显式解). 线性常微分方程的解满足叠加原理,从而他们的求解可归结为求一个特解和相应齐次微分方程的通解.一阶变系数线性微分方程总可用这一思路求得显式解。高阶线性常系数微分方程可用特征根法求得相应齐次微分方程的基本解，再用常数变异法求特解。 一阶场微分方程与高阶微分方程可以互化，已给一个n 阶方程， ),,",',()1()(-=n n y y y t f y 设)1(21 ,,',-===n n y y y y y y ，可将上式化为一阶方程组 ????? ????====-) ,,,,(''''2113221n n n n y y y t f y y y y y y y

常微分方程习题及答案.[1]

第十二章 常微分方程 (A) 一、是非题 1．任意微分方程都有通解。( ) 2．微分方程的通解中包含了它所有的解。( ) 3．函数x x y cos 4sin 3-=是微分方程0=+''y y 的解。( ) 4．函数x e x y ?=2是微分方程02=+'-''y y y 的解。( ) 5．微分方程0ln =-'x y x 的通解是()C x y += 2 ln 2 1 (C 为任意常数)。( ) 6．y y sin ='是一阶线性微分方程。( ) 7．xy y x y +='33不是一阶线性微分方程。( ) 8．052=+'-''y y y 的特征方程为0522=+-r r 。( ) 9． 2 2 1xy y x dx dy +++=是可分离变量的微分方程。( ) 二、填空题 1．在横线上填上方程的名称 ①()0ln 3=-?-xdy xdx y 是 。 ②()()022=-++dy y x y dx x xy 是 。 ③x y y dx dy x ln ?=是 。 ④x x y y x sin 2+='是 。 ⑤02=-'+''y y y 是 。 2．x x y x y cos sin =-'+'''的通解中应含 个独立常数。 3．x e y 2-=''的通解是 。 4．x x y cos 2sin -=''的通解是 。 5．124322+=+'+'''x y x y x y x 是 阶微分方程。 6．微分方程()06 ='-''?y y y 是 阶微分方程。

7．x y 1 =所满足的微分方程是 。 8．x y y 2='的通解为 。 9． 0=+ x dy y dx 的通解为 。 10． ()25 11 2+=+- x x y dx dy ，其对应的齐次方程的通解为 。 11．方程()012=+-'y x y x 的通解为 。 12．3阶微分方程3x y ='''的通解为 。 三、选择题 1．微分方程()043='-'+''y y y x y xy 的阶数是( )。 A ．3 B ．4 C ．5 D ． 2 2．微分方程152=-''-'''x y x y 的通解中应含的独立常数的个数为( )。 A ．3 B ．5 C ．4 D ． 2 3．下列函数中，哪个是微分方程02=-xdx dy 的解( )。 A ．x y 2= B ．2x y = C ．x y 2-= D ． x y -= 4．微分方程32 3y y ='的一个特解是( )。 A ．13+=x y B ．()3 2+=x y C ．()2 C x y += D ． ()3 1x C y += 5．函数x y cos =是下列哪个微分方程的解( )。 A ．0=+'y y B ．02=+'y y C ．0=+y y n D ． x y y cos =+'' 6．x x e C e C y -+=21是方程0=-''y y 的( )，其中1C ，2C 为任意常数。 A ．通解 B ．特解 C ．是方程所有的解 D ． 上述都不对 7．y y ='满足2|0==x y 的特解是( )。 A ．1+=x e y B ．x e y 2= C ．22x e y ?= D ． x e y ?=3 8．微分方程x y y sin =+''的一个特解具有形式( )。 A ．x a y sin *= B ．x a y cos *?=

常微分方程解题方法总结.docx

常微分方程解题方法总结 来源：文都教育 复习过半，课本上的知识点相信大部分考生已经学习过一遍 . 接下来，如何将零散的知识点有机地结合起来，而不容易遗忘是大多数考生面临的问题 . 为了加强记忆，使知识自成体系，建议将知识点进行分类系统总结 . 著名数学家华罗庚的读书方法值得借鉴，他强调读 书要 “由薄到厚、由厚到薄 ”，对同学们的复习尤为重要 . 以常微分方程为例， 本部分内容涉及可分离变量、 一阶齐次、 一阶非齐次、 全微分方程、 高阶线性微分方程等内容， 在看完这部分内容会发现要掌握的解题方法太多， 遇到具体的题 目不知该如何下手， 这种情况往往是因为没有很好地总结和归纳解题方法 . 下面以表格的形 式将常微分方程中的解题方法加以总结，一目了然，便于记忆和查询 . 常微分方程 通解公式或解法 ( 名称、形式 ) 当 g( y) 0 时，得到 dy f (x)dx ， g( y) 可分离变量的方程 dy f ( x) g( y) 两边积分即可得到结果； dx 当 g( 0 ) 0 时，则 y( x) 0 也是方程的 解 . 解法：令 u y xdu udx ，代入 ，则 dy 齐次微分方程 dy g( y ) x dx x u g (u) 化为可分离变量方程 得到 x du dx 一 阶 线 性 微 分 方 程 dy P ( x)dx P ( x) dx Q(x) y ( e Q( x)dx C )e P( x) y dx

伯努利方程解法：令 dy P( x) y Q( x) y n（n≠0,1） 代入得到dx —u y1 n，有 du(1 n) y n dy ， du(1 n) P(x)u(1 n)Q(x) dx 求解特征方程： 2pq 0三种情况： 二阶常系数齐次线性微分方程 y p x y q x y0 二阶常系数非齐次线性微分方程y p x y q x y f ( x) (1)两个不等实根： 1 ,2 通解： y c1 e 1x c2 e 2x (2)两个相等实根：12 通解： y c1c2 x e x (3)一对共轭复根：i , 通解： y e x c1 cos x c2 sin x 通解为y p x y q x y 0 的通解与 y p x y q x y f ( x) 的特解之和. 常见的 f (x) 有两种情况： x （ 1）f ( x)e P m ( x) 若不是特征方程的根，令特解y Q m ( x)e x；若是特征方程的单根，令特 解 y xQ m ( x)e x；若是特征方程的重根， 令特解 y*x2Q m (x)e x； （2）f (x) e x[ P m ( x) cos x p n ( x)sin x] 当i不是特征值时，令 欢迎下载2

2018常微分方程考研复试真题及答案

常微分方程计算题 2.指出下列方程中的阶数，是线性方程还是非线性方程，并说明理由； （1） t 2 2 2dt u d +t dt du +( t 2 -1)u=0 （2） dx dy =x 2+y 2 ; （3）dx dy + 2 x y =0 3.求曲线族y=C 1e x +C 2x e x 所满足的微分方程 4．验证函数y= C 1e x 2+ C 2e x 2-是微分方程y `` -4y=0的解，进一步验证它是通解。 5.试用一阶微分方程形式不变性求解方程dx dy =2x 6.什么叫积分一个微分方程 7．什么是求解常微分方程的初等积分法 8．分离变量一阶方程的特征是什么 9．求下列方程的通解 （1） y ` ＝sinx （2） x 2 y 2 y ` +1=y （3） tgx dx dy =1+y （4） dx dy =exp(2x-y) （5） dx dy =21y 2- （6） x 2 ydx=(1- y 2 +x-2 x 2 y 2 )dx （7）( x 2 +1)( y 2 -1)dx+xydy=0 10.叙述齐次函数的定义 11．试给出一阶方程y ` ＝f(x,y)或p(x,y)dx+ q(x,y)dy=0为齐次方程的特征。说明二

个方程的关系。 12．求解齐次方程通常用什么初等变换，新旧函数导数关系如何 13．求解下列方程 dx dy ＝2 22y x xy - 14．求解下列方程 （1）（x+2y ）dx —xdy=0 (2) dx dy =x y +y x 2 15. dx dy =22y x xy + 16(x 2 +y 2 )dx —2xydy=0 17. dx dy =5 242+---y x x y 18―――――19 20―――――――27

(整理)常微分方程(含解答)

第八章 常微分方程 【教学要求】 一、了解微分方程的基本概念：微分方程，微分方程的阶、解、特解、通解、初始条件和初值问题，线性微分方程。 二、熟练掌握一阶可分离变量微分方程的解法。 三、熟练掌握一阶线性非齐次微分方程)()(x q y x p y =+' 的解法——常数变易法和公式法。 四、理解线性微分方程解的性质和解的结构。 五、熟练掌握二阶线性常系数齐次微分方程0=+'+''qy y p y 的解法——特征根法。 会根据特征根的三种情况，熟练地写出方程的通解，并根据定解的条件写出方程特解。 六、熟练掌握二阶线性常系数非齐次微分方程qy y p y +'+'' )(x f =，当自由项f (x )为某些特殊情况时的解法——待定系数法。 所谓f (x )为某些特殊情况是指f (x )为多项式函数，指数函数 或它们的和或乘积形式、三角函数x x x ββαsin cos ,e 。 关键是依据f (x )的形式及特征根的情况，设出特解y *,代入原方程，定出y *的系数。 【教学重点】 一阶可分离变量微分方程、一阶线性微分方程、二阶线性常系数微分方程的解法。 【典型例题】 。的阶数是微分方程例)(e )(12x y y y =-'+'' 2.1.B A 4. 3.D C 解：B 。的特解形式是微分方程例)( e 232x x y y y +=+'-'' x x x b ax B b ax A e )(.e ).(++ x x c b ax D cx b ax C e ).(e ).(++++ 解：C 是一阶线性微分方程。下列方程中例)( ,3 x x y y x B y A y x cos sin 1.e .2=+'='+ y x y D y y x y C ='=+'+''.0 . 解：B ???=='++1)1(0)1(4y y x y y 求解初值问题例 ??-=+x x y y y d )1(d 解：由变量可分离法得 c x y y ln ln 1ln +-=+∴ 代入上式得通解为由21ln ln 1)1(=?=c y x y y 211=+ 的特解。满足求解微分方程例1)0(e 252==-'y x y y x 解：由公式法得 ]d e e 2[e d 12d 1c x x y x x x +???=---?

2016春 作业 实验1常微分方程

1、 分别用Euler 法与ode45解下列常微分方程并与解析解比较: (1) ,(0)1, 03y x y y x '=+=<< function [ t,y ] = euler(f,ts,y0,h) t=ts(1):h:ts(2); y(1)=y0; for i=1:length(t)-1 y(i+1)=y(i)+h*f(t(i),y(i)); end t=t'; y=y'; end f=@(t,y)t+y; [t1,y1]=euler(f,[0,3],1,0、05); [t2,y2]=ode45(f,[0,3],1); plot(t1,y1,'、-',t2,y2,'ro') hold on y3=dsolve('Dy=x+y','y(0)=1','x') ezplot(y3,[0,3]) hold off legend('euler','ode45','解析解');

（2）22()5()3()45,(0)2,(0)1, 02t x t x t x t e x x t ''''--===<< f=@(t,x)[2*x(2);5*x(2)+3*x(1)+45*exp(2*t)]; [t1,y1]=ode45(f,[0,2],[2,1]); plot(t1,y1)

2. 求一通过原点的曲线,它在(,)x y 处的切线斜率等于2 2,0 1.57.x y x +<<若x 上限增为1、58,1、60会发生什么？ function dy = odefun_2(x,y) dy=2*x+y^2; dy=dy(:); end

[t1,y]=ode45('odefun_2',[0,1、58],0) plot(t1,y); [t2,y]=ode45('odefun_2',[0,1、60],0) plot(t2,y);

二阶常微分方程解

二阶常微分方程解

————————————————————————————————作者: ————————————————————————————————日期:

第七节 二阶常系数线性微分方程 的解法 在上节我们已经讨论了二阶线性微分方程解的结构，二阶线性微分方程的求解问题,关键在于如何求二阶齐次方程的通解和非齐次方程的一个特解。本节讨论二阶线性方程的一个特殊类型，即二阶常系数线性微分方程及其求解方法。先讨论二阶常系数线性齐次方程的求解方法。 §7.1 二阶常系数线性齐次方程及其求解方法 设给定一常系数二阶线性齐次方程为 ?? 22 dx y d +p dx dy ＋ｑy=０ (7.1) 其中p 、q 是常数,由上节定理二知,要求方程(7．1)的通解，只要求出其任意两个线性无关的特解y 1,ｙ2就可以了，下面讨论这样两个特解的求法。 我们先分析方程(7.1)可能具有什么形式的特解, 从方程的形式上来看，它的特点是22dx y d ，dx dy ,y 各乘以 常数因子后相加等于零，如果能找到一个函数ｙ,其

22dx y d ，dx dy ，ｙ之间只相差一个常数因子，这样的函数有可能是方程(７.1)的特解,在初等函数中,指数函数e rx ,符合上述要求，于是我们令 y=e r ｘ (其中r 为待定常数）来试解 将y ＝e rx ,dx dy =re r ｘ,22dx y d ＝r ２e r ｘ 代入方程(7.1) 得 r 2e ｒx ＋ｐre rx ＋ｑｅrx ＝０ 或 e r ｘ(r ２+pr+q ）＝0 因为e rx ≠０,故得 ? r 2 +pr ＋q=0 由此可见，若r 是二次方程 ?? r 2＋pr ＋q=０ (7．2) 的根，那么e r ｘ就是方程(7.１)的特解,于是方程（７.1)的求解问题，就转化为求代数方程(7.2）的根问题。称（7.2)式为微分方程(７.１)的特征方程。 特征方程(7.2)是一个以r 为未知函数的一元二次代数方程。特征方程的两个根r 1，r 2，称为特征根,由代数知识，特征根r １，r 2有三种可能的情况,下面我们分别进行讨论。 (1)若特证方程（7．2）有两个不相等的实根r 1， r 2，此时e r １ｘ ,e r2x 是方程（７.1)的两个特解。

常微分方程应用题和答案

应 用 题（每题10分） 1、设()f x 在(,)-∞∞上有定义且不恒为零，又()f x '存在并对任意,x y 恒有 ()()()f x y f x f y +=，求()f x 。 2、设()()()F x f x g x =，其中函数(),()f x g x 在(,)-∞∞内满足以下条件 ()(),()(),(0)0,()()2x f x g x g x f x f f x g x e ''===+= （1）求()F x 所满足的一阶微分方程； （2）求出()F x 的表达式。 3、已知连续函数()f x 满足条件320 ()3x x t f x f dt e ??=+ ??? ?，求()f x 。 4、已知函数()f x 在(0,)+∞内可导，()0,lim ()1x f x f x →+∞ >=，且满足 1 1 0()lim ()h x h f x hx e f x →? ?+ ?= ? ?? ? ，求()f x 。 5、设函数()f x 在(0,)+∞内连续，5 (1)2 f =，且对所有,(0,)x t ∈+∞，满足条件 1 1 1 ()()()xt x t f u du t f u du x f u du =+? ??，求()f x 。 6、求连续函数()f x ，使它满足10 ()()sin f tx dt f x x x =+?? 。 7、已知可微函数()f t 满足 31() ()1()x f t dt f x t f t t =-+?，试求()f x 。 8、设有微分方程 '2()y y x ?-=， 其中21 ()01x x x ?? 。试求在(,)-∞∞内的连续函 数()y y x =使之在(,1)-∞和()1,+∞内部满足所给方程，且满足条件(0)0y =。 9、设位于第一象限的曲线()y f x = 过点122?? ? ? ?? ，其上任一点(,)P x y 处的法线与y 轴的交点为Q ，且线段PQ 被x 轴平分。 （1）求曲线()y f x =的方程； （2）已知曲线sin y x =在[0,]π上的弧长为l ，试用l 表示曲线()y f x =的弧长s 。 10、求微分方程(2)0xdy x y dx +-=的一个解()y y x =，使得由曲线()y y x =与直线 1,2x x ==以及x 轴所围成的平面图形绕x 轴旋转一周的旋转体体积最小。 11、设曲线L 位于xOy 平面的第一象限内，L 上任一点M 处的切线与y 轴总相交，交点记为

实验一 常微分方程

实验一 常微分方程 1. 分别用Euler 法和ode45解下列常微分方程并与解析解比较： (1) ,(0)1,13y x y y x '=+=<< odefun=inline （‘x+y ’，‘x ’，‘y ’）； [x1,y1]=ode45(odefun,[0,3],1); [x2,y2]=euler(odefun,[0,3],1,0.01); S=dsolve(‘Dy=x+y’,’y(0)=1’,’x’); hold on plot(x1,y1,’o’); plot(x2,y2,’r’); fplot(‘2*exp(x )-x-1’,[0,3]); title(‘Euler 法和ode45法与解析解’)； Legend(‘ode45法’,’Euler 法’,’解析解’); ylabel(‘x 轴’); ylabel(‘y 轴’); hold off (2) 20.01()2sin(),(0)0,(0)1,05y y y t y y t ''''-+===<< odefun=@(t,y)[y(2);0.01*y(2)^2-2*y(1)+sin(t)]; [t,y]=ode45(odefun,[0 5],[0:1]); plot(t,y(:,1)); title(‘第一题（2）图像’); xlabel(‘x 轴’); ylabel(‘y 轴’);

实验一 常微分方程 2. 求一通过原点的曲线，它在(,)x y 处的切线斜率等于2 2,0 1.57.x y x +<<若x 上限增为1.58，1.60会发生什么？ t2(1.57)

实验一 常微分方程 3. 求解刚性方程组： 11212 121100.25999.750.5,(0)1,050. 999.751000.250.5,(0)1,y y y y x y y y y '=-++=?<

《常微分方程》期末模拟试题

《常微分方程》模拟练习题及参考答案 一、填空题（每个空格4分，共80分） 1、n 阶线性齐次微分方程基本解组中解的个数恰好是 n 个。 2、一阶微分方程 2=dy x dx 的通解为 2=+y x C （C 为任意常数） ，方程与通过点（2，3）的特解为 2 1=-y x ，与直线y=2x+3相切的解是 2 4=+y x ，满足条件3 3ydx =?的解为 22=-y x 。 3、李普希兹条件是保证一阶微分方程初值问题解惟一的 必要 条件。 4、对方程 2()dy x y dx =+作变换 =+u x y ，可将其化为变量可分离方程，其通解为 tan()=+-y x C x 。 5、方程 21d d y x y -=过点)1,2 (π 共有 无数 个解。 6、方程 ''2 1=-y x 的通解为 42 12122=-++x x y C x C ，满足初始条件13|2,|5====x x y y 的特解为 4219 12264 =-++x x y x 。 7、方程 x x y x y +-=d d 无 奇解。 8、微分方程2260--=d y dy y dx dx 可化为一阶线性微分方程组 6?=??? ?=+??dy z dx dz z y dx 。 9、方程 y x y =d d 的奇解是 y=0 。 10、35323+=d y dy x dx dx 是 3 阶常微分方程。 11、方程 22dy x y dx =+满足解得存在唯一性定理条件的区域是 xoy 平面 。 12、微分方程22450d y dy y dx dx --=通解为 512-=+x x y C e C e ，该方程可化为一阶线性微分方程组 45?=??? ?=+??dy z dx dz z y dx 。 13、二阶线性齐次微分方程的两个解12(),()y x y x ??==成为其基本解组的充要条件是 线性无关 。

常微分方程练习题及答案(复习题)

常微分方程练习题及答案(复习题)

常微分方程练习试卷 一、 填空题。 1. 方程23 2 10d x x dt +=是 阶 （线性、非线性）微分方程. 2. 方程 ()x dy f xy y dx =经变换_______，可以化为变量分离方程 . 3. 微分方程 3230d y y x dx --=满足条件(0)1,(0)2y y '==的解有 个. 4. 设常系数方程 x y y y e αβγ'''++=的一个特解*2()x x x y x e e xe =++，则此方程的系数α= ，β= ，γ= . 5. 朗斯基行列式 ()0W t ≡是函数组12(),(),,()n x t x t x t L 在a x b ≤≤上线性相关的 条件. 6. 方程 22(2320)0xydx x y dy ++-=的只与y 有关的积分因子为 . 7. 已知 ()X A t X '=的基解矩阵为()t Φ的，则()A t = . 8. 方程组 20'05??=???? x x 的基解矩阵为 ． 9.可用变换 将伯努利方程 化为线性方程. 10 .是满足方程 251y y y y ''''''+++= 和初始条件 的唯一解. 11.方程 的待定特解可取 的形式: 12. 三阶常系数齐线性方程 20y y y '''''-+=的特征根是 二、 计算题 1.求平面上过原点的曲线方程, 该曲线上任一点处的切线与切点和点(1,0)的连线相互垂直. 2．求解方程13 dy x y dx x y +-=-+. 3. 求解方程 222()0d x dx x dt dt += 。 4．用比较系数法解方程. . 5．求方程 sin y y x '=+的通解. 6．验证微分方程 22(cos sin )(1)0x x xy dx y x dy -+-=是恰当方程，并求出它的通解.

常微分方程期末考试练习题及答案.

一，常微分方程的基本概念 常微分方程： 含一个白变量x,未知数y及若干阶导数的方程式。一般形式为：F (x, y, y …y(n)) =0 (n 丰0). 1. 常微分方程中包含未知函数最高阶导数的阶数称为该方程的阶。 如：f(x)⑶ +3f(x)+x=f(x) 为 3 阶方程。 2. 若f (x)使常微分方程两端恒等，则f (x)称为常微分方程的解。 3. 含有独立的任意个常数(个数等于方程的阶数)的方程的解称为常微 分方程的通解。如常系数三阶微分方程F (t , x(3)) =0的通解的形式为：x (t) =cx (t) +C2x (t) +C3x (t )。 4. 满足初值条件的解称为它的特解(特解不唯一，亦可能不存在) 。 5. 常微分方程之线性及非线性：对于F (x, y, y…y(n)) =0而言，如果方程之左端是y, y'…y(n)的一次有理式，则次方程为n阶线性微分方程。(方程线性与否与白变量无关)。如：xy⑵-5y +3xy=sinx 为2阶线性微分方程；y⑵+siny=0为非线性微分方程。 注：a.这里主要介绍几个主要的，常用的常微分方程的基本概念。余者如常微分方程之显隐式解，初值条件，初值问题等概念这里予以略去。另外，有兴趣的同学不妨看一下教材23页的雅可比矩阵。 b.教材28页第八题不妨做做。

二.可分离变量的方程

1. 定义：形如dy=f (x) 4 (y)的方程，称为分离变量方程。这里f dx (x), § (x)分别是x, y的连续函数。 2. 解法：分离变量法』芸七=J f (x)dx+c. (*) 说明：a由于(*)是建立在§ (y)乒0的基础上，故而可能漏解。 需视情况补上§ (y) =0的特解。(有时候特解也可以和通解统一于 一式中) b.不需考虑因白变量引起的分母为零的情况。 例 1. ydx (x2-4x)dy =0 解：由题意分离变量得：2dx dy=0 x -4 y 即：1(工-1)dx 业=。 4 x —4 x y 积分之，得:1(ln x—4 —In x)+ln y =c 故原方程通解为：(x-4)y4=cx (c为任意常数)，特解y=0 包含在通解中(即两者统一于一式中)。 *例2.若连续函数f (x)满足f(x)T f(：)dt+|n2,则f (x)是？ 解：对给定的积分方程两边关于x求导，得： f' (x) = 2 f (x) (变上限求积分求导) 分离变量，解之得：f(x)=Ce2x 由原方程知：f (0) =In2 ,代入上解析式得： C=ln2 ,