1.
使用444(x)对数据进行插值,并写出误差分析理论。
建立脚本
x1=[0.2 0.4 0.6 0.8 1.0];
y1=[0.98 0.92 0.81 0.64 0.38];
n=length(y1);
c=y1(:);
for j=2:n %求差商
for i=n:-1:j
c(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));
end
end
syms x df d;
df(1)=1;d(1)=y1(1);
for i=2:n %求牛顿差值多项式
df(i)=df(i-1)*(x-x1(i-1));
d(i)=c(i)*df(i);
end
disp('4次牛顿插值多项式');
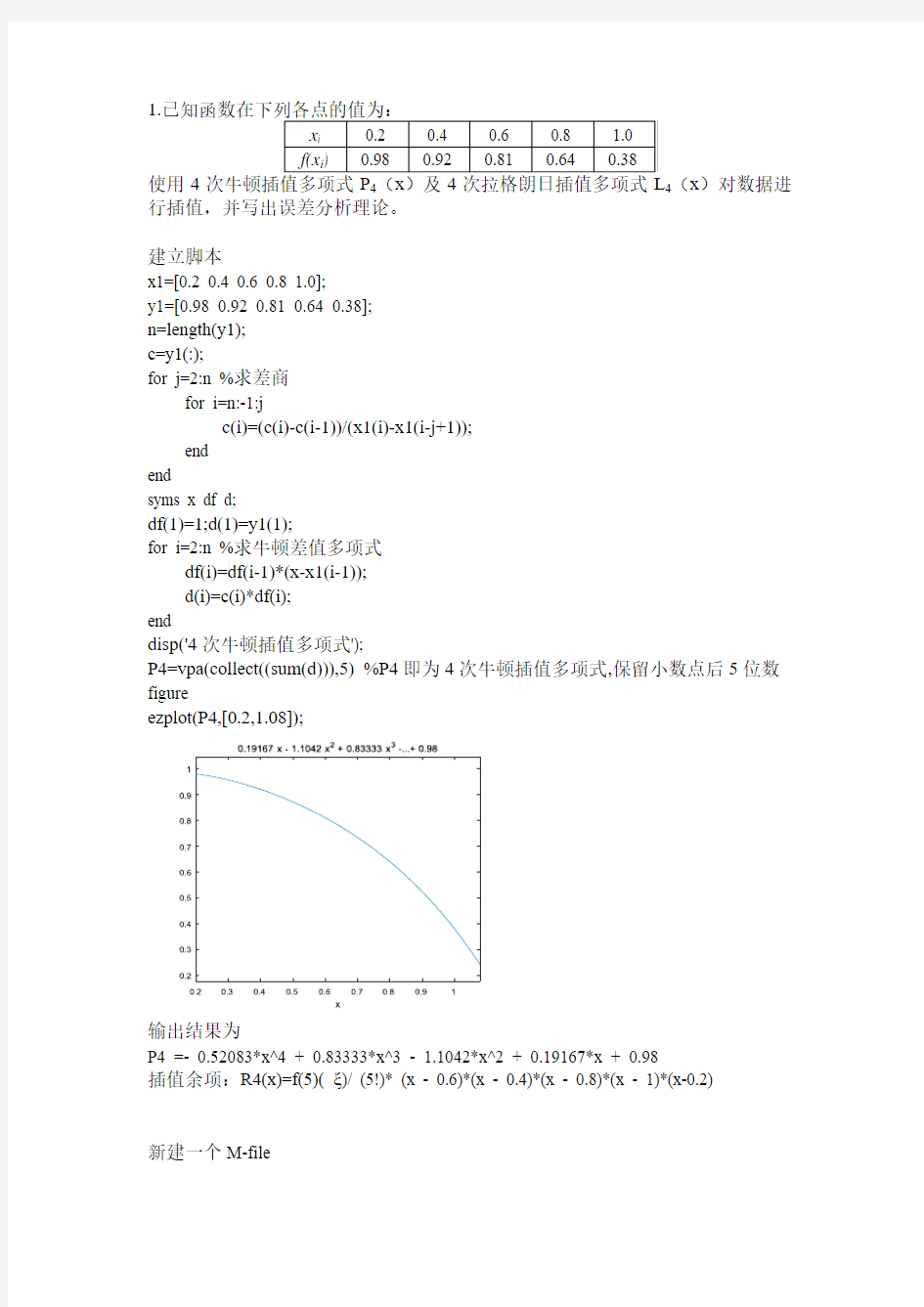
P4=vpa(collect((sum(d))),5) %P4即为4次牛顿插值多项式,保留小数点后5位数figure
ezplot(P4,[0.2,1.08]);
输出结果为
P4 =- 0.52083*x^4 + 0.83333*x^3 - 1.1042*x^2 + 0.19167*x + 0.98
插值余项:R4(x)=f(5)( ξ)/ (5!)* (x - 0.6)*(x - 0.4)*(x - 0.8)*(x - 1)*(x-0.2)
新建一个M-file
syms x l;
x1=[0.2 0.4 0.6 0.8 1.0];
y1=[0.98 0.92 0.81 0.64 0.38];
n=length(x1);
Ls=sym(0);
for i=1:n
l=sym(y1(i));
for k=1:i-1
l=l*(x-x1(k))/(x1(i)-x1(k));
end
for k=i+1:n
l=l*(x-x1(k))/(x1(i)-x1(k));
end
Ls=Ls+l;
end
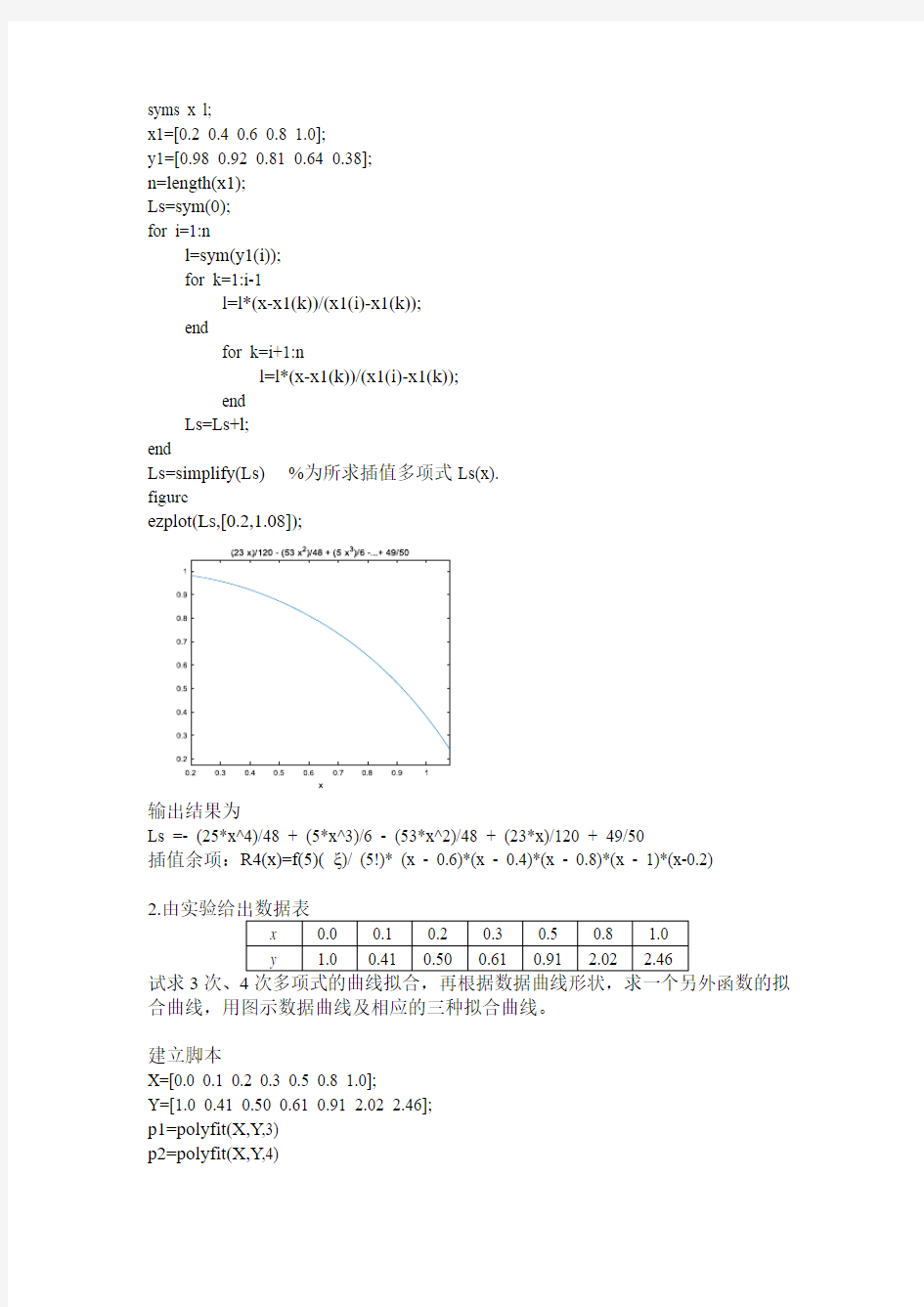
Ls=simplify(Ls) %为所求插值多项式Ls(x).
figure
ezplot(Ls,[0.2,1.08]);
输出结果为
Ls =- (25*x^4)/48 + (5*x^3)/6 - (53*x^2)/48 + (23*x)/120 + 49/50
插值余项:R4(x)=f(5)( ξ)/ (5!)* (x - 0.6)*(x - 0.4)*(x - 0.8)*(x - 1)*(x-0.2) 2.
试求3次、
合曲线,用图示数据曲线及相应的三种拟合曲线。
建立脚本
X=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
Y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];
p1=polyfit(X,Y,3)
p2=polyfit(X,Y,4)
Y1=polyval(p1,X)
Y2=polyval(p2,X)
plot(X,Y,'b*',X,Y1,'g-.',X,Y2,'r--')
f1=poly2sym(p1)
f2=poly2sym(p2)
plot(X,Y,'b*',X,Y1,'m-.',X,Y2,'c--')
legend('数据点','3次多项式拟合','4次多项式拟合') xlabel('X轴'),ylabel('Y轴')
另一个拟合曲线,
新建一个M-file
function [C,L]=lagran(x,y)
w=length(x);
n=w-1;
L=zeros(w,w);
for k=1:n+1
V=1;
for j=1:n+1
if k~=j
V=conv(V,poly(x(j)))/(x(k)-x(j));
end
end
L(k,:)=V;
end
C=y*L
end
%在命令窗口中输入以下的命令:
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];
cc=polyfit(x,y,4);
xx=x(1):0.1:x(length(x));
yy=polyval(cc,xx);
plot(xx,yy,'r');
hold on;
plot(x,y,'x');
xlabel('x');
ylabel('y');
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[0.94 0.58 0.47 0.52 1.00 2.00 2.46]; %y中的值是根据上面两种拟合曲线而得到的估计数据,不是真实数据
function [C,L]=lagran(x,y);
xx=0:0.01:1.0;
yy=polyval(C,xx);
hold on;
plot(xx,yy,'b',x,y,'.');
命令窗口运行
p1 =-6.6221 12.8147 -4.6591 0.9266
p2 =2.8853 -12.3348 16.2747 -5.2987 0.9427
Y1 =0.9266 0.5822 0.4544 0.5034 0.9730 2.0103 2.4602 Y2 =0.9427 0.5635 0.4399 0.5082 1.0005 1.9860 2.4692 f1 =- (3727889208212549*x^3)/562949953421312 +
(3607024445890881*x^2)/281474976710656 -
(1311410561049893*x)/281474976710656 +
4172976892199517/4503599627370496
f2 =(406067862549531*x^4)/140737488355328-
(6943889465038337*x^3)/562949953421312 +
(4580931990070649*x^2)/281474976710656 -
(2982918465844219*x)/562949953421312 +
8491275464650319/9007199254740992
C =
40.6746 -110.2183 110.3671 -57.3264 23.4994 -5.4764 0.9400
3.
对于积分
1
4
9
xdx=-,取不同的步长h。分别用复合梯形及复合辛普森求
积计算积分,给出误差中关于h的函数,并与积分精确值比较两个公式的精度,是否存在一个最小的h,使得精度不能再被改善?
syms x
x=0:0.001:1; % h 为步长,可分别令h=0.1,0.05,0.001,0.005
y=sqrt(x).*log(x+eps);
T=trapz(x,y);
T=vpa(T,7)
f=inline('sqrt(x).*log(x)',x);
S=quadl(f,0,1);
S=vpa(S,7)
运行结果:
T =-0.4443875
S =-0.444444
由结果(1度要高,且当步长取不同值时即n 越大、h 越小时,积分精度越高。实验结果说明不存在一个最小的h ,使得精度不能再被改善。又两个相应的关于h 的误差(余项)其中h 属于a 到b 。可知h h 愈小,余项愈小,从而积分精度越高。
4.用LU 分解及列主元高斯消去法解线性方程组
123410701832.09999962 5.9000015151521021x x x x ??????-??????-??????=??????--??????????????
输出Ax=b 中系数A=LU 分解的矩阵L 及U ,解向量x 及detA;列主元法的行交换次序,解向量x 及detA;比较两种方法所得的结果。
LU 分解法
建立函数
function h1=zhijieLU(A,b) %h1各阶主子式的行列式值
[n n]=size(A);RA=rank(A);
if RA~=n
disp('请注意:因为A 的n 阶行列式h1等于零,所以A 不能进行LU 分解。A 的秩RA 如下:')
RA,h1=det(A);
return
end
if RA==n
for p=1:n
h(p)=det(A(1:p,1:p));
end
h1=h(1:n);
for i=1:n
if h(1,i)==0
disp('请注意:因为A的r阶主子式等于零,所以A不能进行LU 分解。A的秩RA和各阶顺序主子式h1依次如下:')
h1;RA
return
end
end
if h(1,i)~=0
disp('请注意:因为A的r阶主子式都不等于零,所以A能进行LU分解。A的秩RA和各阶顺序主子式h1依次如下:')
for j=1:n
U(1,j)=A(1,j);
end
for k=2:n
for i=2:n
for j=2:n
L(1,1)=1;L(i,i)=1;
if i>j
L(1,1)=1;L(2,1)=A(2,1)/U(1,1);L(i,1)=A(i,1)/U(1,1);
L(i,k)=(A(i,k)-L(i,1:k-1)*U(1:k-1,k))/U(k,k);
else
U(k,j)=A(k,j)-L(k,1:k-1)*U(1:k-1,j);
end
end
end
end
h1;RA,U,L, X=inv(U)*inv(L)*b
end
end
end
命令窗口运行
A=[10 -7 0 1;-3 2.099999 6 2;5 -1 5 -1;2 1 0 2];
b=[8;5.900001;5;1];
h1=zhijieLU(A,b)
请注意:因为A的r阶主子式都不等于零,所以A能进行LU分解。A的秩RA 和各阶顺序主子式h1依次如下:
RA =4
U = 10.0000 -7.0000 0 1.0000
0 2.1000 6.0000 2.3000
0 0 -2.1429 -4.2381
0 -0.0000 0 12.7333
L = 1.0000 0 0 0
-0.3000 1.0000 0 0
0.5000 1.1905 1.0000 -0.0000
0.2000 1.1429 3.2000 1.0000
X = -0.2749
-1.3298
1.2969
1.4398
h1 = 10.0000 -0.0000 -150.0001 -762.0001
列主元法
建立函数
function [RA,RB,n,X]=liezhu(A,b)
B=[A b];n=length(b);RA=rank(A);RB=rank(B);zhicha=RB-RA;
if zhicha>0
disp('请注意:因为RA~=RB,所以方程组无解')
return
warning off MATLAB:return_outside_of_loop
end
if RA==RB
if RA==n
disp('请注意:因为RA=RB,所以方程组有唯一解')
X=zeros(n,1);C=zeros(1,n+1);
for p=1:n-1
[Y,j]=max(abs(B(p:n,p)));C=B(p,:);
B(p,:)=B(j+p-1,:);B(j+p-1,:)=C;
for k=p+1:n
m=B(k,p)/B(p,p);
B(k,p:n+1)=B(k,p:n+1)-m*B(p,p:n+1);
end
end
b=B(1:n,n+1);A=B(1:n,1:n);X(n)=b(n)/A(n,n);
for q=n-1:-1:1
X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);
end
else
disp('请注意:因为RA=RB end end 命令窗口运行 A=[10 -7 0 1;-3 2.099999 6 2;5 -1 5 -1;2 1 0 2]; b=[8;5.900001;5;1]; [RA,RB,n,X]=liezhu(A,b),H=det(A) 请注意:因为RA=RB ,所以方程组有唯一解 RA =4 RB =4 n =4 X = 0.0000 -1.0000 1.0000 1.0000 H = -762.0001 5.线性方程组Ax=b 的A 及b 为 1078732756523,86109337591031A b ????????????==???????????? 则解T x (1,1,1,1)=.用MATLAB 内部函数求detA 及A 的所有特征值和cond(A)2。 若令 1078.17.27.085.04658 5.989.8996.99599.98A A δ??????+=?????? 求解(A+A)(x x)b δδ+=,输出向量x δ和2x δ.从理论结果和实际计算两方面 分析线性方程组Ax=b 解的相对误差22x /x δ及A 的相对误差22/A A δ的关系。 命令窗口运行 A=[10 7 8 7;7 5 6 5;8 6 10 9;7 5 9 10]; b=[32;23;33;31]; dA=det(A),lamda=eig(A),Ac2=cond(A,2) dA = 1.0000 lamda = 0.0102 0.8431 3.8581 30.2887 Ac2 = 2.9841e+03 误差分析 建立函数 function Acp=pjwc(A,jA,b,jb,p) Acp=cond(A,p);dA=det(A);X=A\b; deltaA=jA-A; pndA=norm(deltaA,p);deltab=jb-b; pndb=norm(deltab,p); if pndb>0 jX=A\jb;Pnb=norm(b,p);pnjx=norm(jX,p);deltaX=jX-X; pnjdX=norm(deltaX,p);jxX=pnjdX/pnjX; pnX=norm(X,p);xX=pnjdX/pnX; pndb=norm(deltab,p);xAb=pndb/pnb;pnbj=norm(jb,p);xAbj=pndb/pnbj; Xgxx=Acp*xAb; end if pndA>0 jX=jA\b;deltaX=jX-X;pnX=norm(X,p); pnjdX=norm(deltaX,p); pnjX=norm(jX,p);jxX=pnjdX/pnjX;xX=pnjdX/pnX; pnjA=norm(jA,p);pnA=norm(A,p); pndA=norm(deltaA,p);xAbj=pndA/pnjA;xAb=pndA/pnA; Xgxx=Acp*xAb; end end 命令窗口运行 jA=[10 7 8.1 7.2;7.08 5.04 6 5;8 5.98 9.89 9;6.99 5 9 9.98]; jb=b;p=2; Acp=pjwc(A,jA,b,jb,p) Acp =2.9841e+03 dA =1.0000 ans =1.0000 1.0000 1.0000 1.0000 ans =-9.5863 18.3741 -3.2258 3.5240 xX =10.4661 jxX =0.9842 Xgxx =22.7396 电子科技大学电子工程学院标准实验报告(实验)课程名称MATLAB与数值分析 学生姓名:李培睿 学号:2013020904026 指导教师:程建 一、实验名称 《MATLAB与数值分析》第一次上机实验 二、实验目的 1. 熟练掌握矩阵的生成、加、减、乘、除、转置、行列式、逆、范数等运算 操作。(用.m文件和Matlab函数编写一个对给定矩阵进行运算操作的程序) 2. 熟练掌握算术符号操作和基本运算操作,包括矩阵合并、向量合并、符号 转换、展开符号表达式、符号因式分解、符号表达式的化简、代数方程的符号解析解、特征多项式、函数的反函数、函数计算器、微积分、常微分方程的符号解、符号函数的画图等。(用.m文件编写进行符号因式分解和函数求反的程序) 3. 掌握Matlab函数的编写规范。 4、掌握Matlab常用的绘图处理操作,包括:基本平面图、图形注释命令、 三维曲线和面的填充、三维等高线等。(用.m文件编写在一个图形窗口上绘制正弦和余弦函数的图形,并给出充分的图形注释) 5. 熟练操作MATLAB软件平台,能利用M文件完成MATLAB的程序设计。 三、实验内容 1. 编程实现以下数列的图像,用户能输入不同的初始值以及系数。并以x, y为坐标显示图像 x(n+1) = a*x(n)-b*(y(n)-x(n)^2); y(n+1) = b*x(n)+a*(y(n)-x(n)^2) 2. 编程实现奥运5环图,允许用户输入环的直径。 3. 实现对输入任意长度向量元素的冒泡排序的升序排列。不允许使用sort 函数。 四、实验数据及结果分析 题目一: ①在Editor窗口编写函数代码如下: 数值分析实习报告 姓名:gestepoA 学号:201******* 班级:***班 序言 随着计算机技术的迅速发展,数值分析在工程技术领域中的应用越来越广泛,并且成为数学与计算机之间的桥梁。要解决工程问题,往往需要处理很多数学模型,不仅要研究各种数学问题的数值解法,同时也要分析所用的数值解法在理论上的合理性,如解法所产生的误差能否满足精度要求:解法是否稳定、是否收敛及熟练的速度等。而且还能减少大量的人工计算。 由于工程实际中所遇到的数学模型求解过程迭代次数很多,计算量很大,所以需要借助如MATLAB,C++,VB,JAVA的辅助软件来解决,得到一个满足误差限的解。本文所计算题目,均采用MATLAB进行编程,MATLAB被称为第四代计算机语言,利用其丰富的函数资源,使编程人员从繁琐的程序代码中解放出来MATLAB最突出的特点就是简洁,它用更直观的、符合人们思维习惯的代码。它具有以下优点: 1友好的工作平台和编程环境。MATLAB界面精致,人机交互性强,操作简单。 2简单易用的程序语言。MATLAB是一个高级的矩阵/阵列语言,包含控制语言、函数、数据结构,具有输入、输出和面向对象编程特点。用户可以在命令窗口中将输入语句与执行命令同步,也可以先编好一个较大的复杂的应用程序(M 文件)后再一起运行。 3强大的科学计算机数据处理能力。包含大量计算算法的集合,拥有600多个工程中要用到的数学运算函数。 4出色的图像处理功能,可以方便地输出二维图像,便于我们绘制函数图像。 目录 1 第一题 (4) 1.1 实验目的 (4) 1.2 实验原理和方法 (4) 1.3 实验结果 (5) 1.3.1 最佳平方逼近法 (5) 1.3.2 拉格朗日插值法 (7) 1.3.3 对比 (8) 2 第二题 (9) 2.1实验目的 (9) 2.2 实验原理和方法 (10) 2.3 实验结果 (10) 2.3.1 第一问 (10) 2.3.2 第二问 (11) 2.3.3 第三问 (11) 3 第三题 (12) 3.1实验目的 (12) 3.2 实验原理和方法 (12) 3.3 实验结果 (12) 4 MATLAB程序 (14) 科学计算—理论、方法 及其基于MATLAB 的程序实现与分析 三、 解线性方程组的迭代法(Iteration ) 线性方程组的理论求解公式 b A x 1 -= (1) 在应用于实际问题的计算时,通常面临两方面的问题 1、计算过程复杂, 2、不能保证算法的稳定性; 此外,当初始数据(可能)存在误差时,按公式(1)即使求出了“精确解”意义也不大,因此,对于存在初始数据误差、特别是大型的线性方程组求解,需要寻求能达到精度要求的、操作和计算过程相对简单的求解方法。下面将要介绍的迭代法就属于这类方法。 迭代法求解线性方程组的基本思想是 1) 不追求“一下子”得到方程组的解,而是在逐步逼近方程组的精 确解的迭代过程中获得满足精度要求的近似解,这一点与直接法不同; 2) 通过对问题的转化,避免(困难的)矩阵求逆运算。 用迭代法求解线性方程组,首先要把线性方程组写成等价的形式 f Mx x b Ax +=?= (2) 式(2)的右端称为迭代格式,由迭代格式(2)确定如下的迭代算法: ,2,101=? ??∈?+=+k R x f Mx x n k k (3) 对于给定的线性方程组,可以写成不同的(无穷多)迭代格式,有意义的(可用的)迭代格式应具有收敛性―生成的解向量序列{}x n 收敛于方程组的解;而好的迭代法应具有较高的收敛速度。 关于迭代法收敛性的两个判别条件: a 、充分必要条件是:矩阵M 的谱半径 (){}1,,2,1max <==n i M i i λρ b 、充分条件是:矩阵M 的某个算子 范数 M <1。 设x 是方程组(2)的解,{}m x 是迭代法(3)生成的任一序列,因为 f Mx x +=,f Mx x m m +=+1 所以 ()()()022 1x x M x x M x x M x x m m m m - ==- =-=--- (4) 设1 1--=?=TJT M J MT T ,其中矩阵J 是矩阵M 的Jordan 标准型,那么容易验证1 -=T TJ M m m ,并且 ()[ ]() ()()1 lim ,2,10lim lim 0 lim lim 01 0 用Matlab 软件求解微分方程 1.解析解 (1)一阶微分方程 求21y dx dy +=的通解:dsolve('Dy=1+y^2','x') 求y x dx dy -+=21的通解:dsolve('Dy=1+x^2-y','x') 求?????=+=1 )0(12y y dx dy 的特解:dsolve('Dy=1+y^2',’y(0)=1’,'x') (2)高阶微分方程 求解???-='==-+'+''. 2)2(,2)2(,0)(222πππy y y n x y x y x 其中,21=n ,命令为: dsolve('x^2*D2y+x*Dy+(x^2-0.5^2)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x') 求042=-+'-'''x y y y 的通解,命令为: dsolve('D3y-2*Dy+y-4*x=0','x') 输出为: ans=8+4*x+C1*exp(x)+C2*exp(-1/2*(5^(1/2)+1)*x)+C3*exp(1/2*(5^(1/2)-1)*x) (3)一阶微分方程组 求???+-='+='). (3)(4)(),(4)(3)(x g x f x g x g x f x f 的通解:[f,g]=dsolve('Df=3*f+4*g','Dg=-4*f+3*g','x') 输出为: f =exp(3*x)*(cos(4*x)*C1+sin(4*x)*C2) g =-exp(3*x)*(sin(4*x)*C1-cos(4*x)*C2) 若再加上初始条件1)0(,0)0(==g f ,则求特解: [f,g]=dsolve('Df=3*f+4*g','Dg=-4*f+3*g','f(0)=0,g(0)=1','x') 输出为: f =exp(3*x)*sin(4*x) g =exp(3*x)*cos(4*x) 2.数值解 (1)一阶微分方程 第2章牛顿插值法实现 参考文献:[1]岑宝俊. 牛顿插值法在凸轮曲线修正设计中的应用[J]. 机械工程师,2009,10:54-55. 求牛顿插值多项式和差商的MA TLAB 主程序: function[A,C,L,wcgs,Cw]=newpoly(X,Y) n=length(X);A=zeros(n,n);A(:,1) =Y'; s=0.0;p=1.0;q=1.0;c1=1.0; for j=2:n for i=j:n A(i,j)=(A(i,j-1)-A(i-1,j-1))/(X(i)-X(i-j+1)); end b=poly(X(j-1));q1=conv(q,b);c1=c1*j;q=q1; end C=A(n,n);b=poly(X(n));q1=conv(q1,b); for k=(n-1):-1:1 C=conv(C,poly(X(k)));d=length(C);C(d)=C(d)+A(k,k); end L(k,:)=poly2sym(C);Q=poly2sym(q1); syms M wcgs=M*Q/c1;Cw=q1/c1; (1)保存名为newpoly.m 的M 文件 (2)输入MA TLAB 程序 >> X=[242,243,249,250]; >> Y=[13.681,13.526,13.098,13.095]; >> [A,C,L,wcgs,Cw]=newpoly(X,Y) 输出3阶牛顿插值多项式L 及其系数向量C 差商的矩阵A ,插值余项wcgs 及其 ) ()()1(ξ+n n f x R 的系数向量Cw 。 A = 13.6810 0 0 0 13.5260 -0.1550 0 0 13.0980 -0.0713 0.0120 0 13.0950 -0.0030 0.0098 -0.0003 C = 1.0e+003 * 数值分析作业(1) 1:思考题(判断是否正确并阐述理由) (a)一个问题的病态性如何,与求解它的算法有关系。 (b)无论问题是否病态,好的算法都会得到它好的近似解。 (c)计算中使用更高的精度,可以改善问题的病态性。 (d)用一个稳定的算法计算一个良态问题,一定会得到他好的近似解。 (e)浮点数在整个数轴上是均匀分布。 (f)浮点数的加法满足结合律。 (g)浮点数的加法满足交换律。 (h)浮点数构成有效集合。 (i)用一个收敛的算法计算一个良态问题,一定得到它好的近似解。√2: 解释下面Matlab程序的输出结果 t=0.1; n=1:10; e=n/10-n*t 3:对二次代数方程的求解问题 20 ++= ax bx c 有两种等价的一元二次方程求解公式 2224b x a c x b ac -±==- 对 a=1,b=-100000000,c=1,应采用哪种算法? 4:函数sin x 的幂级数展开为: 357 sin 3!5!7! x x x x x =-+-+ 利用该公式的Matlab 程序为 function y=powersin(x) % powersin. Power series for sin(x) % powersin(x) tries to compute sin(x)from a power series s=0; t=x; n=1; while s+t~=s; s=s+t; t=-x^2/((n+1)*(n+2))*t n=n+2; end (a ) 解释上述程序的终止准则; (b ) 对于x=/2π、x=11/2π、x =21/2π,计算的精度是多少?分别需 要计算多少项? 5:指数函数的幂级数展开 2312!3!x x x e x =+++ + 根据该展开式,编写Matlab 程序计算指数函数的值,并分析计算结果(重点分析0x <的计算结果)。 1、 在MATLAB 中用Jacobi 迭代法讨论线性方程组, 1231231234748212515 x x x x x x x x x -+=?? -+=-??-++=? (1)给出Jacobi 迭代法的迭代方程,并判定Jacobi 迭代法求解此方程组是否收敛。 (2)若收敛,编程求解该线性方程组。 解(1):A=[4 -1 1;4 -8 1;-2 1 5] %线性方程组系数矩阵 A = 4 -1 1 4 -8 1 -2 1 5 >> D=diag(diag(A)) D = 4 0 0 0 -8 0 0 0 5 >> L=-tril(A,-1) % A 的下三角矩阵 L = 0 0 0 -4 0 0 2 -1 0 >> U=-triu(A,1) % A 的上三角矩阵 U = 0 1 -1 0 0 -1 0 0 0 B=inv(D)*(L+U) % B 为雅可比迭代矩阵 B = 0 0.2500 -0.2500 0.5000 0 0.1250 0.4000 -0.2000 0 >> r=eigs(B,1) %B 的谱半径 r = 0.3347 < 1 Jacobi迭代法收敛。 (2)在matlab上编写程序如下: A=[4 -1 1;4 -8 1;-2 1 5]; >> b=[7 -21 15]'; >> x0=[0 0 0]'; >> [x,k]=jacobi(A,b,x0,1e-7) x = 2.0000 4.0000 3.0000 k = 17 附jacobi迭代法的matlab程序如下: function [x,k]=jacobi(A,b,x0,eps) % 采用Jacobi迭代法求Ax=b的解 % A为系数矩阵 % b为常数向量 % x0为迭代初始向量 % eps为解的精度控制 max1= 300; %默认最多迭代300,超过300次给出警告D=diag(diag(A)); %求A的对角矩阵 L=-tril(A,-1); %求A的下三角阵 U=-triu(A,1); %求A的上三角阵 B=D\(L+U); f=D\b; x=B*x0+f; k=1; %迭代次数 while norm(x-x0)>=eps x0=x; x=B*x0+f; k=k+1; if(k>=max1) disp('迭代超过300次,方程组可能不收敛'); return; end end 第四讲Matlab求解微分方程(组) 理论介绍:Matlab求解微分方程(组)命令 求解实例:Matlab求解微分方程(组)实例 实际应用问题通过数学建模所归纳得到得方程,绝大多数都就是微分方程,真正能得到代数方程得机会很少、另一方面,能够求解得微分方程也就是十分有限得,特别就是高阶方程与偏微分方程(组)、这就要求我们必须研究微分方程(组)得解法:解析解法与数值解法、 一.相关函数、命令及简介 1、在Matlab中,用大写字母D表示导数,Dy表示y关于自变量得一阶导数,D2y 表示y关于自变量得二阶导数,依此类推、函数dsolve用来解决常微分方程(组)得求解问题,调用格式为: X=dsolve(‘eqn1’,’eqn2’,…) 函数dsolve用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解、 注意,系统缺省得自变量为t 2、函数dsolve求解得就是常微分方程得精确解法,也称为常微分方程得符号解、但就是,有大量得常微分方程虽然从理论上讲,其解就是存在得,但我们却无法求出其解析解,此时,我们需要寻求方程得数值解,在求常微分方程数值解方 面,MATLAB具有丰富得函数,我们将其统称为solver,其一般格式为: [T,Y]=solver(odefun,tspan,y0) 说明:(1)solver为命令ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb、ode15i之一、 (2)odefun就是显示微分方程在积分区间tspan上从到用初始条件求解、 (3)如果要获得微分方程问题在其她指定时间点上得解,则令tspan(要求就是单调得)、 (4)因为没有一种算法可以有效得解决所有得ODE问题,为此,Matlab提供了多种求解器solver,对于不同得ODE问题,采用不同得solver、 表1 Matlab中文本文件读写函数 列主元法 function lianzhuyuan(A,b) n=input('请输入n:') %选择阶数A=zeros(n,n); %系数矩阵A b=zeros(n,1); %矩阵b X=zeros(n,1); %解X for i=1:n for j=1:n A(i,j)=(1/(i+j-1)); %生成hilbert矩阵A end b(i,1)=sum(A(i,:)); %生成矩阵b end for i=1:n-1 j=i; top=max(abs(A(i:n,j))); %列主元 k=j; while abs(A(k,j))~=top %列主元所在行 k=k+1; end for z=1:n %交换主元所在行a1=A(i,z); A(i,z)=A(k,z); A(k,z)=a1; end a2=b(i,1); b(i,1)=b(k,1); b(k,1)=a2; for s=i+1:n %消去算法开始m=A(s,j)/A(i,j); %化简为上三角矩阵 A(s,j)=0; for p=i+1:n A(s,p)=A(s,p)-m*A(i,p); end b(s,1)=b(s,1)-m*b(i,1); end end X(n,1)=b(n,1)/A(n,n); %回代开始 for i=n-1:-1:1 s=0; %初始化s for j=i+1:n s=s+A(i,j)*X(j,1); end X(i,1)=(b(i,1)-s)/A(i,i); end X 欧拉法 clc clear % 欧拉法 p=10; %贝塔的取值 T=10; %t取值的上限 y1=1; %y1的初值 r1=1; %y2的初值 %输入步长h的值 h=input('欧拉法please input number(h=1 0.5 0.25 0.125 0.0625):h=') ; if h>1 or h<0 break end S1=0:T/h; S2=0:T/h; S3=0:T/h; S4=0:T/h; i=1; % 迭代过程 for t=0:h:T Y=(exp(-t)); R=(1/(p-1))*exp(-t)+((p-2)/(p-1))*exp(-p*t); y=y1+h*(-y1); y1=y; r=r1+h*(y1-p*r1); r1=r; S1(i)=Y; S2(i)=R; S3(i)=y; S4(i)=r; i=i+1; end t=[0:h:T]; % 红线为解析解,'x'为数值解 plot(t,S1,'r',t,S3,'x') MATLAB与数值分析课程总结 姓名:董建伟 学号:2015020904027 一:MATLAB部分 1.处理矩阵-容易 矩阵的创建 (1)直接创建注意 a中括号里可以用空格或者逗号将矩阵元素分开 b矩阵元素可以是任何MATLAB表达式,如实数复数等 c可以调用赋值过的任何变量,变量名不要重复,否则会被覆盖 (2)用MATLAB函数创建矩阵如:a空阵[] b rand/randn——随机矩阵 c eye——单位矩阵 d zeros ——0矩阵 e ones——1矩阵 f magic——产生n阶幻方矩阵等 向量的生成 (1)用冒号生成向量 (2)使用linspace和logspace分别生成线性等分向量和对 数等分向量 矩阵的标识和引用 (1)向量标识 (2)“0 1”逻辑向量或矩阵标识 (3)全下标,单下标,逻辑矩阵方式引用 字符串数组 (1)字符串按行向量进行储存 (2)所有字符串用单引号括起来 (3)直接进行创建 矩阵运算 (1)注意与数组点乘,除与直接乘除的区别,数组为乘方对应元素的幂 (2)左右除时斜杠底部靠近谁谁是分母 (3)其他运算如,inv矩阵求逆,det行列式的值, eig特征值,diag 对角矩阵 2.绘图-轻松 plot-绘制二维曲线 (1)plot(x)绘制以x为纵坐标的二维曲线 plot(x,y) 绘制以x为横坐标,y为纵坐标的二维曲线 x,y为向量或矩阵 (2)plot(x1,y1,x2,y2,。。。。。。)绘制多条曲线,不同字母代替不同颜色:b蓝色,y黄色,r红色,g绿色 (3)hold on后面的pl ot图像叠加在一起 hold off解除hold on命令,plot将先冲去窗口已有图形(4)在hold后面加上figure,可以绘制多幅图形 (5)subplot在同一窗口画多个子图 三维图形的绘制 (1)plot3(x,y,z,’s’) s是指定线型,色彩,数据点形的字 符串 (2)[X,Y]=meshgrid(x,y)生成平面网格点 (3)mesh(x,y,z,c)生成三维网格点,c为颜色矩阵 (4)三维表面处理mesh命令对网格着色,surf对网格片着色 (5)contour绘制二维等高线 (6)axis([x1,xu,y1,yu])定义x,y的显示范围 3.编程-简洁 (1)变量命名时可以由字母,数字,下划线,但是不得包含空格和标点 (2)最常用的数据类型只有双精度型和字符型,其他数据类型只在特殊条件下使用 (3)为得到高效代码,尽量提高代码的向量化程度,避免使用循环结构 Matlab实现数值分析插值及积分 摘要: 数值分析(numerical analysis)是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科,是数学的一个分支,它以数字计算机求解数学问题的理论和方法为研究对象。在实际生产实践中,常常将实际问题转化为数学模型来解决,这个过程就是数学建模。学习数值分析这门课程可以让我们学到很多的数学建模方法。 分别运用matlab数学软件编程来解决插值问题和数值积分问题。题目中的要计算差值和积分,对于问题一,可以分别利用朗格朗日插值公式,牛顿插值公式,埃特金逐次线性插值公式来进行编程求解,具体matlab代码见正文。编程求解出来的结果为:=+。 其中Aitken插值计算的结果图如下: 对于问题二,可以分别利用复化梯形公式,复化的辛卜生公式,复化的柯特斯公式编写程序来进行求解,具体matlab代码见正文。编程求解出来的结果为: 0.6932 其中复化梯形公式计算的结果图如下: 问题重述 问题一:已知列表函数 表格 1 分别用拉格朗日,牛顿,埃特金插值方法计算。 问题二:用复化的梯形公式,复化的辛卜生公式,复化的柯特斯公式计算积分,使精度小于5。 问题解决 问题一:插值方法 对于问题一,用三种差值方法:拉格朗日,牛顿,埃特金差值方法来解决。 一、拉格朗日插值法: 拉格朗日插值多项式如下: 首先构造1+n 个插值节点n x x x ,,,10 上的n 插值基函数,对任一点i x 所对应的插值基函数 )(x l i ,由于在所有),,1,1,,1,0(n i i j x j +-=取零值,因此)(x l i 有因子 )())(()(110n i i x x x x x x x x ----+- 。又因)(x l i 是一个次数不超过n 的多项式,所以只 可能相差一个常数因子,固)(x l i 可表示成: )())(()()(110n i i i x x x x x x x x A x l ----=+- 利用1)(=i i x l 得: MATLAB 编程题库 1.下面的数据表近似地满足函数2 1cx b ax y ++=,请适当变换成为线性最小二乘问题,编程求最好的系数c b a ,,,并在同一个图上画出所有数据和函数图像. 625 .0718.0801.0823.0802.0687.0606.0356.0995 .0628.0544.0008.0213.0362.0586.0931.0i i y x ---- 解: x=[-0.931 -0.586 -0.362 -0.213 0.008 0.544 0.628 0.995]'; y=[0.356 0.606 0.687 0.802 0.823 0.801 0.718 0.625]'; A=[x ones(8,1) -x.^2.*y]; z=A\y; a=z(1); b=z(2); c=z(3); xh=-1:0.1:1; yh=(a.*xh+b)./(1+c.*xh.^2); plot(x,y,'r+',xh,yh,'b*') 2.若在Matlab工作目录下已经有如下两个函数文件,写一个割线法程序,求出这两个函数 10 的近似根,并写出调用方式: 精度为10 解: >> edit gexianfa.m function [x iter]=gexianfa(f,x0,x1,tol) iter=0; while(norm(x1-x0)>tol) iter=iter+1; x=x1-feval(f,x1).*(x1-x0)./(feval(f,x1)-feval(f,x0)); x0=x1;x1=x; end >> edit f.m function v=f(x) v=x.*log(x)-1; >> edit g.m function z=g(y) z=y.^5+y-1; >> [x1 iter1]=gexianfa('f',1,3,1e-10) x1 = 1.7632 iter1 = 6 >> [x2 iter2]=gexianfa('g',0,1,1e-10) x2 = 0.7549 iter2 = 8 第二讲MATLAB的数值分析 2-1矩阵运算与数组运算 矩阵运算和数组运算是MATLAB数值运算的两大类型,矩阵运算是按矩阵的运算规则进行的,而数组运算则是按数组元素逐一进行的。因此,在进行某些运算(如乘、除)时,矩阵运算和数组运算有着较大的差别。在MATLAB中,可以对矩阵进行数组运算,这时是把矩阵视为数组,运算按数组的运算规则。也可以对数组进行矩阵运算,这时是把数组视为矩阵,运算按矩阵的运算规则进行。 1、矩阵加减与数组加减 矩阵加减与数组加减运算效果一致,运算符也相同,可分为两种情况: (1)若参与运算的两矩阵(数组)的维数相同,则加减运算的结果是将两矩阵的对应元素进行加减,如 A=[1 1 1;2 2 2;3 3 3]; B=A; A+B ans= 2 2 2 4 4 4 6 6 6 (2)若参与运算的两矩阵之一为标量(1*1的矩阵),则加减运算的结果是将矩阵(数组)的每一元素与该标量逐一相加减,如 A=[1 1 1;2 2 2;3 3 3]; A+2 ans= 3 3 3 4 4 4 5 5 5 2、矩阵乘与数组乘 (1)矩阵乘 矩阵乘与数组乘有着较大差别,运算结果也完全不同。矩阵乘的运算符为“*”,运算是按矩阵的乘法规则进行,即参与乘运算的两矩阵的内维必须相同。设A、B为参与乘运算的 =A m×k B k×n。因此,参与运两矩阵,C为A和B的矩阵乘的结果,则它们必须满足关系C m ×n 算的两矩阵的顺序不能任意调换,因为A*B和B*A计算结果很可能是完全不一样的。如:A=[1 1 1;2 2 2;3 3 3]; B=A; A*B ans= 6 6 6 12 12 12 18 18 18 F=ones(1,3); G=ones(3,1); F*G ans 3 G*F ans= 1 1 1 1 1 1 1 1 1 (2)数组乘 数组乘的运算符为“.*”,运算符中的点号不能遗漏,也不能随意加空格符。参加数组乘运算的两数组的大小必须相等(即同维数组)。数组乘的结果是将两同维数组(矩阵)的对应元素逐一相乘,因此,A.*B和B.*A的计算结果是完全相同的,如: A=[1 1 1 1 1;2 2 2 2 2;3 3 3 3 3]; B=A; A.*B ans= 1 1 1 1 1 4 4 4 4 4 9 9 9 9 9 B.*A ans= 1 1 1 1 1 4 4 4 4 4 9 9 9 9 9 由于矩阵运算和数组运算的差异,能进行数组乘运算的两矩阵,不一定能进行矩阵乘运算。如 A=ones(1,3); B=A; A.*B ans= 1 1 1 A*A ???Error using= => MATLAB数值计算 (读书日记及程序编写) 第四章方程求根 (2) 第四章 方程求根 #二分法 求2的值 转化成方程02-2 =x 最慢的方法是取初值1001=x 02-21>x ,取502=x 这样得到 也可以x0=a, x1=x0+h, 进行扫描,若f(x0)*f(x1)<0, 则扫描成功,有根区间为[x0,x1],否则继续扫描,如果出现x1>b ,表面扫描失败,再缩小步长h, 再次扫描。 >> format long %让显示的值为 M=2,a=1,b=2,k=0; while b-a>eps x=(a+b)/2; if x^2>M b=x else a=x end k=k+1 end 执行后得到的值为: k = 50 b = 1.414213562373095 k = 51 b = 1.414213562373095 k = 52 最后得到的值就是Matlab 能表达的最接近的值。 #牛顿法 求解f(x)=0的牛顿法是在f(x)画一条切线,确定切线与x 轴的焦点,通过迭代 ) (x f )f(x -n n 1'=+n n x x 对于平方根的问题,牛顿法简洁有效, 换成f(x)=x^2-M, )(x f n ' =2x 这样 ??? ? ??+==+n n n n x M x M x x 212x -x -n 2n 1 该算法就是反复求x 和M/x 的平均值,Matlab 的程序为: format long %让显示的值为 xprev=2; %取的不等于初值x 的一个值,让判断能继续 x=100; %取的初值为3 while abs(x-xprev)>eps*abs(x) xprev=x; x=0.5*(x+2/x) end x = 1.833333333333333 x = 1.462121212121212 x = 1.414998429894803 x = 1.414213780047198 x = 1.414213562373112 x = 1.414213562373095 x = 1.414213562373095 可见6步很快就收敛 然而,若f(x)不具有连续的、有界的一阶、二阶导数,牛顿法的收敛将变得很慢。 #fzero 函数直接求根 求x^3-1在区间[0,10]上的根 fzero(@(x)x^3-1,[0,10]) ans = 1 fzerogui(@(x)x^3-1,[0,10]) 可以通过在图形界面上选择割点来得到 1、%用牛顿法求f(x)=x-sin x 的零点,e=10^(-6) disp('牛顿法'); i=1; n0=180; p0=pi/3; tol=10^(-6); for i=1:n0 p=p0-(p0-sin(p0))/(1-cos(p0)); if abs(p-p0)<=10^(-6) disp('用牛顿法求得方程的根为') disp(p); disp('迭代次数为:') disp(i) break; end p0=p; end if i==n0&&~(abs(p-p0)<=10^(-6)) disp(n0) disp('次牛顿迭代后无法求出方程的解') end 2、disp('Steffensen加速'); p0=pi/3; for i=1:n0 p1=0.5*p0+0.5*cos(p0); p2=0.5*p1+0.5*cos(p1); p=p0-((p1-p0).^2)./(p2-2.*p1+p0); if abs(p-p0)<=10^(-6) disp('用Steffensen加速求得方程的根为') disp(p); disp('迭代次数为:') disp(i) break; end p0=p; end if i==n0&&~(abs(p-p0)<=10^(-6)) disp(n0) disp('次Steffensen加速后无法求出方程的解') end 1、%使用二分法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根, %误差限为 e=10^-4 disp('二分法') a=0.2;b=0.26; tol=0.0001; n0=10; fa=600*(a.^4)-550*(a.^3)+200*(a.^2)-20*a-1; for i=1:n0 p=(a+b)/2; fp=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1; if fp==0||(abs((b-a)/2) roots([1 -1 -1]) x=linspace(0,2*pi,10); y=sin(x); xi=linspace(0,2*pi,100); y1=interp1(x,y,xi); y2=interp1(x,y,xi,'spline'); y3=interp1(x,y,xi,'cublic'); plot(x,y,'o',xi,y1,xi,y2,xi,y3) x=[0 300 600 1000 1500 2000]; y=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491]; xi=linspace(0,2000,20); yi=1.0332*exp(-(xi+500)/7756); y1=interp1(x,y,xi,'spline'); subplot(2,1,1);plot(x,y,'o',xi,yi,xi,y1,'*') p=polyfit(x,y,2); y2=polyval(p,xi); subplot(2,1,2);plot(x,y,'o',xi,yi,xi,y2,'*') x=[0 300 600 1000 1500 2000]; y=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491]; xi=linspace(0,2000,20); y1=interp1(x,y,xi,'spline'); subplot(2,1,1);plot(x,y,'-o', xi,y1,'-*') p=polyfit(x,y,2); y2=polyval(p,xi); subplot(2,1,2);plot(x,y,'-o',xi,y2,'-*') 数值分析MATLAB计算实验报告 姓名班级学号 一、实验名称 用MATLAB编程实现数值微分的外推法计算。 二、实验目的 1.掌握数值微分和定义和外推法的计算过程; 2.了解数值微分外推法的计算方法并且编写出与其算法对应的MATLAB程序代码;3.体会利用MATLAB软件进行数值计算。 三、实验内容 用外推法计算f(x)=x2e?x在x=0.5的导数。 四、算法描述 1.命名函数。 2.如果输入未知数少于四个,默认精度10^-3 3.描述T表矩阵坐标 4.依次赋值计算 T表第一列 5.根据数值微分计算公式求出T表矩阵的值 6.若达到精度则运算结束,若未达到循环计算 7.输出T表,得出的值就是导数值 五、实验结果 六、实验结果分析 此实验通过MATLAB实现外推法数值微分计算,得到相应的数据,方便对数据进行分析。从结果可以看出,当步长h=0.025时用中点微分公式只有3位有效数字,外推一次达到5位有效数字,外推两次达到9位有效数字。 七、附录(程序) function g=waituifa(fname,x,h,e) if nargin<4,e=1e-3; end; i=1; j=1; G(1,1)=(feval(fname,x+h)-feval(fname,x-h))/(2*h); G(i+1,1)=(feval(fname,x+h/2)-feval(fname,x-h/2))/h; G(i+1,j+1)=(4^j*G(i+1,j)-G(i,j))/(4^j-1); while abs(G(i+1,i+1)-G(i+1,i))>e i=i+1; G(i+1,1)=(feval(fname,x+h/2^i)-feval(fname,x-h/2^i))/(2*h/2^i); for j=1:i G(i+1,j+1)=((4^j)*G(i+1,j)-G(i,j))/(4^j-1); end end G g=G(i+1,i+1); 第四讲 Matlab 求解微分方程(组) 理论介绍:Matlab 求解微分方程(组)命令 求解实例:Matlab 求解微分方程(组)实例 实际应用问题通过数学建模所归纳得到的方程,绝大多数都是微分方程,真正能得到代数方程的机会很少.另一方面,能够求解的微分方程也是十分有限的,特别是高阶方程和偏微分方程(组).这就要求我们必须研究微分方程(组)的解法:解析解法和数值解法. 一.相关函数、命令及简介 1.在Matlab 中,用大写字母D 表示导数,Dy 表示y 关于自变量的一阶导数,D2y 表示y 关于自变量的二阶导数,依此类推.函数dsolve 用来解决常微分方程(组)的求解问题,调用格式为: X=dsolve(‘eqn1’,’eqn2’,…) 函数dsolve 用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解. 注意,系统缺省的自变量为t 2.函数dsolve 求解的是常微分方程的精确解法,也称为常微分方程的符号解.但是,有大量的常微分方程虽然从理论上讲,其解是存在的,但我们却无法求出其解析解,此时,我们需要寻求方程的数值解,在求常微分方程数值解方面,MATLAB 具有丰富的函数,我们将其统称为solver ,其一般格式为: [T,Y]=solver(odefun,tspan,y0) 说明:(1)solver 为命令ode45、ode23、ode113、ode15s 、ode23s 、ode23t 、ode23tb 、ode15i 之一. (2)odefun 是显示微分方程'(,)y f t y =在积分区间tspan 0[,]f t t =上从0t 到f t 用初始条件0y 求解. (3)如果要获得微分方程问题在其他指定时间点012,,, ,f t t t t 上的解,则令 tspan 012[,,,]f t t t t =(要求是单调的). (4)因为没有一种算法可以有效的解决所有的ODE 问题,为此,Matlab 提供 数值分析幂法与反幂法 matlab程序 随机产生一对称矩阵,对不同的原点位移和初值(至少取3个)分别使用幂法求计算矩阵的主特征值及主特征向量,用反幂法求计算矩阵的按模最小特征值及特征向量。 要求 1)比较不同的原点位移和初值说明收敛性 2)给出迭代结果,生成DOC文件。 3)程序清单,生成M文件。 解答: >> A=rand(5) %随机产生5*5矩阵求随机矩阵 A = 0.7094 0.1626 0.5853 0.6991 0.1493 0.7547 0.1190 0.2238 0.8909 0.2575 0.2760 0.4984 0.7513 0.9593 0.8407 0.6797 0.9597 0.2551 0.5472 0.2543 0.6551 0.3404 0.5060 0.1386 0.8143 >> B=A+A' %A矩阵和A的转置相加,得到随机对称矩阵B B = 1.4187 0.9173 0.8613 1.3788 0.8044 0.9173 0.2380 0.7222 1.8506 0.5979 0.8613 0.7222 1.5025 1.2144 1.3467 1.3788 1.8506 1.2144 1.0944 0.3929 0.8044 0.5979 1.3467 0.3929 1.6286 B=?? ????? ???? ?? ???6286.13929.03467.15979.08044 .03929.00944 .12144.18506 .13788.13467.12144.15025.17222.08613.05979.08506.17222.02380.09173.08044.03788.18613 .09173 .04187.1 编写幂法、反幂法程序: function [m,u,index,k]=pow(A,u,ep,it_max) % 求矩阵最大特征值的幂法,其中 % A 为矩阵; % ep 为精度要求,缺省为1e-5; % it_max 为最大迭代次数,缺省为100; % m 为绝对值最大的特征值; % u 为对应最大特征值的特征向量; % index ,当index=1时,迭代成功,当index=0时,迭代失败 if nargin<4 it_max=100; end if nargin<3 ep=1e-5; end n=length(A); index=0; k=0; m1=0; m0=0.01; % 修改移位参数,原点移位法加速收敛,为0时,即为幂法 I=eye(n) T=A-m0*I while k<=it_max v=T*u; [vmax,i]=max(abs(v)); m=v(i); u=v/m; if abs(m-m1)《MATLAB与数值分析》第一次上机实验报告
数值分析MATLAB上机实验
数值分析 第四章 基于MATLAB的科学计算—解线性方程组的迭代法
用Matlab解微分方程
数值分析的matlab实现
matlab与数值分析作业
matlab数值分析例题
Matlab求解微分方程(组)及偏微分方程(组)
数值分析的MATLAB程序
MATLAB与数值分析课程总结
matlab实现数值分析插值及积分
同济大学数值分析matlab编程题汇编
第2讲 matlab的数值分析
MATLAB数值计算-第4章-方程求根
数值分析matlab代码
第3章 MATLAB数值计算-习题 答案
数值分析第四章外推法计算数值微分MATLAB计算实验报告.docx
Matlab求解微分方程(组)及偏微分方程(组)
数值分析幂法与反幂法-matlab程序