
第三章 运输问题
主要内容 运输问题的模型、算法 讲授重点 运输问题的模型、算法 讲授方式
讲授式、启发式
第一节 运输问题及其数学模型
一、运输问题的数学模型
设某种物品有m 个产地A 1,A 2,…,A m ,各产地的产量分别是a 1,a 2,…,a m ;有n 个销地B l ,B 2,…,B n ,各销地的销量分别为b l ,b 2,…,b n 。假定从产地A i (i =1,2,…,m)向销地B j (j =1,2,…,n)运输单位物品的运价是c ij ,问怎样调运这些物品才能使总运费最小?
这是由多个产地供应多个销地的单品种物品运输问题。为直观清楚起见,可列出该出该问题的运输表,如表3-1所示。
设
ij
x 表示从A i 运往B j 的物品数量,
ij
c 表示从A i 运往B j 的单位物品的运价。则对于平
衡运输问题(
∑∑===
n
j j
m
i i
b
a
1
1),其数学模型的一般形式可表示为:
∑∑===
n
j m
i ij
ij
x c
s 11
min
()()()?????
????
==≥====∑∑==n j m i x n j b x m i a x ij j
m i ij i
n
j ij ,2,1;,2,10
,,2,1,,2,11
1 (3.1)
二、运输问题数学模型的特点
对于平衡运输问题(
∑∑===
n
j j
m
i i
b
a
1
1
),可以证明其有如下两个特点: (1)矩阵A 的秩R(A)=m+n-1。
(2)问题必有最优解,而且当j
i b a ,皆为整数时,其最优解必为整数最优解。
第二节 表上作业法求解运输问题
一、给出运输问题的初始可行解(初始调运方案) 1、最小元素法 解题步骤:
⑴在运价表中找到最小运价c 1k ; ⑵将的A L 产品给B k ;
①若a L>b k,则将a L改写为a L-b k,划掉b k,同时将运价表中K列的运价划掉;
②若a L
如此重复(1)、(2),直到分配完毕。
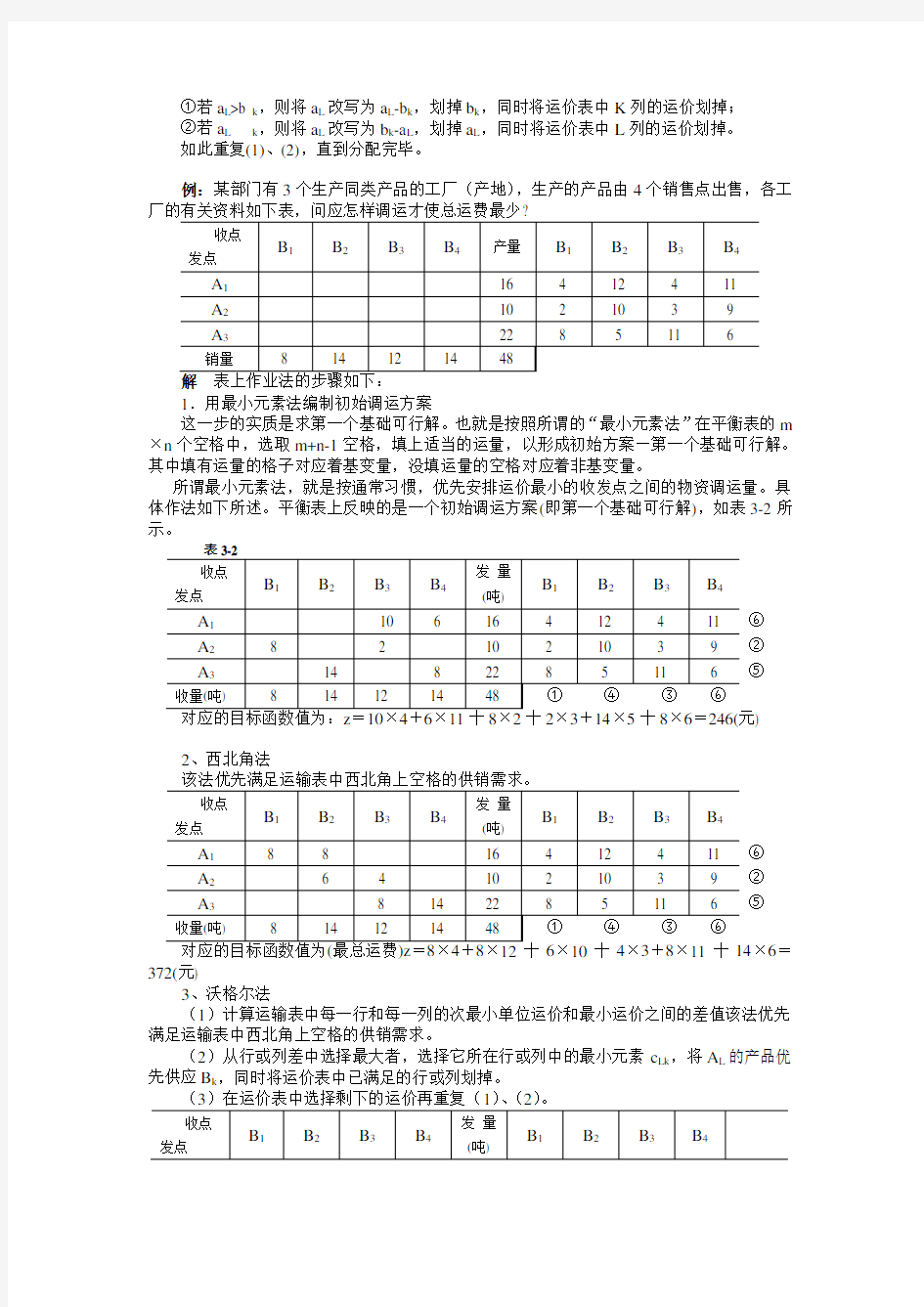
例:某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工
1.用最小元素法编制初始调运方案
这一步的实质是求第一个基础可行解。也就是按照所谓的“最小元素法”在平衡表的m ×n个空格中,选取m+n-1空格,填上适当的运量,以形成初始方案—第一个基础可行解。其中填有运量的格子对应着基变量,没填运量的空格对应着非基变量。
所谓最小元素法,就是按通常习惯,优先安排运价最小的收发点之间的物资调运量。具体作法如下所述。平衡表上反映的是一个初始调运方案(即第一个基础可行解),如表3-2所示。
⑥
②
⑤
)
2、西北角法
⑥
②
⑤
×6=372(元)
3、沃格尔法
(1)计算运输表中每一行和每一列的次最小单位运价和最小运价之间的差值该法优先满足运输表中西北角上空格的供销需求。
(2)从行或列差中选择最大者,选择它所在行或列中的最小元素c Lk,将A L的产品优先供应B k,同时将运价表中已满足的行或列划掉。
244(元)
二、解的最优性检验
1、闭回路法
闭回路法:它是以某一空格为起点,用水平线或垂直线向前画,每碰到一个数字格转90度后,继续前进,直到回到起始空格为止。
判别即考察初始方案对应的基础可行解是否是基础最优解,也就是判别非基变量x ij对应的检验数σij是否全部非负。若是,则初始方案就是最优方案;若否,则初始方案尚需改进调整。那么,这里如何计算σij呢?这个方法就是所谓的“闭回路法”。下面以σ11的计算为例加以说明。
为了计算σ11,我们暂时对初始方案作如下的局部调整:在σ11对应的空格中填入运量1,即非基变量x ll的取值由0增大1,但为了保持收发平衡,从表3-2可以看出:x ll增加1,x l3必需减去1,x23必需增加1,x21必需减去1.这样调整运量以后,依据运价表计算,总运费将要增加的数值为:
c11-c13+c23-c21,
而依据典式目标函数(3.3)计算应为σ11.由此可知
σ11=c11-c13+c23-c21
或
σ11=(c11+c23)-(c13+c21)(3.4)
如果我们把上述调整过运量的格子x ll、x l3、x23、x21(为了叙述方便,我们不妨把每个格子以其对应的变量来表记)连接起来恰巧形成一个封闭的回路。
过每一个空格能且只能做唯一的一条闭回路。例如在表3-2中:
空格x ll对应的闭回路是x ll-x l3-x23一x21一x ll;
空格x l2对应的闭回路是x l2-x14-x34一x32一x12.
以上两条闭回路画于表3-2中。
有了闭回路概念,就可以分析检验数与闭回路的关系:
(1)因为每一个空格x ij都唯一对应一条闭回路,而每一空格又都对应非基变量的检验数σij,因此每一个非基变量的检验数σij也唯一对应一条闭回路(以起始空格为奇数次拐角点)。
(2)由(3.4)知,
σ11=(c11+c23)-(c13+c21)
其中(c13+c21)正是σ11对应的闭回路第偶数次拐角点对应的运价之和,(c11+c23)正是第奇数次拐角点对应的运价之和。一般地,可以证明:空格x ij对应的检验数σij与其相应的闭回路的关系是:
σij=[奇角点对应运价之和]-[偶角点对应运价之和] (3.5)
在上例中,利用表3-2可以求出:
σ11=(4+3)-(2+4)=1
σ22=(10+6+4)-(5+11+3)=1
σ12=(12+6)-(5+11)=2
……
σ24=(9+4)-(11+3)=-1
经过以上分析,至此我们便可对调运方案的判别准则作以下概述:
(1)从调运方案表中的第一行开始,从左到右,按公式(3.5),依次计算每个空格对应的检验数。
(2)若全部检验数σij≥0,则已有方案便是最优方案。
(3)若计算中遇到某检验数小于0,则停止计算其余的检验数,表明方案需要调整,转入下一步—方案的调整。
2、对偶变量法(位势法)
(1)编制位势表:在运价表中,凡是对应于平衡表中有运量的运价都划上圈,同时在右侧和下边分别增加一行和一列;
(2)填写位势数:最后一列为列位势数有m个,最后一行为行位势数有n个。
这m+n个位势数必须满足要求:U K+V L+=V KL
(3)计算检验数:σij=C ij-(U i+V j)
三、解的改进
调整的步骤如下:
(1)作第一个出现的负检验数σkj对应的闭回路;
(2)求调整量ε:ε=闭回路偶拐角点中的最小运量;
(3)调整:闭回路中,奇拐角点处运量加上ε;偶拐角点处运量减去ε(其中出基变量对应的格子变成空格);不在闭回路上的格子,运量不变;最后写出新的调运方案。
四、几点说明
P94
第三节运输问题的进一步讨论
一、产销不平衡的运输问题
我们结合下面的例题作以说明。
吨,1231234
总发量比总收量多4吨。如果各发点把多余的水泥库存下来的话,那么不论怎样组织运输(满足需求)总的库存数部是4吨。这样,我们就在平衡表中增加库存一列;同时在运价表也相
这里要注意,在利用最小元素法编制初始调运方案时,应首先把运价表中库存一列的零运价划去,然后再在其余运价中逐次选取最小运价来编制初始调运方案。最后得到的最优调
二、作物布局问题的表工作业法
作物布局问题同物资调运问题的线性规划数学模型基本类似,只是作物布局问题是求目标函数(总产量或总产值)最大值,而物资调运问题是求目标函数(总运费)最小值,所以它们的解法也是基本相同的。下面只举一个例子,借以说明作物布局问题的表上作业法。 例4 某农场有土地9公顷。这些土地因土壤的肥沃程度和
水源条件不同,可以分成三类。现在农场要在这三类土地上计划种植三种作物。各类土地面积、计划种植面积,以及各种作物在各类土地上的亩产量如下表所示。问应如何因地制宜安排作物布局,才使作物总产量最多?
解 所谓最大元素法,就是按产量高的优先安排种植的原则。比如在表3-19中可以看到在土地B 1上种植作物A 2产量最高,所以B 1的3公顷全部种植A 2……直至三种作物全部安排
⑤ ②
④
先求出初始方案中每个空格对应的检验数λij ,其中计算公式与物资凋运问题一样,即 ????
??-????
??=亩产总和偶拐角点亩产总和奇拐角点ij λ
如果所有检验数λij ≤0,就可判定这个方案是最优方案。否则,就要对方案进行调整。 对于这个例子的初始方案,因为λ11=50,所以需要调整。 (3)调整——用闭回路法求调整方案
作物布局方案的调整与物资调运方案的调整类似,即:过第一个出现的负检验数对应的空格,作一闭回路;在闭回路奇拐角点的数字中,找一个最小的数,称为调整量;然后,在这条闭回路上,凡奇拐角点的数减去调整数,凡偶拐角点的数加上调整数,便得新的种植方案,经过若干次调整,总能得到最优方案。
对表
案。最大总产量为:
s=100×700+200×850+200×700+400×500=580 000公斤第四节应用问题举例
见例6-例7
作业2,3,7,9,10
表上作业法 什么是表上作业法 表上作业法是指用列表的方法求解线性规划问题中运输模型的计算方法。是线性规划一种求解方法。当某些线性规划问题采用图上作业法难以进行直观求解时,就可以将各元素列成相关表,作为初始方案,然后采用检验数来验证这个方案,否则就要采用闭合回路法、位势法等方法进行调整,直至得到满意的结果。这种列表求解方法就是表上作业法。 [编辑] 表上作业法的步骤[1] 1、找出初始基本可行解(初始调运方案,一般m+n-1个数字格),用西北角法、最小元素法; (1)西北角法: 从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数。然后按行(列)标下一格的数。若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。如此进行下去,直至得到一个基本可行解。 (2)最小元素法: 从运价最小的格开始,在格内的右下角标上允许取得的最大数。然后按运价从小到大顺序填数。若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。如此进行下去,直至得到一个基本可行解。 注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元例外(同时划去一行和一列)。当填上一个数后行、列同时饱和时,也应任意划去一行(列),在保留的列(行)中没被划去的格内标一个0。 2、求出各非基变量的检验数,判别是否达到最优解。如果是停止计算,否则转入下一步,用位势法计算; 运输问题的约束条件共有m+n个,其中:m是产地产量的限制;n是销地销量的限制。其对偶问题也应有m+n个变量,据此: σ ij = c ij? (u i + v j) ,其中前m个计为,前n个计为
由单纯形法可知,基变量的σ ij = 0 c ij? (u i + v j) = 0因此u i,v j可以求出。 3、改进当前的基本可行解(确定换入、换出变量),用闭合回路法调整; (因为目标函数要求最小化) 表格中有调运量的地方为基变量,空格处为非基变量。基变量的检验数σ ij = 0,非基变量的 检验数。σ ij < 0表示运费减少,σij > 0表示运费增加。 4、重复②,③,直到找到最优解为止。 [编辑] 表上作业法计算中的问题 1、无穷多最优解 产销平衡的运输问题必定存最优解。如果非基变量的σ ij = 0,则该问题有无穷多最优解。 2、退化 表格中一般要有(m+n-1)个数字格。但有时,在分配运量时则需要同时划去一行和一列,这时需要补一个0,以保证有(m+n-1)个数字格。一般可在划去的行和列的任意空格处加一个0即可。 [编辑] 表上作业法案例分析 [编辑] 案例一:表上作业法在物流配送中的应用[2] 配送是物流系统的一项十分重要的功能。随着物流行业的发展,物流公司迅速增加,各个物流公司之间的竞争日趋激烈。如何加强管理以减少成本问题成为各物流公司非常关注的话题。一般来说,配送中心数量减少,配送中心距离客户的距离就会越长,配送成本就越高;配送中心数量增多,配送中心距离客户的距离就会缩短,配送成本就越少,但是配送中心的管理成本随之增加。本文讨论利用现有的配送中心向客户的配送问题,寻求最小的配送成本。
运输问题的求解方法 ——表上作业法 产销平衡表与单位运价表 表上作业法 一、产销平衡表与单位运价表 运输问题还可用产销平衡表与单位运价表进行描述。 假设某种物资有m个生产地点Ai(i=1,2,…,m),其产量(供应量)分别为ai(i=1,2,…,m),有n个销地Bj(j=1,2,…,n),其销量(需求量)分别为bj(j=1,2,…,n)。从Ai到Bj运输单位物资的运价(单价)为Cij。将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。 表5.3.1 产销平衡表与单位运价表 二、表上作业法 运输这一类特殊问题可用更加简便的求解方法———表上作业法求解,实质仍是单纯形法,步骤如下: (1)确定初始调运方案,即找出初始基可行解,在产销平衡表上给出m+n-1个数字格。 (2)求非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解:是否存在负的检验数?如果存在负的检验数,则初始调运方案不是最优方案;如果所有检验数都非负,则初始调运方案已经是最优方案了。如果已经得到最优调运方案,则停止计算,否则转入下一步。 (3)确定换入变量和换出变量,找出新的调运方案(新的基可行解),即在表上用闭回路法进行调整。 (4)重复(1)~(2),直到求出最优解为止。 (一)确定初始可行基的方法 ?最小元素法 从单位运价表中最小的运价开始确定供销关系,然后考虑运价次小的,一直到给出初始基可行解为止。 ?伏格尔法 采用最小元素法可能造成其他处的更多浪费,伏格尔法考虑最小运费与次小运费之间的差额,差额越大,就按次小运费调运。
(二)最优解的判别 计算非基变量(空格)的检验数,当所有的检验数时,为最优解。 求空格检验数的方法有: ?闭回路法 以某一空格为起点找一条闭回路,用水平或垂直线向前划,每碰到一数字格转900后,继续前进,直到回到起始空格为止。 闭回路如图5.3.1的(a)、(b)、(c)等所示。从每一个空格出发一定存在并且可以找到唯一的闭回路。因为,m+n-1个数字格(基变量)对应的系数向量是一个基,任一空格(非基变量)对应的系数向量是这个基的线性组合。 ?位势法 一种较为简便的求检验数的方法。 设是对应运输问题的m+n个约束条件的对偶变量。B是含有一个人工变量X a的初始基矩阵。X a在目标函数中的系数Ca ,由线性规划的对偶理论可知 而每一个决策变量Xij的系数向量,所以 由单纯形法可知,所有基变量的检验数等于0,即 下面用具体例子说明表上作业法的计算步骤。 例1:假设某种物资共有3个产地,其日产量分别是:A1为7 t,A2为4 t,A3为9 t;该种物资的4个销售地,其日销量分别:B1为3 t,B2为6 t,B3为5 t,B4为6 t;各产地到销售地的单位物资的运价如表5.3.2所示。在满足各销售点需要量的前提下,如何调运该种物资,才能使总运费达到最小? 表5.3.2
谢荣华、林建、岳钱华、叶俊君 【摘要】在物资调运问题中,希望运输费用最少总是人们最为关心的一个 目标。在各种设定条件的约束下,如何寻找使得总运输费用最少的最优的运输方案是运输问题的核心。为给社会生产(生活)提供既便捷又经济实惠的物资调运方案,运输问题模型的求解方法可以产生最优的决策方案。因此对运输问题的深入研究具有极其重要的理论意义和实际应用价值。表上作业法是解决运输问题的重要方法本文讨论了产销平衡运输问题的表上作业法,利用伏格尔法求初始方案,位势法求检验数,闭合回路发对可行解进行调整和改进,直至求出最优解。 【关键词】运筹学、运输问题、改善优化、表上作业法 一、理论依据 运输问题的表上作业法步骤 1、制作初始平衡表 用“西北最大运量,然后,每增加角方法”:即在左上角先给予最大运量,然后,每增加一个运量都使一个发量或手里饱。如果所有运量的数字少于 (m+n-1),则补0使之正好(m+n-1)个。 (注:补零时不能使这些书构成圈。) 2、判断初始方案是否最优 (1)求位势表:对运价表加一行一列,圈出运价表中相应于有运量的项,在增加的行列上分别添上数,使这些元素之和等于圈内的元素。这些元素称为位势数。 (2)求检验数,从而得到检验数表。 结论:若对任意检验数小于等于0,则该方案最优,否则进入3进行调整. 3、调整 (1)找回路:在检验数大于0对应的应量表上对应元素为起点,沿横向或纵向前进,如遇到有运量的点即转向,直至起点,可得到一个回路。 (2)找调整量:沿上述找到的回路,从起点开始,在该回路上奇数步数字的最小者作为调整量ε。 (3)调整方式:在该回路上奇数步-ε,偶数步+ε,得到新回路。 重复上述步骤,使所有检验数小于0,即得到最优方案。 二、背景 鉴于市场竞争日益激烈,消费者需求渐趋多样,工厂作为市场消费品的产出源头,唯有对这种趋势深刻理解、深入分析,同事具体的应用于实际中,才能使自身手艺,断发展壮大,不被新新行业所淘汰。对于今天的重点研究对象食品工厂而言,由于在不同产品在原料使用、物料损耗、市场价格等方面均存在各种差异,如何确定各产品的生产配比,以及在最优的生产配比方案之下工厂能够达到最大的产值,都是值得进行探讨研究的现实问题。 三、实例
三、单纯形法的解题步骤 第一步:作单纯形表. )(1)把原线性规划问题化为标准形式; )(2)找出初始可行基,通常取约束方程组系数矩阵中的单位矩阵; )(3)目标函数非基化; )(4)作初始单纯形表. 第二步:最优解的判定. (1) 若所有检验数都是非正数,即,则此时线性规划问题已取 得最优解. (2) 若存在某个检验数是正数,即,而所对应的列向量无正分量,则线性规划 问题无最优解. 如果以上两条都不满足,则进行下一步. 第三步:换基迭代. ,并确定所在列的非基变量为进基变量. (1)找到最大正检验数,设为 (2)对最大正检验数所在列实施最小比值法,确定出主元,并把主元加上小括号. 主元是最大正检验数 所在列,用常数项与进基变量所对应的列向 量中正分量的比值最小者; 替换出基变量,从而得到新的基变量.也就是主元所在 (3)换基:用进基变量 (4)利用矩阵的行初等变换,将主元变为1,其所在列其他元素都变为零,从此得到新的单纯形表; (5)回到第二步,继续判定最优解是否存在,然后进行新一轮换基迭代,直到问题得到解决为止. 例3 求.
解(1)化标准型:令 ,引进松弛变量 ,其标准型为 求 (2)作单纯形表:在约束方程组系数矩阵中 的系数构成单位矩阵,故取 为基变量,目标函数已非基化了,作初始单纯形表并“换基迭代”(见表6.8).表 6.8
(3)最终结果:此时检验数均为非正数,线性规划问题取得最优解,最优解为 目标函数取得最优值. 原线性规划问题的最优解为:.目标函数的最优值为14,即. 例4 用单纯形方法解线性规划问题. 求. 解此数学模型已是标准型了,其中约束方程含有一个二阶单位矩阵(1、2行,3、4列构成),取为基变量,而目标函数没有非基化.从约束方程找出 ,, 代入目标函数 , 经整理后,目标函数非基化了. 作单纯形表,并进行换基迭代(见表6.9). 最大检验数,由最小比值法知:为主元,对主元所在列施以行初等变出基,非基变量进基. 换,基变量
第三章 运输问题 主要内容 运输问题的模型、算法 讲授重点 运输问题的模型、算法 讲授方式 讲授式、启发式 第一节 运输问题及其数学模型 一、运输问题的数学模型 设某种物品有m 个产地A 1,A 2,…,A m ,各产地的产量分别是a 1,a 2,…,a m ;有n 个销地B l ,B 2,…,B n ,各销地的销量分别为b l ,b 2,…,b n 。假定从产地A i (i =1,2,…,m)向销地B j (j =1,2,…,n)运输单位物品的运价是c ij ,问怎样调运这些物品才能使总运费最小? 这是由多个产地供应多个销地的单品种物品运输问题。为直观清楚起见,可列出该出该问题的运输表,如表3-1所示。 设 ij x 表示从A i 运往B j 的物品数量, ij c 表示从A i 运往B j 的单位物品的运价。则对于平 衡运输问题( ∑∑=== n j j m i i b a 1 1),其数学模型的一般形式可表示为: ∑∑=== n j m i ij ij x c s 11 min ()()()????? ???? ==≥====∑∑==n j m i x n j b x m i a x ij j m i ij i n j ij ,2,1;,2,10 ,,2,1,,2,11 1 (3.1) 二、运输问题数学模型的特点 对于平衡运输问题( ∑∑=== n j j m i i b a 1 1 ),可以证明其有如下两个特点: (1)矩阵A 的秩R(A)=m+n-1。 (2)问题必有最优解,而且当j i b a ,皆为整数时,其最优解必为整数最优解。 第二节 表上作业法求解运输问题 一、给出运输问题的初始可行解(初始调运方案) 1、最小元素法 解题步骤: ⑴在运价表中找到最小运价c 1k ; ⑵将的A L 产品给B k ;
表上作业法解决运输 问题
表上作业法解决运输问题 谢荣华、林建、岳钱华、叶俊君 【摘要】在物资调运问题中,希望运输费用最少总是人们最为关心的一个目标。在各种设定条件的约束下,如何寻找使得总运输费用最少的最优的运输方案是运输问题的核心。为给社会生产(生活)提供既便捷又经济实惠的物资调运方案,运输问题模型的求解方法可以产生最优的决策方案。因此对运输问题的深入研究具有极其重要的理论意义和实际应用价值。表上作业法是解决运输问题的重要方法本文讨论了产销平衡运输问题的表上作业法,利用伏格尔法求初始方案,位势法求检验数,闭合回路发对可行解进行调整和改进,直至求出最优解。 【关键词】运筹学、运输问题、改善优化、表上作业法 一、理论依据 运输问题的表上作业法步骤 1、制作初始平衡表 用“西北最大运量,然后,每增加角方法”:即在左上角先给予最大运量,然后,每增加一个运量都使一个发量或手里饱。如果所有运量的数字少于 (m+n-1),则补0使之正好(m+n-1)个。 (注:补零时不能使这些书构成圈。) 2、判断初始方案是否最优
(1)求位势表:对运价表加一行一列,圈出运价表中相应于有运量的项,在增加的行列上分别添上数,使这些元素之和等于圈内的元素。这些元素称为位势数。 (2)求检验数,从而得到检验数表。 结论:若对任意检验数小于等于0,则该方案最优,否则进入3进行调整. 3、调整 (1)找回路:在检验数大于0对应的应量表上对应元素为起点,沿横向或纵向前进,如遇到有运量的点即转向,直至起点,可得到一个回路。 (2)找调整量:沿上述找到的回路,从起点开始,在该回路上奇数步数字的最小者作为调整量ε。 (3)调整方式:在该回路上奇数步-ε,偶数步+ε,得到新回路。 重复上述步骤,使所有检验数小于0,即得到最优方案。 二、背景 鉴于市场竞争日益激烈,消费者需求渐趋多样,工厂作为市场消费品的产出源头,唯有对这种趋势深刻理解、深入分析,同事具体的应用于实际中,才能使自身手艺,断发展壮大,不被新新行业所淘汰。对于今天的重点研究对象食品工厂而言,由于在不同产品在原料使用、物料损耗、市场价格等方面均存在各种差异,如何确定各产品的生产配比,以及在最优的生产配比方案之下工厂能够达到最大的产值,都是值得进行探讨研究的现实问题。 三、实例 甲、乙、丙三个城市每年需要煤炭分别为:320、250、350万吨,由A、B 两处煤矿负责供应。已知煤炭年供应量分别为:A—400万吨,B—450万吨。
第3章运输问题
第三章运输问题 一、选择 1.运输问题在用表上作业法计算的时候,用闭回路法进行调整检验时,通过任 一空格可以找到()闭回路 A、惟一 B、多个 C、零个 D 不能确定 2.在产销不平衡的运输问题中,如果产大于销,我们(B )把他变成一个产销 平衡的运 输问题 A 假想一个产地 B 假想一个销地 C 去掉一个产地 D 没有办法 3.最小元素法的基本思想就是( D)。 A依次供应B全面供应 C 选择供应 D就近供应 4.运输问题中在闭回路调整中,使方案中有数字的格为( C )。 A m B n C m+n D m+n-1 5.在表上作业法中,调运方案中有数字的格为( C ) A m+n B m-n C m+n-1 D m*n 6.运输问题的数学模型中,包含有( D)变量。 A m+n B m-n C m+n-1 D m*n 7. 运输问题的数学模型中,包含有( A)个约束条件。 A m+n B m-n C m+n-1 D m*n 8. 运输问题的数学模型中,系数矩阵中线性独立的列向量的最大个数为(C ) A m+n B m-n C m+n-1 D m*n 9. 运输问题的解中的基变量数一般为(C ) A m+n B m-n C m+n-1 D m*n
10.运输问题中,在检验数表上所有检验数都(C ),此时运输表中给出的方案就是最优方案。 A大于零B等于零C大于等于零D小于零 11.在产销不平衡的运输问题中,如果销大于产时,可以在产销平衡表上 ( A),把他变成 一个产销平衡的运输问题 A 假想一个产地 B 假想一个销地 C 去掉一个产地 D 没有办法 12.运输问题数学模型的特点之一是() A 一定有最优解 B 不一定有最优解 C 一定有基可行解 D 不一定有基可行解 13.运输问题的数学模型的约束条件的系数矩阵的元素由()组成。 A 0B1C0,1D 不确定 14. 二、填空 1.求解不平衡的运输问题的基本思想是(设立虚供地或虚需求点,化为供求平衡的标准形式) 。 2.运输问题中求初始基本可行解的方法通常有 (最小元素法 )、 (伏格尔法 ) 两种方法。 3.伏格尔法有时就用作求运输问题最优方案的(近似解) 4.运输问题最优性检验通常有(闭回路法、位势法)两种方法。 5.
/* 表上作业法的源代码 */ #include "" #include "" #include "" /* #define debug */ #define a(j) (*(C+(M-1)*N+j)) /*销量数组*/ #define b(i) (*(C+i*N+N-1)) /*产量数组*/ #define c(i,j) (*(C+i*N+j)) /*运价数组*/ #define x(i,j) (*(X+i*(N-1)+j)) /*运量数组 */ /*(<:基本解,>=:运量为0) */ #define s(i,j) (*(S+i*(N-1)+j)) /*检验数数组Sij */ #define u(i) (*(U+i)) /*位势数组Ui*/ #define v(i) (*(V+i)) /*位势数组Vi*/ #define cpi(k) ((CP+k)->i) /*闭回路点i标*/ #define cpj(k) ((CP+k)->j) /*闭回路点i标*/ #define cpf(k) ((CP+k)->f) /*闭回路点i标*/ /* f=0:j++; f=2:j--; f=1;i--; f=3:i++; */ /*void TP(int M,int N,double *C,double *X); */ 10 6 30 0 20 30 40 50 60 12 7 14 16 9 10 9 13 8 14 183 185 119 162 137 102 179 118 114 189 107 169 161 179 169 140 135 112 184 149 128 106 165 178 199 183 194 127 184 173 124 125 151 127 178 160 162 105 150 185 179 153 174 121 142 108 163 157 138 189 171 114 131 165 150 159 131 155 135 165 124 167 107 109 107 149 175 162 108 182 135 181 106 136 183 134 179 188 136 131 189 166 158 159 180 162 104 116 159 111 void main() { int M,N,i,j; double *C; /*存储运价,产量及销量 */ double *X; /*存储运量分配方案 */ float z; FILE *fp; char fn[80]; double sum; void TP(int M,int N,double *C,double *X); printf("please input the data file name: "); scanf("%s",fn); if((fp=fopen(fn,"r"))==NULL) { printf("Cannot open the data file!");
第32卷第3期2000年6月 南 京 航 空 航 天 大 学 学 报 Jo urnal o f Nanjing Univ ersity o f Aeronautics&Astronautics V o l.32No.3 Jun.2000 运输问题表上作业法的改进研究 李时椿 (南京经济学院管理系 南京,210042) 摘要 在传统的“闭回路法”和“位势法”基础上,提出利用“流水原理”来寻求运输问题最优解。即以“最小元素法”求得初始调运方案后,将表中各栏单位物资的运价视为“水位”的高低,将已安排的运输量视为处于一定水位高度的“蓄水量”,依据“水往低处流”的自然界基本原理,考察处于最高“水位”的“蓄水量”沿其所在的行或列的“渠道”流向最低“水位”的可能性,来确定“流向”及其相应的“闭回路”,据此调配运输方案,直至总体“蓄水量”处于最低水位状态,则方案达最优。 关键词:输运理论;流水原理;闭回路法 中图分类号:F224.3 引 言 运输问题通常用“表上作业法”求解——先以“最小元素法”或“西北角法”给出一个初始方案,再以“闭回路法”或“位势法”进行调整改进,直至获得最优方案。但在实际优化调整时,无论采用何种方法,都必须逐一计算每个空栏处的检验数,才可分析比较并作出调整,其过程重复、计算繁冗,极大地影响了实际应用和推广。本文借助自然界“水往低处流”的基本规律,利用“流水原理”寻求最有效的调配路线进行优化,从而使求解过程简捷而又直观,大大克服了传统方法繁锁重复的弊端。 1 流水原理求解供求平衡的运输问题 某运输问题如下,运价(元/吨)标在图1中各栏斜线左上方,问该如何调运可使总运费支出为最少[1](图中O表示产量,S表示销售量或需求量,下同)。 解 (1)以“最小元素法”确定初始方案。图1中圈内数据表示初始方案所安排的运输量,初始方案总运费为86元。 (2)以“流水原理”对初始方案优化调整。 (A)确定“最高水位”。“水位”指各栏中单位运量的运价,“最高水位”系指已安排有运 收稿日期:1999-06-02;修改稿收到日期:1999-09-13 作者:李时椿,男,副教授,1949年9月生。
第八章运输及配送路线的优化 教学目的:使学生理解各种运输方式的特点及运输方式选择的原则,掌握运输方式选择的定量分析法,理解存在中间运转的物资调配方法,掌握旅行 商问题和中国邮递员问题的解法以及扫描法和节约法。 基本要求:1、理解各种运输方式的特点; 2、掌握运输方式选择的定量分析法; 3、理解存在中间运转的物资调配方法; 4、掌握旅行商问题和中国邮递员问题的解法。 教学重点:扫描法、节约法 教学时数:6学时 第一节运输方式的选择 ?运输方式选择的原则 当同时存在多种运输方式可供选择的情况下,就需要进行选优抉择。通常根据各种运输方式的经济特性和服务特征来选择合适的运输方式,即主要依据运输成本、运输速度、可靠性、安全性等指标进行判断和选择。 安全性原则——首要的原则 及时性原则 准确性原则 经济性原则——主要原则 货物运输的六大方式: 根据运输工具的不同,可分为:水路、公路、铁路、航空、管道和多式联运等运输形式。 在各种运输方式中,如何选择适当的运输方式是物流合理化的重要问题。可以选择一种运输方式也可以选择使用联运的方式。 运输方式的选择,需要根据运输环境、运输服务的目标要求,采取定性分析与定量分析的方法进行考虑。 ?运输方式选择的定性分析法 定性分析法主要是依据完成运输任务可用的各种运输方式的运营特点及主要功能、货物的特性以及货主的要求等因素对运输方式进行直观选择的方法。 1.单一运输方式的选择 单一运输方式的选择,就是选择一种运输方式提供运输服务。公路、铁路、水路、航空和管道五种基本运输方式各有自身的优点与不足,可以根据五种基本运输方式的优势、特点,结合运输需求进行恰当的选择。 一般要考虑的因素是:
单纯形法表的解题步骤 单纯形法表结构如下: j c → 对应变量的价值系数 i θ B C b X b 1x 2x 3x " j x 基变量的价值系数 基变量 资源列 θ规则 求的值 j σ 检验数 ①一般形式 若线性规划问题标准形式如下: 123451231425max 23000284164120,1,2,5 j z x x x x x x x x x x x x x j =++++++=??+=?? +=??≥=?" 取松弛变量345,,x x x 为基变量,它对应的单位矩阵为基。这样就得到初始可 行基解:()()0 0,0,8,16,12T X =。将有关数字填入表中,得到初始单纯形表,如表 1-1所示: 表 1-1 ()()00,0,8,16,12T X = j c → 2 3 0 0 0 i θ B C b X b 1x 2x 3x 4x 5x 0 3x 8 1 2 1 0 0 4 0 4x 16 4 0 0 1 0 -
5x 12 0 [4] 0 0 1 3 j σ 2 3 0 0 0 若检验数均未达到小于等于0,则对上表进行调整。选择上表中检验数最大的列,该列对应的非变量为入基变量;再应用θ规则该列对应的各基变量对应的 θ值,选出其中最小的一行,该行对应的基变量为出基变量。修改单纯形表,对各行进行初等变换,确保基变量组成的矩阵为单为矩阵。修改后的单纯形表如表 1-2所示: 表 1-2 ()()10,3,2,16,0T X = 检验数12,0σσ>,则进行继续调整,调整后的单纯形法表如表1-3所示: 表 1-3 ()()22,3,0,8,0T X =
单纯形法求解线性规划的步骤
单纯形法求解线性规划的步骤 1>初始化 将给定的线性规划问题化成标准形式,并建立一个初始表格,它最右边的单元格都是非负的(否则无解),接下来的m列组成一个m*m的单元矩阵(目标行的单元格则不必满足这一条件),这m列确定了初始的基本可行解的基本变量,而表格中行用基本变量来表示 2>最优化测试 如果目标行的所有单元格都是非负的(除了最右列中代表目标函数值的那个单元格),就可以停止了,该表格代表了一个最优解,它的基本变量的值在最右列中,而剩下的非基本变量都为0 3>确定输入变量 从目标行的前n个单元格中选择一个负的单元格(选择绝对值最大的那个)该单元格所在的列确定的输入变量及主元列 4>确定分离变量 对于主元列的每个正单元格,求出θ比率(如果主元格的单元格为负或为0,说明该问题是无解的,算法终止),找出θ比率最小的列,改行确定了分离变量和主元行 5>建立下一张表格 将主元行的所有单元格除以主元得到新的主元行,包括主元行在内的每一行,要减去改行主元列单元格和新主元行的成绩(除主元行为1外,这一步将主元列的所有单元格变成0).把主元列的变量名进行代换,得到新的单纯形表,返回第一步 为求简单 在本程序中,需要自己建立标准矩阵(比如加入松弛变量等工作需要用户自己完成),程序的输入有两种方式: 1:指定行和列,由用户自行输入每一个元素SimpleMatrix(introw=0,int col=0); 2:直接在主程序中初始化一个二维数组,然后利用构造函数SimpleMatrix(introw,int col,double **M) 来初始化和处理(本程序所用的实例用的是这种方法) 程序中主要的函数以及说明 ~SimpleMatrix(); 销毁动态分配的数组.用于很难预先估计矩阵的行和列,所以在程序中才了动态的内存分配.需要重载析构函数 bool Is_objectLine_All_Positive(); //判断目标行是否全部为非负数,最后一列不作考虑 这个函数用来判断是否已经存在最优解 bool Is_MainCol_All_Negative(int col);//判断主元列是否全部为负数或零 这个函数用来判断线性规划是否是无解的 bool Is_column_all_Positive(int col); //判断col列中是否全部为正(不包括目标行)
任务1.3 优化物流运输的线路 ●任务描述 面对高油价以及公路计重收费的到来,物流运输企业的成本剧增,如何应对挑战?运输公司普遍的做法是:强化经营管理,在降本减耗上下功夫,抵御高物流成本经营风险。其中重要的一条就是不断优化运输线路,减少人为加大的运距,节约油耗,避免油资源浪费,提高运输效率。案例1.3就是广西运德物流公司成功地为康鑫全药业集团运输药品的经验。 ■案例放送 【案例1.3】康鑫全药业集团公司有4个药品生产厂:A1(南宁四塘)、A2(巴马)、A3(南丹)和A4(柳州),2008年第二季度生产供应高科技产品——“护肝王”特效药(针剂)分别为+20、+60、+100、+20万盒(供应量记“+”);有5个批发配送中心B1(平果)、B2(合山)、B3(宜州)、B4(河池)、B5(贵州黔南县),负责推销配送“护肝王”分别是-30、-30、-50、-70、-20万盒(需求量或销售量记“-”)。“护肝王”配送的交通线路用图表示,见图1.3-1。图中○表示生产供应点,□表示配送点,站点旁边的数字表示生产(正数)或配送(负数)“护肝王”数量。线路旁括号内标注的数字表示相邻两点间的距离(为了计算方便,未取实际准确数)。 ■案例研讨 优化物流运输线路与运输线路开发有区别,它是在已知货物名称及数量、货源地和目的地的情况下,根据运输合理化原则对运输线路的选择与优化。 物流运输合理化要求以最佳的运输线路、最快的运输速度和最低的运输费用等将物品从原产地运送到目的地,案例中康鑫全集团的4个生产供应点,5个批发配送点,线路图中有成圈的,有不成圈的,属于相对复杂的情况。应该如何安排,才能达到路程最近和时间及费用最省?经过本单元以下内容的学习,可以找到解决问题的办法。
单纯形法求解线性规划的步骤 1>初始化 将给定的线性规划问题化成标准形式,并建立一个初始表格,它最右边的单元格都是非负的(否则无解),接下来的m列组成一个m*m的单元矩阵(目标行的单元格则不必满足这一条件),这m列确定了初始的基本可行解的基本变量,而表格中行用基本变量来表示 2>最优化测试 如果目标行的所有单元格都是非负的(除了最右列中代表目标函数值的那个单元格),就可以停止了,该表格代表了一个最优解,它的基本变量的值在最右列中,而剩下的非基本变量都为0 3>确定输入变量 从目标行的前n个单元格中选择一个负的单元格(选择绝对值最大的那个)该单元格所在的列确定的输入变量及主元列 4>确定分离变量 对于主元列的每个正单元格,求出θ比率(如果主元格的单元格为负或为0,说明该问题是无解的,算法终止),找出θ比率最小的列,改行确定了分离变量和主元行 5>建立下一张表格 将主元行的所有单元格除以主元得到新的主元行,包括主元行在内的每一行,要减去改行主元列单元格和新主元行的成绩(除主元行为1外,这一步将主元列的所有单元格变成0).把主元列的变量名进行代换,得到新的单纯形表,返回第一步 为求简单 在本程序中,需要自己建立标准矩阵(比如加入松弛变量等工作需要用户自己完成),程序的输入有两种方式: 1:指定行和列,由用户自行输入每一个元素SimpleMatrix(introw=0,int col=0); 2:直接在主程序中初始化一个二维数组,然后利用构造函数SimpleMatrix(introw,int col,double **M) 来初始化和处理(本程序所用的实例用的是这种方法) 程序中主要的函数以及说明 ~SimpleMatrix(); 销毁动态分配的数组.用于很难预先估计矩阵的行和列,所以在程序中才了动态的内存分配.需要重载析构函数 bool Is_objectLine_All_Positive();其中row2为主元所在的行,col为主元所在的列,row1为要处理的行 void PrintAnswer();数不合法"< 图解法和单纯形法求解以下线性规划问题 1.1 图解法解线性规划问题 只含两个变量的线性规划问题,可以通过在平面上作图的方法求解,步骤如下: (1)以变量x1为横坐标轴,x2为纵坐标轴,适当选取单位坐标长度建立平面坐标直 角坐标系。由变量的非负性约束性可知,满足该约束条件的解均在第一象限内。 (2)图示约束条件,找出可行域(所有约束条件共同构成的图形)。 (3)画出目标函数等值线,并确定函数增大(或减小)的方向。 (4)可行域中使目标函数达到最优的点即为最优解。 然而,由于图解法不适用于求解大规模的线性规划问题,其实用意义不大。 1.2 单纯形法解线性规划问题 它的理论根据是:线性规划问题的可行域是n维向量空间Rn中的多面凸集,其最优值如果存在必在该凸集的某顶点处达到。顶点所对应的可行解称为基本可行解。 单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。如果问题无最优解也可用此法判别。 单纯形法的一般解题步骤可归纳如下:①把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。②若基本可行解不存在,即约束条件有矛盾,则问题无解。③若基本可行解存在,从初始基本可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。④按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。⑤若迭代过程中发现问题的目标函数值无界,则终止迭代。 1.3 线性规划问题的标准化 使用单纯形法求解线性规划时,首先要化问题为标准形式 第4章 单纯形法的计算方法 单纯形法求解线性规划的思路: 一般线性规划问题具有线性方程组的变量数大于方程个数, 这时有不定的解。但可以从线性方程组中找出一个个的单纯形, 每一个单纯形可以求得一组解, 然后再判断该解使目标函数值是增大还是变小, 决定下一步选择的单纯形。这就是迭代, 直到目标函数实现最大值或最小值为止。 4.1 初始基可行解的确定 为了确定初始基可行解, 要首先找出初始可行基, 其方法如下。 (1)第一种情况:若线性规划问题 max z =n j j j=1c x ∑ 1,1,2,...,0,1,2,...n ij j i j j a x b i m x j n =?==???≥=?∑ 从Pj ( j = 1 , 2 , ? , n )中一般能直接观察到存在一个初始可行基 121(,,...,)n B P P P 0 0?? ?0 1 0 ?== ? ?0 0 1?? (2)第二种情况:对所有约束条件是“ ≤”形式的不等式, 可以利用化为标准型的方法, 在每个约束条件的左端加上一个松弛变量。经过整理, 重新对 j x 及ij a ( i = 1 , 2 , ? , m ; j = 1 , 2 , ? , n )进行编号, 则可得下列方 程组 11,1111 22,1122,1112.........,,...,0 m m n n m m n n m m m m nn n n n x a x a x b x a x a x b x a x a x b x x x +++++++++=?? +++=?? ??+++=??≥? 显然得到一个m ×m 单位矩阵 单纯形法的解题步骤 三、单纯形法的解题步骤 第一步:作单纯形表. (1)(1)把原线性规划问题化为标准形式; (2)(2)找出初始可行基,通常取约束方程组系数矩阵中的单位矩阵; (3)(3)目标函数非基化; (4)(4)作初始单纯形表. 第二步:最优解的判定. (1) 若所有检验数都是非正数,即 ,则此时线性规划问题已取得最优解. (2) 若存在某个检验数是正数,即,而 所对应的列向量无正分量,则线性规划问题无最 优解. 如果以上两条都不满足,则进行下一步. 第三步:换基迭代. (1)找到最大正检验数,设为,并确定 (2)作单纯形表:在约束方程组系数矩阵中的系数构成单位矩阵,故取为基变量,目标函数已非基化了,作初始单纯形表并“换基迭代”(见表6.8). 表 6.8 x1 x2x3x4x5常数 x 3 x 4 x 51 0 1 0 0 1 2 0 1 0 0 (1)0 0 1 5 10 4 S′ 1 3 0 0 0 0 x 3 x 4 x2 1 0 1 0 0 (1)0 0 1 -2 0 1 0 0 1 5 2 4 S′ 1 0 0 0 -3 -12 x 3 x 1 x 20 0 1 -1 2 1 0 0 1 -2 0 1 0 0 1 3 2 4 S′0 0 0 -1 -1 -14 (3)最终结果:此时检验数均为非正数,线性规划问题取得最优解,最优解为 目标函数取得最优值. 原线性规划问题的最优解为:.目标函数的最优值为14,即. 例4 用单纯形方法解线性规划问题. 求. 解此数学模型已是标准型了,其中约束方程含有一个二阶单位矩阵(1、2行,3、4列构成),取为基变量,而目标函数没有非基化.从约束方程找出图解法和单纯形法求解线性规划问题
单纯形法的计算方法
单纯形法的解题步骤