第2章模型论初步
- 格式:ppt
- 大小:424.50 KB
- 文档页数:88

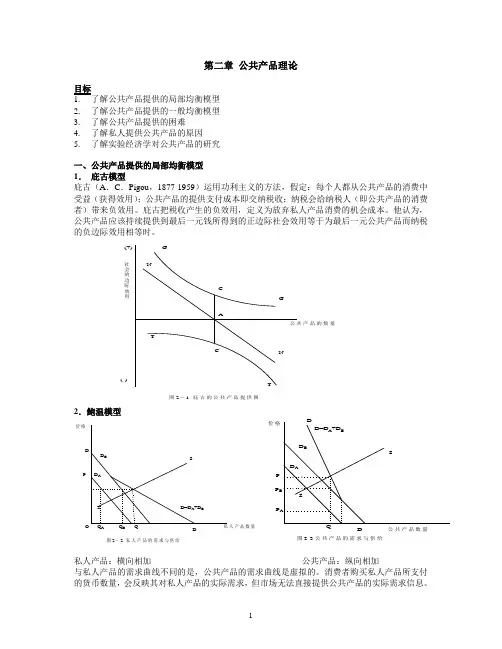
第二章 公共产品理论目标1. 了解公共产品提供的局部均衡模型2. 了解公共产品提供的一般均衡模型3. 了解公共产品提供的困难4. 了解私人提供公共产品的原因5. 了解实验经济学对公共产品的研究一、公共产品提供的局部均衡模型 1. 庇古模型庇古(A .C .Pigou ,1877-1959)运用功利主义的方法,假定:每个人都从公共产品的消费中受益(获得效用);公共产品的提供支付成本即交纳税收;纳税会给纳税人(即公共产品的消费者)带来负效用。
庇古把税收产生的负效用,定义为放弃私人产品消费的机会成本。
他认为,公共产品应该持续提供到最后一元钱所得到的正边际社会效用等于为最后一元公共产品而纳税的负边际效用相等时。
2.鲍温模型私人产品:横向相加 公共产品:纵向相加与私人产品的需求曲线不同的是,公共产品的需求曲线是虚拟的。
消费者购买私人产品所支付的货币数量,会反映其对私人产品的实际需求,但市场无法直接提供公共产品的实际需求信息。
G GT T A (+)(-)社会的边际效用公共产品的数量CC 'NN图2-1 庇古的公共产品提供图D ADBSD D=D A +D BO QA Q BQ P S D 私人产品数量价格图2-2 私人产品的需求与供给S S D A D BD=D A +D BDD Q P AP BP 公共产品数量价格 图2-3 公共产品的需求与供给这里所假定的某人对公共产品的需求曲线,只是模拟市场作出的。
这种假定的意义在于突出私人产品与公共产品需求上存在的差异。
二、 纯公共产品最优提供的一般均衡模型公共产品提供的萨缪尔森条件 消费上的边际替代率之和等于生产上的边际转换率三、公共产品供应的威克塞尔-林达尔模型(W -L 模型) (见图2-7) 四、公共产品提供的困难与公共产品的私人提供 1. “囚徒困境”模型(见图2-8)。
公共产品提供犹如“囚徒困境”,合作与搭便车问题现实中私人提供公共产品:慈善事业(与“搭便车”比较);非营利性组织;科斯:《经济学中的灯塔》B 所消费的私人产品数量XA 所消费的私人产品数量XA 公共产品G 的数量OX (a)公共产品G 的数量X (b)(c)私人产品总数X公共产品G 的数量F X 121⎧⎪⎨⎪⎩X 1A X 'B X '⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩图2-4 资源在私人产品和公共产品之间的配置A AB B 12A O Bh 1h=0h=1A 所支付的税收的比重B 所支付的税收的比公共产品G 的数量图2-7 威克塞尔-林达尔模型囚徒A图2-8 囚徒困境六、公共产品论的实验经济学视角研究1.实验经济学介绍2.公共产品提供实验的分类3.对“搭便车”程度的研究4.减少“搭便车”机制的研究5.对公共产品理论研究的其他影响小结带给他的负边际效用。

第2章多体系统动力学基本理论本章主要介绍多体系统动力学的基本理论,包括多刚体系统动力学建模、多柔体系统动力学建模、多体系统动力学方程求解及多体系统动力学中的刚性(Stiff)问题。
通过本章的学习可以对多体系统动力学的基本理论有较深入的了解,为具体软件的学习打下良好的理论基础。
2.1 多体系统动力学研究状况多体系统动力学的核心问题是建模和求解问题,其系统研究开始于20世纪60年代。
从60年代到80年代,侧重于多刚体系统的研究,主要是研究多刚体系统的自动建模和数值求解;到了80年代中期,多刚体系统动力学的研究已经取得一系列成果,尤其是建模理论趋于成熟,但更稳定、更有效的数值求解方法仍然是研究的热点;80年代之后,多体系统动力学的研究更偏重于多柔体系统动力学,这个领域也正式被称为计算多体系统动力学,它至今仍然是力学研究中最有活力的分支之一,但已经远远地超过一般力学的涵义。
本节将叙述多体系统动力学发展的历史和目前国内外研究的现状。
2.1.1 多体系统动力学研究的发展机械系统动力学分析与仿真是随着计算机技术的发展而不断成熟的,多体系统动力学是其理论基础。
计算机技术自其诞生以来,渗透到了科学计算和工程应用的几乎每一个领域。
数值分析技术与传统力学的结合曾在结构力学领域取得了辉煌的成就,出现了以ANSYS、NASTRAN等为代表的应用极为广泛的结构有限元分析软件。
计算机技术在机构的静力学分析、运动学分析、动力学分析以及控制系统分析上的应用,则在二十世纪八十年代形成了计算多体系统动力学,并产生了以ADAMS和DADS为代表的动力学分析软件。
两者共同构成计算机辅助工程(CAE)技术的重要内容。
多体系统是指由多个物体通过运动副连接的复杂机械系统。
多体系统动力学的根本目的是应用计算机技术进行复杂机械系统的动力学分析与仿真。
它是在经典力学基础上产生的新学科分支,在经典刚体系统动力学上的基础上,经历了多刚体系统动力学和计算多体系统动力学两个发展阶段,目前已趋于成熟。







第2课时价电子对互斥理论等电子原理课标解读重点难点1.了解杂化轨道的三种类型(sp3、sp2、sp)。
2.初步认识分子的空间构型。
3.能运用杂化轨道理论和价层电子对互斥模型判断分子的空间构型。
4.结合实例说明“等电子原理”的应用。
1.判断分子中心原子的杂化轨道类型。
(重点)2.用价层电子对互斥理论及杂化轨道理论推断分子的空间构型。
(难点)课前自主导学一、杂化轨道理论与分子空间构型1.sp3杂化与CH4分子的空间构型(1)杂化轨道的形成碳原子2s轨道上的1个电子进入2p空轨道, 2s轨道和 2p轨道“混合”,形成的4个sp3杂化轨道。
图示为:(2)sp3杂化轨道的空间指向碳原子的4个sp3杂化轨道指向,每个轨道上都有一个未成对电子。
(3)共价键的形成碳原子的4个轨道分别与4个H原子的轨道重叠形成4个相同的σ键。
(4)CH4分子的空间构型CH4分子为空间结构,分子中C—H键之间的夹角都是。
2.sp2杂化与BF3分子的空间构型(1)sp2杂化轨道的形成硼原子2s轨道上的1个电子进入2p轨道。
1个2s轨道和 2p轨道发生杂化,形成能量相等、成分相同的 sp2杂化轨道。
图示为:(2)sp2杂化轨道的空间指向硼原子的3个sp2杂化轨道指向,3个sp2杂化轨道间的夹角为。
(3)共价键的形成硼原子的3个轨道分别与3个氟原子的1个2p轨道重叠,形成3个相同的σ键。
(4)BF3分子的空间构型BF3分子的空间构型为,键角为。
3.sp杂化与BeCl2分子的空间构型(1)杂化轨道的形成Be原子2s轨道上的1个电子进入2p轨道,1个2s轨道和1个2p轨道发生杂化,形成能量相等、成分相同的个sp杂化轨道。
图示为:(2)sp杂化轨道的空间指向两个sp杂化轨道呈,其夹角为。
(3)共价键的形成Be原子的2个sp杂化轨道分别与2个Cl原子的1个轨道重叠形成相同的σ键。
思考交流:1.任意不同的原子轨道都可以杂化吗?二、价层电子对互斥模型1.理论分子中的价电子对(包括电子对和孤电子对)由于相互排斥作用,而趋向于尽可能彼此远离以减小斥力,分子尽可能采取的空间构型。
第2章一元二次函数、方程和不等式2.1等式和不等式性质课程标准:1.梳理等式的性质,理解不等式的概念,掌握不等式的性质,能运用不等式的性质比较大小2能运用不等式的性质证明不等式和解决简单的实际问题.教学重点:1.不等式的性质2用不等式的性质证明不等式.教学难点:用作差法比较代数式的大小.【知识导学】知识点一等式的性质(1)如果a=b,那么a+c=b+c.(2妆口果a=b,那么ac = be或学=#(CH0).(3妆口果a=b, b=c,那么a=c.知识点二作差比较法(1)理论依据:因d_/2>OOa>b:^a-b = 0<^a = b; ^g-b<0<^a<b.⑵方法步骤:①叵I作差;②西整理;③西判断符号;④因下结论.知识点三两个实数大小的比较(1)“> 如凹"-b>0:(2)"=bO"-b 図=0:(3)固αvZ?Ua —b<0.知识点四不等式的性质⑴如果a>b,那么b<a;如果b<cb那么回“>/?,即国台Z?V".(2妆口果a>b,且b>c,那么歴輕,即a>b, b>c=叵I ">c.(3)如果a>b,那么d+o画R+c.(4)如果a>b, c>0,那么ac >bc;如果a>b, c<O,那么UC <bc.(5)如果a>b, OcL那么α+c 画 >/?+〃.(6)如果a>b>O, c>d>O,那么ac回如果α>b>O, c<(l<0,那么ac 回G"∙⑺如果a>b>O,那么0 凹R"(n∈N, π≥2).(8)如果回^/>∕x>0,那么,∖[cι>,yfb(n^N, 2).【新知拓展】1.关于不等式性质的理解两个同向不等式可以相加,但不可以相减,如">/?, c>d不能推出“一c>/?—d.2.常用的结论(1 )a>b,(2)bvO<"W>*;(3)a>b>O,o√>0=>^>p... r,I a a+m a a~m b b+m b b~m(4)右Qb>0,加>0,则沪书p丹百卩一心0); £片;茗二需(方_心0).3.比较大小的方法比较数(式)的大小常用作差与0比较.作差法中常用的变形手段是分解因式和配方等恒等变形,前者将“差”化为“积”,后者将“差”化为一个完全平方式或儿个完全平方式的“和”,也可二者并用.4.利用不等式求范围应注意的问题求指定代数式的取值范围,必须依据不等式的性质进行求解,同向不等式具有可加性与可乘性,但是不能相减或相除,解题时必须利用性质,步步有据,避免改变代数式的取值范围.题型一作差法比较大小例1比较下列各组中两数的大小:(1)已知S 〃为正数,且a≠b,比较/+,与局+“2;⑵已知XV1,比较X3-I与2X2-2X:(3)已知X, y均为正数,设加=出,“=古,比较加与〃的大小.[解](1 )(Λ3 ÷b3)—(a2b ÷ ab2)=a3+b3-a1b-ab2=a2{a-b)-b2(a—b)= (a-b)(a2-b2)= {a~b)2(a+b).Vt∕>O, b>0 且a≠b, Λ(a-b)2>Q9 a+b>O9/. (a y÷ /?3) — (a2b ÷ ab2)>O,即cr+b^>a2b+ab2.(2)X3- 1 — (2x2-2x)=x3-2X2÷2X- 1=(√-X2)-(X2-2X÷1)=X2(Λ:- I)-(X-1)2= (X-I)(X2-χ+1) = (X- 1 {(^-∣)2+∣•Txvl, Λχ- l<0.X^x-^2÷j>0,•••(XT)-(x^⅛+fl <0, ΛX3~1<2Λ2~2X.4 x+y 4 (x+y)2_4Xy (χ∙~y)'χ+y Xy x+y Q(X+y) xy(x÷y)* 乂“ y均为正数,Λ.r>0, y>0, xy>0, x÷y>0, (X-y)2≥0.Λ∕n-∕2≥0,即〃总舁(当x=y时,等号成立)・金版点睛作差比较法的四个步骤[结论〕—(根据差的符号,判断两数(式)的大小「题型二 不等式的性质及应用例2下列命题正确的是 ___________②α>b 且 c>d=>ac>bch解析]①戸’ n 知 当XO, b>0时,满足已知条件,但推不出a>b, IoO (・•・①错误.②当a = 3, b=∖, C= —2, Cl=—3时,命题显然不成立∙ ∙°∙②错误•④显然c 2>0t Λ两边同乘以$得a>b.④正确.[答案]③④金版点睛 解决这类问题,主要是根据不等式的性质判定,其实质是看是否满足性质所 需的条件,若要判断一个命题是假命题,可以从条件入手,推出与结论相反的结 论,也可举出一个反例予以否定・题型三 利用不等式的性质证明不等式例 3 (1)已知e>f 9 c>0,求证:f-ac<e~bc;(2)已知CVdV0,求证:土缶;-∖a>h>09‰>o一成立・・:③正确・ ③a>b>O 且 c>√>0=>=>^>p*0=>(3)已知bc-ad20, bd>O.求证:一T —W 〃・[证明](I)Tα>∕?, c>O, .*.ac>hc./. -ac<-hc.'∙f<e,:・f— ac<e—be.(2) T CVdVO, /. —c>—d>0.乂a>b>O, C. ci—c>b—d>0.(3) •: be—adMO, :∙QdWbc,乂T bcl>O,金版点睛利用不等式的性质证明不等式的实质与技巧(1)实质:就是根据不等式的性质把不等式进行变形,要注意不等式的性质成立的条件.(2)技巧:若不能直接由不等式的性质得到,可先分析需要证明的不等式的结构.然后利用不等式的性质进行逆推,寻找使其成立的充分条件.题型四利用不等式的性质求取值范围例4 (1)已知2vαW5,3WbVl0,求a~b,彳的取值范围;(2)已知一∣≤cc<^≤^,求笞迫,生亍©的取值范圉.[解](I)V3≤∕^<10,・•・一10v-bW-3.乂2<t∕≤5τ •:—8<f∕-Z>≤2.⑵T —彳WaV厂W号,・•・-共鈴γ<⅛两式相加得一两式相加得一又*0,・・・三篡0, Λ[变式探究]将本例(1)中,条件不变,求a+b,“b的取值范围.解由2<t∕≤5,3≤^<10 得2 +3 V/+b<5 ÷ 10,2 ×3<ab<5 ×10,即5<a÷b< 15,6<ab<50.金版点睛利用不等式的性质求取值范围应注意的问题本题中不能直接用G的范围去减或除b的范围,应严格利用不等式的性质去求范围;其次在有些题目中,还要注意整体代换的思想,即弄清要求的与已知的"范围”间的联系.如已知20<x+yV30,15Vχ-y<18,要求2x+3y的范围,不能分别求出X, y的范围,再求"+3y的范围,应把已知的"x+y” “x—y” 视为整体,即2x+3y=I(X+>-)—∣(Λ—y),所以需分别求出∣(x+y), —∣(χ-y)的范围,两范围相加可得2r+3y的范围.“范围”必须对应某个字母变量或代数式,一旦变化出其他的范围问题,则不能再间接得出,必须“直来直去”,即直接找到要求的量与已知的量间的数量关系,然后去求.2.2基本不等式课程标准:1•掌握基本不等式的内容2能熟练地运用基本不等式来比较两个实数的大小.3.能初步运用基本不等式来证明简单的不等式.4 •熟练掌握基本不等式及变形的应用∙5.会用基本不等式解决简单的最大(小)值问题.教学重点:1.理解基本不等式的内容及其证明过程2运用基本不等式来比较两个实数的大小及进行简单的证明.3.运用基本不等式解决简单的最大值或最小值问题.教学难点:基本不等式条件的创设.【知识导学】知识点一基本不等式如果。
王思斌社会工作导论北京大学出版社第二版笔记第一章(选择题)1、社会工作的定义:一、社会工作时科学的社会服务和方法,二、社会工是一个专业和制度,社会工作时以利他主义为指导,以科学的知识为基础,运用科学的方法进行职业性的助人活动社会服务分为公共服务(政府)和社会服务(社会组织)专业(格林伍德):理论体系,社会认可。
专业权威、伦理守则。
专业文化制度:具备社会制度的基本特征,成为社会福利必不可少的组成部分2、社会工作的性质:融价值、理论、实务为一体的多维系统。
实务性、科学性、价值相关性、道德实践3、社会工作的构成要素:社会工作者:角色,贝克把社会工作者角色分为直接服务、间接服务、和合并服务角色服务对象:个体、群体、社区价值观:核心是利他主义助人方法:专业的方法4、社会工作方法分类:直接服务:个案工作、小组工作、社区工作、间接方法:社会工作行政第二章:社会工作发展历史(选择题)时间、人物、意义、特点、什么队个案的影响,什么对社区的影响第一节:社会工作历史起源一。
思想渊源1、古希腊、古罗马及希伯来时期的思想根源古罗马时期。
人们之间的互助主要表现在人们对社会责任观的强调,这种责任的意义在于富人帮助穷人是一种宗教责任希伯来时期:人们对正义的主张表现在公平享有财富的认识中,这种思想对社会工作价值强调社会公平正义的传统起到重要影响2、基督教的博爱思想产生于公元1世纪,教义包含许多利他、奉献、爱人等博爱思想,这种博爱思想对社会工作的价值基础长生影响3、人道主义价值观时间:源于欧洲文艺复兴,强调人生而平等、人的尊严和人的价值的重视对社会工作的出现产生了重要影响,为社会工作的产生奠定了坚实的思想基础二、工业革命与社会救助的发展1、工业革命与社会变迁工业革命促进经济结构的转变同时带来社会关系和社会结构的转变,资本主义的经济体系好人社会关系的确立。
后果是产生大量的农民失业和众多贫民的产生2、英国的(伊丽莎白济贫法)1601年,为应对贫困和其他社会问题,颁布济贫法。
数理逻辑(证明论、递归论、模型论和公理集合论)(2010-10-28 00:14:03)转自新浪博客1930年以后,数学逻辑开始成为一个专门学科,得到了蓬勃发展。
哥德尔的两个定理证明之后,希尔伯特的有限主义纲领行不通,证明论出现新的情况,主要有两方面:通过放宽有限主义的限制来证明算术无矛盾性以及把证明形式化、标准化,这些主要是在三十年代完成。
同时哥德尔引进递归函数,发展成递归论的新分支,开始研究判定问题。
而哥德尔本人转向公理集合论的研究,从此出现公理集合论的黄金时代。
五十年代模型论应运而生,它与数学有着密切联系,并逐步产生积极的作用。
1、证明论证明论又称元数学,它研究数学的最基本活动—证明的合理性问题。
研究这类数学基础的问题原来一直是哲学家的事,后来才成为数学家的事。
这个转变发生在1893年弗雷格发表《算术基础规则》之时,后来希尔伯特和他的许多合作者使这种思想发展成一门学科—元数学,目的是用数学方法来研究整个数学理论。
要使数学理论成为一个合适的研究对象,就必须使之形式化。
自从希尔伯特和阿克曼所著《理论逻辑纲要》第一版在1928年出版以来,在实践中用得最多的是具有等式的一阶谓词演算(以及高阶谓词演算)。
许多理论可以用一阶理论来表述,它比较简单方便,具有多种形式。
从基础的观点来看,有两个理论最为重要,因而研究也最多。
这两个理论就是形式化的皮亚诺算术理论与形式化的集合论。
因为大多数观代数学理论都可以在这两个理论范围内发展,所以这两个理论的合理性如果得到证实,也就是向数学的可靠性迈进了一大步。
“希尔伯特计划”无非就是要找到一个有限的证明步骤来证明算术的无矛盾性。
这里“有限”的意义是由法国年轻数学家厄布朗明确提出的,他认为下列条件必须满足:必须只讨论确定的有限数目的对象及函数;这些对象及函数要能确定它们的真值产生协调一致的计算结果;一个对象如不指出如何构造它就不能肯定其存在;必须永远不考虑一个无穷集体中所有对象的集合;一个定理对于一组对象都成立的意思是,对于每个特殊的对象,可以重复所讲的普遍论证,而这普遍论证只能看成是结果特殊论证的原型。