当前位置：文档之家› 图论及其应用

图论及其应用

图和子图图

图 G = (V, E)，其中 V = {νv v v ,......,,21} V ---顶点集， ν---顶点数

E = {e e e 12,,......,ε}

E ---边集， ε---边数

例。左图中， V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意，左图仅仅是图G 的几何实现（代表），它们有无穷多个。真正的图G 是上面所给出式子，它与顶点的位置、边的形状等无关。不过今后对两者将经常不加以区别。

称边 ad 与顶点 a (及d) 相关联。也称顶点 b(及 f) 与边 bf 相关联。

称顶点a 与e 相邻。称有公共端点的一些边彼此相邻，例如p 与af 。

环（loop ，selfloop ）：如边 l 。棱（link ）：如边ae 。重边：如边p 及边q 。简单图：（simple graph ）无环，无重边平凡图：仅有一个顶点的图（可有多条环）。一条边的端点：它的两个顶点。记号：νε()(),()().G V G G E G ==。

习题

1.1.1 若G 为简单图，则

εν≤?? ??

?2 。

1.1.2 n ( ≥ 4 )个人中，若每4人中一定有一人认识其他3人，则一定有一人认识其他n-1人。

同构

在下图中，图G 恒等于图H , 记为 G = H ? V （G)=V(H), E(G)=E(H)。图G 同构于图F ? V(G)与V(F), E(G)与E(F)之间各存在一一对应关系，且这二对应关系保持关联关系。记为 G ?F 。

注往往将同构慨念引伸到非标号图中，以表达两个图在结构上是否相同。

e f G = (V, E)

y z w c

=(V , E )

w c

z H =(V ?, E ?)

?a ?

c ?

y ?

e ?z ?

F=(V ??, E ??)

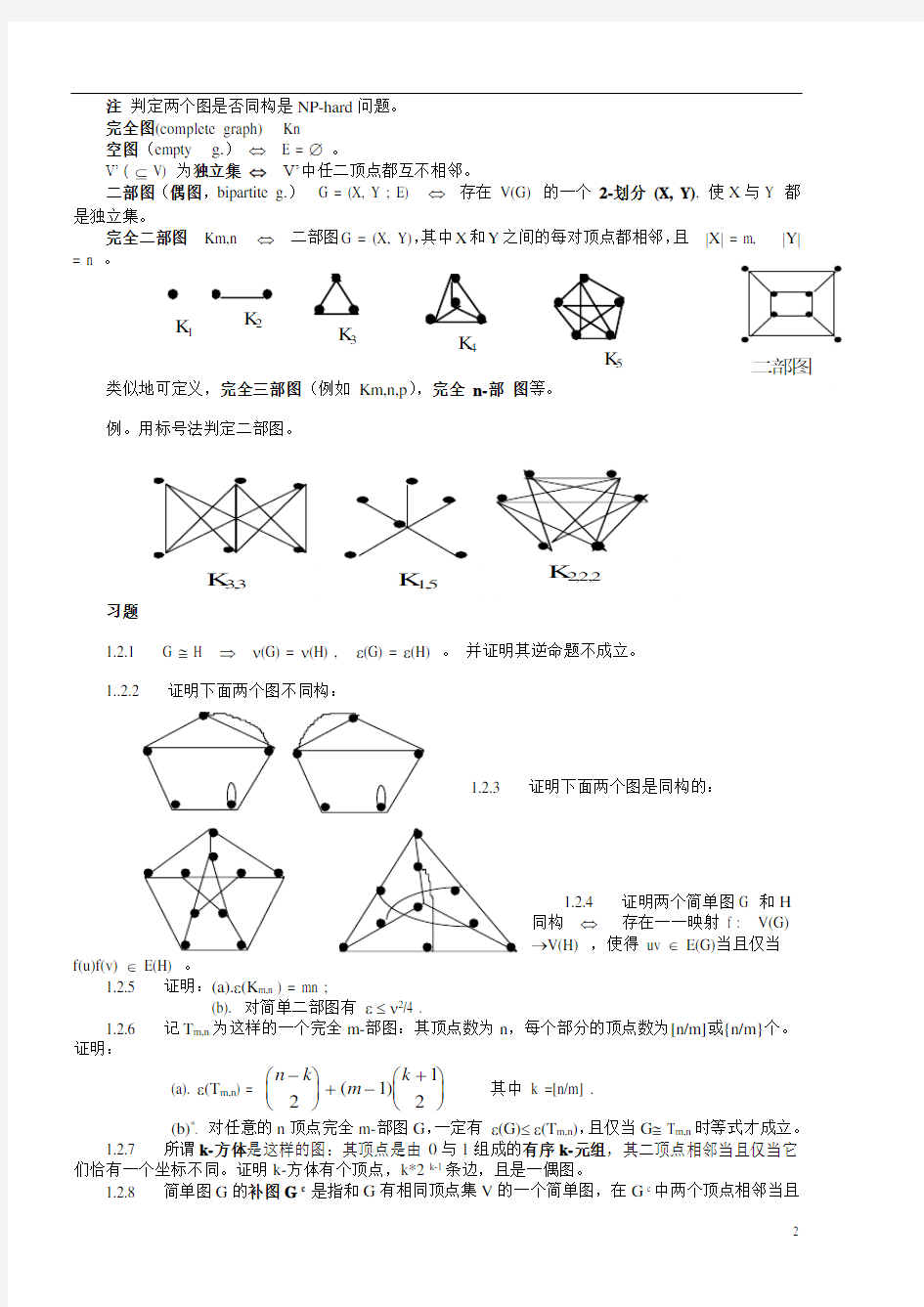
注判定两个图是否同构是NP-hard 问题。完全图(complete graph) Kn

空图（empty g.） ? E = ? 。

V? ( ? V) 为独立集 ? V?中任二顶点都互不相邻。

二部图（偶图，bipartite g.） G = (X, Y ; E) ?存在 V(G) 的一个 2-划分 (X, Y), 使X 与Y 都是独立集。

完全二部图 Km,n ? 二部图G = (X, Y)，其中X 和Y 之间的每对顶点都相邻，且 |X | = m, |Y | = n 。

类似地可定义，完全三部图（例如 Km,n,p ），完全 n-部图等。

例。用标号法判定二部图。

习题

1.2.1 G ? H ? ν(G) = ν(H) , ε(G) = ε(H) 。并证明其逆命题不成立。

1..

2.2 证明下面两个图不同构：

1.2.3 证明下面两个图是同构的：

1.2.4 证明两个简单图G 和H 同构 ? 存在一一映射 f : V(G) →V(H) ，使得 uv ∈ E(G)当且仅当

f(u)f(v) ∈ E(H) 。

1.2.5 证明：(a).ε(K m,n ) = mn ;

(b). 对简单二部图有 ε ≤ ν2/4 .

1.2.6 记T m,n 为这样的一个完全m-部图：其顶点数为n ，每个部分的顶点数为[n/m]或{n/m}个。证明：

(a). ε(T m,n ) = n k m k -?? ???+-+?? ?

?2112() 其中 k =[n/m] .

(b)*. 对任意的n 顶点完全m-部图G ，一定有 ε(G)≤ ε(T m,n )，且仅当G ? T m,n 时等式才成立。

1.2.7 所谓k-方体是这样的图：其顶点是由0与1组成的有序k-元组，其二顶点相邻当且仅当它们恰有一个坐标不同。证明k-方体有个顶点，k*2 k-1条边，且是一偶图。

1.2.8 简单图G 的补图G c 是指和G 有相同顶点集V 的一个简单图，在G c

中两个顶点相邻当且

二部图

K 1

K 3

K 5

K 3

,3K 1

K 2,2,2

仅当它们在G 不相邻。

(a). 画出K c n 和 K c m,n 。

(b). 如果G ? G c 则称简单图G 为自补的。证明：若G 是自补的，则 ν ≡ 0, 1 (mod 4)

关联矩阵M(G)与邻接矩阵A(G)

M(G)=[m i,j ]ν*ε, A(G)=[a i,j ]ν*ν ,

其中 m i,j = 顶点v i 与边e j 的关联次数= 0, 1, 2. a i,j = 连接顶点v i 与 v j 的边数。例。

e e e e e e e M G v v v v 1

234

5671234

1100101111000000110010

0()=????

????????

v v v v A G v v v v 1

2341

234

02112

0101101

1()=????

????????

子图

子图(subgraph) H ? G ? V(H) ? V(G) , E(H) ? E(G) 。真子图 H ? G 。母图（super graph ）。

生成子图（spanning subg.） ? H ? G 且V(H) = V(G) 。生成母图。

基础简单图（underlying simple g.）。

导出子图（induced subg.）G[V?], (非空V?? V ) ? 以V?为顶点集，以G 中两端都在V?上的边全体为边集构成的G 的子图。边导出子图 G[E?] 非空E? ? E ? 以E?为边集，以E?中所有边的端点为顶点集的的子图。例。

e 34

e 5

G = (V , E)

G [{c, d, e}]

[{f, c]}

以上两种子图，其实，对应于取子图的两种基本运算。下面是取子图的另两种基本运算：

G - V’ ? 去掉V?及与V?相关联的一切边所得的剩

余子图。

? 即 G[V \ V?]

G - E’ ? 从中去掉E? 后所得的生成子图

例。G - {b, d, g}, ( = G[E \ {b, d, g}] ) G - {b, c, d, g}, ( ≠ G[E \ {b, c, d, g}] ) G - {a, e, f, g}. ( ≠ G[E \ {a, e, f, g}] )

注意 G[E \ E?] 与G - E? 虽有相同的边集，但两者不一定相等：后者一定是生成子图，而前者则不然。

上述四种运算是最基本取子图运算，今后老要遇到，一定要认真掌握好。关于子图的一些定义还有： G + E? ? 往G 上加新边集E? 所得的（G 的母）图。为简单计，今后将 G ± {e} 简计为 G ± e ； G - {v} 简计为 G - v 。设 G 1, G 2 ? G ，称G 1与G 2为不相交的（disjiont ） ? V(G 1) ? V(G 2) = ? ( ∴ E(G 1) ? E(G 2) = ? )

边不相交（edge-distjiont ）? E(G 1) ? E(G 2 ) = ? 。 ( 但这时G 1与G 2仍可能为相交的）。并图 G 1?G 2 , 当不相交时可简记为 G 1+G 2. 交图 G 1?G 2 .

习题

1.4.1 证明：完全图的每个导出子图是完全图；偶图的每个导出子图是偶图。

1.4.2 设G 为一完全图，1< n < ν-1。证明：若 ν ≥ 4，且G 中每个n 顶点的导出子图均有相同的边数，则 G ? K ν或 K c ν 。

顶点的度

顶点 v 的度 d G (v) = G 中与顶点v 相关联边数。（每一环记为2）最大、最小度 ?，δ 。（?(G) , δ(G) ) 定理1.1 (hand shaking lemma) 任一图中，

d v v V

()∈∑=2ε .

系1.1 任一图中，度为奇数顶点的个数为偶数。

例。任一多面体中，边数为奇数的外表面的数目为偶数。证明。作一图，使其顶点对应于多面体的面，并使其中二顶点相邻当且仅当对应的两个面相邻。...... #

G =(V , E )

G [{u ,w,x ,y }]

G [{u ,w,x }]

k-正则图（k-regular g.) ? d(v) = k, ?v ∈ V . 习题

1.5.1 证明：δ ≤ 2ε/ν ≤ ? 。 1.5.2 若 k-正则偶图(k > 0)的2-划分为 (X, Y),则

|X | = |Y |。

1.5.3 在人数 >1的人群中，总有二人在该人群中有相同的朋友数。

1.5.4 设V(G) = {v v v 12,,......,ν}，则称 ( d(v 1), d(v 2), ...... , d(v ν) ) 为G 的度序列。证明：非负整数序列 ( d 1 ,d 2, ......, d n ) 为某一图的度序列 ?

i n

=∑1

是偶数。

1.5.5 证明：任一无环图G 都包含一偶生成子图H ，使得 d H (v) ≥ d G (v)/2 对所有v ∈ V 成立。

1.5.6*

设平面上有n 个点，其中任二点间的距离 ≥ 1，证明：最多有 3n 对点的距离 = 1 。

路和连通性

途径（walk) 例如（u ，x ）-途径

W = ueyfvgyhwbvgydxdydx (有限非空序列） = uyvywvyxyx (简写法---当不引起混淆时）起点（origin ） u 。终点（terminus ） x 。内部顶点（internal vertex ） y, v, w, x 。

（注意，中间出现的x 也叫内部顶点。）

长 ? 边数（重复计算）。

节（段，section ）。例如W 的(y, w)-节=yvw 。

W -1

（逆途径）, WW ’（两条途径W 与W ?相衔接）。迹( trail) ? 边各不相同的途径。例如，yvwyx 。路 (path) ? 顶点各不相同的途径。（可当作一个图或子图)。例如， yvwx 。

d(u, v) = u 与v 之间最短路的长。例。（命题）G 中存在(u, v)-途径 ? G 中存在(u, v)-路。

G 中顶点u 与v 为连通的(connected) ? G 中存在(u, v)-路

( ? G 中存在(u, v)-途径。)

V 上的连通性是V 上的等价关系，它将V 划分为（等价类）：

V 1,......,V ω

使每个V i 中的任二顶点u 及v 都连通（即存在(u, v)-路）。称每个 G[V i ] i=1,2,......ω

为G 的一个分支（component ）; 称ω(G ）为G 的分支数。 G 为连通图 ? ω(G) = 1

? G 中任两点间都有一条路相连。 G 为非连通图 ? ω(G) > 1。

3-正则图

0-正则图

1-正则

图2-正则图

v w

图 G

记号对任一非 S ?V ，令 S = V\S, 记（称为边割）

[S, S ] = G 中一端在S 中，另一端在S 中的一切边的集合。例。（命题）G 连通 ? 对任 S ? V 都有 [S, S ] ≠ ? 例。（命题）简单图G 中， δ ≥ k ? G 中有长 ≥ k 的路。

习题

1.6.1 证明：G 中长k 为的(v i ,v j )-途径的数目, 就是A k

中的(I, j)元素。 1.6.2 证明：对简单图G 有， εν>-?? ?

?12 ? G 连通。对于ν > 1，试给出εν=-??

?12的不连通简单图。 1.6.3 简单图G 中， δ > [ν/2] - 1 ? G 连通。当ν是偶数时，试给出一个不连通的([ν/2]-1)正则简单图。

1.6.4 G 不连通 ? G c

连通。

1.6.5 对任意图G 的任一边e ，有 ω(G)≤ ω(G-e) ≤ ω(G) +1 。

1.6.6 G 连通，且 d(v)=偶数，? v ∈ V ? ω(G-v)≥ d(v)/2, ? v ∈ V. 1.6.7 连通图中，任二最长路必有公共顶点。

1.6.8 对任一图的任三个顶点 u, v, w 都有 d(u, v)+d(v, w) ≥ d(u, w)。

1.6.9 任一简单图非完全图中，一定有三个顶点 u, v, w ，使得uv, vw ∈ E 而 uw ?E 。

圈

闭途径（closed walk) ? 起点=终点且长 > 0 的途径。闭迹 (closed trail) ?边各不相同的闭途径。

圈（cycle ）? 顶点各不相同的闭迹。（可当作一图或子图。）

例。闭途径： uyvyu ; uywxywvu ； uyuyu 。

闭迹：uyxwyvu 。

圈： yfvgy ; uywvu 。

k-圈（k-cycle ）? 长为k 的圈。

例。1-圈（即一条环）， 2-圈(由重边组成），3-圈（又称三角形）。

奇圈 (odd cycle)。偶圈 (even cycle)。

定理1.2 G 为二部图 ? G 不含奇圈。证明：?：设G 的2-划分为（X, Y ），由G 的定义，G 的任一圈中，X 和Y 的顶点一定交错出现，从而其长必为偶数。

?：不妨设G 为连通的。任取一顶点u,令 X = { x ∈V | d(u, x) = 偶数 }, Y = { y ∈V | d(u, y) = 奇数}。由于，易见，(X, Y)为V 的

2-划分，只要再证X 和Y 都是G

的独立集（即X （或 Y ）中任二顶点v ， w 都不相邻）即可：令

P 与Q 分别为最短(u, v)-路与最短(u, w)-路。设u ?为P 与Q 的

v w

u w

最后一个公共顶点；而 P ?与Q ?分别为P 的(u ?, v)-节与Q 的(u ?, w)-节。则P ?与Q ?只有一公共顶点。又，由于P 与Q 的(u, u ?)-节的长相等， P ?与Q ?的长有相同的奇偶性，因此v 与w 不能相邻，不然，

v( P?)-1 Q?wv 将是一奇圈，矛盾。# 例。（命题）图G 中 δ ≥ 2 ? G 中含圈。例。（命题）简单图G ，δ ≥ 2 ? G 含长 ε ≥ δ+1 的圈。例。（命题）任一图中

(a). ε ≥ ν ? 含圈。

(b)*. ε ≥ ν + 4 ? 含二条边不重的圈。

习题

1.7.1 若边e 在G 的一闭迹中，则e 在G 的一圈中。 1.7.2 证明：(a). ε ≥ ν ? G 含圈。

(b)*. ε ≥ ν + 4 ? G 含两个边不重的圈。

最短路问题

赋权图（weighted g.)(权 ≡ 1 之推广 ) 权( weight ) w(e) ≥ 0. w(H) =

w e e E H ()()

∈∑, H ? G .

路P 的长 = w(P)

顶点u 与v 距离 d(u, v) = 最短(u, v)-路的长。问题求最短( u 0, v 0)-路。

转求最短(u 0, v)-路, ? v ∈ V \ {u 0}. 简化只考虑简单图，且w(e) > 0 ? e ∈ E.

（ w(uv) = 0 时，可合并u 与v 为一顶点）。原理逐步求出顶点序列 u 1, u 2, ............

使 d(u 0, u 1) ≤ d(u 0, u 2) ≤ ...... 记 S 0 = { u 0 },

S k = { u 0, u 1,.............,u k } ， S k = V \ S 。 P i 为最短( u 0, u i )-路 i= 1, 2,......

(1).u 1 ： u 1是使 w(u 0u 1) = min{ w(u 0v)∣ v ≠ u 0 } 者 . 得 S 1 = S 0?{u 1} , P 1 = u 0u 1 .

(2). 若已求得S k-1 ; d(u 0, u 1),.........d(u 0, u k-1) ; 及最短 (u 0, u i )路 P i i=1.2,...,k-1 .

u k ：显然，

d(u 0, u k ) = min{ d( u 0, v) | v ∈ ?S k -1 } = d(u 0, u j ) + w( u j u k ) 某 j ∈{ 1,2,......,k-1 } = min{ d( u o , u ) + w( uu k ) | u ∈ S k-1 }

= min{d( u 0 , u ) + w(uv ) | v ∈ S k -1? , u ∈ S k-1 } = min { l( v ) | v ∈ S k -1}

其中， l( v ) = min { d( u o , u ) + w( uv ) | u ∈ S k-1} ( ∴ l( u k ) = d( u 0 , u k ) ) ∴ S k = S k-1 ? { u k } ,

P k = P j u j u k 某 j ∈{ 1,2,......,k-1 } 。

update 进行下一步时，只要更新 l( v ) 即可：

l( v ) ← min { l( v ) , l( u k ) + w( u k v ) } ? v ∈ S k

Dijkstra 算法

(1).作为开始：l( u 0 ) ← 0 ; l( v ) ← ∞ ? v ≠ u 0 ; S 0 ← { u 0 }; k ← 0 . (2). （这时已有S k = { u 0, u 1,.............,u k }）

l( v ) ← min { l( v ) , l( u k ) + w( u k v ) } ? v ∈ S k 再计算 min { l( v ) }，设其最小值点为 u k+1 ，令 S k+1 = S k ? { u k+1 }。

(3). 若 k = ν - 1 , 仃止；不然，令 k ← k+1 ,并回到 (2) 。

计算复杂性

加法： ν(ν- 1)/2 比较： ν(ν- 1)/2 ? 2

v ∈S ： (ν-1)2

+)________________________________________________ 共 O (ν2 )

凡是复杂性为 p( ν, ε ) 的算法 ( p( . , . ) 为一多项式 ) 称为“好算法”( “good algorithm”------J.Edmonds )。这是相对于指数型算法而言的：在10 - 6秒/步运算速度下：

复杂性

n= 10 20 30 40 50 n 3 .001sec .008sec .027sec .064sec .125sec n 5 .1sec 3.2sec 24.3sec 1.7min 5.2min 2n .001sec 1.0sec 17.9min 12.7days 35.7years 由上表可见，两种算法有天壤之别。

注 1.若只关心求d(u 0 , v 0)则算法进行到v 0 ∈ S k 时停止。

2.计算过程中，所得子图是一棵树。每步都是往其上增加一条边及一个顶点，因此该过程称为 tree growing procedure 。

3.若要计录u 0到每个顶点u 的最短路，只要记录下该路中u 的前一个顶点即可。

习题

1.8.1 描述一个算法以确定 (a). 一图的各个分支；

(b). 一图的围长（即最短圈的长）。并说明你的算法好到什么程度。

树树

无圈图（acyclic g.；林forest ）。树（tree ） ? 连通无圈图。

叶 (leave) ? 树中度为1的顶点。

定理2.1 树中任二顶点间有唯一的路相连。

证明：反证，假设存在树G ，其中有二顶点u 与v ，其间有二不同(u, v)-路P 1 和P 2 相连。因P 1 ≠ P 2 ，一定存在P 1 的一条边e = xy ，它不是P 2 的边。显然，图 P 1 ? P 2 - e 是连通的，从而其中包含一条(x, y)-路P 。于是P + e 是G 中的一圈，这与G 为无圈图相矛盾。 #

注意 (1). 当G 无环时，易见，

G 是树 ? G 中任二顶点间有唯一的路相连。 (2). 以下结论不一定成立： ? 闭途径 ? ? 圈。

定理2.2 G 是树 ? ε = ν - 1。

证明：对 ν 进行归纳。当 ν = 1时，G = K 1 ，成立。假设定理对小于 ν个顶点的树成立，而G 为 ν 个顶点的树。任取G 的一边uv 。它是G 中的一条路，由定理2.1知， G - uv 不连通，且它恰有二分支（习题1.6.5），设为G 1与G 2 。它们都是连通无圈图，因此是树。又，它们的顶点数都小于 ν 。由归纳假设知

ε(G I ) = ν(G I )- 1 I= 1,2 . 故， ε(G) = ε(G 1 ) + ε(G 2 ) + 1 = ν(G 1 ) + ν(G 2 ) - 1 = ν(G) - 1 。 #

推论2.2 每棵非平凡树至少有两个度为1的顶点。证明：由于G 为非平凡连通图， d(v) ≥ 1 , ? v ∈ V 。再由定理1.1 及2.2知，

d v v V

()∈∑==-222εν ，

由此知推论成立。

例。（命题）恰只包含二度为一顶点的树是路。

习题

2.1.1 证明：非平凡树中，任一最长路的起点和终点均是度为 1的顶点。再由此去证明推论2.2。 2.1.2 当 ε = ν - 1 时，证明以下三结论是等价的： (a) G 是连通图； (b) G 是无圈图； (c) G 是树。

2.1.3 一树中若 ? ≥ k ，则其中至少有k 个度为 1 的顶点。 2.1.4 G 为林 ? ε = ν - ω 。

2.1.5 若林G 恰有2k 个奇点，则G 中存在k 条边不重的路P 1 ,P 2 ,..,P k ,使得 E(G) = E(P 1 )?E(P 2 )? ... ?E(P k )。

2.1.6 正整数序列(d 1 ,d 2 ,...,d ν )是一棵树的度序列，当且仅当

i =∑=-1

21ν

ν()。

2.1.7 饱和烃分子形如C m H n ,其中碳原子的价键为4，氢原子的价键为 1，且任何价键序列都不构成圈。证明：对每个m，仅当n = 2m + 2时C m H n方能存在。

割边和键

e为割边( cut edge) ?ω(G-e) > ω(G) 。

（即ω(G-e) = ω(G) + 1 ）

定理2.3 e为G的割边? e不在G的任一圈中。

证明：令 e = xy ，则 x 与 y在G的同一分支中。于是，

e 为G的割边

?ω(G-e) = ω(G) + 1

? x与y不G-e在同一分支中

? G-e中无(x,y)-路

? G中无含e的圈。#

定理2.4图G连通，且每边是割边? G为树。

证明：注意到以下事实即可，

G无圈? G中每边不在任一圈中

? G中每边是其割边。#

连通图G的生成树（spanning tree )

? G的生成子图，且为树。

推论2.4.1每一连通图都包含一生成树。

证明：令 T 为极小( minimal)连通生成子图（意指 T 的任一真子图都不是连通生成子图）（由定义，T 可在保持连通性的前提下，用逐步从G中去边（∴所去的边一定在一圈中（即非割边））（每次破坏一圈）的办法求出。

由T的定义知，ω(T) = 1 ，

ω(T - e) = 2 ? e ∈ E(T) 。

即 T 的每边为割边，故由定理2.4知T为树。#

注也可用极大无圈（生成）子图（即其真生成母图都含圈）来求生成树 T。它可由V上的空图开始，在保持无圈的前提下，逐步由G中取边的办法求出。（为何是生成树？）

推论2.4.2 G ?ε≥ν - 1 。

定理2.4.5 设 T 为G的一生成树，e为G中不属于T的边，则T+e 含唯一的圈。

证明：由于T 无圈，T + e 中的每个圈都包含e 。又，

C为 T + e 的一圈? C - e 为T 中连接e的两个端点的路。

但，由定理2.1知，T中恰只有一条这样的路，因此 T + e中包含唯一的圈。

小结G为树

? G中任二顶点间有唯一的路相连，且无环

? G连通，无圈

? G连通，且每边为割边

? G连通，且ε = ν - 1

? G连通。且ε = ν - 1 。

图G的边割（ edge cut）[S,S] S ? V

? G中一端在S另一端在S中的边的子集合。

显然，在连通图G中，

E??边割?ω(G-E?) > 1 。

键（bond, 割集cut set ) ? 极小非空边割。

例。e 是G 的割边 ? {e} 是G 的键。例。左图G 中，

{uv, zv, zy, vw, yx},

{zu, zv, zy, xy, xw},

{uv, zv, zy} {zu, zv, zy}

都是边割，其中后两个为键。而 E ? ={zu, zv, zy, uv}不是G 的边割，当然更不是G 的键，虽然G- E ? 变成不连

通。易见，当G 连通且 S ≠ ? 时，

边子集B 为G 的键 ? B 是使G 不连通的E 的极小子集。

? ω(G-B)=2，且中每边的两端点分别在二分支中。边割B = [S,S ]为键 ? G[S],G[S ]都连通。（习题）

设H 为G 的子图，称子图 G - E(H) 为G 中H 的补图，记为： ?H(G) 。

特别地，当T 为G 的生成树时，称 ?T 为G 的余树。

定理2.6 设T 为连通图G 的一个生成树， e 为T 的一条边，则

(1).余树?T 不包含G 的键； (2). ?T + e 中唯一包含的G 的一个键。证明：(1).因 G - E(?T )= T 连通，则T 不包含G 的边割，从而也不包含G 的键。 (2).注意到e 为的T 割边，令S 与?S 分别为 T - e 的二分支的顶点集。考虑 B = [S,?S]G

由于G[S] ( 包含T-e 的一个分支T[S]) 与G[?S] ( 包含T-e 的一个分支T[?S]) 都连通，B 必是G 键，包含于??T+e 中。

来证B 为包含在?T+e 中的唯一键,只要再证对包含在?T+e 中的G 的任一键B ?，一定有 B = B ? 即可：假设不然，由于键的极小性，B ?不会包含B ，从而一定存在B 的一边b ? B ? 。于是

G - B ? ? T - e +b ( 注意到 B ? ? ?T+e ? G-B ? ? T-e ) 但T-e+b 也是G 的一生成树（因其边数=ν -1，且连通），从而G - B ? 连通，这与B ? 为G 的键相矛盾。 #

附录设G 连通，T 为其任一生成树。

对每一 e ∈ ?T ，T+e 中有唯一圈C ，因而可得 C 1 ,C 2 ,......,C ε-ν+1

共ε -ν + 1个不同的圈，每个称为G 的一个基本圈。同样，对每一 e ∈ T ，?T+e 中有唯一的键因而可得 B 1 ,B 2 ,......,B ν-1

共ν - 1个不同的键，每个称为的一个基本割集。

设S 1 ,S 2为二集合，记其对称差( 即（S 1?S 2）-（S 1?S 2） )为 S 1 ⊕ S 2

称为它们的环和(ring sum)。性质

1) 图G 的每一边割是G 的一些割集的边不重并。

2) 设B 1 ,B 2 为图的任二边割，则B 1 ⊕ B 2 也是G 的边割。（对任二非空V 1 ,V 2 ? V ，有

G T ?T

[V 1 ,V 1]⊕[V,V] = [V 2 , V 2], 其中V 3 =(V 1 ?V 2)?(?V 1? ?V 2 ) ）。 3) 设边子集E ?与E ”分别为G 中一些圈的边不重并，则E ?⊕E ” 亦然。 4) G 的每个圈可唯一地表为G 的一些基本圈的环和。 5) G 的每个边割可唯一地表为G 的一些基本割集的环和。 6) 边子集E ?为G 中一些边不重圈的并集

? 边子集E ?与G 中每个边割有偶数条公共边。 7) 边子集B 为G 的一个边割

? 边子集B 与G 的每个圈有偶数条公共边。

8) G 为一些圈的边不重并 ? d(v) = 偶数 ? v ∈ V

习题

2.2.1 设G 连通且 e ∈ E ，证明：

(a) e 在G 的每棵生成树中当且仅当e 是G 的边割。 (b) e 不在G 的任一生成树中当且仅当e 是G 的环。

2.2.2 无环图G 恰只有一棵生成树T ，则G = T 。 2.2.3 设F 是G 的极大（maximal ）林，证明： (a) 对G 的每个分支H ， F ?H 是H 的生成树； (b) ε(F) = ν(G)- ω(G)。

2.2.4 证明：任一图G 至少包含 ε - ν + ω 个不同的圈。 2.2.5 (a) 若G 的每个顶点均为偶点（即，度为偶数的顶点），则G 没有割边； (b) 若G 是k-正则偶图且 k ≥ 2，则没有割边。 2.2.6 当G 连通且 S ≠ ? 时，

边割B = [S,S ]为键 ? G[S],G[S ]都连通。 2.2.7 图G 的每一边割是G 的一些键（即，割集）的边不重并。 2.2.8 在图G 中，设B 1和B 2为键，C 1和C 2为圈（看作边子集）。证明： (a) B 1⊕B 2 是G 的键的边不重并集； (b) C 1⊕C 2是G 的圈的边不重并集；

2.2.9 证明：若图G 包含k 棵边不重的生成树，则对于顶点集每一划分(V 1 ,V 2 ,...,V n )，端点在这个划分的不同部分的边的数目至少为 k(n-1)。

割点

称顶点v 为G 的割点(cut vertex) ? E 可划分为二非空子集E 1及E 2，使G[E 1]与G[E 2]只有一公共顶点v 。

显然，当G 无环时，

v 为割点 ? ω(G-v) > ω(G) 。

? 存在二顶点x 及y ，使G 中任一(x, y)-路一定包含v 。

例。（边割）{}{}[]

v , v 为G 的键 ? v 不是的G 的割点。

定理2.7 在树G 中

v 为割点 ? d(v) > 1 。

证明：(i) 若d(v) = 0，则G ? K 1 ，v 不是割点。

(ii) 若 d(v) = 1，则G -v 仍然是树。因此 ω(G-v)= 1 = ω(G)，从而 v 不是割点。 (iii) 若 d(v) > 1，则G 中存在与v 相邻接的二不同顶点u, w 。由定理2.1知，uvw 是G 中的唯一(u, w)-路，因此G-v 中不含(u, w)-路，（即G-v 中u,w 不连通）

∴ ω(G-v) > 1 ，即v 为G 的割点。 #

推论2.7 非平凡、无环、连通图中，至少有二顶点不是割点。证明：令T 为G 的一生成树，由推论2.2及定理2.7知，T 中至少存在二顶点 u 与v 不是T 的割点，则它们也不是G 的割点：这是因为对于u (及v)有

1 = ω(T-u) ≥ ω(G-u) ≥ 1 ， ∴ ω(G-u) = 1 =ω(G) 。 # 习题

2.3.1 设G 为 ν ≥ 3的连通图，证明：

(a) 若G 有割边，则G 有顶点v 使 ω(G-v) > ω(G)；（即，割边必有一端点为割点） (b) (a)的逆命题不成立。

2.3.2 证明：恰有二顶点为非割点的简单连通图必是一条路。 2.3.3 在简单连通图G 中证明：

v 为G 的割点 ? G 的任一生成树不以v 为叶。

生成树的计数及Caley 公式

本节只讨论无环连通图。

将图G 的关联A ν?ε 矩阵中每列的两个1元素之一改为 -1，得一新矩阵，记为A a （它是G 的一个定向图的关联矩阵）。例如：

A e e e e e v v v v a =-----???

?????

???? 1

23451234110000

1101001101

001

1 记A 为从A a 中删去某一行所得的(ν -1)?ε 矩阵。引理1 设A 1 为A 的任一(ν-1) 阶子方阵，则

det(A 1 ) = ± 1 ? A 1 的列对应于G 的一生成树。

证明：令划去的行对应于顶点u ，记H 为以全体与A 1的列相对应的边构成的生成子图。由于 ε(H)= ν-1 ,因此有

H 连通 ? H 为G 的生成树。

（1）当H 不是G 的生成树时，由上述知，H 不连通。令S 为H 中不含u 的一个分支的顶点集。易见，A 1中对应于S 的全体行向量之和为一零向量。因此，det(A 1 ) = 0。

（2）当H 是G 的生成树时，重排A 1 的行、列如下：

取H 的一个度为1的顶点u 1 ，并使 u 1 ≠ u 。记 u 1 在H 中的关联边为e 1 ; 再取 H-u 1

中的一个度为1的顶点u 2 ，并使 u 2 ≠ u ,记 u 2 在H-u 1 中的关联边为 e 2 ;......。

按u 1 ,u 2 ,...及e 1 ,e 2 ,,,,,,,的顺序重排A 1 的行、列，得矩阵A 1? 。易见，A ?1 为下三角型。且主对角线元素全为 ±1 ,因此 |detA 1 | = |detA 1?| =1 。 #

Binet-Cauchy 定理设矩阵 P=[ p ij ]m ?n ， Q=[ q ij ]n ?m ，且m ≤ n 则

2v 3

4e 1

e 3

det()...............

......

.........

...PQ p p p p q q q q ij j mj mj j j m j j m

j j n

m m

m m m =

*≤<<≤∑

111111

引理2 连通图的生成树数目 = det （AA T

）。证明：由Binet-Cauchy 定理知，

det(AA T ) = ∑(detA 1)2

(对A 的所有 v-1阶子方阵A 1求和）但由引理1知

|detA 1| = {

±10

1A G 的列对应于的一生成树

其它

得证。 #

无环图G 的度矩阵 K = [ k ij ]ν ? ν ，其中

k i j v v d v i j

ij ij

i j ij i =-≠=???μμ当且与间有条平行边

当()

例如对本节开头的例子有

K v v v v v v v v =----------????????????1234123

21011

31101211

定理连通图G 的生成树数目 = K 的任一元素的代数余子式

证明：容易验证，K=A a A a T

。又，K 的任一行（列）的元素的代数和 = 0，因此 K 的所有代数余子式都相等。再，设A k 为从A a 中去掉第k 行所得的 (ν-1)?ε 矩阵，易见，

A k A T

k = 从K 中去掉第k 行第k 列后所得的子方阵故由引理2知本定理成立。 #

例。前例的图的生成树数目 = K 的(2,3)-元素的代数余子式

=()-------+12

110

111

23 = 8 。

定理（Cayley ） K n 中共有 n n-2

个不同的生成树。证明：用上述定理可直接证出（习题）。 #

习题

2.4.1 求Ｋ３，３的生成树数目。

2.4.2 若ｅ是Ｋｎ的一条边，则Ｋｎ－ｅ的生成树数目为 (n-2)n n-3

。

连线问题

问题设城市v i 与v j 间建立直接通信线路的费用为c ij （ ≥ 0）。

2v 3

e 1

e 34

建设连接 {v v v 12,,......,ν}的通讯网使造价最省

? 在赋权图G 中求一最小权连通生成子图； ? 在赋权图G 中求一最小权生成树（最优树）。

下面的Kruskal 算法是在非赋权图中求生成树的“极大无圈子图”算法的改进，它是一种贪心算法（greedy algorithm ）：

Kruskal ’s algorithm

(1) 选棱（link ）e 1 使w(e 1)最小；

(2) 若已选定 e 1 ,e 2 ,...,e i ，则从 E\{e 1 ,e 2 ,...,e i }中选取 e i+1 使 (i) G[{e 1 ,e 2 ,...,e i }? {e i+1 }]无圈； (ii) w(e i+1)是满足(i)之最小者。

(3) 若(2)不能再进行下去时，停止。否则，回到 (2)。

定理2.10 Kruskal 算法求出的生成树 = G[{e 1 ,e 2 ,...,e ν-1 }] 是最优树。

证明：反证，假设T *

不是G 的最优树。取G 的一最优树T 。令e k 为{e 1 ,e 2 ,...,e ν-1 }中（按顺序）第一个不属于T 的边，且令T 为最优树中使k 为最大者。则T+e k 中唯一的圈C 包含e k ，且C 中

必含一条边e ?k ? T * (不然，C ? T *

，矛盾。）但

T ? = T + e k -e ?k 也是G 的生成树。（因e ?k 不是T + e k 的割边（定理2。3），从而T ? 连通，且其边数=ν -1。）又，由于T 的子图

G[{e 1 ,e 2 ,...,e k-1 }? {e ?k }] 也不含圈，由法算法知

w(e k )≤ w(e ?k ) ∴ w(T ?) ≤ w(T)，

即T ?也是G 的最优树，且{e 1 ,e 2 ,...,e ν-1 }中第一个不属于T ?的边的下标 > k 。这与k 的取法相矛盾。 #

实现先按权的不减顺序将边集重排成 a 1 ,a 2 ,...,a ε 。

关于算法中无圈性的判定，我们有一简单的办法：当S={e 1 ,e 2 ,...,e i }已取定时，对候选边a j G[S ? {a j }] 无圈 ? a j 的两端点在林G[S]（此处当作生成子图）的不同分支中。

从而我们有求最优树的标记法：

开始：取a 1为候选边；并将v k 标以k ， k = 1,2,...,ν 。

若S={e 1 ,e 2 ,...,e i }已取定，当候选边a j 的两端点有相同标号时，改取a j+1为候选边（丢掉a j 永不再考虑）；否则选定e i+1=a j ，并将G[S]中a j 两端点所在的二分支的顶点重新标号，标以两者中的最小者。

算法复杂性

边排序 O( ε?log 2ε ) 比较边两端的标号 ε

重新标号 O(( ν -1)ν ) 故为好算法（ ≤ O( ν3

) ）。

附录（A ） Prim ’s algorithm （也是一种贪心算法） T ← ? , V ? ← {u}

for all v ∈?V ? do L(v) ← w(uv) //initializing L(.); ?V ?=V\V ? while ?V ?≠V do begin

find vertex w s.t. L(w)=min{ L(v) | v ∈ ?V ? } and denote the associated edge from V ?

to w by e

T ← T ? {e}, V ? ← V ? ? {w}

for all v ∈?V ? do //updating L(v) from new vertex w L(v) ← if w(vw) < L(v) then w(vv) end

Prim 算法的复杂性为 O(ν2

)

（B ）Steiner tree prob.：（NP-hard prob.)

已给赋权连通图G 中，任给定 V ? ? V ，求一最小权树 T 使 V(T) ? V ? 。

习题

2.5.1 用Kruskal 算法解带约束的连线问题：用最小费用建立一连接若干城市的网络。但某些特定的城市对间要求有直通线路相连。

2.5.2 连通图G 的树图是这样的一个图：其顶点集是G 的全体生成树{T 1 ,T 2 ,...,T τ}，且 T i 和T j 相连 ? 它们恰有 v-2条公共边。证明：任何连通图的树图是连通的。

连通度问题连通度

B ? E(G)为图G 的k-边割 ? |B | = k 。

图G 的边连通度（edge connectivity)

κ'()min{''}

G E E G G G =??

为的边割当为非平凡图当为平凡图

( = 使G 变成不连通或平凡图所需去掉的最少边数。）易见，当G 为非平凡连通图时， κ' = G 的最小键的边数。

例。κ' = 0 ? G 平凡或不连通。 κ' = 1 ? G 连通且含割边。 κ'(K n )= n-1 ( n > 0 )。当G 为简单图时，

κ' = ν -1 ? G ? K ν 。称图G 为 k-边连通的（k-edge connected ） ? κ'(G) ≥ k ? 至少去掉k 条边才能使G 变成不连通或平凡图。

例如，所有非平凡连通图都是 1-边连通的。

称顶点子集V?为G 的顶点割(vertex cut) ? G - V? 不连通。

称顶点子集V?为G 的k-(顶)点割(vertex cut) ? V?为G 的顶点割，且 | V? | = k 。显然，当G 为无环连通图时， v 为G 的1-点割 ? v 为G 的割点。

κ=κ'=2κ=1,κ'=2

κ=1,κ'=2

κ=κ'=0κ=2,κ'=3

κ=κ'

完全图无点割。 G 的连通度(connectivity)

}

{

κν()min G =??

? V' V'G G -1为的点割

当有二不相邻接顶点时

其它

（ = 使G 变成不连通或平凡图所需去掉的最少的顶点数。）

例。当 ν ≥ 3时， κ = 1 ? G 连通且有1-点割。 κ(K ν) = ν-1 。

κ(G) = ν -1 ? G 的基础简单图为完全图。称图G 为k-连通的（k-connected ） ? κ(G) ≥ k ? 至少去掉k 个顶点才能使G 变成不连通或平凡图。例如，所有非平凡连通图都是 1-连通的。

定理3.1 κ ≤ κ' ≤ δ 。

证明：先证κ' ≤ δ ：当G 为平凡图时，κ' =0 ≤ δ ，结论成立；当G 为非平凡图时，选取v 使d(v) = δ , 则 E? =

{}{}[]v , v 是G 的一个边割，因此

κ' ≤ |E'| ≤ δ

结论成立。再来证 κ ≤ κ' ：不妨设G 为简单、连通、非完全图，于是 κ' ≤ ν -2。任取一 κ'-边割B ，及B 中任一边 e = xy 。今，在B-e 的每边上各取一个端点使之不等于x 及y 。令这些端点的集合为S 。易见，

| S | ≤ κ'-1 。记 H = G-S 。

(i) 若H 不连通，则S 为G 的点割，从而 κ ≤ | S | ≤ κ'-1 。

(ii) 若H 连通，则e = xy 为H 的割边。但，ν(H) = ν(G)- | S | ≥ ν - ( κ'-1)≥ 3 ，因此，x 与y 必有一个为H 的割点，设为 x 。于是

S ? {x} 为G 的点割，故

κ ≤ | S | + 1 ≤ κ' 。 #

习题 3.1.1 (a) 证明：若G 是k-边连通的，且k > 0 ，又E ?为G 的任k 条边的集合，则 ω（G-E ?) ≤ 2。

(b) 对 k >0，找出一个k-连通图G 以及G 的k 个顶点的集合S ，使ω(G-S)> 2 。 3.1.2 证明：若G 是k-边连通的，则 ε ≥ k ν/2 。

3.1.3 (a) 证明：若G 是简单图且 δ ≥ ν -2，则 κ = δ 。 (b) 找出一个简单图G ，使得δ =ν-3且 κ <δ 。

3.1.4 (a) 证明：若G 是简单图且 δ ≥ ν/2，则 κ' = δ 。

(b) 找出一个简单图G ，使得 δ = [（ν/2）-1] 且 κ' < δ 。

3.1.5 证明：若G 是简单图且δ ≥ (ν +k-2)/2 ( k < ν )，则G 是k 连通的。 3.1.6 证明：若G 是正则简单图，则 κ = κ' 。

3.1.7 证明：若l ，m 和n 是适合0

块

块（block ） ? 无割点连通图。显然，当 v ≥ 3时，

G 为块 ? G 为无环、2-连通图。

例。 v ≥ 3的块中无割边。

定理3.2 (Whiteney,1932) 当 v ≥ 3时，

G 为2-连通图 ? G 中任二顶点间则至少被两条内部不相交（internally disjoint ）的路连接。（两条路P 与Q 内部不相交 ? P 与Q 无公共内部顶点）

证明：? ：显然，G 连通，且无1-点割，因此G 为2-连通。

? ：对G 中二顶点间的距离d(?,?)进行归纳。当d(u,v) = 1 时（即uv 为G 的边)，因G 为2-连通，边uv 是G 的非割边( ∵ κ ≥ κ' ≥ 2)。因此，由定理2.3 ，边uv 在G 的某一圈内，成立。

假设定理对 d(?,?)

d(u,w)= k-1 。

因此，由归纳假设，存在二内部不相交的

（u,w)-路P 及Q 。因G 为2-连通，G-w 中一定存在一 (u,v)-路P ? 。令x 为P ?在 P ? Q 中的最后一个顶点。不

失一般性。不妨设x 在P 上。这时G 中有二内部不

相交的(u,v)-路：

( P 的(u,x)-节)( P ?的(x,v)-节) Quv 。 #

推论3.2.1 当ν ≥ 3时，

图G 为2-连通的 ? G 的任二顶点共圈。证明：由定理3.2 ，显然。 #

称边e 被剖分 ? 用连接e 的两端点的长2为的新路去替换e 。容易验证，当ν ≥ 3时，块的一些边被剖分后仍然保持是块。推论3.2.2 G 为块 ? G 的任二边共圈。

证明：? ：当ν ≤ 2时，显然成立。当ν ≥ 3时，将G 的任二边e 1 和e 2 分别用新顶点v 1 和v 2 加以剖分，得新图G ? 。它是块，因此为2-连通的。由推论3.2.1知，v 1 与v 2 共圈。从而e 1 与e 2共圈。

? ：由条件知，G 无环。只要再证G 也不会有割点即可：假设u 为G 的割点。由割点定义知，存在E(G)的一个2-划分（E 1 ,E 2 )使边导出子图G[E 1]与G[E 2]恰只有一公共顶点u 。由边导出子图定义知，E 1 和E 2 各含一边 e 1 和e 2 ，它们有一公共端点u 。从而，易见， e 1 和e 2不能共圈，矛盾。 #

附录 Menger 定理若ν ≥ k+1，则

G 为k-连通的 ? G 中任二不同顶点至少被k-条内部不相交的路所连接。 G 为k-边连通的 ? G 中任二不同顶点至少被k-条边不重的路所连接。

当一个图G 有割点时，我们可沿G 的割点将G 逐步划分为一些不含割点的极大连通子图，它们每个称为G 的块。例如

性质

(1) G 的两个块之间至多有一公共顶点，它一定是G 的割点。

(2) G 的任一割点至少是G 的两个块的公共顶点。 (3) G 是它的块的边不重并。

(4) 含割点的连通图G 中，至少有两个G 的块每个恰含G 的一个割点。 (5)*

任一图G 中，易证，两边之间的共圈关系是一等价关系。它将E(G)划分为一些等价类 (E 1 ,E 2 ,...,E p )，而每个G[E i ]就是G 每个的块。

划分图G

G 的块

习题

3.2.1 证明：一图是边连通的当且仅当任二顶点至少被两条边不重的路所连接。

3.2.2 举例说明：若P 为2-连通图G 中一给定的(u,v)-路，则G 不一定有一条与P 内部不相交的（u,v)-路。

3.2.3 证明：若G 没有偶圈及孤立点，则G 的每个块为K 2 或奇圈。

3.2.4 证明：不是块的连通图G 中，至少有两个G 的块每个恰含G 的一个割点。

3.2.5 证明：G 的块的数目 = ?+

-∈∑(())b v v V

1 ，其中b(v)是G 中含顶点v 的块的个数。

3.2.6 设G 为2-连通，而X 和Y 是V 的不相交子集，它们各至少包含二顶点。证明：G 包含二不

相交的路P 和Q 使得

(i) P 和Q 的起点在X 中； (ii) P 和Q 的终点在Y 中；

(iii) P 和Q 的内部顶点都不在X ? Y 中。 3.2.7 叙述求图的块的好算法。

可靠通信网的建设

κ 及κ'越大越可靠（造价越贵：δ ≥ κ' ≥ κ ）

问题已给赋权图G 及正整数k ，求G 的最小权k-连通（k-边连通）生成子图。解当 k = 1 , optimal tree (connector prob.) 当k > 1 , NP-hard prob. 当每边权≡ 1且G 为任意图时，问题变成求边数最少的k-连通生成子图。( 仍然是 NP-hard prob.)

当G ? K ν 且每边权为 1 时，Harary (1962)作出边数最少的G 的k-连通（k-边连通）生成子图H k,ν（边数={k ν/2}) （∴有好算法。）

Hamilton 圈与Euler 环游 Euler 环游

环游（tour ）? 通过图中每边至少一次的闭途径。 Euler 环游 ? 通过图中每边恰一次的闭途径。 Euler 迹 ? 通过图中每边的迹。

? 通过图中每边恰一次的途径。（可“一笔画成”。） Euler 图 ? 包含Euler 环游的图

? 包含Euler 闭迹的图。 ? 本身为闭迹的图。

定理4.1 设G 为非空连通图，则

G 为 Euler 图 ? G 中无度为奇数的顶点。

证明：? ：令 C = u 0 e 1 u 1 e 2 u 2 ...e ε u ε (u ε = u 0 )为G 的一 Euler 环游，起点为u 0 。则对任一顶点v ≠ u 0 ，当v 每次作为内部顶点出现于C 时，C 上有二边与v 相关联。由于C 上包含了G 的所有边且不重复，因此d(v)=偶数。类似地，d(u 0)=偶数。

? ：反证，假设存在非空连通图，它的每个顶点的度都是偶数，但却不是Euler 图。在这种图中选取G 使其边数最少。由于 δ(G) ≥ 2，G 包含圈。令C 为G 中的最长闭迹。由假设，C 不会是 Euler 环游。因此

G - E(C)

中一定有一分支G?使ε(G?)>0。由于C本身为 Euler图，（由定理的必要条件知）C中每个顶点的

度都是偶数，因此G?中无度为奇数的顶点。但

ε(G?) < ε(G)

由G的选择知，G?中含一 Euler环游 C?。又，由于G连通，C与C?至少有一公共顶点，设为v，

且不妨设它同时为它们的起点。于是，

CC?

是G的一闭迹，其长大于C的长，矛盾。#

附录定理4.1?:之新证法（J.G.T.Fall 1986)：对ε进行归纳。当ν=2时，显然成立。只

要再考虑ν≥ 3情形。假设对ε < q成立，而ε(G)=q 。选取顶点v ，使v有二不同顶点u及w与

它相邻。考虑图

H = (G - {uv,vw})+uw （uw 为一新加边——不管G中是否有以u，w

为两端点的边）显然，

ω(H) ≤ 2 , Arrayε(H) = q-1 ,

d H(x) = 偶数? x ∈ V 。

(i) 当ω(H)=1时，由归纳假设，H中有Euler环游 C?。把C?中

一边uw代之以路uvw，即得G的Euler环游。

(ii) 当ω(H)=2时，由归纳假设，H的二分支各有其Euler环游 C1

及C2。不妨设uw在C2中。将C2中的边uw代之以迹 uvC1vw，即得G

的Euler环游。#

推论4.1若G连通，则

G有一Euler迹? G中至多有二度为奇数顶点。

证明：?：类似定理4.1中?：的证明。

?：若G中无度为奇数顶点，则由定理4.1 ，G中有Euler迹。否则，G中恰有二度

为奇数顶点，设为u，v 。考虑图

G + e ，

其中e为连接u与v的新边。显然，G+e中无度为奇数顶点，从而包含一Euler环游

C = v0 e1 v1 e2 v2 ...eε+1vε+1，

其中，vε+1 = v0 =u ，v1 =v 。易见

v1 e2 v2 ...eε+1vε+1

就是G的Euler迹。#

习题

4.1.1 若可能，画出一个ν为偶数，而ε为奇数的Euler图。否则说明理由。

4.1.2 证明：若G无奇点，则G的每个块也是Euler图。

4.1.3 若G无奇点，则存在边不重的圈C1 ,C2 ,...,C m 使得

E(G) = E(C1) ? E(C2)? ...? E(C m)。

4.1.4 若连通图G有2k >0 个奇点，则G中存在k条边不重的迹Q1 ,Q2 ,...,Q k 使得

E(G) = E(Q1) ? E(Q2)? ...? E(Q k)。

4.1.5 设G为非平凡Euler图，且v ∈V。证明：G中任一条以v为起点的迹都能延伸成一Euler

环游当且仅当 G-v为林。（O.Ore）

中国邮递员问题

问题在一赋权图G中，求一最小权环游（即最优环游）。

当G 为Euler图时，其任一Euler环游都是最优环游，此时有求最优环游的好算法，如

Fleury算法（“过河拆桥，尽量不走独木桥“）

任取一顶点v0 ，令w0 = v0 。

答案(电子科大版)图论及其应用第一章

习题一： ● 。证明:作映射f : v i ? u i (i=1,2….10) 容易证明，对?v i v j ∈E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图(a)与(b)是同构的。 ● 5.证明：四个顶点的非同构简单图有11个。证明：设四个顶点中边的个数为m ，则有： m=0: m=1 ： m=2： m=3： m=4： (a) v 23 4 (b)

m=5： m=6：因为四个顶点的简单图最多就是具有6条边，上面所列出的情形是在不同边的条件下的不同构的情形，则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。 ● 11.证明：序列（7,6,5,4,3,3,2）和（6,6,5,4,3,3,1）不是图序列。证明：由于7个顶点的简单图的最大度不会超过6，因此序列（7,6,5,4,3,3,2）不是图序列；（6,6,5,4,3,3,1）是图序列 1 1 12312(1,1,,1,,,)d d n d d d d d π++=---是图序列（5,4,3,2,2,0）是图序列，然而（5,4,3,2,2,0）不是图序列，所以（6,6,5,4,3,3,1）不是图序列。 ● 12.证明：若，则包含圈。证明：下面仅对连通图的下的条件下进行证明，不连通的情形可以通过分成若干个连通的情形来证明。设 , 对于中的路若与邻接，则构成一个闭路。若是一条路，由于，因此，对于，存在与之邻接，则构成一个圈。 ● 17.证明：若G 不连通，则连通。证明：对于任意的 ,若与属于G 的连通分支，显然与在中连通；

如何将PDF转换成WORD PDF转WORD

如何把PDF转换成WORD 先了解一下: PDF文档到底是什么？ PDF是出版和图形领域的软件厂商Adobe制定的电子文档格式标准。Adobe为之提供了免费的文档浏览器--Adobe Acrobat Reader以及相应的编辑软件--Adobe Acrobat，后者可以对PDF文档中页面的组织、链接进行编辑，对文档进行批注等等。而Adobe的另外一款软件--Illustrator则可以从各个细致入微处修整PDF文件。与普通格式的电子文档(如纯文本、超文本、RTF格式以及Word文档等)相比，PDF文档具有能够完善保持版面样式、跨平台等优越性，所以国外许多组织机构在发放无需再次编辑的文件时通常选择使用PDF格式。在我国，许多电子书籍也开始采用PDF格式。创建PDF文件的典型方法并不是使用Illustrator等软件来编辑，而是先用普通的文字处理和桌面排版软件如Word、WordPerfect和PageMaker等编排好文档，然后通过Adobe的PDF Distiller或者PDF Writer等仿打印机引擎制作PDF文件。另外也有一些PDF文档是直接使用Adobe Acrobat配合扫描仪将原书稿扫描制作完成的，虽然该软件配有支持对多种西方文字进行光学字符识别(OCR)的插件，但是为了保证文字的可靠性，多数情况下采用这种方法制作的PDF文件没有进行字符识别。如何把PDF文档转换成Word文档一款非常好的Pdf向Doc格式转换的工具，ScanSoft PDF Converter for Microsoft Word v1.0。它是由ScanSoft公司同微软共同组队开发了一个全新的Office 2003 插件。该插件可以帮助你通过Word直接将Pdf文档转换为Word文档，并且完全保留原来的格式和版面设计。这个名为 ScanSoft PDF Converter for Microsoft Word 的插件是首先捕获Pdf文档中的信息，分离文字同图片，表格和卷，再将其统一到Word格式。现在你可以重新利用早先你从网络上下载或Email中收到的Pdf文件中的信息，而无需添加任何其他软件。 ScanSoft PDF Converter for Microsoft 已经非常紧密的同Office 2003整合在一起了，有两种方式可以将Pdf格式转换成Doc文件。第一种方式，在Microsoft Word 2003中你可以直接通过“文件”—>“打开”来打开Pdf文件。ScanSoft PDF Converter for Microsoft Word插件会自动弹出了，经过转换后我们就可以得到想要的Doc文件。第二种方式，ScanSoft公司也已经开发了基于此的Smart Tag(Office 2003中重要的功能元件)能够轻松的通过右键来将PDF文件转换成为 Microsoft Word 文件。 =========================== PDF文件中的文字存在两种可能性: 其一，可能是以计算机字符代码的形式被包裹在文件中; 其二，也可能只是一个页面图像中的像素组成的线条，没有字符代码信息。很明显，只有第

电子科技大学研究生试题《图论及其应用》(参考答案)

电子科技大学研究生试题《图论及其应用》(参考答案) 考试时间：120分钟一．填空题(每题3分，共18分) 1．4个顶点的不同构的简单图共有__11___个； 2．设无向图G 中有12条边，已知G 中3度顶点有6个，其余顶点的度数均小于3。则G 中顶点数至少有__9___个； 3．设n 阶无向图是由k(k ?2)棵树构成的森林，则图G 的边数m= _n-k____; 4．下图G 是否是平面图？答__是___; 是否可1-因子分解？答__是_. 5．下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。图G 二．单项选择(每题3分，共21分) 1．下面给出的序列中，是某简单图的度序列的是( A ) (A) (11123); (B) (233445); (C) (23445); (D) (1333). 2．已知图G 如图所示，则它的同构图是（ D ） 3．下列图中，是欧拉图的是（ D ） 4．下列图中，不是哈密尔顿图的是（B ） 5．下列图中，是可平面图的图的是（B ） A C D A B C D

6．下列图中，不是偶图的是（ B ） 7．下列图中，存在完美匹配的图是（B ）三．作图(6分) 1．画出一个有欧拉闭迹和哈密尔顿圈的图； 2．画出一个有欧拉闭迹但没有哈密尔顿圈的图； 3．画出一个没有欧拉闭迹但有哈密尔顿圈的图；解：四．(10分)求下图的最小生成树，并求其最小生成树的权值之和。解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20. 五．(8分)求下图G 的色多项式P k (G). 解：用公式 (G P k -G 的色多项式： )3)(3)()(45-++=k k k G P k 。六．(10分) 22，n 3个顶点的度数为3，…，n k 个顶点的度数为k ，而其余顶点的度数为1，求1度顶点的个数。解：设该树有n 1个1度顶点，树的边数为m. 一方面：2m=n 1+2n 2+…+kn k 另一方面：m= n 1+n 2+…+n k -1 v v 1 3 图G

图论及其应用答案电子科大

图论及其应用答案电子科大 This model paper was revised by the Standardization Office on December 10, 2020

习题三：证明：e是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意u ∈V 1及v ∈V 2, G 中的路（u，v）必含e . 证明：充分性: e是G的割边，故G ?e至少含有两个连通分支，设V 1是其中一个连通分支的顶点集，V 2是其余分支的顶点集，对12,u V v V ?∈?∈，因为G中的u ,v不连通，而在G中u与v连通，所以e在每一条(u ,v )路上，G中的(u ,v )必含e。必要性：取12,u V v V ∈∈，由假设G中所有(u ,v )路均含有边e，从而在G ?e中不存在从 u与到v的路，这表明G不连通，所以e 是割边。 3.设G 是阶大于2的连通图，证明下列命题等价：（1） G 是块（2） G 无环且任意一个点和任意一条边都位于同一个圈上；（3） G 无环且任意三个不同点都位于同一条路上。（1）→（2）： G是块，任取G的一点u，一边e，在e边插入一点v，使得e成为两条边，由此得到新图G 1，显然G 1的是阶数大于3的块，由定理，G中的u,v 位于同一个圈上，于是G 1中u 与边e都位于同一个圈上。（2）→（3）： G无环，且任意一点和任意一条边都位于同一个圈上，任取G的点u ，边e ，若u在e 上，则三个不同点位于同一个闭路，即位于同一条路，如u不在e上，由定理，e的两点在同一个闭路上，在e边插入一个点v ，由此得到新图G 1，显然G 1的是阶数大于3的块，则两条边的三个不同点在同一条路上。（3）→（1）： G连通，若G不是块，则G中存在着割点u，划分为不同的子集块V 1, V 2, V 1, V 2无环，12,x v y v ∈∈，点u在每一条(x ,y )的路上，则与已知矛盾，G是块。 7.证明：若v 是简单图G 的一个割点，则v 不是补图G ?的割点。证明：v是单图G的割点，则G ?v有两个连通分支。现任取x ,y ∈V (G ?v ), 如果x ,y 不在G ?v的同一分支中，令u是与x ,y处于不同分支的点，那么，x ,与y在G ?v的补图中连通。若x ,y在G ?v的同一分支中，则它们在G ?v的补图中邻接。所以，若v是G 的割点，则v不是补图的割点。 12.对图3——20给出的图G1和G2，求其连通度和边连通度，给出相应的最小点割和最小边割。解：()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{（6,5），（8,5）}

介绍几款word和PDF互相转换的软件

介绍几款word和PDF互相转换的软件，轻松办公今天向大家介绍几款word和PDF互相转换的软件，由于许多人在使用不同的办公软件，在传输和交流文档以及打印文档的时候，都会遇到这样或者那样的问题。所以在进行这些活动之前，建议把你所要使用的文档转换为PDF文档，以保证在他人电脑上可以无障碍的打开，和避免打印时所出现的字体变更，格式变更等问题。虽然pdf的交互性很好，但是却不便于编辑，所以你要编辑pdf文档的话，建议把pdf文档转换为office文档。所以，今天向大家介绍几款这方面的软件。一，首推adobe acrobat x 10 Adobe acrobat x 10是adobe公司最新推出的PDF创建、编辑和查看软件，功能强大，相比上一版的acrobat 9提高了许多，首先从打开文档的速度上来说，个人觉得比上一般快许多，打开一般的文档比adobe reader快一倍多，和foxit reader相比来说，速度差不多。界面上，编辑的按钮主要集中在了右侧，上方按钮较少，这样方便编辑。从功能上来说，增加了保存为word,excel和图片等格式，支持保存为word 2003和2007，excel2003和2007，图片可以保存为jpg,TIFF等格式，并且把菜单集中到word和excel中，在word和excel 中你可以把word和excel文档输出成为PDF格式，如果你是office 2010的用户，你可以使用backstage就是文件背景视图中的save as来把word和excel文档保存成为PDF文档。从界面上看，现在还没有官方的中文版本，只有英文等版本供大家使用，对于不懂英文的朋友来说，就有一些困难了，个人还是期待中文版早点推出，方便亿万中国用户。当然adobe 晚推出或者不推出有些软件的中文版，主要是由于中国的盗版太猖獗了，所以大家有条件的话，还是要支持正版，终究老用盗版也不好，做软件要花费大量的精力和人员，所以取得一定的报酬也是对的。在转换速度上来说，从PDF转换成word和excel的速度非常快。从质量上来看，转换出来的文档的格式都没有变，和原word文档一样，我现在使用的结果是，会丢掉word里原先插好的目录标题文字，这个主要用来作自动目录的，还有有些下划线会稍微变化一下，有部分图片的一小部分会发生变化，其他的都很好。在这一点上，比其他的转换软件好许多。从word，excel转换到PDF的速度和质量也很好，但个人觉得没有用office2010直接保存成pdf的速度和质量好，也不如doPDF的转换速度。但是好的地方在于和office的高度集成，还有转换文档的平滑性，同时还可以随意创建和编辑pdf文档。这个版本还强化了社交和分享的功能，你可以方便的添加评论和与他人分享文档。从体积上来看，许多人都觉得体积大，现在的安装包体积有400多M，相对于foixt要打30多倍，但是呢，其功能比较全一些，对不同种类和不同语言的pdf文档支持好许多。Adobe acrobat和foxit，就相当于microsoft office和金山的wps一样的。Office虽然臃肿体积大，但是它对office文档的支持和兼容性最好了。wps体积小，功能也很多，对于一般办公已经足够应付了，但是你在使用的过程中，有时候会遇到较大的或者某些office文档用wps不能打开，但是用microsoft office就可以打开。所以还是推荐大家使用这个体积大的adobe acrobat x 10。官方网站试用链接（需要有adobe账号）： verycd程序下载安装地址：二，Nitro PDF Professional

图论及其应用答案电子科大

图论及其应用答案电子科大 Newly compiled on November 23, 2020

图论及其应用第三章答案电子科大

习题三： ● 证明：e 是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意u ∈V 1及v ∈V 2, G 中的路（u ，v ）必含e . 证明：充分性: e 是G 的割边，故G ?e 至少含有两个连通分支，设V 1是其中一个连通分支的顶点集，V 2是其余分支的顶点集，对12,u V v V ?∈?∈，因为G 中的u,v 不连通，而在G 中u 与v 连通，所以e 在每一条(u,v)路上，G 中的(u,v)必含e 。必要性：取12,u V v V ∈∈，由假设G 中所有(u,v)路均含有边e ，从而在G ?e 中不存在从u 与到v 的路，这表明G 不连通，所以e 是割边。 ● 3.设G 是阶大于2的连通图，证明下列命题等价：（1） G 是块（2） G 无环且任意一个点和任意一条边都位于同一个圈上；（3） G 无环且任意三个不同点都位于同一条路上。（1）→（2）： G 是块，任取G 的一点u ，一边e ，在e 边插入一点v ，使得e 成为两条边，由此得到新图G 1，显然G 1的是阶数大于3的块，由定理，G 中的u,v 位于同一个圈上，于是G 1中u 与边e 都位于同一个圈上。（2）→（3）： G 无环，且任意一点和任意一条边都位于同一个圈上，任取G 的点u ，边e ，若u 在e 上，则三个不同点位于同一个闭路，即位于同一条路，如u 不在e 上，由定理，e 的两点在同一个闭路上，在e 边插入一个点v ，由此得到新图G 1，显然G 1的是阶数大于3的块，则两条边的三个不同点在同一条路上。（3）→（1）： G 连通，若G 不是块，则G 中存在着割点u ，划分为不同的子集块V 1, V 2, V 1, V 2无环， 12,x v y v ∈∈，点u 在每一条(x,y)的路上，则与已知矛盾，G 是块。 ● 7.证明：若v 是简单图G 的一个割点，则v 不是补图G ?的割点。证明：v 是单图G 的割点，则G ?v 有两个连通分支。现任取x,y ∈V(G ?v), 如果x,y 不在G ?v 的同一分支中，令u 是与x,y 处于不同分支的点，那么，x,与y 在G ?v 的补图中连通。若x,y 在G ?v 的同一分支中，则它们在G ?v 的补图中邻接。所以，若v 是G 的割点，则v 不是补图的割点。 ● 12.对图3——20给出的图G1和G2，求其连通度和边连通度，给出相应的最小点割和最小边割。解：()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{（6,5），（8,5）} ()25G κ= 最小点割{6,7,8,9,10} 2()5G λ= 最小边割{（2,7）…（1,6）} ● 13.设H 是连通图G 的子图，举例说明：有可能k(H)> k(G). 解：通常k (H )

图论及其应用

图和子图图图 G = (V, E)，其中 V = {νv v v ,......,,21} V ---顶点集， ν---顶点数 E = {e e e 12,,......,ε} E ---边集， ε---边数例。左图中， V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意，左图仅仅是图G 的几何实现（代表），它们有无穷多个。真正的图G 是上面所给出式子，它与顶点的位置、边的形状等无关。不过今后对两者将经常不加以区别。称边 ad 与顶点 a (及d) 相关联。也称顶点 b(及 f) 与边 bf 相关联。称顶点a 与e 相邻。称有公共端点的一些边彼此相邻，例如p 与af 。环（loop ，selfloop ）：如边 l 。棱（link ）：如边ae 。重边：如边p 及边q 。简单图：（simple graph ）无环，无重边平凡图：仅有一个顶点的图（可有多条环）。一条边的端点：它的两个顶点。记号：νε()(),()().G V G G E G ==。习题 1.1.1 若G 为简单图，则 εν≤?? ?? ?2 。 1.1.2 n ( ≥ 4 )个人中，若每4人中一定有一人认识其他3人，则一定有一人认识其他n-1人。同构在下图中，图G 恒等于图H , 记为 G = H ? V （G)=V(H), E(G)=E(H)。图G 同构于图F ? V(G)与V(F), E(G)与E(F)之间各存在一一对应关系，且这二对应关系保持关联关系。记为 G ?F 。注往往将同构慨念引伸到非标号图中，以表达两个图在结构上是否相同。 d e f G = (V, E) y z w c G =(V , E ) w c y z H =(V ?, E ?) ?a ? c ? y ? e ?z ? F=(V ??, E ??)

图论及应用第一章完整作业

习题 1 1. 证明在n 阶连通图中（1）至少有n -1条边。（2）如果边数大于n -1，则至少有一条闭通道。（3）如恰有n -1条边，则至少有一个奇度点。证明 (1) 若对?v ∈V(G),有d(v)≥2,则：2m=∑d(v)≥2n ? m ≥n >n-1,矛盾！若G 中有1度顶点，对顶点数n 作数学归纳。当n=2时，G 显然至少有一条边，结论成立。设当n=k 时，结论成立，当n=k+1时，设d(v)=1，则G-v 是k 阶连通图，因此至少有k-1条边，所以G 至少有k 条边。 (2) 考虑v 1→v 2→?→v n 的途径，若该途径是一条路，则长为n-1,但图G 的边数大于n-1,因此存在v i ,v j ,使得v i adgv j ,这样，v i →v i+1→?→v j 并上v i v j 构成一条闭通道；若该途径是一条非路，易知，图G 有闭通道。 (3) 若不然，对?v ∈V(G),有d(v)≥2,则：2m=∑d(v)≥2n ? m ≥n >n-1,与已知矛盾！ 2. 设G 是n 阶完全图，试问（1）有多少条闭通道？（2）包含G 中某边e 的闭通道有多少？（3）任意两点间有多少条路？答 (1) (n-2)! (2) (n-1)!/2 (3) 1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n -2)…1. 3. 证明图1-27中的两图不同构：证明容易观察出两图中的点与边的邻接关系各不相同，因此，两图不同构。 4. 证明图1-28中的两图是同构的证明将图1-28的两图顶点标号为如下的(a)与(b)图图 1-27 图1-28

图论及应用第一章完整作业

习题 1 1. 证明在n阶连通图中（1）至少有n-1条边。（2）如果边数大于n-1，则至少有一条闭通道。（3）如恰有n-1条边，则至少有一个奇度点。证明(1) 若对v V(G),有d(v)2,则：2m=d(v)2n m n n-1,矛盾！若G中有1度顶点，对顶点数n作数学归纳。当n=2时，G显然至少有一条边，结论成立。设当n=k时，结论成立，当n=k+1时，设d(v)=1，则G-v是k阶连通图，因此至少有k-1条边，所以G至少有k条边。 (2) 考虑v 1v 2v n的途径，若该途径是一条路，则长为n-1,但图G的边数大于n-1,因此存在v i,v j,使得v i adgv j,这样，v i v i+1v j并上v i v j构成一条闭通道；若该途径是一条非路，易知，图G有闭通道。 (3) 若不然，对v V(G),有d(v)2,则：2m=d(v)2n m n n-1,与已知矛盾！ 2.设G是n阶完全图，试问（1）有多少条闭通道？（2）包含G中某边e的闭通道有多少？（3）任意两点间有多少条路？答(1) (n-2)! (2) (n-1)!/2 (3) 1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n-2)…1. 3.证明图1-27中的两图不同构：图1-27 证明容易观察出两图中的点与边的邻接关系各不相同，因此，两图不同构。 4.证明图1-28中的两图是同构的图1-28 证明将图1-28的两图顶点标号为如下的(a)与(b)图

作映射f : f(v i )u i (1 i 10) 容易证明，对v i v j E((a)),有f(v i v j )u i u j E((b)) (1 i 10, 1j 10 ) 由图的同构定义知，图1-27的两个图是同构的。 5. 证明：四个顶点的非同构简单图有11个。证明 m=0 1 2 3 4 5 6 由于四个顶点的简单图至多6条边，因此上表已经穷举了所有情形，由上表知：四个顶点的非同构简单图有11个。 6. 设G 是具有m 条边的n 阶简单图。证明：m =??? ? ??2n 当且仅当G 是完全图。证明必要性若G 为非完全图，则 v V(G),有d(v) n-1 d(v) n(n-1) 2m n(n-1) m n(n-1)/2=??? ? ??2n , 与已知矛盾！充分性若G 为完全图，则 2m= d(v) =n(n-1) m= ??? ? ??2n 。 7. 证明：（1）m (K l ,n ) = ln ， (a) v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 v 10 u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 (b)

如何将有密码的PDF转换成WORD

如何将有密码的PDF转换成WORD 可以试试下面的方法：打开PDF格式文件选择打印（如果有打印限制，抱歉，暂时没办法啊）打印机名称选择Microsoft Office Document Image Write（没有？在安装Office时选择安装高级服务程序）打印成mdi格式将自动打开的mdi文件进行OCR识别（工具栏里找，注意识别时间很长) 识别完后将文件导出到Word（工具栏里）最后，将导出的html文件另存为DOC文件 Pdf格式文件向Doc文件转换相对比较难，因为Pdf格式与Doc 格式解码格式不同，在Pdf下的回车符、换行符以及相关的图片格式无法直接转换为Doc文件，笔者之前一直使用复制文本，然后粘贴到Word中实现Pdf向Doc格式的转换。今天突然发现了一款非常好的Pdf向Doc格式转换的工具，ScanSoft PDF Converter for Microsoft Word v1.0。它是由ScanSoft公司同微软共同组队开发了一个全新的Office 2003 插件。该插件可以帮助你通过Word直接将Pdf文档转换为Word文档，并且完全保留原来的格式和版面设计。这个名为 ScanSoft PDF Converter for Microsoft Word 的插件是首先捕获Pdf文档中的信息，分离文字同图片，表格和卷，再将其统一到Word格式。现在你可以重新利用早先你从网络上下载或Email

中收到的Pdf文件中的信息，而无需添加任何其他软件。 ScanSoft PDF Converter for Microsoft 已经非常紧密的同Office 2003整合在一起了，有两种方式可以将Pdf格式转换成Doc文件。第一种方式，在Microsoft Word 2003中你可以直接通过“文件”—>“打开”来打开Pdf文件。ScanSoft PDF Converter for Microsoft Word 插件会自动弹出了，如图3所示，经过转换后我们就可以得到想要的Doc文件。第二种方式，ScanSoft公司也已经开发了基于此的Smart Tag(Office 2003中重要的功能元件)能够轻松的通过右键来将PDF文件转换成为 Microsoft Word 文件注意，在安装ScanSoft PDF Converter for Microsoft Word的时候建议关闭正在运行的Office Word，Internet Explorer和Outlook等软件。 OFFICE使用技巧FAQ宝典-PDF文件处理问：PDF与WORD之间如何通过软件实现格式转换？答：PDF—>DOC 使用软件Acrobat，pdf2word；DOC—>PDF 使用软件Acrobat pdf->Tiff(JPEG,PNG)->OCR输出word，效果极佳，如果是English几乎不用怎么修改就可以用了。推荐OCR软件：ABBYY FineReader 7.0；ScanSoft OmniPage Pro 14.0（最强）问：如何把WORD文档转换成PDF？答：安装Acrobat（不只是Reader）完全版，在安装选项里有的，把这一项选上，选pdfmaker。在word的工具条上会有一个转换按钮。

图论及其应用(精)

图论及其应用学时：40 学分：2 课程属性：专业选修课开课单位：理学院先修课程：高等代数后续课程：无一、课程的性质《图论及其应用》是数学与应用数学专业的专业选修课程。二、教学目的通过教学，使学生掌握图论及其算法的基本理论和基本技巧，初步掌握图论及其算法的基本应用手段、基本算法设计及编程，并能用所学理论解决一些应用问题。三、教学内容 1.图的基本概念 2.图的连通性 3.树的基本性质及其应用 4.Euler Graphs and Hamilton Graphs with Applications 5.平面图性质 6.匹配，求最大匹配算法及应用 7.图的染色及应用 8.极图理论四、学时分配章课程内容学时 1 图的基本概念 4 2 图的连通性 6 3 树的基本性质及其应用 6 4 Euler Graphs and Hamilton Graphs with Applications 4 5 平面图性质 6 6 匹配，求最大匹配算法及应用 6

7 图的染色及应用 4 8 极图理论 4 合计40 五、教学方式本课程采用多媒体课堂讲授，结合实际范例深入浅出讲解讨论。六、考核方式本课程考核采用平时与期末考核相结合的办法，特别注重平时的考核，作业采用简单练习、论文等形式，期末考试采用简单考题或论文形式。七、教材及教学参考书参考教材： [1] J.A.Bondy and U.S.R.Murty. Graph Theory with Applications, The Macmillan Press LTD,1976. [2] 蒋长浩．图论与网络流．北京：中国林业出版社，2000．参考书目： [1] Bela Bollobas．Modern Graph Theory（现代图论，影印版）．北京：科学出版社，2001． [2] 殷剑宏、吴开亚．图论及其算法．合肥：中国科学技术大学出版社，2003． [3] 谢金星、邢文训．网络优化．北京：清华大学出版社．2000． [4] 程理民、吴江、张玉林．运筹学模型与方法教程．北京：清华大学出版社，2000． [5] 三味工作室．SPSS V10.0 for Windows 实用基础教程．北京：北京希望电子出版社2001． [６] 孙魁明、张海彤．Mathematica工具软件大全．北京：中国铁道出版社，1994． [７] 楼顺天、于卫、闫华梁．MATLAB程序设计语言．西安：西安电子科技大学出版社，1997．八、教学基本内容及要求第一章图的基本概念 1．教学基本要求掌握的图的基本概念、特殊图概念，了解最短路问题。 2．教学具体内容图的基本概念，路和圈，最短路问题。

如何将PDF转化成word

教你如何将打印稿变成电子稿最近，我的一个刚刚走上工作岗位上的朋友老是向我报怨，说老板真的是不把我们这些新来工作的人不当人看啊，什么粗活都是让我们做，这不，昨天又拿了10几页的文件拿来，叫他打成电子稿，他说都快变成打字工具了，我听之后既为他感到同情，同时教给他一个简单的方法，可以轻松将打印稿变成电子稿，我想以后对大家也有用吧，拿出来给大家分享一下。首先你得先把这些打印稿或文件通过扫描仪扫到电脑上去，一般单位都有扫描仪，如果没有也没关系，用数码相机拍也行，拍成图片放到WORD里面去，不过在些之前，你还得装一下WORD自带的组件，03和07的都行。点开始-程序-控制面板-添加/删除程序，找到Office-修改找到Microsoft Office Document Imaging 这个组件，Microsoft Office Document Imaging Writer 点在本机上运行，安装就可以了。首先将扫描仪安装好，接下来从开始菜单启动“Microsoft Office/ Microsoft Office 工具/Microsoft Office Document Scanning”即可开始扫描。提示:Office 2003默认安装中并没有这个组件，如果你第一次使用这个功能可能会要求你插入Office2003的光盘进行安装。由于是文字扫描通常我们选择“黑白模式”，点击扫描，开始调用扫描仪自带的驱动进行扫描。这里也要设置为“黑白模式”，建议分辨率为300dpi。扫描完毕后回将图片自动调入Office 2003种另外一个组件“Microsoft Office Document Imaging”中。点击工具栏中的“使用OCR识别文字”按键，就开始对刚才扫描的文件进行识别了。按下“将文本发送到Word”按键即可将识别出来的文字转换到Word中去了。如果你要获取部分文字，只需要用鼠标框选所需文字，然后点击鼠标右键选择“将文本发送到Word”就将选中区域的文字发送到Word中了。此软件还有一小技巧：通过改变选项里的OCR语言，可以更准确的提取文字。例如图片里为全英文，把OCR语言改为“英语”可以确保其准确率，而如果是“默认”则最终出现的可能是乱码～还有：应该说，PDF文档的规范性使得浏览者在阅读上方便了许多，但倘若要从里面提取些资料，实在是麻烦的可以。回忆起当初做毕业设计时规定的英文翻译，痛苦的要命，竟然傻到用Print Screen截取画面到画图板，再回粘到word中，够白了：（最近连做几份商务标书，从Honeywell本部获取的业绩资料全部是英文版的PDF，为了不再被折磨，花费了一个晚上的时间研究PDF和Word文件的转换，找到下面2种方法，出于无产阶级所谓的同甘共苦之心，共享下：） 1、实现工具：Office 2003中自带的Microsoft Office Document Imaging 应用情景：目前国外很多软件的支持信息都使用PDF方式进行发布，如果没有Adobe Reader，无法查看其内容，如果没有相关的编辑软件又无法编辑PDF文件。转换为DOC格式则可以实现编辑功能。尽管有些软件也可以完成PDF转换为DOC的工作，但很多都不支持中文，我们利用Office 2003中的Microsoft Office Document Imaging组件来实现这一要求最为方便。

万能的pdf转word工具

万能的pdf转word工具我们有时候希望将别的格式（比如图片、PDF等不可编辑的格式）转换为Word，这样方便我们进行后续的加工、修改工作。 PDF分为两种类型，一种是文字型PDF（也就是里面的文字你是可以直接选取的），还有一种是图片性PDF（比如扫描实体书制作的PDF，里面其实就是一张张的图片，内容是无法选取复制的），前者转换简单，后者转换会困难很多。但是，无论是图片好还是文字PDF，用捷速PDF文字识别软件一样可以快速识别出来，转换成你想要的文档格式。下面来看看怎样操作的吧。第一步：双击打开已经下载好的软件，可以看到弹出的对话框，选择“从PDF读文件”。接着会弹出打开对话框，选择保存PDF的文件夹，打开需要编辑的PDF。或直接进入到操作界面，点击“读取”按钮，然后到打开对话框中选择你需要识别的PDF，添加进去。第二步：PDF文档就会出现在编辑页面中了。这时我们点击上面的“纸面解析”，软件就会自动对文件进行分解排版，以便于后续的识别过程。第三步：点击上面的“识别”按钮，软件就会自动对文件上的文字进行识别，不一会儿就会把识别结果呈现在右边。大家可以对识别结果进行校对，如果发现错误可以进行改正。如果是多页内容进行识别的话，我们可以点击识别按钮选择下方的“全部”，就能对所有内容进行识别了。如果只想对几页进行识别的话，只要选定该页进行识别就可以了。第四步：最后得到的识别结果根据自身的要求选择保存格式，这里需要保存为word 就直接点击Word就可以了。有了捷速PDF文字识别软件之后，我们将PDF转换成Word就会变得简单许多，这样可以大大提高我们工作和学习的效率。

PDF转换word的方法

PDF转换Word方法在工程上，我们用的很多图纸都是PDF格式的。PDF格式的文件图纸虽然很流行，但是有时我们需要它转换成word可编辑文字形式来为我们服务，比如做施工组织设计需要图纸里面的设计说明，要是我们照着图纸一个字一个字往上敲，不知道需要多少时间。当然网上也有PDF转换word的软件，但是需要花钱，而且不能一次性买断它。在这里我教大家一种可以将PDF文件转换成word文档的方法，非常不错，而且永久免费。 PDF转换成WORD的步骤： 1、首先下载汉王PDF OCR 并安装，这个软件是免费的所以放心使用。运行PDF OCR，单击文件—打开，选择你要转换的PDF文件，如图所示。 2、打开选中的PDF文件后，你就可以在这个软件里查看文件的内容，因为它也是一个P DF文件的阅读器。打开文件以后有页面选择，你可以自己选择要转换的页码范围。

备注：很多图纸为了方便打印，都是横着的，你可以点编辑，转换图像，左转900就变成上面这样了。3、打开图纸以后，点击识别，版面分析。备注：在版面分析中，调整红线范围可以调整你需要的具体内容，这点很重要，如果你连旁边的专业、日期、签字页圈上，结果会出现一堆乱码。

4、版面分析完以后，点击识别，开始识别。 5、识别完以后，点击输出，到指定格式文件。备注：我是喜欢保存到桌面上，保存类型格式txt会以记事本的方式打开。

6、保存到文件夹以后，打开它，选择格式，然后点击字体，选择宋体（这一步也很关键）。 7、最后把所选内容文字复制，粘贴到新建WORD中。最会就变成我们自己想要的可用于编辑的word形式。

图论及其应用第一章答案(电子科大版)

习题一(yangchun)： 4.证明下面两图同构。证明:作映射f : v i ? u i (i=1,2….10) 容易证明，对?v i v j ∈ E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图(a)与(b)是同构的。 5.证明：四个顶点的非同构简单图有11个。证明：设四个顶点中边的个数为m ，则有： m=0: m=1 ： m=2： m=3： m=4： (a) v 23 4 (b)

m=5： m=6：因为四个顶点的简单图最多就是具有6条边，上面所列出的情形是在不同边的条件下的不同构的情形，则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。 11.证明：序列（7,6,5,4,3,3,2）和（6,6,5,4,3,3,1）不是图序列。证明：由于7个顶点的简单图的最大度不会超过6，因此序列（7,6,5,4,3,3,2）不是图序列；（6,6,5,4,3,3,1）是图序列 1 1 12312(1,1,,1,,,)d d n d d d d d π++=--- 是图序列（5,4,3,2,2,0）是图序列，然而（5,4,3,2,2,0）不是图序列，所以（6,6,5,4,3,3,1）不是图序列。 ● 12.证明：若，则包含圈。证明：下面仅对连通图的下的条件下进行证明，不连通的情形可以通过分成若干个连通的情形来证明。设 , 对于中的路若与邻接，则构成一个闭路。若是一条路，由于，因此，对于，存在与之邻接，则构成一个圈。 ● 17.证明：若G 不连通，则连通。证明：对于任意的 ,若与属于G 的连通分支，显然与在中连通；

5款免费PDF转换成WORD软件下载

Pdf转换成Word软件在哪下载? 近日，有许多网友提问说要给个转换软件下载地址。这里再重新发布五款免费Pdf转换成Word软件供大家下载。 1、e-PDF To Word Converter v2.5 软件大小：2.93MB 软件类型：汉化版软件性质：共享版热门程度：★★★★★ 本地下载 115网盘 BRSBOX网盘 ------------------------------------------------------------------------------------------------- 2、VeryPDF PDF2Word V03.0 软件大小：5.17MB 软件类型：汉化版软件性质：共享版热门程度：★★★★★ 本地下载 115网盘 BRSBOX网盘 ------------------------------------------------------------------------------------------------- 3、PDF2Word(pdf to word)2.1 大小：253KB 类型：汉化版性质：免费软件热门程度：★★★★ 本地下载 115网盘 BRSBOX网盘 ------------------------------------------------------------------------------------------------- 4、Easy PDF to Word Converter V2.0.3 体积：538KB 类型：汉化版热门程度：★★★★ 本地下载 115网盘BRSBOX网盘

PDF转word哪个软件比较好用

使用过PDF文件的朋友都知道，PDF文件不可以直接修改，当我们需要撰写一份活动方案，或者策划书的时候，我们要传送给领导查看修改，如果传送的文件是PDF格式的文件，领导就无法直接修改，很麻烦，就要将PDF文件转换成Word文档。那么今天就给大家分享一个方法。 1.因为PDF文件不能进行编辑，因此就需要借助转换工具才能实现转换。大家在百度中搜索关键词PDF转换器，将此软件下载安装到电脑内。

2.下面大家需要打开刚安装好的转换器，进入转换器界面后先要进行功能地选择。鼠标点击选中界面上方的【PDF转换】按钮，在点击左侧的【PDF转换其他】下拉框中的【文件转word】的按钮，就可以了。 3.接下来就要将PDF文件置入PDF转换器，鼠标点击界面中的

【添加文件】，再从跳出的窗口中找到PDF文件并用鼠标左击选中它，接着再点击窗口内的打开键，将文件添加到处理列表中。 4.如果大家只需要转换PDF文件中的部分文件页面，则可点击界面内页面选择文字下方的全部选项，在弹出的窗口中的页面栏内输入要转换的页面页码数，再点击确定键即可。

5.接着要为转换后的Word文档设置保存路径，鼠标点击界面中输出目录旁的自定义按钮，再点击右侧的浏览选项，之后在跳出的窗口内找到保存路径并用鼠标单击选中，然后再点击选择文件夹选项即可设定成功。

6.大家即可点击转换器界面右下角的【开始转换】选项，等到界面中状态栏内转换进度显示100%的时候，也就意味着PDF文件已成功转换。直接点击页面上方的【打开】按钮，就可以查看转换完成的文件了。 PDF文件与Word文档都是工作必备文件格式，因此小编今天将PDF文件转换为Word的操作方法教给大家。大家在工作中遇到类似问题后，可以使用工具快速解决。

图论及其应用答案电子科大

习题三： ● 证明：是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意及, G 中的路必含. 证明：充分性: 是的割边，故至少含有两个连通分支，设是其中一个连通分支的顶点集，是其余分支的顶点集，对12,u V v V ?∈?∈，因为中的不连通，而在中与连通，所以在每一条路上，中的必含。必要性：取12,u V v V ∈∈，由假设中所有路均含有边，从而在中不存在从与到的路，这表明不连通，所以e 是割边。 ● 3.设G 是阶大于2的连通图，证明下列命题等价：（1） G 是块（2） G 无环且任意一个点和任意一条边都位于同一个圈上；（3） G 无环且任意三个不同点都位于同一条路上。：是块，任取的一点，一边，在边插入一点，使得成为两条边，由此得到新图，显然的是阶数大于3的块，由定理，中的u,v 位于同一个圈上，于是中u 与边都位于同一个圈上。：无环，且任意一点和任意一条边都位于同一个圈上，任取的点u ，边e ，若在上，则三个不同点位于同一个闭路，即位于同一条路，如不在上，由定理，的两点在同一个闭路上，在边插入一个点v ，由此得到新图，显然的是阶数大于3的块，则两条边的三个不同点在同一条路上。：连通，若不是块，则中存在着割点，划分为不同的子集块,,,无环，12,x v y v ∈∈，点在每一条的路上，则与已知矛盾，是块。 ● 7.证明：若v 是简单图G 的一个割点，则v 不是补图的割点。证明：是单图的割点，则有两个连通分支。现任取, 如果不在的

同一分支中，令是与处于不同分支的点，那么，与在的补图中连通。若在的同一分支中，则它们在的补图中邻接。所以，若是的割点，则不是补图的割点。 ● 12.对图3——20给出的图G1和G2，求其连通度和边连通度，给出相应的最小点割和最小边割。解：()12G κ= 最小点割 {6,8} 1()2G λ= 最小边割{（6,5），（8,5）} ()25G κ= 最小点割{6,7,8,9,10} 2()5G λ= 最小边割{（2,7）…（1,6）} ● 13.设H 是连通图G 的子图，举例说明：有可能k(H)> k(G). 解：通常. 整个图为，割点左边的图为的的子图，，则. e H

文档之家

图论及其应用

答案(电子科大版)图论及其应用第一章

如何将PDF转换成WORD PDF转WORD

电子科技大学研究生试题《图论及其应用》(参考答案)

图论及其应用答案电子科大

介绍几款word和PDF互相转换的软件

图论及其应用答案电子科大

图论及其应用第三章答案电子科大

图论及其应用

图论及应用第一章完整作业

图论及应用第一章完整作业

如何将有密码的PDF转换成WORD

图论及其应用(精)

如何将PDF转化成word

万能的pdf转word工具

PDF转换word的方法

图论及其应用第一章答案(电子科大版)

5款免费PDF转换成WORD软件下载

PDF转word哪个软件比较好用

图论及其应用 答案电子科大

图论及其应用答案电子科大