高中数列知识大总结(绝对全)

第六章 数列

二、重难点击

本章重点：数列的概念，等差数列，等比数列的定义，通项公式和前n 项和公式及运用，等差数列、等比数列的有关性质。注重提炼一些重要的思想和方法，如：观察法、累加法、累乘法、待定系数法、倒序相加求和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。

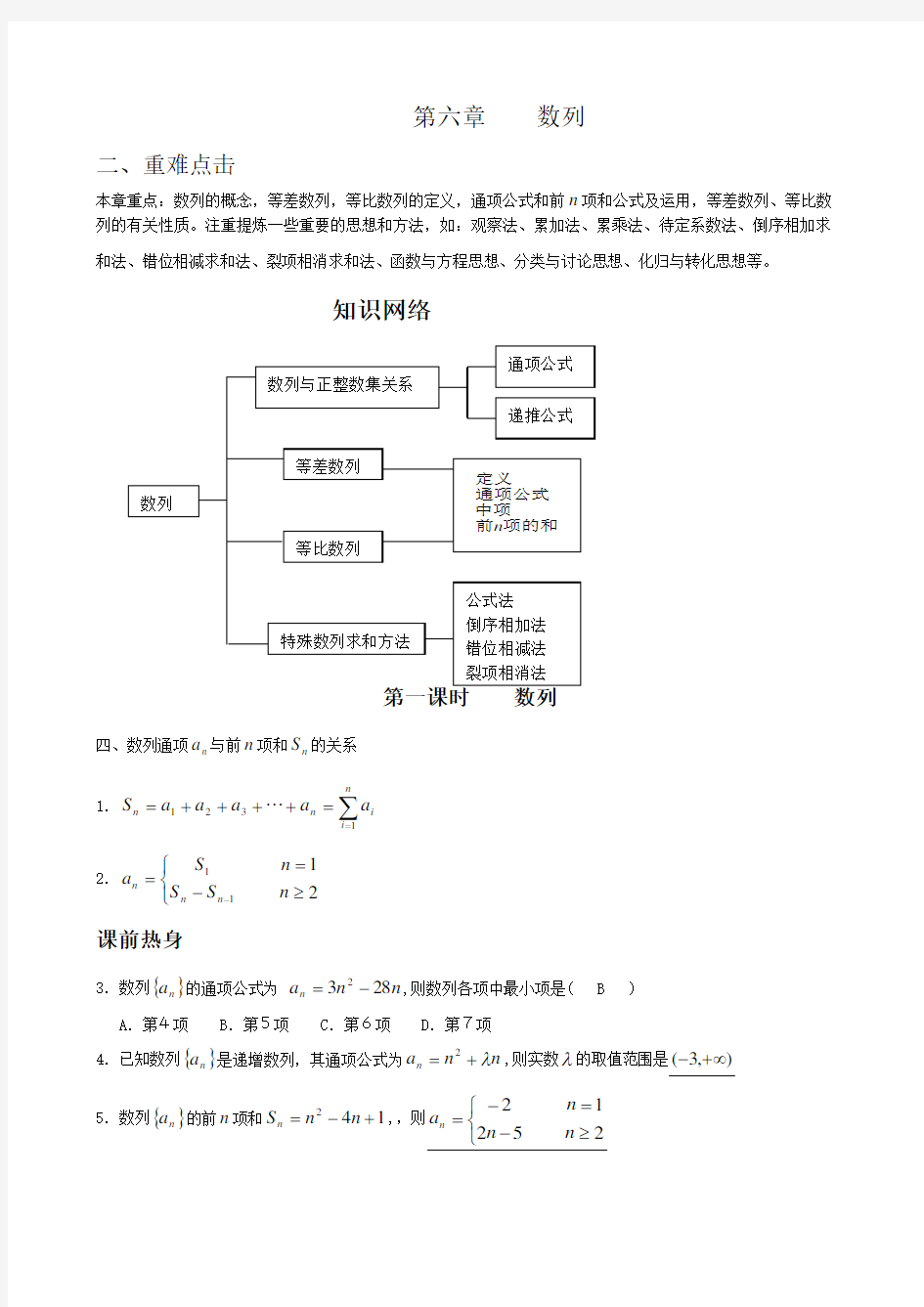
知识网络

四、数列通项n a 与前n 项和n S 的关系 1．∑==

++++=n

i i

n n a

a a a a S 1

321

2．??

?≥-==-2

1

1

1

n S S n S a n n n 课前热身

3．数列{}n a 的通项公式为 n n a n 2832

-=,则数列各项中最小项是( B )

A ．第４项

B ．第５项

C ．第６项

D ．第７项

4．已知数列{}n a 是递增数列，其通项公式为n n a n λ+=2

,则实数λ的取值范围是),3(+∞-

5．数列{}n a 的前n 项和142

+-=n n S n ,，则??

?≥-=-=2

5

21

2

n n n a n

题型一 归纳、猜想法求数列通项

【例1】根据下列数列的前几项，分别写出它们的一个通项公式 ⑴7，77，777，7777，…

⑶1，3，3，5，5，7，7，9，9… 解析：⑴将数列变形为

),110(9

7-?),110(972-)110(973-，, )110(97

-n

⑶将已知数列变为1+0，2+1，3+0，4+1，5+0，6+1，7+0，8+1，9+0，…。可得数列的通项公式为

2

)1(1n

n n a -++=

解析：⑴当123,11

11=-===S a n 时， 当)23

()23(,21

1---=-=≥--n n

n n n S S a n 时

132-?=n

又11=a 不适合上式，故???≥?==-)

2(3

2)1(1

1

n n a n n

解析：⑴因为141

2

1

-+

=+n a a n n ，所以

)1

21

121(2114121+--=-=-+n n n a a n n

所以)31

11(2112-=-a a

)51

31(2123-=-a a

43111

()257

a a -=-

…，…，

1111

()22321

n n a a n n --=---

以上)1(-n 个式相加得

)1

211(211--=

-n a a n 即：243

42411--=--=n n n a n

课外练习

解：因为

02213211

1

3212211<+-+=+-

+++=

-+n n n n n a a n n

所以n n a a <+1，选Ｃ．

解：构造函数

99

9899199

98--+

=--=

x x x y

由函数性质可知，函数在)99(，-∞上递减，且1y

最小

最大，）

，又9109

21301211101109(99a a a a a a a a a ∴>>>>>>>>>∴∈ 三、解答题

6.2等差数列

课前热身

165

1203232)(32)

2(3

1

318999119=?==-=+-=-a d a d a a a a

。

解：0912129=-=S S S S ，

003011111121110>=∴=∴=++∴a a a a a a ，又，，

∴{}n a 为递减等差数列∴1110S S =为最大。 解：∵

，，，，，1001102030102010S S S S S S S ---

成等差数列，公差为D 其首项为

10010=S ，前10项的和为10100=S

110

2210101001022102

9

101010011010100110

-=-?++=∴+=--=∴=??+?∴）（又，S D

S S S D D 102

10102)10(29840242)1(129850max 22==+--=-+-=?

?

????

?-+--=y n n n n n n n n y 时，所以当 ６．设等差数列{}n a 的前n 项和为n S ，已知

001213123<>=S S a ，，

①求出公差d 的范围，

②指出1221S S S ，，

， 中哪一个值最大，并说明理由。

d )(n f a n =n n a n S {}n a "2"≥n

解：①)(6)(610312112a a a a S +=+=

解

3

7

24

3

08240)82(2

13

)

(213

2)(137

240

7240)72(63113131133-<<--<∴<+∴<+=+=+=-

>∴>+∴>+=d d d d a a a a a S d d d a 从而又 ②

最大。

，66771376120

00130)(6S a a a S a a S ∴><∴<=>+=

课外练习 一、 选择题

1． 已知{}n a 数列是等差数列，1010=a ，其前10

项的和7010=S ，则其公差d 等于( D )

3

23

13132

．．．．D C B A -

-

2． 已

知

等差数列

{}

n a 中

，

12497116a a a a ，则，===+等于（ A ）

A ．15

B ．30

C ．31

D ．64

15

1212

497=∴+=+a a a a a 解：

二、填空题

3． 设n S 为等差数列{}n a 的前n 项和，

971043014S S S S ，则，=-==54

4． 已知等差数列{}n a 的前n 项和为n S ，若

=+++=118521221a a a a S ，则

5． 设F 是椭圆16

72

2=+y x 的右焦点，且椭圆上至少有21个不同点

,),2,1(321F P F P F P i P i ，，使=

组成公差为

d 的等差数列，则d 的取值范围为

??

? ?????????-10100101，， 解：椭圆的焦点F 到椭圆上的点最大、最小距离分别

为）和（17)17(-+，由题意得：

101001010

101

20

11

2

17)117≤

<<≤-∴≠≤∴≥--=

∴+=-+-d d d d n n d d n 或，又（）（ 三、解答题

6． 等差数列{}n a 的前n 项和记为n S ，已知

50302010==a a ，

①求通项n a ；②若n S =242，求n

解：d n a a n )1(1-+=

1022

12501930

950

3011

12010+=∴???==∴???=+=+==n a d a d a d a a a n 解方程组，

由2

)1(1d

n n na S n -+

=，n S =242 舍去）

或解得(2211242

22

)

1(12-===?-+

∴n n n n n 7． 甲、乙两物体分别从相距70m 的两处同时相向运

动，甲第一分钟走2m ，以后每分钟比前一分钟多

走1m ，乙每分钟走5m ，①甲、乙开始运动后几分钟相遇？②如果甲乙到对方起点后立即折返，甲继续每分钟比前一分钟多走1m ，乙继续每分钟走5m ，那么，开始运动几分钟后第二次相遇？ 解：①设n 分钟后第一次相遇，依题意有：

舍去），解得(20770

52

)

1(2-===+-+

n n n n n n 故第一次相遇是在开始运动后7分钟。 ②设n 分钟后第二次相遇，则：

舍去），解得(281570

352

)

1(2-==?=+-+

n n n n n n 故第二次相遇是在开始运动后15分钟 10．已知数列

{}

n a 中，，31=a 前n 和

1)1)(1(2

1

-++=

n n a n S ①求证：数列{}n a 是等差数列 ②求数列{}n a 的通项公式

③设数列?

??

??

?

+11n n a a 的前n 项和为n T ，是否存在实

数M ，使得M T n ≤对一切正整数n 都成立？若存在，求M 的最小值，若不存在，试说明理由。 解：①∵1)1)(1(2

1

-++=

n n

a n S []n

n n n n n n n n n n

n n n n a n a n na a n a n a n a n na a n a n S S a a n S )1()2()1(1)2()1(1

)1()1)(1()1)(2(2

1

1)1)(2(2

1

11212111111+-+=-+∴-+=+∴-+=++-++=

-=∴-++=∴+++++++++++整理得，

n

n n n n n a a a a a n a n +=∴++=+∴++++21212))(1()1(2

∴数列{}n a 为等差数列。 ②1)1(311-+==+n n a n na a ，

{}1

22)1(3)1(22

51211212+=?-+=-+=∴=-∴=-=∴n n d n a a a a a a a n n 的公差为即等差数列

③)

32)(12(1

11++=+n n a a n n

61

)3

2131(21)

321

12171515131(2132112121<

∈+-=+-+++-+-=∴?

?

?

??+-+=

*n n T N n n n n T n n 时，又当 要使得M T n ≤对一切正整数n 恒成立，只要M ≥

6

1

，所以存在实数M 使得M T n ≤对一切正整数n 都成立，M 的最小值为6

1。

6.3等比数列

知识要点

1． 定义：如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，记为

)0≠q q ，（。

2． 递推关系与通项公式

m

n m n n n n n q a a q a a qa a --+?=?==推广：通项公式：递推关系：111 3． 等比中项：若三个数c b a ,,成等比数列，则称b 为

c a 与的等比中项，且为ac

b a

c b =±=2，注：是成等比数列的必要而不充分条件。 4． 前n 项和公式

)1(11)1()1(111

≠??

?

??--=

--==q q q

a a q q a q na S n n n

5． 等比数列的基本性质，),,,(*

∈N q p n m 其中 ①q p n m a a a a q p n m ?=?+=+，则若反之不真！ ②)(2

*+--∈?==

N n a a a a a q

m n m n n m

n m

n ， ③{}n a 为等比数列，则下标成等差数列的对应项成等比数列。

④ ，

，，时，n n n n n S S S S S q 2321---≠仍成等比数列。

6． 等比数列与等比数列的转化 ①{}n a 是等差数列?{}

)10(≠>c c c n

a ，是等

比数列； ②

{}

n a 是正项等比数列?{}

)10(log ≠>c c a n c ，是等差数列；

③{}n a 既是等差数列又是等比数列?{}n a 是各项不为零的常数列。 7． 等比数列的判定法 ①定义法：

?=+（常数）q a a n

n 1

{}n a 为等比数列； ②中项法：?≠?=++)0(2

2

1n n n n a a a a {}n a 为

等比数列；

③通项公式法：

??=为常数）q k q k a n

n ,({}

n a 为等比数列；④前

n 项和法：

?-=为常数）（q k q k S n n ,)1({}n a 为等比数

列。

1． 10310

7

4

22

222)(++++++=n n f 设

)18(7

2)18(72)18(72)18(72)()(431----∈+++*n n n n D C B A D n f N n ．．．．）

（等于，则

2． 已知数列

{}

n a 是等比数列，且

===m m m S S S 323010，则，70 （问题引入）

猜想：{}n b 是等比数列，公比为21

。 证明如下：∵4

1

21412121

-=-=++n n n a a b

n

n n b a a 21)41(214

1

)41(211212=-=-+=

--

即：

2

11=+n n b b ，∴{}n b 是首项为41

-a ，公比

为2

1

的等比数列。

二、性质运用 例

2：⑴在等比数列

{}

n a 中，

143613233+>==+n n a a a a a a ，，

①求n a ，

②若n n n T a a a T 求,lg lg lg 21+++= ⑵在等比数列{}n a 中，若015=a ，则有等式

n

n a a a a a a -+++=+++292121 )29(*∈

在等比数列{}n b 中，若119=b 则有等式 成立。 解：⑴①由等比数列的性质可知：

n

n n a q q a a a a a a a a a a a a --=?==∴====>=+=?=?6151661616143612)2

1

(322

13213211323332所以，，即所以

，解得，又

②由等比数列的性质可知，{}n a lg 是等差数列，因为

2

lg 2

)11(2)lg (lg 2lg 5lg 2lg )6(2lg lg 116n n n a a T a n a n n n n -=+==-==-所以，

⑵由题设可知，如果0=m a 在等差数列中有

n m n a a a a a a --+++=+++122121 )12(*∈-

等

比

数

列

{}

n b ，则有

q p n m a a a a q p n m ?=?+=+，则若所以可以得

出结论，若

n

m n m b b b b b b b --==1221211 ，则有)12(*∈-

n

n b b b b b b -=372121 则有)37(*∈

点拨：历年高考对性质考查较多，主要是利用“等积性”，题目“小而巧”且背景不断更新，要熟练掌握。 典例精析

一、 错位相减法求和 例1：求和：n n a

n

a a a S ++++=

32321 解：⑴

2

)

1(3211+=

+++==n n n S a n 时， ⑵01≠≠a a

时，因为

n n a n

a a a S ++++=

32321① 1321211++-+++=n n n a

n a n a a S a ② 由①－②得：

???

????≠----=+=----=

---=-+++=-++)

1)1()1()1()1(2)1()1()

1()1(11)

11(1111)11(2211

2a a a a n a a a n n S a a a n a a S a n a

a a

a

n

a a a S a n n

n n n n n n n n n 综上所述，

所以

点拨：①若数列{}n a 是等差数列，{}n b 是等比数列，

则求数列{}n n b a ?的前n 项和时，可采用错位相减法；

②当等比数列公比为字母时，应对字母是否为1进行

讨论；

③当将n S 与q n S 相减合并同类项时，注意错位及未

合并项的正负号。

二、 裂项相消法求和 例

2

：

数

列

{}

n a 满足

1

a =8，

022124=+-=++n n n a a a a ，且 （*∈N n ）

①求数列{}n a 的通项公式；

则21

41

4-=--=

a a d

所以，n a =8＋（n －1）×（－2）＝―10－2n ②32)2(41)1(4183)2111211(41)211()4121()3111(41)211(41)

2(21

)14(121m n n n n n n b b b T n n n n a n b n

n n n >+-+-=+-+-+=??????+-++-+-=

+++=+-=+=

-=

所以

对一切*

∈N n 恒成立。

3163

1621811812)2

8

18122

81812min <=+-+-=+-+-∈∈+-+-

<∴**m n n N n N n n n m 所以，（对恒成立。

对一切故

m 的最大整数值为5。

点拨：①若数列

{}

n a 的通项能转化为

)()1(n f n f -+的形式，常采用裂项相消法求和。

②使用裂项消法求和时，要注意正负项相消时，消去了哪些项，保留了哪些项。 三、 奇偶分析法求和

例3：设二次函数[]

1)(2

+∈+=n n x x x x f ，，当

1． 在等差数列{}n a 中，1a =1，前n 项和n S 满足

，，，211

2

42=++=n n n S S n n ①求数列{}n a 的通项公式 ②记)0(>=p p

a b n

a n n ，求数列{}n

b 的前n 项和

n T 。

解：①设数列

{}

n a 的公差为

d ，由

，，，211

2

42=++=n n n S S n n 1

)1(22

)(22)(12412311212212

1+++=

+++=

=++=-===+n n n n n n

a n a n

a a n

a nd a S S n n a a d a a a a 又

即，所以得

所以n a =n ②由)0(>=p p a b n a n n ，有n

n np b = 所以n

n np p p p T ++++= 3232① 2

)1(1+==n n T p n 时，当 时，

当1≠p 132)1(2++-+++=n n n np p n p p pT ②

①－②得

???

????

≠----=+=----=---=-+++=-++++)

1(1)1()1()1(2

)1(1)1()1(1)1()1(121

2

1

1

2p p np p p p p n n T p np p p p T np p

p p np p p p T p n n

n n n n n n n n n 即：所以

课外练习 １． 数列

{}

n a 的前n 项和为n S ，若

5)

1(1

S n n a n ，则+=

等于（ B ）

6

5)

61

51()3121()2111(1

1

1)1(130

1

616

5

15=-++-+-=+-

=+= S n n n n a D C B A n 所以解：因为．

．．

．

４．)(x f 的定义域为R ，且)(x f 是以2为周期的周期函数，数列{}n a 是首项为)(*∈N a a ，公差为1的等差数列，那么)()()(1021a f a f a f +++ 的值为（ C ）

A ．－1

B ．1

C ．0

D ．10a 解：因为函数)(x f 的定义域为R ，且)(x f 是以2为周期的周期函数， 所以

)()2(00(x f x f f =+=，且）

又数列{}n a 是首项为a ，公差为1的等差数列

[]0

)1()

1()1()1()21()1()1(5)1()0(5)1(5)(5)

()()()1()()(11021==-=+--=+=++=+++??

?+=∈-+=*f f f f f f f f f a f a f a f a f a f n a f n a f a f N a n a a n n 即所以又所以为偶数）

（为奇数）

（，又所以

故原式=0，选C 。 二、填空题

５．设等比数列{}n a 的公比与前n 项和分别为q 和

n S ，且q ≠1，8

1810

20

10=+=q

S S ，则

8

1)1(8)1(1()1(18

21)

1(1010

20

10101010102012111020102011020101==++=+=++++==-+-=+∴=--S q S q S S q S a a a S S q q q a q S q a 所以

方法二、）方法一、

6．数列{}n a 满足1212

1n

n

a n n n =

+++

+++， 1

2n n n b a a +=

又，则数列

{}n b 的前n 项和为

1

8+n n

1(12)12n n a n n =

+++=+解： 128(1)n n n b a a n n +==+=118(1

n n -+） 1211

11118()()()12231188111n

b b b n n n n n +++??=-+-++-??

+??

?

?=-=??++??所以７．数列 ，，，，，，，，，，4

141414131313121211

的前100项的和为14

913

。（*

∈N n ）

典例精析

一、 函数与数列的综合问题

的等差数列。

，公差为是首项为，，，设，

且：已知例24)()()()()10(log )(121*∈≠>=N n a f a f a f a a x x f n a ①设a 是常数，求证：{}n a 成等差数列； ②若)(n n n a f a b =，{}n b 的前n 项和是n S ，当2=a 时，求n S

解：①222)1(4)(+=?-+=n n a f n ，

{}为等比数列。

所以为定值所以，所以即n n n n n n n n a a n a a a a a a a n a )2(22log 2222122≥===+=+-+

②)(n n n a f a b =

3

3

143254332542

5432

2222222222)1(2

1)

21(2162)1(222222)1(2232222)1(2423222)1()2()22(2)22(log ++-++++++++++?=?+---+=?+-++++?=-?++?++?+?=?+++?+?+?=?+=?+==+==n n n n n n n n n n n n n n n n n a n n S n n S n n S n S n n b a a n a a 所以两式相减得

时，

当 点拨：本例是数列与函数综合的基本题型之一，特 征是以函数为载体构建数列的递推关系，通过由函数的解析式获知数列的通项公式，从而问题得到求解。 １． 已知正项数列{}n a 的前n 项和为n S ，

2)1(4

1

+n n a S 与是的等比中项，

①求证：数列{}n a 是等差数列；

②若n

n

n a b 2=

，数列{}n b 的前n 项和为n T ，求n T ③在②的条件下，是否存在常数λ，使得数列?

??

??

?++2n n a T λ为等比数列？若存在，试求出λ；若不存在，说明理由。

解：①

2)1(4

1

+n n a S 与是的等比中项，

)2)(()22(4

1)1(4

1

21

)1(41

1)1(4

1

1112

12121112112=--+-+-=

-=+=≥=∴+==+=

-------n n n n n n n n n n n n n n n a a a a a a a a S S a a S n a a a n a S 即所以时，当，时，当所以

2

02011=-=-->--n n n n n a a a a a 即：，所以因为

所以数列{}n a 是等差数列。 ②n

n

n T 2

3

23+-

= 321

)2

323(2+?++-=++n n a T n

n n λλ n n 2

1

323-++=

λ

所以当且仅当3+λ=0，即λ=－3时，数列 ?

??

???++2n n a T λ为等比数列。

２． 已知在正项数列{}n a 中，1a =2，且

）

，1(+n n n a a A 在双曲线12

2=-x y 上， 数列{}n b 中，

点（n b ，n T ）在直线

12

1

+-=x y 上，其中n T 是数列{}n b 的前n 项和，①求数列{}n a 的通项公式；②求证：数列{}n b 是

等比数列。③若n n n n n C C b a C

，1(

+n n n a a A 在12

2=-x y 上知， 1+n a －n a ＝１，所以数列{}n a 是以2为首项，以1为公差的等差数列。

所以1)1(1+=-+=n d n a a n ②因为点（n b ,n T ）在直线12

1

+-

=x y 上，

1111

1

1

21

1211

22

n n n n n n n n n T b T b b T T b b ----=-+=-+=-=-+所以所以两式相减得：

{}111111

3

12

1123

23

1

3

212

()333

n n n n n n

b b n b b b b b --===-+=

=?=所以，

令得，所以所以是一个以为首项，以为公比的等比数列。所以 ③n n n n

n b a C 3

2

)1(?

+=?= n

n n n

n n n C C n n n C C <<--?=+-?

+=-++++11

1

10

)12(3

232)

1(32)2(所以所以

一、选择题

1.（2009广东卷理）已知等比数列

{}

n a 满足

0,1,2,

n a n >=，且

25252(3)

n n a a n -?=≥，则当1n ≥时，

2123221log log log n a a a -+++=

A. (21)n n -

B. 2(1)n +

C. 2n

D. 2(1)n -

【解析】由

25252(3)

n n a a n -?=≥得

n

n a 22

2=，

>n a ，则

n

n a 2=，

+???++3212log log a a 2

122)12(31log n n a n =-+???++=-，选C.

答案 C

2.（2009辽宁卷理）设等比数列{

n

a }的前n 项和为

n

S ，若

6

3

S S =3 ，则

6

9S S =

A. 2

B. 7

3 C. 83 D.3

【解析】设公比为q ,则363

33

(1)S q S S S +=＝1＋q3＝3 ? q3＝2

于是6369311247

1123

S q q S q ++++===++

【答案】B

14.(2009湖北卷理)已知数列{}n a 满足：1a ＝m （m 为正整数），1,2

31,n

n n n n a a a a a +??=??+?当为偶数时，当为奇数时。若6a ＝1，则m 所有

可能的取值为__________。

答案 4 5 32

解析 （1）若1a m =为偶数，则12a 为偶,故

223 a 224a m

m a === ①当4m 仍为偶数时，46832m m a a =??????= 故132

32m

m =?=

②当4m 为奇数时，433

3114a a m =+=+63

1

4

4m a +??????= 故3

1414m +=得m=4。

（2）若1a m

=为奇数，则213131

a a m =+=+为偶数，故

331

2m a +=

必为偶数

63116m a +??????=

，所以31

16m +=1可得m=5

16.（2009陕西卷文）设等差数列{}n a 的前n 项和为n s ,若6312a s ==,则n a = .

解析:由

6312

a s ==可得

{}n a 的公差d=2,首项1a =2,故易得n a =2n.

答案:2n

17.(2009陕西卷理)设等差数列{}n a 的前n 项和为n S ,若6312a S ==,则2lim

n

n S n →∞= .

611223

112512211

(1)lim lim 112122n n n n n a a d a S S n n S n n s a d d n n n n →∞→∞=+==???++???=+?=?==???=+==???解析：

答案：1

22.（2009全国卷Ⅰ理）在数列{}n a 中，

1111

1,(1)2n n n n a a a n ++==++ （I ）设

n

n a b n =

，求数列{}n b 的通项公式 （II ）求数列

{}

n a 的前n 项和

n

S

分析：（I ）由已知有1112

n n n a a n n +=++11

2n n n

b b +∴-=

利用累差迭加即可求出数列

{}

n b 的通项公式:

11

22n n b -=-

(*n N ∈)

（II ）由（I ）知

122n n n a n -=-

,

∴n S =11(2)2n

k k k k -=-∑1

11(2)2n n

k k k k k -===-∑∑

而1

(2)(1)

n

k k n n ==+∑,又1

12n

k k k

-=∑是一个典型的错位相减法模型，

易得1112422n

k n k k n --=+=-∑∴n S =(1)n n +1242n n -++-

23.（2009北京理）已知数集

{}()

1212,,1,2n n A a a a a a a n =≤<<≥具有性质P ；对任意的

()

,1i j i j n ≤≤≤，

i j

a a 与

j

i a a 两数中至少有一个属于A .

（Ⅰ）分别判断数集

{}1,3,4与{}1,2,3,6是否具有性质P ，并说明理由；

（Ⅱ）证明：11a =，且12111

12n

n

n a a a a a a a ---+++=+++；

（Ⅲ）证明：当5n =时，

12345

,,,,a a a a a 成等比数列.

【解析】本题主要考查集合、等比数列的性质，考查运算能力、推理论证能力、分

分类讨论等数学思想方法．本题是数列与不等式的综合题，属于较难层次题.

（Ⅰ）由于34?与4

3均不属于数集

{}1,3,4，∴该数集不具有性质P.

由于

661236

12,13,16,23,,,,,,

231236????都属于数集{}1,2,3,6， ∴该数集具有性质P.

（Ⅱ）∵{}

12,,n A a a a =具有性质P ，∴

n n

a a 与

n

n

a a 中至少有一个属于A ， 由于

121n

a a a ≤<<<，∴

n n n

a a a >，故

n n a a A

?.

从而1n

n

a A a =

∈，∴

11

a =.

∵

121n

a a a =<<<， ∴

k n n

a a a >，故

()

2,3,,k n a a A k n ?=.

由A 具有性质P 可知()

1,2,3,,n

k

a A k n a ∈=.

又∵1

21n n n n

n

n a a a a a a a a -<<<

<

，

∴21121

1,,,n n n n n n n

n a a

a a

a a a a a a a --====， 从而1211

21

n n n n

n n

n

n a a a a a a a a a a a a --=++

+=++++，

∴1211112n

n

n a a a a a a a ---+++=+++.

（Ⅲ）由（Ⅱ）知，当5n =时，有5523

43,a a

a a a a ==，即2

5243a a a a ==，

∵

125

1a a a =<<<，∴

34245

a a a a a >=，∴

34a a A

?，

由A 具有性质P 可知4

3a A a ∈.

2

243a a a =，得3423a a A a a =∈，且3221a a a <=，∴3

4232

a a a a a ==，

∴53422

4321a a a a a a a a a ====，即12345,,,,a a a a a 是首项为1，公比为2a 成等比数列.

25（2009江苏卷）对于正整数n ≥2，用n

T 表示关于x 的一元二次方程2

20x ax b ++=有实数根的有序数组(,)a b 的

组数，其中

{}

,1,2,,a b n ∈（a 和b 可以相等）；对于随机选取的

{}

,1,2,,a b n ∈（a 和b 可以相等），记

n

P 为关于

x 的一元二次方程220x ax

b ++=有实数根的概率。

（1）求

2

n T 和

2

n P ；

（2）求证：对任意正整数n ≥2，有

1n P >【解析】 [必做题]本小题主要考查概率的基本知识和记数原理，考查探究能力。满分10分。

29.（2009江西卷理）各项均为正数的数列

{}

n a ，

12,a a a b

==，且对满足m n p q +=+的正整数,,,m n p q 都有

.

(1)(1)(1)(1)

p q m n

m n p q a a a a a a a a ++=++++

（1）当

14,25a b ==

时，求通项;n a （2）证明：对任意a ，存在与a 有关的常数λ，使得对于每个正整数n ，都有1

.

n a λλ

≤≤

解：（1）由

(1)(1)(1)(1)

p q m n

m n p q a a a a a a a a ++=

++++得

121

121.(1)(1)(1)(1)n n n n a a a a a a a a --++=++++将1214

,25a a ==代入化简得 1121

.

2n n n a a a --+=

+ 所以1

1111,131n n n n a a a a ----=?++

故数列1{}1n n

a a -+为等比数列，从而

11

,13n n

n a a -=+即

31.

31n n n a -=+ 可验证，

31

31n n n

a -=+满足题设条件.

(2) 由题设

(1)(1)m n m n a a a a +++的值仅与m n +有关,记为,m n b +则111.

(1)(1)(1)(1)n n

n n n a a a a b a a a a +++==++++

考察函数

()(0)

(1)(1)a x

f x x a x +=

>++,则在定义域上有

1

,

111

()(),1

2,011a a f x g a a a

a a ?>?+??≥==???<

故对*

n N ∈，

1()

n b g a +≥恒成立.

又

22

2()

(1)n

n n a b g a a =

≥+,

注意到

1

0()2g a <≤

,解上式得

n a =≤≤

取

λ=

,即有 1

.

n a λλ≤≤.

30. (2009湖北卷理)已知数列{}n a 的前n 项和1

1()22n n n S a -=--+（n 为正整数）。

（Ⅰ）令

2n n n

b a =，求证数列

{}n b 是等差数列，并求数列{}n a 的通项公式；

(Ⅱ）令

1n n n c a n +=

，12........n

n T c c c

=+++试比较n T 与521n

n +的大小，并予以证明。 解（I ）在11()22n n n S a -=--+中，令n=1，可得11

12n S a a =--+=，即11

2a = 当2n ≥时，21

111111

()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++，， 11n 111

2a (),21

2n n n n n a a a ----∴=+=+n 即2. 112,1,n 21

n n n n n n b a b b b --=∴=+≥-=n 即当时，b .

又

1121,b a ==∴

数列

}{n

b 是首项和公差均为1的等差数列.

于是

1(1)12,2n n n n n n b n n a a =+-?==∴=

.

(II)由（I ）得

11

(1)()2n n n n c a n n +=

=+，所以

231111

23()4()(1)()2222n

n T n =?+?+?+++

2341111112()3()4()(1)()22222n n T n +=?+?+?+++ 由①-②得231

111

11

1()()()(1)()2

2222n n n T n +=+++

+-+

111

11

[1()]

133421(1)()1222123

32n n n n n

n n n T -++-+=+-+=--+∴=-

535(3)(221)

3212212(21)n n n n n n n n n T n n n ++---=--=

+++

于是确定

521n n

T n +与

的大小关系等价于比较221n

n +与的大小

由

23

45

2211;2221;2231;2241;225;

可猜想当

322 1.n

n n ≥>+时，证明如下： 证法1：（1）当n=3时，由上验算显示成立。 （2）假设1n k =+时1

2

222(21)422(1)1(21)2(1)1k k k k k k k +=>+=+=+++->++

所以当1n k =+时猜想也成立

综合（1）（2）可知 ，对一切3n ≥的正整数，都有22 1.n

n >+ 证法2：当3n ≥时

012

10112(11)2221

n n n n n n

n n n n n n n n n C C C C C C C C C n n --=+=+++

++≥+++=+>+

综上所述，当1,2n =时

521n n T n <

+，当3n ≥时521n n

T n >

+

31.（2009四川卷文）设数列{}n a 的前n 项和为n S ，

对任意的正整数n ，都有51n n a S =+成立，记

*4()1n

n n

a b n N a +=

∈-。

（I ）求数列

{}n a 与数列{}n b 的通项公式；

（II ）设数列

{}n b 的前n 项和为n R ，是否存在正整数k ，使得4n R k ≥成立？若存在，找出一个正整数k ；若不存在，

请说明理由；

（III ）记

*

221()

n n n c b b n N -=-∈，设数列

{}n c 的前n 项和为n T ，求证：对任意正整数n 都有

32n T <

；

解（I ）当1=n 时，111151,4=+∴=-

a S a

又

1151,51

++=+=+n n n n a S a S

1111

5,4即

+++∴-==-n n n n n a a a a a

∴数列

{}n a 是首项为

114=-

a ，公比为1

4=-

q 的等比数列，

∴1()4=-n n a ，*14()4()11()4+-=

∈--n

n n

b n N …………………………………3分

（II ）不存在正整数k ，使得

4n R k

≥成立。

证明：由（I ）知1

4()5441(4)11()4+-==+----n

n n

n b

2122125

5520151640

8888.(4)1(4)1161164(161)(164)--?-+=++=+-=-<-----+-+k k k k k k k k k

b b

∴当n 为偶数时，设

2()n m m N *

=∈ ∴

1234212()()()84n m m R b b b b b b m n

-=++++++<=

当n 为奇数时，设

21()n m m N *=-∈ ∴

1234232221()()()8(1)4844n m m m R b b b b b b b m m n ---=+++++++<-+=-=

∴对于一切的正整数n ，都有4n R k

<

∴不存在正整数k ，使得

4n R k

≥成立。 …………………………………8分

（III ）由

5

4(4)1n n b =+

--得

212221225515161516151615

4141(161)(164)(16)3164(16)16n n n n n n n n n n n n n n

c b b --???=+=+==<=

-+-++?-又

1221343,,33b b c ==

∴=， 当1=n 时，

13

2T <

，

当2n ≥时，

2

223211[1()]41114161625()25131616

16311614693162513482116n n n T --<

+?+++=+?

-<+?=<-

32.（2009湖南卷文）对于数列

{}

n u ,若存在常数M ＞0,对任意的*

n N ∈，恒有

1121n n n n u u u u u u M

+--+-++-≤, 则称数列

{}

n u 为B -数列.

（Ⅰ）首项为1，公比为1

2-

的等比数列是否为B-数列？请说明理由;

（Ⅱ）设

n

S 是数列

{}

n x 的前n 项和.给出下列两组判断：

A 组：①数列{}

n x 是B-数列, ②数列{}

n x 不是B-数列; B 组：③数列

{}n S 是B-数列, ④数列

{}

n S 不是B-数列.

请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题. 判断所给命题的真假，并证明你的结论； (Ⅲ)若数列

{}

n a 是B-数列，证明：数列

2{}

n a 也是B-数列。

解: （Ⅰ）设满足题设的等比数列为{}n a ,则1

1()2n n a -=-.于是 12211131

()()(), 2.

2222n n n n n a a n -----=---=?≥ 1121||||||

n n n n a a a a a a +--+-+

+-

=2

n 311112222???+++

+????-1（）（）=n 131 3.2?

??-

所以首项为1，公比为1

2-

的等比数列是B-数列 .

（Ⅱ）命题1：若数列

{}

n x 是B-数列，则数列

{}

n S 是B-数列.此命题为假命题.

数列知识点归纳及例题分析

《数列》知识点归纳及例题分析 一、数列的概念： 1.归纳通项公式：注重经验的积累 例1.归纳下列数列的通项公式： (1)0，-3,8，-15,24，....... (2)21,211,2111,21111,...... (3), (17) 9 ,107,1,23 2.n a 与n S 的关系：???≥-==-) 2(,) 1(,11n S S n a a n n n 注意：强调2,1≥=n n 分开，注意下标；n a 与n S 之间的互化（求通 项） 例2：已知数列}{n a 的前n 项和???≥+==2,11 ,32n n n S n ，求n a . 3.数列的函数性质： （1）单调性的判定与证明：定义法；函数单调性法 （2）最大（小）项问题： 单调性法；图像法 （3）数列的周期性：（注意与函数周期性的联系）

例3：已知数列}{n a 满足????? <<-≤≤=+121,12210,21n n n n n a a a a a ，531 =a ，求2017a . 二、等差数列与等比数列 1.等比数列与等差数列基本性质对比（类比的思想，比较相同之处和不同之处）

例题： 例4（等差数列的判定或证明）：已知数列{a n }中，a 1＝35，a n ＝2－1 a n －1 (n ≥2，n ∈N * )，数列{b n }满足b n ＝1a n －1 (n ∈N *)． (1)求证：数列{b n }是等差数列； (2)求数列{a n }中的最大项和最小项，并说明理由． (1)证明 ∵a n ＝2－1 a n －1 (n ≥2，n ∈N * )，b n ＝1 a n －1 . ∴n ≥2时，b n －b n －1＝1a n －1－1 a n －1－1 ＝ 1? ?? ??2－1a n －1－1 －1 a n －1－1 ＝a n －1 a n －1－1－1a n －1－1 ＝1. ∴数列{b n }是以－5 2 为首项，1为公差的等差数列．

高中数学数列知识点总结

数列基础知识点 《考纲》要求： 1、理解数列的概念，了解数列通项公式的意义，了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项； 2、理解等差数列的概念，掌握等差数列的通项公式与前n 项和公式，并能解决简单的实际问题； 3、理解等比数列的概念，掌握等比数列的通项公式与前n 项和公式，并能解决简单的实际问题。 数列的概念 1 ．数列的概念：数列是按一定的顺序排列的一列数，在函数意义下，数列是定义域为正整数N *或 其子集{1，2，3，……n}的函数f(n)．数列的一般形式为a 1，a 2，…，a n …，简记为{a n }，其中a n 是数列{a n }的第项． 2．数列的通项公式 一个数列{a n }的与之间的函数关系，如果可用一个公式a n ＝f(n)来表示，我们就把这个公式叫做这个数列的通项公式． 3．在数列{a n }中，前n 项和S n 与通项a n 的关系为： =n a ?????≥==21n n a n 4．求数列的通项公式的其它方法 ⑴公式法：等差数列与等比数列采用首项与公差(公比)确定的方法． ⑵观察归纳法：先观察哪些因素随项数n 的变化而变化，哪些因素不变；初步归纳出公式，再取n 的特珠值进行检验，最后用数学归纳法对归纳出的结果加以证明． ⑶递推关系法：先观察数列相邻项间的递推关系，将它们一般化，得到的数列普遍的递推关系，再通过代数方法由递推关系求出通项公式. 例1.根据下面各数列的前n 项的值，写出数列的一个通项公式． ⑴－3 12?，534?，－758?，9716?…； ⑵ 1，2，6，13，23，36，…； ⑶ 1，1，2，2，3，3， 解：⑴ a n ＝(－1) n )12)(12(12+--n n n ⑵ a n ＝)673(21 2+-n n （提示：a 2－a 1＝1，a 3－a 2＝4，a 4－a 3＝7，a 5－a 4＝10，…，a n －a n －1＝1＋3(n －2)=3n －5．各式相加得

数列知识点归纳及

数列知识点归纳及例题分析

《数列》知识点归纳及例题分析 一、数列的概念： 1.归纳通项公式：注重经验的积累 例1.归纳下列数列的通项公式： (1)0，-3,8，-15,24，....... (2)21,211,2111,21111,...... (3), (17) 9 ,107,1,23 2.n a 与n S 的关系：???≥-==-)2(,) 1(,11n S S n a a n n n 注意：①强调2,1≥=n n 分开，注意下标；②n a 与n S 之间的互化（求通项） 例2：已知数列}{n a 的前n 项和???≥+==2 ,11 ,32n n n S n ，求n a . 3.数列的函数性质： （1）单调性的判定与证明：①定义法；②函数单调性法 （2）最大（小）项问题：①单调性法；②图像法 （3）数列的周期性：（注意与函数周期性的联系） 例3：已知数列}{n a 满足?? ??? <<-≤≤=+121,12210,21n n n n n a a a a a ，531 =a ，求2017a . 二、等差数列与等比数列 1.等比数列与等差数列基本性质对比（类比的思想，比较相同之处和不同之处） 等差数列 等比数列 定义 1n n a a d +-=（d 是常数1,2,3n =，…） 1 n n a q a +=（q 是常数，且0≠q ，1,2,3n =，…） 通项 公式 ()11n a a n d =+- ()n m a a n m d =+- 11n n a a q -= 推广：n m n m a a q -= 求和 公式 () 112 n n n S na d -=+=()12n n a a + ()111 (1)1(1)11n n n na q S a q a a q q q q =?? =-?-=≠? --? 中项 公式 2 n k n k a a A -++=（*,,0n k N n k ∈>>） k n k n a a G +-±=（*,,0n k N n k ∈>>）

高中数学数列知识点总结精华版

一、数列 1.数列的定义：按照一定顺序排列的一列数称为数列，数列中的每个数称为该数列的项. ⑴数列中的数是按一定“次序”排列的，在这里，只强调有“次序”，而不强调有“规律”．因此，如果组成两个数列的数相同而次序不同，那么它们就是不同的数列． ⑵在数列中同一个数可以重复出现． ⑶项a n 与项数n 是两个根本不同的概念． ⑷数列可以看作一个定义域为正整数集(或它的有限子集)的函数当自变量从小到大依次取值时对应的一列函数值，但函数不一定是数列 2.通项公式：如果数列{}n a 的第n 项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式，即)(n f a n =. 3.递推公式：如果已知数列{}n a 的第一项（或前几项），且任何一项n a 与它的前一项1-n a （或前几项）间的关系可以用一个式子来表示，即)(1-=n n a f a 或),(21--=n n n a a f a ，那么这个式子叫做数列{}n a 的递推公式. 如数列{}n a 中，12,11+==n n a a a ，其中12+=n n a a 是数列{}n a 的递推公式. 4.数列的前n 项和与通项的公式 ①n n a a a S +++= 21； ②???≥-==-)2()1(11n S S n S a n n n . 5. 数列的表示方法：解析法、图像法、列举法、递推法. 6. 数列的分类：有穷数列，无穷数列；递增数列，递减数列，摆动数列，常数数列；有界数列，无界数列. ①递增数列:对于任何+∈N n ,均有n n a a >+1. ②递减数列:对于任何+∈N n ,均有n n a a <+1. ③摆动数列:例如: .,1,1,1,1,1 --- ④常数数列:例如:6,6,6,6,……. ⑤有界数列:存在正数M 使+∈≤N n M a n ,. ⑥无界数列:对于任何正数M ,总有项n a 使得M a n >. 1、已知*2()156 n n a n N n =∈+，则在数列{}n a 的最大项为（答：125）； 2、数列}{n a 的通项为1 +=bn an a n ，其中b a ,均为正数，则n a 与1+n a 的大小关系为（答：n a <1+n a ）； 3、已知数列{}n a 中，2n a n n λ=+，且{}n a 是递增数列，求实数λ的取值范围（答：3λ>-）； 4、一给定函数)(x f y =的图象在下列图中，并且对任意)1,0(1∈a ，由关系式) (1n n a f a =+得到的数列}{n a 满足)(*1N n a a n n ∈>+，则该函数的图象是 （）（答：A ）

高中数列知识点总结

数列知识点总结 第一部分 等差数列 一 定义式： 1n n a a d --= 二 通项公式：n a 1()(1)m a n m d a n d =+-??=+-? 一个数列是等差数列的等价条件：b an a n +=(a ，b 为常数)，即n a 是关于n 的一次函数，因为n Z ∈，所以n a 关于n 的图像是一次函数图像的分点表示形式。 三 前n 项和公式： 1()2n n n a a S +=na =中间项 1(1)2 n n na d -=+ 一个数列是等差数列的另一个充要条件：bn an S n +=2(a ，b 为常数，a ≠0)，即n S 是关于n 的二次函数，因为n Z ∈，所以n S 关于n 的图像是二次函数图像的分点表示形式。 四 性质结论 1.3或4个数成等差数列求数值时应按对称性原则设置， 如：3个数a-d,a,a+d ； 4个数a-3d,a-d,a+d,a+3d 2.a 与b 的等差中项2 a b A +=； 在等差数列{}n a 中，若m n p q +=+，则 m n p q a a a a +=+；若2m n p +=，则2m n p a a a +=； 3.若等差数列的项数为2() +∈N n n ，则，奇偶nd S S =- 1 +=n n a a S S 偶奇 ； 若等差数列的项数为()+∈-N n n 12，则()n n a n S 1212-=-，且n a S S =-偶奇，1 -=n n S S 偶奇 4.凡按一定规律和次序选出的一组一组的和仍然成等差数列。设12,n A a a a =++?+，122n n n B a a a ++=++?+， 21223n n n C a a a ++=++?+，则有C A B +=2； 5.10a >,m n S S =,则前2m n S +(m+n 为偶数)或12 m n S +±(m+n 为奇 数)最大 第二部分 等比数列 一 定义：1 (2,0,0){}n n n n a q n a q a a -=≥≠≠?成等比数列。 二 通项公式：11-=n n q a a ，n m n m a a q -= 数列{a n }是等比数列的一个等价条件是： (1),(0,01n n S a b a b =-≠≠，） 当0q >且0q ≠时，n a 关于n 的图像是指数函数图像的分点表示形式。

高中数学必修5数列知识点总结

数列 1. 等差数列 通项公式：1(1),n a a n d n *=+-∈N 等差中项：如果2 a b A += ，那么A 是a 与b 的等差中项 前n 项和：11()(1)22n n n a a n n S na d +-==+ 若n a 是等差数列，且k l m n +=+，则k l m n a a a a +=+ ? 等差数列的通项求法应该围绕条件结合1,a d ，或是利用特殊项。 ? 等差数列的最值问题求使0(0)n n a a ≥≤成立的最大n 值即可得n S 的最值。 例1.{}n a 是等差数列，538,6a S ==，则9a =_________ 解析：513113248,33362 a a d S a d a d ?=+==+ =+=，解得10,2a d ==，916a = 例2.{}n a 是等差数列，13110,a S S >=，则当n 为多少时，n S 最大？ 解析：由311S S =得1213 d a =- ，从而 21111(1)249()(7)2131313n a n n S na a n a -=+?-=--+，又10a >所以1013 a -< 故7n = 2. 等比数列 通项公式：11(0)n n a a q q -=≠ 等比中项：2G ab = 前n 项和：111(1)(1)(1)11n n n na q S a a q a q q q q =??=--?=≠?--? 若{}n a 是等比数列，且m n p q +=+，则m n p q a a a a ?=? 例.{}n a 是由正数组成的等比数列，2431,7a a S ==，则5S =__________

高中数列知识点总结

高中数列知识点总结 Written by Peter at 2021 in January

数列知识点总结 第一部分 等差数列 一 定义式： 1n n a a d --= 二 通项公式：n a 1 ()(1)m a n m d a n d =+-??=+-? 一个数列是等差数列的等价条件：b an a n +=(a ，b 为常数)，即n a 是关于n 的一次函数，因为n Z ∈，所以n a 关于n 的图像是一次函数图像的分点表示形式。 三 前n 项和公式： 一个数列是等差数列的另一个充要条件：bn an S n +=2(a ，b 为常数，a ≠0)，即n S 是关于n 的二次函数，因为n Z ∈，所以n S 关于n 的图像是二次 函数图像的分点表示形式。 四 性质结论 或4个数成等差数列求数值时应按对称性原则设置， 如：3个数a-d,a,a+d ； 4个数a-3d,a-d,a+d,a+3d 2.a 与b 的等差中项2 a b A +=； 在等差数列{}n a 中，若m n p q +=+，则 m n p q a a a a +=+；若2m n p +=，则2m n p a a a +=； 3.若等差数列的项数为2()+∈N n n ，则，奇偶nd S S =- 1+=n n a a S S 偶 奇 ； 若等差数列的项数为()+∈-N n n 12，则()n n a n S 1212-=-，且n a S S =-偶奇，1 -=n n S S 偶奇 4.凡按一定规律和次序选出的一组一组的和仍然成等差数列。设 12,n A a a a =++?+，122n n n B a a a ++=++?+， 21223n n n C a a a ++=++?+，则有C A B +=2； 5.10a >,m n S S =,则前2m n S +(m+n 为偶数)或12 m n S +±(m+n 为奇 数)最大 第二部分 等比数列 一 定义：1 (2,0,0){}n n n n a q n a q a a -=≥≠≠?成等比数列。 二 通项公式：11-=n n q a a ，n m n m a a q -=

人教版高中数列知识点总结(知识点+例题)

人教版高中数列知识点总结(知识点+例题) Lesson6 数列 知识点1：等差数列及其前n 项 1．等差数列的定义 2．等差数列的通项公式 如果等差数列{a n }的首项为a 1，公差为d ，那么它的通项公式a n ＝a 1＋(n －1) d . 3．等差中项 a ＋b 如果 A ＝2 ，那么A 叫做a 与b 的等差中项． 4．等差数列的常用性质 (1)通项公式的推广：a n ＝a m ＋（n-m ）d ，(n ，m ∈N *) ． (2)若{a n }为等差数列，且k ＋l ＝m ＋n ，(k ，l ，m ，n ∈N *) ，则 (3)若{a n }是等差数列，公差为d ，则{a 2n }也是等差数列，公差为. (4)若{a n }，{b n }是等差数列，则{pa n ＋qb n }也是等差数列． (5)若{a n }是等差数列，公差为d ，则a k ，a k ＋m ，a k ＋2m ，…(k ，m ∈N *) 是公差为的等差数列． 5．等差数列的前n 项和公式 n (a 1＋a n )n (n －1) 设等差数列{a n }的公差d ，其前n 项和S n 或S n ＝na 1＋22. 6．等差数列的前n 项和公式与函数的关系 d d 2? S n 2＋ a 1－2n . 数列{a n }是等差数列?S n ＝An 2＋Bn ，(A 、B 为常数) ． ?? 7．等差数列的最值 在等差数列{a n }中，a 1>0，d 0，则S n 存在最小值． [难点正本疑点清源] 1．等差数列的判定 (1)定义法：a n －a n －1＝d (n ≥2) ； (2)等差中项法：2a n ＋1＝a n ＋a n ＋2.

数列知识点总结及题型归纳总结

数列知识点总结及题型归纳总结

高三总复习----数列 一、数列的概念 （1）数列定义：按一定次序排列的一列数叫做数 列； 数列中的每个数都叫这个数列的项。记作n a ，在数 列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n 的项叫第n 项（也叫通项）记作n a ； 数列的一般形式：1a ，2a ，3a ，……，n a ，……，简记作 {}n a 。 例：判断下列各组元素能否构成数列 （1）a, -3, -1, 1, b, 5, 7, 9; (2)2010年各省参加高考的考生人数。 （2）通项公式的定义：如果数列}{n a 的第n 项与n 之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式。 例如：①：1 ，2 ，3 ，4， 5 ，… ②：5 1 4131211，，，，… 数列①的通项公式是n a = n （n ≤7，n N + ∈）， 数列②的通项公式是n a = 1n （n N + ∈）。 说明： ①{}n a 表示数列，n a 表示数列中的第n 项，n a = ()f n 表 示数列的通项公式； ② 同一个数列的通项公式的形式不一定唯一。例如，n a = (1)n -=1,21 ()1,2n k k Z n k -=-?∈?+=? ； ③不是每个数列都有通项公式。例如，1，1.4，

1.41，1.414，…… （3）数列的函数特征与图象表示： 序号：1 2 3 4 5 6 项 ：4 5 6 7 8 9 上面每一项序号与这一项的对应关系可看成是一 个序号集合到另一个数集的映射。从函数观点看，数列实质上是定义域为正整数集N + （或它的有限子集）的函数()f n 当自变量n 从1开始依次取值时对应的一系列函数值(1),(2),(3),f f f ……，()f n ，……．通常用n a 来代替()f n ，其图象是一群孤立点。 例：画出数列12+=n a n 的图像. （4）数列分类：①按数列项数是有限还是无限分： 有穷数列和无穷数列；②按数列项与项之间的大小关系分：单调数列（递增数列、递减数列）、常数列和摆动数列。 例：下列的数列，哪些是递增数列、递减数列、常 数列、摆动数列？ （1）1，2，3，4，5，6，… (2)10, 9, 8, 7, 6, 5, … (3) 1, 0, 1, 0, 1, 0, … (4)a, a, a, a, a,… （5）数列{n a }的前n 项和n S 与通项n a 的关系： 1 1(1)(2)n n n S n a S S n -=?=?-?≥ 例：已知数列}{n a 的前n 项和3 22+=n s n ，求数列}{n a 的通

重点高中数学数列知识点总结

重点高中数学数列知识点总结

————————————————————————————————作者：————————————————————————————————日期：

定义：1n n a a d +-=（d 为常数），()11n a a n d =+- 等差中项：x A y ，，成等差数列2A x y ?=+ 前n 项和()()11122 n n a a n n n S na d +-==+ 性质：{}n a 是等差数列 （1）若m n p q +=+，则m n p q a a a a +=+； （2）数列{}{}{}12212,,+-n n n a a a 仍为等差数列，232n n n n n S S S S S --，，……仍为等差数列，公差为d n 2； （3）若三个成等差数列，可设为a d a a d -+，， （4）若n n a b ，是等差数列，且前n 项和分别为n n S T ，，则2121 m m m m a S b T --= （5）{}n a 为等差数列2n S an bn ?=+（a b ，为常数，是关于n 的常数项为0的二次函数） n S 的最值可求二次函数2n S an bn =+的最值；或者求出{}n a 中的正、负分界项， 即：当100a d ><，，解不等式组100 n n a a +≥??≤?可得n S 达到最大值时的n 值. 当100a d <>，，由1 00n n a a +≤??≥?可得n S 达到最小值时的n 值. (6)项数为偶数n 2的等差数列{}n a ，有 ),)(()()(11122212为中间两项++-+==+=+=n n n n n n n a a a a n a a n a a n S Λ nd S S =-奇偶，1 +=n n a a S S 偶奇. （7）项数为奇数12-n 的等差数列{} n a ，有 )()12(12为中间项n n n a a n S -=-， n a S S =-偶奇， 1-=n n S S 偶奇.

高中数列知识大总结(绝对全)

第六章 数列 重难点击 本章重点：数列的概念，等差数列，等比数列的定义，通项公式和前n 项和公式及运用，等差数列、等比数列的有关性质。注重提炼一些重要的思想和方法，如：观察法、累加法、累乘法、待定系数法、倒序相加求和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。 知识网络 第一课时 数列 四、数列通项n a 与前n 项和n S 的关系 1．∑== ++++=n i i n n a a a a a S 1 321 2．?? ? ≥-==-2 11 1n S S n S a n n n 课前热身 3．数列{}n a 的通项公式为 n n a n 2832 -=,则数列各项中最小项是( B ) A ．第４项 B ．第５项 C ．第６项 D ．第７项 4．已知数列{}n a 是递增数列，其通项公式为n n a n λ+=2 ,则实数λ的取值范围是),3(+∞- 5．数列{}n a 的前n 项和142 +-=n n S n ,，则?? ?≥-=-=2 5 212n n n a n 数列与正整数集关系 等差数列 等比数列 特殊数列求和方法 公式法 倒序相加法 错位相减法 裂项相消法 n 定义 通项公式中项 前项的和 递推公式 通项公式 数列

题型一 归纳、猜想法求数列通项 【例1】根据下列数列的前几项，分别写出它们的一个通项公式 ⑴7，77，777，7777，… ⑶1，3，3，5，5，7，7，9，9… 解析：⑴将数列变形为 ), 110(9 7-?), 110 (9 72 -)110 (9 73 -，, )110 (9 7-n ⑶将已知数列变为1+0，2+1，3+0，4+1，5+0，6+1，7+0，8+1，9+0，…。可得数列的通项公式为 2 ) 1(1n n n a -++ = 点拨：本例的求解关键是通过分析、比较、联想、归纳、转换获得项与项数的一般规律，从而求得通项。 题型二 应用?? ? ≥-==-) 2()1(1 1n S S n S a n n n 求数列通项 例2．已知数列{}n a 的前n 项和n S ，分别求其通项公式. ⑴23-=n n S 解析：⑴当123,11 11=-===S a n 时， 当)23 ()23(,21 1---=-=≥--n n n n n S S a n 时 1 3 2-?=n 又11=a 不适合上式，故???≥?==-) 2(32)1(11 n n a n n 三、利用递推关系求数列的通项 【例3】根据下列各个数列{}n a 的首项和递推关系，求其通项公式 ⑴141 , 2 12 11-+ == +n a a a n n 解析：⑴因为1 41 2 1 -+=+n a a n n ，所以 )1 21121 ( 21 1 41 2 1+- -= -= -+n n n a a n n 所以)31 11(2112-=-a a )51 31(2123-=-a a 43111()257 a a -= -

数列全章知识点总结

数列知识点题型方法总复习 一．数列的概念：数列是一个定义域为正整数集N*（或它的有限子集｛1,2，3，…，n ｝）的特殊函 数，数列的通项公式也就是相应函数的解析式。如 （1）已知* 2 () 156 n n a n N n = ∈+，则在数列{}n a 的最大项为__（125）； （2）数列}{n a 的通项为1 +=bn an a n ，其中 b a ,均为正数，则n a 与1+n a 的大小关系为___（n a <1+n a ）； （3）已知数列{}n a 中，2n a n n λ=+，且{}n a 是递增数列，求实数λ的取值范围（3λ>-）；（4）一给定函数)(x f y =的图象在下列图中，并且对任意)1,0(1∈a ，由关系式)(1n n a f a =+得到的数 列}{n a 满足)(* 1N n a a n n ∈>+，则该函数的图象是（A ） A B C D 二．等差数列的有关概念： 1．等差数列的判断方法：定义法1(n n a a d d +-=为常数）或11(2)n n n n a a a a n +--=-≥。如设{}n a 是等差数列，求证：以b n = n a a a n +++ 21 *n N ∈为通项公式的数列{}n b 为等差数列。 2．等差数列的通项：1(1)n a a n d =+-或()n m a a n m d =+-。如(1)等差数列{}n a 中，1030a =，2050a =，则通项n a = 210n +；（2）首项为-24的等差数列，从第10项起开始为正数，则公差的取值范围是______ 8 33 d <≤ 3．等差数列的前n 和：1()2n n n a a S += ，1(1) 2n n n S na d -=+。如（1）数列 {}n a 中，*11(2,)2 n n a a n n N -=+≥∈，32n a =，前n 项和15 2n S =-，则13a =-，10n =； （2）已知数列 {}n a 的前n 项和2 12n S n n =-，求数列{||}n a 的前n 项和n T （答：2* 2* 12(6,) 1272(6,) n n n n n N T n n n n N ?-≤∈?=?-+>∈??）. 4．等差中项：若,,a A b 成等差数列，则A 叫做a 与b 的等差中项，且2 a b A +=。 提醒：（1）等差数列的通项公式及前n 和公式中，涉及到5个元素：1a 、d 、n 、n a 及n S ，其中1a 、 d 称作为基本元素。只要已知这5个元素中的任意3个，便可求出其余2个，即知3求2。 （2）为减少运算量，要注意设元的技巧，如奇数个数成等差，可设为…，2,,,,2a d a d a a d a d --++…（公差为d ）；偶数个数成等差，可设为…，3,,,3a d a d a d a d --++,…（公差为2d ） 三．等差数列的性质： 1．当公差0d ≠时，等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函数，且斜率 为公差d ；前n 和211(1)()222 n n n d d S na d n a n -=+=+-是关于n 的二次函数且常数项为0. 2．若公差0d >，则为递增等差数列，若公差0d <，则为递减等差数列，若公差0d =，则为常数 列。

2019年高一数列知识点总结

2019年高一数列知识点总结 数列是高一数学的重点，以下是整理的高一数列知识点总结，欢迎参考阅读！ 求数列通项公式常用以下几种方法： 一、题目已知或通过简单推理判断出是等比数列或等差数列，直接用其通项公式。 例：在数列{an}中，若a1=1，an+1=an+2（n1），求该数列的通项公式an。 解：由an+1=an+2（n1）及已知可推出数列{an}为a1=1，d=2的等差数列。所以an=2n—1。此类题主要是用等比、等差数列的定义判断，是较简单的基础小题。 二、已知数列的前n项和，用公式 S1（n=1） Sn—Sn—1（n2）

例：已知数列{an}的前n项和Sn=n2—9n，第k项满足5 （A）9（B）8（C）7（D）6 解：∵an=Sn—Sn—1=2n—10，∴5<2k—10 此类题在解时要注意考虑n=1的情况。 三、已知an与Sn的关系时，通常用转化的方法，先求出Sn与n的关系，再由上面的（二）方法求通项公式。 例：已知数列{an}的前n项和Sn满足an=SnSn—1（n2），且a1=—，求数列{an}的通项公式。 解：∵an=SnSn—1（n2），而an=Sn—Sn—1，SnSn—1=Sn—Sn —1，两边同除以SnSn—1，得———=—1（n2），而—=—=—，∴{—}是以—为首项，—1为公差的等差数列，∴—=—，Sn=—， 再用（二）的方法：当n2时，an=Sn—Sn—1=—，当n=1时不适合此式，所以， —（n=1）

—（n2） 四、用累加、累积的方法求通项公式 对于题中给出an与an+1、an—1的递推式子，常用累加、累积的方法求通项公式。 例：设数列{an}是首项为1的正项数列，且满足（n+1）an+12—nan2+an+1an=0，求数列{an}的通项公式 解：∵（n+1）an+12—nan2+an+1an=0，可分解为[（n+1）an+1—nan]（an+1+an）=0 又∵{an}是首项为1的正项数列，∴an+1+an≠0，∴—=—，由此得出：—=—，—=—，—=—，…，—=—，这n—1个式子，将其相乘得：∴—=—， 又∵a1=1，∴an=—（n2），∵n=1也成立，∴an=—（n∈N*） 五、用构造数列方法求通项公式

高三复习数列知识点总结

数列专题解析方法 一、数列通项公式的求解 类型一：观察法 例 1: 写出下列数列的一个通项公式 （1）3,5,9,17,33 ，； （2）11,22,33,44, ; 2345 （3）7,77.777.7777. （4）2, 1,10, 17,26, ; 3 7 9 11 （5）3,9,25,65, ; 2 4 8 16 类型二：公式法 (1) a n a1 (n 1)d a m (n m)d 例 2：已知等差数列a n 中，a1 1,a3 3,求a n 的通项公式 n 1 n m (2)a n a1q n1 a m q n m 例 3：已知等比数列a n 中，a2 6,6a1 a3 30, 求a n 的通项公式类型三：利用“ S n ”求解 S1,(n 1) (1) (1) a n n S n S n 1(n 2)

例 4：已知数列a n 的前n项和S n n2 24n(n N* )，求a n 的通项公例 5：已知数列a n 的前n项和为S n，且有a1 3,4S n 6a n a n 1 4S n 1,求a n 的通项公式 例 6：已知数列a n 的前n 项和为S n，且有a1 1,a n 1 2S n 1(n 1), 求a n 的通项公式 例 7：已知正数数列a n 的前n项和为S n ，且对任意的正整数n满足 2 S n a n 1, 求a n 的通项公式 (2)S n S n 1的推广 例 8：设数列a n满足a13a232a33n 1a n n,n N*求a n的通项公 3 式 类型四：累加法 形如a n 1 a n f (n)或a n a n 1 f (n)型的递推数列(其中f(n)是关于n 的函数) (1)若 f (n)是关于n的一次函数，累加后可转化为等差数列求和例 9：a n 1 a n 2n 1,a1 2, 求a n 的通项公式 (2)若 f (n)是关于n的指数函数，累加后可转化为等比数列求和例 10：a n 1 a n 2n,a1 2, 求a n 的通项公式 (3)若 f (n) 是关于n 的二次函数，累加后可分组求和 例11：a n 1 a n n n 1,a1 1, 求a n 的通项公式 (4)若 f (n)是关于n的分式函数，累加后可裂项求和 例 12：a n 1 a n 21,a1 1, 求a n的通项公式 n 2 2n n 类型五：累乘法 形如an1f(n)或an f (n)型的递推数列(其中f(n)是关于n的函数) a n a n 1

高中数列知识大总结(绝对全)

第六章 数列 二、重难点击 本章重点：数列的概念，等差数列，等比数列的定义，通项公式和前n 项和公式及运用，等差数列、等比数列的有关性质。注重提炼一些重要的思想和方法，如：观察法、累加法、累乘法、待定系数法、倒序相加求和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。 知识网络 四、数列通项n a 与前n 项和n S 的关系 1．∑== ++++=n i i n n a a a a a S 1 321 2．?? ?≥-==-2 1 1 1 n S S n S a n n n 课前热身 3．数列{}n a 的通项公式为 n n a n 2832 -=,则数列各项中最小项是( B ) A ．第４项 B ．第５项 C ．第６项 D ．第７项 4．已知数列{}n a 是递增数列，其通项公式为n n a n λ+=2 ,则实数λ的取值范围是),3(+∞- 5．数列{}n a 的前n 项和142 +-=n n S n ,，则?? ?≥-=-=2 5 21 2 n n n a n

题型一 归纳、猜想法求数列通项 【例1】根据下列数列的前几项，分别写出它们的一个通项公式 ⑴7，77，777，7777，… ⑶1，3，3，5，5，7，7，9，9… 解析：⑴将数列变形为 ),110(9 7-?),110(972-)110(973-，, )110(97 -n ⑶将已知数列变为1+0，2+1，3+0，4+1，5+0，6+1，7+0，8+1，9+0，…。可得数列的通项公式为 2 )1(1n n n a -++= 解析：⑴当123,11 11=-===S a n 时， 当)23 ()23(,21 1---=-=≥--n n n n n S S a n 时 132-?=n 又11=a 不适合上式，故???≥?==-) 2(3 2)1(1 1 n n a n n 解析：⑴因为141 2 1 -+ =+n a a n n ，所以 )1 21 121(2114121+--=-=-+n n n a a n n 所以)31 11(2112-=-a a )51 31(2123-=-a a 43111 ()257 a a -=- …，…， 1111 ()22321 n n a a n n --=--- 以上)1(-n 个式相加得 )1 211(211--= -n a a n 即：243 42411--=--=n n n a n 课外练习 解：因为

高中数列知识点总结(很实用!!)

第二章 数列 复习要点 1. 等差数列的定义与性质 定义：1n n a a d +-=（d 为常数），()11n a a n d =+- 等差中项：x A y ，，成等差数列2A x y ?=+ 前n 项和()()11122 n n a a n n n S na d +-==+ 性质：{}n a 是等差数列 （1）若m n p q +=+，则m n p q a a a a +=+； （2）数列{}{}{}12212,,+-n n n a a a 仍为等差数列，232n n n n n S S S S S --，，……仍为等差数列， 公差为d n 2； （3）若三个成等差数列，可设为a d a a d -+，， （4）若n n a b ，是等差数列，且前n 项和分别为n n S T ，，则2121 m m m m a S b T --= （5）{}n a 为等差数列2n S an bn ?=+（a b ，为常数，是关于n 的常数项为0的二次函数） n S 的最值可求二次函数2n S an bn =+的最值；或者求出{}n a 中的正、负分界项， 即：当100a d ><，，解不等式组1 00n n a a +≥??≤?可得n S 达到最大值时的n 值. 当100a d <>，，由100 n n a a +≤??≥?可得n S 达到最小值时的n 值. (6)项数为偶数n 2的等差数列{} n a ，有 ),)(()()(11122212为中间两项++-+==+=+=n n n n n n n a a a a n a a n a a n S nd S S =-奇偶，1 +=n n a a S S 偶奇 .

高中数学必修等差数列知识点总结和题型归纳

等差数列 一．等差数列知识点： 知识点1、等差数列的定义: ①如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示 知识点2、等差数列的判定方法: ②定义法：对于数列{}n a ，若d a a n n =-+1(常数)，则数列{}n a 是等差数列 ③等差中项：对于数列{}n a ，若212+++=n n n a a a ，则数列{}n a 是等差数列 知识点3、等差数列的通项公式: ④如果等差数列{}n a 的首项是1a ，公差是d ，则等差数列的通项为 d n a a n )1(1-+= 该公式整理后是关于n 的一次函数 知识点4、等差数列的前n 项和: ⑤2 )(1n n a a n S += ⑥d n n na S n 2) 1(1-+ = 对于公式2整理后是关于n 的没有常数项的二次函数 知识点5、等差中项: ⑥如果a ，A ，b 成等差数列，那么A 叫做a 与b 的等差中项即：2 b a A += 或b a A +=2 在一个等差数列中，从第2项起，每一项（有穷等差数列的末项除外）都是它的前一项与后一项的等差中项；事实上等差数列中某一项是与其等距离的前后两项的等差中项 知识点6、等差数列的性质: ⑦等差数列任意两项间的关系：如果n a 是等差数列的第n 项，m a 是等差数列的第m 项，且n m ≤，公差为d ，则有d m n a a m n )(-+= ⑧ 对于等差数列{}n a ，若q p m n +=+，则q p m n a a a a +=+ 也就是：ΛΛ=+=+=+--23121n n n a a a a a a ⑨若数列{}n a 是等差数列，n S 是其前n 项的和，*N k ∈，那么k S ，k k S S -2，k k S S 23-成等差数列如下图所示： 4444444444484444444444476443 4421Λ4434421Λ444344421Λk k k k k S S S k k S S k k k a a a a a a a a 3232k 31221S 321-+-+++++++++++ 10、等差数列的前n 项和的性质：①若项数为() *2n n ∈N ，则 ()21n n n S n a a +=+，且 S S nd -=偶奇， 1 n n S a S a +=奇偶．②若项数为() *21n n -∈N ，则()2121n n S n a -=-，且n S S a -=奇偶， 1 S n S n = -奇偶（其中n S na =奇，()1n S n a =-偶）． 二、题型选析： 题型一、计算求值（等差数列基本概念的应用） 1、.等差数列{a n }的前三项依次为 a-6，2a -5， -3a +2，则 a 等于（ ) A . -1 B . 1 C .-2 D. 2 2．在数列{a n }中，a 1=2，2a n+1=2a n +1，则a 101的值为 （ ） A ．49 B ．50 C ．51 D ．52 3．等差数列1，－1，－3，…，－89的项数是（ ）

高中数学必修等差数列知识点总结和题型归纳

二、题型选析： 题型一、计算求值（等差数列基本概念的应用） 1、.等差数列{a n }的前三项依次为 a-6 ，2a -5 ， -3a +2 ，则 a A . -1 B . 1 C .-2 D. 2 2．在数列 {a n } 中， a 1=2，2a n+1=2a n +1，则 a 101的值为 （ ） A ．49 B ．50 C ． 51 D ．52 3．等差数列 1，－ 1，－ 3，?，－ 89的项数是（ ） 等差数列 一．等差数列知识点： 知识点 1、等差数列的定义 : ①如果一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，那么这个数列 就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母 d 表示 知识点 2、等差数列的判定方法 : ②定义法：对于数列 a n ，若a n 1 a n d （常数） ，则数列 a n 是等差数列 ③等差中项：对于数列 a n ，若2a n 1 a n a n 2，则数列 a n 是等差数列 知识点 3、等差数列的通项公式 : 的首项是 a 1 ，公差是 d ，则等差数列的通项为 该公式整理后是关于 n 的一次函数 n 项和 : n （n 1） ⑥ S n na 1 d 2 ④如果等差数列 a n a n a 1 （n 1）d 知识点 4、等差数列的前 ⑤ Sn n （a 1 a n ） 2 对于公式 2整理后是关于 n 的没有常数项的二次函数 知识点 5、等差中项 : ⑥如果 a ， A ， b 成等差数列，那么 A 叫做 a 与b 的等差中项即： A a b 或2A a b 在一个等差数列中，从第 2 项起，每一项（有穷等差数列的末项除外）都是它的前一项 与后一项的等差中项；事实上等差数列中某一项是与其等距离的前后两项的等差中项 知识点 6、等差数列的性质 : ⑦等差数列任意两项间的关系：如果 且 m n ，公差为 d ，则有 a n a m （n ⑧ 对于等差数列 a n ，若 n m p a n 是等差数列的第 n 项， a m 是等差数列的第 m 项， m ）d q ，则 a n a m a p a q 也就是： a 1 a n a 2 a n 1 a 3 a n 2 ⑨若数列 a n 是等差数列， 等差数列如下图所示： S n 是其前 n 项的和， k N ，那么 S k ， S 2k S k ， S 3k S 2k 成 S 3k a 1 a 2 a 3 S k a k a k 1 S 2k a 2k S k a 2k 1 S 3k S 2k a 3k ①若项数为 2n n * ， 则 S 2n n a n a n 1 ， 且 S 偶 S 奇 S 奇 nd ， 奇 an ． ②若项数为 2n 1 n S 偶 a n 1 S 奇 n （其中 S 奇 na n ， S 偶 n 1 a n ）． S 偶 n 1 奇 等差数列的前 n 项和的性质： 10、 ，则 S 2n 1 2n 1 a n ，且 S 奇 S 偶 a n ， 等于（ ）