
动点问题专题训练
1、如图,已知ABC
△中,10
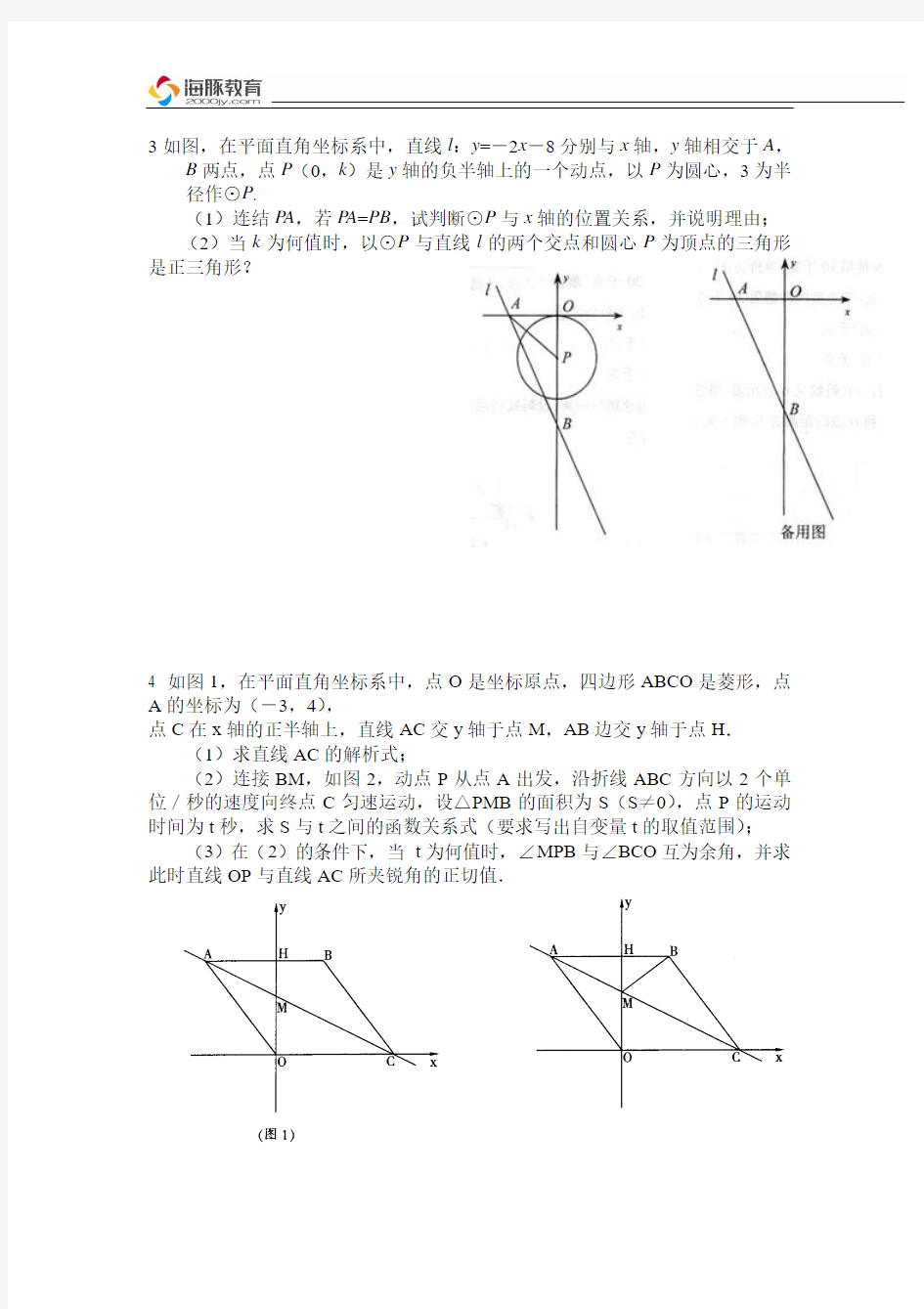
AB AC
==厘米,8
BC=厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q 在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,BPD
△与
CQP
△是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度
为多少时,能够使BPD
△与CQP
△全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度
从点B同时出发,都逆时针沿ABC
△三边运动,求经过多长时间点P
与点Q第一次在ABC
△的哪条边上相遇?
2、直线
3
6
4
y x
=-+与坐标轴分别交于A B
、两点,动点P Q
、同时从O点出发,
同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
(1)直接写出A B
、两点的坐标;
(2)设点Q的运动时间为t秒,OPQ
△的面积为S,求出S 与t之间的函数关系式;
(3)当
48
5
S=时,求出点P的坐标,并直接写出以点
O P Q
、、为顶点的平行四边形的第四个顶点M的坐标.
运动型问题 第17课时 几何图形中的动点问题 (58分) 一、选择题(每题6分,共18分) 1.[·安徽]如图6-1-1,在矩形ABCD 中,AB =5,AD =3,动点P 满足S △ PAB =S 矩形ABCD ,则点P 到A ,B 两点距离之和PA +PB 的最小值为( D )13A. B. C.5 D. 2934241 图6-1-1 第1题答图 【解析】 令点P 到AB 的距离为h ,由S △PAB =S 矩形ABCD ,得×5h =×5131213 ×3,解得h =2,动点P 在EF 上运动,如答图,作点B 关于EF 的对称点B ′,BB ′=4,连结AB ′交EF 于点P ,此时PA +PB 最小,根据勾股定理求得最小值为=,选D. 52+42412.如图6-1-2,在矩形ABCD 中,AB =2a ,AD =a ,矩 形边上一动点P 沿A →B →C →D 的路径移动.设点P 经 过的路径长为x ,PD 2=y ,则下列能大致反映y 与x 的 函数关系的图象是 ( D )【解析】 ①当0≤x ≤2a 时,∵PD 2=AD 2+AP 2,AP = x ,∴y =x 2+a 2;② 图6-1-2
当2a <x ≤3a 时,CP =2a +a -x =3a -x ,∵PD 2=CD 2+CP 2,∴y =(3a -x )2+(2a )2=x 2-6ax +13a 2;③当3a <x ≤5a 时,PD =2a +a +2a -x =5a -x , ∴PD 2=y =(5a -x )2,y =∴能大致反映y {x 2+a 2(0≤x ≤2a ),x 2-6ax +13a 2(2a 二次函数的动点问题 1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长. (2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度. (3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =o ∠的点P 有 个. (抛物线()2 0y ax bx c a =++≠的顶点坐标是2424b ac b a a ?? -- ??? ,. [解] (1)作BF y ⊥轴于F . ()()01084A B Q ,,,, 86FB FA ∴==,. 10AB ∴=. (2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=Q ,. P Q ∴,两点的运动速度均为每秒1个单位. (3)方法一:作PG y ⊥轴于G ,则PG BF ∥. GA AP FA AB ∴ =,即610 GA t =. 35GA t ∴=. 3 105OG t ∴=-. 4OQ t =+Q , ()113410225S OQ OG t t ? ?∴= ??=+- ?? ?. 立体几何与平面解析几何的交汇问题 在教材中,立体几何与解析几何是互相独立的两章,彼此分离不相联系,实际上,从空间维数看,平面几何是二维的,立体几何是三维的,因此,立体几何是由平面几何升维而产生;另一方面,从立体几何与解析几何的联系看,解析几何中的直线是空间二个平面的交线,圆锥曲线(椭圆、双曲线、抛物线)是平面截圆锥面所产生的截线;从轨迹的观点看,空间中的曲面(曲线)是空间中动点运动的轨迹,正因为平面几何与立体几何有这么许多千丝万缕的联系,因此,在平面几何与立体几何的交汇点,新知识生长的土壤特别肥沃,创新型题型的生长空间也相当宽广,这一点,在高考卷中已有充分展示,应引起我们在复习中的足够重视。 一、动点轨迹问题 这类问题往往是先利用题中条件把立几问题转化为平面几何问题,再判断动点轨迹。 例1定点A 和B 都在平面α内,定点α?P ,α⊥PB , C 是α内异于A 和B 的动点,且AC PC ⊥。那么,动点C 在平面α内的轨迹是( ) A. 一条线段,但要去掉两个点 B. 一个圆,但要去掉两个点 C. 一个椭圆,但要去掉两个点 D. 半圆,但要去掉两个点 例2若三棱锥A —BCD 的侧面ABC 内一动点P 到平面BCD 距离与到棱AB 距离相等,则动点P 的轨迹与△ABC 组成的图形可能是( ) ) 解:设二面角A —BC —D 大小为θ,作PR ⊥面BCD ,R 为垂足,PQ ⊥BC 于Q ,PT ⊥AB 于T ,则∠PQR =θ, 且由条件PT=PR=PQ·sinθ,∴ 为小于1的常数,故轨迹图形应选(D )。 二、几何体的截痕 例3:球在平面上的斜射影为椭园:已知一巨型广告汽球直径6米,太阳光线与地面所成角为60°,求此广告汽球在地面上投影椭圆的离心率和面积(椭圆面积公式为S=πab ,其中a,b 为长、短半轴长)。 解:由于太阳光线可认定为平行光线,故广告球的投影 椭园等价于以广告球直径为直径的圆柱截面椭园:此时 b=R ,a= =2R ,∴离心率 , 投影面积S=πab=π·k·2R=2πR 2=18π。 三、动点与某点(面)的距离问题 , 例4.正方体1111D C B A ABCD -中,棱长为a ,E 是 1AA 的中点, 在对角面D D BB 11上找一动点M ,使AM+ME 最小.a 23. 四、常见的轨迹问题 (1) 轨迹类型识别 此类问题最为常见,求解时,关注几何体的特征,灵活选择几何法与代数法. 例5、(北京)平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交 α于点C ,则动点C 的轨迹是( ) A .一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支 【解析】直线l 运动后形成的轨迹刚好为线段AB 的垂面,由公理二易知点C 刚好落在平面α与线段AB 的垂面的交线上,所以动点C 的轨迹是一条直线.选择 A. 总结:空间的轨迹最简单的一直存在形式就是两个平面的交线,处理问题中注意识别即可. 例6、如图,在正方体ABCD A 1 B 1C 1D 1 中,若四边形A 1BCD 1 内一动点P 到AB 1和 BC 的距离相等,则点P 的轨迹为( ) … A .椭圆的一部分 B .圆的一部分 C .一条线段 D .抛物线的一部分 O E 例4题图 A % C D A 1 C 1 D 1 B 1 M - C D B C P O 例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P ,PH ⊥O A,垂足为H,△OPH 的重心为G. (1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度. (2)设PH x =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围). (3)如果△P GH 是等腰三角形,试求出线段PH 的长. 解:(1)当点P在弧A B上运动时,OP 保持不变,于是线段GO 、GP 、 GH 中,有长度保持不变的线段,这条线段是GH=32NH=2 1 32?OP=2. (2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴ 2362 1 21x OH MH -== . 在Rt △MPH 中, . ∴y =GP= 32M P=23363 1x + (0 中考数学动点几何问题 ※动点求最值: 两定一动型(“两个定点,一个动点”的条件下求最值。例如上图中直线l的同侧有两个定点A、B,在直线l上有一动点) 例1、以正方形为载体如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上有一动点P,使PD+PE的值最小,则其最小值是 例2、以直角梯形为载体如图,在直角梯形中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P 在BC上移动,当PA+PD取得最小值时,△APD中AP边上的高为 一定两动型(“一个定点”+“两个动点”) 例3、以三角形为载体如图,在锐角△ABC中,AB=4√2,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD、AB上的动点,则BM+MN的最小值是 例4、以正方形、圆、角为载体正方形ABCD的边长为2,E为AB的中点,P是AC上的一动点.连接BP,EP,则PB+PE的最小值是 例5、⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB, ∠AOC=60°,P是OB上的一动点,PA+PC 的最小值是 例6、如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值是 . 例7:在△ABC中,∠B=60°,BA=24CM,BC=16CM,(1)求△ABC的面积; (2)现有动点P从A点出发,沿射线AB向点B方向运动,动点Q从C点出发,沿射线CB也向点B方向运动。如果点P的速度是4CM/秒,点Q的速度是2CM/秒,它们同时出发,几秒钟后,△PBQ的面积是△ABC的面积的一半? (3)在第(2)问题前提下,P,Q两点之间的距离是多少?A C B 动态问题 所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静. 数学思想:分类思想数形结合思想转化思想 1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始 沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P, Q分别从A,C同时出发,设移动时间为t秒。 当 t= 时,四边形是平行四边形;6 当t= 时,四边形是等腰梯形. 8 2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点, 则DN+MN的最小值为 5 3、如图,在Rt ABC △中,9060 ACB B ∠=∠= °,°,2 BC=.点O是AC的中点,过 点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE AB ∥交直线l于点E,设直线l的旋转角为α. (1)①当α=度时,四边形EDBC是等腰梯形,此时AD的长为; ②当α=度时,四边形EDBC是直角梯形,此时AD的长为; (2)当90 α=°时,判断四边形EDBC是否为菱形,并说明理由. 解:(1)①30,1;②60,; (2)当∠α=900时,四边形EDBC是菱形. ∵∠α=∠ACB=900,∴BC∵CE∴AB=4,AC=23. ∴AO= 1 2 AC = 3 .在Rt△AOD 中,∠A=300,∴AD=2. O E C D A α l O C A (备用图) ∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形, ∴四边形EDBC 是菱形 4、在△ABC 中,∠ACB =90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E. (1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE=AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE=AD-BE ; (3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系请写出这个等量关系,并加以证明. 解:(1)① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB ② ∵△ADC ≌△CEB ∴CE=AD ,CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ,CD=BE ∴DE=CE-CD=AD-BE (3) 当MN 旋转到图3的位置时,DE=BE-AD(或AD=BE-DE ,BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE , 又∵AC=BC , ∴△ACD ≌△CBE , ∴AD=CE ,CD=BE , ∴DE=CD-CE=BE-AD. 5、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=o ,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF . 经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证 AME ECF △≌△,所以AE EF =. 在此基础上,同学们作了进一步的研究: (1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗如果正确,写出证明过 C B A E D 图1 N M A B C D E M N 图2 A C B E D N M 图3 立体几何的动态问题 立体几何的动态问题,主要有五种:动点问题、翻折问题、旋转问题、投影与截面问题以及轨迹问题。基本类型:点动问题;线动问题;面动问题;体动问题;多动问题等。解题时一般可以通过改变视角、平面化或者寻找变化过程中的不变因素而把问题回归到最本质的定义、定理或现有的结论中,若能再配以沉着冷静的心态去计算,那么相信绝大多数问题可以迎刃而解。 动点轨迹问题 空间中动点轨迹问题变化并不多,一般此类问题可以从三个角度进行分析处理,一是从曲线定义或函数关系出发给出合理解释;二是平面与平面交线得直线或线段;三是平面和曲面(圆锥,圆柱侧面,球面)交线得圆,圆锥曲线。很少有题目会脱离这三个方向。(注意:阿波罗尼斯圆,圆锥曲线第二定义) 1.(2015·浙江卷8)如图11-10,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB =30°,则点P的轨迹是( ) A.直线 B.抛物线C.椭圆 D.双曲线的一支 式题如图,平面α的斜线AB交α于B点,且与α所成的角为θ,平面α内有一动点满足∠=π 6 ,若动 点C的轨迹为椭圆,则θ的取值范围为________. 3.(2015春?龙泉驿区校级期中)在棱长为1的正方体ABCD﹣A1B1C1D1中,M是A1D1的中点,点P在侧面BCC1B1上运动.现有下列命题: ①若点P总保持PA⊥BD1,则动点P的轨迹所在的曲线是直线; ②若点P到点A的距离为,则动点P的轨迹所在的曲线是圆; ③若P满足∠MAP=∠MAC1,则动点P的轨迹所在的曲线是椭圆; ④若P到直线BC与直线C1D1的距离比为2:1,则动点P的轨迹所在的曲线是双曲线; ⑤若P到直线AD与直线CC1的距离相等,则动点P的轨迹所在的曲线是抛物线. 其中真命题的个数为() A.4 B.3 C.2 D.1 动态问题 所谓“动点型问题”是指题设图形中存在一个或多个动点 ,它们在线段、射线或弧线上运动的一类 6 c N t4 o o AD 的长为 度时 AD 的长为 ②当 .度时 o C B C B A (备用图) E N E A B B B A A E 时 时 M C ” 图1 l E EDBC 是否为菱形,并说明理由 C ,且 (1)① 当 四边形EDBC 是直角梯形,此时 开放性题目 关键: 数学思想 1、如图1 C 开始沿向点 秒 当 当 CE // AB 交直线I 于点E ,设直线I 的旋转角为 2、如图2,正方形的边长为 4,点M 为 5 90 ° ,直线经过点 3、如图,在只也ABC 中,ACB 四边形是平行四边形; 四边形是等腰梯形?8 90° B 60°, BC 2 .点O 是AC 的中点,过 四边形EDBC 是等腰梯形,此时 (2 )当 90「时,判断四边形 解:(1 [① 30, 1 :② 60, 1.5 ; (2)当/% =900时,四边形是菱形? ???/a =Z 90°,.?..???,???四边形是平行四边形 在△中,/ 900,/ 6002, ???/ 30°. 在边上,且1 , N 为对角线上任意一点,则的最小值 .解决这类问题的关键是动中求静 ,灵活运用有关数学知识解决问题 . 动中求静? 分类思想 数形结合思想转化思想 梯形中,// ,/ 90°, 141821,点P 从A 开始沿边以1秒的速度移动,点 Q 从 B 以2秒的速度移动,如果 P , Q 分别从A , C 同时出发,设移动时间为 t D ,丄于 E M C 点o 的直线l 从与AC 重合的位置开始,绕点0作逆时针旋转,交AB 边于点D ?过点C 作 ? 2. ???. 又??四边形是平行四边形 ?四边形是菱形 4、在△中 M D C A D 1 42 . 3. ? 2AC 3 .在△中,/ 3。0, (2) 图2 N 立体几何中的动点问题 1、如图,四棱锥ABCD P -的底面是边长为2的正方形,⊥PA 平面ABCD ,且4=PA ,M 是PB 上的一个动点(不与B P ,重合),过点M 作平面//α平面PAD ,截棱锥所得图形的面积为y ,若平面α与平面PAD 之间的距离为x ,则函数()x f y =的图象是C 2、在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑BCD A -中,⊥AB 平面BCD ,且CD BD ⊥,CD BD AB ==,点P 在棱AC 上运动,设CP 的长度为x ,若PBD ?的面积为()x f ,则()x f 的图象大致是A 3、 如图所示,侧棱与底面垂直,且底面为正方形的四棱柱1111D C B A ABCD -中,21=AA ,1=AB ,N M ,分别在BC AD ,1上移动,始终保持//MN 平面11D DCC ,设x BN =,y MN =,则函数()x f y =的图象大致是 C 4、如图,已知正方体1111D C B A ABCD -的棱长为2,长为2的线段MN 的一个端点M 在棱1DD 上运动,点N 在正方体的底面ABCD 内运动,则MN 的中点P 的轨迹的面积是________2π 5、点P 在正方体1111D C B A ABCD -的面对角线1BC 上运动,给出下列命 题: ①三棱锥PC D A 1-的体积不变; ②//1P A 平面1ACD ; ③1BC DP ⊥; ④平面⊥1PDB 平面1ACD ; 其中正确的命题序号是_______①②④ 6、在正方体1111D C B A ABCD -中,F E ,分别为11C B ,11D C 的中点,点P 是底面1111D C B A 内一点,且//AP 平面EFDB ,则1tan APA ∠的最大值是_______22 7、已知直三棱柱111C B A ABC -中的底面为等腰直角三角形,AC AB ⊥,点N M ,分别是边C A AB 11,上动点,若直线//MN 平面11B BCC ,点Q 为线段MN 的中点,则点Q 的轨迹为 C .A 双曲线的一支(一部分) .B 圆弧(一部分) .C 线段(去掉一个端点) .D 抛物线的一部分 解:以AB 为轴,AC 为轴,1AA 为轴建系 设()b ta M ,0,1,()tb ta M ,0,,()b ta N ,,01,则()()b t ta N -1,,0,()tb ta M ,0,()10<≤t 则N M ,中点?? ? ??2,2,2b ta ta Q (通过作与平面11B BCC 平行的平面交C A AB 11,来找N M ,进而找中点Q ) 动点问题 灵活运用有关数学知识解决问题 转化思想 6 c 1 8 4 0 0 II ②当 0 C B C AB=4,AC=2 B A (备用图) D C E N D E A B B B A A E (1)①当 点M 在边 5 图1 l E - 2 .点°是AC 的中点,过 BE 丄MN 于E 60° BC 且AD 丄MN 于 度时,四边形EDBC 是直角梯形,此时 AD 的长为 DC 上,且 CE // AB 交直线l 于点E ,设直线I 的旋转角为 交AB 边于点D .过点C 作 度时,四边形EDBC 是等腰梯形,此时AD 的长为 放性题目?解决这类问题的关键是动中求静 关键:动中求静. 数学思想:分类思想 数形结合思想 1、如图 1,梯形 ABCD 中,AD // BC , A 开始沿AD 边以1cm/秒的速度移动,点 如果P , Q 分别从A , C 同时出发,设移动时间为 当t= 时,四 边形是平行四边形 当t= 时,四边形是等腰梯形 2、如图2,正方形 ABCD 的边长为 意一点,贝U DN+MN 的最小值为 / B=90 ° , AB=14cm,AD=18cm,BC=21cm,点 P 从 -Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动, t 秒。 3、如图,在 Rt △ ABC 中,ACB 90° B 解:(1)① 30, 1;② 60, 1.5; (2)当/a =900 时,四边形EDBC 是菱形. ???/a = / ACB=90°,「. BC//ED. ?/ CE//AB,二四边形 EDBC 是平行四边形 在 Rt △ ABC 中,/ ACB=900,/ B=600,BC=2, /./ A=30°. (2)当 90°时,判断四边形 EDBC 是否为菱形,并说明理由 点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转 M D C ??? BD=2. ??? BD=BC. 又??四边形 EDBC 是平行四边形, ???四边形EDBC 是菱形 4、在厶ABC 中,/ ACB=90° , AC=BC ,直线 MN 经过点C M C 1 AC AO= 2 = ■ 3 .在 Rt △ AOD 中,/ A=30°,二 AD=2 A D 所谓“动点型问题”是指题设图形中存在一个或多个动点 ,它们在线段、射线或弧线上运动的一类开 N 图2 A ____________ …n 1 DM=1 , N 为对角线AC 上任 动点问题专题训练 1、(09包头)如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. (1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等? (2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇? 解:(1)①∵1t =秒, ∴313BP CQ ==?=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米. 又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =. 又∵AB AC =, ∴B C ∠=∠, ∴BPD CQP △≌△. ································································································· (4分) ②∵P Q v v ≠, ∴BP CQ ≠, 又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,, ∴点P ,点Q 运动的时间4 33 BP t ==秒, ∴515 443 Q CQ v t = ==厘米/秒. · ·················································································· (7分) (2)设经过x 秒后点P 与点Q 第一次相遇, 由题意,得15 32104 x x =+?, 解得80 3 x = 秒. 1 A 1.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=2 2 , 则下列结论中错误 ..的个数是( ) (1) AC⊥BE. (2) 若P为AA1上的一点,则P到平面BEF的距离为2 2 . (3) 三棱锥A-BEF的体积为定值. (4) 在空间与DD1,AC,B1C1都相交的直线有无数条. (5) 过CC1的中点与直线AC1所成角为40?并且与平面BEF所成角为50?的直线有2条. A.0 B.1 C.2 D.3 2.如图,正方体的棱长为1,线段上有两个动点 ,且 2 2 = EF,则下列结论中错误 ..的是() A.B.∥平面 C.三棱锥的体积为定值 D.△AEF与△BEF的面积相等 3.关于图中的正方体1 1 1 1 D C B A ABCD-,下列说法正确的有 ___________________. ①P点在线段BD上运动,棱锥1 1 D AB P-体积不变; ②P点在线段BD上运动,二面角 A D B P- - 1 1不变; ③一个平面 α截此正方体,如果截面是三角形,则必为锐角三角形; ④一个平面 α截此正方体,如果截面是四边形,则必为平行四边形; ⑤平面 α截正方体得到一个六边形(如图所示),则截面α在平面 1 1 D AB 与平面1 BDC 间平行移动时此六边形周长先增大,后减小。 4、如图,正方体1111 ABCD A BC D - 的棱长为1,P为BC的中点,Q为线段1 CC 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是___________(写 出所有正确命题的编号). ①当 1 2 CQ << 时,S为四边形; ②当 1 2 CQ= 时,S不为等腰梯形; ③当 3 4 CQ= 时,S与11 C D 的交点R满足 1 1 3 C R= ; 1 1 1 1 D C B A ABCD- 1 1 D B F E, BE AC⊥EF ABCD BEF A- 初二数学“动点问题”分析 所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静. 数学思想:分类思想函数思想方程思想数形结合思想转化思想 注重对几何图形运动变化能力的考查。 从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。选择基本的几何图形,让学生经历探索的过程,以能力立意,考查学生的自主探究能力,促进培养学生解决问题的能力.图形在动点的运动过程中观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程。 在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。 课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展.这些压轴题题型繁多、题意创新,目的是考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等.从数学思想的层面上讲:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想;(5)转化思想等. 一、建立动点问题的函数解析式 函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢? 1.应用勾股定理建立函数解析式。 2.应用比例式建立函数解析式。 3.应用求图形面积的方法建立函数关系式。 二、动态几何型压轴题 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。 (一)以动态几何为主线的压轴题。 1.点动问题。 2.线动问题。 3.面动问题。 (二)解决动态几何问题的常见方法有: 1.特殊探路,一般推证。 2.动手实践,操作确认。 3.建立联系,计算说明。 (三)本大类习题的共性: 1.代数、几何的高度综合(数形结合);着力于数学本质及核心内容的考查;四大数学思想:数学结合、分类讨论、方程、函数. 2.以形为载体,研究数量关系;通过设、表、列获得函数关系式;研究特殊情况下的函数值。 三、双动点问题 点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力. 其中以灵活多变而著称的双动点问题更成为中考试题的热点, 1.以双动点为载体,探求函数图象问题。 2.以双动点为载体,探求结论开放性问题。 3.以双动点为载体,探求存在性问题。 4.以双动点为载体,探求函数最值问题。 双动点问题的动态问题是近几年来中考数学的热点题型.这类试题信息量大,对同学们获取信息和处理信息的能力要求较高;解题时需要用运动和变化的眼光去观察和研究问题,挖掘运动、变化的全过程,并特别关注运动与变化中的不变量、不变关系或特殊关系,动中取静,静中求动。 四:函数中因动点产生的相似三角形问题五:以圆为载体的动点问题 动点问题是初中数学的一个难点,中考经常考察,有一类动点问题,题中未说到圆,却与圆有关,只要巧妙地构造圆,以圆为载体,利用圆的有关性质,问题便会迎刃而解;此类问题方法巧妙,耐人寻味。 初中几何的动点问题专题练习(答案) 1、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. (1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等? (2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇? 1.解:(1)①∵1t =秒, ∴313BP CQ ==?=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米. 又∵8PC BC BP BC =-=,厘米, ∴835PC =-=厘米, ∴PC BD =. 又∵AB AC = , ∴B C ∠=∠, ∴BPD CQP △≌△. ··························· (4分) ②∵P Q v v ≠, ∴BP CQ ≠, 又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,, ∴点P ,点Q 运动的时间4 33 BP t = =秒, ∴515 443 Q CQ v t = ==厘米/秒. ······················· (7分) (2)设经过x 秒后点P 与点Q 第一次相遇, 由题意,得 15 32104x x =+?, 解得80 3 x =秒. ∴点P 共运动了80 3803 ?=厘米. ∵8022824=?+, ∴点P 、点Q 在AB 边上相遇, L F E H F G E C G 图2 F H 动态问题 所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静. 数学思想:分类思想 数形结合思想 转化思想 一、单动点问题 小菜一碟:如图 2,正方形 ABCD 的边长为 4,点 M 在边 DC 上,且 DM=1,N 为对角线 AC 上任意一点,则 DN+MN 的最小值为 例 (10 年房ft 二模压轴)25. (1)如图 1,已知矩形 ABCD 中,点 E 是 BC 上的一动点,过点 E D A D A D B C B B C 图1 图3 作 EF ⊥BD 于点 F ,EG ⊥AC 于点 G ,CH ⊥BD 于点 H ,试证明 CH=EF+EG; (2) 若点 E 在BC的延长线上,如图 2,过点 E 作 EF ⊥BD 于点 F ,EG ⊥AC 的延长线于点 G ,CH ⊥BD 于点 H , 则 EF 、EG 、CH 三者之间具有怎样的数量关系,直接写出你的猜想; (3) 如图 3,BD 是正方形 ABCD 的对角线,L 在 BD 上,且 BL=BC, 连结 CL ,点 E 是 CL 上任一点, EF ⊥BD 于点 F ,EG ⊥BC 于点 G ,猜想 EF 、EG 、BD 之间具有怎样的数量关系,直接写出你的猜想; (4) 观察图 1、图 2、图 3 的特性,请你根据这一特性构造一个图形, 使它仍然具有 EF 、EG 、CH 这样的线段,并满足(1)或(2)的结论,写出相关题设的条件和结论. 学生姓名 年级 授课时间 教师姓名 课时 2 1.(2013年普通等学校招生统一试大纲版数学(理)WORD 版含答案(已校对))如图四棱锥P ABCD -902,ABC BAD BC AD PAB ∠=∠==?,与PAD ?都是等边三角形 (I)证明:; PB CD ⊥ (II)求二面角A PD C --的大小 (2012年高考(四川理))如图,在三棱锥P ABC -中,90APB ∠=,60PAB ∠=,AB BC CA ==,平面PAB ⊥平面ABC . (Ⅰ)求直线PC 与平面ABC 所成角的大小; (Ⅱ)求二面角B AP C --的大小. (2012年高考(辽宁理)) 如图,直三棱柱///ABC A B C -,90BAC ∠=, /,AB AC AA λ==点M ,N 分别为/A B 和//B C 的中点. (Ⅰ)证明:MN ∥平面//A ACC ; (Ⅱ)若二面角/A MN C --为直二面角,求λ的值 . (2012年高考(北京理))如图1,在Rt△ABC 中,∠C=90°,BC=3,AC=6,D,E 分别是AC,AB 上的点, 且DE∥BC,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C⊥CD,如图2. (1)求证:A 1C⊥平面BCDE; (2)若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小; (3)线段BC 上是否存在点P,使平面A 1DP 与平面A 1BE 垂直?说明理由. (2012年高考(安徽理))平面图形111ABB AC C 如图4所示,其中11BB C C 是矩 形,12,4BC BB ==,AB AC ==1111A B AC ==现将该平面图形分别沿 BC 和11B C 折叠,使ABC ?与111A B C ?所在平面都与平面11BB C C 垂直,再分别连接111,,AA BA CA ,得到如图2所示的空间图形,对此空间图形解答下列问题 . (Ⅰ)证明:1AA BC ⊥; (Ⅱ)求1AA 的长; (Ⅲ)求二面角1A BC A --的余弦值. 初中数学几何动点问题专题训练 所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静. 数学思想:分类思想函数思想方程思想数形结合思想转化思想 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。 例题1.梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从点A开始,沿AD边,以1厘米/秒的速度向点D运动;动点Q从点C开始,沿CB边,以3厘米/秒的速度向B点运动。已知P、Q两点分别从A、C同时出发,,当其中一点到达端点时,另一点也随之停止运动。假设运动时间为t秒,问: (1)t为何值时,四边形PQCD是平行四边形? (2)t为何值时,四边形PQCD是直角梯形? (3)在某个时刻,四边形PQCD可能是菱形吗?为什么? (4)t为何值时,四边形PQCD是等腰梯形? 练习1. 如右图,在矩形ABCD中,AB=20cm,BC=4cm,点P从A开始沿折线A—B—C —D以4cm/s的速度运动,点Q从C开始沿CD边1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为t(s),t 为何值时,四边形APQD也为矩形? 初二上动点问题 1.如图,已知△ABC中,∠B=90 o,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒. (1)出发2秒后,求线段PQ的长? (2)当点Q在边BC上运动时,出发几秒钟后,△PQB是等腰三角形? (3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间? 2.如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=10cm,直线CM⊥BC,动点D从点C开始沿射线 ....CB..方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM..上以每秒2厘米的速度运动,连接AD、AE,设运动时间为t秒. (1)求AB的长;(2)当t为多少时,△ABD的面积为15cm2? (3)当t为多少时,△ABD≌△ACE,并简要说明理由.(请在备用图中画出具体图形) 3.(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系. 小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是; (2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的 点,且∠EAF=∠BAD上述结论是否仍然成立,并说明理由; (3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进 1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F 处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离. 4.(12分)在等腰△ABC中,AB=AC=2, ∠BAC=120°,AD⊥BC于D,点O、点P分别在射线AD、BA上的运动,且保证∠OCP=60°,连接OP. (1)当点O运动到D点时,如图一,此时AP=______,△OPC是什么三角形。 (2)当点O在射线AD其它地方运动时,△OPC还满足(1)的结论吗?请用利用图二说明理由。 (3)令AO=x,AP=y,请直接写出y关于x的函数表达式,以及x的取值范围。 图一图二最新最新中考二次函数动点问题(含答案)
立体几何动点问题
初中数学动点问题专题讲解
八年级几何之动点问题
初二数学动点问题练习(含答案)
立体几何动态问题专题
初二数学动点问题练习(含答案)
立体几何中的动点问题
初二动点问题(含答案)
初中数学几何的动点问题专题练习
立体几何动点问题
初二数学动点问题专题分析
初中几何的动点问题专题练习(答案)
(完整版)初二动点问题(含答案)2
2014高考理科立体几何难建系和动点问题(考前必做的立几大题)
初中数学几何动点问题专题训练
初二上动点问题