
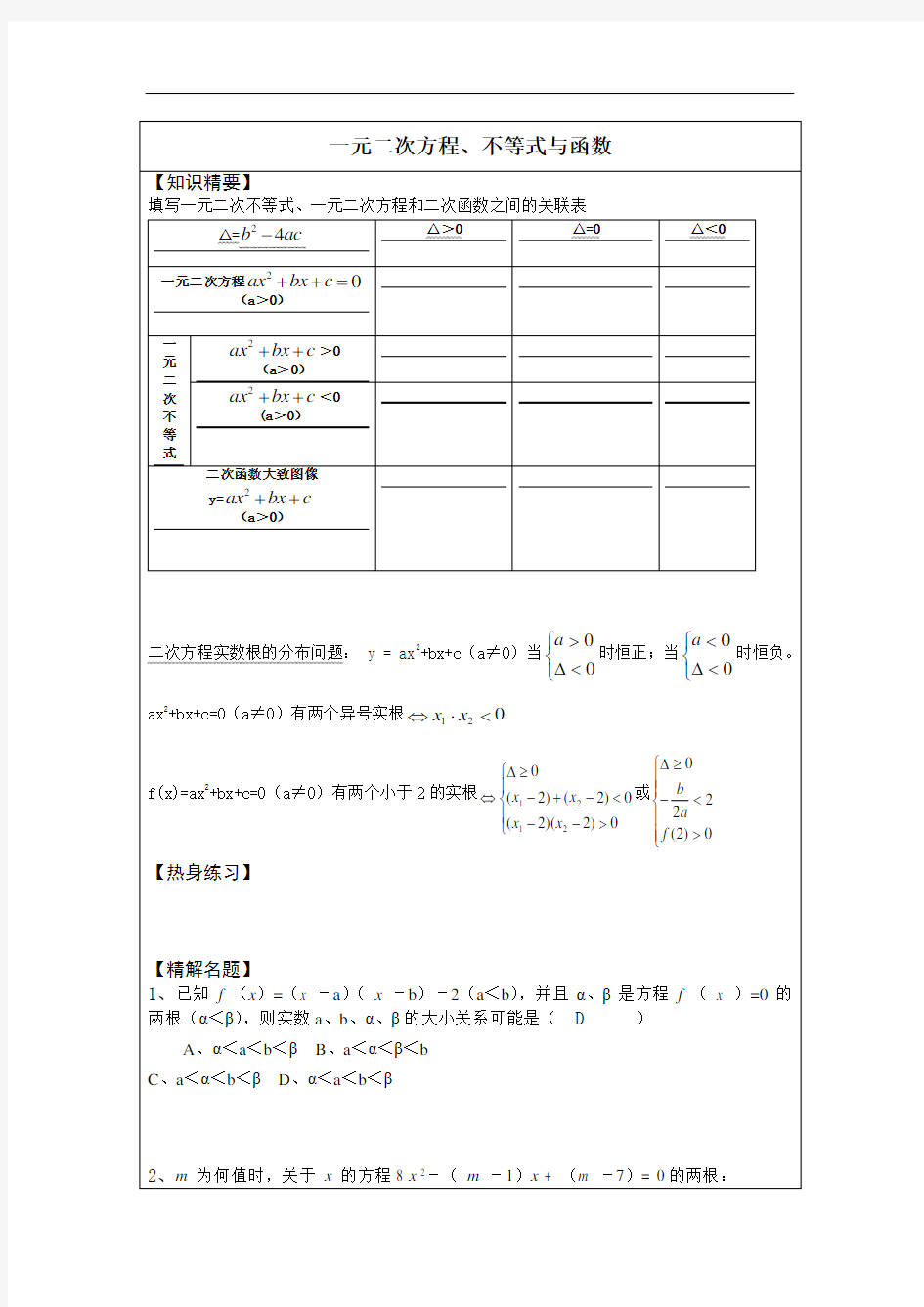
一元二次方程及根的定 义 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】
一元二次方程及根的定义 1.已知关于的方程的一个根为2,求另一个根及 的值. 思路点拨:从一元二次方程的解的概念入手,将根代入原方程解的值,再代回原方程,解方程求出另一个根即可. 解:将代入原方程,得 即 解方程,得 当时,原方程都可化为 解方程,得. 所以方程的另一个根为4,或-1. 总结升华:以方程的根为载点.综合考查解方程的问题是一个常考问题,解这类问题关键是要抓住“根”的概念,并以此为突破口. 举一反三: 【变式1】已知一元二次方程的一个根是,求代数式 的值. 思路点拨:抓住为方程的一个根这一关键,运用根的概念解题. 解:因为是方程的一个根, 所以, 故, , 所以.
. 总结升华:“方程”即是一个“等式”,在“等式”中,根据题目的需要,合理地变形,是一种对代数运算综合要求较高的能力,在这一方面注意丰富自己的经验. 类型二、一元二次方程的解法 2.用直接开平方法解下列方程: (1)3-27x2=0; (2)4(1-x)2-9=0. 解:(1)27x2=3 . (2)4(1-x)2=9 3.用配方法解下列方程: (1);(2). 解:(1)由, 得, ,
, 所以, 故. (2)由, 得, , , 所以 故 4.用公式法解下列方程: (1);(2);(3). 解:(1)这里 并且 所以, 所以,. (2)将原方程变形为, 则 , 所以,
所以. (3)将原方程展开并整理得, 这里, 并且, 所以. 所以. 总结升华:公式法解一元二次方程是解一元二次方程的一个重点,要求熟练掌握,它对我们的运算能力有较高要求,也是提高我们运算能力训练的好素材. 5.用因式分解法解下列方程: (1);(2); (3). 解:(1)将原方程变形为, 提取公因式,得, 因为,所以 所以或, 故 (2)直接提取公因式,得 所以或,(即 故. (3)直接用平方差公式因式分解得
方程与不等式之一元二次方程技巧及练习题含答案 一、选择题 1.某果园2011年水果产量为100吨,2013年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x ,则根据题意可列方程为( ) A .144(1﹣x )2=100 B .100(1﹣x )2=144 C .144(1+x )2=100 D .100(1+x )2=144 【答案】D 【解析】 试题分析:2013年的产量=2011年的产量×(1+年平均增长率)2,把相关数值代入即可. 解:2012年的产量为100(1+x ), 2013年的产量为100(1+x )(1+x )=100(1+x )2, 即所列的方程为100(1+x )2=144, 故选D . 点评:考查列一元二次方程;得到2013年产量的等量关系是解决本题的关键. 2.上海世博会的某纪念品原价168元,连续两次降价a %后售价为128元,下面所列方程中正确的是( ) A .168(1+a %)2=128 B .168(1-a %)2=128 C .168(1-2a %)=128 D .168(1-a 2%)=128 【答案】B 【解析】 【分析】 【详解】 解:第一次降价a%后的售价是168(1-a%)元, 第二次降价a%后的售价是168(1-a%)(1-a%)=168(1-a%)2; 故选B. 3.将方程()2 2230x x x m n --=-=化为的形式,指出,m n 分别是( ) A .1和3 B .-1和3 C .1和4 D .-1和4 【答案】C 【解析】 【分析】 此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数. 【详解】 移项得x 2-2x=3, 配方得x 2-2x+1=4, 即(x-1)2=4, ∴m=1,n=4.
一元二次方程根与系数的关系(附答案) 评卷人得分 一.选择题(共6小题) 1.已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是() A.方程有两个相等的实数根B.方程有两个不相等的实数根 C.没有实数根D.无法确定 · 2.关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是()A.m≥﹣1 B.m>﹣1 C.m≤﹣1 D.m<﹣1 3.关于x的一元二次方程x2+3x﹣1=0的根的情况是() A.有两个不相等的实数根B.有两个相等的实数根 C.没有实数根D.不能确定 4.设x1、x2是一元二次方程2x2﹣4x﹣1=0的两实数根,则x12+x22的值是()A.2 B.4 C.5 D.6 5.若α、β是一元二次方程x2﹣5x﹣2=0的两个实数根,则α+β的值为()A.﹣5 B.5 C.﹣2 D. 6.已知关于x的方程x2﹣4x+c+1=0有两个相等的实数根,则常数c的值为()》 A.﹣1 B.0 C.1 D.3 评卷人得分 二.填空题(共1小题) 7.若关于x的一元二次方程x2﹣3x+a=0(a≠0)的两个不等实数根分别为p,q,且p2﹣pq+q2=18,则的值为.
评卷人· 得分 三.解答题(共8小题) 8.已知关于x的方程x2﹣(2k+1)x+k2+1=0. (1)若方程有两个不相等的实数根,求k的取值范围; (2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L 的长. 9.已知关于x的方程x2+ax+a﹣2=0. (1)若该方程的一个根为1,求a的值; (2)求证:不论a取何实数,该方程都有两个不相等的实数根. · 10.已知关于x的一元二次方程(x﹣m)2﹣2(x﹣m)=0(m为常数). (1)求证:不论m为何值,该方程总有两个不相等的实数根; (2)若该方程一个根为3,求m的值. 11.已知关于x的一元二次方程x2﹣x+a﹣1=0. (1)当a=﹣11时,解这个方程; (2)若这个方程有两个实数根x1,x2,求a的取值范围; (3)若方程两个实数根x1,x2满足[2+x1(1﹣x1)][2+x2(1﹣x2)]=9,求a的值.12.已知x1,x2是关于x的一元二次方程4kx2﹣4kx+k+1=0的两个实数根.(1)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣成立若存在,求出k的值;若不存在,说明理由; (2)求使+﹣2的值为整数的实数k的整数值; : (3)若k=﹣2,λ=,试求λ的值. 13.已知关于x的方程(k+1)x2﹣2(k﹣1)x+k=0有两个实数根x1,x2. (1)求k的取值范围;
《二次函数与一元二次方程、一元二次不等式》复习题汇编 【知识梳理】: 1.二次函数与一元二次方程关系非常密切,可以相互转化,若已知函数值,可以利用一元二次方程的知识求自变量的值。 2.从“形”的方面看,函数2 y ax bx c =++的图像与 轴交点的横坐标,即为方程 20ax bx c ++=的解;从“数”的方面看,当二次函数2y ax bx c =++的函数值为 时,相应的自变量的值即为方程2 0ax bx c ++=的解。 3.抛物线2 y ax bx c =++与x 轴有 个, 个, 个交点,相应的一元二次方程 20ax bx c ++=有两个不相等的实数根,两个相等的实数根,没有实数根;反过来,如 果一元二次方程2 0ax bx c ++=有两个不相等的实数根,两个相等的实数根,没有实数 根,那么抛物线2 y ax bx c =++与x 轴有 个, 个, 个交点。 4.二次函数2 y ax bx c =++与一元二次方程2 的关系如下: 5.直线y=kx+b 与抛物线y ax bx c =++有0个、1个、2个交点,则由方程y ax bx c =++; y=kx+b 联立并消元后的一元二次方程分别满足24b ac -<0、24b ac -=0、2 4b ac ->0. 6.二次函数与一元二次不等式的关系也非常密切,当c bx ax ++2 >0时,则相应的二次函 数图象2y ax bx c =++上的点位于x 轴的上方;当c bx ax ++2 <0时,则相应的二次函 数图象2 y ax bx c =++上的点位于x 轴的下方。 7.抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2 与x 轴两交点为 ()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故12b x x a +=- 、12c x x a = ; ()()a a ac b a c a b x x x x x x x x AB ?= -=-?? ? ??-=--= -= -=44422 212 212 2121【典型例题】 例1.已知函数()()()() 2 2 113513x x y x x ?--? =?--??≤>,则使y=k 成立的x 值恰好有三个,则k 的值为( ) A .0 B .1 C .2 D .3 例2.已知函数12)3(2++-=x x k y 的图象与x 轴有交点,则k 的取值范围是 A.4 一元二次方程02 =++c bx ax 根的分布情况 设方程()2 00ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=, 方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件) 表一:(两根与0的大小比较即根的正负情况) 分 布情况 两个负根即两根都小于0 ()120,0x x << 两个正根即两根都大于0 ()120,0x x >> 一正根一负根即一个根小于0,一个大于0()120x x << 大致图象( >a ) 得出的结论 ()00200b a f ?>??? -?? ()0 0200 b a f ?>??? ->??>?? ()00 分 布情况 两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即 21x k x << 大致图象( >a ) 得出的结论 ()020b k a f k ?>??? -?? ()0 20 b k a f k ?>??? ->??>?? ()0 §2.3.1 二次函数与一元二次方程、不等式(第一课时) 导学目标: 1.从函数观点看一元二次方程.会结合一元二次函数的图象,求解一元二次方程. 2.从函数观点看一元二次不等式.会结合一元二次函数图像,求解一元二次不等式. 3.借助一元二次函数的图象,了解一元二次不等式、方程与其相应函数的联系. (预习教材P 51~ P 53,回答下列问题) 情景:学校要在长为8,宽为6 的一块长方形地面上进行绿化, 计划四周种花卉,花卉带的宽度相同, 中间种植草坪(图中阴影部分)为了美观, 现要求草坪的种植面积超过总面积的一半, 此时花卉带的宽度的取值范围是什么? 【知识点一】一元二次不等式的定义 只含有一个未知数,并且未知数最高次数是2 的不等式叫做一元二次不等式. 其一般形式可表示为:2 0ax bx c ++>或2 0ax bx c ++<()0a ≠ 自我检测1:下列不等式中是一元二次不等式的是( ) A .22 20a x x +≥ B . 2 1 3x < C .20x x m -+-≤ D .32 410x x x +-+> 【知识点二】一元二次不等式的解法 下图是一元二次函数76y x x =--的图像,请根据图像回答: (1)当x 取 时,0y = 当x 取 时,0y < 当x 取 时,0y > 由上面可知: (2)一元二次不等式2 760x x --<的解集为 一元二次不等式2 760x x --<的解集为 有何发现: 第二章 一元二次函数、方程和不等式 - 2 - (3)一元二次方程2760x x --=的解集为 有何发现: 请归纳求解一元二次不等式()2 00ax bx c ++><的解集的步骤? 自我检测2:一元二次不等式2 20x x -<的解集是 【知识点三】三个二次之间的关系 请根据右图回答: 一元二次方程()2 00ax bx c a ++=≠、 一元二次不等式()2 00ax bx c a ++>≠ 与其对应的一元二次函数()2 0y ax bx c a =++≠图像的关系? (1)一元二次方程()2 00ax bx c a ++=≠的两根为21,x x 是一元二次函数 ()20y ax bx c a =++≠图像与x 轴 . (2)一元二次方程()2 00ax bx c a ++>≠的解集的端点是一元二次方程 ()200ax bx c a ++=≠的 . (3)一元二次方程()2 00ax bx c a ++=≠的两根为21,x x ,则 . 自我检测3:不等式2 50ax x c ++>的解集为1 13 2x x ??<≠恒成立的充要条件是:0a >且2 40()b ac x -<∈R . (2)2 0(0)ax bx c a ++<≠恒成立的充要条件是:0a <且2 40()b ac x -<∈R . 一元二次方程(根与系数关系专题测试) 一、单选题(共10题;共30分) 1.已知x1,x2是方程x2﹣3x﹣2=0的两根,则x12+x22的值为() A. 5 B. 10 C. 11 D. 13 2.已知关于x的一元二次方程x2+5x﹣m=0的一个根是2,则另一个根是() A. ﹣7 B. 7 C. 3 D. ﹣3 3.一元二次方程x2-5x+6=0的两根分别是x1、x2,则x1+x2等于() A. 5 B. 6 C. -5 D. -6 4.是方程的两根, 的值是() A. 2017 B. 2018 C. 2019 D. 2020 5.关于x的方程有两个实数根,,且,那么m的值为() A. -1 B. -4 C. -4或1 D. -1或4 6.关于x的方程(为常数)根的情况下,下列结论中正确的是() A. 两个正根 B. 两个负根 C. 一个正根,一个负根 D. 无实数根 7.已知一元二次方程x2﹣4x+m=0有一个根为2,则另一根为() A. ﹣4 B. ﹣2 C. 4 D. 2 8.已知,是一元二次方程的两个实数根且,则的值为(). A. 0或1 B. 0 C. 1 D. -1 9.若α,β是方程x2﹣2x﹣3=0的两个实数根,则α2+β2+αβ的值为() A. 10 B. 9 C. 7 D. 5 10.若a≠b,且则的值为() A. B. 1 C. .4 D. 3 二、填空题(共6题;共18分) 11.如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么x1+x2=﹣, x1x2= ,这就是一元二次方程根与系数的关系(韦达定理).利用韦达定理解决下面问题:已知m与n是方程x2﹣5x﹣25=0的两根,则+ =________. 12.一元二次方程的两根为,则________ 怀文中学2014—2015学年度第一学期随堂练习 初 三 数 学(5.3二次函数与一元二次方程和不等式(1)) 设计:吴兵 审校:蔡应桃 班级__________ 学号___________ 姓名____________ 一、知识点 1.二次函数与一元二次方程之间的关系是通过 与 的交点来体现的:若抛物线0(2 ≠++=a c bx ax y )与x 轴的交点为(m ,0)、(n ,0),则对应的一元二次方程 02=++c bx ax 的两根为 . 一元二次方程根的情况对应决定着抛物线与x 轴的交点个数. (1)抛物线2 (0)y ax bx c a =++≠与x 轴有两个交点, 02 =+ +c bx ax ac b 42- 0; (2)抛物线2 (0)y ax bx c a =++≠与x 轴只有一个交点, 02 =++c bx ax ac b 42- 0; (3)抛物线2 (0)y ax bx c a =++≠与x 轴没有交点, 02 =++c bx ax ac b 42- 0. 2.抛物线与直线的交点: ①二次函数图象与x 轴及平行于x 轴的直线; ②二次函数图象与y 轴及平行于y 轴的直线; ③二次函数图象与其它直线(不平行于坐标轴,即一次函数图象). 3.根据示意图求一元二次不等式的解集. 二、典型例题 不画图象,你能判断函数 的图象与x 轴是否有公共点吗?请说明理由。 三、适应练习 1、方程 的根是 ;则函数 的图象与x 轴的交点有 个,其坐标是 . 2、方程 的根是 ;则函数 的图象与x 轴的 交点有 个,其坐标是 . 3、下列函数的图象中,与x 轴没有公共点的是( ) 62 -+=x x y 0542 =-+x x 025102=-+-x x 25102 -+-=x x y 542 -+=x x y 2)(2-=x y A x x y B -=2)(96)(2-+-=x x y C 2)(2+-=x x y D 九年级数学第十周拓展训练(部分习题选自《新思维》)(2017.11.5) 1.(永州)抛物线122-++=m x x y 与x 轴有两个不同的交点,则m 的取值范围是----( ) A .m <2 B .m >2 C .0<m≤2 D .m <﹣2 2.(陕西)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值,可判断该二次函数的图 ( ) x … 1- 0 1 2 … y … 1- 47- 2- 4 7- … A.只有一个交点 B.有两个交点,且它们分别在y 轴两侧 C.有两个交点,且它们均在y 轴同侧 D.无交点 3.(宜昌)已知抛物线122+-=x ax y 与x 轴没有交点,那么该抛物线的顶点所在的象限是------( ) A.第四象限 B.第三象限 C.第二象限 D.第一象限 4.(南宁)二次函数)0(2≠++=a c bx ax y 和正比例函数x y 3 2=的图象如图所示,则方程0)3 2(2=+-+c x b ax 的两根之和-------------------------------------------------------( ) A .大于0 B .等于0 C .小于0 D .不能确定 5.(安徽)如图,一次函数x y =1与二次函数c bx ax y ++=22的图象相交于P 、Q 两点,则函数 c x b ax y +-+=)1(2的图象可能为-----------------------------------------------------( ) 6.(绵阳)若)(,2121x x x x <是方程)(1))((b a b x a x <=--的两个根,则b a x x ,,,21的大小关系( ) A. b a x x <<<21 B. b x a x <<<21 C. 21x b a x <<< D. 21x b x a <<< 7.(泰安)二次函数bx ax y +=2 的图象如图所示,若一元二次方程02=++m bx ax 有实数根,则m 的最大值为-----------------------------------------------------------------------------( ) A.-3 B.3 C.-6 D.9 第4题 第5题 第7题 复系数方程的求解 知识点: 1.复系数方程的一般求解方法; 2.复系数方程与实系数方程解的关联性; 教学过程: 1.系数为复数的方程统称为复系数方程; 2.复系数方程的一般求解方程方法为待定系数法; 3.复系数一元二次方程的根满足韦达定理; 4.复系数一元n次方程有且仅有n个根(k重根按k个根记),此结论由高斯在1797年的博士论文中严格证明。并称为代数基本定理 ......。 例1.解关于x的方程: (1)2340 --= x i (2)2(1)0 -++= x i x i (3)2 i x i x i +----= (1)(1)260 (4)2(3)430 -+++= x i x i (5)22 -++--= 252(2)0 x x x x i 例2.设方程20x px k -+=有一个根是12i +。 (1)若p R ∈,求实数k 的值; (2)若4p =,求复数k 的值; 例3.解关于x 的方程(1)(1)0,n n x x n N +--=∈。 例4.设1,,x u vi u v R =+∈是关于x 的方程20,,ax ibx c a b R ++=∈的根,求方程的另一个根; 例5.设k R ∈,关于x 的方程2(2)20x k i x ki ++++=有实数解,求k 的值,并求方程的根。 例6.已知关于x 的方程222(1)(1)0a i x a i a i +++++=有实数解,求实数a 积方程的根。 例7.已知关于x 的方程09)6(2=+++-ai x i x ,a R ∈有实数根b 。 (1)求实数,a b 的值; (2)若复数z 满足02=---- z bi a z ,求z 为何值时,z 有最小值,并求出z 的值。 例8.关于x 的二次方程2120x z x z m +++=中,12,,z z m 均是复数,且i z z 20164221+=-. 设这个方程的两个根为α、β,且满足72||=-βα.求|m |的最大值和最小值。 一元二次方程练习题 1. 解下列方程:(1)2(1) 9x -=; (2)2(21)3x +=; (3)2(61)250x --=. (4)281(2)16x -=. 2. 用直接开平方法解下列方程: (1)25(21)180y -=; (2)21(31)644 x +=; (3)26(2) 1x +=; (4)2()(00)ax c b b a -=≠,≥ 3. 填空 (1)28x x ++( )=(x + )2.(2)223x x -+( )=(x - )2. (3)2b y y a -+( )=(y - )2. 4. 用适当的数(式)填空: 23x x -+ (x =- 2);2x px -+ =(x - 2) 23223(x x x +-=+ 2)+ . 5. 用配方法解方程. 23610x x --= 22540x x --= 6. 关于x 的方程22291240x a ab b ---=的根1x = ,2x = . 7. 用适当的方法解方程(1)23(1) 12x +=; (2)2410y y ++=; (3)2884x x -=; (4)2310y y ++=. (5) ()9322=-x ; (6)162=-x x ; 一元二次不等式 2.一元二次不等式20(0)ax bx c a ++>>与相应的函数2(0)y ax bx c a =++>、相应的方程20(0)ax bx c a ++=>之间 1、把二次项的系数变为正的。(如果是负,那么在不等式两边都乘以-1,把系数变为正) 2、解对应的一元二次方程。(先看能否因式分解,若不能,再看△,然后求根) 3、求解一元二次不等式。(根据一元二次方程的根及不等式的方向) 一元二次方程求解 一、一周知识概述 1、一元二次方程的求根公式 将一元二次方程ax2+bx+c=0(a≠0)进行配方,当b2-4ac≥0时的根为 . 该式称为一元二次方程的求根公式,用求根公式解一元二次方程的方法称为求根公式法,简称公式法. 说明:(1)一元二次方程的公式的推导过程,就是用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0); (2)由求根公式可知,一元二次方程的根是由系数a、b、c的值决定的; (3)应用求根公式可解任何一个有解的一元二次方程,但应用时必须先将其化为一般形式. 2、一元二次方程的根的判别式 (1)当b2-4ac>0时,方程有两个不相等的实数根; (2)当b2-4ac=0时,方程有两个相等的实数根; (3)当b2-4ac<0时,方程没有实数根. 二、重难点知识 1、对于一元二次方程的各种解法是重点,难点是对各种方法的选择,突破这一难点的关键是在对四种方法都会使用的基础上,熟悉各种方法的优缺点。 (1) “开平方法”一般解形如“”类型的题目,如果用“公式 法”就显得多余的了。 (2)“因式分解法”是一种常用的方法,一般是首先考虑的方法。 (3) “配方法”是一种非常重要的方法,一般不使用,但若能恰当地使用,往往能起到简化作用,思考于“因式分解法”之后,“公式法”之前。如方程;用因式分解,则6391这个数太大,不易分解;用公式法,也太繁;若配方,则方程化为,就易解,若一次项系数中有偶因数,一般也应考虑运用。 (4)“公式法”是一般方法,只要明确了二次项系数、一次项系数及常数项,若方 程有实根,就一定可以用求根公式求出根,但因为要代入(≥0)求值,所以对某些特殊方程,解法又显得复杂了。 2、在运用b2-4ac的符号判断方程的根的情况时,应注意以下三点: (1)b2-4ac是一元二次方程的判别式,即只有确认方程为一元二次方程时,才能确定a、b、c,求出b2-4ac; (2)在运用上述结论时,必须先将方程化为一般形式,以便确认a、b、c; (3)根的判别式是指b2-4ac,而不是 三、典型例题讲解 例1、解下列方程: (1); (2); (3). 分析:用求根公式法解一元二次方程的关键是找出a、b、c的值,再代入公式计算, 典型例题一 例 求证:如果关于x 的方程922+=+m x x 没有实数根,那么,关于y 的方程0522=+-+m my y 一定有两个不相等的实数根. 分析:由已知,可根据一元二次方程的根的判别式证之. 证明 设方程922+=+m x x 即0922=--+m x x 的根的判别式为1?,方程 0522=+-+m my y 的根的判别式为2?,则 . 36)4( 208)25(4. 440)9(42222221-+=-+=--=?+=++=?m m m m m m m ∵方程922+=+m x x 无实数根, 01+∴m ,即036)4(2>-+m . 故方程0522=+-+m my y 有两个不相等的实数根. 说明:上述证明中,判定02>?用到了01 分析:运用根的判别式判定根的情况时,要首先把方程变形为一元二次方程的一般形式,然后从求出的判别式的值来判定根的判别式的符号,尤其是当方程系数中含有字母时,一般利用配方法将“?”化成完全平方式或完全平方式加上(或减去)一个常数,再根据完全平方式的非负性判断“?”的符号,从而判定方程的根的情况,有时还需要对字母进行讨论.这是不解方程判别根的情况的关键. 解:(1)),1(4,2,1-=-==k c k b a )1(414)2(422-??--=-=?∴k k ac b )2(4)44(416 16422 2≥-=+-=+-=k k k k k ∴方程有两个实数根. (2)0≠a , ∴方程02=+bx ax 是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项,将常数项看作零. ∴2204b a b =?-=?. ∴不论b 取任何实数,2b 均为非负数, 02≥=?b 恒成立. ∴方程有两个实数根. (3)0≠a , ∴方程02=+c ax 是缺少一次项的不完全的一元二次方程,它的一次项系数0=b . ac a 40402-=?-=?, ∴需要讨论a 、c 的符号,才能确定?的符号. 当0=c 时,0=?,方程有两个相等的实数根; 当a 、c 异号时,0>?,方程有两个不相等的实数根; 当a 、c 同号时,0 二次方程根的分布与二次函数在闭区间上的最值归纳 1、一元二次方程02 =++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=, 方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件) 表一:(两根与0的大小比较即根的正负情况) a 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧 12,x m x n <>,(图形分别如下)需满足的条件是 (1)0a >时,()()00f m f n ???>?? 对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况: 若()0f m =或()0f n =,则此时()()0f m f n 第4节从函数的观点看一元二次方程和 一元二次不等式 知识梳理 1.一元二次不等式 只含有一个未知数,并且未知数的最高次数为2的整式不等式叫作一元二次不等式. 2.三个“二次”间的关系 判别式Δ=b2-4ac Δ>0Δ=0Δ<0 二次函数 y=ax2+bx+c (a>0)的图象 一元二次方程ax2+bx+c=0 (a>0)的根有两相异实根x1, x2(x1<x2) 有两相等实根x1= x2=- b 2a 没有实数根 ax2+bx+c>0 (a>0)的解集{x|x>x2 或x<x1}?? ? ? ? ? x|x≠- b 2a R ax2+bx+c<0 (a>0)的解集 {x|x1<x<x2}??3.(x-a)(x-b)>0或(x-a)(x-b)<0型不等式的解集 不等式 解集 ab (x-a)·(x-b)>0{x|x (1)f (x ) g (x )>0(<0)?f (x )·g (x )>0(<0). (2)f (x ) g (x )≥0(≤0)?f (x )·g (x )≥0(≤0)且g (x )≠0. [微点提醒] 1.绝对值不等式|x |>a (a >0)的解集为(-∞,-a )∪(a ,+∞);|x |0)的解集为(-a ,a ). 记忆口诀:大于号取两边,小于号取中间. 2.解不等式ax 2+bx +c >0(<0)时不要忘记当a =0时的情形. 3.不等式ax 2+bx +c >0(<0)恒成立的条件要结合其对应的函数图象决定. (1)不等式ax 2+bx +c >0对任意实数x 恒成立????a =b =0,c >0或???a >0,Δ<0. (2)不等式ax 2 +bx +c <0对任意实数x 恒成立????a =b =0,c <0或???a <0, Δ<0. 基 础 自 测 1.判断下列结论正误(在括号内打“√”或“×”) (1)若不等式ax 2+bx +c >0的解集是(-∞,x 1)∪(x 2,+∞),则方程ax 2+bx +c =0的两个根是x 1和x 2.( ) (2)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( ) (3)不等式x 2≤a 的解集为[-a ,a ].( ) (4)若方程ax 2+bx +c =0(a <0)没有实数根,则不等式ax 2+bx +c >0(a <0)的解集为R .( ) 解析 (3)错误.对于不等式x 2≤a ,当a >0时,其解集为[-a ,a ];当a =0时,其解集为{0},当a <0时,其解集为?. (4)若方程ax 2+bx +c =0(a <0)没有实根,则不等式ax 2+bx +c >0(a <0)的解集为?. 答案 (1)√ (2)√ (3)× (4)× 2.(必修5P103A2改编)已知集合 A =???? ?? x ???12x -1≤0,B ={x |x 2-x -6<0},则A ∩B 一元二次方程和不等式 1. 如图,抛物线从 c bx ax y ++=2与x 轴交于点A (1,0),B (3,0),则 (1) a 0, b 0, c 0; (2) 方程02=++c bx ax 的解集为 ; (3) 不等式02>++c bx ax 的解集为 ; (4) 不等式02<++c bx ax 的解集为 ; 2. 如图,是二次函数 c bx ax y ++=21和一次函数n mx y +=2的图象, (1) n x c bx ax +=++m 2的解为 ; (2) 不等式n x c bx ax +>++m 2的解集为 ; (3) 不等式n x c bx ax +<++m 2的解集为 ; 3. 解一元二次不等式 (1) 解不等式0342<+-x x (2) 已知二次函数21x y -=与一次函数432--=x y 交于A 、B 两点 a 、 求A 、B 两点的坐标; b 、判断x 为何值时,21 y y < 4、抛物线c bx ax y ++=2分别交坐标轴于A (-2,0),B (6,0),C (0,4),则402<++≤c bx ax 的解集是 。 y y 2y 1 根与系数关系(一) 基本问题:直线与抛物线相交所截线段长度可用根与系数关系得到。 例1:基本图形,抛物线所截弦长。如图,直线1+=x y 与m m mx x y ++-=222交于A ,B 两点(A 在B 左边)。求证无论m 为任何值,AB 的长总为定值。 例2:(线段和差)如图,抛物线342+-=x x y 与x 轴交于A ,B 两点,与y 轴交于点C ,将直线BC 向上平移交抛物线于M ,N ,交y 轴于点P ,求PM-PN 的 值。 例3:(线段乘积)如图,已知直线k kx 9y -=(k<0)与抛物线322 --=x x y 交于A,B 两点,与x 轴交于点P ,过点A 做AC ⊥x 轴于点C ,过点B 做BD ⊥x 轴于点D ,求证:PC PD ? 为定值。 例4.抛物线L :y =-x 2+bx +c 经过点A (0,1),与它的对称轴直线x =1交于点B (1) 直接写出抛物线L 的解析式 (2) 如图1,过定点的直线y =kx -k +4(k <0)与抛物线L 交于点M 、N .若 △BMN 的面积等于1,求k 的值 一元二次方程根的两个特性及简单运用 我们知道方程的解是由方程的系数(包括常数项)决定的。因此,一元二次方程的根与其系数有着密切的联系。教材中我们探索了一元二次方程的二次项系数为1的情况下的两根之和、两根之积与系数的关系。现在我们接着来探索一般形式下的一元二次方程20(0) ax bx c a ++=≠的两根之和、两根之积与系数的关系。 例1、先阅读,再填空解题: (1)方程:x2-4x-12=0 的根是:x 1=6, x 2 =-2,则x 1 +x 2 =4,x 1 ·x 2 =-12; (2)方程2x2-7x+3=0的根是:x 1= 1 2 , x 2 =3,则x 1 +x 2 = 7 2 ,x 1 ·x 2 = 3 2 ; (3)方程3x2+6x-2=0的根是:x 1= , x 2 = .则x 1 +x 2 = , x 1·x 2 = ; 根据以上(1)(2)(3)你能否猜出:如果关于x的一元二次方程ax2+bx+c=0 (a≠0且a、b、c为常数)的两根为x 1、x 2 ,那么x 1 +x 2 、x 1 x 2 与系数a、b、c有 什么关系?请写出来你的猜想并说明理由。 解析:方程3x2+5x-2=0的根是:x 1= 1 3 x 2 =-2。则x 1 +x 2 = 5 3 -,x1·x2= 2 3 -。 能猜出:如果关于x的一元二次方程ax2+bx+c=0(a≠0且a、b、c为常数) 的两根为x 1、x 2 ,那么x 1 +x 2 a b - =、x1x2 a c =。理由如下: 根据求根公式可知,关于x的一元二次方程ax2+bx+c=0(a≠0且a、b、c 为常数)的两根为: a ac b b x 2 4 2 1 - + - =, a ac b b x 2 4 2 2 - - - = 所以x 1+x 2 = a ac b b 2 4 2- + - + a ac b b 2 4 2- - - a b - = x 1x 2 = a ac b b 2 4 2- + - · a ac b b 2 4 2- - - a c = 也就是说,对于任何一个有实数根的一元二次方程,这个方程的两个根与系数的关系是:两根之和,等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积,等于常数项除以二次项系数所得的商. 《一元二次方程的解法》规律总结 1.一元二次方程的解法 (1)直接开平方法:根据平方根的意义,用此法可解出形如a x 2=(a ≥0), b )a x (2=-(b ≥0)类的一元二次方程.a x 2=,则a x ±=;b )a x (2=-,b a x ±=-,b a x +=.对有些一元二次方程,本身不是上述两种形式,但可以化为a x 2=或b )a x (2 =-的形式,也可以用此法解. (2)因式分解法:当一元二次方程的一边为零,而另一边易分解成两个一次因式的积时,就可用此法来解.要清楚使乘积ab =0的条件是a =0或b =0,使方程x(x -3)=0的条件是x =0或x -3=0.x 的两个值都可以使方程成立,所以方程x(x -3)=0有两个根,而不是一个根. (3)配方法:任何一个形如bx x 2 +的二次式,都可以通过加一次项系数一半的平方的方法配成一个二项式的完全平方,把方程归结为能用直接开平方法来解 的方程.如解07x 6x 2=++时,可把方程化为7x 6x 2-=+,2 2226726x 6x ??? ??+-=??? ??++,即2)3x (2=+,从而得解. 注意:(1)“方程两边各加上一次项系数一半平方”的前提是方程的二次项系数是1. (2)解一元二次方程时,一般不用此法,掌握这种配方法是重点. (3)公式法:一元二次方程0c bx ax 2=++(a ≠0)的根是由方程的系数a 、b 、 c 确定的.在0ac 4b 2≥-的前提下,a 2ac 4b b x 2-±-=.用公式法解一元二次方 程的一般步骤: ①先把方程化为一般形式,即0c bx ax 2 =++(a ≠0)的形式; ②正确地确定方程各项的系数a 、b 、c 的值(要注意它们的符号); ③计算0ac 4b 2<-时,方程没有实数根,就不必解了(因负数开平方无意义); ④将a 、b 、c 的值代入求根公式,求出方程的两个根. 说明:象直接开平方法、因式分解法只是适宜于特殊形式的方程,而公式法则是最普遍,最适用的方法.解题时要根据方程的特征灵活选用方法. 2.一元二次方程根的判别式 一元二次方程的根有三种情况:①有两个不相等的实数根;②有两个相等的 实数根;③没有实数根.而根的情况,由ac 4b 2-的值来确定.因此ac 4b 2-=?叫做一元二次方程0c bx ax 2 =++的根的判别式. △>0?方程有两个不相等的实数根. △=0?方程有两个相等的实数根. △<0?方程没有实数根. 方程与不等式之一元二次方程技巧及练习题 一、选择题 1.已知x 1、x 2是关于x 的方程x 2﹣ax ﹣2=0的两根,下列结论一定正确的是( ) A .x 1≠x 2 B .x 1+x 2>0 C .x 1?x 2>0 D .x 1<0,x 2<0 【答案】A 【解析】 分析:A 、根据方程的系数结合根的判别式,可得出△>0,由此即可得出x 1≠x 2,结论A 正确; B 、根据根与系数的关系可得出x 1+x 2=a ,结合a 的值不确定,可得出B 结论不一定正确; C 、根据根与系数的关系可得出x 1?x 2=﹣2,结论C 错误; D 、由x 1?x 2=﹣2,可得出x 1<0,x 2>0,结论D 错误. 综上即可得出结论. 详解:A ∵△=(﹣a )2﹣4×1×(﹣2)=a 2+8>0, ∴x 1≠x 2,结论A 正确; B 、∵x 1、x 2是关于x 的方程x 2﹣ax ﹣2=0的两根, ∴x 1+x 2=a , ∵a 的值不确定, ∴B 结论不一定正确; C 、∵x 1、x 2是关于x 的方程x 2﹣ax ﹣2=0的两根, ∴x 1?x 2=﹣2,结论C 错误; D 、∵x 1?x 2=﹣2, ∴x 1<0,x 2>0,结论D 错误. 故选A . 点睛:本题考查了根的判别式以及根与系数的关系,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键. 2.从4-,2-,1-,0,1,2,4,6这八个数中,随机抽一个数,记为a .若数a 使关于x 的一元二次方程()22 240x a x a --+=有实数解.且关于y 的分式方程1311y a y y +-=--有整数解,则符合条件的a 的值的和是( ) A .6- B .4- C .2- D .2 【答案】C 【解析】 【分析】 由一元二次方程()22240x a x a --+=有实数解,确定a 的取值范围,由分式方程1311y a y y +-=--有整数解,确定a 的值即可判断. 【详解】一元二次方程根的分布情况归纳总结
2.3.1 二次函数与一元二次方程、不等式(第一课时)导学案
一元二次方程(根与系数关系)
二次函数与一元二次方程和不等式教学提纲
二次函数与一元二次方程不等式之间的关系
复系数一元二次方程求解
解一元二次方程及一元二次不等式练习题 -
一元二次方程求根公式
一元二次方程根的差别式
一元二次方程根的分布情况归纳(完整版)
第4节 从函数的观点看一元二次方程和一元二次不等式
一元二次方程和不等式
一元二次方程根的两个特性及简单运用
《一元二次方程的解法》规律总结
方程与不等式之一元二次方程技巧及练习题