
62
第六讲 向量代数与空间解析几何(数一)
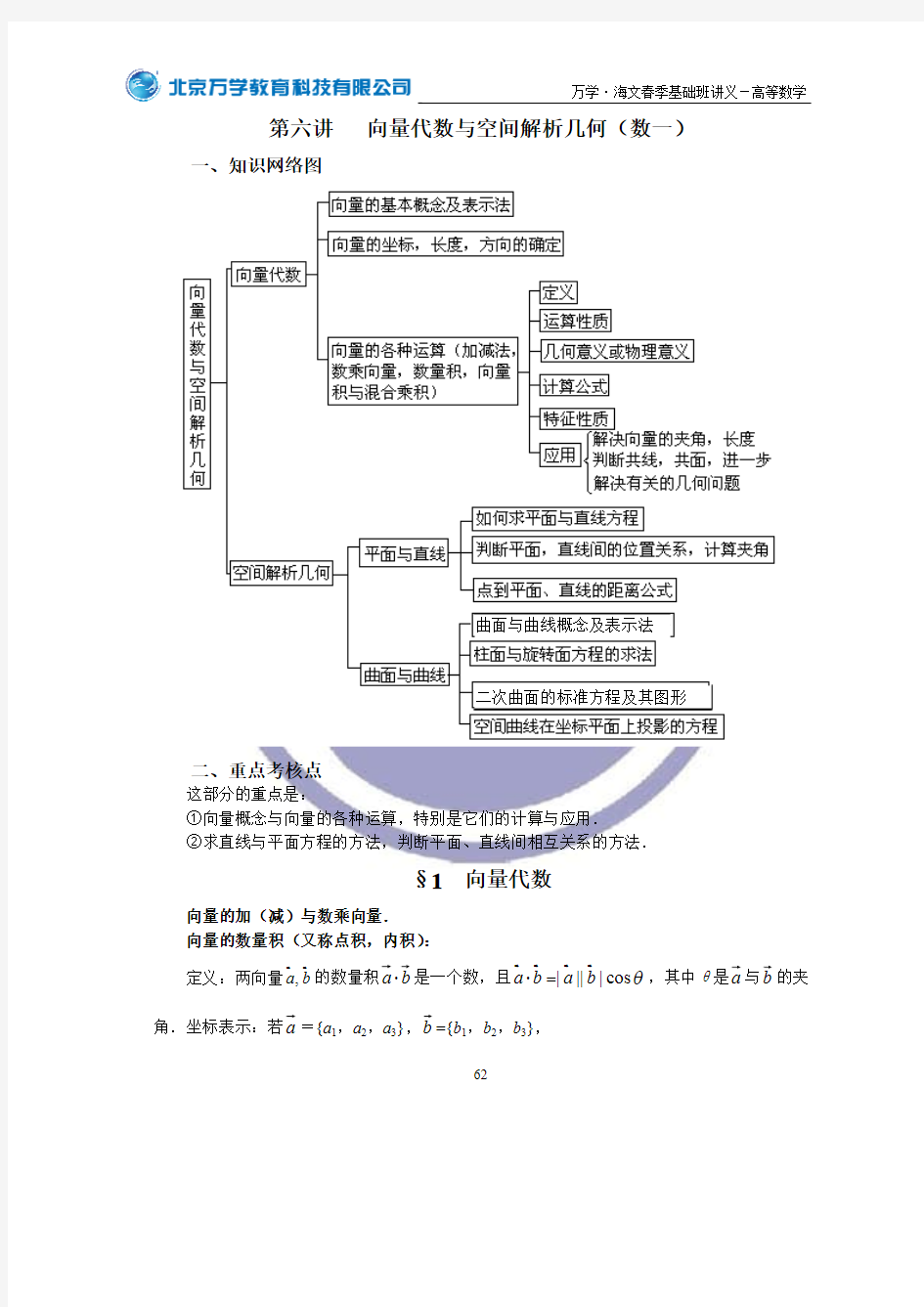
一、知识网络图
二、重点考核点
这部分的重点是:
①向量概念与向量的各种运算,特别是它们的计算与应用.
②求直线与平面方程的方法,判断平面、直线间相互关系的方法.
§1 向量代数
向量的加(减)与数乘向量. 向量的数量积(又称点积,内积):
定义:两向量,a b
的数量积?是一个数,且||||cos a b a b θ=? ,其中θ是与的夹角.坐标表示:若={a 1,a 2,a 3},={b 1,b 2,b 3},
曲面与曲线概念及表示法
二次曲面的标准方程及其图形
63
则·=a 1b 1+a 2b 2+a 3b 3.
特征性质:a ⊥b ?a ·b =0,即a 1b 1+a 2b 2+a 3b 3 = 0 主要应用:
①判定两向量垂直;
②求两向量、两直线、两平面以及直线与平面间的夹角; ③建立平面的点法式方程.
向量的向量积(又称叉积,外积):
定义:两向量,a b
的向量积×是一个向量,其模θsin ||||||=×,其中θ是与
的夹角,又×同时与和都垂直且、、×构成右手系.
坐标表示:若a ={a 1,a 2,a 3},b ={b 1,b 2,b 3},则
a ×
b =3
2
1321
b b b a a a k
j i
特征性质://0a b a b ?×=
.
主要应用:
①判定两向量平行;
②求平行四边形面积,求点到直线的距离;
③求两平面交线的方向向量,化直线的一般方程为标准方程. 向量的混合积:
定义:三向量a ,b ,c 的混合积[a ,b ,c ]是一个数,且[a ,b ,c ]=(a ×
)·.
坐标表示:若a ={a 1,a 2,a 3},b ={b 1,b 2,b 3},c ={c 1,c 2,c 3}则
[a ,b ,c ]=3
2
1
32
1
321
c c c b b b a a a 特征性质:a ,b ,c 共面?[a ,b ,c ]= 0 主要应用:
①判定三向量或四个点共面,建立平面方程;
②求平行六面体的体积,求点到平面或两条异面直线间的距离; ③建立异面直线公垂线的方程.
【例1】设(a ×b )·c =2,则[(a +b )×(b +c )]·(c +a )=________.
【解】
64
【例2】||a =2,||b =2,a ·b =2,则||b a ×=________. 【解】
【例3】指出下列等式成立的充要条件,并证明: (1)||||b a b a ?=+;
(2)+与?共线,其中,0b ≠
.
【证明】(1)||||b a b a ?=+?(+)·(+)=(?)·(?)
?2222
22a a b b a a b b ++=?+??? a ·b = 0
? a ⊥b (2)a +b 与b a ?平行?(a +b )×(b a ?)=θ?b ×a -a ×b =θ?a ×b =
θ ? a 与b 平行.
§2 平面与直线
【例1】过直线L 1:13
0211??=
?=?z y x 且平行于直线L 2:1
1122z y x =?=+的平面方程是________.
【解】
65
【例2】过点(1,2,1)?且与直线??
?
???=?=+?=1432t z t y t x 垂直的平面方程是________.
【解】
【例3】设直线L 为??
?=+??=+++0
31020
123z y x z y x ,平面Π为4x -2y + z -2 = 0,则( ).
(A )L ∥Π (B )L 在Π上 (C )L ⊥Π (D )L 与Π斜交
【分析】
【例4】已知直线L在平面Π:x + y + z -1 = 0上,并且与直线??
?
??=+?=+=t z t y t x L 110垂直相交,
求L 的方程.
【分析与解法】1)将L 0的参数方程代入平面Π的方程,得
(t + 1)+(-t + 1)+ t -1 = 0,t = -1
?L0与Π的交点M0(0,2,-1),它就是L与Π的交点.
2)L 0的方向向量0l =(1,-1,1),平面Π的法向量n =(1,1,1),L的方向向量l
∥n × 0l
×n 0l 1
11(2,02)//(1,0,1)111
i j k
==???
3)L 即是过M0以l
为方向向量的直线
1
1
021?+=?=z y x
另解 若用两面式更简单.过M0与L0垂直的平面是 (2)(1)0x y z ??++=,即x -y + z + 3=0
L 为交线??
?=?++=++?0
10
3z y x z y x
66
§3 曲面方程
【例1】 求①直线L:
1
1
111??=
=?z y x 在平面Π:x -y + 2z -1=0上的投影L0的方程.②直线L0绕y 轴旋转一周而成的曲面方程.
【分析与求解】①求L0即求过L与平面Π垂直的平面Π1与Π的交线.
平面Π1由点0(1,0,1)M 及与之平行的向量(1,1,1)l =? 与(1,1,2)n =?
所确定.方程为
02
1
1
1111
1
=????z y x 即 x -3y -2z + 1 = 0 L 0的方程为?
?
??=??=+?1231
2z y x z y x
②为求L0绕y 轴旋转的旋转面方程,先把L0的交面式方程化为以y 为参数的方程.
????????===)
1(21
2y z y y y x 按参数式表示的旋转面方程得????
?
?????+==?+=θθsin ))1(21()2(cos ))1(21()2(2222y y z y y y y x
消去θ得 22
2
2
)1(4
1
4y y z x ?+
=+ 即 2224174210x y z y +++?= 【评注】转参数来旋曲面用方程描述是方便的.
求一条直线L绕某坐标轴旋转产生的旋转面方程,如绕y 轴,先将L写成以y 为参数的方程.
???
??+==+=d cy z y
y b
ay x 旋转面的参数方程???????+==+=θ
θsin )()(cos )()(2
222y z y x z y y y z y x x 消去θ得旋转面方程
2222()()x z ay b cy d +=+++
【例2】求直线L:1,x y z ==绕z 轴旋转一周所生成的旋转面方程.
67
【解】直线L的参数方程是?????===z
z z y x 1,旋转面的参数方程是???
??
??=+=+=z z z y z x θθ
sin 1cos 12
2
消去θ得旋转面方程 x 2 + y 2 = 1 + z 2
§4 空间曲线在坐标面上的投影曲线
【例1】求曲线C :???=++=++1
1
222z y x z y x 在xy 平面上的投影曲线的方程.
【解】投影曲线的方程是
???==??++0
1)1(222z y x y x
68
第七讲 常微分方程
一、知识网络图
二、重点考核点
①掌握方程类型的判别,根据类型选择合适的方法求解方程,会利用初值条件定出任意常数。
69
②掌握列方程的常用方法.根据题意,分析条件,搞清问题所涉及的物理或几何意义,结合其他相关的知识和掌握的方法列出方程和初条件. ③一、二阶线性方程解的性质.
④对数三还要求差分方程,其重点是求解一阶线性差分方程与简单的经济应用. (注意,全微分方程的求解放在多元积分学部分介绍)
§1 微分方程的有关基本概念
微分方程:含有自变量,未知函数以及未知函数的导数(或微分)的函数方程,称为微
分方程.当方程中的未知函数是一元函数时,称为常微分方程.
微分方程的阶:出现在微分方程中的未知函数的最高阶导数或微分的阶数称为微分方程的阶.
设x 为自变量,()y y x =为未知函数,则n 阶微分方程的一般形式为 F (x ,y ,()
,,,n y y y
′′′ )= 0,
且在方程中)
(n y 一定要出现.
微分方程的解:若把已知函数及其导数或微分代入微分方程后能使其成为恒等式,则称该函数为这个微分方程的一个解.含有与方程阶数相同个数的独立任意常数的解,称为微分方程的通解;不含任意常数的解称为微分方程的特解.
为了确定微分方程的特解,需要给出方程中未知函数应满足的附加条件,这种条件称为定解条件,通常给出的是未知函数及其若干阶导数在某点处的值,称为初始条件. 例如:对方程F (x ,y ,()
,,,n y y y
′′′ )= 0,初始条件可设为
,,,
,,10)
1(201000)()()()(??==′′=′=n n y x y y x y y x y y x y
其中x 0,y 0,y 1,y 2,…,y n -1都是给定的常数.
求微分方程满足初始条件的特解的问题称为初值问题.
§2 一阶微分方程的解法
(1)变量可分离方程 变量可分离方程的常见形式是
)()(d d y g x f x
y
=, 若()0g y ≠,方程可改写为
x x f y g y d )()(d =, 求积分即得通解∫∫
=x x f y g y
d )()(d . 若存在y 0使g (y 0)=0,直接验算可知常值函数y = y 0也是原方程的一个解.
更一般的变量可分离方程是0d )()(d )()(=+y y Q x N x y P x M . 当0)()(≠y P x N 时,经分离变量,方程可改写成
0d )()(d )()(=+x x N x M y y P y Q ,于是,积分可得通解∫∫=+C x x N x M y y P y Q d )
()
(d )()(.
70
若0y 是函数()P y 的一个零点,则0y y =也是方程的一个解.如果不限定自变量是x ,未知函数是y ,且x 0是函数()N x 的一个零点,则常值函数0x x =也是方程的一个解.在求解变量可分离的方程时,注意不要遗漏了这类常值函数解.如果在积分所得的通解表达式里,未知函数包含在对数中,应尽可能通过恒等变形把未知函数从对数中“解脱”出来. (2)齐次微分方程 齐次微分方程的标准形式是
)(d d x
y f x y =, 作变换,ux y x y
u =?=由于d y = u d x +x d u ,
代入方程可得u u f x u
x u f x u x u ?=?=+)(d d )(d d ,这是关于u 与x 的可分离变量方程.当
()0f u u ?≠时,分离变量并积分可得ln ()du x C f u u
=+?∫
. 把u 换回y
x ,即得原方程的
通解.同样,若存在0u u =是()0f u u ?=的根,则0y u x =也是原方程的一个解. (3)一阶线性微分方程
一阶线性方程的标准形式是)()(x Q y x P y =+′,其中()P x 与()Q x 是已知函数.当
()0Q x ≡时,称为一阶齐次线性方程,否则称为一阶非齐次线性方程.一阶线性方程的通解
为()d ()d ()d e
e ()e d p x x
p x x
p x x
y C Q x x ??∫
∫
∫
=+∫.
注意,通解公式中的第一项∫?x
x p C d )(e 是对应齐次线性方程0)(=+′y x P y 的通解,通
解公式中的第二项()d ()e
()e d p x x
p x dx
Q x x ?∫∫∫
是非齐次线性方程的一个特解.一阶线性方程通解的这种结构是所有线性微分方程通解的共同特点.
除了直接用上述通解公式求解外,还可用积分因子法求解.即用函数∫
x
x p d )(e (称为方程
的积分因子)同乘方程两端,按乘积的导数公式有 ()d ()d (e )()e p x x
p x x y Q x ∫∫′=,两端再积分
一次,移项后就得出了通解公式.
【例1】已知函数()y x 在任意点x 处的增量α++Δ=
Δ2
1x x
y y ,且当0→Δx 时,α是比x Δ较高阶的无穷小,(0)y π=,则(1)y =( )
(A )2π. (B )π. (C )4
πe . (D )4
ππe .
71
【例2】设函数()y x 连续,求解方程:
∫
=+
x
x x y s s y 0
2)(2
1
d )(. 【解】实质上()y x 可导.求导得 x x y x y 2)(2
1
)(=′+
又原方程中令x = 0得y (0)=0. 求解初值问题 ??
?==+′0
)0(42y x y y 两边乘x x 2d 2e e ==∫μ,得 x
x x y 22e 4)e (=′
积分得C x C x x y x x x x
+?=+=∫2222e e 2d e 4e
由(0)01y C =?=.x
e
x y 212?+?=
【例3】设函数()f x 在[)1,+∞连续,且满足 ∫
?=x
f x f x t t f 1
22)]1()([3
1
d )(.
求函数()f x . 【解】实质上()f x 可导,求导得)]()(2[3
1
)(22
x f x x xf x f ′+=
原方程中令x = 1, 得0 = 0自然成立,不必另加条件.求解方程y x xy y ′+=2
2
23(其中()y f x =)得
()y f x ==
常数为?+C Cx
x
,13
. §3 二阶常系数线性微分方程及其解法
二阶常系数线性微分方程的标准形式为)(x f by y a y =+′+′′,其中a ,b 是已知常数,右端项()f x 是已知函数.当()0f x ≡时,方程称为齐次的,否则,方程称为非齐次的. 引入记号by y a y y L +′+′′=][,则方程)(][)(x f y L x f by y a y ==+′+′′可写成. 二阶常系数线性微分方程的解满足叠加原理:若y 1是方程11[]()L y f x =的一个解,y 2是方程22[]()L y f x =的一个解,A ,B 是两个常数,则Ay 1 + By 2就是方程12[]()()L y Af x Bf x =+的一个解.
二阶常系数线性微分方程通解结构定理:方程[]()L y f x =的通解是
y = C 1 y 1 + C 2y 2 + y *.
其中y 1和y 2是对应齐次方程L [y ] = 0两个线性无关的解,即L [y 1]≡0和L [y 2]≡0,且不存在常数k 使得y 1≡ky 2,y *是非齐次方程的一个解,即[]()L y f x ?
=,而C 1,C 2是两个任意常数.
(1)齐次方程两个线性无关解的求法:二次方程02
=++b a λλ称为二阶常数系线性微分方
72
程)(x f by y a y =+′+′′的特征方程,它的两个根12,λλ称为特征根.按照特征根的不同情况,可得齐次方程0=+′+′′b y a y 两个线性无关的解,如下表.
特征根 线性无关二解
实根21λλ≠ x x ,21e e λλ 实根21λλ= x x x 11e ,e λλ
复根)0>(ββαi ±
cos ,sin x x e x e x ααββ
(2)非齐次方程一个特解的求法:当()f x 是多项式,指数函数,正弦函数,余弦函数以及它们的和与乘积时,可根据()f x 的形式选取适当形式的特解,然后代入非齐次方程并确定特解中的待定系数,即可求得所需的一个特解.若rx
m e x P x f )()(=,其中()m P x 是一个x 的m 次多项式,r 是一个实数,则可按照下表选取特解:(其中()m Q x 是系数待定的m 次多项式)
()f x
r 与特征根1λ,2λ的关系 特解y *的形式
rx m x P e )( r ≠1λ,r ≠2λ rx m x Q e )( rx m x P e )(
r =1λ,r ≠2λ rx m x xQ e )(
rx m x P e )( r =1λ,r =2λ
rx m x Q x e )(2
若非齐次项()()m f x P x =,只需把它看成rx
m x P x f e )()(=,且r = 0的特殊情形即可.若
)sin cos (e )(x N x M x f rx ωω+=,其中M,N,r ,ω都是实数,且ω>0.特解的取法如
下表:(其中A ,B 是两个待定的常数)
()f x ωi r ±与特征值的关系 特解y *的形式
)sin cos (e x N x M rx ωω+ωi r ±不是特征根 )sin cos (e x B x A rx ωω+ )sin cos (e x N x M rx ωω+
ωi r ±是特征根
)
sin cos (e x B x A x rx ωω+ 若非齐次项()cos sin f x M x N x ωω=+,只需把它看成是)sin cos (e )(x N x M x f rx
ωω+=,且r = 0的特殊情形即可.另外,无论系数M与N中是否有等于零的,在特解y *中仍应当假设包含两个待定系数A 与B .
【例1】设线性无关的函数y 1,y 2,y 3都是微分方程)()()(x f y x q y x p y =+′+′′的解,其中()p x ,()q x , ()f x 是连续的,且C 1和C 2是任意常数,则此方程的通解是y =( ). (A )C 1y 1 + C 2y 2+y 3. (B )C 1y 1 + C 2y 2-(C 1 + C 2)y 3.
(C )C 1y 1 + C 2y 2-(1-C 1-C 2)y 3. (D )C 1y 1 + C 2y 2 +(1-C 1-C 2)y 3.
73
【例2】设x c by y a y e =+′+′′有一个特解为x x
x y e )1(e 2++=,求常数a ,b ,c 的值及
此方程的通解.
【例3】微分方程x x y y sin 12
++=+′′的特解形式可设为 (A )y * = ax 2 + bx + c + x (A sinx + Bcosx ). (B )y * = x (ax 2 + bx + c + A sinx + Bcosx ). (C )y * = ax 2 + bx + c + Asinx . (D )y * = ax 2 + bx + c + Acosx . 【例4】设∫
??
=x
dt t f t x x x f 0
)()(sin )(,其中()f x 连续.求()f x .
【分析与求解】1)化为求解常微分方程的初值问题,事实上()f x 可导.先将方程写成 ∫
∫+?=x
x
dt t tf dt t x x x f 0
)()(sin )( ①
两边求导得 ∫
+??
=′x
x xf x xf dt t f x x f 0
)()()(cos )(
即 t t f x x f x
d )(cos )(0
∫
?
=′ ②
在①式中令x = 0得(0)0f = ③ 求解①转化为求解② + ③
再将②求导得)(sin )(x f x x f ??=′′ ④ 在②中令x = 0得1)0(=′f ⑤ 求解② + ③又转化为求解④ + ③ + ⑤ 2)求解初值问题.
令()y f x =,求解①转化为求解二阶线性常系数方程的初值问题:
?
?
?=′=?=+′′1)0(,0)0(sin y y x
y y 特征方程012
=+λ,特征根λ=±i ,相应齐次方程的通解
74
y =1c cos x +2c sin x 再求原非齐次方程的如下特解(cos sin )y x A x B x ?
=+
记y =A cos x + B sin x ,
于是y *=x y ,且无论系数A ,B 取何值,其中的函数y =A cos x + B sin x 都满足对应的齐次方程.计算可得
,2)(,)(**y y x y y y x y ′+′′=′′+′=′?y y y y x y y ′=′++′′=+′′22)()(*
*.
代入方程就有 x x B x A y sin )cos sin (22?=+?=′,
由此可得02
1==
B A 于是原方程的通解为x x x c x c y cos 21
sin cos 21++=
由初条件(0)0y =,121(0)102
y c c ′== ,=定出.因此求得x x x x f y cos 21
sin 21)(+==
§4 某些高阶微分方程
§5 应用问题
一、利用定积分的几何意义列方程
【例1】设()y f x =是第一象限内连接()()0,1,1,0A B 的一段连续曲线,(,)M x y 为该曲线上任意一点,C 为M 在x 轴上的投影,O 为坐标原点,若梯形OCMA 的面积与曲边三角
形CBM 的面积之和为
3
1
63+x ,求()f x 的表达式. 【分析与求解】(见右图)
1)列方程,定附加条件,按题意
[]311
1()()263
x x x f x f t dt ++=+∫ ①
并有
(0)1f = ② (1)0f = ③ 2)转化,将①求导并化简得 ])10((1
)(1)(,x x
x x f x x f ∈?=?
′ ④ 在①中令x = 1?(1)0f =与③一致. 3)求解④并满足②与③.
75
解一阶线方程④并定常数得2()(1)f x x =? (0≤x ≤1).
【例2】设函数()f x 区间[1,+ ∞]上连续,由曲线()y f x =与直线x = 1,x = t (t >1)及x 轴围成的平面图形绕x 轴旋一周所得旋转体的体积为)]1()([3
π)(2
f t f t t V ?=求: (1)()y f x =所满足的微分方程;
(2)该微分方程满足条件9
2
2
=
=x y
的解. 【解】(1)()V t 的积分表达式是
21
()()d t V t f x x π=∫,按题意得221
()d [()(1)]3
t
f x x t f t f ππ=
?∫
如同§2例3,()f t 满足此积分方程等价于()f t 满足微分方程)]()(2[3
1)(22t f t t tf t f ′+= (2)将t 换成x ,记()y f x =,解y x xy y ′+=223 得通解3
1Cx x
y +=,由初值92)2(=
y 得C = 1,于是3
1x
x
y +=
. 【例3】(数一,数二)设曲线()r r θ=上任意点为(,)M r θ,一个定点为0(2,0)M ,由此曲线与极径0OM ,OM 围成的曲边扇形的面积等于两点0M 与M 间弧长的一半,求此曲线的方程.
【分析与求解】1)首先用极坐标写出曲边扇形的面积与弧长表达式.
见右图.极径0OM ,OM 与曲线()r r θ=围成的曲边扇形面积∫=
θθθθ0
2
d )(21)(r S 0M ,M 间的弧长∫
′+=θ
θθθθ0
22d )()()(r r s
2)按题意列方程并给出初值.)(2
1
)(θθs S =
即22200()d ()()d r r r θθθθθθθ′=+∫∫还有(0)2r =
3)转化 将方程求导,原问题转化为求解
????
?=
′+=2
)0()
()()(222r r r r θθθ? ????
?=?±=′2
)0(1
)()()(2r r r r θθθ 4)求解初值问题
76
这是变量可分离的方程.用变量分离法求出通解C r
+±=?θ1
arcsin 由6
2)0(π
?
=?=c r .于是求得)
6
πsin(1
θ±=
r 即 23=±y x . 二、利用导数的几何意义列方程
【例4】设曲线L位于Oxy 平面的第一象限内,过L上任意一点M 处的切线与y 轴总相交,交点记作A ,且长度OA AM =.又L过点2
3,23(,求L的方程.
【分析与求解】设L的方程为y = y (x )
.由L上?点M(x ,y )处的切线方程为 ))(()(x X x y x y Y ?′+=令X = 0得A 点坐标为.x y x x ,y ))()(0(′?由
得AM OA =
2222)(y x x y x y ′+=′?化简得 y
x
x y y 22?=?
′ 初条件 23)23(=y 解初值问题????
??
?=?=?′23
)2
3(22y y x x y y 这是齐次方程(也是伯努利方程).解得)3(,32
2
x x y x y x ?=?=+(0<x <3)
三、利用导数的经济意义列方程(数三,数四)
【例5】某商品的需求量Q 对价格的弹性为3
3p ?=η,市场对该商品的最大需求量为1(万件),求需求函数.
【解】设需求函数为()Q p ,需求弹性即
p Q Q p d d ,按题意得p
Q
Q p d d = -3p 3,(0)1Q = 这是可分离变量的方程,用分离变量法求得通解,再由初值定常数,最后得3
e p Q ?=.
四、利用变化率满足的条件列方程
【例6】设在一人群中推广某种新技术是通过其中已掌握技术的人进行的.已知该人群的总数为N,在t = 0时刻,已掌握新技术的人数为x 0,在时刻t ,已掌握新技术的人数为()x t (设()x t 是连续可微的),其变化率与已掌握新技术的人数和未掌握新技术的人数之积成正比,且比例常数k >0,求变量()x t .
【解】t 时刻已掌握新技术人数为()x t ,它的变化率即
t
x
d d ,按题意:
77
0d (),(0)d x
kx N x x x t =?=这是可分离变量的,求出通解后定常数,得000e e Nkt Nkt
Nx x N x x =?+ 五、利用牛顿第二定律列方程(数一,数二)
【例7】从船上向海里沉放某种探测仪器时,需要确定仪器下沉深度y (从海平面算起)与下沉速度v 的函数关系.设仪器在重力作用下,从海平面由静止开始铅直下沉,在下沉过程中还受到阻力与浮力的作用.设仪器的质量为m ,体积为B ,海水比重为ρ,仪器所受的阴力与下沉速度成正比,比例系数为k (k >0).试建立y 与v 所满足的微分方程,并求出函数关系式()y y v =.
【分析与求解】建立坐标系:沉放点为原点0,Oy 轴正向铅直向下. 1)仪器受力:重力mg ,阻力t
y
k
d d ?,浮力-B ρ.按牛顿第二定律列方程 22d d d d y y
m mg k B t t
ρ=??初条件 0)0(,0)0(=′=y y 2)转化:为求()y y v =,将方程改写.22d d d d d d d d y y
v v v v
v t y t
=== 于是方程化为d ,d y mv
H kv H mg Bg v =??记
即d d y mv v H kv =?相应的初值0)(0
==v v y 3)求解 直接积分并由初值定常数得2ln m mH H
y v k H kv k
=?
+? 六、利用微元法列方程(数一,数二)
【例8】要设计一形状为旋转体的水泥桥墩,桥墩高为h ,上底面直径为2a ,要求桥墩在任一水平截而上所受上部桥墩的平均压强为一常数p ,设水泥的比重为ρ,试求桥墩的形状.
【分析与求解】首先建立坐标系,如图所示,x 轴为桥墩中心轴,y 轴为水平轴,设桥墩侧面的曲线方程为()y y x =,下面列方程并给初条件,然后求解. 【方法1】用微元法
任取[,][0,]x x x h +Δ?所对应桥墩的小薄片. 下层压力-上层压力=薄片的重量 222π()π()()p y x p y x x y x x ρπ?+Δ≈Δ 2()()
[()()]
()y x x y x p y x x y x y x x
ρ+Δ??+Δ+≈Δ
令0→Δx 得 )(d d )
(22x y x
y
x py ρ=?
78
即
y p
x y 2d d ρ?=初条件 ()y h a = 解一阶线性齐次方程的初值问题??
???==+
a h y y p x y )(02d d ρ
得 )
(2e
h x p
a y ??
=ρ
【方法2】用积分法
基本关系式 x 截面处所受压力=顶面压力+该截面上方桥墩的重量t t y a p x y p h
x
d )(ππ)(π22
2
∫
+=ρ
这是变限积分方程.
将上式求导,在上式中令x = h ,分别得?????
=?=a
h y y x
y py
)(d d 22ρ其余同方法1. §6 一阶常系数线性差分方程及其解法(数学三)
一阶常系数线性差分方程标准形式为 1()t t y ay f t ++=,其中t = 0,1,2,…,常数a ≠0,已知函数()f t 当 t = 0,1,2,…时有定义.如果当t = 0,1,2,…时有()0f t ≡,则称方程为一阶常系数齐次线性差分方程,否则,称为一阶常系数非齐次线性差分方程.
可以证明一阶常系数线性差分方程的通解与一阶线性微分方程有相同的结构,即一阶常系数线性差分方程1()t t y ay f t ++=的通解可表示为()(0,1,2,,),t
t t y C a y t ?
=?+=
其中C 是一个任意常数,y t *是非次齐次差分方程1()t t y ay f t ++=的一个特解. 注意,在上述非齐次方程通解的表达式中,()c
t
t y C a =?是对应齐次差分方程
10t t y ay ++=的通解.代入方程不难验证这一结论.
当()f t 是多项式,指数函数,正弦函数,余弦函数以及它们的和差或乘积时,常用待定系数法求非齐次差分方程1()t t y ay f t ++=的一个特解.与二阶常系数微分方程类似,仍分为两大类来讨论:
(1)若()()t m f t P t d =
,其中()m P t 是t 的m 次多项式,常数d ≠0.非齐次项()()m f t P t =可看成d = 1的特例.
这时非齐次差分方程1()t
t t m y ay P t d ++=的一个特解的取法如下表:(其中()m Q t 是待定系数的m 次多项式)
79
()f t
d 与系数a 的关系
特解y t *的形式
()t m P t d a + d ≠0 ()t m Q t d ()t m P t d
a + d = 0
()t m tQ t d
(2)若()f t = Mc os ωt +Nsi n ωt ,其中M,N,ω是常数,且0<ω<2π,ω≠π.这时总可以取函数y t * =Ac os ωt + B si n ωt 为非齐次方程的一个特解,其中A ,B 是待定常数. 【例1】差分方程2y t + 1 + 10y t -5t = 0的通解为________.
【解】写成标准形式t y y t t 25
51=
++(a = 5,d = 1,a + d ≠0)特解形式:y t *=At + B 代入方程得725
,125,25)6(6,25)(5)1(?===++=++++B A t B A At t B At B t A
通解为 )6
1(125)5(?+?=t c y t
t
【例2】差分方程y y + 1-y t = t 2t 的通解为________.
【解】a =-1,()f t =
t 2t ,d = 2,a + d ≠0特解形式y t *
=(At + B )2t ,代入方程得 1((1))2()22,2t t t A t B At B t At A B t +++?+=++=?A = 1,B =-2
即y t *
=(t -2)2t 因此,通解为 (2)2t
t y c t =+?
【例3】差分方程y t + 1-2y t = 3t 2π
cos
的通解为________. 【解】2
π=?,特解y t *
=t B t A 2πsin 2πcos +,代入方程得
t t B t A t B t A 2
π
cos 32πsin 22πcos 2)2π2πsin()2π2πcos(=??+++
t t B A t A B 2πcos 32πsin )2(2πcos )2(=+???B -2A = 3,A + 2B = 0?5
6
?=A ,
5
3
=B .?通解为)2πsin 2πcos 2(532t t c y t t +?+=
【例4】设某人于某年年底在银行存款a 元,其年利率是r ,且按复利计算利息,又该存
款人从存款满一年起每年年底均取出固定数额为b 元的部分存款,求该存款人每年年底在银行存款余额的变化规律.
【解】设y t 是存款t (t = 0,1,2…)年整时该存款人的存款余额,于是可得 11(1)(1)t t t t y r y b y r y b ++=+???+=?,且y 0 = a .注意,方程的通解是 r
b
r C y t
t +
+=)1(.
80
利用初值r
b C a y +==0可确定常数C =r b a ?,故该存款人每年年底在银行存款余额的
变化服从如下规律:
)2,1,0()1)(( =++?=t r
b
r r b a y t t .
第八讲多元函数微分学
一、知识网络图
二、重点考核点
这部分的重点是:
①偏导数、全微分的计算,尤其是求复合函数的二阶偏导数(包括带函数记号的复合函数,隐函数,变量替换下方程的变形及初等函数等).
②多元函数的简单极值与条件极值问题特别是有关的应用题(几何、物理与经济上的应用题).
③几何应用(求曲面的切平面和法线,空间曲线的切线和法平面)(只对数一)
④求方向导数和梯度(只对数一).
⑤可微性概念.
81
平行线动点问题 模块一 课前检测 【题1】将一块等腰直角三角板与一把直尺如图放置,若∠1=60°,则∠2的度数为 . 【题2】如图,AB ∥DE ,∠1=25°,∠2=110°,求∠BCD 的度数. 【题3】如图AM ∥BN ,C 是BN 上一点,O 是射线CP 上的点,∠MAO 的平分线与∠OBN 的平分线交于点D . (1)当点O 在AM 与BN 之间时,如图1所示,求证:∠D =12 ∠AOB ; (2)当点O 在AM 上方时,如图2所示,试判断(1)中的结论是否依然成立,给出结论,并对你给出的结论加以证明. 模块二 动点与角度 21E D C B A 21图1 N M O A B C D P 图2M N A B C O D P
知识点睛 变相考察平行线四大模型,依然遵循“逢拐作平行”原则. 典型例题 【例1】已知AB ∥CD ,线段EF 分别与AB 、CD 相交于E 、F . (1)如图1,当∠A =20°,∠APC =70°时,求∠C 的度数; (1)如图2,当点P 在线段EF 上运动时(不包括E 、F 两点),∠A 、∠APC 与∠C 之间有怎样的数量关系?试证明你的结论; (3)如图3,当点P 在线段EF 的延长线上时,(2)中的结论还成立吗?如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明. 【巩固】直线AB ∥CD ,直线a 分别交AB 、CD 于E 、F ,点M 在直线EF 上,点P 是直线CD 上的一个动点(点P 不与点F 重合). (1)如图,当点P 在射线FC 上移动时,∠FMP +∠FPM 与∠AEF 有什么数量关系,请说明理由; (2)当点P 在射线FD 上移动时,请画出图形并探究∠BEM 、∠DPM 、∠EMP 有什么数量关系,请说明图3 图1图2A E B C F D P A E B C F D P A B C D P E F A B E M
一、基础知识 1、将直接引语中若干句子改成对话的形式 周萍说:“我对吴林描述了电影《想飞的钢琴少年》的内容,维达斯有着敏感的听觉,与众不同。她问我什么时候上映,很想去看。我说下周就上映了。” 周萍说:“” 吴林说:“” 周萍问答:“” 2、写出十个汉语中表示眼部动作的字 例:看 ()()()()()()()()()() 二、阅读练习 (一)士别三日刮目相看 三国时,吴国有一员大将,名叫吕蒙。吕蒙从小炼就了一身武艺,十几岁就开始在军队中服役了。打仗时,他冲锋陷镇,十分勇敢,常常手提大刀,第一个杀入敌阵,为吴国立下了汗马功劳。因此,“吴下阿蒙”成了家喻户晓的大英雄。 可是,吕蒙识字不多,自称“大老粗”,不爱学习。吴国国君孙权劝他要多读点书,对他说:“你身上的担子很重,没有文化是不能统帅千军的,一个将军()要勇敢,()要有智谋,这样才能服众。”吕蒙听了不以为然,心想:“我没读多少书,也不比别人打的胜仗少啊!”他对孙权说:“军营里的事情太多了,没有多余的时间读书啊!”孙权知道吕蒙在找借口,就例举了许多刻苦学习才成就不凡伟人的例子,并说:“()想读书学习,时间()可以找到。” 吕蒙听了孙权的教导以后,发奋读书,白天处理军务,晚上常常挑灯夜读,逐渐喜欢上了读书。果然,几个月下来,吕蒙的知识明显丰富多了。 有一次吴国的军师鲁肃到军营来看望吕蒙,两人一起讨论一些问题。鲁肃发现吕蒙的举止谈吐跟以前相比判若两人,感到惊讶,问道:“吕将军好像跟以前不大一样,是怎么回事?”吕蒙听后哈哈大笑,“朋友相处,三日不见,当刮目相看。我早就不是以前那个粗鲁的阿蒙了!” 孙权也听说了吕蒙发奋读书的事,对他更器重了,还经常在别人面前称赞吕蒙,要求其他将领要以吕蒙为榜样,好好学习文化。 1、圈出第一节中的两个错别字,依次改在后面的括号里:()() 2、在文中的括号里填上合适的关联词 3、联系上下文,理解词语的意思 (1)不以为然: (2)判若两人: 4、根据文章内容填空 文章通过吕蒙___________________________________,让鲁肃____________,让孙权_____________________。“士别三日刮目相看”的意思是_______________________________。“吴下阿蒙”指的是___________。原先,吕蒙认为_______________________________________,因此以_________________________________为借口不想读书。但是他听了________的教导后,______________________________________________________,结果让________刮目相看。5、“士别三日刮目相看”的故事,给了你什么启示?(50字以上)
第一讲 极限与连续 主要内容概括(略) 重点题型讲解 一、极限问题 类型一:连加或连乘的求极限问题 1.求下列极限: (1)???? ? ?+-++?+?∞→)12)(12(1 531311lim n n n Λ; (2)1 1 lim 332+-=∞→k k n k n π; (3)∑=∞ →+n k n n k k 1]) 1(1 [ lim ; 2.求下列极限: (1)???? ??++++++∞→n n n n n 22241 2411 41lim Λ; 3.求下列极限: (1)??? ? ??++++++∞→2222221 211 1lim n n n n n Λ; (2)n n n n !lim ∞ →; (3)∑ =∞ →++ n i n n i n 1 2 11 lim 。 类型二:利用重要极限求极限的问题 1.求下列极限: (1))0(2 cos 2cos 2cos lim 2≠∞→x x x x n n Λ; (2)n n n n n n 1sin )1(lim 1+∞→+; 2.求下列极限: (1)( ) x x x cos 11 20 sin 1lim -→+; (3)) 21ln(103 sin 1tan 1lim x x x x x +→?? ? ??++; (4)2 1cos lim x x x ?? ? ?? ∞ →; 类型三:利用等价无穷小和麦克劳林公式求极限的问题 1.求下列极限: (1)) cos 1(sin 1tan 1lim 0x x x x x -+-+→; (2))cos 1(lim tan 0x x e e x x x --→; (3)]1)3cos 2[(1lim 30 -+→x x x x ; (4))tan 1 1(lim 220x x x -→;
有理数是初中数学六年级下学期第一章第一节的内容.重点是有理数的相关概念辨析,利用对数轴的理解对有理数进行大小比较,绝对值的化简等.难点是绝对值的化简及运算.本讲会在讲解有理数的意义和数轴的知识之后,学习一些绝对值的基础知识,并会在下一讲中,着重讲解绝对值相关的化简及运算. 1、正数和负数 在现实生活中,用正数和负数表示具有相反意义的量. 2、有理数的概念 整数和分数统称为有理数. 3、有理数的分类 按意义分: ?? ?? ? ? ?? ?? ? ? ? ? ?? ? 正整数 整数零 负整数 有理数 正分数 分数 负分数 ;按符号分: ?? ?? ? ? ? ? ?? ?? ?? ? 正整数 正有理数 正分数 有理数零 负整数 负有理数 负分数 . 注意:(1)零既不是正数,也不是负数,零是正数和负数的分界; (2)零和正数统称为非负数;零和负数统称为非正数. 有理数 内容分析 知识结构 模块一:有理数的意义 知识精讲
例题解析 【例1】下列说法错误的是() A.盈利2000元和亏损100元是相反意义的量 B.向西走5千米和向北走5千米是相反意义的量 C.增加20人和减少10人是相反意义的量 D.支出600元和收入800元是相反意义的量 【难度】★ 【答案】B 【解析】B答案错误,向西走5千米和向东走5千米是相反意义的量. 【总结】考察正数、负数表示的意义. 【例2】如果5 -米表示向南走5米,那么下列各数分别表示什么意义? (1)8+米;(2)3-米;(3)0米;(4)6米. 【难度】★ 【答案】(1)向北走8米;(2)向南走3米;(3)停留在原地;(4)向北走6米.【解析】向南为负数,则向北为正数. 【总结】考察正数、负数表示的意义. 【例3】下列说法错误的是() A.正整数、0、负整数统称整数B.0既不是正数,也不是负数 C.有理数包括正数和负数D.有理数包括整数和分数 【难度】★ 【答案】C 【解析】C答案错误,有理数包括正数和负数和0. 【总结】考察有理数的分类. 2/ 16
二年级超常班第一讲 要想数得快,规律用起来【例1】数一数,下图中共有多少条线段? 【分析】数一数一共有6个端点,那么基本线段就有(条),这个图中一共就有 条线段. 【例2】数一数,图①中共有多少个锐角?图②中共有多少个 三角形?
【分析】 【例3】数一数,下图中共有多少个长方形? 【分析】 上面第一层以AB为宽的有6个长方形,下面第二层以BC为宽的也就有6个长方形.另外把第一层和第二层合在一起以AC为宽的长方形还有6个,一层有6个,共3层,这样一共就有 个长方形.
【例4】数一数,下图中共有多少个三角形? 【分析】 方法一:可以分类来数.具体分析如下: (1)左边:左边三角形ABD中有 个三角形; (2)右边:右边三角形ADC中有 个三角形; (3)左边+右边:左右合起来三角形ABC中有3个三角形;
一共有:个三角形. 方法二:可根据三角形包含基本图形的个数来分类数.具体分析如下: 只含1个基本图形的三角形有6个; 只含2个基本图形的三角形有5个; 只含3个基本图形的三角形有2个; 只含4个基本图形的三角形有1个; 只含5个基本图形的三角形有0个;
个; 一共有:个三角形. 【例5】数一数,下图中共有多少个三角形? 【分析】根据三角形包含基本图形的个数分类数.先按顺时针的方向给基本图形标上序号,如图:
个,分别是:①、②、③、④、⑤、⑥; 只含2个基本图形的三角形有3个,分别是:②③、④⑤、⑥①;只含3个基本图形的三角形有6个,分别是:①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②;只含4个或5个基本图形的三角形有0个;只含6个基本图形的三角形有1个,是:①②③④⑤⑥.图中共有三角形: (个). 【超常挑战】1.数一数,下图中
第十二讲:长方体再认识 1.能说出长方体的特征及概念 2.能应用长方体的特征及概念解决具体问题 掌握特殊角之间的数量关系 长方体的元素:六个面、八个顶点、十二条棱 长方体的三元素的特点:(主要是外观特征和数量关系) ①长方体的每个面都是长方形;②长方体的十二条棱可以分为三组,每组中的四条棱的长度相等。 ③长方体的六个面可以分为三组,每组中的两个面形状大小都相同。正方体是特殊的长方体。 平面是平的,无边无沿,没有厚度和大小,一般用平行四边形来表示。记作:平面ABCD或平面 。 将水平放置的平面画成一边是水平位置,另一边与水平线成45度角的平行四边形。 斜二侧画法画长方体时要注意:宽画成标注尺寸的一半;看不到的线画成虚线;要标字母和尺寸,要写结论。 长方体ABCD-EFGH、平面ABCD、棱AB、顶点A。 空间中两直线的位置关系有三种:相交、平行、异面 如果两条直线在同一平面内,有唯一公共点,称这两条直线的位置关
系是相交; 如果两条直线在同一平面内,没有唯一公共点,称这两条直线的位置 关系是平行; 如果两条直线既不平行也不相交,称这两条直线的位置关系是异面。 直线垂直于平面记作:直线PQ ⊥平面ABCD ;直线平行于平面记作: 直线PQ ∥平面ABCD 。 计算公式之一:(三条棱长分别是a 、b 、c 的长方体) 棱长和 = 4()a b c ++ ; ② 体积 = abc ;③ 表面积 = 2()ab bc ac ++ ; ④ 无盖表面积 = S ab -、S bc -、S bc - 10、计算公式之二:(边长是a 正方体)① 棱长和= 12a ;②体积= 3a ;③表面积= 26a ;④无盖表面积 =25a 。 11、长方体不一定是正方体;正方体一定是长方体。 12、长方体中棱与棱的位置关系有3种,分别是平行、相交、异面。 13、长方体中棱与面的位置关系有2种,分别是:平行、垂直。 14、长方体中面与面的位置关系有2种,分别是:平行、垂直。 二、检验垂直或平行的方法: 1、检验直线与平面垂直的方法: ① 铅垂线法:将铅垂线靠近被测直线,如果铅垂线能够紧贴被测 直线,说明直线垂直于水平面。(可用于检验细棒是否垂直于水平面、 黑板的边沿是否垂直于水平面) ② 三角尺法:将两把三角尺的一条直角边分别紧贴已知平面并且位 置交叉,将两把三角尺的另一条直角边分别靠近被测细棒,如果两条
课程配套讲义说明1、配套课程名称2013年考研数学高数中值定理及定积分公开课(汤家凤) 2、课程内容 此课程为2013年考研数学高数部分的公开课,主要讲授定积分部分。 3、主讲师资 汤家凤——主讲高等数学、线性代数。 著名考研辅导专家,南京大学博士,南京工业大学教授,江苏省大学生数学竞赛优秀指导教师。凭借多年从事考研阅卷工作的经验,通过自己的归纳总结,在课堂上为学生列举大量以往考过的经典例子。深入浅出,融会贯通,让学生真正掌握正确的解题方法。 4、讲义: 6页(电子版) 文都网校 2011年5月27日
公开课二:定积分理论 一、实际应用背景 1、运动问题—设物体运动速度为)(t v v =,求],[b a t ∈上物体走过的路程。 (1)取b t t t a n =<<<= 10,],[],[],[],[12110n n t t t t t t b a -???= , 其中)1(1n i t t t i i i ≤≤-=?-; (2)任取)1](,[1n i x x i i i ≤≤∈-ξ,i n i i t f S ?≈ ∑=)(1ξ; (3)取}{max 1i n i x ?=≤≤λ,则i n i i x f S ?=∑=→)(lim 1 ξλ 2、曲边梯形的面积—设曲线)(0)(:b x a x f y L ≤≤≥=,由b x a x L ==,,及x 轴围成的区域称为曲边梯形,求其面积。 (1)取b x x x a n =<<<= 10,],[],[],[],[12110n n x x x x x x b a -???= , 其中)1(1n i x x x i i i ≤≤-=?-; (2)任取)1](,[1n i x x i i i ≤≤∈-ξ,i n i i x f A ?≈ ∑=)(1ξ; (3)取}{max 1i n i x ?=≤≤λ,则i n i i x f A ?=∑=→)(lim 1 ξλ。 二、定积分理论 (一)定积分的定义—设)(x f 为],[b a 上的有界函数, (1)取b x x x a n =<<<= 10,],[],[],[],[12110n n x x x x x x b a -???= , 其中)1(1n i x x x i i i ≤≤-=?-; (2)任取)1](,[1n i x x i i i ≤≤∈-ξ,作 i n i i x f ?∑=)(1 ξ; (3)取}{m a x 1i n i x ?=≤≤λ, 若i n i i x f ?∑=→)(lim 1 ξλ存在,称)(x f 在],[b a 上可积,极限称为) (x f 在],[b a 上的定积分,记 ? b a dx x f )(,即?b a dx x f )(i n i i x f ?=∑=→)(lim 1 ξλ。
第一讲 定义新运算(又名:自定义) 例1:规定一种运算: a△b=3×a+4×b,例如,2△5=3×2+4×5=6+20=26,5△ 2=3×5+4×2=15+8=23, ……,根据以上规律计算: ①10△2 ② 2△10 简析: 本题属于“用字母表示数”的学习内容,重点是弄清规定,找出规律. ①含义为:给定两个数a和b,用3乘第一个数a,用4乘第二个数b,并将结果相 加 10△2 2△10 =3×10+4×2 = 3×2+4×10 =30+8 = 6+40 =38 =46 ②式中的“△”为“关系符号”,不是运算符号,可以是任意的字符,图片,实 物等 ③计算完毕后比较一下:定义新运算中,交换律适用吗? 配套练习: 1.规定一种运算:m□n=4×m-3×n,根据以上规律计算:5□3 2.规定一种运算:a△b=﹙a+b﹚×﹙a-b﹚,试求: 6△4 例2:对于两个数a和b,规定:a△b=﹙a+3﹚×﹙b+4﹚,试求:①1△2△3 ② 1△﹙2△3﹚ 简析: 本题是例1的发展,重点在于弄清运算顺序。 ①其运算顺序与四则混合运算顺序相同,但要注意,先计算部分是个整体,应加 括号,没算到的部分往下带。 ②应该用发展的、动态的眼光对待a和b. 1△2△3 =[﹙1+3﹚×﹙2+4﹚]△3 ﹙a=1,b=2﹚ =[4×6]△3 =24△3 =﹙24+3﹚×﹙3+4﹚﹙a=24,b=3﹚ =27×7 =189 1△﹙2△3﹚ =1△[﹙2+3﹚×﹙3+4﹚]﹙a=2,b=3﹚ =1△[5×7] =1△35 =﹙1+3﹚×﹙35+4﹚﹙a=1,b=35﹚ =4×39 =156 配套练习: 1.对于两个数a和b,规定a○b=a+5b,试求① 1○2○3 ② 1○﹙2○3﹚注 意:5b表示5×b或b×5 2.对于两个数a和b,规定:a□b=﹙a-2﹚×﹙b÷2﹚.试求:3□﹙5□4﹚ 例3:如果2☆3=2+3+4,5☆2=5+6,4☆5=4+5+6+7+8,......照此规律,计算① 3
春季班·初三物理 第一讲:机械运动 【精讲精练】 知识点一、长度、时间的测量 1. 工具:刻度尺、卷尺、游标卡尺、螺旋测微器等,常用工具为刻度尺。 2. 在国际单位制中,长度的基本单位是米(m ),常用的单位还有千米(km )、分米(dm )、厘米(cm )、 毫米(mm )、微米(um )、纳米(nm );还有英尺、码、光年等也是 的单位。 1km= m 1m = dm = cm = mm = μm = nm 3. 刻度尺 (1)零刻度线:刻度尺的起始刻度。使用时要看刻度尺的零刻度线是否在尺端,是否磨损。 (2)分度值:两条相邻刻度线之间的距离。 (3)量程(测量范围):从零刻度线到这把刻度尺的最后一条刻度线的距离。 4. 刻度尺的正确使用: (1)测量前首先要观察刻度尺的 、 和零刻线是否磨损; (2)测量时的方法:零刻线与被测物体对齐,且尺要 被测物体,读数时视线与刻度尺尺面 ,厚刻度尺有刻度的面要紧贴被测物体,计数时要估读到 的下一位, 测量结果由 和 组成 。多次测量取 作为测量结果。这样可减少误差。 【归纳总结】 (1)选:根据测量要求,选择适当量程及分度值的刻度尺; (2)放:刻度尺与被测物平行,刻度线紧贴被测物,零刻度线与被测物一端对齐; (3)看:视线正对刻度尺的刻度线,不要斜视; (4)读:读数时要估读到分度值的下一位; (5)记:记录的测量结果要有准确值、估读值和单位。 例1、如图1,图中物体的长度为 cm ,其中的估读值为 cm 。 图1 例2、小明用刻度尺和三角板按右图测一个纽扣的直径,该刻度尺的分度值是 mm ,纽扣的直径是 cm 。 变式1、某同学用刻度尺测同一本物理课本的宽度,你的结果是 18.41cm 。 结果由三部分组成,分别是准确值、估计值、单位,你的结果的准确值是 ,估计值是 , 单位是 。 变式2、如图2,图中物体的长度为 cm 。 图3中物体的长度记为 cm 。 1 2 3 4 5 6
考研数学春季基础班线性代数辅导讲义汤家凤 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】
2013考研数学春季基础班线性代数辅导讲义- 主 讲 : 汤 家 凤 第一讲 行列式 一、基本概念 定义1 逆序—设j i ,是一对不等的正整数,若j i >,则称),(j i 为一对逆序。 定义2 逆序数—设n i i i 21是n ,,2,1 的一个排列,该排列所含逆序总数称为该排列的逆序数,记为)(21n i i i τ,逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列。 定义3 行列式—称nn n n n n a a a a a a a a a D 21 2222111211 = 称为n 阶行列式,规定 n n n nj j j j j j j j j a a a D 21212121) ()1(∑-= τ 。 定义4 余子式与代数余子式—把行列式nn n n n n a a a a a a a a a D 21 22221 112 11 = 中元素ij a 所在的i 行元素和 j 列元素去掉,剩下的1-n 行和1-n 列元素按照元素原来的排列次序构成的1-n 阶行列式,称为元素ij a 的余子式,记为ij M ,称ij j i ij M A +-=)1(为元素ij a 的代数余子式。 二、几个特殊的高阶行列式
1、对角行列式—形如 n a a a 0 000 021 称为对角行列式,n n a a a a a a 2121 00 00 0=。 2、上(下)三角行列式—称 nn n n a a a a a a 0 0222112 11 及nn n n a a a a a a 21 22 21 11 0为上(下)三角行列 式, nn nn n n a a a a a a a a a 2211222112110 0=,nn nn n n a a a a a a a a a 221121222111 0=。 3、 ||||B A B O O A ?=, ||||B A B O C A ?=, ||||B A B C O A ?=。 4、范得蒙行列式—形如1121 121211 11 ),,,(---= n n n n n n a a a a a a a a a V 称为n 阶范得蒙行列式,且 n i j j i n n n n n n a a a a a a a a a a a V ≤<≤----== 11121 121 21)(1 11 ),,,(。 【注解】0),,,(21≠n a a a V 的充分必要条件是n a a a ,,,21 两两不等。 三、行列式的计算性质 (一)把行列式转化为特殊行列式的性质 1、行列式与其转置行列式相等,即T D D =。 2、对调两行(或列)行列式改变符号。
第一讲等差数列基础 关于第一讲等差数列,是中年级学习的一个重点。高年级的很多题虽不是直接考察等差数列,但往往中间的某一步需要用到等差数列的知识。等差数列这讲公式繁多,但希望孩子们千万不要死记硬背这些公式,一定要理解着记忆。死记硬背公式不易记牢,往往容易出错,考试中一旦出现,背错公式,分数就得不到了;在在我总结的知识点解析里每个公式,我都讲了理解的方法。可以在做题时反复理解几次,就不容易出错了。 关于计算这里,再啰嗦几句。很多孩子的计算基本功不过关,所以往往上课时算式列出来了,但不会算,算得慢或算不准,这样就太可惜了。所以希望孩子们能够每天坚持练几道大数乘除法。乘法可以按照三位数×一位数,两位数×两位数,三位数×两位数,四位数×两位数,三位数×三位数,四位数×三位数。除法可以从三位数÷一位数,四位数÷一位数,三位数÷两位数,四位数÷一位数,五位数÷一位数,五位数÷三位数等等这样的顺序练起。 一、通项公式 知识点解析: ⒈第n项=首项+(n-1)×公差 理解方法:可以对比植树问题来理解等差数列,第二项比第一项多一个公差,第三项比第一项多两个公差,……第n项比第一项多(n-1)个公差。 辅助练习:等差数列5、8、11……求这个数列的第2011项是多少? 答:5+(2011-1)×3=6035 这个公式含有四个量首项,第n项,项数n,公差,这四个其实是知三求一的。 ⒉首项=第n项-(n-1)×公差 理解方法:同1,第n项比第一项多(n-1)个公差,用第n项剪去多出的即可。 辅助练习:等差数列……91,95,99共17项,求第一项是多少? 分析:已知第17项是99,项数n为17,公差95-91=4 答:99-(17-1)×4=35 (此公式本讲没有涉及) ⒊项数n=(第n项-首项)÷公差+1 理解方法:对比植树问题,第n个数与第一个数之间共差了第n项-首项,那么间隔数应为(第n项-首项)÷公差,项数n应该比间隔数多1,所以,项数n=(第n项-首项)÷公差+1 此公式为求和公式的基础,往往一道题第一步需要孩子判断一下共有多少项,第二步利用求和公式求和。 辅助练习:等差数列105,111,117……,567共多少项? 分析:首项105,末项567,公差111-105=6 答:(567-105)÷6+1=78 ⒋公差=(第n项-首项)÷(项数n-1)
2013考研数学春季基础班线性代数辅导讲义- 主讲:汤家凤 第一讲 行列式 一、基本概念 定义1 逆序—设j i ,是一对不等的正整数,若j i >,则称),(j i 为一对逆序。 定义2 逆序数—设n i i i 21是n ,,2,1 的一个排列,该排列所含逆序总数称为该排列的逆序数,记为 )(21n i i i τ,逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列。 定义3 行列式—称nn n n n n a a a a a a a a a D 21 22221 11211 = 称为n 阶行列式,规定 n n n nj j j j j j j j j a a a D 21212121)()1(∑ -= τ。 定义4 余子式与代数余子式—把行列式nn n n n n a a a a a a a a a D 21 22221 11211 = 中元素ij a 所在的i 行元素和j 列元 素去掉,剩下的1-n 行和1-n 列元素按照元素原来的排列次序构成的1-n 阶行列式,称为元素ij a 的余子式,记为ij M ,称ij j i ij M A +-=)1(为元素ij a 的代数余子式。 二、几个特殊的高阶行列式 1、对角行列式—形如 n a a a 000 21 称为对角行列式,n n a a a a a a 2121 00 =。
2、上(下)三角行列式—称 nn n n a a a a a a 0 022211211 及 nn n n a a a a a a 21 2221 11 0为上(下)三角行列式, nn nn n n a a a a a a a a a 2211222112110 0=,nn nn n n a a a a a a a a a 2211212221 11 0=。 3、 ||||B A B O O A ?=, ||||B A B O C A ?=, ||||B A B C O A ?=。 4、范得蒙行列式—形如1121 121211 11 ),,,(---= n n n n n n a a a a a a a a a V 称为n 阶范得蒙行列式,且 n i j j i n n n n n n a a a a a a a a a a a V ≤<≤----== 11121 121 21)(1 11 ),,,(。 【注解】0),,,(21≠n a a a V 的充分必要条件是n a a a ,,,21 两两不等。 三、行列式的计算性质 (一)把行列式转化为特殊行列式的性质 1、行列式与其转置行列式相等,即T D D =。 2、对调两行(或列)行列式改变符号。 3、行列式某行(或列)有公因子可以提取到行列式的外面。 推论1行列式某行(或列)元素全为零,则该行列式为零。 推论2行列式某两行(或列)相同,行列式为零。 推论3行列式某两行(或列)元素对应成比例,行列式为零。 4、行列式的某行(或列)的每个元素皆为两数之和时,行列式可分解为两个行列式,即 nn n n in i i n nn n n in i i n nn n n in in i i i i n a a a b b b a a a a a a a a a a a a a a a b a b a b a a a a 2 121112112 121112 11212 21 111211 +=+++。 5、行列式的某行(或列)的倍数加到另一行(或列),行列式不变,即
考研数学春季强化班高数讲义
第一章 函数 极限 连续 一.函数 1. 函数的概念(定义、定义域、对应法则、值域) 2. 函数的性态 1)单调性 定义:单调增: ).()(2121x f x f x x '单调增; 2)奇偶性 定义:偶函数 );()(x f x f =- 奇函数 ).()(x f x f -=- 判定:(1)定义: (2)设)(x f 可导,则: a))(x f 是奇函数? )(x f '是偶函数; b))(x f 是偶函数? )(x f '是奇函数; (3)连续的奇函数其原函数都是偶函数; 连续的偶函数其原函数之一是奇函数。 3)周期性 定义:)()(x f T x f =+ 判定:(1)定义; (2)可导的周期函数其导函数为周期函数; (3)周期函数的原函数不一定是周期函数;
4)有界性 定义:若;)(,,0M x f I x M ≤∈?>?则称)(x f 在I 上有界。 判定:(1)定义: (2))(x f 在],[b a 上连续)(x f ?在],[b a 上有界; (3))(x f 在),(b a 上连续,且)0()0(-+b f a f 和存在)(x f ?在 )(b a ,上有界; (4))(x f '在区间I (有限)上有界)(x f ?在I 上有界; 3.复合函数与反函数 (函数分解成简单函数的复合,分段函数的复合) 4.基本的初等函数与初等函数 基本初等函数: 常数,幂函数 ,指数,对数,三角,反三角。了解它们定义域,性质,图形. 初等函数: 由基本初等函数经过有限次的加、减、乘、除和复合所得到且能用一个 解析式表示的函数. 题型一 复合函数 例1设)1(-x f 的定义域为),0(],,0[>a a ,则)(x f 的定义域为 (A) ]1,1[+a (B) ]1,1[--a (C) ],1[a a - (D) ]1,[+a a 例2已知,1)]([,)(2x x f e x f x -==?且,0)(≥x ?求)(x ?及其定义域。 =)((x ?)0,)1ln(≤-x x 例3设???≥<=0,10,0)(x x x f , ? ??≤-<-=||1,2||1||,2)(2x x x x x g 试求)]([)],([x f g x g f . ( ???≤<<≤=||21||,12||1,0)]([x x x x g f 或 ???≥-<=0 ,10,2)]([x x x f g ) 题型二 函数性态
文都教育2014年考研数学春季基础班线性代数辅导讲义 主讲:汤家凤 第一讲 行列式 一、基本概念 定义1 逆序—设j i ,是一对不等的正整数,若j i >,则称),(j i 为一对逆序。 定义2 逆序数—设n i i i Λ21是n ,,2,1Λ的一个排列,该排列所含逆序总数称为该排列的逆序数,记为)(21n i i i Λτ,逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列。 定义3 行列式—称nn n n n n a a a a a a a a a D Λ ΛΛΛΛΛ Λ21 222 2111211 = 称为n 阶行列式,规定 n n n nj j j j j j j j j a a a D ΛΛΛ21212121) ()1(∑-= τ 。 定义 4 余子式与代数余子式—把行列式nn n n n n a a a a a a a a a D Λ ΛΛΛΛΛ Λ21 222 2111211= 中元素ij a 所在的i 行元 素和j 列元素去掉,剩下的1-n 行和1-n 列元素按照元素原来的排列次序构成的1-n 阶行列式,称为元素ij a 的余子式,记为ij M ,称ij j i ij M A +-=)1(为元素ij a 的代数余子式。 二、几个特殊的高阶行列式 1、对角行列式—形如 n a a a Λ ΛO ΛΛΛΛ00 000021称为对角行列式, n n a a a a a a ΛΛΛO ΛΛΛΛ2121 000000=。 2、上(下)三角行列式—称 nn n n a a a a a a Λ ΛO ΛΛΛΛ 0022211211及 nn n n a a a a a a Λ ΛO Λ ΛΛΛ21 222111 0为上(下)三角行列式, nn nn n n a a a a a a a a a ΛΛ Λ O ΛΛΛΛ 2211222112 11 0=, nn nn n n a a a a a a a a a ΛΛ ΛO Λ ΛΛΛ221121222111 0=。
第7讲长方体的再认识(三视图) (一)长方体直观图的画法 知识点1 数学中平面的特征 数学中的平面是平的,无边无沿,没有厚度,它是可以无限延伸的。 知识点2 数学中平面的画法和表示方法 数学中用一个平行四边形来表示平面,把水平放置的平面画成一边(AB边)是水平位置, 另一边(BC边)与水平线所成的角为45°且长度等于水平线一边的一半( 1 2 BC AB =)的平 αD C B A 行四边形。记作:平面ABCD或平面α。 知识点3 用斜二测画法画出长方体直观图。 1.注意线段的长度:使AB等于长方体的长,AD等于长方体宽的二分之一,AE等于长方体的高; 2.注意角度,45 DAB ∠=?; 3.注意虚实线的应用:由于图中,, AD DC DH被遮住的线段,因此要用虚线(隐藏线)表示。 长方体的每个面均为长方形,即对边相等,四个角均为直角。长方体的六个面可以分为三组(上下两个,左右两个,前后两个),每组中的两个面的形状和大小都相同。 H G F E D C B A
(三)长方体中棱与棱的位置关系的认识 知识点1 如果直线'',','C D A B DD 与直线CD 在同一平面内,具有唯一公共点,那么称这两条直线的位置关系为相交,读作:直线AB 与直线CD 相交。 知识点2 如果直线AB 与直线CD 在同一平面内,但无公共点,那么称这两条直线的位置关系为平行,读作:直线AB 与直线CD 平行,即AB 平行于CD ,CD 平行于AB 。 知识点3 如果直线AB 与直线1CC 既不平行,也不相交,那么称这两条直线的位置关系为异面,读作:直线AB 与直线1CC 异面。 (四)长方体中棱与平面位置关系的认识 知识点 1 直线PQ 垂直于平面ABCD ,记作:直线PQ ⊥平面ABCD ,读作:直线PQ 垂直于平面ABCD 。如图 Q P A B C D D C B A P Q 知识点2 直线PQ 平行于平面ABCD ,记作:直线//PQ 平面ABCD ,读作:直线 PQ 平行于平面ABCD 。如图 (五)长方体中平面与平面位置关系的认识 知识点1 平面α垂直平面β,记作: 平面α⊥平面β,读作:平面α垂直于平面β。如图① β α D 1 C 1B 1 A 1 A B C D ① ②
初一数学春季班
知识点1:实数的概念 1、无限不循环的小数叫做无理数. 注意: 1)整数和分数统称为有理数; 2)圆周率π是一个无理数. 2、无理数也有正、负之分. 如2、π、0.101001000100001L 等这样的数叫做正无理数; 2-、π-、0.101001000100001-L 这样的数叫做负无理数; 只有符号不同的两个无理数,如2与2-,π与π-,称它们互为相反数. 实数、数的开方 知识结构 模块一 实数的概念和分类 知识精讲
3、有理数和无理数统称为实数. (1)按定义分类 ??????????? ? →?整数有理数有限小数或无限循环小数 实数分数无理数无限不循环小数 (2)按性质符号分类 0???? ?? ??? ?????? 正有理数正实数正无理数实数负有理数负实数负无理数 【例1】 写出下列各数中的无理数: 3.1415926,2 π,16,.0.5,0,2 3-,0.1313313331…(两个1之间依次多一个3), 0.2121121112. 【难度】★ 【答案】2π 、0.1313313331…. 【解析】无限不循环小数都是无理数. 【总结】考查无理数的概念. 【例2】 判断正误,在后面的括号里对的用“√”,错的记“×”表示. (1)无限小数都是无理数. ( ) (2)无理数都是无限小数. ( ) (3)带根号的数都是无理数. ( ) (4)不带根号的数一定不是无理数. ( ) 【难度】★ 【答案】(1)×; (2)√; (3)×; (4)×. 【解析】(1)无限不循环小数才是无理数;(2)无理数是无限不循环小数当然是无限小数; (3)开方开不尽的数是无理数;(4)π没带根号但是无理数. 【总结】考查无理数的概念及无理数与小数的关系. 例题解析
word文档下载后可自由复制编辑 第一讲绪论 心理学的研究对象是心理现象。心理现象是多种多样的,也是非常复杂的。心理学主要研究人的心理现象,也研究动物的心理现象;既研究个体的心理现象,也研究群体的社会心理现象。与物理、化学等现象不同,心理现象不具形体性,是人的内部世界的精神生活,他人无法直接进行观察。但是通过对行为的观察和分析,却可以客观地研究人的心理。因此,心理学还研究行为及其与心理的关系。 第一节心理学的研究对象 心理学是对心理现象的阐述并揭露其本质和规律的科学。心理现象(心理过程、个性心理、群体心理) 一、心理过程 人的心理过程就其性质与功能来说可以分为认识过程、情绪过程和意志过程三个方面。 (一)认识过程 认识过程是指人由表及里、由现象到本质地反映客观事物的特性与联系的心理活动。人的认识过程包括对客观事物的感觉、知觉、记忆、思维和想象等过程。 (二)情绪/情感过程 情绪/情感过程是指人对客观事物是否满足自身物质和精神上的需要而产生的主观体验的心理活动,它反映的是客观事物同人的需要之间的关系,包括喜、怒、哀、乐、爱、憎、惧等情绪和情感。 (三)意志过程 意志过程是指人为了满足某种需要,在一定动机的激励下,自觉确定目标,克服内部和外部困难并力求实现目标的心理活动,意志过程是人的意识能动性的表现,即人不仅能认识客观事物,而且还能根据对客观事物及其规律的认识自觉地改造世界。 二、个性 人的心理活动具有共同规律的特征。个性是指一个人的整个心理面貌,它是个人心理活动的稳定的心理倾向和心理特征的总和。个性的心理结构主要包括个性倾向性和个性心理特征两个方面。 (一)个性倾向性 个性倾向性是推动人进行活动的动力系统,是个性结构中最活跃的因素。个性倾向性是指人所具有的意识倾向,它决定着人对现实的态度以及对认识活动对象的趋向和选择。个性倾向性主要包括需要、动机和价值观。 (二)个性心理特征 个性心理特征是人的多种心理特征的一种独特的组合。它集中反映了一个人的精神面貌的稳定的类型差异。例如,有的人聪明,有的人愚笨;有的人有高度发展的数学才能,有的人有高度发展的音乐才能。这是能力上的差异。能力标志着人在完成某项活动时的潜在可能
考研数学春季基础班线性代数辅导讲义汤家凤 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】
2013考研数学春季基础班线性代数辅导讲义- 主讲:汤家凤 第一讲 行列式 一、基本概念 定义1 逆序—设j i ,是一对不等的正整数,若j i >,则称),(j i 为一对逆序。 定义2 逆序数—设n i i i 21是n ,,2,1 的一个排列,该排列所含逆序总数称为该排列的逆序数,记为)(21n i i i τ,逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列。 定义3 行列式—称nn n n n n a a a a a a a a a D 21 2222111211 = 称为n 阶行列式,规定 n n n nj j j j j j j j j a a a D 21212121) ()1(∑-= τ 。 定义4 余子式与代数余子式—把行列式nn n n n n a a a a a a a a a D 21 22221112 11 = 中元素ij a 所在的i 行元 素和j 列元素去掉,剩下的1-n 行和1-n 列元素按照元素原来的排列次序构成的1-n 阶行列式,称为元素ij a 的余子式,记为ij M ,称ij j i ij M A +-=)1(为元素ij a 的代数余子式。 二、几个特殊的高阶行列式
1、对角行列式—形如 n a a a 0 00 021 称为对角行列式, n n a a a a a a 2121 00 0=。 2、上(下)三角行列式—称 nn n n a a a a a a 0 0222112 11 及nn n n a a a a a a 21 2221 11 0为上(下)三角 行列式, nn nn n n a a a a a a a a a 2211222112 11 0=,nn nn n n a a a a a a a a a 2211212221 11 0=。 3、 ||||B A B O O A ?=, ||||B A B O C A ?=, ||||B A B C O A ?=。 4、范得蒙行列式—形如1121 121211 11 ),,,(---= n n n n n n a a a a a a a a a V 称为n 阶范得蒙行列式,且 n i j j i n n n n n n a a a a a a a a a a a V ≤<≤----== 11121 12 121)(1 11),,,(。 【注解】0),,,(21≠n a a a V 的充分必要条件是n a a a ,,,21 两两不等。 三、行列式的计算性质 (一)把行列式转化为特殊行列式的性质 1、行列式与其转置行列式相等,即T D D =。 2、对调两行(或列)行列式改变符号。