
毕业论文开题报告
数学与应用数学
随机利率下的寿险精算模型
一、选题的背景与意义
二战结束以来,随着保险精算行业的迅速发展,各式各样的风险也逐渐显露。其中,利率波动带来的风险对寿险行业的负面影响极大。现实生活中为计算简便,通常采用固定利率的做法,计算保险的各项费用。然而,大多数情况下利率并不是一层不变的,利率随着经济周期、国家宏观政策等的变动而变动,这就不可避免地对保险行业造成冲击,从而导致寿险业在经营上困难重重。以美国为例,从1989年开始就有大量保险公司倒闭,其中不乏财力雄厚的公司。这些公司破产的原因固然很多,但都或多或少与利率风险有关。
就中国的寿险业状况看,自改革开放以来,我国寿险业也取得了巨大的发展空间。但我国由于寿险行业起步较晚,各项政策措施都不是很完善,更容易受到来自利率的冲击。中国寿险公司的资金一直以来主要存放在银行,适用的是普通银行相应的基准利率。从1985年开始,由于我国面临着越来越严重的通货膨胀,导致银行利率不断攀升,在传统寿险精算固定利率的情况下,中国寿险公司损失日趋严重,利差严重成了寿险业的心腹大患。如何解决这个问题,显得至关重要,故此,对影响利差的因素——利率波动的研究迫在眉睫。
传统精算理论中,预定利率是确定的,它往往决定了一个保单十几年甚至几十年的评估利率水平。当实际利率与预定利率之间只有很小的出入时,经过一二十年的利滚利之后就会产生巨额差别。通常情况下,保期越长,保费越高,付费期越短。则利率风险的影响越大。预定利率越高,保费越低,反之则越高。在寿险实务中,利率具有随机性,由利率波动产生的风险较之保险公司面临的死亡风险更为危险。因而,随机利率下的寿险研究逐步受到重视。越来越多的专家、学者投入到寿险中的随机利率波动性研究,以期解决利率风险给保险行业带来的毁灭性灾难。
基于寿险行业面临的利率风险的现状,本文选择对随机利率下的寿险精算模型进行了构建,使寿险行业能够更好的应对利率波动带来的风险,保持保险行业的稳定增长。
二、研究的基本内容与拟解决的主要问题
1、研究的基本内容
本文主要对随机利率下的寿险精算进行研究。首先,从理论分析角度,简要说明利率波动对寿险行业的影响;其次,在国内外学者研究的基础上,假定随机利率的基本分布,讨论相应的精算问题。本文着重讨论随机利率下的生存年金组合和寿险准备金问题。
2、拟解决的主要问题
(1)介绍各种利率的不同表达方式。
(2)在随机利率下,给出生存年金组合值和寿险准备金的计算表达式。
(3)该随机利率模型的一个应用。
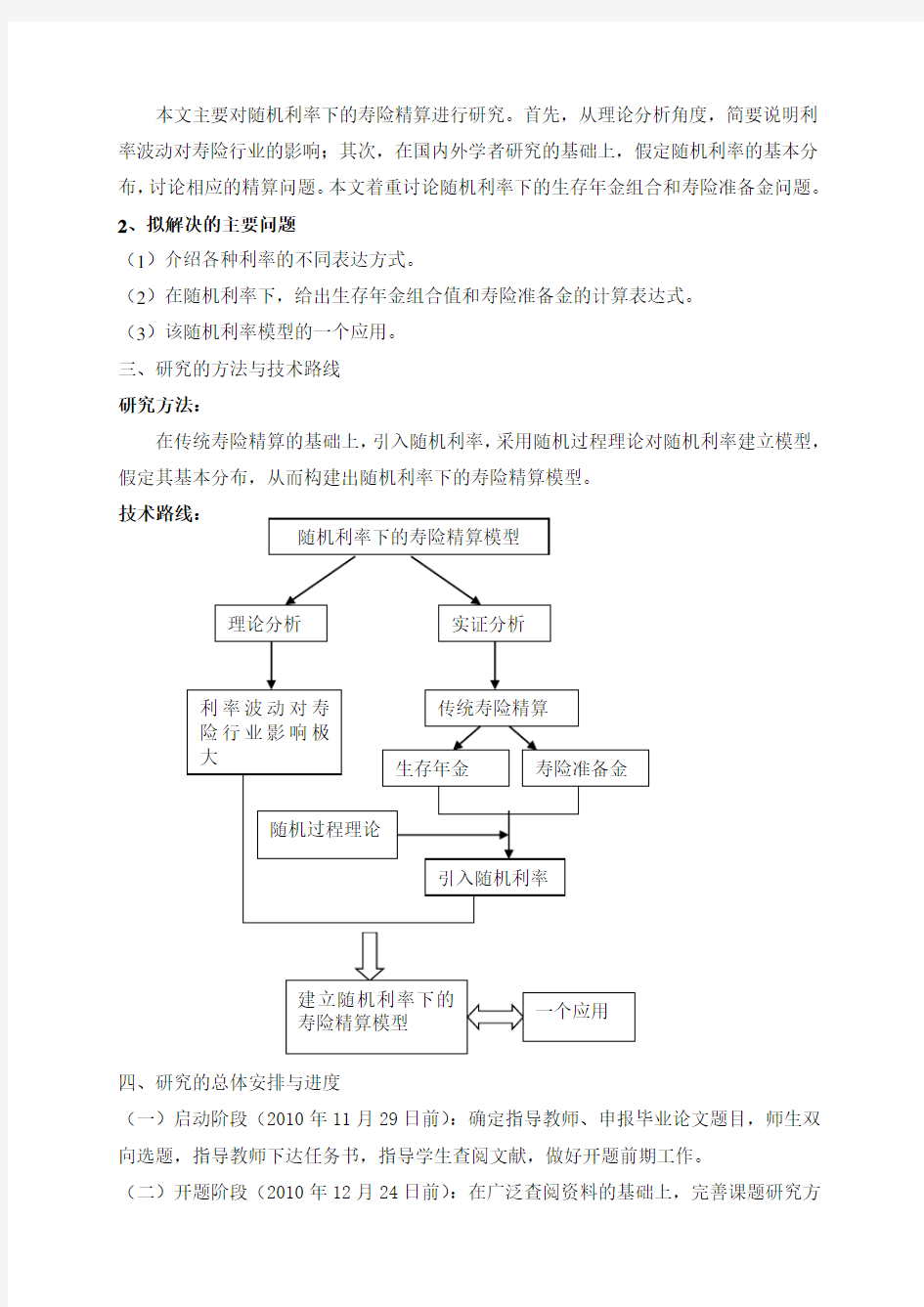
三、研究的方法与技术路线
研究方法:
在传统寿险精算的基础上,引入随机利率,采用随机过程理论对随机利率建立模型,假定其基本分布,从而构建出随机利率下的寿险精算模型。
四、研究的总体安排与进度
(一)启动阶段(2010年11月29日前):确定指导教师、申报毕业论文题目,师生双向选题,指导教师下达任务书,指导学生查阅文献,做好开题前期工作。
(二)开题阶段(2010年12月24日前):在广泛查阅资料的基础上,完善课题研究方
案,完成文献综述和开题报告等工作,准备开题论证和初期检查工作。
(三)实施阶段(2011年4月29日前):查找资料,广泛阅读,进行课题的实验、设计、调研及结果的处理与分析等,完成论文写作或毕业设计说明书,进行毕业论文的审阅和修改完善。
五、主要参考文献
[1] Bellhouse D.R.,H.H. Panjer.Stochastic modeling of interest rates with
applications to life contingencies-PartII[J].Journal of Risk and Insurance.1981.
(47):628-637.
[2] Beekman J.A.,Fueling C.P..Interest and mortality randomness in some
annuities[J] .Insurance:Mathematics and Economics.1990.(9):185-196.
[3] Beekman J.A.,Fueling C.P..Extra randomness in certain annuity models[J].
Insurance: Mathematics and Economics.1991.(10):275-287.
[4] Etienne Marceau, Patrice Gaillardetz.On life insurance reserves in a stochastic mortality and interest rates environment[J]. Insurance: Mathematics and Economics.1999.(25):261-280.
[5] Zaks A.Annuities under random rates of interest[J]. Insurance: Mathematics and Economics.2001.(28):1-11.
[6] Perry D.,E..Long-term stochastic interest rate models[J]. Insurance: Mathematics and Economics.2001.(29):73-82.
[7] Parker G..Two stochastic approaches for discounting actuarial function[J].
Astin Bulletin.1996.(26):167-181.
[8] Parker G..Stochastic analysis of the interaction between investment and insurance risks[J].North American Actuarial Journal.1997.(12):55-84.
[9] James M.Carson..Interest rate risk and equity values of life insurance companies:A GERCH-M model[J].2007.(74):401-423.
[10] Michael Ludkovski, Virginia R.Young.Indifference pricing of pure endowments and life annuities under stochastic hazard and interest rates[J].2008.(42):14-30.
[11] 吴金文,杨静平,周俊.随机利率寿险模型[J].经济数学.2001.18(3):1-8.
[12] 刘凌云,汪荣明.一类随机利率下的增额寿险模型[J].应用概率统计.2001.17(3):283-290.
[13] 欧阳资生,鄢茵.随机利率下增额寿险现值函数矩的一些结果[J].经济数学.2003.20(1):41-47.
[14] 郎艳怀.随机利率下的寿险模型研究[J].中国管理科学.2004(12):326-318
[15] 高建伟,丁克诠.MA(q)利率下企业生存年金精算现值模型[J].系统工程学报.2006.21(2):131-135.
[16] 东明.随机利率下寿险保单组的均衡保费模型[J].系统工程学报.2007.22
(4):394-400.
[17] 陈海兵,韩素芳.一类随机利率下的变额寿险模型研究[J].数学理论与应用.2008.28(3):1-4.
[18] 关清元,陶菊春.随机利率下寿险组合精算现值模型研究[J].佳木斯大学学报(自然科学版).2009.27(6):933-935.
等额本息和等额本金计算公式 等额本金: 本金还款和利息还款: 月还款额=当月本金还款+当月利息式1 其中本金还款是真正偿还贷款的。每月还款之后,贷款的剩余本金就相应减少: 当月剩余本金=上月剩余本金-当月本金还款 直到最后一个月,全部本金偿还完毕。 利息还款是用来偿还剩余本金在本月所产生的利息的。每月还款中必须将本月本金所产生的利息付清: 当月利息=上月剩余本金×月利率式2 其中月利率=年利率÷12。据传工商银行等某些银行在进行本金等额还款的计算方法中,月利率用了一个挺孙子的算法,这里暂且不提。 由上面利息偿还公式中可见,月利息是与上月剩余本金成正比的,由于在贷款初期,剩余本金较多,所以可见,贷款初期每月的利息较多,月还款额中偿还利息的份额较重。随着还款次数的增多,剩余本金将逐渐减少,月还款的利息也相应减少,直到最后一个月,本金全部还清,利息付最后一次,下个月将既无本金又无利息,至此,全部贷款偿还完毕。 两种贷款的偿还原理就如上所述。上述两个公式是月还款的基本公式,其他公式都可由此导出。下面我们就基于这两个公式推导一下两种还款方式的具体计算公式。 1. 等额本金还款方式 等额本金还款方式比较简单。顾名思义,这种方式下,每次还款的本金还款数是一样的。因此: 当月本金还款=总贷款数÷还款次数 当月利息=上月剩余本金×月利率 =总贷款数×(1-(还款月数-1)÷还款次数)×月利率
当月月还款额=当月本金还款+当月利息 =总贷款数×(1÷还款次数+(1-(还款月数-1)÷还款次数)×月利率) 总利息=所有利息之和 =总贷款数×月利率×(还款次数-(1+2+3+。。。+还款次数-1)÷还款次数) 其中1+2+3+…+还款次数-1是一个等差数列,其和为(1+还款次数-1)×(还款次数-1)/2=还款次数×(还款次数-1)/2 :总利息=总贷款数×月利率×(还款次数+1)÷2 由于等额本金还款每个月的本金还款额是固定的,而每月的利息是递减的,因此,等额本金还款每个月的还款额是不一样的。开始还得多,而后逐月递减。 等额本息还款方式: 等额本金还款,顾名思义就是每个月的还款额是固定的。由于还款利息是逐月减少的,因此反过来说,每月还款中的本金还款额是逐月增加的。 首先,我们先进行一番设定: 设:总贷款额=A 还款次数=B 还款月利率=C 月还款额=X 当月本金还款=Yn(n=还款月数) 先说第一个月,当月本金为全部贷款额=A,因此: 第一个月的利息=A×C 第一个月的本金还款额 Y1=X-第一个月的利息
毕业论文开题报告 数学与应用数学 随机利率下的寿险精算模型 一、选题的背景与意义 二战结束以来,随着保险精算行业的迅速发展,各式各样的风险也逐渐显露。其中,利率波动带来的风险对寿险行业的负面影响极大。现实生活中为计算简便,通常采用固定利率的做法,计算保险的各项费用。然而,大多数情况下利率并不是一层不变的,利率随着经济周期、国家宏观政策等的变动而变动,这就不可避免地对保险行业造成冲击,从而导致寿险业在经营上困难重重。以美国为例,从1989年开始就有大量保险公司倒闭,其中不乏财力雄厚的公司。这些公司破产的原因固然很多,但都或多或少与利率风险有关。 就中国的寿险业状况看,自改革开放以来,我国寿险业也取得了巨大的发展空间。但我国由于寿险行业起步较晚,各项政策措施都不是很完善,更容易受到来自利率的冲击。中国寿险公司的资金一直以来主要存放在银行,适用的是普通银行相应的基准利率。从1985年开始,由于我国面临着越来越严重的通货膨胀,导致银行利率不断攀升,在传统寿险精算固定利率的情况下,中国寿险公司损失日趋严重,利差严重成了寿险业的心腹大患。如何解决这个问题,显得至关重要,故此,对影响利差的因素——利率波动的研究迫在眉睫。 传统精算理论中,预定利率是确定的,它往往决定了一个保单十几年甚至几十年的评估利率水平。当实际利率与预定利率之间只有很小的出入时,经过一二十年的利滚利之后就会产生巨额差别。通常情况下,保期越长,保费越高,付费期越短。则利率风险的影响越大。预定利率越高,保费越低,反之则越高。在寿险实务中,利率具有随机性,由利率波动产生的风险较之保险公司面临的死亡风险更为危险。因而,随机利率下的寿险研究逐步受到重视。越来越多的专家、学者投入到寿险中的随机利率波动性研究,以期解决利率风险给保险行业带来的毁灭性灾难。 基于寿险行业面临的利率风险的现状,本文选择对随机利率下的寿险精算模型进行了构建,使寿险行业能够更好的应对利率波动带来的风险,保持保险行业的稳定增长。 二、研究的基本内容与拟解决的主要问题 1、研究的基本内容
等额本息还款公式推导 设贷款总额为A,银行月利率为β,总期数为m(个月),月还款额设为X,则各个月所欠银行贷款为: 第一个月A 第二个月A(1+β)-X 第三个月(A(1+β)-X)(1+β)-X=A(1+β)2-X[1+(1+β)]第四个月((A(1+β)-X)(1+β)-X)(1+β)-X =A(1+β)3-X[1+(1+β)+(1+β)2] … 由此可得第n个月后所欠银行贷款为 A(1+β)n –X[1+(1+β)+(1+β)2+…+(1+β)n-1]= A(1+β)n –X [(1+β)n-1]/β 由于还款总期数为m,也即第m月刚好还完银行所有贷款,因此有 A(1+β)m –X[(1+β)m-1]/β=0 由此求得
X = Aβ(1+β)m /[(1+β)m-1] ======================================================= ===== ◆关于A(1+β)n –X[1+(1+β)+(1+β)2+…+(1+β)n-1]= A(1+β)n –X[(1+β)n-1]/β的推导用了等比数列的求和公式 ◆1、(1+β)、(1+β)2、…、(1+β)n-1为等比数列 ◆关于等比数列的一些性质 (1)等比数列:An+1/An=q, n为自然数。 (2)通项公式:An=A1*q^(n-1); 推广式:An=Am·q^(n-m); (3)求和公式:Sn=nA1(q=1) Sn=[A1(1-q^n)]/(1-q) (4)性质: ①若m、n、p、q∈N,且m+n=p+q,则am·an=ap*aq; ②在等比数列中,依次每k项之和仍成等比数列. (5)“G是a、b的等比中项”“G^2=ab(G≠0)”. (6)在等比数列中,首项A1与公比q都不为零. ◆所以1+(1+β)+(1+β)2+…+(1+β)n-1 =[(1+β)n-1]/β 等额本金还款不同等额还款 问:等额本金还款是什么意思?与等额还款相比是否等额本金还款更省钱?
习题 第一章人寿保险 一、n 年定期寿险 【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。 I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。 解:I 表4–1 死亡赔付现值计算表 年份 年内死亡人数 赔付支出 折现因子 赔付支出现值 (1) (2) (3)=1000*(2) (4) (5)=(3)*(4) 1 1 1000 103.1- 970.87 2 2 2000 203.1- 1885.19 3 3 3000 303.1- 2745.43 4 4 4000 403.1- 3553.9 5 5 5 5000 503.1- 4313.04 合计 --- 15000 --- 13468.48 根据上表可知100张保单未来赔付支出现值为: 48.13468)03.1503.1403.1303.1203.11(100054321=?+?+?+?+??-----(元) 则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。 解:II 表4–2 死亡赔付现值计算表 年份 年内死亡人数 赔付支出 折现因子 赔付支出现值 (1) (2) (3)=1000*(2) (4) (5)=(3)*(4) 1 1000*40q =1.650 1650 103.1- 1601.94 2 1000*40|1q =1.809 1809 203.1- 1705.16 3 1000*40|2q =1.986 1986 303.1- 1817.47 4 1000*40 | 3q =2.181 2181 403.1- 1937.79
《精算技术》公式 第一章 利息理论 1n n v a i -=; ()11n n n v a a i d -=+=&&; () ()11 1n n n n i s a i i +-=+= ; ?? ? ?? -=11511000x l x ; 1a i ∞=; 1a d ∞ =&&; 1n n v a δ -= ; ()11 n n i s δ +-= ; ()n n n a nv Ia i -= &&; ()()()1n n n n s n Is Ia i i -=+=&&; ()n n n a Da i -=; ()()1n n n n i s Ds i +-= ; ()211 Ia i i ∞ =+。
第二章 生命表 22x x x m q m = +; 1x x x l l d +=-; x x x d q l =; ()11 2 x x x L l l += +; 1 x x x t t T L ?--+== ∑ ; x x x T e l = 。 第三章 生存年金 生存年金的概念及其种类。 生存年金现值计算公式
各种年金之间的关系式: x a =:x n a +|n x a | n x a =n x E x n a + x a &&=1+x a :x n a &&=1+:1x n a - | n x a &&=1|n x a - |n m x a &&=1|n m x a - :x n s =:x n a 1 n x E :x n s &&=:x n a &&1n x E ()m x a &&=()m x a + 1 m ()m x a =():m x n a +()|m n x a () | m n x a =n x E ()m x n a + 转换函数的定义
保险精算(第二版) 第一章:利息的基本概念 练 习 题 1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。 800元在28%i =,第3为 t (t=0),i 积累; 11. 某人1999年初借款3万元,按每年计息3次的年名义利率6%投资,到2004年末的积累值为( )万元。 A. 7.19 B. 4.04 C. 3.31 D. 5.21 12.甲向银行借款1万元,每年计息两次的名义利率为6%,甲第2年末还款4000元,则此次还款后所余本金部分为( )元。 A.7 225 B.7 213 C.7 136 D.6 987 第二章:年金 练习题 1.证明() n m m n v v i a a -=-。
2.某人购买一处住宅,价值16万元,首期付款额为A ,余下的部分自下月起每月月初付1000元,共付10年。年计息12次的年名义利率为8.7% 。计算购房首期付款额A 。 3. 已知7 5.153a = , 117.036a =, 189.180a =, 计算 i 。 4.某人从50岁时起,每年年初在银行存入5000元,共存10年,自60岁起,每年年初从银行提出一笔款作为生活费用,拟提取10年。年利率为10%,计算其每年生活费用。 5.年金A 的给付情况是:1~10年,每年年末给付1000元;11~20年,每年年末给付2000元;21~30年,每年年末给付1000元。年金B 在1~10年,每年给付额为K 元;11~20年给付额为0;21~30年,每年年末给付K 元,若A 与B 的现值相等,已知10 1 2 v = ,计算K 。 6. 化简() 1020101a v v ++ ,并解释该式意义。 5 。 n 年每年,那么v=( 2. 已知Pr [5<T(60)≤6]=0.1895,Pr [T(60)>5]=0.92094,求60q 。 3. 已知800.07q =,803129d =,求81l 。 4. 设某群体的初始人数为3 000人,20年内的预期死亡人数为240人,第21年和第22年的死亡人数分别为15人和18人。求生存函数s(x)在20岁、21岁和22岁的值。 5. 如果221100x x x μ= ++-,0≤x ≤100, 求0l =10 000时,在该生命表中1岁到4岁之间的死亡人数为( )。 A.2073.92 B.2081.61 C.2356.74 D.2107.56
一)准精算师部分 准精算师部分由八门专业课程及一门职业道德教育课程组成。 具体课程名称和主要内容如下: 课程名称 考试内容 A1 数学 1)概率论(30%); 2)数理统计(20%); 3)随机过程(20%); 4)应用统计(20%); 5)随机微积分(10%)。 A2 金融数学 1)复利数学(40%); 2)利率期限结构和随机利率模型(20%); 3)未定权益基本分析和风险中性评估(20%); 4)投资组合理论基础(20%)。 A3 精算模型 1)基本模型:生存模型和多状态模型、财产责任保险常见风险标的模型、个体模型和聚合模型;(40%)2)统计建模初步:参数估计和校验:频率和索赔额模型、信度理论;(20%) 3)统计模型的进一步分析:修匀原理和方法(10%)
4)破产模型;(20%) 5)情景及敏感性测试:随机模拟(10%) A4 经济学 宏观经济学(30%)、微观经济学(50%)、金融学(20%)A5 寿险精算 1)寿险精算数学(60%) 2)寿险精算实务(40%) A6 非寿险精算 1)非寿险精算数学(60%) 2)非寿险精算实务(40%) A7 会计与财务 1)会计基本原理(25%); 2)会计准则(25%); 3)各种经营实体介绍(20%); 4)企业会计的基本结构(15%); 5)企业会计的解释能力和局限性(15%)。 A8 精算管理 1)企业运营的一般环境(10%); 2)风险评估、风险类型和风险度量(15%);
3)产品(或服务)的设计和开发(10%); 4)产品和服务的定价及定价假设(10%); 5)准备金和负债评估(15%); 6)风险管理基本方法(15%); 7)资产负债管理基础(10%); 8)经验监测(10%); 9)偿付能力、盈利能力和资本管理(5%)。 (注:1、课程A1-A8均为3小时笔试。2、考生在通过了A1-A8全部课程后,还需参加为期一天的中国准精算师《A9职业道德教育》课程的培训,方可获得中国准精算师资格。) 一)科目名称:数学基础I 1、科目代码:01中国精算师资格考试 2、考试时间:3小时中国精算师资格考试 3、考试形式:标准化试题中国精算师资格考试 4、考试内容:中国精算师资格考试 (1)微积分(分数比例:60%)中国精算师资格考试 ①函数、极限、连续中国精算师资格考试 函数的概念及性质反函数复合函数隐函数分段函数基本初等函数的性质初等函数数列极限与函数极限的概念函数的左、右极限无穷小和无穷大的概念及其关系无穷小的比较极限的四则运算中国精算师资格考试 函数连续与间断的概念初等函数的连续性闭区间上连续函数的性质中国精算师资格考试 ②一元函数微积分中国精算师资格考试 导数的概念函数可导性与连续性之间的关系导数的四则运算基本初等函数的导数复合函数、反函数和隐函数的导数高阶导数微分的概念和运算法则微分在近似计算中的应用中值定理及其应用洛必达(L’Hospital)法则函数的单调性函数的极值函数图形的凹凸性、拐点及渐近线函数的最大值和最小值中国精算师资格考试 原函数与不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理变上限定积分及导数不定积分和定积分的换元积分法和分部积分法广义积分的概念及计算定积分的应用中国精算师资格考试 ③多元函数微积分中国精算师资格考试 多元函数的概念二元函数的极限与连续性有界闭区间上二元连续函数的性质偏导数的概念与计算多元复合函数及隐函数的求导法高阶偏导数全微分多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算***区域上的简单二重积分的计算曲线的切线方程和法线方程中国精算师资格考试 ④级数中国精算师资格考试 常数项级数收敛与发散的概念级数的基本性质与收敛的必要条件几何级数与p级数的收敛性正项级数收敛性的判断任意项级数的绝对收敛与条件收敛交错级数莱布尼茨定理幂级数的概念收敛半
精品文档 等本息法和等本金法的两种算公式 一: 按等额本金还款 法:贷款额为: a, 月利率为: i , 年利率为: I , 还款月数: n, an 第 n 个月贷款剩余本金: a1=a, a2=a-a/n, a3=a-2*a/n ...次类推 还款利息总和为Y 每月应还本金: a/n 每月应还利息: an*i 每期还款 a/n +an*i 支付利息 Y=( n+1)*a*i/2 还款总额 =( n+1)*a*i/2+a 等本金法的算等本金(减法):算公式: 每月本金=款÷期数 第一个月的月供 =每月本金+款×月利率 第二个月的月供 =每月本金+(款-已本金)×月利率 申10 万 10 年个人住房商性款,算每月的月供款?(月利率: 4.7925 ‰)算果: 每月本金: 100000÷120= 833 元 第一个月的月供:833+ 100000×4.7925 ‰=1312.3 元 第二个月的月供:833+( 100000- 833)×4.7925 ‰= 1308.3 元 如此推?? 二 : 按等本息款法:款 a,月利率 i ,年利率 I ,款月数n,每月款 b,款利息和 Y 1: I =12×i 2: Y=n×b- a 3:第一月款利息:a×i 第二月款利息:〔a-( b- a×i )〕×i =( a×i -b)×( 1+ i ) ^1 +b 第三月款利息:{ a-( b- a×i )-〔 b-( a×i - b)×( 1+ i ) ^1 -b〕}×i =( a×i -b)×( 1+i ) ^2 + b 第四月款利息:=( a×i - b)×( 1+ i ) ^3 + b 第 n 月款利息:=(a×i - b)×( 1+ i ) ^( n- 1)+ b 求以上和:Y=( a×i -b)×〔( 1+ i ) ^n- 1〕÷i + n×b 4:以上两Y 相等求得 月均款 :b = a×i ×( 1+ i ) ^n ÷〔( 1+ i )^n - 1〕 支付利息 :Y = n×a×i ×( 1+i ) ^n ÷〔( 1+ i ) ^n - 1〕- a 款 :n ×a×i ×( 1+ i )^n ÷〔( 1+ i ) ^n- 1〕 注:a^b 表示 a 的 b 次方。 等本息法的算 ----- 例如下: 如款 21 万, 20 年,月利率 3.465 ‰按照上 面的等本息公式算 月均款 :b = a×i ×( 1+ i ) ^n ÷〔( 1+ i )^n - 1〕即: =1290.11017 即每个月款1290 元。 。 1欢迎下载
第一章人寿保险的主要类型 一、普通型人寿保险 定期寿险:以死亡为给付条件且期限固定。 优点:保费低廉 可以无现金价值,可续保性,可转换性 终身寿险:以死亡为给付条件且期限为终身。 优点:可得到永久保障,有退费权利,获得退保现金价值 分类:普通终身寿险、限期交费终身寿险、趸交终身保险 两全保险:以死亡或生存为给付条件的。储蓄性极强。 定期死亡险与生存险的结合,净保费由危险保费和储蓄保费组成。 年金保险:以生存为给付条件,按约定分期给付生存保险金,且给付间隔不超过一年。 ◆交费方式:趸交年金、期交年金 ◆给付开始日期:即期年金、延期年金 终身年金 ◆给付方式:最低保证年金确定给付年金(规定了最低保证年数) 退还年金(退还购买金额与领取金额的差额) 定期生存年金 个人年金 ◆被保险人数联合年金(均生存为给付条件) 最后生存者年金(至少一个生存为给付条件,给付金
额不变) 联合及生存者年金(至少一个生存为给付条件,给付 金额随被保险人减少调整) ◆给付额是否变动:定额年金、变额年金 二、新型人寿保险 (1)分红保险 ?分红保险、非分红保险以及分红保险产品与其附加的非分红保险产品必须分设帐户、独立核算。 采用固定费用率的,相应的附加保费收入和佣金、管理费用等不列入分红保险帐户; 采用固定死亡率方法的,相应的死亡保费收入和风险保额给付等不列入分红保险帐户 ?特点: ○1保单持有人享受经营成果。至少将当年可分配盈余的70%分配给客户 ○2保单持有人承担一定风险 ○3定价精算假设比较保守 ○4保险给付、退保金中含有红利 ?保单红利 利源:利差益、死差益、费差益、失效收益、资产增值、预期利润、残疾给付等与实际给付的差额 分配:满足公平性原则和可持续性原则 分配方式:现金红利、增额红利
精算数学读书笔记 ————数学班 王秋阳 09080124 摘要:利用生命函数,以预定利率和预定死亡率为基础计算定期寿险、终身寿险、延期寿险、生存保险、两全保险的精算现值。 关键字:生命函数、剩余寿命、生命表、精算现值、定期寿险、终身寿险、延期寿险、生存保险、两全保险 一、生命函数 1、初生婴儿未来寿命X 的分布函数()()Pr F x X x =≤ 0x ≥ 生存函数()()Pr S x X x =≥ 初生婴儿在x 至z 之间死亡的概率()()()Pr x X z S x S z <≤=- 3、剩余寿命F (x ):分布函数Pr(())()()()() t x q T X t pr x X x t X x s x s x t s x =≤=<≤+>-+= 生存函数 Pr(())Pr()() () t x p T x t X x t X t s x t s x =>=>+>+= :x 岁的人至少能活到x+1岁的概率 :x 岁的人将在1年内去世的概率 :x 岁的人将在x+t 岁至x+t+u 岁之间去世的概率 整值剩余寿命T(x):(), ()1,0,1,K X k k T x k k =≤<+= 概率函数 ()()()()1 1Pr(())Pr(()1) Pr 1Pr k x k x k x k x k x x k x k K X k k T x k T x k T x k q q p p p q q +++==≤<+=≤+-≤= -=-=?= 死力()() ln[()]()() x s x f x s x s x s x μ''=- ==- 死力与生存函数的关系 0()exp{} exp{} x s x t t x s x s x ds p ds μμ+=-=-?? 死力与密度函数的关系()()}0 exp x x x s f x s x ds μμμ?=?=?-??? x p x q x t u q
汽车保险论文关于汽车保险论文: 汽车保险精算定价模型研究综述 摘要:汽车保险定价模型在非寿险精算领域内占有重要地位,本文对车险定价模型一百多年来的研究进展作了综述性的回顾。首先,本文介绍了车险定价模型的先验估费方法;其次着重介绍了时齐的后验估费方法,以及时变的先验后验相结合的精算模型;最后提出了车险定价模型的未来发展方向。 关键词:汽车保险;先验估费;后验估费;索赔频率;索赔额 一、前言 汽车保险是承保汽车因自然灾害或意外事故导致的损失或民事赔偿责任的综合性财产保险,属于运输工具保险。汽车保险是伴随着19世纪后期汽车在欧洲的普及而出现的。当时,汽车交通事故导致的意外伤害和财产损失不断增加,引起了精明的保险商对汽车保险的关注。第一张汽车保险单是由英国的“法律意外保险有限公司”于1895年签发的保费为10至100英镑的汽车第三者责任保险,随后汽车保险又扩展到了汽车火灾险和汽车碰撞损失险[1]。第二次世界大战结束后,发达国家汽车制造工业迅速扩张,汽车保险业也得到飞速发展,成为各国财产保险中最重要的业务险种。在发达国家,汽车保险的保费收入一般要占财产险总保费的50%左右。在我国实施交通事故强制保险制度后,汽车保险也约占到总财产险保费的70%。 汽车保险的精算定价是与汽车保险同时诞生的,至今已经有一百多年的历史了。由于汽车保险已成为财产保险中名副其实的“龙头险种”,其经营效益的优劣直接影响到各财险公司财务盈亏,因此,各
家保险公司对车险精算定价极其重视,车险精算也成为非寿险精算领域的重要研究内容。汽车保险的精算定价是保险公司承保风险之前最主要和最重要的风险管理工具。精算师和学者进行了广泛研究,定价模型也历经先验估费模型、后验估费模型、先验与后验相结合模型,得到不断的改进和应用。本文将概括性介绍汽车保险精算研究中的经典模型、研究进展和重要热点,为今后的研究提供一些启示和借鉴作用。 二、先验估费阶段 在20世纪50年代之前,汽车保险的定价方法是按照寿险均衡保费定价原则进行定价的。投保人的风险纯保费P为 P=E(L)(1) L表示被保险人的损失风险。为了体现定价的公平性,和寿险精算(生命表)中选择年龄、性别等作为风险分类的先验风险变量一样,非寿险精算师们依据投保人先前影响风险的先验变量(风险因素)确定其风险保费水平(费率等级)。在这种先验估费方法中,汽车的类型、用途和被保险人居住区域是最主要的先验定价变量。例如,欧洲大多数国家把汽车的排气量作为汽车保险的主要车型风险分类变量;荷兰的保险公司还把投保人的行驶里程作为先验风险分类变量[1]。 先验估费的基本原理就是把具有相同先验风险因素的投保人分入同一风险等级(收取相同保险费),在同一风险等级的保单组合内进行均衡保费定价。先验估费方法移植了寿险精算均衡保费定价方法,简便易行。但是由于相比人寿保险,汽车保险的保险标的具有更
《保险精算学》笔记:生命表函数与生命表构造 第一节生命表函数 一、生存函数 1、定义: 2、概率意义:新生儿能活到的概率 3、与分布函数的关系: 4、与密度函数的关系: 二、剩余寿命 1、定义:已经活到x岁的人(简记),还能继续存活的时间,称为剩余寿命,记作T(x)。 2、剩余寿命的分布函数 5、:, 它的概率意义为:将在未来的年去世的概率,简记 3、剩余寿命的生存函数:, 它的概率意义为:能活过岁的概率,简记 特别: (1) (2) (3) (4):将在岁与岁之间去世的概率 4、整值剩余寿命
(1)定义:未来存活的完整年数,简记 (2)概率函数: 5、剩余寿命的期望与方差 (1)期望剩余寿命:剩余寿命的期望值(均值),简记 (2)剩余寿命的方差: 6、整值剩余寿命的期望与方差 (1)期望整值剩余寿命:整值剩余寿命的期望值(均值),简记 (2)整值剩余寿命的方差: 2 三、死亡效力 1、定义:的人瞬时死亡率,记作 2、死亡效力与生存函数的关系 3、死亡效力与密度函数的关系 4、死亡效力表示剩余寿命的密度函数
记为剩余寿命的分布函数,为的密度函数,则 第二节生命表的构造 一、有关寿命分布的参数模型 1、de Moivre模型(1729) 2、Gompertz模型(1825) 3、Makeham模型(1860) 4、Weibull模型(1939) 二、生命表的起源 1、参数模型的缺点 (1)至今为止找不到非常合适的寿命分布拟合模型。这四个常用模型的拟合效果不令人满意。 (2)使用这些参数模型推测未来的寿命状况会产生很大的误差 (3)寿险常不使用参数模型拟合寿命分布,而是使用非参数方法确定的生命表拟合人类寿命的分布。 (4)在非寿险领域,常用参数模型拟合物体寿命的分布。 2、生命表的起源
保险精算中的人寿保险的精算现值的模型 一、人寿保险简介 保险精算学主要分为两大类:一个是所谓的人寿保险(寿险精算),另一个是非人寿保险。前者主要以人的寿命、身体或健康为“保险标的”的保险。 非人身保险主要包括:汽车保险、屋主保险、运输保险、责任保险、信用保险、保证保险等。而这次我们主要讨论人寿保险。 狭义的人寿保险是以被保险人在保障期是否死亡作为保险标的的一种保险。 广义的人寿保险是以被保险人的寿命作为保险标的的一种保险。它包括以保障期内被保险人死亡为标的的狭义寿险,也包括以保障期内被保险人生存为标底的生存保险和两全保险。 人寿保险的分类 根据不同的标准,人寿保险有不同的分类: (1)以被保险人的受益金额是否恒定进行划分,可分为:定额受益保险,变额受益保险。 (2)以保障期是否有限进行划分,可分为:定期寿险和终身寿险。 (3)以保单签约日和保障期是否同时进行划分分为:非延期保险和延期保险。(4)以保障标的进行划分,可分为:人寿保险(狭义)、生存保险和两全保险。人寿保险的特点 1:保障的长期性 这使得从投保到赔付期间的投资收益(利息)成为不容忽视的因素。 2:保险赔付金额和赔付时间的不确定性 人寿保险的赔付金额和赔付时间依赖于被保险人的生命状况。被保险人的死亡时间是一个随机变量。这就意味着保险公司的赔付额也是一个随机变量,它依赖于被保险人剩余寿命分布。 3:被保障人群的大多数性 保险公司可以依靠概率统计的原理计算出平均赔付并可预测将来的风险。 人寿保险趸缴纯保费厘定的原理 1、假定 传统的人寿保险产品的趸缴纯保费是在如下假定下厘定的:假定一:同性别、同年龄、同时参保的被保险人的剩余寿命独立同分布。假定二:被保险人的剩
一、按揭贷款等额本息还款计算公式 1、计算公式 每月还本付息金额=[本金×月利率×(1+月利率)还款月数]/(1+月利率)还款月数-1] 其中:每月利息=剩余本金×贷款月利率 每月本金=每月月供额-每月利息 计算原则:银行从每月月供款中,先收剩余本金利息,后收本金;利息在月供款中的比例中虽剩余本金的减少而降低,本金在月供款中的比例因而升高,但月供总额保持不变。 2、商业性房贷案例 贷款本金为300000元人民币 还款期为10年(即120个月) 根据5.51%的年利率计算,月利率为4.592‰ 代入等额本金还款计算公式计算: 每月还本付息金额=[300000×4.592‰×(1+月利率)120]/[(1+月利率)120-1] 由此,可计算每月的还款额为3257.28元人民币 二、按揭贷款等额本金还款计算公式 1、计算公式 每月还本付息金额=(本金/还款月数)+(本金-累计已还本金)×月利率 每月本金=总本金/还款月数 每月利息=(本金-累计已还本金)×月利率 计算原则:每月归还的本金额始终不变,利息随剩余本金的减少而减少 2、商业性房贷案例 贷款本金为300000元人民币 还款期为10年(即120个月) 根据5.51%的年利率计算,月利率为4.592‰ 代入按月递减还款计算公式计算: (第一个月)还本付息金额=(300000/120)+ (300000-0)×4.592‰ 由此,可计算第一个月的还款额为3877.5元人民币 (第二个月) 还本付息金额=(300000/120)+ (300000-2500)×4.592‰ 由此,可计算第一个月的还款额为3866.02元人民币 (第二个月) 还本付息金额=(300000/120)+ (300000-5000)×4.592‰
第一章生命表 1.给出生存函数() 2 2500 x s x e- =,求: (1)人在50岁~60岁之间死亡的概率。 (2)50岁的人在60岁以前死亡的概率。 (3)人能活到70岁的概率。(4)50岁的人能活到70岁的概率。 () () () 1050 2050 (5060)50(60) 50(60) (50) (70)(70) 70 (50) P X s s s s q s P X s s p s <<=- - = >= = 2.已知生存函数S(x)=1000-x3/2 ,0≤x≤100,求(1)F(x)(2)f(x)(3)F T(t)(4)f T(f)(5)E(x) 3. 已知Pr[5<T(60)≤6]=,Pr[T(60)>5]=,求q65。 ()() () 5|60560 65 65(66)65 0.1895,0.92094 (60)(60) 65(66) 0.2058 (65) s s s q p s s s s q s - ==== - ∴== 4.已知Pr[T(30)>40]=,Pr[T(30)≤30]=,求10p60 Pr[T(30)>40]=40P30=S(70)/S(30)= S(70)=×S(30) Pr[T(30)≤30]=S(30)-S(60)/S(30)= S(60)=×S(30)
∴10p 60= S(70)/S (60)== 5.给出45岁人的取整余命分布如下表: k 0 1 2 3 4 5 6 7 8 9 45k q .0050 .0060 .0075 .0095 .0120 .0130 .0165 .0205 .0250 .0300 求:1)45岁的人在5年内死亡的概率;2)48岁的人在3年内死亡的概率;3)50岁的人在52岁至55岁之间死亡的概率。 (1)5q 45=(++++)= 6.这题so easy 就自己算吧 7.设一个人数为1000的现年36岁的群体,根据本章中的生命表计算(取整) (1)3年后群体中的预期生存人数(2)在40岁以前死亡的人数(3)在45-50之间挂的人 (1)l 39=l 36×3P 36=l 36(1-3q 36)=1500×()≈1492 (2)4d 36=l 36×4q 36=1500×(+)≈11 (3)l 36×9|5q 36=l 36×9P 35×5q 45=1500××=1500×≈33 8. 已知800.07q =,803129d =,求81l 。 808081 808080 0.07d l l q l l -= ==
保险精算(寿险)模拟教学系统 第一章前言 一、系统概述 本技术白皮书主要阐述保险精算系统的项目背景和使用现状以及建设目标、总体解决方案,从多个 角度描述本系统的优势和特点,并结合产品特点提出适合贵校的系统总体框架。 本设计方案是公司组织多名在保险行业有多年从业经验的精算师开发而成,是目前国内专业精算软件 中唯一针对高校保险专业而开发的教学系统。 本系统可以为金融实验室构建一个精算实训平台,是保险精算信息化处理、操作和管理平台,充分利 用科技手段实现精算理论教学和精算实际应用相结合的目标。 二、发展趋势 9 0 年代以来,保险精算在中国保险业得到了很大的发展,这种发展不仅表现在保险精算算法上,还 表现在保险教育上,目前国内综合性高校相继开办保险精算专业或保险精算课程,教授保险精算理论知识, 部份高校还开设培养保险精算专业研究生,而且更主要的发展体现在保险精算从理念接受、学习借鉴和探 索阶段,开始向着保险业乃至相关行业的实际操作和应用阶段迈进,即精算理论与技术在中国保险实务中 得到了不同程度的应用。 三、开发背景 随着保险精算信息处理技术的发展,为了适应新形势的要求,各高校基于保险专业教学的需要,开始 希望有一套保险精算软件系统来构建一个模拟保险精算实验室,模拟整个精算过程、结果,让学生有一个 完善、实用、真实的实践环境,去检验所学到的保精算理论知识。正是基于这种市场需求,公司I T 技术 专家、美国/ 香港/ 大陆注册精算师及知名财经高校保险精算教授等核心开发力量共同合作,历经一年时 间开发了本系统,以满足高校保险精算教学需求。 通过对本系统的实训操作,可以促使学生关注最新的信息技术,训练学生的实际操作能力,为金融专 业及其它相关专业的学生走向社会提供一个理论结合实际的实习环境。 本系统是金融保险人才培养和科学研究的重要工具。为了培养面向2 1 世纪的新型实用人才,本系统 提供的真实的操作环境,使学生在掌握理论知识的同时熟悉实际操作过程,改变其知识结构,培养保险行 业真正需要的实用性人才,增强学生的社会就业竞争力。 第二章解决方案 一、概述
燕山大学 寿险精算课程设计论文 题目:寿险责任准备金的两类精算模型应用研究 学院(系):理学院 年级专业:数理统计 学号: 110108020037 学生姓名:黎骕骦 指导教师:王永茂 教授职称:教授 燕山大学课程设计(论文)任务书
院(系):基层教学单位: 说明:此表一式四份,学生、指导教师、基层教学单位、系部各一份。 年月日 燕山大学课程设计评语表
摘要 正确的预估责任准备金,是为更好预估保险公司的负债。本论文直接探讨寿险责任准备金的两类精算模型,即在换算函数下的过去法和未来法在计算机系统中实现时的比较,通过数据比较分析发现在计算机系统中应采用未来法计算准备金,对类似的寿险精算概念在计算机中实现有较高的借鉴价值。 关键词:寿险;责任准备金;精算;计算机实现。 Abstract The correct estimated liability reserve funds, to better forecast the liabilities of insurance company. This paper discusses two types of life insurance liability reserve funds directly actuarial model, namely the conversion under the function of the past and the future method is implemented in a computer system, by comparing and analyzing the data found in the computer system should be adopted in the future method to calculate reserves, the similar life insurance actuarial concepts in computer in implementing the existing of high reference value. Key words: life insurance; Liability reserve funds; Actuarial science. Computer implementation
1.(x)=1-F ()=P (X>x) >=0x X r S r x x 生存函数: 2.我们约定:x (0)=0,S (0)=1;x F 3.r ()(X>y )= ()X X S y P X x S x > 4. =Pr(T(x)>t)=Pr(X>x+t ) (+)=()t x X X p X x S x t S x > 5. ++q =Pr[t 等额本息和等额本金还款的解释及公式推导过程 住房贷款的分期还款方式分为等额本息付款和等额本金方式付款两种方式,两种付款方式的月付款额各不相同,计算方式也不一样。网上分别有着两种还款方式的计算公式,然而,对于这两个公式的来源却很少有解释,或者解释是粗略的或错误的。本人经过一段时间的思考,运用数学理论推导出了这两个计算公式。本文将从原理上解释一下这两种还款方式的原理及计算公式的推导过程。 无论哪种还款方式,都有一个共同点,就是每月的还款额(也称月供)中包含两个部分:本金还款和利息还款。 月还款额 = 当月本金还款 + 当月利息 其中本金还款是真正偿还贷款的,每月还款之后,贷款的剩余本金就相应减少:当月剩余本金=上月剩余本金 — 当月本金还款 直到最后一个月,全部本金偿还完毕。 利息还款是用来偿还剩余本金在本月所产生的利息,每月还款中必须将本月本金所产生的利息付清。 当月利息 = 上月剩余本金 × 月利率 其中月利率=年利率÷12,由上面利息偿还公式中可见,月利息是与上月剩余本金成正比的,由于在贷款初期,剩余本金较多,所以贷款初期每月的利息较多,月还款额中偿还利息的份额较重。随着还款次数的增多,剩余本金将逐渐减少,月还款的利息也相应减少,直到最后一个月,本金全部还清,利息付最后一次,下个月将既无本金又无利息,至此,全部贷款偿还完毕。 两种贷款的偿还原理就如上所述,下面推导一下两种还款方式的具体计算公式。1. 等额本金还款方式 等额本金还款方式比较简单顾名思义,这种方式下,每次还款的本金还款数是一样的。以下结合一事例帮助理解公式推导过程。比如贷款24万,年利率7.2%,则月利率为7.2%÷12=0.6%,分20年还完。 当月本金还款=总贷款数÷还款次数=240000÷(12×20) =1000 寿险精算数学 考试时间:4小时 考试形式:客观判断题 考试内容和要求: 考生应掌握生命表、纯保费(趸缴、均衡)、责任准备金(均衡、修正)、总保费、多元生命函数、多元风险模型等主要内容。能够熟练运用精算现值的概念以及平衡原理计算纯保费、年金和责任准备金。理解纯保费与总保费的影响因素的差别。对于多元生命函数和多元风险模型,能够熟练运用精算现值的概念以及平衡原理计算纯保费和年金。初步了解养老金计划的精算方法。 A. 生存分布和生命表(分数比例约为10%) 1. 各种生存分布及其特征,例如:密度函数、死亡力、剩余寿命变量和的矩 2. 生命表的结构及其度量指标,如,, 3. 关于分数年龄的假设 B. 趸缴纯保费(分数比例约为10%) 1. 精算现值 2. 离散型与连续型的各种寿险模型及其纯保费的计算 3. 现值变量的方差 4. 在死亡均匀假设下离散型与连续型纯保费的关系 C. 生存年金(分数比例约为10%) 1. 离散型与连续型的各种生存年金模型及其纯保费的计算 2. 现值随机变量的方差 3. 特殊的两种生存年金 a. 完全期末年金 b. 比例期初年金 4. 寿险与生存年金纯保费的递推关系 5. 寿险纯保费与生存年金纯保费的关系 D. 均衡纯保费(分数比例约为15%) 1. 平衡原理 2. 各种寿险模型(完全离散、完全连续、半连续、每年缴次)的年缴纯保费 3. 亏损变量的方差 4. 特殊的两种寿险模型 a. 保费可部分返还的寿险(对应的纯保费称为比例保费) b. 累积增额受益的寿险 E. 均衡纯保费的责任准备金(分数比例约为20%) 1. 平衡原理与责任准备金的出现 2. 各种寿险模型(完全离散、完全连续、半连续、每年缴次)的责任准备金 3. 亏损变量的方差 4. 责任准备金通常的四种计算方法 5. 比例责任准备金等额本息和等额本金还款原理解释及公式推导过程
寿险精算数学