通7-2

息化主管部⻔的共同努⼒下，在各乘⽤⻋制造企业、整⻋物流企业、⾏业协会的积极⽀持下，整⻋物流市场秩规运输承担⼀部分责任。

严格执法 禁⽌
⻋辆运输⻋“6+2”违法装载
⻋辆运输⻋“7+2”违法装载. All Rights Reserved.
深⼊推进⻋辆运输⻋治理⼯作的通知》（交办运函〔 〕 号）的要求，强化路⾯执法检查，重点加强对⻋辆运输⻋“ + ”“ + ”超⻓违法运输⾏为的查处，⼀经发现，严格依据《中华⼈⺠共和国道路交通安全法》《中华⼈⺠共和国辆运输⻋，吊销其⻋辆营运证；
对 年内违法超限运输超过 次的⻋辆运输⻋驾驶⼈，责令其停⽌从事营业性运输；
整⻋物流企业 年内违法超限运输的⻋辆运输⻋超过本单位货运⻋辆总数 %的，责令整⻋物流企业停业整顿；情节严重的，吊销其道路运输经营许可证，并向社
. All Rights Reserved.
⼈、整⻋物流企业以及指使、强令⻋辆运输⻋驾驶⼈违法运输乘⽤⻋的企业纳⼊严重违法超限超载运输失信当事⼈名单，按照《交通⻋辆运输⻋合规装载⽰意图
平头铰接⻋辆运输⻋
⻓头铰接⻋辆运输⻋
中置轴⻋辆运输⻋
. All Rights Reserved.。

爆破安全监理停工整改通知CSJL-2016-016贵州六盘水滕达爆破工程服务有限公司印象城爆破施工项目部：受“六盘水恒维房地产开发有限公司”的委托，我公司承接了“凤凰城市综合体A-23#-1、A-23#-2号地块平场爆破工程”的爆破安全监理工作，监理工作自2016年3月1日开始至今，我公司安排了专业监理人员对整个爆破施工过程和流程进行了爆破安全监理。

爆破施工单位基本实现了爆破施工的安全和规范，爆破有害效应基本能控制在《爆破安全规程》（GB6722-2014）要求的范围之内，但贵单位在爆破施工过程中仍存在部分安全隐患及不规范施工现象，为了确保爆破施工的安全顺利进行，现特书面告知贵单位对在爆破施工过程中存在的安全隐患、不规范操作、违规现象等进行认真停工整改，以确保该爆破施工项目的安全实施，具体整改情况如下：一、施工资料有待完善，《爆破施工日志》必须及时祥细填写。

二、不符合《爆破设计施工方案》的情况：1、爆破作业必须按照经过爆破评估单位已安全评估的《爆破设计方案》进行施工，不得进行深孔爆破，只能进行浅孔爆破作业。

2、爆破作业过程中必须严格控制最大单孔装药量和一次起爆总药量，必须确保填塞质量，必须进行有效的安全防护。

3、由于爆破施工位于市中心，爆破区域地处繁华交通要道，爆破时爆破安全警戒距离范围过小、警戒力量不足、警戒距离过近，警戒时警戒哨子配备不足，存在安全警戒死角现象。

爆破区域周围安全警戒人员配备不足、安全警戒人员分工不明确、责任不到位时不得进行起爆。

4、实施爆破时必须申请实施交通管制，以确保爆破施工安全。

5、爆破施工现场安全警示标志设置不到位，通往爆区路口警戒线和警戒标识设置不足。

6、通往爆破区路口未及时设置爆破公告和施工公告。

7、盛夏且多雨，爆破施工现场临时堆放的爆破器材未及时覆盖。

8、现场临时存放的民用爆炸物品堆放不符合规范，炸药与雷管之间的堆放间距不符合《爆破安全规程》-GB6722-2014要求。

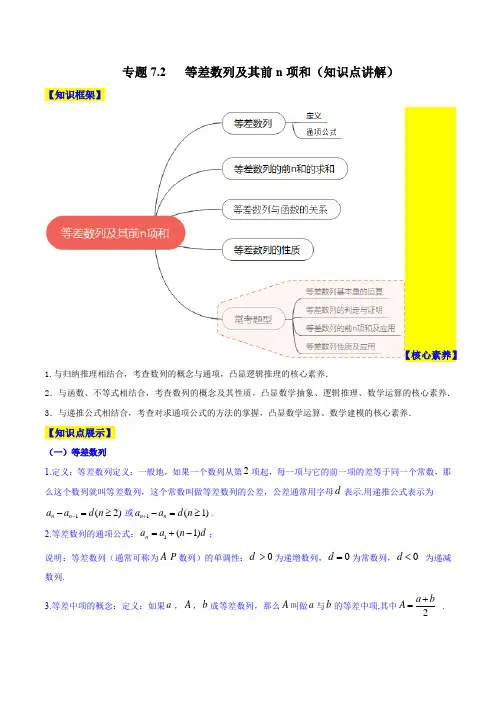
专题7.2 等差数列及其前n 项和（知识点讲解）【知识框架】【核心素养】1.与归纳推理相结合，考查数列的概念与通项，凸显逻辑推理的核心素养．2．与函数、不等式相结合，考查数列的概念及其性质，凸显数学抽象、逻辑推理、数学运算的核心素养． 3．与递推公式相结合，考查对求通项公式的方法的掌握，凸显数学运算、数学建模的核心素养．【知识点展示】（一）等差数列1.定义：等差数列定义：一般地，如果一个数列从第项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫等差数列，这个常数叫做等差数列的公差，公差通常用字母表示.用递推公式表示为或.2.等差数列的通项公式：；说明：等差数列（通常可称为数列）的单调性：为递增数列，为常数列， 为递减数列.3.等差中项的概念：定义：如果，，成等差数列，那么叫做与的等差中项,其中 . 2d 1(2)n n a a d n --=≥1(1)n n a a d n +-=≥1(1)n a a n d =+-A P d 0>0d =0d <a A b A a b 2a bA +=，，成等差数列. 4.要注意概念中的“从第2项起”．如果一个数列不是从第2项起，而是从第3项或第4项起，每一项与它前一项的差是同一个常数，那么此数列不是等差数列． 5.注意区分等差数列定义中同一个常数与常数的区别． （二）等差数列的前和的求和公式：. （三）等差数列的通项公式及前n 项和公式与函数的关系(1)当d ≠0时，等差数列{a n }的通项公式a n ＝dn ＋(a 1－d )是关于d 的一次函数． (2)当d ≠0时，等差数列{a n }的前n 项和S n ＝d2n 2＋⎝⎛⎭⎫a 1－d 2n 是关于n 的二次函数． （四）等差数列的前n 项和的最值在等差数列{a n }中，a 1>0，d <0，则S n 存在最大值；若a 1<0，d >0，则S n 存在最小值． （五）等差数列的性质：（1）在等差数列中，从第2项起，每一项是它相邻二项的等差中项；（2）在等差数列中，相隔等距离的项组成的数列是等差数列， 如：，，，，……；，，，，……；（3）在等差数列中，对任意，，，；（4）在等差数列中，若，，，且，则,特殊地，时，则，是的等差中项.（5）等差数列被均匀分段求和后，得到的数列仍是等差数列，即成等差数列.（6）两个等差数列{}n a 与{}n b 的和差的数列{}n n a b ±仍为等差数列． （7）若数列{}n a 是等差数列,则{}n ka 仍为等差数列．（8）设数列是等差数列，且公差为，（Ⅰ）若项数为偶数，设共有项，则①-S S nd =奇偶； ②；（Ⅱ）若项数为奇数，设共有项，则①S S -偶奇(中间项)；②. （9）等差数列中，(),p q a q a p p q ==≠,则0p q a +=,m n m n S S S mnd +=++.a Ab ⇔2a bA +=n 11()(1)22n n n a a n n S na d +-==+{}n a {}n a 1a 3a 5a 7a 3a 8a 13a 18a {}n a m n N +∈()n m a a n m d =+-n ma a d n m-=-()m n ≠{}n a m n p q N +∈m n p q +=+m n p q a a a a +=+{}n a d 2n 1n n S a S a +=奇偶21n -n a a ==中1S nS n =-奇偶（10）如果两个等差数列有公共项，那么由它们的公共项顺次组成的新数列也是等差数列，且新等差数列的公差是两个原等差数列公差的最小公倍数．（11）若与{}n b 为等差数列，且前n 项和分别为n S 与'n S ，则2121'm m m m a Sb S --=. （12）等差数列的增减性：0d >时为递增数列，且当10a <时前n 项和n S 有最小值．0d <时为递减数列，且当10a >时前n 项和n S 有最大值．【常考题型剖析】题型一：等差数列基本量的运算例1.（2019·全国·高考真题（理））记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则（ ） A ．25n a n =- B ．310n a n =- C ．228n S n n =-D ．2122n S n n =-【答案】A 【解析】 【分析】等差数列通项公式与前n 项和公式．本题还可用排除，对B ，55a =，44(72)1002S -+==-≠，排除B ，对C ，245540,25850105S a S S ==-=⨯-⨯-=≠，排除C ．对D ，24554150,5250522S a S S ==-=⨯-⨯-=≠，排除D ，故选A ． 【详解】由题知，41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩，解得132a d =-⎧⎨=⎩，∴25n a n =-，故选A ．例2．（2022·全国·高考真题（文））记n S 为等差数列{}n a 的前n 项和．若32236S S =+，则公差d =_______． 【答案】2 【解析】【分析】转化条件为()112+226a d a d =++，即可得解. 【详解】由32236S S =+可得()()123122+36a a a a a +=++，化简得31226a a a =++， 即()112+226a d a d =++，解得2d =. 故答案为：2.{}n a【总结提升】1.解决等差数列运算问题的思想方法(1)方程思想：等差数列的基本量为首项a 1和公差d ，通常利用已知条件及通项公式或前n 项和公式列方程(组)求解，等差数列中包含a 1，d ，n ，a n ，S n 五个量，可“知三求二”．(2)整体思想：当所给条件只有一个时，可将已知和所求都用a 1，d 表示，寻求两者间的联系，整体代换即可求解．(3)利用性质：运用等差数列性质可以化繁为简、优化解题过程． 2.等差数列的通项公式及前n 项和公式，共涉及五个量1,,,,n n a d n a S ，知其中三个就能求另外两个,即知三求二，多利用方程组的思想，体现了用方程的思想解决问题.3.特殊设法:三个数成等差数列，一般设为,,a d a a d -+；四个数成等差数列，一般设为3,,,3a d a d a d a d --++.这对已知和,求数列各项,运算很方便.题型二：等差数列的判定与证明例3. （2020·山东·高考真题）某男子擅长走路，9天共走了1260里，其中第1天、第4天、第7天所走的路程之和为390里.若从第2天起，每天比前一天多走的路程相同，问该男子第5天走多少里.这是我国古代数学专著《九章算术》中的一个问题，请尝试解决. 【答案】140里. 【解析】 【分析】由条件确定，该男子这9天中每天走的路程数构成等差数列，根据等差数列的通项公式，和前n 项和公式，列式求解.【详解】解：因为从第2天起，每天比前一天多走的路程相同， 所以该男子这9天中每天走的路程数构成等差数列， 设该数列为{}n a ，第1天走的路程数为首项1a ，公差为d ， 则91260S =，147390a a a ++=. 因为1(1)2n n n S na d -=+，1(1)n a a n d =+-， 1(1)n a a n d =+-11()(1)22n n n a a n n S na d +-==+所以11119(91)91260236390a d a a d a d ⨯-⎧+=⎪⎨⎪++++=⎩，解得110010a d =⎧⎨=⎩，则514100410140a a d =+=+⨯=， 所以该男子第5天走140里.例4.（2021·全国·高考真题（文））记n S 为数列{}n a 的前n 项和，已知210,3n a a a >=，且数列是等差数列，证明：{}n a 是等差数列. 【答案】证明见解析. 【解析】 【分析】的公差d，进一步写出的通项，从而求出{}n a 的通项公式，最终得证. 【详解】∵数列是等差数列，设公差为d(n -()n *∈N∴12n S a n =，()n *∈N∴当2n ≥时，()221111112n n n a S S a n a n a n a -=-=--=- 当1n =时，11121=a a a ⨯-，满足112n a a n a =-， ∴{}n a 的通项公式为112n a a n a =-，()n *∈N ∴()()111111221=2n n a a a n a a n a a --=----⎡⎤⎣⎦∴{}n a 是等差数列.例5．（2021·全国·高考真题（理））已知数列{}n a 的各项均为正数，记n S 为{}n a 的前n 项和，从下面①①①中选取两个作为条件，证明另外一个成立． ①数列{}n a是等差数列：②数列是等差数列；③213a a =． 注：若选择不同的组合分别解答，则按第一个解答计分． 【答案】证明过程见解析 【解析】 【分析】选①②作条件证明③时，结合,n n a S 的关系求出n a ，利用{}n a 是等差数列可证213a a =；也可分别设出公差，写出各自的通项公式后利用两者的关系，对照系数，得到等量关系，进行证明.选②③作条件证明①时，an b =+，结合,n n a S 的关系求出n a ，根据213a a =可求b ，然后可证{}n a 是等差数列；也可利用前两项的差求出公差，然后求出通项公式，进而证明出结论. 【详解】选①②作条件证明③：[方法一]：待定系数法+n a 与n S 关系式(0)an b a +>，则()2n S an b =+， 当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为{}n a 也是等差数列，所以()()222a b a a a b +=-+，解得0b =；所以()221n a a n =-，21a a =，故22133a a a ==.[方法二] ：待定系数法设等差数列{}n a 的公差为d，等差数列的公差为1d ，1(1)n d -，将1(1)2n n n S na d -=+1(1)n d -，化简得())2222211111222d d n a n d n d n d ⎛⎫+-=+-+⎪⎝⎭对于n +∀∈N恒成立．则有21211112,240,d d a d d d ⎧=⎪⎪-=-⎨=，解得112d d a =．所以213a a =． 选①③作条件证明②：因为213a a =，{}n a 是等差数列， 所以公差2112d a a a =-=， 所以()21112n n n S na d n a -=+=，)1n =+=所以是等差数列. 选②③作条件证明①： [方法一]：定义法(0)an b a +>，则()2n S an b =+， 当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为213a a =，所以()()2323a a b a b +=+，解得0b =或43a b =-； 当0b =时，()221,21n a a a a n ==-，当2n ≥时，2-1-2n n a a a =满足等差数列的定义，此时{}n a 为等差数列；当43a b =-4=3an b an a +-03a=-<不合题意，舍去. 综上可知{}n a 为等差数列. [方法二]【最优解】：求解通项公式因为213a a =，因为也为等差数列，所以公差1d()11n d =-=故21n S n a =，当2n ≥时，()()221111121n n n a S S n a n a n a -=-=--=-，当1n =时，满足上式，故{}n a 的通项公式为()121n a n a =-，所以()1123n a n a -=-，112n n a a a --=，符合题意. 【整体点评】这类题型在解答题中较为罕见，求解的关键是牢牢抓住已知条件，结合相关公式，逐步推演，选①②时，法一：利用等差数列的通项公式是关于n(0)an b a =+>，平方后得到n S 的关系式，利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩得到{}n a 的通项公式，进而得到213a a =，是选择①②证明③的通式通法；法二：分别设出{}n a 与{}n S的公差，写出各自的通项公式后利用两者的关系，对照系数，得到等量关系1d =12d a =，进而得到213a a =；选①③时，按照正常的思维求出公差，表示出n S进行证明；选②③时，法一：利用等差数列的通项公式是关于n 的一次函数，(0)an b a =+>，结合,n n a S 的关系求出n a ，根据213a a =可求b ，然后可证{}n a两项的差1d11,1,2n nn S n a S S n -=⎧=⎨-≥⎩，求出{}n a 的通项公式，进而证明出结论. 【总结提升】等差数列的四种判断方法(1) 定义法：对于数列{}n a ，若d a a n n =-+1()n N ∈*(常数)，则数列{}n a 是等差数列； (2) 等差中项：对于数列{}n a ，若212+++=n n n a a a ()n N ∈*，则数列{}n a 是等差数列; (3)通项公式：n a pn q =+(,p q 为常数,n N ∈*)⇔是等差数列;(4)前n 项和公式：2n S An Bn =+(,A B 为常数, n N ∈*)⇔是等差数列;(5)是等差数列⇔n S n ⎧⎫⎨⎬⎩⎭是等差数列. 提醒：判断时易忽视定义中从第2项起，以后每项与前一项的差是同一常数，即易忽视验证a 2－a 1＝d 这一关键条件.题型三：等差数列的前n 项和例6．【多选题】（2022·湖南永州·三模）已知等差数列{}n a 是递减数列，n S 为其前n 项和，且78S S =，则（ ）A ．0d ＞B ．80a =C ．150S >D ．7S 、8S 均为n S 的最大值【答案】BD 【解析】【分析】根据等差数列的性质以及其前n 项和的性质，逐个选项进行判断即可求解 【详解】因为等差数列{}n a 是递减数列，所以，10n n a a +-<，所以，0d <，故A 错误； 因为78S S =，所以8870a S S =-=，故B 正确； 因为()115158151502a a S a +===，故C 错误； 因为由题意得，789000a a a >⎛ = <⎝，所以，*78()n S S S n N =≥∈，故D 正确；故选：BD例7.（2020·全国·高考真题（文））记n S 为等差数列{}n a 的前n 项和．若1262,2a a a =-+=，则10S =__________． 【答案】25 【解析】 【分析】因为{}n a 是等差数列，根据已知条件262a a +=，求出公差，根据等差数列前n 项和，即可求得答案. 【详解】{}n a 是等差数列，且12a =-，262a a +=设{}n a 等差数列的公差d根据等差数列通项公式：()11n a a n d +-= 可得1152a d a d +++= 即：()2252d d -++-+= 整理可得：66d = 解得：1d =根据等差数列前n 项和公式：*1(1),2n n n S na d n N -=+∈ 可得：()1010(101)1022045252S ⨯-=-+=-+=∴1025S =. 故答案为：25.例8.（2018·全国·高考真题（文））记n S 为等差数列{}n a 的前n 项和，已知17a =-，315S =-． （1）求{}n a 的通项公式； （2）求n S ，并求n S 的最小值．【答案】（1）n a =2n –9，（2）Sn =n 2–8n ，最小值为–16． 【解析】 【详解】分析：（1）根据等差数列前n 项和公式，求出公差，再代入等差数列通项公式得结果，（2）根据等差数列前n 项和公式得nS 的二次函数关系式，根据二次函数对称轴以及自变量为正整数求函数最值.详解：（1）设{}n a 的公差为d ，由题意得3a 1+3d =–15．由a 1=–7得d =2．所以{n a }的通项公式为n a =2n –9． （2）由（1）得Sn =n 2–8n =（n –4）2–16． 所以当n =4时，Sn 取得最小值，最小值为–16．例9.（2021·全国·高考真题）记n S 是公差不为0的等差数列{}n a 的前n 项和，若35244,a S a a S ==． （1）求数列{}n a 的通项公式n a ； （2）求使n n S a >成立的n 的最小值． 【答案】(1)26n a n =-；(2)7. 【解析】 【分析】(1)由题意首先求得3a 的值，然后结合题意求得数列的公差即可确定数列的通项公式； (2)首先求得前n 项和的表达式，然后求解二次不等式即可确定n 的最小值. 【详解】(1)由等差数列的性质可得：535S a =，则：3335,0a a a =∴=，设等差数列的公差为d ，从而有：()()22433a a a d a d d =-+=-，()()()41234333322S a a a a a d a d a a d d =+++=-+-++-=-， 从而：22d d -=-，由于公差不为零，故：2d =， 数列的通项公式为：()3326n a a n d n =+-=-.(2)由数列的通项公式可得：1264a =-=-，则：()()214252n n n S n n n -=⨯-+⨯=-，则不等式n n S a >即：2526n n n ->-，整理可得：()()160n n -->， 解得：1n <或6n >，又n 为正整数，故n 的最小值为7.例10．（2022·福建·厦门一中模拟预测）已知数列{}n a 的前n 项和n S ，11a =，0n a >，141n n n a a S +=-． (1)计算2a 的值，求{}n a 的通项公式；(2)设1(1)nn n n b a a +=-，求数列{}n b 的前2n 项和2n T ．【答案】(1)23a =，21n a n =- (2)24(21)n T n n =+ 【解析】 【分析】（1）根据11,1,2n nn S n a S S n -=⎧=⎨-≥⎩，作差得到24n n a a +-=，再根据等差数列通项公式计算可得；（2）由（1）可得(1)(21)(21)n n b n n =--+，利用并项求和法计算可得； (1)解：当1n =时，12141a a a =-，解得23a =， 由题知141n n n a a S +=-①，12141n n n a a S +++=-②，由②-①得121()4n n n n a a a a +++-=，因为0n a >，所以24n n a a +-=， 于是：数列{}n a 的奇数项是以11a =为首项，以4为公差的等差数列， 即()2114(1)432211n a n n n -=+-=-=--，偶数项是以23a =为首项，以4为公差的等差数列，即234(1)41n a n n =+-=- 所以{}n a 的通项公式21n a n =-； (2)解：由（1）可得(1)(21)(21)n n b n n =--+，212(43)(41)(41)(41)4(41)n n b b n n n n n -=---+-+=-+21234212(341)()()()4[37(41)]44(21)2n n n n n T b b b b b b n n n -+-=++++++=+++-=⨯=+. 【总结提升】1.利用等差数列的单调性或性质，求出其正负转折项，便可求得和的最值．当10a >，0d <时，n S 有最大值；10a <，0d >时，n S 有最小值；若已知n a ，则n S 最值时n 的值（n N +∈）则当10a >，0d <，满足100n n a a +≥⎧⎨≤⎩的项数n 使得n S 取最大值，(2)当10a <，0d >时，满足10n n a a +≤⎧⎨≥⎩的项数n 使得n S 取最小值.2.利用等差数列的前n 项和：2n S An Bn =+(,A B 为常数, n N ∈*)为二次函数，通过配方或借助图像，二次函数的性质，转化为二次函数的最值的方法求解；有时利用数列的单调性（0d >,递增；0d <，递减）；3. 利用数列中最大项和最小项的求法：求最大项的方法：设为最大项，则有11n n n n a a a a -+≥⎧⎨≥⎩；求最小项的方法：设为最小项，则有11n n n n a a a a -+≤⎧⎨≤⎩.只需将等差数列的前n 项和1,2,3,n =依次看成数列{}n S ，利用数列中最大项和最小项的求法即可.4.在解含绝对值的数列最值问题时,注意转化思想的应用. 题型四：等差数列性质及应用例11.（2020·浙江·高考真题）已知等差数列{an }的前n 项和Sn ，公差d ≠0，11a d≤．记b 1=S 2，bn+1=S2n+2–S 2n ，n *∈N ，下列等式不可能．．．成立的是（ ） A ．2a 4=a 2+a 6 B ．2b 4=b 2+b 6 C ．2428a a a = D ．2428b b b =【答案】D 【解析】 【分析】根据题意可得，21212222n n n n n b S a a S ++++=+=-，而1212b S a a ==+，即可表示出题中2468,,,b b b b ，再结合等差数列的性质即可判断各等式是否成立． 【详解】对于A ，因为数列{}n a 为等差数列，所以根据等差数列的下标和性质，由4426+=+可得，4262a a a =+，A 正确；对于B ，由题意可知，21212222n n n n n b S a a S ++++=+=-，1212b S a a ==+， ∴234b a a =+，478b a a =+，61112b a a =+，81516b a a =+． ∴()47822b a a =+，26341112b b a a a a +=+++．根据等差数列的下标和性质，由31177,41288+=++=+可得()26341112784=2=2b b a a a a a a b +=++++，B 正确；对于C ，()()()()2224281111137222a a a a d a d a d d a d d d a -=+-++=-=-， 当1a d =时，2428a a a =，C 正确； 对于D ，()()22222478111213452169b a a a d a a d d =+=+=++，n a n a()()()()2228341516111125229468145b b a a a a a d a d a a d d =++=++=++，()22428112416832b b b d a d d d a -=-=-．当0d >时，1a d ≤，∴()113220d a d d a -=+->即24280b b b ->；当0d <时，1a d ≥，∴()113220d a d d a -=+-<即24280b b b ->，所以24280b b b ->，D 不正确．故选：D.例12．（2014·北京高考真题（理））若等差数列{}n a 满足7897100,0a a a a a ++>+<，则当n =__________时，{}n a 的前n 项和最大． 【答案】8 【解析】由等差数列的性质，，，又因为，所以所以，所以，，故数列的前8项最大.例13．（2016·北京·高考真题（理））已知{}n a 为等差数列，n S 为其前n 项和，若16a =，350a a +=，则6=S _______. 【答案】6 【解析】 【详解】试题分析：因为{}n a 是等差数列，所以35420a a a +==，即40a =，又4136a a d -==-，所以2d =-， 所以616156615(2)6S a d =+=⨯+⨯-=．故答案为6．例14.（2021·江西新余四中高二月考（理））等差数列{}n a 、{}n b 的前n 项和分别为n S 和n T ，若2132n n S n T n +=+，则2517208101214a a a ab b b b +++=+++________．【答案】4365【分析】 证明得出2121n n n n a S b T --=，结合等差中项的基本性质可求得结果. 【详解】因为等差数列{}n a 、{}n b 的前n 项和分别为n S 和n T ，则()()()()()()12121121212121221212n n n n n n n nn a a n a S a n b b T n b b -----+-===-+-，所以，25172011218101214112142211434321265a a a a a Sb b b b b T +++⨯+====+++⨯+.故答案为：4365. 【温馨提醒】等差数列的性质主要涉及“项的性质”和“和的性质”，因此，要注意结合等差数列的通项公式、前n 项和公式求解．。

附件：江阴市建筑原材料登记程序第一条根据《江阴市建筑原材料登记管理办法（试行）》（以下简称《管理办法》）制定本程序。

第二条江阴市建筑原材料登记程序一、原材料生产供应企业根据《管理办法》的要求，结合企业自身的实际情况向江阴市建设工程质量监督站（以下简称市质监站）申请办理原材料登记。

二、市质监站对企业申报材料进行审查，确定是否准予登记；同时市质监站每月将通过核查的备案材料单位在网上公布登记信息，在全市范围内有效。

三、原材料生产供应企业在申请办理原材料登记时，应提供以下文件：1、《江阴市建筑原材料质量信息登记表》三份（见附表一）。

2、附件资料一份，附件资料应包括下列内容（附件内材料提供复印件一份，并提供原件审核）：（1）企业法人营业执照、组织机构代码证，委托办理的，提供受委托人身份证明和法定代表人出具的授权办理委托书。

（2）申请登记产品近2个月内指定法定资质检测机构出具的一年有效期内的产品型式检验报告。

（3）产品执行的质量标准（图集），对执行企业标准的产品，应提供经企业注册地质量技术监督部门备案的企业产品标准，产品技术说明书、出厂合格证和出厂检验报告。

（4）产品相关的施工验收标准或应用技术导则。

适用时，应提供相关的资质、许可、认证、鉴定等证书，如工业产品生产许可、强制性产品认证、管理体系认证证书等。

第三条市质监站在受理并接受符合本程序要求的相关资料后，即办理建筑原材料登记手续，将登记信息公布在江阴市建设局质量监督板块（/c/zhiliangjiandu.shtml）。

第四条根据《管理办法》要求，建筑原材料登记实施动态管理，登记有效期为一年，生产企业在登记有效期到期前一个月应重新申请办理登记；登记信息变更时，应重新申请办理登记。

第五条登记监督管理1、市质监站承担原材料登记名录管理、申报材料验证、审核和公布登记信息等工作。

2、对不符合国家法律法规、技术标准的原材料，或企业提供虚假登记资料的，不予办理登记或取消登记。