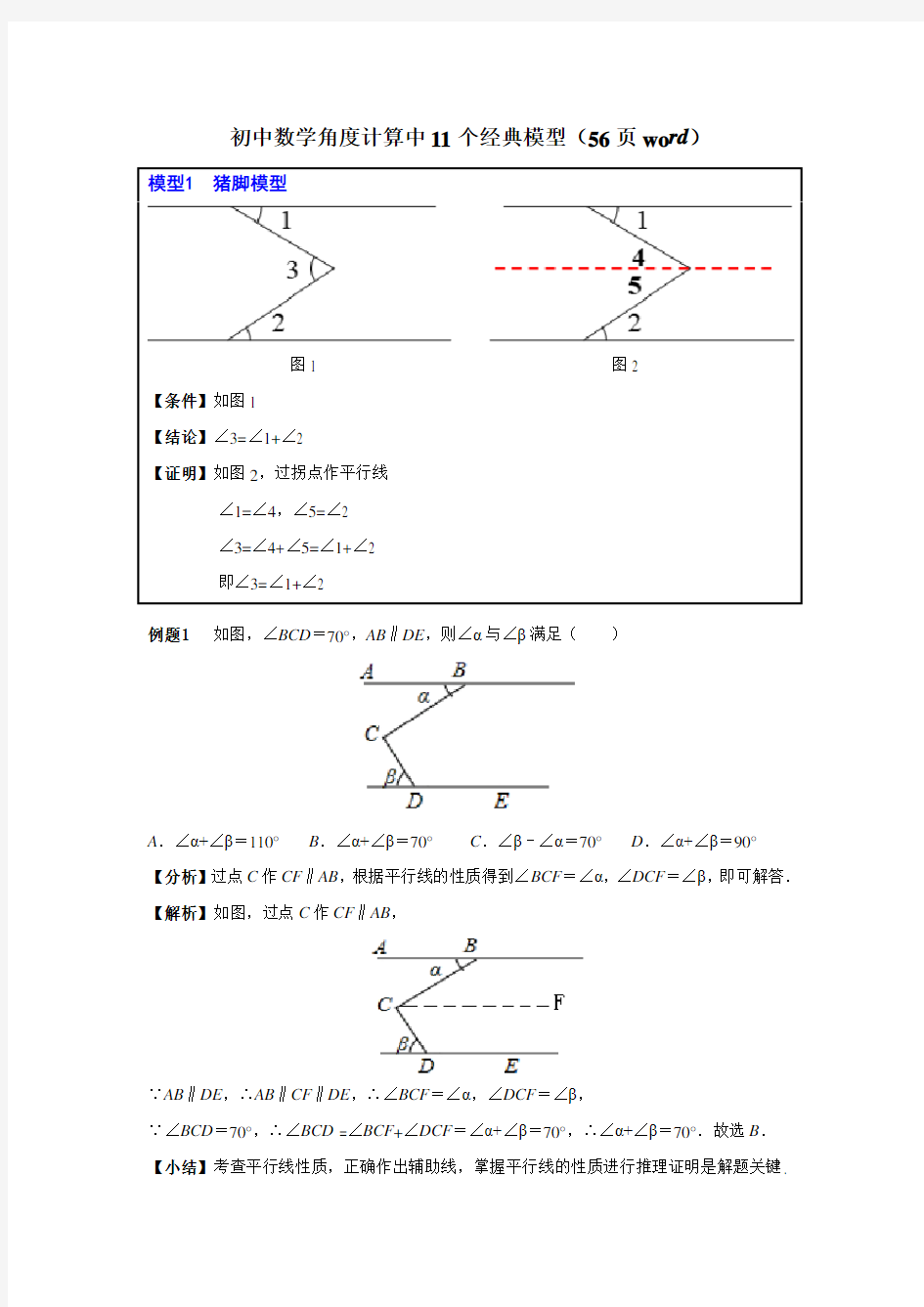

初中数学角度计算中11个经典模型(56页wo rd)
模型1猪脚模型
图1 图2
【条件】如图1
【结论】∠3=∠1+∠2
【证明】如图2,过拐点作平行线
∠1=∠4,∠5=∠2
∠3=∠4+∠5=∠1+∠2
即∠3=∠1+∠2
例题1 如图,∠BCD=70°,AB∥DE,则∠α与∠β满足()
A.∠α+∠β=110°B.∠α+∠β=70°C.∠β﹣∠α=70°D.∠α+∠β=90°
【分析】过点C作CF∥AB,根据平行线的性质得到∠BCF=∠α,∠DCF=∠β,即可解答.【解析】如图,过点C作CF∥AB,
∵AB∥DE,∴AB∥CF∥DE,∴∠BCF=∠α,∠DCF=∠β,
∵∠BCD=70°,∴∠BCD =∠BCF+∠DCF=∠α+∠β=70°,∴∠α+∠β=70°.故选B.【小结】考查平行线性质,正确作出辅助线,掌握平行线的性质进行推理证明是解题关键.
变式1 如图,AB //EF ,∠D =90°
,则α,β,γ的大小关系是( )
A .βαγ=+
B .90βαγ=+-?
C .90βγα=+?-
D .90βαγ=+?-
【解析】如图,过点C 和点D 作CG //AB ,DH //AB ,
∵CG //AB ,DH //AB ,∴CG //DH //AB ,∵AB //EF ,∴AB //EF //CG //DH ,
∵CG //AB ,∴∠BCG =α,∴∠GCD =∠BCD -∠BCG =β-α,∵CG //DH ,∴∠CDH =∠GCD =β-α, ∵HD //EF ,∴∠HDE =γ,∵∠EDC =∠HDE +∠CDH =90°,∴γ+β-α=90°,∴β=α+90°-γ.故选:D . 模型2 铅笔模型
图1 图2
【条件】如图1
【结论】∠1+∠2+∠3=360°
【证明】如图2,过拐点作平行线
根据同旁内角互补得,∠1+∠4=180°,∠2+∠5=180°
又∠3=∠4+∠5
所以∠1+∠2+∠3=∠1+∠2+∠4+∠5=360°
【推广】∠1+∠2+∠3+…+∠n = 180°(n -1)【即变异铅笔模型】
变式2 综合探究:已知//AB CD ,点M 、N 分别是AB 、CD 上两点,点G 在AB 、CD 之间,连接MG 、NG .
图1 图2 (1)如图1,若GM GN ⊥,求AMG CNG +∠∠的度数;
(2)如图2,若点P 是CD 下方一点,MG 平分BMP ∠,ND 平分GNP ∠,已知40BMG ∠=?,求MGN MPN ∠+∠的度数.
【解析】(1)如图1,过G 作//GH AB ,//AB CD ,////GH AB CD ∴
AMG HGM ∴∠=∠,CNG HGN =∠∠,MG NG ⊥
90MGN MGH NCH AMG CNG ∴∠=∠+∠=∠+∠=?
图1
(2)如图2,过G 作//GK AB ,过点P 作//PQ AB 设GND α∠=
//GK AB ,//AB CD ,//GK CD ∴KGN GND α∴∠=∠=,
//GK AB ,40BMG ∠=?,40MGK BMG ∴∠=∠=? MG 平分BMP ∠,ND 平分GNP ∠,40GMP BMG ∴∠=∠=?,80BMP ∴∠=?, //PQ AB ,80MPQ BMP ∴∠=∠=?,ND 平分CNP ∠,DNP GND α∴∠=∠=, //AB CD ,//PQ CD ∴,QPN DNP α∴∠=∠=,40MGN α∴∠=?+,
80MPN α∠=?-,4080120MGN MPN αα∴∠+∠=?++?-=?
图2
模型3双垂直模型
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE,∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°
∴∠BAC+∠ACB=90°
又∠ECD+∠ACB=90°
∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°,且∠CED+∠DCE =90°
∴∠ACB=∠CED,得证。
例题2 如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.
【解析】∵FD⊥AB于D,∴∠BED+∠B=90°,
∵∠ACB=90°,∴∠A+∠B=90°,∴∠A=∠BED=55°.
变式3如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.
【解析】∵DF⊥BC,∴∠FDC=90°,
∵∠AFD=152°,∴∠C=∠AFD﹣∠FDC=152°﹣90°=62°,
∵∠B=∠C,∴∠A=180°﹣∠B﹣∠C=180°﹣62°﹣62°=56°.
变式4如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
【解析】证明:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B;
(2)在Rt△AFC中,∠CF A=90°﹣∠CAF,
同理在Rt△AED中,∠AED=90°﹣∠DAE.
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
变式5(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B 有什么关系?为什么?
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状是什么?为什么?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,点C,B,E在同一直线上,∠A与∠D有什么关系?为什么?
【解析】(1)∠ACD=∠B,理由如下:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠DCB=90°,∴∠ACD=∠B;
(2)△ADE是直角三角形.
∵在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,∠A为公共角,
∴∠AED=∠ACB=90°,∴△ADE是直角三角新;
(3)∠A+∠D=90°.∵在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,
∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,∴∠A+∠D=90°.
模型4A字模型
图1
【条件】图1中三种情况
【结论】∠1=∠2
例题3 如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?
【解析】∵∠A+∠B+∠C=180°,∴∠A+∠B=180°﹣∠C,
∵∠C=75°,∴∠A+∠B=180°﹣75°=105°,∵∠1+∠2+∠A+∠B=360°,
∴∠1+∠2=360°﹣(∠A+∠B),∴∠1+∠2=360°﹣105°=255°.
变式6如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.
【解析】∵∠A=40°,∴∠1+∠2=∠3+∠4=180°﹣∠A=140°.
∴∠1+∠2+∠3+∠4=280°.
模型5双内角平分线模型
【条件】B P、C P分别为∠ABC、∠ACB的角平分线.
1∠A.
【结论】∠P=90°+
2
例题4 如图,△ABC中,
(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.
【解析】(1)∵∠B=70°,∴∠BAC+∠BCA=110°,
∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA)=×110°=55°,∴∠P=180°﹣55°=125°;
(2)∵点P是△ABC的∠BAC和∠ACB的平分线的交点,
∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA),
∴∠P=180°﹣(∠P AC+∠PCA)=180°﹣(∠BAC+∠BCA)=180°﹣(180°﹣∠B)=90°+∠B.
变式7如图,在△ABC中,∠ABC与∠ACB的平分线交于点O.
(1)如图1,已知∠ABC=40°,∠ACB=60°,求∠BOC的度数.
(2)如图2,已知∠A=90°,求∠BOC的度数.
(3)如图1,设∠A=m°,求∠BOC的度数.
【解析】(1)∵BC平分∠ABC,∠ABC=40°,∴∠OBC=∠ABC=20°,
∵CO平分∠ACB,∠ACB=60°,∴∠OCB=∠ACB=30°,
∴∠BOC=180°﹣20°﹣30°=130°.
(2)∵∠A=90°,∴∠ABC+∠ACB=180°﹣90°=90°,
又∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=45°,
∴∠BOC=180°﹣45°=135°.
(3)∵∠A=m°∴∠ABC+∠ACB=180°﹣m°,
又∵∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=90°﹣m°,∴∠BOC=90°+m°.
变式8已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.
(1)如图1,求∠BDC的度数;
(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.
【解析】(1)∵∠A=100°,∴∠ABC+∠ACB=80°,
又∵∠ABD=∠CBD,∠ACD=∠BCD,∴∠CBD=∠ABC,∠BCD=∠ACB,
∴∠CBD+∠BCD=(∠ABC+∠ACB)=40°,∴∠BDC=180°﹣40°=140°;
(2)设∠ACF=α,则∠BCD=α,∵∠BDC=140°,∴∠CBD=40°﹣α=∠ABD,
∵∠AED是△DCE的外角,∠AFD是△BDF的外角,
∴∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,
∴∠AED﹣∠AFD=∠ACF+∠CDF﹣∠ABE﹣∠BDE=α﹣(40°﹣α)=12°,
解得α=26°,∴∠ACF=26°.
变式9已知任意一个三角形的三个内角的和是180°.如图1,在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=a,求∠BOC的度数;
1∠ABC,∠(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=
3
1∠ACB,∠A=a,求∠BOC的度数.
OCB=
3
【解析】(1)∵∠A=70°,∴∠ABC+∠ACB=180°﹣∠A=110°,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=∠ABC,∠OCB=ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=125°;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=∠ABC,∠OCB=ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣)=90°+;(3)∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,
∵∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=60°﹣,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(60°﹣)=120°+.模型6内外角平分线模型
【条件】B P、C P分别为∠ABC、∠ACE的角平分线
1∠A
【结论】∠P=
2
例题5 如图,△ABC中,∠ABC与∠ACB的外角的平分线相交于点E.(1)已知∠A=60°,求∠E的度数;
(2)直接写出∠A与∠E的数量关系:.
【解析】(1)∵CE、BE分别平分∠ACD、∠ABC,
∴∠ECD=∠ACD,∠EBC=∠ABC,
∴∠E=∠ECD﹣∠EBD=(∠ACD﹣∠ABC)=∠A=30°;
(2)由(1)得,∠E=∠A,∴∠A=2∠E
变式10如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.
【解析】在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=∠ACD,∠PBC=∠ABC,
∴∠PCD=∠BPC+∠PBC=40°+∠ABC,∴∠ACD=∠ABC+40°,
∴∠ACD﹣∠ABC=80°,∴∠BAC=∠ACD﹣∠ABC=80°,即∠CAB=80°.
变式11如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE
的平分线,且与BD交于点D;
(1)若∠ABC=60°,∠DCE=70°,则∠D=°;
(2)若∠ABC=70°,∠A=80°,则∠D=°;
(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)
【解析】(1)∵BD为△ABC的角平分线,∠ABC=60°,∴∠DBC=30°,
∵∠DCE=70°,∴∠D=∠DCE﹣∠DBC=70°﹣30°=40°;
(2)∵∠ABC=70°,∠A=80°,∴∠ACE=150°
∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,
∴∠DBC=∠ABC=35°,∠DCE=∠ACE=75°,
∴∠D=∠DCE﹣∠DBC=75°﹣35°=40°;
(3)不变化,理由:∵∠DCE=∠DBC+∠D,
∴∠D=∠ACE﹣∠ABC=(∠A+∠ABC)﹣∠ABC=∠A.
变式12如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A=50°,则∠D=;
(2)若∠A=80°,则∠D=;
(3)若∠A=130°,则∠D=;
(4)若∠D=36°,则∠A=;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
【解析】如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,∵∠ACE=∠ABC+∠A,∴2∠2=2∠1+∠A,
而∠2=∠1+∠D,∴2∠2=2∠1+2∠D,∴∠A=2∠D,即∠D=∠A,
(1)当若∠A=50°,则∠D=25°;
(2)若∠A=80°,则∠D=40°;
(3)若∠A=130°,则∠D=65°.
(4)若∠D=36°,则∠A=72°,
(5)综上所述,∠D=∠A;
模型7双外角平分线模型
【条件】B P、C P分别为∠EBC、∠BCF的角平分线.
1∠A.
【结论】∠P=90°-
2
例题6 如图,△ABC 中,分别延长△ABC 的边AB 、AC 到D 、E ,∠CBD
与∠BCE 的平分线相交于点P ,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A =60°,则∠P = °; (2)若∠A =40°,则∠P = °;
(3)若∠A =100°,则∠P = °; (4)请用数学表达式归纳∠A 与∠P 的关系 .
【解析】(1)∵∠A =60°,
∴∠ABC +∠ACB =180°﹣60°=120°,∠DBC +∠BCE =360°﹣120°=240°,
又∵∠CBD 与∠BCE 的平分线相交于点P ,∴∠PBC =∠DBC ,∠PCB =∠BCE , ∴∠PBC +∠PCB =(∠DBC +∠ECB )=120°,∴∠P =60°.
(2)70°;(3)40°(4)∠P =90°﹣∠A .理由如下:
∵BP 平分∠DBC ,CP 平分∠BCE ,∴∠DBC =2∠CBP ,∠BCE =2∠BCP
又∵∠DBC =∠A +∠ACB ∠BCE =∠A +∠ABC ,
∴2∠CBP =∠A +∠ACB ,2∠BCP =∠A +∠ABC ,
∴2∠CBP +2∠BCP =∠A +∠ACB +∠A +∠ABC =180°+∠A ,∴∠CBP +∠BCP =90°+∠A 又∵∠CBP +∠BCP +∠P =180°,∴∠P =90°﹣∠A .
变式13 BD 、CD 分别是△ABC 两个外角∠CBE 、∠BCF 平分线,求证∠BDC =90°2
1
∠A .
【解析】证明:∵BD 、CD 分别是∠CBE 、∠BCF 的平分线
∴∠DBC =∠EBC ,∠BCD =∠BCF ,
∵∠CBE 、∠BCF 是△ABC 的两个外角
∴∠CBE +∠BCF =360°﹣(180°﹣∠A )=180°+∠A
∴∠DBC+∠BCD=(∠EBC+∠BCF)=(180°+∠A)=90°+∠A,
在△DBC中,∠BDC=180°﹣(∠DBC+∠BCD)=180°﹣(90°+∠A)=90°﹣∠A.变式14如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
(1)若∠ABC=40°,∠ACB=36°,求∠BIC的大小;
(2)若∠A=96°,试求∠BIC;
(3)根据前面问题的求解,请归纳∠BIC和∠A的数量关系并进行证明.
【解析】(1)如图所示,∵∠ABC=40°,∠ACB=36°,
∴∠DBC=140°,∠ECB=144°,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,
∴∠3=∠DBC=70°,∠4=∠ECB=72°,∴△BCI中,∠I=180°﹣70°﹣72°=38°;(2)∵∠A=96°,∴∠1+∠2=84°,∴∠DBC+∠ECB=276°,
又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,
∴∠3+∠4=(∠DBC+∠ECB)=×276°=138°,∴△BCI中,∠I=180°﹣138°=42°;(3)∠BIC=90°﹣∠A.证明:△ABC中,∠1+∠2=180°﹣∠A,
∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,
又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,
∴∠3+∠4=(∠DBC+∠ECB)=×(180°+∠A)=90°+∠A,
∴△BCI中,∠I=180°﹣(∠3+∠4)=180°﹣(90°+∠A)=90°﹣∠A.
变式15如图,在△ABC中,BD,CD是内角平分线,BP,CP是∠ABC,∠ACB的外角平分线,分别交于点D,P.
(1)若∠A=30°,求∠BDC,∠BPC的度数.
(2)若∠A=m°,求∠BDC,∠BPC的度数(直接写出结果,不必说明理由)
(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由,若无影响,直接求出其值.
【解析】(1)∵BD,CD是内角平分线,∴∠CBD+∠BCD=(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,∠A=30°,∴∠ABC+∠ACB=150°,∴∠CBD+∠BCD=75°.又∵∠BDC+∠CBD+∠BCD=180°,∴∠BDC=105°.
∵∠CBE+∠BCF=360°﹣(∠ABC+∠ACB)=210°,BP,CP是∠ABC,∠ACB外角平分线
∴∠CBP+∠BCP=(∠CBE+∠BCF)=105°,
∵∠BPC+∠CBP+∠BCP=180°,∴∠BPC=75°.
(2)根据(1)的求角过程可知:∠BDC=90°+°,∠BPC=90°﹣°.
(3)∵∠D+∠P=90°+°+90°﹣°=180°为定值,
∴∠A的大小变化,对∠D+∠P的值无影响.
模型8共定点角平分线和高线模型
【条件】△ABC中,AH是高、AD是∠BAC的角平分线
1(∠B-∠C),即共顶点高线与角平分线夹角等于两底角之差的一半
【结论】∠HAD=
2
例题7 如图,在ABC ?中,AD 、AE 分别是ABC ?的高和角平分线,50B ∠=?,60C ∠=°,则DAE =∠__________度.
【解析】在△ABC 中,∵∠B =50°,∠C =60°,∴∠BAC =180°-∠B -∠C =180°-50°-60°=70°,
∵AE 是ABC ?的角平分线,∴∠EAC =12∠BAC =12×70°=35°, ∵AD 是△ABC 的高,∴∠ADC =90°
∴在△ADC 中,∠DAC =180°-∠ADC -∠C =180°-90°-60°=30°,
∴∠DAE =∠EAC -∠DAC =35°-30°=5°.
变式16 如图所示,在ABC ?中,AD 是高,AE 、BF 是角平分线,它们相交于点O ,50BAC ∠=?,70C ∠=?,求DAC ∠、BOA ∠的度数.
【解析】AD 是ABC ?的高,90ADC ∴∠=?
在ADC ?中,90907020DAC C ∠=?-∠=?-?=?
在ABC ?中,180180507060ABC BAC C ∠=?-∠-∠=?-?-?=?
AE ∵、BF 是角平分线,11603022
∴∠=∠=??=?ABO ABC 11502522
BAO BAC ∠=∠=??=? 在ABC ?中,1801803025125BOA ABO BAO ∠=?-∠-∠=?-?-?=?
变式17 在△ABC 中,AD 是BC 边上的高,AE 是∠BAC 的平分线,∠EAD =15°,∠B =40°. (1)求∠C 的度数.
(2)若:∠EAD =α,∠B =β,其余条件不变,直接写出用含α,β的式子表示∠C 的度数.
【解析】(1)∵AD ⊥BC ,∴∠ADC =∠ADB =90°,
∵∠B =40°,∴∠BAD =90°-40°=50°,∵∠EAD =15°,∴∠BAE =50°-15°=35°,
∵AE 平分∠BAC ,∴∠CAE =∠BAE =12∠BAC =35°,∴∠BAC =70°, ∴∠C =180°-∠BAC -∠B =180°-70°-40°=70°;
(2)∵AD ⊥BC ,∴∠ADC =∠ADB =90°,∵∠B =β,∴∠BAD =90°
-β, ∵∠EAD =α,∴∠BAE =90°-β-α,∵AE 平分∠BAC ,∴∠CAE =∠BAE =12
∠BAC =90°-β-α, ∴∠BAC =180°-2β-2α,∴∠C =180°-∠BAC -∠B =180°-(180°-2β-2α)-β=β+2α. 变式18 如图,BD 、BE 分别是ABC ?的高和角平分线,46A ∠=?,74ABC ∠=?,求DBE ∠的度数.
【解析】∵BD 是ABC ?的高,∴∠ABD =90904644A ?-∠=?-?=?,
∵BE 是ABC ?的角平分线,∴∠ABE =11743722
ABC ∠=??=?, ∴44377DBE ABD ABE ∠=∠-∠=?-?=?.
模型9 8字模型
【条件】AE 、BD 相交于点C
【结论】∠A +∠B =∠D +∠E .
例题8 图1,线段AB 、CD 相交于点O ,连接AD 、CB ,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ,并且与CD 、AB 分别相交于M 、N .试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;
(2)仔细观察,在图2中“8字形”的个数:个;
(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).
【解析】(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠P AB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠P AB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠P AB+∠P,
即2∠P=∠D+∠B,又∵∠D=50度,∠B=40度,
∴2∠P=50°+40°,∴∠P=45°;
(4)关系:2∠P=∠D+∠B.由∠D+∠1+∠2=∠B+∠3+∠4①
由∠ONC=∠B+∠4=∠P+∠2,②
①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,
∠D+2∠B=2∠P+∠B,即2∠P=∠D+∠B.
变式19 已知:如图,AM ,CM 分别平分∠BAD 和∠BCD .
①若∠B =32°,∠D =38°,求∠M 的度数;
②探索∠M 与∠B 、∠D 的关系并证明你的结论.
【解析】①根据三角形内角和定理,∠B +∠BAM =∠M +∠BCM ,
∴∠BAM ﹣∠BCM =∠M ﹣∠B ,同理,∠MAD ﹣∠MCD =∠D ﹣∠M ,
∵AM 、CM 分别平分∠BAD 和∠BCD ,∴∠BAM =∠MAD ,∠BCM =∠MCD , ∴∠M ﹣∠B =∠D ﹣∠M ,∴∠M =(∠B +∠D )=(32°+38°)=35°;
②根据三角形内角和定理,∠B +∠BAM =∠M +∠BCM ,∴∠BAM ﹣∠BCM =∠M ﹣∠B , 同理,∠MAD ﹣∠MCD =∠D ﹣∠M ,
∵AM 、CM 分别平分∠BAD 和∠BCD ,∴∠BAM =∠MAD ,∠BCM =∠MCD , ∴∠M ﹣∠B =∠D ﹣∠M ,∴∠M =(∠B +∠D ).
变式20 如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A +∠C =∠B +∠D ;
(2)如图2,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,且与CD 、AB 分别相交于点M 、N .
①以线段AC 为边的“8字型”有 个,以点O 为交点的“8字型”有 个; ②若∠B =100°,∠C =120°,求∠P 的度数;
③若角平分线中角的关系改为“∠CAP=31∠CAB ,∠CDP=3
1∠CDB ”,试探究∠P 与∠B 、∠C 之间存在的数量关系,并证明理由.
【解析】(1)证明:在图1中,有∠A +∠C =180°﹣∠AOC ,∠B +∠D =180°﹣∠BOD , ∵∠AOC =∠BOD ,∴∠A +∠C =∠B +∠D ;
(2)解:①3;4;②以M 为交点“8字型”中,有∠P +∠CDP =∠C +∠CAP ,
以N 为交点“8字型”中,有∠P +∠BAP =∠B +∠BDP
∴2∠P +∠BAP +∠CDP =∠B +∠C +∠CAP +∠BDP ,
∵AP 、DP 分别平分∠CAB 和∠BDC ,
∴∠BAP =∠CAP ,∠CDP =∠BDP ,∴2∠P =∠B +∠C ,
∵∠B =100°,∠C =120°,∴∠P =(∠B +∠C )=(100°+120°)=110°; ③3∠P =∠B +2∠C ,其理由是:
∵∠CAP =∠CAB ,∠CDP =∠CDB ,∴∠BAP =∠CAB ,∠BDP =∠CDB , 以M 为交点“8字型”中,有∠P +∠CDP =∠C +∠CAP ,
以N 为交点“8字型”中,有∠P +∠BAP =∠B +∠BDP
∴∠C ﹣∠P =∠CDP ﹣∠CAP =(∠CDB ﹣∠CAB ),
∠P ﹣∠B =∠BDP ﹣∠BAP =(∠CDB ﹣∠CAB ).
∴2(∠C ﹣∠P )=∠P ﹣∠B ,∴3∠P =∠B +2∠C .
变式21 (1)如图1的图形我们把它称为“8字形”,请说理证明∠A +∠B =∠C +∠D
(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC =20°,∠ADC =26°,求∠P 的度数(可直接使用问题(1)中的结论)
(3)如图3,直线AP 平分∠BAD 的外角∠F AD ,CP 平分∠BCD 的外角∠BCE ,若 ∠ABC =36°,∠ADC =16°,猜想∠P 的度数为
(4)在图4中,若设∠C =x ,∠B =y ,∠CAP=31
∠CAB ,∠CDP=3
1∠CDB ,试问∠P 与
初中数学常用几何模型及构造方法大全几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间… 全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角 旋转:相邻等线段绕公共顶点旋转 对称全等模型 角分线模型 往角两边作垂线 往角两边截取等线段 过角分线某点作垂线 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。
对称半角模型 说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 旋转全等模型 半角:有一个角含1/2角及相邻线段 自旋转:有一对相邻等线段,需要构造旋转全等 共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题 旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型 构造方法: 遇60度旋60度,造等边三角形 遇90度旋90度,造等腰直角 遇等腰旋顶点,造旋转全等 遇中点旋180度,造中心对称 共旋转模型 说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。
模型变换 说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
初中几何常见模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。(2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有;③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形)
模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE; ②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等边三角形。(3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③.
?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②; ③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导?
初中数学九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED O D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A C D E 图 2 O A B C D E O C D E 图 1 图 2
二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEA=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BE=∠BOA ; ③ ===OA OB OC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有22 22CD AB B C AD +=+;⑥BD AC 2 1 S △BCD ?= 三、模型三、对角互补模型 (1)全等型-90° 【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 2 1 S S S =+= 证明提示: ①作垂直,如图2,证明△CDM ≌△CEN ②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21 S S =- O C O C D E O B C D E O C D A O B C D E 图 1 A O B C D E M N 图 2 A O B C D E F 图 3 A O B C D E M N 图 4
初中数学几何模型 中点模型 【模型1】倍长 1、倍长中线;2、倍长类中线;3、中点遇平行延长相交 E D A B C F D A B C E 【模型2】遇多个中点,构造中位线 1、直接连接中点;2、连对角线取中点再相连 【例1】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE. (1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长; (2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的关系,写出你的猜想;并给予证明; (3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗写出你的猜想,并给予证明. 图3 图2 图1 G F D C G F D C G F D C A B E E B A E B A 【例2】如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,BAF DAE∠ = ∠. (1)求证:CE=CF; (2)若? = ∠120 ABC,点G是线段AF的中点,连接DG,EG.求证:DG上GE. 【例3】如图,在四边形ABCD中,AB=CD,E、F分别为BC、AD中点,BA交EF延长线于G,CD交EF 于H.求证:∠BGE=∠CHE. H G E F A B D C
E A B C O D E A B C O D B O A C 角平分线模型 【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形 【例4】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为. H G F E A D B C 手拉手模型 【条件】OA OB OC OD AOB COD ==∠=∠ ,, 【结论】OAC OBD ?;AEB OAB COD ∠=∠=∠(即都是旋转角);OE AED ∠ 平分; - 【例5】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为. 【例6】如图,ABC中,90 BAC? ∠=,AB=AC,AD⊥BC于点D,点E在AC边上,连结BE,AG⊥BE 于F,交BC于点G,求DFG ∠ G F D C B A E
初中几何常见九大模型解析(完美版) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
初中几何常见九大模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有;③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) 模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE;②; ③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③
?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②;③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导? 模型四:角含半角模型90° (1)角含半角模型90°-1 ?条件:①正方形;②; ?结论:①;②的周长为正方形周长的一半; 也可以这样: ?条件:①正方形;② ?结论:
全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转 对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 旋转全等模型 半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题
旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 自旋转模型构造方法: 遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称
共旋转模型 说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。
模型变形 说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转: 说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中数学几何经典模型 范文 集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]
如图,正方形ABCD DE=2CE,过点C作CF 如图,ABC中,∠如图,在边长为6 ,连接EG,
中,AB=AD,
H G F C B D A E H G F B C A D E 点E 旋转,旋转过程中,线段DE 与线段A B 相交于点P ,射线EF 与线段AB 相交于点G ,与射线CA 相交于点Q .若AQ =12,BP =3,则PG =. 【例12】如图,在菱形ABCD 中,AB =BD ,点E 、F 分别在AB 、AD 上,且AE =DF .连接 BF 与DE 交于点G ,连接CG 与BD 交于点H ,若CG =1,则BCDG S =四边形. 一线三等角模型【条件】EDF B C DE DF ∠=∠=∠=,且【结论】BDE CFD ? 【例13】如图,正方形ABCD 中,点E 、F 、G 分别为AB 、BC 、CD 边上的点,EB =3,GC =4,连接EF 、FG 、GE 恰好构成一个等边三角形,则正方形的边长为 . 最短路径模型【两点之间线段最短】 1、将军饮马 2、费马点【垂线段最短】 【两边之差小于第三边】 【例16】如图,矩形ABCD 是一个长为1000米,宽为600米的货场,A 、D 是入 口.现拟在货场内建一个收费站P ,在铁路线BC 段上建一个发货站台H ,设铺设公路l .求l 的最小值. AP 、DP 以及PH 之长度和为【例17】如图,E 、F 是正方形ABCD 的边AD 上两个动点,满足AE =DF ,连接CF 交BD 于G ,连接 BE 交AG 于点H ,若正方形的边 长为2,则线段DH 长度的最小值是. 中,4,42AB AD ==,E 是线【例18】如图所示,在矩形ABCD 段AB 的中点,F 是线段BC 上的动点,BEF ?沿直线EF 翻折到'B EF ?,连接'DB ,'DB 最短为 . 《三垂直模型》 课后练习题 【练习1】 问题1:如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =BC =CD ,点M ,N 分别在AD ,CD 上,∠MBN =12 ∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系请直接写出你的猜想; 问题2:如图2,在四边形ABCD 中,AB =BC ,∠ABC +∠ADC =180°,点M ,N 分别在 DA ,CD 的延长线上,若∠MBN =12 ∠ABC 仍然成立,请你进一步探究线段MN ,AM ,CN 又有怎样的数量关系写出你的猜想,并给予证明. 【练习2】已知:如图1,正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG .
如果您喜欢这份文档,欢迎下载! 精品文档,名师推荐! 初中几何必杀技一一八大模型 MH)手拉手模型一旋转型全等 1.等边三角形 条件:如图1,AOAB,△OCD均为等边三角形. 结论:①左OAC^AOBD;②ZAEB= 60°;③EO平分匕AED. 2.等腰直角三角形 条件:如图2.AOAB,△OCD均为等腰直角三角形. 结论:①左QAC丝△OBD ;②ZAEB= 90°;③EO平分/AED. 3.任意等腰三角形 条件:如图3,AQAB,AOCD均为等腰三角形,OA=OB,OC=OD,ZAOB=ZCOD. 结论:①左OAC^/\OBD;② ZAEB=ZAOB;③ EO 平分/AED. 模型二)手拉手模型一旋转型相似 1.一般情况 条件:如图4,CD//AB,将△OCD旋转至右图位置. 结论:右图中①左OCDw AOAB, AOACco AOBD;②延长AC交BD于点E,必有ZBEC=ZBOA. 2.特殊情况 条件:如图5,CD//AB,ZAOB=90°,将△OCD旋转至右图位置. 结论:右图中①左OCD GO AOAB, AOACco AOBD,②连接AC,BD交于点E,必有ZBEC=ZBOA;?|^ = ^ = ^ = tanZOCD;@BD±AC;⑤连接 AD,BC,必有AD2 +BC2=AB2+CD2;⑥S mABCD = yACX BD(对角线互相垂直的四边形). 对角互补模型 1.全等型一90° 条件:如图6①,①ZAOB = ZDCE= 90°;②OC平分ZAOB. 结论:?CD=CE;② OD+OE=7^OC;③=扌8气 证明提示: ①过点C作CM丄OA于点M,CN丄OB于点N,如图②,证明△ CDM^ △ CEN; ②过点C作CF丄。C,如图③,证明△ ODC^AFEC. 当ZECD的一边交A。的延长线于点D时,如图④, 结论:(DCD=CE(不变);②OE— OD=72OC;③ S ACCE—S A0CD =yOC2. 以上结论证明方法与前一种一致,可自行尝试. A 图4 图6
g a t a t i m e a n d A l l t h i n g s i n t h e i r b e i n g a r e g o o d f o r s o 初中数学常用几何模型及构造方法大全, 掌握它轻松搞定压轴题! 几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握哦~全等变换 平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。对称半角模型 说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。旋转全等模型 半角:有一个角含1/2角及相邻线段 自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题
g a t a t i m e a n d A l l t h i n g s i n t h e i r b e i n g a r e g o o d f o r s o 旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。自旋转模型构造方法: 遇60度旋60度,造等边三角形; 遇90度旋90度,造等腰直角;遇等腰旋顶点,造旋转全等; 遇中点旋180度,造中心对称. 共旋转模型
初中数学几何模型 【模型1】倍长 1、 倍长中线; 2、倍长类中线; 3、中点遇平行延长相交 E D A B C F D A B C E ---------------------------------------------------------------------------------------------------------------------- 【模型2】遇多个中点,构造中位线 1、 直接连接中点; 2、连对角线取中点再相连 【例1】在菱形ABCD 和正三角形BEF 中,∠ABC =60°,G 是DF 的中点,连接GC 、GE . (1)如图1,当点E 在BC 边上时,若AB =10,BF =4,求GE 的长; (2)如图2,当点F 在AB 的延长线上时,线段GC 、GE 有怎样的数量和位置关系,写出你的猜想;并给予证明; (3)如图3,当点F 在CB 的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明. 图3 图2图1G F D C G F D C G F D C A B E E B A E B A 中点模型
【例2】如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,BAF DAE∠ = ∠. (1)求证:CE=CF; (2)若? = ∠120 ABC,点G是线段AF的中点,连接DG,EG.求证:DG上GE. 【例3】如图,在四边形ABCD中,AB=CD,E、F分别为BC、AD中点,BA交EF延长线于G,CD交EF于H.求证:∠BGE=∠CHE. H G E F A B D C 【模型1】构造轴对称 【模型2】角平分线遇平行构造等腰三角形 ---------------------------------------------------------------------------------------------------------------------- 角平分线模型
初中几何常见九大模型解析模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?】 ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?` ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ' ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) 模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE;②;③ ?证明提示: ①作垂直,如图,证明; - ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?<
?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等 边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?' ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②;③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导 ? 模型四:角含半角模型90°
初中数学九大几何模型 Prepared on 24 November 2020
初中数学九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED 二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; O A B C D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A B C D E 图 2 O A B C D E O C D E 图 1图 2O C O C D E O B C D E O C D
③ ===OA OB OC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有22 22CD AB B C AD +=+;⑥BD AC 21 S △BCD ?= 三、模型三、对角互补模型 (1)全等型-90° 【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 2 1 S S S =+= 证明提示: ①作垂直,如图2,证明△CDM ≌△CEN ②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21 S S =- (2)全等型-120° 【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43 S S S =+= 证明提示:①可参考“全等型-90°”证法一; ②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。 (3)全等型-任意角ɑ 【条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE ; 【结论】:①OC 平分∠AOB ;②OD+OE=2OC ·cos ɑ; ③α cos αsin OC S S S 2△OCE △OCD △DCE ??=+= ※当∠DCE 的一边交AO 的延长线于D 时(如右下图): 原结论变成:①; ②; ③。 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 A O B C D E 图 1 A O B C D E M N 图 2 A O B C D E F 图 3 A O B C D E M N 图 4 A
初中数学几何模型大全+ 经典题型(含答案) 全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角 旋转:相邻等线段绕公共顶点旋转 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。 垂直也可以做为轴进行对称全等。 说明:上图依次是45°、30°、°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等 共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全 构造方法:遇60 度旋60 度,造等边三角形 遇90 度旋90 度,造等腰直角 遇等腰旋顶点,造旋转全等遇中点旋180 度,造中心对称
说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“ 8”字模型可以证明。 说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。 说明:两个正方形、两个等腰直角三角形或者一个正方形一个等 腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和
初中数学几何公式和九大几何模型 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12 两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等 24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理(SSS) 有三边对应相等的两个三角形全等 26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等
27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角) 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 33 推论3 等边三角形的各角都相等,并且每一个角都等于60° 34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35 推论1 三个角都相等的三角形是等边三角形 36 推论2 有一个角等于60°的等腰三角形是等边三角形 37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半 38 直角三角形斜边上的中线等于斜边上的一半 39 定理线段垂直平分线上的点和这条线段两个端点的距离相等 40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上 41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合 42 定理1 关于某条直线对称的两个图形是全等形 43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线 44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上 45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称 46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2 47勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形 48定理四边形的内角和等于360°
初中常见几何模型汇总 全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角 旋转:相邻等线段绕公共顶点旋转 对称全等模型 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 对称半角模型 说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 旋转全等模型 半角:有一个角含1/2角及相邻线段
自旋转:有一对相邻等线段,需要构造旋转全等 共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题 旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 自旋转模型 构造方法: 遇60度旋60度,造等边三角形 遇90度旋90度,造等腰直角 遇等腰旋顶点,造旋转全等 遇中点旋180度,造中心对称
共旋转模型 说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。 模型变换
说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。 中点旋转:
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。 几何最终模型 对称最值(两点间线段最短)
初中数学常用几何模型及构造方法大全, 掌握它轻松搞定压轴题! 几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握哦~ 全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角 旋转:相邻等线段绕公共顶点旋转 对称全等模型 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 对称半角模型 说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 旋转全等模型 半角:有一个角含1/2角及相邻线段 自旋转:有一对相邻等线段,需要构造旋转全等 共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题
旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 自旋转模型 构造方法: 遇60度旋60度,造等边三角形; 遇90度旋90度,造等腰直角; 遇等腰旋顶点,造旋转全等; 遇中点旋180度,造中心对称. 共旋转模型
说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。 模型变形 说明: 模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
初中几何常见九大模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有 (2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) 模型三:对角互补模型
(1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE;②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明 为等边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②;③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导?模型四:角含半角模型90°
初中数学几何模型大全+经典题型(含答案) 全等变换 平移:平行等线段(平行四边形) 对称:角平分线或垂直或半角 旋转:相邻等线段绕公共顶点旋转 对称全等模型 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 对称半角模型 说明:上图依次是45°、30°、°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 旋转全等模型
半角:有一个角含1/2角及相邻线段 自旋转:有一对相邻等线段,需要构造旋转全等 共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题 旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 自旋转模型 构造方法: 遇60度旋60度,造等边三角形 遇90度旋90度,造等腰直角 遇等腰旋顶点,造旋转全等 遇中点旋180度,造中心对称
共旋转模型 说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。 模型变形 说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。 中点旋转: 说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与
初中数学九大几何模型 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】
初中数学 九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED 二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; O A B C D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A B C D E 图 2 O A B C D E O C D E 图 1图 2O A B C D O B C D E O B C D E O C D
三线八角 同位角找F型内错角找Z型同旁内角找U型 拐角模型 1.锯齿形 ∠2=∠1+∠3 ∠1+∠2=∠3+∠4 2.鹰嘴型 鹰嘴+小=大 ∠2=∠1+∠3 ∠2=∠1+∠3 3.铅笔头型 ∠1+∠2+∠3=360° ∠1+∠2+∠3+∠4=540°180×(n-1)
等积变换模型 S△ACD=S△BCD 八字模型 ∠A+∠B=∠C+∠D AD+BC>AB+CD 飞镖模型 ∠D=∠B+∠C+∠A AB+AC>BD+CD 内内角平分线模型 ∠A ∠D=90°+1 2 内外角平分线模型 ∠D=1 ∠A 2
外外角平分线模型 ∠D=90°-1 ∠A 2 平行平分出等腰模型 HG=HM 等面积模型 D是BC的中点 S△ABD= S△ACD 倍长中线模型:D是BC的中点 S△FBD= S△ECD 角平分线构造全等模型 角平分线垂直两边角平分线垂直中间
角平分线构造轴对称 以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,垂直也可以做为轴进行对称全等。 三垂模型 拉手模型 大小等边三角形虚线相等且夹角为60° 大小等腰三角形顶角为a,虚线相等,且夹角为a 大小等腰直角三角形虚线相等且夹角为90°
大小正方形虚线相等,且夹角为90° 半角模型 正方形ABCD ∠EDF=45° 得:EF=AE+CF CD=AD,∠ADC=90°,∠EDF=45°,∠A+∠C=180° 得:EF=AE+CF ∠BAD AB=AD,∠B+∠D=180°,∠EAF=1 2 得:EF=BE+DF AB=AC,∠BAC=90°,∠DAE=45° 得:DE2=BD2+CE2 △CEF为直角三角形
初中几何模型及常见结论的总结归纳 三角形的概念 三角形边、角之间的关系:①任意两边之和大于第三边(任意两边之差小于第三边);②三角形内角和为0 180(外角和为0360);③三角形的外角等于不相邻的两内角和。 三角形的三线:(1)中线(三角形的顶点和对边中点的连线);三角形三边中线交于一点(重心) 如图,O 为三角形的重心,重心O 分中线长度之比为1:2(1:2=OE BO :); DF EF DE 、、分别为三角形AC AB BC 、、边上的中位线(三角形任意两边中点的连线),DE ∥BC 且BC DE 2 1=。 几何问题中的“中点”与“中线”常常是联系再一起的。因此遇到中点这样的条件(或关键词)我们可以考虑中线定理与中位线定理进行思考。 中线(中点)的应用: ①在面积问题中,中线往往把三角形的面积等分,如果两三角形高相同,我们往往把面积之比转化为底边之比。(面积问题转化为线段比的问题)如上图,我们可以得到2:1===????AO OF S S S S ABO BO F ACF ABF ::, ②在涉及中线有关的线段长度问题,我们往往考虑倍长中线。
如图,已知AB ,AC 的长,求AF 的取值范围时。我们可以通过倍长中线。利用三角形边的关系在三 角形ABD 中构建不等关系。(AC AB AF AC AB +- 2). (2)角平分线(三角形三内角的角平分线);三角形的三条内角平分线交于一点(内心) 如图,O 为三角形ABC 的内心(内切圆的圆心);内心O 到三边的距离相等r OD OF OE ===(角平分线的性质定理);090=∠+∠+∠ACO CBO BAO ;ABC ABC C S r ??= 2(ABC S ?表示ABC ?的面积,ABC C ?表示ABC ?的周长); 关于角平分线角度问题的常见结论: