初中数学二次函数综合题及答案

二次函数题 选择题：

１、y=(m-2)x m2- m 是关于ｘ的二次函数，则m=( ) A -1 B 2 Ｃ －１或2 D m 不存在

2、下列函数关系中，可以看作二次函数y ＝ax ２

＋b ｘ+c （a ≠0)模型的是( ） A 在一定距离内，汽车行驶的速度与行驶的时间的关系

Ｂ 我国人中自然增长率为１％，这样我国总人口数随年份变化的关系 Ｃ 矩形周长一定时,矩形面积和矩形边长之间的关系 D 圆的周长与半径之间的关系

4、将一抛物线向下向右各平移2个单位得到的抛物线是y=-x 2，则抛物线的解析式是( ) A y=—( x-2）2+2 B y=—( x+2)２+2 C ｙ＝— （ ｘ＋2）2+2 D y=—( x-2)2—2 ５、抛物线y=

2

1 x 2-６x+2４的顶点坐标是(

)

A （—6,—6)

B (—６,6）

C (6,6)

D （6,—6) 6、已知函数ｙ＝a ｘ２

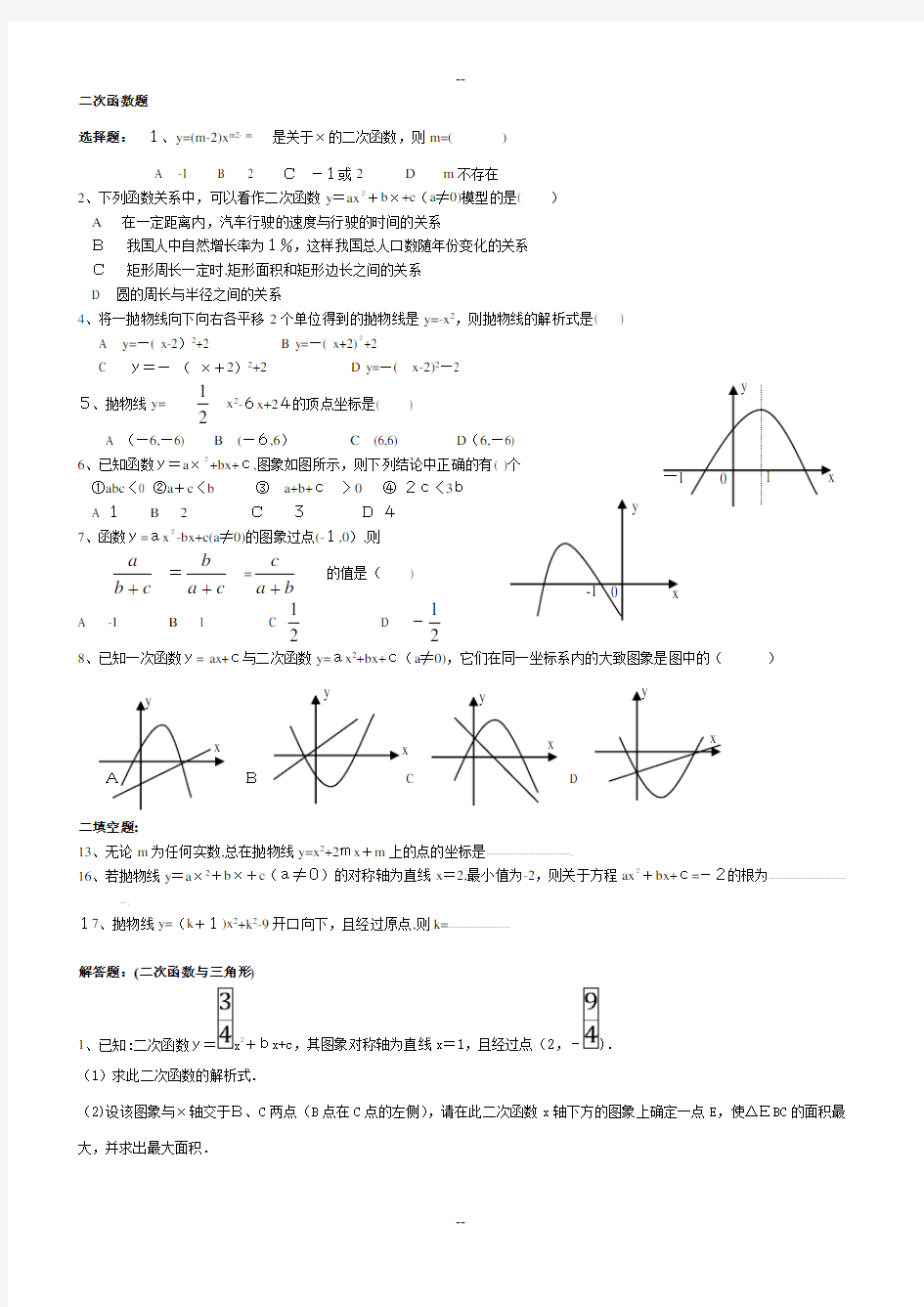
+bx+ｃ,图象如图所示，则下列结论中正确的有( )个 ①abc 〈0 ②a ＋c 〈b ③ a+b+ｃ 〉0 ④ ２ｃ〈3ｂ A １ B 2 Ｃ ３ Ｄ ４ 7、函数ｙ=ａx ２

-bx+c(a ≠0)的图象过点(-１,0）,则

c

b a + ＝

c a b + =b

a c

+ 的值是（ )

A -1

B 1

C 21

D －2

1

8、已知一次函数ｙ= ax+ｃ与二次函数y=ａx 2+bx+ｃ（a ≠0)，它们在同一坐标系内的大致图象是图中的（ ）

Ａ Ｂ C D

二填空题:

13、无论m 为任何实数,总在抛物线y=x 2+2ｍx ＋m 上的点的坐标是————————————。

16、若抛物线y ＝a ｘ2＋b ｘ＋c （ａ≠０）的对称轴为直线x ＝2,最小值为-2，则关于方程ax ２

＋bx+ｃ=－２的根为———————————

—。

１7、抛物线y=（k ＋１)x 2+k 2-9开口向下，且经过原点,则k=—————————

解答题：(二次函数与三角形)

1、已知:二次函数ｙ＝x 2

＋ｂx+c ，其图象对称轴为直线x ＝1，且经过点（2，﹣

)．

（1）求此二次函数的解析式.

（2)设该图象与ｘ轴交于Ｂ、C 两点（B 点在C 点的左侧），请在此二次函数x 轴下方的图象上确定一点E ，使△ＥBC 的面积最大，并求出最大面积．

1 —1 0

x

y

y

x

-1

x

y

y

x

y

x

y

2、如图,在平面直角坐标系中，抛物线与x 轴交于A 、B 两点（A 在B 的左侧）,与y 轴交于点C (0,4),顶点为(１，错误!). (1)求抛物线的函数表达式；

（2）设抛物线的对称轴与轴交于点Ｄ，试在对称轴上找出点P ，使△C ＤP 为等腰三角

形，请直接写出满足条件的所有点P 的坐标．

（3）若点Ｅ是线段ＡB 上的一个动点（与A 、B 不重合)，分别连接AC 、ＢC ,过点E 作

ＥF ∥AC 交线段BC 于点F ，连接CE ，记△CEF 的面积为Ｓ，S 是否存在最大值?

若存在,求出S 的最大值及此时E 点的坐标；若不存在，请说明理由．

3、如图,一次函数y ＝－4ｘ-4的图象与x 轴、y 轴分别交于A 、Ｃ两点，抛物线ｙ＝4

3

x 2+bx ＋c

的图象经过A 、C 两点,且与x 轴交于点Ｂ． （1）求抛物线的函数表达式；

(2)设抛物线的顶点为D ,求四边形A ＢD Ｃ的面积；

（3)作直线MN 平行于x 轴，分别交线段AC 、B Ｃ于点M 、Ｎ.问在x 轴上是否存在点P ，使得

△PMN 是等腰直角三角形?如果存在，求出所有满足条件的P 点的坐标;如果不存在,请说明理由．

(二次函数与四边形）4、已知抛物线

217222

y x mx m =

-+-． (1)试说明：无论ｍ为何实数，该抛物线与x 轴总有两个不同的交点；

(2)如图,当该抛物线的对称轴为直线x =3时,抛物线的顶点为点C ，直线y =ｘ－1与抛物线交于A 、Ｂ两点,并与它的对称轴交于点D ．

①抛物线上是否存在一点P 使得四边形AC ＰD 是正方形？若存在,求出点P 的坐标；若不存在,说明理由；

②平移直线ＣD ,交直线AB 于点Ｍ,交抛物线于点Ｎ，通过怎样的平移能使得C 、D 、Ｍ、N 为顶点的四边形是平行四边形．

C

O

A

y

x

D

B C O

A

y

x

D

B M

N

l :x ＝n

5、如图，抛物线ｙ＝mx 2-１1mx +2４ｍ (m <0) 与x 轴交于Ｂ、C 两点(点B 在点C 的左侧）,抛物线另有一点Ａ在第一象限内,

且∠BAC ＝90°.

(1)填空：O Ｂ=_ ▲ ，OC ＝＿ ▲ ；

(2）连接OA ，将△OAC 沿x 轴翻折后得△ODC ,当四边形OAC Ｄ是菱形时,求此时抛物线的解析式；

(３)如图２,设垂直于x 轴的直线l ：ｘ=ｎ与（2）中所求的抛物线交于点M ,与ＣＤ交于点Ｎ,若直线l 沿x 轴方向左右平移，

且交点Ｍ始终位于抛物线上Ａ、Ｃ两点之间时,试探究：当n 为何值时，四边形A ＭＣN 的面积取得最大值,并求出这个最大值.

６、如图所示,在平面直角坐标系中，四边形ＡBCD 是直角梯形,BC ∥AD,∠BA Ｄ=９0°，ＢC 与y 轴相交于点M,且M 是ＢC 的中点,Ａ、B 、D 三点的坐标分别是A （ 1 0-，)，B （ 1 2-，),D （３，0）.连接ＤM,并把线段DM 沿DA 方向平移到ＯN.若抛物线

2y ax bx c =++经过点D 、M 、N ．

（1)求抛物线的解析式．

(2)抛物线上是否存在点P,使得PA=ＰC,若存在，求出点P 的坐标;若不存在,请说明理由．

(3)设抛物线与ｘ轴的另一个交点为Ｅ,点Q 是抛物线的对称轴上的一个动点,当点Q 在什么位置时有|QE-Q Ｃ|最大?并求出最大值.

７、已知抛物线

223 (0)y ax ax a a =--<与x 轴交于A 、B 两点(点A 在点B 的左侧）,与ｙ轴交于点C ，点D 为抛物线

的顶点．(１）求A 、B 的坐标；

（2)过点D 作DH 丄y 轴于点Ｈ,若ＤＨ=ＨC ，求ａ的值和直线CD 的解析式;

（3)在第(２)小题的条件下，直线ＣD 与ｘ轴交于点E,过线段OB 的中点N 作N Ｆ丄x 轴,并交直线ＣD 于点F ，则直线N Ｆ上是否存在点Ｍ,使得点M 到直线CD 的距离等于点M 到原点Ｏ的距离?若存在,求出点M 的坐标;若不存在，请说明理由．

(二次函数与圆)

8、如图，在平面直角坐标系中，抛物线y=ax ２

+bx ＋c （ａ≠0)的图象经过M （1，0)和N （３,０)两点，且与ｙ轴交于Ｄ(0，3），直线l 是抛物线的对称轴．1)求该抛物线的解析式．

2)若过点Ａ（﹣1,0)的直线AB 与抛物线的对称轴和ｘ轴围成的三角形面积为6，求此直线的解析式． 3）点Ｐ在抛物线的对称轴上，⊙Ｐ与直线AB 和ｘ轴都相切，求点P 的坐标.

９、如图，y 关于x 的二次函数y ＝﹣（ｘ+ｍ)（x ﹣3ｍ)图象的顶点为M,图象交

ｘ轴于A 、B 两点，交y 轴正半轴于D 点．以AB 为直径作圆，圆心为C.定点E 的坐标

为(﹣3，0),连接ＥD.（m ＞0） （１)写出A 、Ｂ、D 三点的坐标；

（2）当m 为何值时M 点在直线E Ｄ上?判定此时直线与圆的位置关系;

（３)当m 变化时，用m 表示△AED 的面积S ，并在给出的直角坐标系中画出S 关于m 的函数图象的示意图。

1０、已知抛物线

2y ax bx c =++的对称轴为直线2x =，且与x 轴交于A 、Ｂ两点.与y 轴交于点C.其中AI(1,0),C(0,3-).

(１)（３分)求抛物线的解析式;

（2)若点Ｐ在抛物线上运动(点P 异于点A ）.

①（4分)如图l ．当△PBC 面积与△ABC 面积相等时．求点Ｐ的坐标；

②（5分)如图2．当∠PCB=∠ＢＣA 时,求直线ＣP 的解析式。

答案:

１、解:(1）由已知条件得，(2分)

解得b=﹣,ｃ=﹣,∴此二次函数的解析式为ｙ=x 2

﹣

x ﹣；（1分）

（2）∵x 2

﹣

x ﹣=0，∴x 1=﹣１，x ２=3，

∴B(﹣1，０),C （3，0）,∴ＢC=4，（1分)

∵E 点在x 轴下方，且△EBC 面积最大,∴E 点是抛物线的顶点,其坐标为(１,﹣3）,(1分)

∴△EBC 的面积＝×4×3=6.(1分)

2、（1）∵抛物线的顶点为(1,＼f(9,２)) ∴设抛物线的函数关系式为y =a ( x －1） ２

+错误!

∵抛物线与ｙ轴交于点C （0,4)， ∴ａ (0－1)

2＋＼f （9，２）=4 解得ａ=-＼f(1，２)

∴所求抛物线的函数关系式为y =-＼f(1,2)( x －1) ２

+错误!

（2)解:P 1 (1，＼r(,17)），P 2 (1，-，17)， Ｐ3 （1,８),P ４ (1,17

8

）,

(3）解:令－错误!（ x －1) 2

+错误!＝0，解得x １＝-2，x 1＝4

∴抛物线y ＝-错误!( x －1） 2+错误!与x 轴的交点为A (-２,0) Ｃ （4,0） 过点Ｆ作FM ⊥ＯＢ于点Ｍ,

∵E Ｆ∥AC ,∴△BEF ∽△BAC ,∴MF

OC

＝＼ｆ(ＥB ,AB ) 又 ∵OC ＝4，AB =6,∴MF ＝错误!×ＯC ＝错误!EB

设E 点坐标为 (ｘ，0）,则ＥB =４-x ,MF ＝＼f(2,3) (4-x ) ∴S =Ｓ△BCE -S △BEF ＝错误! ＥB ·OC -错误! EB ·MF ＝错误! ＥＢ(Ｏ

C －M Ｆ)=＼f(1,2） (4-x )[4-２

３

(4-x ）]=－错误!x 2＋错误!x +错误!=-错误!( x －1) 2＋3

∵a ＝-＼f(1,3)＜0,∴S 有最大值 当x ＝1时,S 最大值=3 此时点E 的坐标为 (１,0） 3、（１)∵一次函数y ＝-４x -4的图象与x 轴、y 轴分别交于A 、C 两点,

∴A (－１,0) C （0，-４） 把Ａ （-１,0) C (0，-4)代入ｙ=错误!x 2+bx +c 得 ∴错误! 解得错误! ∴y ＝错误!ｘ2-错误!x －4

(2)∵ｙ=错误!x 2-错误!ｘ－４＝错误!（ x -1) 2－错误! ∴顶点为Ｄ（１,－错误!） 设直线DC 交x 轴于点E 由D (１，-错误!）C (０，-４)

易求直线CD 的解析式为y ＝－错误!x －4

易求E (-3，0),B （3,0） Ｓ△EDB ＝1

２

×6×＼ｆ(１６,３)=16

S △E ＣA =＼ｆ（1,２)×2×4＝4 S 四边形ＡBDC ＝S △ED Ｂ-S △E ＣA ＝12 (3)抛物线的对称轴为x =-1

做BC 的垂直平分线交抛物线于E,交对称轴于点D 3 易求AB 的解析式为y ＝－错误!x +错误!

∵D 3E 是BC 的垂直平分线 ∴D 3E ∥A Ｂ

设Ｄ3E 的解析式为y =-３x +ｂ

∵D ３E 交ｘ轴于（-1，0)代入解析式得b =-＼r(,3), ∴y ＝－＼r(,3)ｘ-错误!

把ｘ＝-１代入得y =0 ∴D 3 （-1，０), 过B 做B Ｈ∥x 轴，则BH =1错误!

在Ｒt △D 1ＨＢ中，由勾股定理得D 1Ｈ=错误! ∴D １（－1,错误!＋错误!)同理可求其它点的坐标。 可求交点坐标Ｄ1（－1，错误!＋错误!）， D 2（-１,2错误!)， D 3 (-1,0), D ４ (-１, 错误!-错误!)D ５(－１,-２错误!)

B x

y O (第3题图) C

A D

E B x

y

O (第3题图)

C

A P

M N

4、(１)?＝

()

2

174222m m ??--??- ???

=247m m -+=2443m m -++=()2

23m -+,∵不管ｍ为何实数,总有

()

2

2m -≥0，∴?=

()

2

23m -+>0,∴无论m 为何实数,该抛物线与ｘ轴总有两个不同的交点.

（２)∵ 抛物线的对称轴为直线x ＝3,∴3m =， 抛物线的解析式为

215322y x x =

-+=()2

1322

x --，顶点C 坐标为（3，－2）

， 解方程组21,

15322

y x y x x =-??

?=-+??，解得1110x y =??

=?或2276x y =??=?,所以A 的坐标为(１,0）、B 的坐标为（7,６）,∵3x =时

y =x －1=3－１=２,∴Ｄ的坐标为（3,2）,设抛物线的对称轴与x 轴的交点为E ,则E 的坐标为(3，０),所以A Ｅ=BE =3,D Ｅ＝CE =2，

① 假设抛物线上存在一点Ｐ使得四边形A ＣPD 是正方形，则A Ｐ、CD 互相垂直平

分且相等,于是P 与点B 重合，但AP=6，CD=4,ＡP ≠CD ,故抛物线上不存在一点P 使得四边形AC ＰＤ是正方形．

② (Ⅰ）设直线CD 向右平移n 个单位(n >0）可使得C 、D 、M 、N 为顶点的四边形

是平行四边形，则直线C Ｄ的解析式为x =3n +,直线C Ｄ与直线y =ｘ-1交于点Ｍ(3n +，2n +),又∵Ｄ的坐标为（3,2）,C 坐标为(３，-2)，∴Ｄ通过向下平移４个单位得到C ．

∵C 、D 、Ｍ、Ｎ为顶点的四边形是平行四边形，∴四边形CDMN 是平行四边形或四边形ＣD ＮＭ是平行四边形． （ⅰ）当四边形CD ＭN 是平行四边形，∴M 向下平移4个单位得N ,∴N 坐标为（3n +，2n -）, 又N 在抛物线215322y x x =

-+上,∴()()2

15233322

n n n -=+-++, 解得1

0n =(不合题意，舍去），22n =,

(ⅱ）当四边形C ＤNM 是平行四边形，∴M 向上平移４个单位得N ,∴N 坐标为(3n +,6n +）, 又N 在抛物线215322y x x =

-+上，∴()()2

15633322

n n n +=+-++, 解得1

117n =-(不合题意,舍去)，2117n =+，

(Ⅱ) 设直线ＣＤ向左平移n 个单位（n ＞0)可使得C 、Ｄ、M 、N 为顶点的四边形是平行四边形，则直线CD 的解析式为

ｘ=3n -，直线C Ｄ与直线ｙ＝x -1交于点Ｍ（3n -,2n -）,又∵D 的坐标为(3,2)，C 坐标为（３，－2），∴D 通过向下

平移４个单位得到C .

∵C 、D 、M 、N 为顶点的四边形是平行四边形,∴四边形CDM Ｎ是平行四边形或四边形CDNM 是平行四边形. （ⅰ）当四边形CD ＭN 是平行四边形,∴M 向下平移4个单位得N ，∴Ｎ坐标为（3n -，2n --)， 又Ｎ在抛物线215322y x x =

-+上，∴()()2

15233322

n n n --=---+, 解得1

0n =(不合题意,舍去），22n =-(不合题意,舍去),

(ⅱ)当四边形CD ＮM 是平行四边形,∴M 向上平移4个单位得N ,∴N 坐标为(3n -,6n -)， 又N 在抛物线215322y x x =

-+上,∴()()2

15633322

n n n -=---+， 解得1

117n =-+,2117n =--（不合题意，舍去)，

C O A

y

x D B E C O A

y x D

B M

N

l :x ＝n E 综上所述，直线CD 向右平移２或(117+)个单位或向左平移(117-+)个单位,可使得C 、Ｄ、M 、N 为顶点的四边

形是平行四边形．

５、解：（1）O Ｂ=3,OC =8

(2)连接O Ｄ，交OC 于点Ｅ

∵四边形ＯA ＣD 是菱形 ∴AD ⊥O Ｃ,ＯE ＝EC ＝错误! ×8＝4 ∴ＢE ＝4-3＝１ 又∵∠B ＡC ＝９０°, ∴△A ＣE ∽△BAE ∴AE

BE

=错误!

∴ＡＥ2＝B Ｅ·ＣＥ＝１×4 ∴A Ｅ=2

∴点A 的坐标为 (4,2)

把点A 的坐标 (４，2)代入抛物线y =mx ２

-11ｍx +２4ｍ,

得m ＝-1２

∴抛物线的解析式为y ＝-错误!ｘ2＋错误!x －12 （3)∵直线ｘ=n 与抛物线交于点Ｍ ∴点M 的坐标为 (n ,－12

n 2＋错误!n -12)

由（2)知,点D 的坐标为（4,－2)，

则Ｃ、Ｄ两点的坐标求直线CD 的解析式为ｙ＝＼f （1，2）x －4 ∴点N 的坐标为 (n ,错误!n -４) ∴MN =（-错误!n 2+错误!n －12)-（错误!n -4）=－错误!n 2+５n －8

∴S 四边形A ＭＣN ＝S △AM Ｎ+S △CMN =错误!M Ｎ·CE =错误!(-错误!n 2+5n -８）×4＝－(ｎ-５)2＋9 ∴当n ＝5时,S 四边形ＡMCN ＝9

6、解:（1)∵ＢC ∥AD,B(－1,2），M 是B Ｃ与ｘ轴的交点，∴M(0,2）,

∵D Ｍ∥ON ，Ｄ(3，０)，∴Ｎ（-3，2)，则9302930a b c c a b c ++=??=??-+=?，解得19132

a b c ?

=-??

?=-??

=???

，∴211293y x x =--+; （２)连接AC 交y 轴与Ｇ，∵M 是B Ｃ的中点,∴AO=BM=MC,AB=BC=2,∴ＡG=ＧC ，即G （0,１）,

∵∠ABC=９0°，∴ＢG ⊥AC ，即BG 是ＡC 的垂直平分线，要使PA=PC,即点Ｐ在AC 的垂直平分线上，故Ｐ在直线BG 上,∴点P 为直线ＢG 与抛物线的交点,

设直线ＢＧ的解析式为y kx b =+,则21k b b -+=??=?,解得11k b =-??=?,∴1y x =-+，

∴2111

293y x y x x =-+??

?=--+??

,解得11332232x y ?=+??=--??,22332232x y ?=-??=-+??， ∴点P(332 232+-- ，)或P （3-32 232-+ ，),

(3）∵

22111392()93924y x x x =--+=-++，∴对称轴32

x =-,

令211

2093

x x --+=,解得13x =，26x =，∴E(6-,0），

故E 、D 关于直线3

2

x =-对称,∴ＱＥ=ＱD ，∴|Q Ｅ-Q Ｃ|=｜QD-ＱC|，

要使｜ＱＥ-ＱC|最大,则延长DC 与3

2

x =-相交于点Q,即点Q 为直线ＤC 与

直线3

2

x

=-

的交点, 由于M 为ＢC 的中点，∴C(1，2),设直线CD 的解析式为y ＝ｋx+b, 则302k b k b +=??

+=?，解得1

3k b =-??=?，∴3y x =-+,

当32x

=-

时，39322y =+=，故当Q 在（39

22

-，）的位置时,｜Q Ｅ－Q Ｃ｜最大, 过点C 作C Ｆ⊥x 轴,垂足为F,则CD=

22222222CF DF +=+=.

7、解：(1)由y=０得，ax 2－2ax-3a=0，

∵a≠0,∴x 2-2x-３=0, 解得x 1=-１，x ２=３， ∴点A 的坐标(-1，０),点B 的坐标(3，０）；

（2）由y=a ｘ2-2ax －3a ，令x ＝0,得y=-3a ， ∴Ｃ(０,-3a)，

又∵y=ax 2-2ａx －3ａ＝a （x －1）2－4a ， 得D(1,－4a)，

∴DH=１，CH=-4a －（－3ａ）=-a, ∴－ａ=1,∴ａ=-1， ∴C(０，３)，D(1,4）,

设直线ＣD 的解析式为y=kx+b ，把Ｃ、Ｄ两点的坐标代入得, ,解得

，

∴直线ＣD 的解析式为y=x+3; （3）存在.

由（２)得,E(-３,0),N （-

,０) ∴F(

, ）,ＥN=

，

作MQ ⊥CD 于Q ，设存在满足条件的点M （ ,m ）,则FM= -m ，

EF= = ，M Ｑ=ＯＭ=

由题意得：Rt △ＦQ Ｍ∽R ｔ△FNE ，∴ ＝

，整理得4m 2+36m －６３=０，∴ｍ2+９m ＝ ， m 2＋9ｍ+

=

+

(ｍ＋ ）2=

m+

=±

∴ｍ1= ,m 2=-

,

∴点Ｍ的坐标为M １（ , ）,Ｍ２（

，- ).

8、解：(1）∵抛物线y=ａx ２

＋b ｘ+c （ａ≠0)的图象经过M （1，0)和N(3，0）两点,且与ｙ轴交于D(0,3），

∴假设二次函数解析式为:ｙ＝a(ｘ﹣1)（x ﹣3)，

将Ｄ(０，３），代入y=ａ(x ﹣１)（x ﹣3)，得：3＝3a ， ∴a=１, ∴抛物线的解析式为:y=（x ﹣1)（ｘ﹣3)＝ｘ２

﹣4x+3；

(2）∵过点A(﹣1，０)的直线ＡＢ与抛物线的对称轴和x 轴围成的三角形面积为6，∴AC×ＢC ＝６,

∵抛物线ｙ=ax 2+bx+c （a≠０)的图象经过M （１,0)和N(3，０）两点,∴二次函数对称轴为x=２,

∴ＡC=3，∴BC=4，∴Ｂ点坐标为:(2，4)，一次函数解析式为；y=kx ＋b ，

∴，解得:，y=x+；

x

y

O A B

E

P

P 3

(3）∵当点P 在抛物线的对称轴上,⊙P 与直线A Ｂ和x 轴都相切,

∴M Ｏ⊥ＡB,AM ＝A Ｃ，P Ｍ=ＰC ，

∵ＡＣ=1＋2＝3，BC=4， ∴A Ｂ=5，ＡM ＝3， ∴B Ｍ=2， ∵∠ＭＢＰ=∠ABC ，∠ＢMP=∠ACB ，

∴△AB Ｃ∽△ＣBM,∴，

∴,∴ＰＣ＝1．5，P 点坐标为:(2,1．5).

９、解：（１)A （﹣m ，0)，Ｂ（３ｍ,0）,D(0,

m ）．

(２）设直线ED 的解析式为y=kx ＋b ，将Ｅ（﹣3，0）,Ｄ(0，

m)代入得：

解得,k=，ｂ=m. ∴直线ＥD 的解析式为ｙ=ｍx+m.

将y=﹣(ｘ+m ）（ｘ﹣3ｍ)化为顶点式：y=﹣（ｘ＋m ）2+m ．

∴顶点M 的坐标为（ｍ，ｍ）．代入y=mx+m 得：m 2=m

∵m>0，∴m=1.所以,当m ＝1时,M 点在直线D Ｅ上.连接CD,C 为AB 中点，C 点坐标为C （m ，0）. ∵ＯD=

,ＯＣ＝1,∴CD ＝2,D 点在圆上

又OE ＝３,D Ｅ2=ＯＤ２

＋ＯＥ2＝12，EC ２

=16,CD ２

=4,∴ＣＤ２

+DE 2=EC 2.∴∠FDC=9０°∴直线ＥD 与⊙C 相切.

(３)当0

当m ＞3时，S △AED ＝AE ．?ＯD=m(m ﹣３）. 即S=m 2

＿

ｍ.

１0、解:(１）由题意,得

0322a b c c b a

?

?++=?

=-???-=?，解得

143a b c =-??

=??=-?

∴抛物线的解析式为243y x x =-+-。

（２)①令2

430x

x -+-=，解得1213x x ==， ∴B(3, 0）

当点P 在x 轴上方时，如图1，过点A 作直线BC 的平行线交抛物线于点Ｐ, 易求直线BC 的解析式为

3y x =-，∴设直线AP 的解析式为y x n =+,

圆的综合大题

二次函数与圆 1、如图，AB 是⊙O 的直径，弦BC=2cm ，∠ABC=60o． （1）求⊙O 的直径； （2）若D 是AB 延长线上一点，连结CD ，当BD 长为多少时，CD 与⊙O 相切； （3）若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动，同时动点F 以1cm/s 的 速度从B 点出发沿BC 方向运动，设运动时间为)20)((<

2、如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）． （1）求此抛物线的解析式 （2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明； （3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

3、如图，抛物线2 23y x x =-++与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D . （1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴； （2）连接BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作 PF DE ∥交抛物线于点F ，设点P 的横坐标为m ； ①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？ ②设BCF △的面积为S ，求S 与m 的函数关系式.

初三数学二次函数知识点总结

初三数学 二次函数 知识点总结 一、二次函数概念： 1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数， 0a ≠）的函数，叫做二次函数。 这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征： ⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项． 二、二次函数的基本形式 1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。 2. 2y ax c =+的性质： 上加下减。 3. ()2 y a x h =-的性质： 左加右减。

4. ()2 y a x h k =-+的性质： 三、二次函数图象的平移 1. 平移步骤： 方法一：⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下： 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二： ⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成 m c bx ax y +++=2（或m c bx ax y -++=2） ⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成 c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2） 四、二次函数()2 y a x h k =-+与2y ax bx c =++的比较 从解析式上看，()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即2 2424b ac b y a x a a -? ?=++ ?? ?，其中2424b ac b h k a a -=-= ，．

初中数学二次函数综合题及答案

二次函数题 选择题： １、y=(m-2)x m2- m 是关于ｘ的二次函数，则m=( ) A -1 B 2 Ｃ －１或2 D m 不存在 2、下列函数关系中，可以看作二次函数y ＝ax ２ ＋b ｘ+c （a ≠0)模型的是( ） A 在一定距离内，汽车行驶的速度与行驶的时间的关系 Ｂ 我国人中自然增长率为１％，这样我国总人口数随年份变化的关系 Ｃ 矩形周长一定时,矩形面积和矩形边长之间的关系 D 圆的周长与半径之间的关系 4、将一抛物线向下向右各平移2个单位得到的抛物线是y=-x 2，则抛物线的解析式是( ) A y=—( x-2）2+2 B y=—( x+2)２+2 C ｙ＝— （ ｘ＋2）2+2 D y=—( x-2)2—2 ５、抛物线y= 2 1 x 2-６x+2４的顶点坐标是( ) A （—6,—6) B (—６,6） C (6,6) D （6,—6) 6、已知函数ｙ＝a ｘ２ +bx+ｃ,图象如图所示，则下列结论中正确的有( )个 ①abc 〈0 ②a ＋c 〈b ③ a+b+ｃ 〉0 ④ ２ｃ〈3ｂ A １ B 2 Ｃ ３ Ｄ ４ 7、函数ｙ=ａx ２ -bx+c(a ≠0)的图象过点(-１,0）,则 c b a + ＝ c a b + =b a c + 的值是（ ) A -1 B 1 C 21 D －2 1 8、已知一次函数ｙ= ax+ｃ与二次函数y=ａx 2+bx+ｃ（a ≠0)，它们在同一坐标系内的大致图象是图中的（ ） Ａ Ｂ C D 二填空题: 13、无论m 为任何实数,总在抛物线y=x 2+2ｍx ＋m 上的点的坐标是————————————。 16、若抛物线y ＝a ｘ2＋b ｘ＋c （ａ≠０）的对称轴为直线x ＝2,最小值为-2，则关于方程ax ２ ＋bx+ｃ=－２的根为——————————— —。 １7、抛物线y=（k ＋１)x 2+k 2-9开口向下，且经过原点,则k=————————— 解答题：(二次函数与三角形) 1、已知:二次函数ｙ＝x 2 ＋ｂx+c ，其图象对称轴为直线x ＝1，且经过点（2，﹣ )． （1）求此二次函数的解析式. （2)设该图象与ｘ轴交于Ｂ、C 两点（B 点在C 点的左侧），请在此二次函数x 轴下方的图象上确定一点E ，使△ＥBC 的面积最大，并求出最大面积． 1 —1 0 x y y x -1 x y y x y x y

二次函数和圆综合(压轴题+例题+巩固+答案解析)

【例1】.如图，点()40M ，，以点M 为圆心、2为半径的圆与x 轴交于点A B ，．已知抛物 21 6 y x bx c =++过点A 和B ，与y 轴交于点C ． ⑴ 求点C 的坐标，并画出抛物线的大致图象． ⑵ 点()8Q m ，在抛物线21 6 y x bx c =++上，点P 为此抛物线对称轴上一个动点，求 PQ PB + 最小值． ⑶ CE 是过点C 的M ⊙的切线，点E 是切点，求OE 所在直线的解析式．

【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ，顶点为M ，直线CM 的解析式 2y x =-+并且线段CM 的长为（1）求抛物线的解析式。 （2）设抛物线与x 轴有两个交点A （X 1 ，0）、B （X 2 ，0），且点A 在B 的左侧，求线段AB 的长。 （3）若以AB 为直径作⊙N ，请你判断直线CM 与⊙N 的位置关系，并说明理由。 【例2】如图，在平面直角坐标系中，以点(04)C ，为圆心，半径为4的圆交y 轴正半轴于点A ， AB 是C ⊙的切线． 动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动，点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动，且动点P 、 Q 从点A 和点O 同时出发，设运动时间为t (秒)． ⑴当1t =时，得到1P 、1Q 两点，求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ；

⑵当t 为何值时，直线PQ 与C ⊙相切？并写出此时点P 和点Q 的坐标； ⑶在⑵的条件下，抛物线对称轴l 上存在一点N ，使NP NQ +最小，求出点N 的坐标并说明理由． 提示：（1）先求出t=1时，AP 和OQ 的长，即可求得P 1，Q 1的坐标，然后用待定系数法即可得出抛物线的解析式．进而可求出对称轴l 的解析式． （2）当直线PQ 与圆C 相切时，连接CP ，CQ 则有Rt △CMP ∽Rt △QMC （M 为PG 与圆的切点），因此可设当t=a 秒时，PQ 与圆相切，然后用a 表示出AP ，OQ 的长即PM ，QM 的长（切线长定理）．由此可求出a 的值． （3）本题的关键是确定N 的位置，先找出与P 点关于直线l 对称的点P ′的坐标，连接P ′Q ，那么P ′Q 与直线l 的交点即为所求的N 点，可先求出直线P ′Q 的解析式，进而可求出N 点的坐标． 【巩固】已知二次函数图象的顶点在原点O ，对称轴为y 轴．一次函数1y kx =+的图象与 二次函数的图象交于A B ，两点(A 在B 的左侧)，且A 点坐标为()44-，．平行于x 轴的直线 l 过()01-，点． ⑴ 求一次函数与二次函数的解析式； ⑵ 判断以线段AB 为直径的圆与直线l 的位置关系，并给出证明； ⑶ 把二次函数的图象向右平移2个单位，再向下平移t 个单位()0t >，二次函数的图象与x

(完整版)初中数学二次函数综合题及答案

二次函数题 选择题： 1、y=(m-2)x m2- m 是关于x 的二次函数，则m=（ ） A -1 B 2 C -1或2 D m 不存在 2、下列函数关系中，可以看作二次函数y=ax 2+bx+c(a ≠0)模型的是（ ） A 在一定距离内，汽车行驶的速度与行驶的时间的关系 B 我国人中自然增长率为1%，这样我国总人口数随年份变化的关系 C 矩形周长一定时，矩形面积和矩形边长之间的关系 D 圆的周长与半径之间的关系 4、将一抛物线向下向右各平移2个单位得到的抛物线是y=-x 2，则抛物线的解析式是（ ） A y=—（ x-2）2+2 B y=—（ x+2）2+2 C y=— （ x+2）2+2 D y=—（ x-2）2—2 5、抛物线y= 2 1 x 2 -6x+24的顶点坐标是（ ） A （—6，—6） B （—6，6） C （6，6） D （6，—6） 6、已知函数y=ax 2+bx+c,图象如图所示，则下列结论中正确的有（ ）个 ①abc 〈０ ②a ＋c 〈b ③ a+b+c 〉０ ④ ２c 〈３b A １ B ２ C ３ D ４ 7、函数y=ax 2-bx+c （a ≠0）的图象过点（-1，0），则 c b a + =c a b + =b a c + 的值是（ ） A -1 B 1 C 21 D -2 1 8、已知一次函数y= ax+c 与二次函数y=ax 2+bx+c （a ≠0），它们在同一坐标系内的大致图象是图中的（ ） A B C D 二填空题： 13、无论m 为任何实数，总在抛物线y=x 2＋2mx ＋m 上的点的坐标是————————————。 16、若抛物线y=ax 2+bx+c （a ≠0）的对称轴为直线x ＝２，最小值为－２，则关于方程ax 2+bx+c ＝－２的根为————————————。 17、抛物线y=（k+1）x 2+k 2-9开口向下，且经过原点，则k ＝————————— 解答题：（二次函数与三角形） 1、已知：二次函数y=x 2 +bx+c ，其图象对称轴为直线x=1，且经过点（2，﹣）． （1）求此二次函数的解析式． （2）设该图象与x 轴交于B 、C 两点（B 点在C 点的左侧），请在此二次函数x 轴下方的图象上确定一点E ，使△EBC 的面积最大，并求出最大面积． 1 —1 0 x y y x -1 x y y x y x y

人教版初中数学二次函数-教案-习题总汇-含答案

一、教学目标 1． 使学生会用描点法画出二次函数k h x a y +-=2 )(的图像； 2． 使学生知道抛物线k h x a y +-=2 )(的对称轴与顶点坐标； 3．通过本节的学习，继续培养学生的观察、分析、归纳、总结的能力； 4．通过本节的教学，继续向学生进行数形结合的数学思想方法的教育，同时向学生渗透事物间互相联系、以及运动、变化的辩证唯物主义思想； 5．通过本节课的研究，充分理解并认识到二次函数图像可运动变化的和谐美，通过数学思维的审美活动，提高对数学美的追求。 二、教学重点 会画形如k h x a y +-=2 )(的二次函数的图像，并能指出图像的开口方向、对称轴及顶点坐标。 三、教学难点：确定形如 k h x a y +-=2 )(的二次函数的顶点坐标和对称轴。 4．解决办法： 四、教具准备 三角板或投影片 1．教师出示投影片，复习2 2 2 )(,,h x a y k ax y ax y -=+==。 2．请学生动手画1)1(2 1 2-+- =x y 的图像，正好复习图像的画法，完成表格。 3．小结k h x a y +-=2 )(的性质??? ?? ??平移顶点坐标对称轴开口方向 4．练习 五、教学过程 提问：1．前几节课，我们都学习了形如什么样的二次函数的图像？ 答：形如2 2 2 )(,h x a y k ax y ax y -=+==和。（板书） 2．这节课我们将来学习一种更复杂的二次函数的图像及其相关问题，你能先猜测一下我们将学习形如什么样的二次函数的问题吗？

由学生参考上面给出的三个类型，较容易得到：讨论形如k h x a y +-=2 )(的二次函数的有关问题．（板书） 一、复习引入 首先，我们先来复习一下前面学习的一些有关知识．（出示幻灯） 请你在同一直角坐标系内，画出函数222)1(2 1 ,121,21+-=--=-=x y x y x y 的图像，并指出它们的开口方向，对称轴及顶点坐标． 这里之所以加上画函数2)1(2 1 +- =x y 的图像， 是为了使最后通过图像的观察能更全面一些，也更直观一些，可以同时给出图像先沿y 轴，再沿x 轴移动的方式，也可以给出图像 先沿x 轴再沿y 轴移动的方式，使这部分知识能更全面，知识与知识之间的联系能更清晰、 更具体． 画这三个函数图像，可由学生在同一表中列值，但是要根据各自的不同特点取自变量x 的值，以便于学生进行观察．教师可事先准备好表格和画有直角坐标系的小黑板，由一名同 学上黑板完成，其他同学在练习本上完成，待同学们基本做完之后加以总结，然后再找三名 同学，分别指出这三个图像的开口方向、对称轴及顶点坐标，填入事先准备好的表格中． 然后提问：你能否在这个直角坐标系中，再画出函数1)1(2 1 2-+- =x y 的图像？ 由于前面几节课我们已经画了不少二次函数的图像，学生对画图已经有了一定的经验， 同时可在画这个图时，把这些经验形成规律，便于学生以后应用． （l ）关于列表：主要是合理选值与简化运算的把握，是教学要点．在选值时，首先要考虑的是函数图像的对称性，因此首先要确定中心值，然后再左，右取相同间隔的值；其次，选值时尽量选取整数，便于计算和描点． 在选取x 的值之后，计算y 的值时，考虑到对称性，只需计算中心值一侧的值，另一侧由对称性可直接填入，但一定要保证运算正确． （2）关于描点：一般可先定顶点（即中心值对应的点，然后利用对称性描出各点，以逐步提高速度．） （3）关于连线：特别要注意顶点附近的大致走向。最后画的抛物线应平滑，对称，并符合抛物线的特点． 由学生在上面的练习中所列的表中填上这个函数及其对应值，然后画出它的图像，同样 找一名同学板演． 学生画完，教师总结完之后，让学生观察黑板上画出的四条抛物线，提问： （1）你能否指出抛物线1)1(2 1 2-+- =x y 的开口方向，对称轴，顶点坐标？ 将在上面练习中三条抛物线的性质填入所列的有中，如下表：

-圆与二次函数综合题精练(带答案)教学文案

圆与二次函数综合题 1、已知：二次函数y=x2-kx+k+4的图象与y轴交于点c，且与x轴的正半轴交于A、B两点（点A 在点B左侧）。若A、B两点的横坐标为整数。 （1）确定这个二次函数的解析式并求它的顶点坐标；（2）若点D的坐标是(0,6），点P（t,0)是线段AB上的一个动点，它可与点A重合，但不与点B重合。设四边形PBCD的面积为S，求S与t的函数关系式； （3）若点P与点A重合，得到四边形ABCD，以四边形ABCD的一边为边，画一个三角形，使它的面积等于四边形ABCD的面积，并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识，画一个三角形，使它的面积等于四边形ABCD的面积（画示意图，不写计算和证明过程）。 2、（1）已知：关于x、y的方程组有两个实数解，求m的取值范围； (2）在（1）的条件下，若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点，与y轴交于点C，且△ABC的面积等于12，确定此抛物线及直线y=(m+1)x-2的解析式； （3）你能将（2）中所得的抛物线平移，使其顶点在（2）中所得的直线上吗？请写出一种平移方法。 3、已知：二次函数y=x2-2(m-1)x+m2-2m-3，其中m为实数。 （1）求证：不论m取何实数，这个二次函数的图像与x轴必有两个交点；（2）设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式。 4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像，确定当x取什么值时，y1>0,y1=0,y1<0; (2)根据（1）的结论，确定函数y2= (|y1|-y1)关于x的解析式； （3）若一次函数y=kx+b(k 0)的图像与函数y2的图像交于三个不同的点，试确定实数k与b应满足的条件。 5、已知：如图，直线y= x+ 与x轴、y轴分别交于A、B两点，⊙M经过原点O及A、B两点。 （1）求以OA、OB两线段长为根的一元二次方程； （2）C是⊙M上一点，连结BC交OA于点D，若∠COD=∠CBO, 写出经过O、C、A三点的二次函数的解析式； （3）若延长BC到E，使DE=2,连结EA，试判断直线EA与 ⊙M的位置关系，并说明理由。（河南省） 6、如图，已知点A（tan ,0）B(tan ,0)在x轴正半轴上，点A在点B的左 边，、是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角。 （1）若二次函数y=-x2- 5/2kx+(2+2k-k2)的图像经过A、B两点，求它的解析式； （2）点C在（1）中求出的二次函数的图像上吗？请说明理由。（陕西省）

2020年初三数学二次函数经典练习全集

1.一跳水运动员从米高台上跳下，他的高度h(单位：米)与所用的时间t(单位：秒)的关系为h=-5(t-2)(t+1),你能帮助该运动员计算一下他跳起来后多长时间达到最大高度？最大高度是多 少米？ 2．篱笆墙长30m ，靠墙围成一个矩形花坛，写出花坛面积y(m 2 )与长x 之间的函数关系式，并指出自变量的取值范围． 3.已知二次函数y=ax 2 ＋bx ＋c ，当 x=0时，y=0；x=1时，y=2；x=-1时，y=1．求a 、b 、c ，并写出函数解析式． 4.求经过A(0，-1)、B(-1，2)，C(1，-2)三点且对称轴平行于y 轴的抛物线的解析式． 5.已知二次函数为x ＝4时有最小值-3且它的图象与x 轴交点的横坐标为1，求此二次函数解析式． 6. 已知抛物线经过点(-1，1)和点(2，1)且与x 轴相切． (1)求二次函数的解析式； (2)当x 在什么范围时，y 随x 的增大而增大； (3)当x 在什么范围时，y 随x 的增大而减小． 7.已知122 12 ++-=x x y (1)把它配方成y ＝a(x-h)2 ＋k 形式； (2)写出它的开口方向、顶点M 的坐标、对称轴方程和最值； (3)求出图象与y 轴、x 轴的交点坐标； (4)作出函数图象； (5)x 取什么值时y ＞0，y ＜0； (6)设图象交x 轴于A ，B 两点，求△AMB 面积． 8．在长20cm ，宽15cm 的矩形木板的四角上各锯掉一个边长为xcm 的正方形，写出余下木 板的面积y(cm 2 )与正方形边长x(cm)之间的函数关系，并注明自变量的取值范围． 9．已知二次函数y=4x 2 ＋5x ＋1，求当y=0时的x 的值． 10．已知二次函数y=x 2 -kx-15，当x=5时，y=0，求k ． 12．已知二次函数y=ax 2＋bx ＋c 中，当x=0时，y=2；当x=1时，y=1；当x=2时，y=-4，试求a 、b 、c 的值． 13.有一个半径为R 的圆的内接等腰梯形，其下底是圆的直径． (1)写出周长y 与腰长x 的函数关系及自变量x 的范围； (2)腰长为何值时周长最大，最大值是多少？ 14.二次函数的图象经过()()()4,2,4,0,0,4--C B A 三点： ① 求这个函数的解析式 ② 求函数图顶点的坐标 ③ 求抛物线与坐标轴的交点围成的三角形的面积。 15．如图，抛物线y=x 2 +bx+c 与x 轴的负半轴相交于A 、B 两点，与y 轴的正半轴相交于C 点，与双曲线y= x 6 的一个交点是(1，m)，且OA=OC.求抛物线的解析式． 16．如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P 从点O 开始沿OA 边向点A 以l 厘米／秒的速度移动；点Q 从点B 开始沿BO 边向点O 以l 厘米，秒的速度移动．如果P 、Q 同时出发，用t(秒)表示移动的时间(0≤t≤6)，那么 (1)设△POQ 的面积为y ，求y 关于t 的函数解析式； (2)当△POQ 的面积最大时，将△POQ 沿直线PQ 翻折后得到△PCQ，试判断点C 是否落在直线AB 上，并说明理由； (3)当t 为何值时，△POQ 与△AOB 相似． 17、水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克. 经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克.

初中数学二次函数综合应用

学 科 中考数学 课题名称 二次函数综合应用 教学目标 二次函数属于中考压轴题，知识点不仅多，考点灵活多变，而且难度较高，这就要求学生在复习二次函数时，须得把相关性质及相关解题技巧掌握扎实，理解透彻。本专题通过梳理二次函数的知识点(拓展知识点)，并结合近几年上海市中考数学最后2道题二次函数的考点，把握中考二次函数命题方向，提高学生利用二次函数和结合相似等综合知识点解决问题的能力。 教学重难点 重点：二次函数解析式的确定，二次函数与x 轴交点问题，二次函数最值问题，二次函数图像上点的 存在问题，二次函数与相似等其它知识点的结合。 难点：二次函数与相似等其它知识点的结合。 知识精解 二次函数性质及相关扩展 1、一般式：y=ax 2+bx+c(a≠0), 函数图像是抛物线； 2、开口方向：（1）a>0, 开口向上， （2）a<0, 开口向下; 3、顶点坐标：（-b/2a, (4ac-b 2)/4a ）, 对称轴：x= -b/2a 4、 顶点式：y=a(x+h)2+k(a≠0) h= -b/2a, k=(4ac-b 2)/4a 5、平移问题： ①将一般式化为顶点式； ②遵循原则：“左+ 右-，上+ 下-”（左右是指沿x 轴平移，上下是指沿y 轴平移） 例：将y=x 2+4x+3先向右平移2个单位，再向上平移1个单位，得到的新抛物线解析式是多少？ 6、交点式：y=a(x-x 1)(x-x 2)(a≠0) ①一元二次方程根与系数的关系：x 1+x 2= -b/a, x 1.x 2=c/a ②求根公式：x ＝2 42b b ac a -±-，其中△＝b 2－4ac 叫做根的判别式。 当△＞0时，抛物线与x 轴有两个交点； 当△＝0时，抛物线与x 轴有一个交点； 当△＜0时，抛物线与x 轴没有交点。 ③运用抛物线的对称性： 若已知抛物线上两点12(,)(,)、x y x y ， 则对称轴方程可以表示为：12 2 x x x += 7、增减性： ①a>0时，在对称轴的左侧，y 随x 的增大而减小； 在对称轴的右侧，y 随x 的增大而增大。 ②a<0时，在对称轴的左侧，y 随x 的增大而增大；

人教版初中数学二次函数解析

人教版初中数学二次函数解析 一、选择题 1．若平面直角坐标系内的点M 满足横、纵坐标都为整数，则把点M 叫做“整点”．例如：P （1，0）、Q （2，﹣2）都是“整点”．抛物线y ＝mx 2﹣4mx +4m ﹣2（m ＞0）与x 轴交于点A 、B 两点，若该抛物线在A 、B 之间的部分与线段AB 所围成的区域（包括边界）恰有七个整点，则m 的取值范围是（ ） A ．12≤m ＜1 B ．12＜m ≤1 C ．1＜m ≤2 D ．1＜m ＜2 【答案】B 【解析】 【分析】 画出图象，利用图象可得m 的取值范围 【详解】 ∵y ＝mx 2﹣4mx +4m ﹣2＝m （x ﹣2）2﹣2且m ＞0， ∴该抛物线开口向上，顶点坐标为（2，﹣2），对称轴是直线x ＝2． 由此可知点（2，0）、点（2，﹣1）、顶点（2，﹣2）符合题意． ①当该抛物线经过点（1，﹣1）和（3，﹣1）时（如答案图1），这两个点符合题意． 将（1，﹣1）代入y ＝mx 2﹣4mx +4m ﹣2得到﹣1＝m ﹣4m +4m ﹣2．解得m ＝1． 此时抛物线解析式为y ＝x 2﹣4x +2． 由y ＝0得x 2﹣4x +2＝0．解得12120.622 3.42 x x ==- ≈+≈，． ∴x 轴上的点（1，0）、（2，0）、（3，0）符合题意． 则当m ＝1时，恰好有 （1，0）、（2，0）、（3，0）、（1，﹣1）、（3，﹣1）、（2，﹣1）、（2，﹣2）这7个整点符合题意． ∴m ≤1．【注：m 的值越大，抛物线的开口越小，m 的值越小，抛物线的开口越大】 答案图1（m ＝1时） 答案图2（ m ＝时） ②当该抛物线经过点（0，0）和点（4，0）时（如答案图2），这两个点符合题意． 此时x 轴上的点 （1，0）、（2，0）、（3，0）也符合题意． 将（0，0）代入y ＝mx 2﹣4mx +4m ﹣2得到0＝0﹣4m +0﹣2．解得m ＝12 ．

初中中招二次函数和圆的综合体包含答案

二次函数和圆 【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x = (1)k >图象上，并与x 轴相交于A 、B 两点． 且始终与y 轴相切于定点C (0，1)． (1) 求经过A 、B 、C 三点的二 次函数图象的解析式; (2) 若二次函数图象的顶点为D ， 问当k 为何值时，四边形ADBP 为菱形． 【例题2】(湖南省韶关市) 25.如图6，在平面直角坐标系中，四边形OABC 是矩形，OA=4，AB=2，直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点，P 是线段DE 上的动点. （1）求M 、D 两点的坐标； （2）当P 在什么位置时，PA=PB ？求出此时P 点的坐标； （3）过P 作PH ⊥BC ，垂足为H ，当以PM 为直径的⊙F 与BC 相切于点N 时，求梯形PMBH 的面积.

【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B． （1）求直线CB的解析式； （2）若抛物线y=ax2+b x+c的顶点在直线BC上，与x 轴的交点恰为点E、F，求该抛物线的解析式； （3）试判断点C是否在抛物线上？ （4）在抛物线上是否存在三个点，由它构成的三角形与 △AOC相似？直接写出两组这样的点． 【例题4】（绵阳市）25.如图，已知抛物线y = ax2 + bx－3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为5．设⊙M与y轴交于D，抛物线的顶点为E． （1）求m的值及抛物线的解析式； （2）设∠DBC = α，∠CBE = β，求sin（α－β）的值； （3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由． 【例题5】（南充市）25.如图，点M（4，0），以点M为圆心、2为半径的圆与x轴交于点A、B．已

初中数学二次函数课件及练习题

第二课时 一、教学目标 1． 使学生会用描点法画出二次函数k h x a y +-=2 )(的图像； 2． 使学生知道抛物线k h x a y +-=2 )(的对称轴与顶点坐标； 3．通过本节的学习，继续培养学生的观察、分析、归纳、总结的能力； 4．通过本节的教学，继续向学生进行数形结合的数学思想方法的教育，同时向学生渗透事物间互相联系、以及运动、变化的辩证唯物主义思想； 5．通过本节课的研究，充分理解并认识到二次函数图像可运动变化的和谐美，通过数学思维的审美活动，提高对数学美的追求。 二、教学重点 会画形如k h x a y +-=2 )(的二次函数的图像，并能指出图像的开口方向、对称轴及顶点坐标。 三、教学难点：确定形如 k h x a y +-=2 )(的二次函数的顶点坐标和对称轴。 4．解决办法： 四、教具准备 三角板或投影片 1．教师出示投影片，复习2 2 2 )(,,h x a y k ax y ax y -=+==。 2．请学生动手画1)1(2 1 2-+- =x y 的图像，正好复习图像的画法，完成表格。 3．小结k h x a y +-=2 )(的性质??? ?? ??平移顶点坐标对称轴开口方向 4．练习 五、教学过程 提问：1．前几节课，我们都学习了形如什么样的二次函数的图像？ 答：形如2 2 2 )(,h x a y k ax y ax y -=+==和。（板书） 2．这节课我们将来学习一种更复杂的二次函数的图像及其相关问题，你能先猜测一下

我们将学习形如什么样的二次函数的问题吗？ 由学生参考上面给出的三个类型，较容易得到：讨论形如k h x a y +-=2 )(的二次函数的有关问题．（板书） 一、复习引入 首先，我们先来复习一下前面学习的一些有关知识．（出示幻灯） 请你在同一直角坐标系内，画出函数222)1(2 1 ,121,21+-=--=-=x y x y x y 的图像，并指出它们的开口方向，对称轴及顶点坐标． 这里之所以加上画函数2)1(2 1 +- =x y 的图像， 是为了使最后通过图像的观察能更全面一些，也更直观一些，可以同时给出图像先沿y 轴，再沿x 轴移动的方式，也可以给出图像 先沿x 轴再沿y 轴移动的方式，使这部分知识能更全面，知识与知识之间的联系能更清晰、 更具体． 画这三个函数图像，可由学生在同一表中列值，但是要根据各自的不同特点取自变量x 的值，以便于学生进行观察．教师可事先准备好表格和画有直角坐标系的小黑板，由一名同 学上黑板完成，其他同学在练习本上完成，待同学们基本做完之后加以总结，然后再找三名 同学，分别指出这三个图像的开口方向、对称轴及顶点坐标，填入事先准备好的表格中． 然后提问：你能否在这个直角坐标系中，再画出函数1)1(2 1 2-+- =x y 的图像？ 由于前面几节课我们已经画了不少二次函数的图像，学生对画图已经有了一定的经验， 同时可在画这个图时，把这些经验形成规律，便于学生以后应用． （l ）关于列表：主要是合理选值与简化运算的把握，是教学要点．在选值时，首先要考虑的是函数图像的对称性，因此首先要确定中心值，然后再左，右取相同间隔的值；其次，选值时尽量选取整数，便于计算和描点． 在选取x 的值之后，计算y 的值时，考虑到对称性，只需计算中心值一侧的值，另一侧由对称性可直接填入，但一定要保证运算正确． （2）关于描点：一般可先定顶点（即中心值对应的点，然后利用对称性描出各点，以逐步提高速度．） （3）关于连线：特别要注意顶点附近的大致走向。最后画的抛物线应平滑，对称，并符合抛物线的特点． 由学生在上面的练习中所列的表中填上这个函数及其对应值，然后画出它的图像，同样 找一名同学板演． 学生画完，教师总结完之后，让学生观察黑板上画出的四条抛物线，提问： （1）你能否指出抛物线1)1(2 1 2-+- =x y 的开口方向，对称轴，顶点坐标？

初中数学二次函数综合题及答案(经典题型)

二次函数试题 选择题： 1、y=(m-2)x m2- m 是关于x 的二次函数，则m=（ ） A -1 B 2 C -1或2 D m 不存在 2、下列函数关系中，可以看作二次函数y=ax 2 +bx+c(a ≠0)模型的是（ ） A 在一定距离，汽车行驶的速度与行驶的时间的关系 B 我国人中自然增长率为1%，这样我国总人口数随年份变化的关系 C 矩形周长一定时，矩形面积和矩形边长之间的关系 D 圆的周长与半径之间的关系 4、将一抛物线向下向右各平移2个单位得到的抛物线是y=-x 2 ，则抛物线的解析式是（ ） A y=—（ x-2）2 +2 B y=—（ x+2）2 +2 C y=— （ x+2）2 +2 D y=—（ x-2）2 —2 5、抛物线y= 2 1 x 2 -6x+24的顶点坐标是（ ） A （—6，—6） B （—6，6） C （6，6） D （6，—6） 6、已知函数y=ax 2 +bx+c,图象如图所示，则下列结论中正确的有（ ）个 ①abc 〈０ ②a ＋c 〈b ③ a+b+c 〉０ ④ ２c 〈３b A １ B ２ C ３ D ４ 7、函数y=ax 2 -bx+c （a ≠0）的图象过点（-1，0），则 c b a + =c a b + =b a c + 的值是（ ）A -1 B 1 C 21 8、已知一次函数y= ax+c 与二次函数y=ax 2 +bx+c （a ≠0 ），它们在同一坐标系的大致图象是图中的（ ） 二填空题： 13、无论 m 为任何实数，总在抛物线y=x 2 ＋2mx ＋m 上的点的坐标是————————————。 16、若抛物线y=ax 2+bx+c （a ≠0）的对称轴为直线 x ＝２，最小值为－２，则关于方程ax 2 +bx+c ＝－２的根为————————————。 17、抛物线y=（k+1）x 2 +k 2 -9开口向下，且经过原点，则k ＝————————— 解答题：（二次函数与三角形） 1、已知：二次函数y=错误!未找到引用源。x 2 +bx+c ，其图象对称轴为直线x=1，且经过点（2，﹣错误!未找到引用源。）．（1）求此二次函数的解析式．（2）设该图象与x 轴交于B 、C 两点（B 点在C 点的左侧），请在此二次函数x 轴下方的图象上确定一点E ，使△EBC 的面积最大，并求出最大面积 2、如图，在平面直角坐标系中，抛物线与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C (0，4)，顶点为（1，92）．（1）求抛物线的函数表达式；（2）设抛物线的对称 轴与轴交于点D ，试在对称轴上找出点P ，使△CDP 为等腰三角形，请直接写出满足条件的所有点P 的坐标． （3）若点E 是线段AB 上的一个动点（与A 、B 不重合），分别连接AC 、BC ，过点E 作EF ∥AC 交线段BC 于点F ，连接CE ，记△CEF 的面积为S ，S 是否存在最大值？若存在，求出S 的最大值及此时E 点的坐标；若不存在，请说明理由． x

专题63 构造圆与隐形圆在二次函数中的综合问题(解析版)

专题63 构造圆与隐形圆在二次函数中的综合问题 1、如图，在直角坐标系中，直线y=﹣1 3x ﹣1与x 轴，y 轴的交点分别为A 、B ，以x=﹣1为对称轴的抛物线 y=x 2+bx+c 与x 轴分别交于点A 、C ，直线x=﹣1与x 轴交于点D ． （1）求抛物线的解析式； （2）在线段AB 上是否存在一点P ，使以A ，D ，P 为顶点的三角形与△AOB 相似？若存在，求出点P 的坐标；如果不存在，请说明理由； （3）若点Q 在第三象限内，且tan△AQD=2，线段CQ 是否存在最小值，如果存在直接写出最小值；如果不存在，请说明理由． 【答案】（1）y=x 2+2x ﹣3；（2）存在；点P 坐标为（﹣1，?23 ）或（-65 ，-3 5 ）； （3）存在，CQ 最小值为 √37?√5 2 . 【解析】（1）△直线y=﹣1 3x ﹣1与x 轴交于A 点， △点A 坐标为（﹣3，0）， 又△直线x=﹣1为对称轴， △点C 坐标为（1，0）， △抛物线解析式为：y=（x+3）（x ﹣1）=x 2+2x ﹣3； （2）存在；

由已知，点D 坐标为（﹣1，0），点B 坐标为（0，﹣1）， 设点P 的坐标为（a ，﹣13 a ﹣1）， △当△AOB△△ADP 时， AD AO = DP OB ，即23 = 1 3 a+11 ， 解得：a=﹣1； 点P 坐标为（﹣1，?2 3）； △当△AOB△△APD 时， 过点P 作PE△x 轴于点E ， 则△APE△△PED ， △PE 2=AE?ED ， △（﹣1 3a ﹣1）2=（a+3）（﹣a ﹣1）， 解得a 1=﹣3（舍去），a 2=﹣6 5， △点P 坐标为（﹣6 5 ，﹣3 5 ）； （3）存在，CQ 最小值为 √37?√5 2 ； 如图，取点F （﹣1，﹣1），过点ADF 作圆，则点E （﹣2，﹣1 2）为圆心，

圆与二次函数综合练习

圆与二次函数综合题 1.已知圆P 的圆心在反比例函数k y x =(1)k >图象上，并与x 轴相交于A 、B 两点． 且始终与y 轴相切于定点C (0，1)． (1) 求经过A 、B 、C 三点的二次 函数图象的解析式; (2) 若二次函数图象的顶点为 D ，问当k 为何值时，四边形ADBP 为菱形． 2.如图6，在平面直角坐标系中，四边形OABC 是矩形，OA=4，AB=2，直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点，P 是线段DE 上的动点. （1）求M 、D 两点的坐标； （2）当P 在什么位置时，PA=PB ？求出此时P 点的坐标； （3）过P 作PH ⊥BC ，垂足为H ，当以PM 为直径的⊙F 与BC 相切于点N 时，求梯形PMBH 的 面积. （3） （2） 3.如图，已知抛物线y = ax 2 + bx －3与x 轴交于A 、B 两点，与y 轴交于C 点，经过A 、B 、 C 三点的圆的圆心M （1，m ）恰好在此抛物线的对称轴上，⊙M 的半径为5．设⊙M 与y 轴 交于D ，抛物线的顶点为E ． （1）求m 的值及抛物线的解析式； （2）设∠DBC = α，∠CBE = β，求sin （α－β）的值；

（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由． 4.如图，点P在y轴上，半径为3的⊙P分别交x轴于A、B两点，AB=4，交y轴负半轴于点C，连接AP并延长交⊙P于点D，过D作⊙P的切线分别交x轴、y轴于点F、G； （1）求直线FG的解析式； （2）连接CD交AB于点E，求PCD ∠ tan的值； （3）设M是劣弧BC上的一个动点，连接DM交x轴于点N，问：是否存在这样的一个常数k，始终满足AN·AB+DN·DM=K，如果存在，请求出K的值，如果不存在，请说明理由； （图1） （图2） 5.已知：如图， 抛物线2 33 y x x =--x轴分别交于A B ，两点，与y轴交于C点，M经过原点O及点A C ，，点D是劣弧OA上一动点（D点与A O ，不重合）．（1）求抛物线的顶点E的坐标；（2）求M的面积； （3）连CD交AO于点F，延长CD至G，使2 FG=，试探究当点D运动到何处时，直线GA与M相切，并请说明理由． 6.(0) A m，(0) m<，以AB为边在x轴下方作正方形ABCD，点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点，连结BE与AD相交于点F． （1）求证：BF DO =； （2）设直线l是BDO △的边BO的垂直平分线，且与BE相交于点G．若G是BDO △的

人教版初中数学二次函数图文解析

人教版初中数学二次函数图文解析 一、选择题 1．已知二次函数y ＝ax 2+bx +c (a ＞0)经过点M (﹣1，2)和点N (1，﹣2)，则下列说法错误的是( ) A ．a +c ＝0 B ．无论a 取何值，此二次函数图象与x 轴必有两个交点，且函数图象截x 轴所得的线段长度必大于2 C ．当函数在x ＜110 时，y 随x 的增大而减小 D ．当﹣1＜m ＜n ＜0时，m +n ＜ 2a 【答案】C 【解析】 【分析】 根据二次函数的图象和性质对各项进行判断即可． 【详解】 解：∵函数经过点M (﹣1，2)和点N (1，﹣2)， ∴a ﹣b +c ＝2，a +b +c ＝﹣2， ∴a +c ＝0，b ＝﹣2， ∴A 正确； ∵c ＝﹣a ，b ＝﹣2， ∴y ＝ax 2﹣2x ﹣a ， ∴△＝4+4a 2＞0， ∴无论a 为何值，函数图象与x 轴必有两个交点， ∵x 1+x 2＝2a ，x 1x 2＝﹣1， ∴|x 1﹣x 2|＝＞2， ∴B 正确； 二次函数y ＝ax 2+bx +c (a ＞0)的对称轴x ＝﹣ 2b a ＝1a ， 当a ＞0时，不能判定x ＜ 110时，y 随x 的增大而减小； ∴C 错误； ∵﹣1＜m ＜n ＜0，a ＞0， ∴m +n ＜0， 2a ＞0， ∴m +n ＜2a ；

∴D正确， 故选：C． 【点睛】 本题考查了二次函数的问题，掌握二次函数的图象和性质是解题的关键． 2．二次函数y＝x2+bx的对称轴为直线x＝2，若关于x的一元二次方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是（） A．0＜t＜5 B．﹣4≤t＜5 C．﹣4≤t＜0 D．t≥﹣4 【答案】B 【解析】 【分析】 先求出b，确定二次函数解析式，关于x的一元二次方程x2+bx﹣t＝0的解可以看成二次函数y＝x2﹣4x与直线y＝t的交点，﹣1＜x＜4时﹣4≤y＜5，进而求解； 【详解】 解：∵对称轴为直线x＝2， ∴b＝﹣4， ∴y＝x2﹣4x， 关于x的一元二次方程x2+bx﹣t＝0的解可以看成二次函数y＝x2﹣4x与直线y＝t的交点，∵﹣1＜x＜4， ∴二次函数y的取值为﹣4≤y＜5， ∴﹣4≤t＜5； 故选：B． 【点睛】 本题考查二次函数图象的性质，一元二次方程的解；将一元二次方程的解转换为二次函数与直线交点问题，数形结合的解决问题是解题的关键． 3．抛物线y＝-x2+bx+3的对称轴为直线x＝-1．若关于x的一元二次方程-x2+bx+3﹣t＝0（t为实数）在﹣2＜x＜3的范围内有实数根，则t的取值范围是（） A．-12＜t≤3B．-12＜t＜4 C．-12＜t≤4D．-12＜t＜3 【答案】C 【解析】 【分析】 根据给出的对称轴求出函数解析式为y＝－x2?2x＋3，将一元二次方程－x2＋bx＋3?t＝0的实数根看做是y＝－x2?2x＋3与函数y＝t的交点，再由﹣2＜x＜3确定y的取值范围即可求解. 【详解】 解：∵y＝－x2＋bx＋3的对称轴为直线x＝－1， ∴b＝?2， ∴y＝－x2?2x＋3，