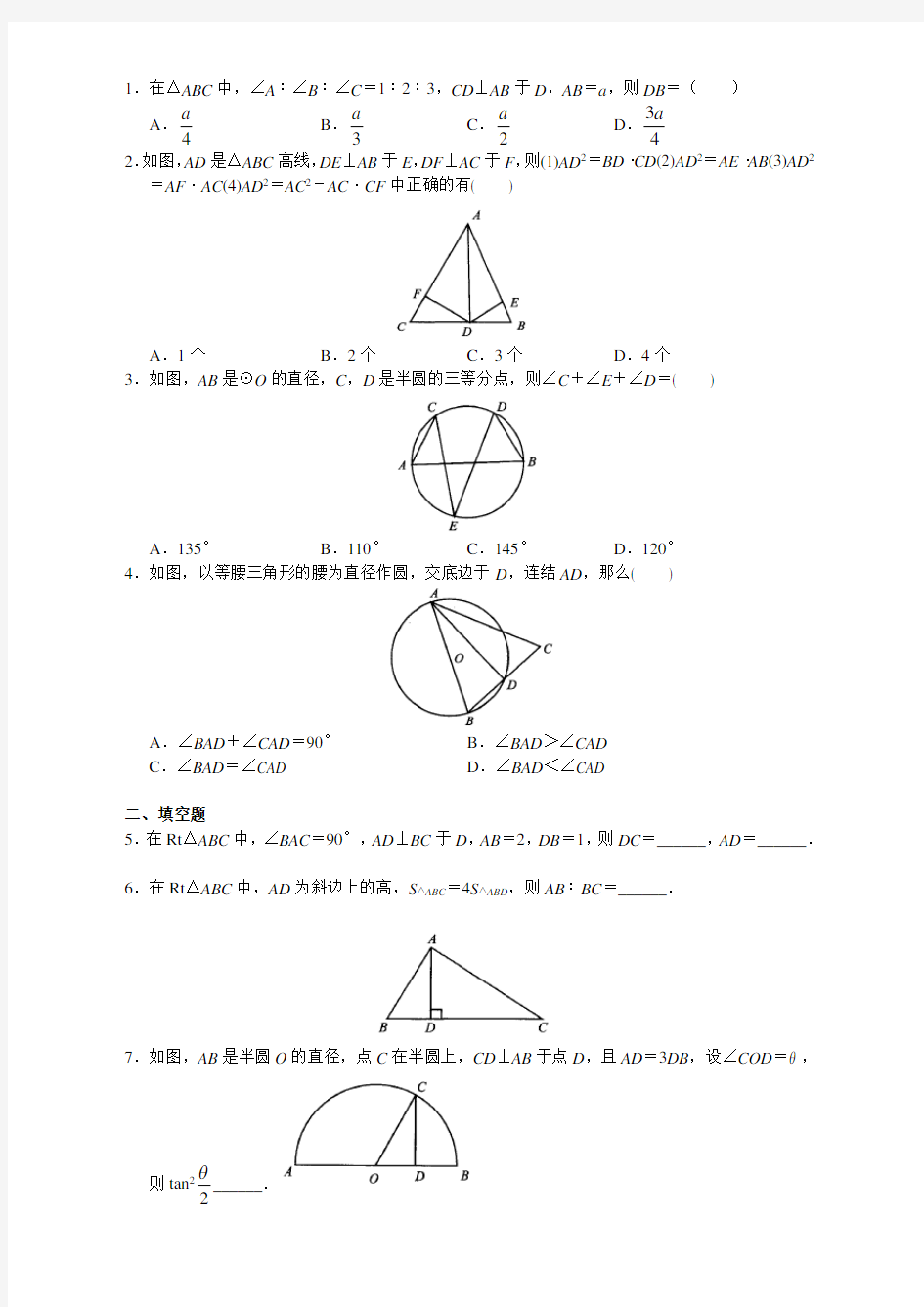
1.在△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,CD ⊥AB 于D ,AB =a ,则DB =( ) A .
4
a B .
3
a C .
2
a D .
4
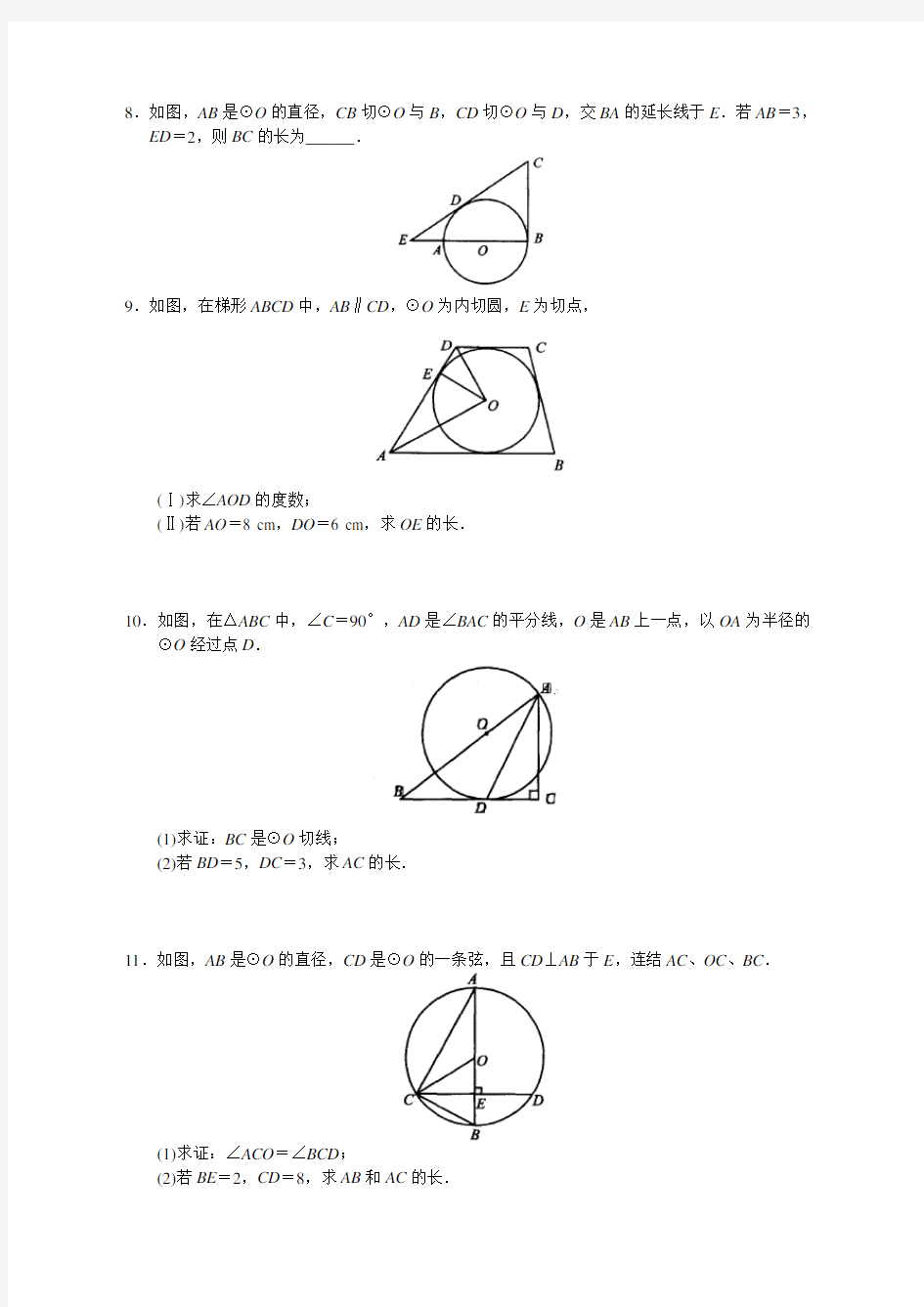
3a 2.如图,AD 是△ABC 高线,DE ⊥AB 于E ,DF ⊥AC 于F ,则(1)AD 2=BD ·CD (2)AD 2=AE ·AB (3)AD 2
=AF ·AC (4)AD 2=AC 2-AC ·CF 中正确的有( )
A .1个
B .2个
C .3个
D .4个
3.如图,AB 是⊙O 的直径,C ,D 是半圆的三等分点,则∠C +∠E +∠D =( )
A .135°
B .110°
C .145°
D .120° 4.如图,以等腰三角形的腰为直径作圆,交底边于D ,连结AD ,那么( )
A .∠BAD +∠CAD =90°
B .∠BAD >∠CAD
C .∠BA
D =∠CAD D .∠BAD <∠CAD
二、填空题
5.在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于D ,AB =2,DB =1,则DC =______,AD =______.
6.在Rt △ABC 中,AD 为斜边上的高,S △ABC =4S △ABD ,则AB ∶BC =______.
7.如图,AB 是半圆O 的直径,点C 在半圆上,CD ⊥AB 于点D ,且AD =3DB ,设∠COD =θ ,
则tan 2
2
θ
______.
8.如图,AB是⊙O的直径,CB切⊙O与B,CD切⊙O与D,交BA的延长线于E.若AB=3,ED=2,则BC的长为______.
9.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点,
(Ⅰ)求∠AOD的度数;
(Ⅱ)若AO=8 cm,DO=6 cm,求OE的长.
10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
11.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连结AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若BE=2,CD=8,求AB和AC的长.
专题十三 相似三角形定理与圆幂定理参考答案
习题13
一、选择题:
1.A 2.C 3.D 4.C 二、填空题
5.3,3 6.1∶2 7.
3
1
8.3 三、解答题
9.(Ⅰ)∵AB ∥CD ,
∴∠BAD +∠ADC =180°.∵⊙O 内切于梯形ABCD ,
∴AO 平分∠BAD ,有∠DAO =21
∠BAD , 又DO 平分∠ADC ,有∠ADO =2
1
∠ADC .
∴∠DAO +∠ADO =2
1
(∠BAD +∠ADC )=90°,∴∠AOD =180°-(∠DAO +∠ADO )=
90°.
(Ⅱ)∵在Rt △AOD 中,AO =8cm ,DO =6cm , ∴由勾股定理,得
.cm 1022=+DO AO
∵E 为切点,∴OE ⊥AD .有∠AEO =90°,∴∠AEO =∠AOD . 又∠CAD 为公共角,∴△AEO ∽△AOD . ∴
cm 8.4,==∴=?AD
OD
AO OE AD AO OD OE . 10.(1)连接OD .∵OA =OD ,AD 平分∠BAC ,
∴∠ODA =∠OAD ,∠OAD =∠CAD .∴∠ODA =∠CAD . ∴OD ∥AC .∴∠ODB =∠C =90°.∴BC 是⊙O 的切线. (2)过D 作DE ⊥AB 于E .∴∠AED =∠C =90°.
又∵AD =AD ,∠EAD =∠CAD ,∴△AED ≌△ACD . ∴AE =AC ,DE =DC =3.
在Rt △BED 中,∠BED =90°,由勾股定理,得
422=-=
DE BD BE ,设AC =x (x >0),则AE =x .
在Rt △ABC 中,∠C =90°,BC =BD +DC =8,AB =x +4,由勾股定理,得 x 2+82=(x +4)2.解得x =6.即AC =6.
11.(1)连结BD ,∵AB 是⊙O 的直径,CD ⊥AB ,
∴=.∴∠1=∠2.
又∵OA =OC ,∴∠1=∠A .∴∠1=∠2. 即:∠ACO =∠BCD .
(2)由(1)问可知,∠A =∠2,∠AEC =∠CEB .
∴△ACE ∽△CBE .∴
CE
AE
BE CE =
.∴CE 2=BE ·AE . 又CD =8,∴CE =DE =4. ∴AE =8.∴AB =10.∴AC =
.548022==+CE AE
模拟题集锦:
1、 如图,已知⊙O 的直径5AB =,C 为圆周上一 点,4=BC ,过点C 作⊙O 的切线l ,过点A 作
l 的垂线AD ,垂足为D ,则CD =___________.
2、如图,已知PA 是圆O 的切线,切点为A ,PO 交圆O 于,B C 两点,3,1PA PB ==,
则圆O 的半径为 ,C ∠= .
3、如图,PAB 、PC 分别是圆O 的割线和切线(C 为切点),若3PA AB ==,则PC 的长为
A .62
B .6
C .32
D .3
l
O
A
D
C
B
A
B P
C
O
A
B
C O
P
4、如图,PC 切O 于点C ,割线PAB 经过圆心O ,弦C D A B ⊥于点E ,已知
O 的半径为3,2PA =,则PC =_________,
OE =_________.
5、如图,圆O 和圆O '相交于A ,B 两点,AC 是圆O '的切线,AD 是
圆O 的切线,若BC =2,AB =4,则=BD _.
6、如右图:PA 切
O 于点A ,4PA =,PBC 过圆心O ,且与圆相交于B 、C 两点,
:1:2AB AC =,则O 的半径为 .
7、如下图,在圆内接四边形ABCD 中, 对角线, AC BD 相交于
点E .已知23BC CD ==,2AE EC =,30CBD ∠=, 则CAB ∠= 30 ,AC 的长是 6 .
8、如图所示,过⊙O 外一点A 作一条直线与⊙O 交于C ,D 两点,AB 切⊙O 于B ,弦MN 过CD 的中点P .已知AC =4,AB =6,则MP ·NP = 254
.
·
P
C
B
A D
E
O . .'O
C
O B
D
A B C
O
A
P
C D M N
O
B A
P
圆 【知识点梳理】 一、圆的概念 集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念: 1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; (补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内?d r ?点A在圆外; A
三、直线与圆的位置关系 1、直线与圆相离 ? d r > ? 无交点; 2、直线与圆相切 ? d r = ? 有一个交点; 3、直线与圆相交 ? d r < ? 有两个交点; 四、圆与圆的位置关系 外离(图1)? 无交点 ? d R r >+; 外切(图2)? 有一个交点 ? d R r =+; 相交(图3)? 有两个交点 ? R r d R r -<<+; 内切(图4)? 有一个交点 ? d R r =-; 内含(图5)? 无交点 ? d R r <-; 五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即: ①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧 AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 B D
圆幂定理及其应用 教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系,并能综合运用它们解决有关问题; 2.通过对例题的分析,提高学生分析问题和解决问题的能力,并领悟添加辅助线的方法; 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的 观点的教育. 教学重点和难点 相交弦定理、切割线定理及其推论之间的关系以及应用是重点;灵活运用圆幂定理解题是难点. 教学过程设计 一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3),让学生结合图形,说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考,在学生回答的基础上,教师用电脑或投影演示图形的变化过程,从相交弦定理出发,用运动的观点来统一认识定理. (1)如图7-163,⊙O的两条弦AB,CD相交于点P,则PA·PB=PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例: 一是如果圆内的两条弦交于圆心O,则有PA=PB=PC=PD=圆的半径R,此时AB,CD 是直径,相交弦定理当然成立.(如图7-164)
二是当P点逐渐远离圆心O,运动到圆上时,点P和B,D重合,这时PB=PD=O,仍然有PA·PB=PC·PD=O,相交弦定理仍然成立.(图7-165) (2)点P继续运动,运动到圆外时,两弦的延长线交于圆外 一点P,成为两条割线,则有PA·PB=PC·PD,这就是我们学过 的切割线定理的推论(割线定理).(图7-166) (3)在图7-166中,如果将割线PDC按箭头所示方向绕P点 旋转,使C,D两点在圆上逐渐靠 近,以至合为一点C,割线PCD变成切线PC.这时有PA·PB=PC·PD =PC2,这就是我们学过的切割线定理.(图7-167) (4)如果割线PAB也绕P点向外旋转的话,也会成为一条切线PA.这时应有PA2=PB2,可 得PA=PB,这就是我们学过的切线长定理.(图7-168) 至此,通过点的运动及线的运动变化,我们发现,相交弦定理、切割线定理及其推论和切线长定理之间有着密切的联系. 3.启发学生理解定理的实质. 经过一定点P作圆的弦或割线或切线,如图7-169. 观察图7-169,可以得出:(设⊙O半径为R) 在图(1)中,PA·PB=PC·PD=PE·PF =(R-OP)(R+OP) =R2-OP2; 在图(2)中,PA·PB=PT2=OP2-OT2 =OP2-R2 在图(3)中,PA·PB=PC·PD=PT2 =OP2-R2. 教师指出,由于PA·PB均等于|OP2-R2|,为一常数,叫做点P关于⊙O的幂,所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理. 二、例题分析(采用师生共同探索、讲练结合的方式进行) 例1 如图7-170,两个以O为圆心的同心圆,AB切大圆于B,AC切小圆于C,交大圆
[文件] sxc3jja0008.doc [科目] 数学 [年级] 初三 [章节] [关键词] 圆/圆幂定理/应用 [标题] 圆幂定理及其应用 [内容] 教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系,并能综合运用它们解 决有关问题; 2.通过对例题的分析,提高学生分析问题和解决问题的能力,并领悟添加辅助线的方 法; 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的 观点的教育. 教学重点和难点 相交弦定理、切割线定理及其推论之间的关系以及应用是重点;灵活运用圆幂定理解题是难点. 教学过程设计 一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3),让学生结合图形,说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考,在学生回答的基础上,教师用电脑或投影演示图形的变化过程, 从相交弦定理出发,用运动的观点来统一认识定理. (1)如图7-163,⊙O的两条弦AB,CD相交于点P,则PA·PB=PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例: 一是如果圆内的两条弦交于圆心O,则有PA=PB=PC=PD=圆的半径R,此时AB,CD是直径,相交弦定理当然成立.(如图7-164)
二是当P点逐渐远离圆心O,运动到圆上时,点P和B,D重合,这时PB=PD=O,仍然有PA·PB=PC·PD=O,相交弦定理仍然成立.(图7-165) (2)点P继续运动,运动到圆外时,两弦的延长线交于圆外一 点P,成为两条割线,则有PA·PB=PC·PD,这就是我们学过的 切割线定理的推论(割线定理).(图7-166) (3)在图7-166中,如果将割线PDC按箭头所示方向绕P点旋 转,使C,D两点在圆上逐渐靠 近,以至合为一点C,割线PCD变成切线PC.这时有PA·PB=PC·PD =PC2,这就是我们学过的切割线定理.(图7-167) (4)如果割线PAB也绕P点向外旋转的话,也会成为一条切线PA.这时应有PA2=PB2,可得PA=PB,这就是我们学过的切线长定理.(图7-168) 至此,通过点的运动及线的运动变化,我们发现,相交弦定理、切割线定理及其推论和 切线长定理之间有着密切的联系. 3.启发学生理解定理的实质. 经过一定点P作圆的弦或割线或切线,如图7-169. 观察图7-169,可以得出:(设⊙O半径为R) 在图(1)中,PA·PB=PC·PD=PE·PF =(R-OP)(R+OP) =R2-OP2;
(完整)圆幂定理讲义(带答案) 编辑整理: 尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)圆幂定理讲义(带答案))的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)圆幂定理讲义(带答案)的全部内容。 1 / 29
圆幂定理 STEP 1:进门考 理念:1。检测垂径定理的基本知识点与题型。 2。垂径定理典型例题的回顾检测。 3. 分析学生圆部分的薄弱环节. (1)例题复习。 1.(2015?夏津县一模)一副量角器与一块含30°锐角的三角板如图所示放置,三角板的直角顶点C落在量角器的直径MN上,顶点A,B恰好都落在量角器 的圆弧上,且AB∥MN.若AB=8cm,则量角器的直径MN=cm. 【考点】M3:垂径定理的应用;KQ:勾股定理;T7:解直角三角形. 【分析】作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E,首先求得CD的长,即OE的长,在直角△A OE中,利用勾股定理求得半径OA的长,则MN即可求解. 【解答】解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E. 在直角△ABC中,∠A=30°,则BC=AB=4cm,在直角△BCD中,∠B=90°﹣∠A=60°, ∴CD=BC?sinB=4×=2(cm), ∴OE=CD=2, 在△AOE中,AE=AB=4cm, 则OA===2(cm),则MN=2OA=4(cm).故答案是:4. 2 / 29
1.在△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,CD ⊥AB 于D ,AB =a ,则DB =( ) A . 4 a B . 3 a C . 2 a D . 4 3a 2.如图,AD 是△ABC 高线,DE ⊥AB 于E ,DF ⊥AC 于F ,则(1)AD 2=BD ·CD (2)AD 2=AE ·AB (3)AD 2 =AF ·AC (4)AD 2=AC 2-AC ·CF 中正确的有( ) A .1个 B .2个 C .3个 D .4个 3.如图,AB 是⊙O 的直径,C ,D 是半圆的三等分点,则∠C +∠E +∠D =( ) A .135° B .110° C .145° D .120° 4.如图,以等腰三角形的腰为直径作圆,交底边于D ,连结AD ,那么( ) A .∠BAD +∠CAD =90° B .∠BAD >∠CAD C .∠BA D =∠CAD D .∠BAD <∠CAD 二、填空题 5.在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于D ,AB =2,DB =1,则DC =______,AD =______. 6.在Rt △ABC 中,AD 为斜边上的高,S △ABC =4S △ABD ,则AB ∶BC =______. 7.如图,AB 是半圆O 的直径,点C 在半圆上,CD ⊥AB 于点D ,且AD =3DB ,设∠COD =θ , 则tan 2 2 θ ______.
8.如图,AB是⊙O的直径,CB切⊙O与B,CD切⊙O与D,交BA的延长线于E.若AB=3,ED=2,则BC的长为______. 9.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点, (Ⅰ)求∠AOD的度数; (Ⅱ)若AO=8 cm,DO=6 cm,求OE的长. 10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D. (1)求证:BC是⊙O切线; (2)若BD=5,DC=3,求AC的长. 11.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连结AC、OC、BC. (1)求证:∠ACO=∠BCD; (2)若BE=2,CD=8,求AB和AC的长.
圆幂定理 STEP 1:进门考 理念:1. 检测垂径定理的基本知识点与题型。 2. 垂径定理典型例题的回顾检测。 3. 分析学生圆部分的薄弱环节。 (1)例题复习。 1.(2015?夏津县一模)一副量角器与一块含30°锐角的三角板如图所示放置,三角板的直角顶点C落在量角器的直径MN上,顶点A,B恰好都落在量角器的圆弧上,且AB∥MN.若AB=8cm,则量角器的直径MN=cm. 【考点】M3:垂径定理的应用;KQ:勾股定理;T7:解直角三角形. 【分析】作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E,首先求得CD的长,即OE的长,在直角△AOE中,利用勾股定理求得半径OA的长,则MN即可求解. 【解答】解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E. 在直角△ABC中,∠A=30°,则BC=AB=4cm,在直角△BCD中,∠B=90°﹣∠A=60°,∴CD=BC?sinB=4×=2(cm),∴OE=CD=2, 在△AOE中,AE=AB=4cm, 则OA===2(cm),则MN=2OA=4(cm).故答案是:4.
【点评】本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中,常用的方法是转化为解直角三角形.
2.(2017?阿坝州)如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为() A.2cm B.cm C.2cm D.2cm 【考点】M2:垂径定理;PB:翻折变换(折叠问题). 【分析】通过作辅助线,过点O作OD⊥AB交AB于点D,根据折叠的性质可知OA=2OD,根据勾股定理可将AD的长求出,通过垂径定理可求出AB的长. 【解答】解:过点O作OD⊥AB交AB于点D,连接OA, ∵OA=2OD=2cm,∴AD===(cm), ∵OD⊥AB,∴AB=2AD=2cm.故选:D. 【点评】本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键. 3.(2014?泸州)如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()
1.在△ ABC中,∠ A∶∠ B∶∠ C=1∶ 2∶ 3, CD⊥ AB 于 D,AB= a,则 DB=() a a a3a A.B.C.D. 4324 2.如图, AD 是△ ABC高线, DE⊥ AB 于 E,DF⊥ AC于 F,则 (1)AD2= BD·CD(2)AD2= AE·AB(3)AD2=AF· AC(4)AD2= AC2- AC· CF 中正确的有 () A. 1 个B. 2 个C.3 个D.4 个 3.如图, AB 是⊙ O 的直径, C, D 是半圆的三等分点,则∠C+∠ E+∠ D=() A. 135°B. 110°C.145°D.120° 4.如图,以等腰三角形的腰为直径作圆,交底边于D,连结 AD,那么 () A.∠ BAD+∠ CAD= 90°B.∠ BAD>∠ CAD C.∠ BAD=∠ CAD D.∠ BAD<∠ CAD 二、填空题 5.在 Rt△ABC中,∠ BAC= 90°, AD⊥ BC于 D, AB= 2, DB= 1,则 DC= ______, AD=______.6.在 Rt△ABC中, AD 为斜边上的高,S△ABC=4S△ABD,则 AB∶ BC=______. 7.如图, AB 是半圆 O 的直径,点 C 在半圆上, CD⊥ AB 于点 D,且 AD= 3DB,设∠ COD=,则 tan 2______. 2
8.如图, AB 是⊙ O 的直径, CB 切⊙ O 与 B,CD 切⊙ O 与 D,交 BA 的延长线于E.若 AB= 3,ED =2,则 BC的长为 ______. 9.如图,在梯形ABCD中, AB∥ CD,⊙ O 为内切圆, E 为切点, (Ⅰ)求∠ AOD的度数; (Ⅱ)若 AO=8 cm, DO= 6 cm,求 OE的长. 10.如图,在△ ABC中,∠ C= 90°, AD 是∠ BAC的平分线, O 是 AB 上一点,以OA 为半径的⊙ O 经过点 D. (1)求证: BC是⊙ O 切线; (2)若 BD= 5, DC=3 ,求 AC的长. 11.如图, AB 是⊙ O 的直径, CD 是⊙ O 的一条弦,且CD⊥ AB 于 E,连结 AC、 OC、BC. (1)求证:∠ ACO=∠ BCD; (2)若 BE= 2, CD=8,求 AB 和 AC 的长.
【精品】
(托勒密定理)四边形ABCD 内接于圆,求证:AC BD AD BC AB CD ?=?+ ?. 【解析】如图,在BD 上取一点P ,使其满足12∠=∠. ∵34∠=∠,∴ACD BCP △∽△,AC AD BC BP = , 即AC BP AD BC ?=? ① 又ACB DCP ∠=∠,56∠=∠, ∴ACB DCP △∽△,AB AC DP CD = ,AC DP AB CD ?=?. ② ①+②,有AC BP AC PD AD BC AB CD ?+?=?+?. 即()AC BP PD AD BC AB CD +=?+?,故AC BD AD BC AB CD ?=?+?. 【教师备课提示】这道题主要考查利用圆幂定理证明四点共圆. (1)如图2-1,点P 为等边ABC △外接圆的?BC 上一点,线段PA 、PB 、PC 间的数量关系为____. (2)如图2-2,AB 为⊙O 的直径,∠ABD =45°,点C 为ABD △外接圆的?AB 上一点,线段CA 、CB 、CD 间的数量关系为____________. (3)如图2-3,30ABC ACB ∠=∠=?,点D 为ABC △外接圆的?BC 上一点,线段DA 、DB 、DC 间的数量关系为_____________. 图2-1 图2-2 图2-3 【解析】(1)PA PB PC =+;(2)2CA CB CD +=;(3)3DB DC DA +=. 【教师备课提示】这道题主要利用托勒密定理解决圆中的Y 字模型,建议讲2中方法. O D C B A B C P O g D A g O C D C A B D C 126345P A B
圆幂定理讲义(带答案 解析)
圆幂定理 STEP 1:进门考 理念:1. 检测垂径定理的基本知识点与题型。 2. 垂径定理典型例题的回顾检测。 3. 分析学生圆部分的薄弱环节。 (1)例题复习。 1.(2015?夏津县一模)一副量角器与一块含30°锐角的三角板如图所示放置,三角板的直角顶点C落在量角器的直径MN上,顶点A,B恰好都落在量角器的圆弧上,且AB∥MN.若AB=8cm,则量角器的直径MN= cm. 【考点】M3:垂径定理的应用;KQ:勾股定理;T7:解直角三角形. 【分析】作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E,首先求得CD的长,即OE的长,在直角△AOE中,利用勾股定理求得半径OA的长,则MN 即可求解. 【解答】解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E. 在直角△ABC中,∠A=30°,则BC=AB=4cm,在直角△BCD中,∠B=90°﹣∠A=60°, ∴CD=BC?sinB=4×=2(cm),∴OE=CD=2, 在△AOE中,AE=AB=4cm,
则OA===2(cm),则MN=2OA=4(cm).故答案是:4. 【点评】本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中,常用的方法是转化为解直角三角形.
2.(2017?阿坝州)如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为() A.2cm B.cm C.2cm D.2cm 【考点】M2:垂径定理;PB:翻折变换(折叠问题). 【分析】通过作辅助线,过点O作OD⊥AB交AB于点D,根据折叠的性质可知OA=2OD,根据勾股定理可将AD的长求出,通过垂径定理可求出AB的长.【解答】解:过点O作OD⊥AB交AB于点D,连接OA, ∵OA=2OD=2cm,∴AD===(cm), ∵OD⊥AB,∴AB=2AD=2cm.故选:D. 【点评】本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键. 3.(2014?泸州)如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()
C.3个 是半圆的三等分点,则∠ C.145° .如图,以等腰三角形的腰为直径作圆,交底边于D,连结 B.∠BAD>∠ D.∠BAD<∠ AD⊥BC于D,AB=2,DB 为斜边上的高,S△ABC=4S△ABD,则AB C在半圆上,CD⊥AB于点 百度文库爱是看得见萨科技的沃尔克我去额咳咳,省得麻烦迫 .
8.如图,AB是⊙O的直径,CB切⊙O与B,CD切⊙O与D,交BA的延长线于E.若 AB=3,ED=2,则BC的长为______. 9.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点, (Ⅰ)求∠AOD的度数; (Ⅱ)若AO=8 cm,DO=6 cm,求OE的长. 10.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D. (1)求证:BC是⊙O切线; (2)若BD=5,DC=3,求AC的长. 11.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连结AC、OC、BC. (1)求证:∠ACO=∠BCD; 百度文库爱是看得见萨科技的沃尔克我去额咳咳,省得麻烦迫 (2)若BE=2,CD=8,求AB和AC的长.
8cm ,DO =6cm ,. cm 102=DO .有∠AEO =90°,∴∠AEO =∠AEO ∽△AOD ..cm 8.4=AD OD 平分∠BAC ,
的直径,CD ⊥AB ,∴=.∴∠. 又∵OA =OC A .∴∠1=∠2.即:∠ACO ,∠AEC =∠CEB ..∴CE 2=BE ·CE AE =.= 8022=+CE AE ,为圆周上一5C 的切线,过点作 l A ___________. CD =的切线,切点为,交圆于A PO O B , . C ∠=
a a a 3a A. — B. — C. — D.—— 4 3 2 4 如图,AD是^ ABC高线,DE丄AB于E, DF丄AC于F,则(1)AD2= BD ? CD(2)AD2= AE- AB(3)AD2 =AF- A0(4)AD2= AC2- AC- CF 中正确的有( ) 2 . 3.A. 1个B. 2个 C. 3个 如图,AB是O O的直径,C, D是半圆的三等分点,则/ D. 4个 C+/ E+Z D=(
4. D. 120° 二、填空题 在RtAABC中,/ BAC= 90°, AD丄BC于D, AB= 2, DB= 1,贝U DC= 5. ,AD = 6. 在RtAABC 中,AD 为斜边上的高,&ABC= 4S A ABD,则AB : BC = 7. tan22 CD丄AB 于点D,且AD= 3DB,设/ COD=,贝U B C. ° A. 135 B. 110如图,AB是半圆
3. 2 AB 是O O 的直径,CB 切O O 与B , CD 切O O 与D ,交BA 的延长线于 E.若AB = 3, ED 则BC 的长 为 ________________ . (I )求/ AOD 的度数; (n )若 A0= 8 cm , D0= 6 cm ,求 OE 的长. 10.如图,在△ ABC 中,/ C = 90°, AD 是/ BAC 的平分线,O 是AB 上一点,以 OA 为半径的O O 经过点D . (1)求证:BC 是O O 切线; ⑵若BD = 5, DC = 3,求AC 的长. 11.如图,AB 是O O 的直径,CD 是O O 的一条弦,且 CD 丄AB 于E,连结 AC 0C 、BC. (1)求证:/ ACO =/ BCD; ⑵若BE = 2, CD = 8,求AB 和AC 的长. &如图, =2, 9.如图 , 在梯形 ABCD 中,AB// CD,
第四章 特瓦尔特定理及应用 【基础知识】 斯特瓦尔特定理 设P 为ABC △的BC 边上任一点(P B ≠,P C ≠),则有 222AB PC AC BP AP BC BP PC BC ?+?=?+?? ① 或 2222P C B P B P P C A P A B A C B C B C B C B C B C =? +?-??. ② 证明 如图4-1,不失一般性,不妨设90APC
圆补充定理及习题(20151218) 板块一:圆幂定理 (1)相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。 即:在⊙O 中,∵弦AB 、CD 相交于点P , ∴PA PB PC PD ?=? (2)相交弦定理推论:如果弦与直径垂直相交,那么弦的一半是它分直径所 成的两条线段的比例中项。 即:在⊙O 中,∵直径AB CD ⊥, ∴2CE AE BE =? (3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。 即:在⊙O 中,∵PA 是切线,PB 是割线 ∴ 2PA PC PB =? (4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如图)。 即:在⊙O 中,∵PB 、PE 是割线 ∴PC PB PD PE ?=? A D B
1:如图,圆中两条弦AB,CD 相交于圆内一点P,已知PA=PB=4,PC=14 PD,求CD 的长 2:E 是圆内两弦AB 和CD 的交点,直线EF//CB,交AD 的延长线于F,切圆于G 。 求证(1) EFA DFE ??: (2)EF=FG 3:两圆相交于A,B 两点,P 为两圆公共弦AB 上任一点,从P 引两圆的切线PC,PD,求证PC=PD 4.如图,在半径为4的⊙O 中,AB 、CD 是两条直径,M 为OB 的中点,CM 的延长线交⊙O 于点E ,且EM>MC.连接DE , DE 求EM 的长.
板块二:两圆公共弦定理 圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。 如图:12O O 垂直平分AB 。 即:∵⊙1O 、⊙2O 相交于A 、B 两点,∴12O O 垂直平分AB 练习1:如图1,半径为5的两个等圆⊙O 1与⊙O 2相交于A 、B ,公共弦AB=8.由点O 1向⊙O 2作切线O 1C ,切点为C , 则O 1C 的长为 图1 图2 练习2:如图2,⊙O 1与⊙O 2相交于A 、B .已知两圆的半径r 1=10,r 2=17,圆心距O 1O 2=21,公共弦AB 等于( ) A .2 B .16 C .6 D .17 练习3:已知相交两圆的半径分别为5cm 和4cm ,公共弦长为6cm ,则这两个圆的圆心距是 cm . 分析:此题综合运用了相交两圆的性质以及勾股定理.注意此题应考虑两种情况. 注意此题应考虑两种情况(图3和图4). 练习4:如图5,⊙O 1和⊙O 2相交于点A ,B ,它们的半径分别为2和 ,公共弦AB 长为2,若圆心O 1、O 2在AB 的同侧,则∠O 1AO 2= 度. B A O1O2 . C A B . . 1 o 2 o 图4 图5 图3 2
高中数学几何证明选讲过关模拟卷(十三) 高中数学 题号 一 二 三 总分 得分 一、选择题(本大题共10小题,每小题4分,共40分) o 20D ∠=, 则1.如图,CD 是 O 的直径,AE 切O 于点B ,连接DB 。若 DBE ∠的大小为 A .20° B .40° C .60° D .70° 2.如图,AB 是半圆O 的直径,点C 在半圆上,CD AB ⊥于点D , 且DB AD 3=, 设COD θ∠=,则2tan 2 θ =( ) A .13 B .1 4 C .423- D .3 3.已知圆C 与圆(x -1)2+y 2=1关于直线y =-x 对称,则圆C 的方程为( ) A .(x +1)2+y 2=1 B .x 2+y 2=1 C .x 2+(y +1)2=1 D .x 2+(y -1)2=1 4.已知直线kx y =与圆???=+=t y t x sin 2cos 24(t 为参数)相切,则直线的倾斜角为 A 6π B 3π C 323ππ或 D 656ππ或 5.如图,AB 是圆O 的直径,C 、D 是圆上的点, 20=∠BAC ,弧 和弧 的长相等,DE 是圆O 的切 线,则=∠EDC A . 70 B . 40 C . 20 D . 35 6.如图4所示,圆O 的直径AB=6,C 为圆周上一点,BC=3过C 作圆的切线l,过A 作l 的垂线AD,垂足为D,则∠DAC = A.15? B.30? C.45? D.60? 7.在Rt ABC ?中,CD 、CE 分别是斜边AB 上的高和中线,则该图中共有x 个三角形与ABC ?相似,则 x =( ) A.0 B.1 C.2 D.3 8.正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,1 3 AE BF == 。动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为 (A )8 (B )6 (C )4 (D )3 9.若圆C 的半径为1,圆心在第一象限,且与直线430x y x -=和轴都相切,则该圆的标准方程是( ) A .3 2 7(3)()13 x y -+= = B .22(2)(1)1x y -+-= C .22 (1)(3)1x y -+-= D .223()(1)12 x y -+-= 10.如图,在正方形ABCD 中,E 为AB 中点,BF⊥CE 于F ,那么S △BFC :S 正方形ABCD =( ). 姓名:__________班级:__________考号:__________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●
圆的相关定理及其几何证明 典题探究 例1:如图,圆O 是ABC ?的外接圆,过点C 作圆O 的切线交BA 的延长线于点D .若 CD =2AB AC ==,则线段AD 的长是 ;圆O 的半径是 . 例2:如图,在圆O 中,直径AB 与弦CD 垂直,垂足为E (E 在A ,O 之间),,垂足为F .若,,则 例3:如图已知PA 与圆O 相切于A ,半径OC OP ⊥,AC 交PO 于B , 若1OC =,2OP =,则PA = ,=PB . 例4:如图,从圆O 外一点P 引圆O 的切线PA 和割线PBC ,已知30BPA ∠=?,11BC =,1PB =, 则PA = ,圆O 的半径等于 EF BC ^6AB =5CF CB ?AE =A B C O P P A
F 演练方阵 A 档(巩固专练) 1.如图,已知直线PD 切⊙O 于点D ,直线PO 交⊙O 于点E,F. 若21PF PD ==,则⊙O 的半径为 ;EFD ∠= . 2. 如图,与切于点,交弦的延长线于点,过点作圆的切线交于点. 若,,则弦的长为_______. 3. 如图:圆O 的割线PAB 经过圆心O ,C 是圆上一点,PA =AC =1 2 AB ,则以下结论不正确...的是( ) A.CB CP = B. PCAC PABC = C. PC 是圆O 的切线 D. BC BABP = 4.如图,已知AB 是圆O 的直径,P 在AB 的延长线上,PC 切圆O 于点C ,CD OP ⊥于D .若6CD =,10CP =,则圆O 的半径长为______;BP =______. 5.如图所示,以直角三角形ABC 的直角边AC 为直径作⊙O ,交斜边AB 于点D ,过点D 作⊙O 的切线,交BC 边于点E .则 =BC BE . AP O A DB P B O AP C 90ACB ∠=?3,4BC CP ==DB D C B P A O
专题27数形结合 例1 5提示作出B 点关于轴的对称点B '(2,-3),连结AB '交轴于C ,则AB '=AC 十CB ' 为所要求的最小值. 例 2 D 提示设两直角边长为a ,b ,斜边长为c ,由题意得a +b +c =,x ab =21,又222c b a =+,得().424b b a --=.因a ,h 为边长且是整数.故当???>->-,04,02b b 得b<2,取34,1==a b 不是整数;当???<-<-,04,02b b 得b>4,要使a ,b 为整数,只有两种取法若b =5时,a =12(或b = 12,a =5);若b =8时,a =6(或b =6,a =8). 例3设AB =,则BC =2,AC =x 3, BE = x 21,DF =DA=.32,31x BD x =.在Rt △AEB 中求得AE=,,23x BF x =代入证明即可. 例4如图,作出函数x x y 52-=图象,由图象可以看出当a =0时,y =0与 x x y 52-=有且只有相异二个交点;当4250< a 时,y =a 与x x y 52-=图象有且只有相异二个交点. 例5由L c s c b s b a s a =+=+=+222 ①,知正数 c b a ,,适合方程.2L x s x =+当0≠x 时,有022=+-s Lx x ②,故c b a ,,是方程②的根.但任何二次方程至多只有两个相异的根,所以c b a ,,中的某两数必相同.设b a =,若a c ≠,由①得()()c a ac s a c s c a -=??? ??-=-2112,则ac =2s =a a h ,这样△ABC 就是以∠B 为直角的直角三角形,b >a ,矛盾,故a =c ,得证. 例6,ABC AOC BOC AOB S S S S ????=++Θ
【例题求解】 【例1】如图,⊙O l与半径为4的⊙O2内切于点A,⊙O l经过圆心O2,作⊙O2的直径BC交⊙O l于点D,EF 为过点A的公切线,若O2D=2 2,那么∠BAF= 度. (重庆市中考题) 思路点拨直径、公切线、O2的特殊位置等,隐含丰富的信息,而连O2O l必过A点,先求出∠D O2A的度数. 注:(1)两圆相切或相交时,公切线或公共弦是重要的类似于“桥梁”的辅助线,它可以使弦切角与圆周角、圆内接四边形的内角与外角得以沟通.同时,又是生成圆幂定理的重要因素. (2)涉及两圆位置关系的计算题,常作半径、连心线,结合切线性质等构造直角三角形,将分散的条件集中,通过解直角三角形求解. 【例2】如图,⊙O l与⊙O2外切于点A,两圆的一条外公切线与⊙O1相切于点B,若AB与两圆的另一条外公切线平行,则⊙O l 与⊙O2的半径之比为( ) A.2:5 B.1:2 C.1:3 D.2:3 (全国初中数学联赛试题) 思路点拨添加辅助线,要探求两半径之间的关系,必须求出∠CO l O2 (或∠DO2O l)的度数,为此需寻求∠
CO1B、∠CO1A、∠BO1A的关系. 【例3】如图,已知⊙O l与⊙O2相交于A、B两点,P是⊙O l上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O l于点N. (1)过点A作AE∥CN交⊙O l l于点E,求证:PA=PE; (2)连结PN,若PB=4,BC=2,求PN的长. (重庆市中考题) 思路点拨 (1)连AB,充分运用与圆相关的角,证明∠PAE=∠PEA;(2)PB·PC=PD·PA,探寻PN、PD、PA 对应三角形的联系. 【例4】如图,两个同心圆的圆心是O,AB是大圆的直径,大圆的弦与小圆相切于点D,连结OD并延长交大圆于点E,连结BE交AC于点F,已知AC=2 4,大、小两圆半径差为2. (1)求大圆半径长; (2)求线段BF的长; (3)求证:EC与过B、F、C三点的圆相切. (宜宾市中考题)
学科教师辅导讲义 学员编号:年级:课时数: 学员姓名:辅导科目:学科教师: 授课类型T相交弦定理C切割线定理T相交弦定理与切割线定理综合星级★★★★★★★★ 授课日期及时段 教学内容
相交弦定理 (1)会在相应的图中确定相交弦定理的条件和结论 (2)能用圆幂定理解决有关问题 四 【知识点梳理】 1、相交弦定理、切割线定理、割线定理统称为圆幂定理。其可统一地表示为:过定点的弦被该点内分(或外分)成 的两条线段的积为定值(该点到圆心的距离与圆的半径的平方差的绝对值)。如图,即2 2r OP PB PA -=?=定值。 相交弦定理通常是通过相似三角形而得到的,所以,研究圆中一些线段的比例关系总离不开相似三角形。 相交弦定理揭示了与圆相关的线段间的比例,应用较多,特别是在处理有关计算、作比例中项、证明角相等、四点共圆等问题时是重要的理论依据。 板块一:相交弦定理 相交弦定理:圆内的两条相交弦被交点分成的两条线段长的乘积相等. 题型1相交弦定理 P O D C B A
如图,弦AB 和CD 交于O ⊙内一点P ,则PA PB PC PD ?=?. 相交弦定理的推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项. 1、如下左图,在O ⊙中,弦AB 与CD 相交于点P ,已知3cm 4cm 2cm PA PB PC ===,,,那么PD = cm . O P D C B A 2、如下中图,在O ⊙中,弦AB 与半径OC 相交于点M ,且OM MC =,若 1.54AM BM ==, ,则OC 的长为( ) A .26 B .6 C .23 D .22 M O C B A 3、如下右图,在O ⊙中,P 为弦AB 上一点,PO PC ⊥,PC 交O ⊙于C ,那么( ) A .2OP PA P B =? B .2P C PA PB =? C .2PA PB PC =? D .2PB PA PC =? O P C B A 4、在△ABC 中,AM 、AD 分别是其中线和角平分线,⊙ADM 交AB 于L ,交AC 于N 。 求证:BL =CN 。
【点评】 本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中, 常用 的方法是转化为解直角三角形. 圆幂定理 STEP 1: 进门考 理念: 1. 检测垂径定理的基本知识点与题 型 2. 垂径定理典型例题的回顾检测。 3. 分析学生圆部分的薄弱环节。 1)例题复习 1. (2015?夏津县一模)一副量角器与一块含 30°锐角的三角板如图所示 放置,三角板的直角顶点 C 落在量角器的直径 MN 上,顶点 A ,B 恰好都落在量角 器的圆弧上,且 AB ∥MN .若 AB=8cm ,则量角器的直径 MN= cm . 【考点】 M3:垂径定理的应用; KQ :勾股定理; T7:解直角三角形. 【分析】 作 CD ⊥ AB 于点 D ,取圆心 O ,连接 OA ,作 OE ⊥AB 于点 E ,首先求得 CD 的长,即 OE 的长,在直角△ AOE 中,利用勾股定理求得半径 OA 的长,则 MN 即可求解. 解答】 解:作 CD ⊥AB 于点 D ,取圆心 O ,连接 OA ,作 OE ⊥ AB 于 点 E . 在直角△ ABC 中,∠ A=30°,则 BC= AB=4cm , 在直角△ BCD 中,∠ B=90°﹣∠ A=60°, =2 (cm ), ∴ OE=CD=2 , 在△ AOE 中, AE= AB=4cm , ∴CD=BC?sinB=×4 则 OA= = =2 ( cm ), 则 MN=2OA=4 ( cm ). 故答案是: 4 .
2. (2017?阿坝州)如图将半径为 2cm 的圆形纸片折叠后,圆弧恰好经过 【考点】 M2:垂径定理; PB :翻折变换(折叠问题). 【分析】 通过作辅助线, 过点 O 作 OD ⊥AB 交 AB 于点 D ,根据折叠的性质可知 OA=2O ,D 根据 勾股定理可将 AD 的长求出,通过垂径定理可求出 AB 的长. 【解答】 解:过点 O 作 OD ⊥ AB 交 AB 于点 D ,连接 OA , ∵OA=2OD=2c ,m ∴ AD= = = ( cm ), 点评】 本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键. 3. (2014?泸州)如图,在平面直角坐标系中,⊙ P 的圆心坐标是( 3,a ) a >3),半径为 3,函数 y=x 的图象被⊙ P 截得的弦 AB 的长为 ,则 a 的值 A .4 考点】 M2:垂径定理; F8:一次函数图象上点的坐标特征; KQ :勾股定理. cm D .2 cm 故选: D . cm .