第一部分函数极限连续
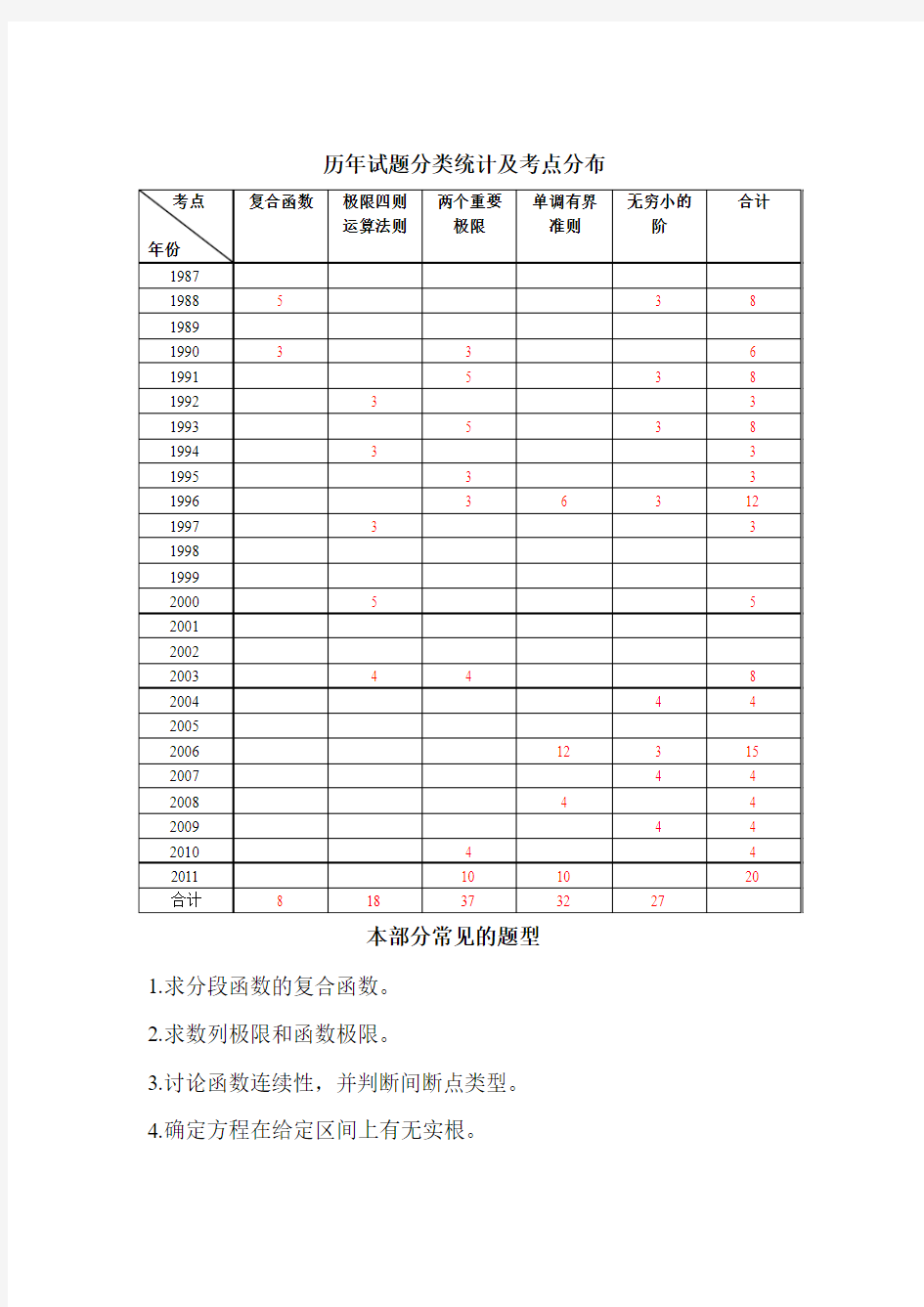
历年试题分类统计及考点分布
本部分常见的题型
1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性,并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数 例1 (1988, 5分) 设2
(),[()]1x f x e f x x
?==-且()0x ?≥,求()x ?及其定义
域。
解: 由2
()x f x e =知2
()
[()]1x f x e x
?
?==-,又()0x ?≥,
则()0
x x ?=
≤.
例2 (1990, 3分) 设函数
1,1
()0,1
x f x x ?≤?=?>??,则[()]f f x =1.
练习题: (1)设
1,1,
()0,1,(),1,1,
x
x f x x g x e x ?
->?求[()]f g x 和[()]g f x ,
并作出这
两个函数的图形。 (2)
设
20,0,0,0,
()(),
,0,,0,
x x f x g x x x x x ≤≤??==??>->??求
[()],[()],[()],[()]f f x g g x f g x g f x .
二、 求数列的极限
方法一 利用收敛数列的常用性质
一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。 性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。 性质3(收敛数列的保号性) 如果lim n
n x
a
→∞
=,且0a >(或0a <),那么存在
0n N
+
∈,使得当0n n >时,都有0n x >(或0n x <).
性质4(数列极限的四则运算法则) 如果,,
lim lim n
n n n x
a y
b →∞
→∞
==那么
(1)()lim n
n n x
y a b →∞
±=±;
(2)lim n
n n x
y a b
→∞
?=?;
(3)当0()n
y
n N +
≠∈且0
b ≠时,lim
n n n
x a y b
→∞
=
.
例3 若 lim n
n x
a
→∞
=,则 lim
n n x a
→∞
=.
注: 例3的逆命题是不对的, 例如我们取(1)
n
n
x =-, 显然1lim
n n x →∞
=,
但数列(1)
n
n
x
=-没有极限。
例4 如果数列{}n x 收敛, 那么数列{}n x 一定有界。 注: 例4的逆命题是不对的, 例如我们取(1)
n
n
x =-, 显然数列{}n x 有界,
但数列(1)
n
n
x
=-没有极限。
例5 设{}{}{},,n n n a b c 均为非负数列, 且0,1,lim lim lim n
n n n n n a
b c →∞
→∞
→∞
===+∞
.
下列陈述中哪些是对的, 哪些是错的? 如果是对的, 说明理由;如果是错的, 试给出一个反例。 (1)
,n n a b n N
+
<∈; (2)
,n n b c n N
+
<∈; (3) lim n
n
n a
c →∞
不存在; (4)
lim n
n
n b c →∞
不存在.
解: (1)是错的, 我们可以令1,1
n
n n a b n
n =
=
+, 显然0,
1lim lim n
n
n n a
b
→∞
→∞
==,
但1
111,2
a
b ==
, 从而11a b >.
(2)是错的, 我们可以令1,1
3n n n b c n
n =
=
+, 显然
1,lim lim n n n n b c →∞
→∞
==+∞
, 但1
111,2
3b
c =
=
, 从而11b c >.
(3)是错的, 我们可以令11,3n
n a c n n
=
=
,
显然0,lim lim n
n n n a
c →∞
→∞
==+∞
,
但111
()33lim lim n n n n a c n n →∞→∞=?=.
(4)是对的, 由于10,lim lim n
n n n b
c →∞
→∞
=≠=+∞
, 则lim n
n n b
c →∞
=+∞
, 即极
限lim n
n
n b
c →∞
不存在。
注1: 极限的保序性是说, “若,,lim lim n
n n n a
a b b a b
→∞
→∞
==>, 则存在0
n
N
+
∈
使得当0n n >时有n n a b >.”, 而不是对任意的n N +∈有n n a b >.
注2: 事实上我们可以得到如下一个常用的结论:
若0,lim lim n
n n n a
a b →∞
→∞
=≠=∞
, 则lim n
n n a
b →∞
=∞
.
练习题: 设数列{}n x 与{}n y 满足0
lim n
n n x
y →∞
=, 则下列断言正确的是( )
(A) 若{}n x 发散, 则{}n y 必发散. (B) 若{}n x 无界, 则{}n y 必无界. (C) 若{}n x 有界, 则{}n y 必为无穷小. (D)
若1n x ??
????
为无穷小, 则{}n y 必为无穷小.
方法二 利用一些常用的结论 (1) 设数列{}n x 有界, 又0
lim n
n y
→∞
=, 则0
lim n
n n x
y →∞
=.
(2) 0,10(1),1,1,1
lim lim n
n
n n q q q q
q q →∞
→∞
?
=<==??
+∞>?. (3) 1
1(0)
lim n
n a a →∞=>. 例6 1cos
2
lim
n n n
π→∞
=0
.
练习题:
(1)1)sin
2lim n n π→∞
=
_______.
(2)1)sin
2
lim n n π→∞
-=__________.
例7 1
()lim n
n
n
n n a
b c →∞
++={}max ,,a b c (0,0,0a b c ≥≥≥).
解: 由于{}{}1
1
max ,,()3max ,,n
n
n
n n a b c a
b c a b c ≤++≤,故1
()lim n
n
n
n n a b c →∞
++=
{}max ,,a b c .
练习题: 已知10,......,
m a a ≥≥, 求极限1
1
(......)lim n
n
n
m n a a →∞
++.
例8 2211lim n
n
n x
x x
→∞-=+,10,1,1
x x x x x ?
=??
->?. 解: 当1x
<时
2211lim n n
n x
x x x
→∞
-=+;
当
1x =时
2210
1lim n n
n x
x x
→∞
-=+;
当1x >时
22221
1
1111
lim lim
n n
n
n n n
x
x x x x x
x
→∞→∞
--=
=-++.
故 2211lim n
n
n x
x x
→∞-=+,10,1,1
x x x x x ?
=??
->?. 练习题: 211lim n
n x
x →∞
+=+________. 方法三 利用Heine 定理将抽象数列的极限转化为具体函数的极限 Heine 定理: 0
()lim x x
f x A
→=的充分必要条件是: 对于任意满足条件
lim
n n x x →∞=且0()
n
x
x n N +
≠∈的数列{}n x , 相应的函数值数列{}()n f x 成立
()lim n
n f x
A →∞
=.
例9 设数列{}n x 满足0()n
x
n N +
≠∈且0lim n n x →∞
=,
计算2
1
sin (
)
lim n
x n
n n
x x →∞
.
解: 我们考虑函数极限
2
2
2
2
3
2
sin sin sin ln(
)ln(11)
1
1
sin cos 1
30
sin (
)lim lim lim lim lim lim x x x x x x x x x
x x
x
x
x
x
x x x x x x x e
e
e
e
e
x
+
----→→→→→→=
=
=
=
=
sin 166
lim x
x
x e
e
--
→=
=
从而2
2
1
1
16
sin sin (
)
(
)lim lim n
x n
x n x n
x x e
x x
-
→∞
→=
=.
练习题: 设数列{}n x 满足0()
n
x n N +
>∈且0lim n
n x
→∞
=,计算1
ln(1)
[
]
lim n
x n n n
x x →∞
+.
方法四 利用夹逼准则 例10 计算2
2
2
111(
......)2lim n n n n n n π
π
π
→∞
+
++
+++.
解: 由于
2
2
2
2
2
2
2
1
1
1
(
(2)
n
n n n n n n n n π
π
π
π
π
≤+
++
≤
+++++, 故
2
2
2
1
11(......)12lim n n n n n n ππ
π
→∞
+
++
=+++.
练习题: (1)
计算......lim n →∞
++
.
(2) 计算2
2
2
12(
......)1
2
lim n n n n n n n n n
→∞
+
++
++++++.
(3) 计算1
111(1......)2
3
lim n
n n
→∞
+
+++.
(4)
计算......lim n →∞
+
.
方法五 利用单调有界准则 适用题型: (1)由递推关系1()n n x f x +=
定义的数列{}n x 极限问题,
一般先
用单调有界准则证明极限存在, 然后等式两边取极限求出极限。 (2)有些题目直接给出了数列{}n x 的通项公式, 要求我们证明数列{}n x 的极限存在, 这时优先考虑用单调有界准则证明其极限存在。
例11 (1996, 6分)
设1110,)n x x n N ++==∈,
试证数列{}n x 极限存在,
并求此极限。
证明: 先证明数列{}n x 是单调减少的。
由于10()n n
n x x x n N
+
+-=
=
≤?∈, 所以数列{}n x 是单
调减少的。 注意到10()
n x x n N +
≤≤?∈, 于是数列{}n x 有界, 故数列{}n x 极限存在。
设lim n
n x
a
→∞
=, 等
式1n x +=
两边取极限
得a =
, 即3a =或
2
a =-, 又1010a x ≤≤
=,
所以3a =, 亦即3lim n
n x
→∞
=.
练习题: (1)
的极限存在, 并求此极
限。
(2)
设11)
n x x n N +
+==∈, 试证数列{}n x 极限存在, 并求
此极限。
(3)
设111,)
n x x n N +
+==∈, 试证数列{}n x 极限存在, 并
求此极限。 (4) 设1101,(2)()
n n n x x x x n N +
+<<=-∈, 试证数列{}n x 极限存在,
并求此极限。
例12 (2008, 4分) 设函数()f x 在(,)-∞+∞内单调有界, {}n x 为数列, 下列命题正确的是( B )
( A ) 若{}n x 收敛, 则{}()n f x 收敛. ( B ) 若{}n x 单调, 则{}()n f x 收敛. ( C ) 若{}()n f x 收敛, 则{}n x 收敛. ( D ) 若{}()n f x 单调, 则{}n x 收敛.
解: 由于()f x 在(,)-∞+∞上单调有界, 若{}n x 单调, 则{}()n f x 是单调有界数列, 故{}()n f x 收敛。
事实上(A)、(C)、(D)都是错误的。若令(1)()
n
n
x n N n
+
-=∈, 显然
(1)0
l i m
n
n n
→∞
-=, 即{}n x 收敛, 再令
1a r c t a n ,0
()arctan ,0
x
x f x x x +≥?=?
()
f x 在
(,)
-∞+∞上单调有界,
但{}()n f x 不收敛。由于
11a r c t a n ,2()()1arctan(),21()n n k k N n
f x n k k N n +
+?+=∈??=?
?-=-∈??
, 所以()lim n n f x →∞
不存在, 故(A)不正
确。 若令(),()a r c t a n n
x
n n N f x x +
=∈=,
显然{}()n f x 收敛且单调, 但{}n x 不收
敛, 故(C)和(D)不正确。
例13 (2006, 12分) 设数列{}n x 满足110,sin ()
n n x x x n N π+
+<<=∈.
( I )证明lim n
n x →∞
存在, 并求该极限;
( II )计算2
1
1(
)
lim n
x n n n
x x +→∞
.
解: ( I )用数学归纳法证明数列{}n x 是单调减少的且有界。 由10x π<
<得2110sin x x x π
<
=≤<;
设0n x π
<<, 则10sin n n n x x x π
+<
=≤<, 所以数列{}n x 是单调减少的且有
界, 故lim n
n x →∞
存在。
记lim n
n x
a
→∞
=, 于是0a π≤≤.由
1sin n n
x x +=得sin a a =, 注意到函数()sin f x x x =-在区间[0,]π上是单调增加的, 所以0a =, 即0lim n
n x
→∞
=.
( II )见例9.
注1: 在判别一个函数()f x 的单调性时, 我们经常用到下面两个孰知的结论。
(1) 设函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 若(,)a b 中除至多有限个点有'()0f x =之外都有'()0f x >, 则()f x 在[,]a b 上单调增加。
(2) 设函数()f x 在[,]a b 上连续, 在(,)a b 内可导, 若(,)a b 中除至多有限个点有'()0f x =之外都有'()0f x <, 则()f x 在[,]a b 上单调减少。
注2: 记住一些基本的不等式可以帮助考研学子在考试时节省大量的时间, 例如sin (),ln(1)(0)x
x x R x x x ≤?∈+等。
练习题: 设数列{}n x 满足1
10,ln(1)()
n n x
x x n N +
+>=+∈.
( I )证明lim n
n x →∞
存在, 并求该极限; ( II )计算1
1(
)
lim n
x n n n
x x +→∞
.
例14 (2011, 10分) 证明: (1)对任意正整数n , 都有111ln(1)1
n n n
<+
<
+;
(2)设111......ln ()2
n
x
n n N n
+=+
++
-∈,
证明数列{}n x 收敛。
证明: (1)由于函数()ln(1)f x x x =-+在[0,)+∞上单调增加, 从而当0x >时()(0)0f x f >
=,
所以对任意正整数n , 都有11ln(1)n
n
+
<
.
由于函数()ln(1)1
x g x x x =+-
+在[0,)+∞上单调增加, 从而当0x >时
()(0)0g x g >=,
所以对任意正整数n , 都有
11ln(1)1
n n <+
+.
故对任意正整数n , 都有
111ln(1)1
n n n
<+
<
+.
(2)先证明数列{}n x 是单调减少的。
我们考虑
11111[1......ln(1)](1......ln )
2
1
2
n n x x n n n n
+-=+++
-+-+
++
-+
11ln(1)0()1
n N n n
+
=
-+
注意到
11311......ln ln 2ln
......ln(1)ln ln(1)ln 0()
22
n x n n n n n N n
n
+
=+
++
->++++
-=+->?∈从而数列{}n x 有界, 故数列{}n x 收敛。 练习题: 设2
2
111......()2
n
x
n N n
+=+
++
∈,
证明数列{}n x 收敛。
方法六 利用定积分的定义 设函数()f x 在[,]a b 上连续, 则1
1
[()]()lim
b
n
n i a
i f a b a f x dx n
n
→∞
=+
-=
∑?.
例15 计算极限111(
......)1
2
2lim n n n n
→∞
+
++
++.
解:
1
11111111
(
......)(
......)ln 2121
2
211
111lim lim
n n dx n n n
n
x n
n
→∞
→∞
+
++
=
+
++
=
=+++++
+
?.
例16 (1998, 6分) 求2sin
sin
sin lim (
......)111
2n n n n n n n
π
π
π→∞++++++
.
解: 注意到
1
1
1
1
1
sin
sin
sin
11
n
n
n
i i i i i i n n
n
n
n i
πππ===≤
≤
++
∑∑
∑
而
1
1
1
2
lim
sin
sin n
n i i xdx n
n πππ
→∞
==
=
∑?,
1
1
1
112
lim
sin
lim (
sin
)sin 1
1
n
n
n n i i i n
i xdx n n
n n
n
ππππ
→∞
→∞
===?
==
++∑
∑?
故2sin
sin
sin 2lim (
......)111
2n n n n n n n
π
π
ππ→∞
+++=+++
.
练习题: (1)
计算1
1
lim n
n i n
→∞
=∑
(2) 计算1
12......(0)lim
p p
p
p n n
p n
+→∞
+++>.
(3) 计算12(1)[sin
sin
(i)
]lim
n n n
n
n
n
π
ππ→∞
-+++.
三、 求函数的极限
方法一 利用函数极限的常用性质
一般而言,函数极限有以下四种常用的性质。 性质1(函数极限的唯一性) 如果0
lim
()
x x f x →存在,那么这极限唯一。
性质2(函数极限的局部有界性) 如果0
lim ()x x f x A →=,那么存在常数0
M >和0
δ
>,使得当00x x δ
<
-<时,有
()f x M
≤.
性质3(函数极限的局部保号性) 如果0
()lim x x f x A
→=
,且0A >(或0A <),
那么存在常数0
δ
>,使得当00x x δ
<
-<时,有()0f x >(或()0f x <).
性质4(函数极限的四则运算法则)如果00()
()
(),
(),lim lim x x x x f x A g x B →∞→∞==那么
(1)0()
[()()]lim x x f x g x A B →∞±=
±;
(2)0()
[()()]lim x x f x g x A B
→∞?=
?;
(3)若又有0B ≠,则0()
()()
lim
x x f x A g x B
→∞=.
例17下列陈述中哪些是对的, 哪些是错的? 如果是对的, 说明理由;如果是错的, 试给出一个反例。
(1)如果0
()lim x x f x →存在, 但0
()lim x x g x →不存在, 那么0
[()()]lim x x f x g x →+不存在;
(2)如果0
()lim x x f x →和0
()lim x x g x →都不存在, 那么0
[()()]lim x x f x g x →+不存在;
(3)如果0
()lim x x f x →存在, 但0
()lim x x g x →不存在, 那么0
()()lim x x f x g x →?不存在.
解: (1)对, 因为, 假若0
[()
()]l i m x x
f x
g x
→+存在, 则
()[()()]()lim lim lim x x x x x x g x g x f x f x →→→=+
-也存在,
这与已知条件矛盾。
(2)错, 例如
1,01,0
()0,0,()0,0
1,01,0x x f x x g x x x x >->????
====????-<
当0x →时的极限都不
存在, 但()()0f x g x +≡当0x →时的极限存在。
(3)错, 例如0
01,0
()0,()0,()0,0,()
1,0
lim
lim x x x f x f x g x x g x x →→->??
≡===??
不存在,
但0
()()0lim x x f x g x →?=.
例18(函数极限的局部保号性) (1)如果0
()lim x x f x A →=,且0A >(或0A <),
那么存在常数0
δ
>,使得当00x x δ
<
-<时,有()0f x >(或()0f x <);
(2)如果()lim x f x A →∞
=且0A >(或0A <), 那么存在常数0
X >使得当x
X
>时有()0f x >(或()0f x <).
注: 例18是一些非常适用的结论, 它们经常可以帮助我们确定方程在给定区间上实根的个数。 方法二 利用一些常用的结论
(1) 有界函数与无穷小的乘积是无穷小。 (2) 当0
00,0,a b m
≠≠和n 为非负整数时, 有
01011
01,......0,......,lim
m m m n
n x n
a n m
b a x a x a n m
b x b x
b n m
--→∞
?=???+++?
>=?+++?
???
∞
x x x
→∞=0
. 注: sin 0lim
x x x
→∞
=,
但0
sin 1lim
x x x
→=, 我们强烈建议考研学子在计算函数
极限时务必要仔细地观察自变量的变化过程, 稍有不慎就会出现重大差错。
练习题: (1)20
1sin
lim x x x
→=________.
(2)arctan lim
x x
x
→∞
=________.
例20 3
2
3
2
341751
lim
x x x x x →∞
++=
++37
.
练习题: (1) 2
3
2
32121lim
x x x x x →∞-+=-+________.
(2) 3
2
221461lim
x x x x x →∞-+=
-+________.
(3) 22121
lim
x x x x →∞
-=--________.
方法三 利用左、右极限 由于0
()()()lim lim lim x x x x x x f x A f x f x A
+
-
→→→=
?
==
, 鉴于此, 如果我们要考查
函数()f x 当0x x →
时极限是否存在, 我们可以去考查函数()f x 在0x 处
的左、右极限是否存在并相等。
适用题型:多用于判别一个分段函数()f x 在分段点0x 处的极限是否存在。
例21 (1992, 3分) 当1x →时, 函数
1
2
111
x x e x ---的极限
( D )
(A)等于2. (B)等于0. (C)为∞. (D)不存在但不为∞. 解: 由于
11
11
221
1
1
1
1
1
1
1
11(1)0,(1)1
1
lim
lim lim
lim x x x x x x x x x x e
x e
e
x e
x x -
-
+
+
----→→→→--=
+==
+=+∞
--
则当1x →时, 函数
1
21
11
x x e
x ---的极限不存在但不为∞.
注: 这里特别应注意的是11
,0
lim lim x
x x x e
e +
-
→→=+∞=.
练习题: (1) (2000, 5分) 求1
4
2sin [
]1lim x
x x
e x x
e →++
+.
(2)设
21sin ,0(),0x x f x x
x x ?>?
=??≤?
, 求0
()lim x f x →.
(3) 设
1
ln(1),0(),0
x x x f x e x +≥??
=??
()lim x f x →.
方法四 利用两个重要极限:1(1)lim x
x e
x
→∞
+
=(或者1
(1)lim x
x x e
→+=) ,
sin 1lim
x x x
→=
在处理1∞型极限时, 经常将所求极限“凑”成基本极限1(1)
lim x
x x
→∞
+
的
形式, 然后求出极限。
注: 洛必达法则也是一种常用的处理1∞型极限的方法, 但鉴于它的重要性, 我们将在第二部分(一元函数微分学)做专门的总结。 例22 (1991, 5分)
求0
(cos
lim x
x π
+
→.
解
: 2
(cos
[1(cos
lim lim x x x e
ππ
+
+
-
→→=
+=.
例23 (2011, 10分) 求极限1
1
ln(1)
[
]lim x
e
x x x
-→+.
解:
1
ln(1)
1[1]1
1
ln(1)
1
1
1
1
ln(1)
ln(1)
ln(1)
[
]
[11]
[11]
lim lim lim x
x
x
x x x
e e e x
x x x x x x x
x
x
+?-?
+----→→→+++=
+
-=
+
-
而2
ln(1)
1ln(1)ln(1)1[
1]2
1
(1)
lim lim
lim
x
x
x x x x x x x x
x
e x e x
→→→++-+--?
=
=
=-
-?-
故1
11
2
ln(1)
[
]lim x
e
x x e
x
-
-→+=.
练习题: (1) (1990, 3分) 设a 是非零常数, 则lim (
)x
x x a x a
→∞+=
-________.
(2) (1993, 5分) 求极限21lim (sin
cos
)
x
x x
x
→∞
+.
(3) (1995, 3分) 2
sin 0(13)
lim x
x x →+=
________. (4) (1996, 3分) 设2lim (
)8x
x x a x a
→∞
+=-,
则a =________.
(5) (2003, 4分) 2
1
ln(1)
(cos )lim x
x x +→=
________.
(6) 求极限2
(2sin )lim x
x
x x e
→+.
(7) 求极限1
1cos 0
sin (
)lim x
x x x
-→.
(8) 求极限1
1
(1)[
]lim x
x
x x e
→+.
(9) 求极限2
(
arctan )
lim x
x x π
→+∞
.
(10) 求极限1
(
)(0,0,0)3
lim x x
x
x x a b c
a b c →++>>>.
(11) 求极限tan 2
(sin )lim x x x π
→
.
(12) 求极限1
11
lim x x x -→.
(13) 求极限1
23lim (
)
21
x x x x +→∞
++.
方法五 利用等价无穷小代换
在处理函数极限的过程中, 如果我们能恰当地利用等价无穷小代换, 可以使计算简化。为了便于考研学子复习, 我们把常用的等价无穷小代换列举如下:
当0x →时
, 2
sin ~,arcsin ~,tan ~,arctan ~111cos ~
,1~
2
ln(1)~,1~x
x x x x x x x x
x x x
n
x x e x
-+-
例24 (1994, 3分) 设2
tan (1cos )2ln(12)(1)
lim
x
x a x b x c x d e
-→+-=-+-, 其中220a c +≠, 则必
有( D ) (A)
4b d
= (B)
4b d
=- (C)
4a c
= (D)
4a c
=-
解: 2
2
tan 1cos tan (1cos )2
2ln(12)(1)
ln(12)
1lim
lim
x
x
x x x x
a
b
a x
b x a x x c
c x
d e
x e
c
d
x
x
--→→-++-===--+---+, 从而
4a c =-.
例25 (2008, 9分) 求极限4
[sin sin(sin )]sin lim
x x x x
x
→-.
解: 444
000
[sin sin(sin )]sin [sin sin(sin )]sin (sin )(sin )lim lim lim x x t x x x x x x t t t
x x t →→→---== 3
2
sin 1cos 136
lim
lim
t t t t t t
t
→→--=
=
.
练习题: (1) (1991, 3分) 已知当0x →时, 1
2
3(1)1
ax +-与cos 1x -是等价
无穷小, 则常数a =_______. (2) (1992, 5分)
求0
lim
x
x → (3) (1993, 3分) 设sin 2
3
4
()sin ,()x
f x t dt
g x x x
==+?
, 则当0x →时,
()f x 是()g x 的( )
(A)等价无穷小 (B)同阶但非等价的无穷小
(C)高价无穷小 (D)低价无穷小
(4) (1994, 3分)
11lim cot (
)sin x x x
x
→-
=
_________.
(5) (1997, 3分) 2
01
3sin cos
(1cos )ln(1)
lim
x x x x x x →+=
++__________.
(6) (1999, 3分) 2
11lim (
)tan x x
x x
→-
=
________.
(7) (2004, 4
分) 把
x +
→时的无穷小
量
2
2
3
cos ,tan ,sin x
x
t dt t dt
αβγ=
=
=
??
?
排列起来, 使排在后面的
是前一个的高阶无穷小, 则正确的排列次序是( ) (A)
,,αβγ
(B)
,,αγβ
(C)
,,βαγ
(D)
,,βγα
(8) (2006, 3分) 0
ln(1)1cos lim
x x x x
→+=
-_________.
(9) (2007, 4分) 当0x +→时,
等价的无穷小量是( )
(A)
1-
(B)
ln
(C)
1
(D) 1cos -
(10) (2009, 4分) 当0x →时, ()sin f x x ax =-与2
()ln(1)
g x x bx =
-
是等价无穷小, 则( ) (A) 11,6a b ==- (B) 11,6
a b ==
(C)
11,6
a b =-=-
(D)
11,6
a b =-=
(11)
求极限0
lim
x +
→(12)
2
sin lim
(1)
x
x x x x e →-=-________.
(13) 求极限3
tan sin (sin )
lim
x x x x →-.
(14)
求极限0
lim
x →.
(15) 求极限0
11lim[
]ln(1)
x x x
→-
+.
方法六 利用Heine 定理
Heine 定理被经常用于证明某个函数极限的不存在性。为了证明函数
()f x 当0
x x →时极限不存在, 我们计划构造两个点列{}{},n n x y 满足如
下条件: (1) 0lim n n x x →∞
=且0()n x x n N +
≠?∈;
(2)
0lim n n y x →∞
=且0()
n y x n N +
≠?∈;
(3)
lim ()lim ()n n n n f x f y →∞
→∞
≠.
从而我们可以说明函数()f x 当0x x →时极限不存在。
例26 证明0
1
lim sin x x
→不存在。
证明: 我们特殊地取
11,()
22
n n x y n N n n π
π
π+
=
=
?∈+
, 则显然有
lim 0,0()n n n x x n N +
→∞
=≠?∈与lim 0,0()n n n y y n N +
→∞
=≠?∈.但由于1lim sin
n n
x →∞
=而
1lim sin
1n n
y →∞
=, 故0
1
lim sin x x
→不存在。
练习题: 证明0
1
lim cos x x
→不存在。
四、 讨论函数连续性,并判断间断点类型 例27 讨论函数221()1lim
n n
n x f x x
x
→∞
-=+的连续性, 若有间断点, 判别其类
型。
解: 由例8知,1()0,1,1
x x f x x x x ?
==??
->?,
从而1x =和1x =-均为()f x 的第一类间
断点。 例28 设函数
,0
(),0x e x f x a x x ?<=?+≥?,
应当怎样选择数a , 使得()f x 成为在
(,)-∞+∞内的连续函数。
解: 要使
()
f x 成为在
(,)
-∞+∞内的连续函数, 我们只需
lim ()lim ()(0)x x f x f x f a
+-→→===, 故1a =.
练习题: (1)求函数3
2
2
33()6
x x x f x x x +--=
+-的连续区间。
(2)设函数()f x 与()g x 在点0x 连续, 证明函数
1. 解: (1)相等. 因为两函数的定义域相同,都是实数集R ; x =知两函数的对应法则也相同;所以两函数相等. (2)相等. 因为两函数的定义域相同,都是实数集R ,由已知函数关系式显然可得两函数的对应法则也相同,所以两函数相等. (3)不相等. 因为函数()f x 的定义域是{,1}x x x ∈≠R ,而函数()g x 的定义域是实数集R ,两函数的定义域不同,所以两函数不相等. 2. 解: (1)要使函数有意义,必须 400x x -≥?? ≠? 即 40x x ≤?? ≠? 所以函数的定义域是(,0)(0,4]-∞U . (2)要使函数有意义,必须 30lg(1)010x x x +≥?? -≠??->? 即 301x x x ≥-?? ≠??
《高等数学》考研辅导练习4 不定积分 1. 求()x f x e -=在R 上的一个原函数。 2. 已知2 2 2 (sin )cos tan f x x x '=+,求()01f x x <<。 3. 设 2 ()f x dx x C =+?,则2(1)xf x dx -=? 。 4. 计算 3。 5。 计算。 6. 计算 71 (2) dx x x +?。 7。 计算。 8. 计算 21 13sin dx x +?。 9。 计算172 2 1sin cos dx x x ? 。 10. 计算 () 2 2 sin cos x dx x x x +?。 11. 计算 ()()2 ln ()ln ()()()()f x f x f x f x f x dx ''''++?。 12. 设()arcsin xf x dx x C =+? ,则 1 () dx f x =? 。 13. 设2 2 2(1)ln 2 x f x x -=-,且(())ln f x x ?=,求()x dx ??。 14. 计算arctan 23/2(1)x xe dx x +?。 15. 计算x 。 16. 计算 1sin 22sin dx x x +?。 17. 计算ln t tdt α ? 。 18. 计算()ln n x dx ?。 《高等数学》考研辅导练习5 定积分 1.设02 ()2 l kx x f x l c x l ? ≤≤??=??<≤??,求0 ()()x x f t dt Φ=?。 2. 设1 ()2()f x x f x dx =+? ,则()f x = 。 3. 计算 {}2 23 min 2,x dx -? 。 4. 已知()f x 连续,且满足()()1f x f x -=,则 2 2cos 1()x dx f x π π-+?= 。
高等数学辅导资料一 主 题:准备知识 学习时间:2014年9月29日—10月5日 内 容: 同学们在学习《高等数学》之前,要对初等数学的知识有一定的了解,因为它里面包含了很多公式、定理的运用。如基本初等函数及其计算公式会在高等数学中再次重述;常用几何公式、不等式会对求函数极限及微积分的学习有所帮助等等。这周我们将学习准备知识。其内容归纳总结如下: 一、初等数学 2、实数的基本性质 (1)实数与数轴上的点是一一对应的; (2)a 、b 为任意的两个实数,则a>b 、a>=?=y x y x y x αα 2、指数函数 )1,0(≠>=a a a y x ,1>a 时,x a 在),0(+∞;0<。