数字信号处理实验报告 - 3
- 格式:doc
- 大小:188.50 KB
- 文档页数:4

数字信号处理实验报告⼀、课程设计(综合实验)的⽬的与要求⽬的与要求:1.掌握《数字信号处理基础》课程的基本理论; 2.掌握应⽤MATLAB 进⾏数字信号处理的程序设计;实验内容:已知低通数字滤波器的性能指标如下:0.26p ωπ=,0.75dB p R =,0.41s ωπ=,50dB s A =要求:1. 选择合适的窗函数,设计满⾜上述指标的数字线性相位FIR 低通滤波器。
⽤⼀个图形窗⼝,包括四个⼦图,分析显⽰滤波器的单位冲激响应、相频响应、幅频响应和以dB 为纵坐标的幅频响应曲线。
2. ⽤双线性变换法,设计满⾜上述指标的数字Chebyshev I 型低通滤波器。
⽤⼀个图形窗⼝,包括三个⼦图,分析显⽰滤波器的幅频响应、以dB 为纵坐标的幅频响应和相频响应。
3. 已知模拟信号1234()2sin(2)5sin(2)8cos(2)7.5cos(2)x t f t f t f t f t ππππ=+++其中10.12f kHz =,2 4.98f kHz =,3 3.25f kHz =,4 1.15f kHz =,取采样频率10s f kHz =。
要求:(1) 以10s f kHz =对()x t 进⾏取样,得到()x n 。
⽤⼀个图形窗⼝,包括两个⼦图,分别显⽰()x t 以及()x n (0511n ≤≤)的波形;(2) ⽤FFT 对()x n 进⾏谱分析,要求频率分辨率不超过5Hz 。
求出⼀个记录长度中的最少点数x N ,并⽤⼀个图形窗⼝,包括两个⼦图,分别显⽰()x n 以及()X k 的幅值; (3) ⽤要求1中设计的线性相位低通数字滤波器对()x n 进⾏滤波,求出滤波器的输出1()y n ,并⽤FFT 对1()y n 进⾏谱分析,要求频率分辨率不超过5Hz 。
求出⼀个记录长度中的最少点数1y N ,并⽤⼀个图形窗⼝,包括四个⼦图,分别显⽰()x n (01x n N ≤≤-)、()X k 、1()y n (101y n N ≤≤-)和1()Y k 的幅值;(4) ⽤要求2中设计的Chebyshev 低通数字滤波器对()x n 进⾏滤波,求出滤波器的输出2()y n ,并⽤FFT 对2()y n 进⾏谱分析,要求频率分辨率不超过5Hz 。

数字信号处理实验实验一信号、系统及系统响应1、实验目的认真复习采样理论、离散信号与系统、线性卷积、序列的z 变换及性质等有关内容;掌握离散时间序列的产生与基本运算,理解离散时间系统的时域特性与差分方程的求解方法,掌握离散信号的绘图方法;熟悉序列的z 变换及性质,理解理想采样前后信号频谱的变化。
2、实验内容a. 产生长度为500 的在[0,1]之间均匀分布的随机序列,产生长度为500 的均值为0 单位方差的高斯分布序列。
b. 线性时不变系统单位脉冲响应为h(n)=(0.9)nu(n),当系统输入为x(n)=R10(n)时,求系统的零状态响应,并绘制波形图。
c. 描述系统的差分方程为:y(n)-y(n-1)+0.9y(n-2)=x(n),其中x(n)为激励,y(n)为响应。
计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位脉冲响应h(n);计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位阶跃响应s(n);由h(n)表征的这个系统是稳定系统吗?d. 序列x(n)=(0.8)nu(n),求DTFT[x(n)],并画出它幅度、相位,实部、虚部的波形图。
观察它是否具有周期性?e. 线性时不变系统的差分方程为y(n)=0.7y(n-1)+x(n),求系统的频率响应H(ejω),如果系统输入为x(n)=cos(0.05πn)u(n),求系统的稳态响应并绘图。
f. 设连续时间信号x(t)=e-1000|t|,计算并绘制它的傅立叶变换;如果用采样频率为每秒5000 样本对x(t)进行采样得到x1(n),计算并绘制X1(ejω),用x1(n)重建连续信号x(t),并对结果进行讨论;如果用采样频率为每秒1000 样本对x(t)进行采样得到x2(n),计算并绘制X2(ejω),用x2(n)重建连续信号x(t),并对结果进行讨论。
加深对采样定理的理解。
g. 设X1(z)=z+2+3z-1,X2(z)=2z2+4z+3+5z-1,用卷积方法计算X1(z)X2(z)。

数字信号处理实验报告设计数字低通IIR和FIR滤波器对语音信号进行滤波处理班级:物联网1104班学号:**********姓名:***指导老师:***一、实验内容1.选择一个.wav格式的语音信号作为分析的对象,对其进行频谱分析。
2.设计FIR和IIR数字滤波器,并对带噪语音信号进行滤波,分析滤波后信号的时域和频域特征。
二、实验目的1.学会使用Matlab来分析音频信号的时域和频域特性。
2.熟悉用双线性变换法设计IIR和FIR数字滤波器的原理与方法。
3.学会设计各种IIR数字滤波器,学会根据滤波需求确定滤波器指标参数。
4.掌握IIR\FIR数字滤波器的MATLAB实现方法。
5.通过观察滤波器输入输出信号的时域波形及其频谱,建立数字滤波的概念。
三、实验原理1.IIR滤波器:利用双线性变换设计IIR滤波器(只介绍巴特沃斯数字低通滤波器的设计),首先要设计出满足指标要求的模拟滤波器的传递函数,然后由通过双线性变换可得所要设计的IIR滤波器的系统函数。
如果给定的指标为数字滤波器的指标,则首先要转换成模拟滤波器的技术指标,这里主要是边界频率的转换,对指标不作变化。
边界频率的转换关系为。
接着,按照模拟低通滤波器的技术指标根据相应设计公式求出滤波器的阶数和截止频率;根据阶数查巴特沃斯归一化低通滤波器参数表,得到归一化传输函数;最后,将代入去归一,得到实际的模拟滤波器传输函数。
之后,通过双线性变换法转换公式,得到所要设计的IIR滤波器的系统函数。
2.FIR滤波器:如果所希望的滤波器的理想频率响应函数为(e )j d H ω,则其对应的单位脉冲响应为⎰-=πππdwe e Hn h jwn jw dd )(21)(窗函数设计法的基本原理是用有限长单位脉冲响应(n)h 逼近(n)d h 。
由于(n)d h 往往是无限长序列,且是非因果的,所以用窗函数(n)w 将(n)d h 截断,并进行加权处理,得到:)()()(n w n h n h d ⋅=(n)h 就作为实际设计的FIR 数字滤波器的单位脉冲响应序列,其频率响应函数(e )j d H ω为∑-=-=10)()(N n jwnjwe n h e H式中,N为所选窗函数(n)w 的长度。

数字信号处理实验报告班级:09050741姓名:杨建国学号:0905074128实验一频谱分析与采样定理一、实验目的1、观察模拟信号经理想采样后的频谱变化关系。
2、验证采样定理,观察欠采样时产生的频谱混叠现象。
3、加深对DFT算法原理和基本性质的理解。
4、熟悉FFT算法原理和FFT的应用。
二、实验原理根据采样定理,对给定信号确定采样频率,观察信号的频谱。
三、实验内容和步骤1)实验内容在给定信号为:1.x(t)=cos(100*π*at)2.x(t)=exp(-at)3.x(t)=exp(-at)cos(100*π*at)其中a为实验者的学号,记录上述各信号的频谱,表明采样条件,分析比较上述信号频谱的区别。
2)实验步骤1.根据采样理论、DFT的定义、性质和用DFT作谱分析的有关内容。
2.根据FFT算法原理和基本思想。
3.确定实验给定信号的采样频率,编制对采样后信号进行频谱分析的程序四、实验过程%实验一:频谱分析与采样定理T=0.0001; %采样间隔T=0.0001F=1/T; %采样频率为F=1/TL=0.02; %记录长度L=0.02N=L/T;t=0:T:L;a=28;f1=0:F/N:F;f2=-F/2:F/N:F/2;%%%%%%%%%%%%%%%%%%%%%%%%%x1=cos(100*pi*a*t);y1=T*abs(fft(x1)); % 求复数实部与虚部的平方和的算术平方根y11=fftshift(y1);figure(1),subplot(3,1,1),plot(t,x1);title('正弦信号');subplot(3,1,2),stem(y1);title('正弦信号频谱'); subplot(3,1,3),plot(f2,y11);title('正弦信号频谱'); %%%%%%%%%%%%%%%%%%%%%x2=exp(-a*t);y2=T*abs(fft(x2));y21=fftshift(y2);figure(2),subplot(3,1,1),stem(t,x2);title('指数信号');subplot(3,1,2),stem(f1,y2);title('指数信号频谱'); subplot(3,1,3),plot(f2,y21);title('指数信号频谱'); %%%%%%%%%%%%%%%%%%%%%x3=x1.*x2;y3=T*abs(fft(x3));y31=fftshift(y3);figure(3),subplot(3,1,1),stem(t,x3);title('两信号相乘'); subplot(3,1,2),stem(f1,y3);title('两信号相乘频谱'); subplot(3,1,3),plot(f2,y31);title('两信号相乘频谱');正弦信号频谱:指数信号频谱:两信号相乘频谱:五、实验结果及分析奈奎斯特抽样定理为抽样频率必须大于或等于信号频谱最高频率的2倍,即h s 2Ω≥Ω。

数字信号处理报告IIR数字滤波器上海理工大学教师:苏湛组员:王世豪徐骞刘新2016.1.4一、实验简介Butterworth 和Chebyshev 低通滤波器方法:1) 根据性能参数,先设计一个模拟滤波器,按照一定的算法转换为满足预定指标的数字滤波器。
利用模拟原型滤波器的逼近算法和特性。
2)计算机辅助设计,从统计概念出发,对所要提取的有用信号从时域进行估计,在统计指标最优的意义下,使得估计值最优逼近有用信号,减弱或消除噪声。
1)Butterworth 低通滤波器 1 幅频特性:21|()|1()a NcH j Ω=Ω+Ω,其中N 为滤波器的阶数,c Ω为通带截止频率。
在Ω=0处,有最大值|(0)|1a H =;2)在通带截止频率c Ω=Ω处,不同阶次的幅频量值都相同,即为|()|0.707|(0)|a a H j H Ω=;3)阶数N 增加时,通带幅频特性变平,阻带衰减更快,逐渐趋近于理想滤波器的幅频特性。
幅频特性通常用衰减函数1020log |()/(0)|a a H j H α=-Ω描述。
分贝(dB ) 2 极点一共有2N 个,并且以圆点为对称中心成对的出现。
21()22k j N k c s eππ-+=Ω k=1,2,…,N系统函数:122()()()()N a c N KH s K s s s s s s ==Ω--- …3 通带衰减函数p α、阻带衰减函数s α 和系统幅频特性20log |()|a H j -Ω的关系:10p 20log |()|a p H j α-Ω≤Ω≤Ω p Ω为通带截止频率 10s 20log |()|a s H j α-Ω≥Ω≥Ω s Ω为阻带截止频率4 阶数N 0.10.11010log [(101)/(101)]2log (/)p s p s N αα----≥ΩΩ5 通带截止频率c Ω 0.10.11/21/2(101)(101)ps psc NNαα--ΩΩΩ==--确定了滤波器的阶数N 和通带截止频率c Ω,就可以求出系统的极点,从而求出系统函数()a H s ,这样就完成了Butterworth 低通滤波器的设计。

数字信号处理实验报告-FIR滤波器的设计与实现在数字信号处理中,滤波技术被广泛应用于时域处理和频率域处理中,其作用是将设计信号减弱或抑制被一些不需要的信号。
根据滤波器的非线性抑制特性,基于FIR(Finite Impulse Response)滤波器的优点是稳定,易设计,可以得到较强的抑制滤波效果。
本实验分别通过MATLAB编程设计、实现、仿真以及分析了一阶低通滤波器和平坦通带滤波器。
实验步骤:第一步:设计一阶低通滤波器,通过此滤波器对波型进行滤波处理,分析其对各种频率成分的抑制效果。
为此,采用零极点线性相关算法设计滤波器,根据低通滤波器的特性,设计的低通滤波器的阶次为n=10,截止频率为0.2π,可以使设计的滤波器被称为一阶低通滤波器。
第二步:设计平坦通带滤波器。
仿真证明,采用兩個FIR濾波器組合而成的阻礙-提升系統可以實現自定義的總三值響應的設計,得到了自定義的總三值響應函數。
实验结果:1、通过MATLAB编程,设计完成了一阶低通滤波器,并通过实验仿真得到了一阶低通滤波器的频率响应曲线,证明了设计的滤波器具有良好的低通性能,截止频率为0.2π。
在该频率以下,可以有效抑制波形上的噪声。
2、设计完成平坦通带滤波器,同样分析其频率响应曲线。
从实验结果可以看出,此滤波器在此频率段内的通带性能良好,通带范围内的信号透过滤波器后,损耗较小,滞后较小,可以满足各种实际要求。
结论:本实验经过实验操作,设计的一阶低通滤波器和平坦通带滤波器具有良好的滤波特性,均已达到预期的设计目标,证明了利用非线性抑制特性实现FIR滤波处理具有较强的抑制滤波效果。
本实验既有助于深入理解FIR滤波器的设计原理,也为其他应用系统的设计和开发提供了指导,进而提高信号的处理水平和质量。
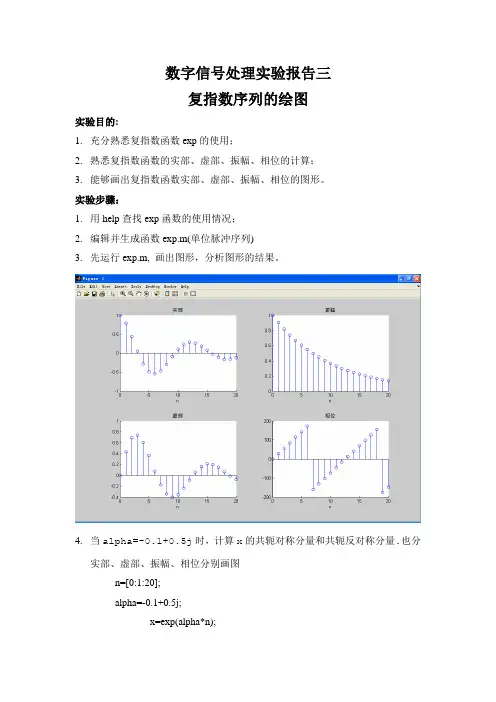
数字信号处理实验报告三复指数序列的绘图实验目的:1.充分熟悉复指数函数exp的使用;2.熟悉复指数函数的实部、虚部、振幅、相位的计算;3.能够画出复指数函数实部、虚部、振幅、相位的图形。
实验步骤:1.用help查找exp函数的使用情况;2.编辑并生成函数exp.m(单位脉冲序列)3.先运行exp.m, 画出图形,分析图形的结果。
4.当alpha=-0.1+0.5j时,计算x的共轭对称分量和共轭反对称分量.也分实部、虚部、振幅、相位分别画图n=[0:1:20];alpha=-0.1+0.5j;x=exp(alpha*n);[y1,n1]=sigfold(x,n);y2=conj(y1);y3=0.5*[x-y2]; %共轭对称分量subplot(2,2,1);stem(n,real(y3));title('实部');xlabel('n')subplot(2,2,3);stem(n,imag(y3));title('虚部');xlabel('n')subplot(2,2,2);stem(n,abs(y3));title('振幅');xlabel('n')subplot(2,2,4);stem(n,(180/pi)*angle(y3));title('相位');xlabel('n')共轭对称分量n=[0:1:20];alpha=-0.1+0.5j;x=exp(alpha*n);[y1,n1]=sigfold(x,n);y2=conj(y1);y3=0.5*[x+y2]; %共轭反对称分量subplot(2,2,1);stem(n,real(y3));title('实部');xlabel('n')subplot(2,2,3);stem(n,imag(y3));title('虚部');xlabel('n')subplot(2,2,2);stem(n,abs(y3));title('振幅');xlabel('n')subplot(2,2,4);stem(n,(180/pi)*angle(y3));title('相位');xlabel('n')共轭反对称分量5.再改变alpha=1.5, alpha=-2, 画出图形,分析图形的结果。


第1篇一、实验目的1. 理解开关信号的基本特性及其在数字信号处理中的应用。
2. 学习使用模拟和数字信号处理技术来分析和处理开关信号。
3. 掌握开关信号的时域和频域分析方法。
4. 熟悉实验设备和软件的使用。
二、实验原理开关信号是一种在特定时刻从一种状态跳变到另一种状态的信号,通常在数字电路和通信系统中广泛应用。
本实验将探讨开关信号的时域和频域特性,并通过实验验证理论分析。
三、实验设备与材料1. 数字信号处理实验箱2. 双踪示波器3. 信号发生器4. 计算机及Matlab软件四、实验步骤1. 开关信号的生成:- 使用信号发生器生成一个理想的开关信号,其状态在0和1之间切换。
- 使用示波器观察并记录开关信号的波形。
2. 时域分析:- 使用示波器观察开关信号的上升时间、下降时间、占空比等时域特性。
- 使用Matlab软件对开关信号进行时域分析,计算其时域统计特性,如均值、方差、自相关函数等。
3. 频域分析:- 使用快速傅里叶变换(FFT)将开关信号从时域转换为频域。
- 使用Matlab软件观察并分析开关信号的频谱,确定其频率成分和幅度分布。
4. 开关信号滤波:- 使用模拟滤波器对开关信号进行低通滤波,去除高频噪声。
- 使用数字滤波器对开关信号进行滤波,验证滤波效果。
5. 开关信号的调制与解调:- 使用模拟调制器将开关信号调制到高频载波上。
- 使用模拟解调器将调制信号解调回原始开关信号。
五、实验结果与分析1. 时域分析:- 示波器显示开关信号的上升时间和下降时间分别为10ns和20ns。
- Matlab软件计算得到开关信号的均值为0.5,方差为0.25。
2. 频域分析:- FFT分析显示开关信号的频谱主要集中在0Hz附近,并存在高频谐波成分。
- 频谱分析表明开关信号的频率成分为基波及其整数倍谐波。
3. 滤波效果:- 模拟滤波器成功去除开关信号中的高频噪声,滤波后的信号波形更加平滑。
- 数字滤波器也有效降低了开关信号的噪声,滤波效果与模拟滤波器相当。

实验3 用FFT 对信号作频谱分析1.实验目的学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便正确应用FFT 。
2.实验原理用FFT 对信号作频谱分析是学习数字信号处理的重要内容。
经常需要进行谱分析的信号是模拟信号和时域离散信号。
对信号进行谱分析的重要问题是频谱分辨率D 和分析误差。
频谱分辨率直接和FFT 的变换区间N 有关,因为FFT 能够实现的频率分辨率是2N π,因此要求2N D π≤。
可以根据此式选择FFT 的变换区间N 。
误差主要来自于用FFT 作频谱分析时,得到的是离散谱,而信号(周期信号除外)是连续谱,只有当N 较大时离散谱的包络才能逼近于连续谱,因此N 要适当选择大一些。
周期信号的频谱是离散谱,只有用整数倍周期的长度作FFT ,得到的离散谱才能代表周期信号的频谱。
如果不知道信号周期,可以尽量选择信号的观察时间长一些。
对模拟信号进行谱分析时,首先要按照采样定理将其变成时域离散信号。
如果是模拟周期信号,也应该选取整数倍周期的长度,经过采样后形成周期序列,按照周期序列的谱分析进行。
3.实验内容及步骤(1)对以下序列进行谱分析14()()x n R n =2103()8470n n x n nn else +≤≤⎧⎪=-≤≤⎨⎪⎩3403()3470n n x n n n else-≤≤⎧⎪=-≤≤⎨⎪⎩ 选择FFT 的变换区间N 为8和16 两种情况进行频谱分析。
分别打印其幅频特性曲线, 并进行对比、分析和讨论。
(2)对以下周期序列进行谱分析4()cos 4x n n π⎛⎫= ⎪⎝⎭5()cos cos 48x n n n ππ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭选择FFT 的变换区间N 为8和16 两种情况分别对以上序列进行频谱分析。
分别打印其幅频特性曲线,并进行对比、分析和讨论。
(3)对模拟周期信号进行谱分析()()()6()cos 8cos 16cos 20x t t t t πππ=++选择采样频率64Hz s f =,变换区间16,32,64N =三种情况进行谱分析。
数字信号处理实验报告一、 实验目的1. 熟练掌握用DFT 对离散序列进行频谱分析;2. 掌握DET 对连续函数频谱分析的方法;3. 了解频谱泄露的原因并解决;4. 对比矩形窗、汉宁窗处理连续函数的优劣并分析;5. 了解FDMA 处理音频信号。
二、 实验内容1. 已知序列 12()=0.5sin(2f n)+sin(2n),015x n f n ππ≤≤,令12f 0.22,0.34f ==,取N=16,32,64,128,画出4个DFT 的频谱图,分析DFT 长度对频谱特性的影响;取12f 0.22,0.25f ==,如何选择DFT 参数才能在频谱分析中分辨出两个频率分量。
2. 假设实际测得的一段信号的表达式为:12()=cos(2f t)+0.75cos(2t)x t f ππ,其中12,f f 自定,试确定一合适的采样频率s f ,利用fft 分析该信号的频谱。
在信号截短时要求:1)使用矩形窗,考虑频谱泄露和频率分辨率等的影响,确定采样数据的长度。
画出信号的时域和频域波形。
2)使用汉宁窗,确定能够分辨出最小谱峰间距的信号长度,并画出对应的信号时域和频域波形图。
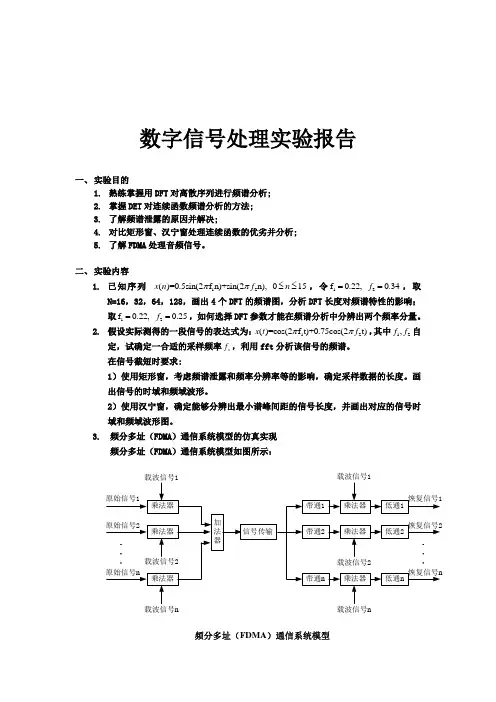
3. 频分多址(FDMA )通信系统模型的仿真实现频分多址(FDMA )通信系统模型如图所示:载波信号n载波信号n频分多址(FDMA )通信系统模型要求:1)读入或录制2路及以上的语音信号。
2)将多路语音信号分别与各自的高频载波信号相乘,由于各高频载波信号将各语音信号频谱移到不同频段,复用信号频谱为各信号频谱的叠加,因此,只需传输该复用信号便可在同一信道上实现多路语音信号的同时传输。
3)传输完成后,通过选择合适的带通滤波器,即可获得多个已调信号。
4)再进行解调,即将多个已调信号分别乘以各自的高频载波信号,这样,原始低频信号被移到低频段。
5) 最后通过选择合适的低通滤波器恢复出各原始语音信号,从而实现FDMA通信传输。
三、 分析处理及结论1. 已知序列 12()=0.5sin(2f n)+sin(2n),015x n f n ππ≤≤,令12f 0.22,0.34f ==,取N=16,32,64,128,画出4个DFT 的频谱图,分析DFT 长度对频谱特性的影响;取12f 0.22,0.25f ==,如何选择DFT 参数才能在频谱分析中分辨出两个频率分量(1) 原理分析离散序列存在两个基频f1和f2,对于第一个要求,直接做DFT 变换即可;至于第二个要求,能在频谱分析中分辨出两个频率分量,则分辨率至少满足两个频率之差,此时所取得DFT 点数才能分辨出f1和f2两个频率。
数字信号处理实验数字信号处理实验讲义前⾔ (2)实验⼀MATLAB简介 (3)实验⼆⽤FFT实现信号的谱分析 (5)实验三IIR数字巴特沃思滤波器的设计 (8)实验四FIR数字滤波器的设计 (9)前⾔信号处理与计算机的应⽤紧密结合。
⽬前⼴泛应⽤的MA TLAB⼯具软件包,以其强⼤的分析、开发及扩展功能为信号处理提供了强有⼒的⽀持。
在数字信号处理实验中,我们主要应⽤MA TLAB的信号处理⼯具箱及其灵活、便捷的编程⼯具,通过上机实验,帮助学⽣学习、掌握和应⽤MA TLAB软件对信号处理所学的内容加以分析、计算,加深对信号处理基本算法的理解。
实验⼀ MATLAB 简介实验⽬的1.熟悉MATLAB 软件的使⽤⽅法; 2.MA TLAB 的绘图功能;3.⽤MA TLAB 语句实现信号的描述及变换。
实验原理1.在MA TLAB 下编辑和运⾏程序在MA TLAB 中,对于简单问题可以在命令窗(command windows )直接输⼊命令,得到结果;对于⽐较复杂的问题则可以将多个命令放在⼀个脚本⽂件中,这个脚本⽂件是以m 为扩展名的,所以称之为M ⽂件。
⽤M ⽂件进⾏程序的编辑和运⾏步骤如下:(1)打开MA TLAB ,进⼊其基本界⾯;(2)在菜单栏的File 项中选择新建⼀个M ⽂件;(3)在M ⽂件编辑窗⼝编写程序;(4)完成之后,可以在编辑窗⼝利⽤Debug ⼯具调试运⾏程序,在命令窗⼝查看输出结果;也可以将此⽂件保存在某个⽬录中,在MATLAB 的基本窗⼝中的File 项中选择Run The Script ,然后选择你所要运⾏的脚本⽂件及其路径,即可得出结果;也可以将此⽂件保存在当前⽬录中,在MA TLAB 命令窗⼝,“>>”提⽰符后直接输⼊⽂件名。
2.MA TLAB 的绘图功能plot(x,y) 基本绘图函数,绘制 x 和y 之间的坐标图。
figure(n ) 开设⼀个图形窗⼝nsubplot(m,n,N) 分割图形窗⼝的MATLAB 函数,⽤于在⼀个窗⼝中显⽰多个图形,将图形窗⼝分为m ⾏n 列,在第N 个窗⼝内绘制图形。
数字信号处理软件实验——MatLab仿真实验报告学院:电子工程学院班级:2013211202姓名:学号:实验一:数字信号的 FFT 分析1、实验内容及要求(1) 离散信号的频谱分析:设信号 此信号的0.3pi 和 0.302pi 两根谱线相距很近,谱线 0.45pi 的幅度很小,请选择合适的序列长度 N 和窗函数,用 DFT 分析其频谱,要求得到清楚的三根谱线。
(2) DTMF 信号频谱分析用计算机声卡采用一段通信系统中电话双音多频(DTMF )拨号数字 0~9的数据,采用快速傅立叶变换(FFT )分析这10个号码DTMF 拨号时的频谱。
2、实验目的通过本次实验,应该掌握:(a) 用傅立叶变换进行信号分析时基本参数的选择。
(b) 经过离散时间傅立叶变换(DTFT )和有限长度离散傅立叶变换(DFT ) 后信号频谱上的区别,前者 DTFT 时间域是离散信号,频率域还是连续的,而 DFT 在两个域中都是离散的。
(c) 离散傅立叶变换的基本原理、特性,以及经典的快速算法(基2时间抽选法),体会快速算法的效率。
(d) 获得一个高密度频谱和高分辨率频谱的概念和方法,建立频率分辨率和时间分辨率的概念,为将来进一步进行时频分析(例如小波)的学习和研究打下基础。
(e) 建立 DFT 从整体上可看成是由窄带相邻滤波器组成的滤波器组的概念,此概念的一个典型应用是数字音频压缩中的分析滤波器,例如 DVD AC3 和MPEG Audio 。
3.设计思路及实验步骤1)离散信号的频谱分析:该信号中要求能够清楚的观察到三根谱线。
由于频率0.3pi 和0.302pi 间隔非常小,要清楚的显示,必须采取足够大小的N ,使得分辨率足够好,至少到0.001单位级,而频率0.45pi 的幅度很小,要清楚的观察到它的谱线,必须采取幅度够大的窗函数,使得它的频谱幅度变大一些。
同时还要注意频谱泄漏的问题,三个正弦函数的周期(2pi/w )分别为20,40,1000,所以为了避免产生频谱泄漏(k=w/w0为整数),采样点数N 必须为1000的整数倍。
数字信号处理课程实验实验报告实验一 利用FFT 分析连续信号频谱一、 实验目的1、 进一步加深离散傅里叶变换DFT 原理的理解;2、 应用离散傅里叶变换DFT (实际应用FFT 计算)分析连续信号的频谱;3、 深刻理解利用DFT 分析连续信号的频谱的原理,分析工程中常出现的现象及解决方法。
二、 实验原理1、 利用DFT 分析连续时间周期信号的频谱周期为Tp 的周期性连续时间信号)(t x p 的频谱(傅里叶级数的系数))(Ωjk x p 是非周期离散谱,定义为)(Ωjk x p =dt e t x p1tjk p p 0Ω-⎰)(T T 其中f 2p2ππ==ΩT 为信号的基频,Ωk 为信号的谐频,谱线间隔为Ω。
通过时域采样就可以利用DFT 分析连续周期信号的频谱。
其步骤为: ① 确定周期信号的基本周期Tp ;② 计算一个周期内的采样点数N ,若周期信号的最高频谱为Ωp ,则频谱中有2p+1 根谱线;若周期信号的频谱无限宽,则认为集中信号90%以上(或根据实际需要)能量的前p+1 个谐波为近似的频谱范围,其余的谐波忽略不计。
取N ≥2p+1; ③ 对连续周期信号以采样间隔NT T p=进行采样 ; ④ 利用FFT 计算采样信号的N 点DFT ,得到()k X ; ⑤ 最后求出连续周期信号的频谱为)(Ωjk x p =N1()k X 。
因为对连续周期信号按采样间隔NT T p=进行采样,每个周期抽取N 点时,则有 t=nT ,Tp=NT那么 )(Ωjk x p =dt et x p 1tjk p p 0Ω-⎰)(T T =∑-=-10n n p 2jk e n x p N T T T T T π)( =∑-=-1n n N 2jk e n x N 1N T π)(=)(k N 1X若能按照满足采样定理的采样间隔进行抽样,并且采取整周期为信号分析的长度,则利用FFT 计算得到的离散频谱值等于连续周期信号频谱)(Ωjk x p 的准确值。
南京邮电大学实验报告实验名称熟悉MATLAB环境快速傅里叶变换(FFT)及其应用 IIR数字滤波器的设计FIR数字滤波器的设计课程名称数字信号处理A班级学号_ 12006311____ 姓名_______张文欣_____________开课时间 2014/2015学年,第二学期实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容(1) 数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3,4,5,6],求C=A+B, D=A-B,E=A.*B,F=A./B,G=A.^B 。
并用stem语句画出A、B、C、D、E、F、G。
n = 0:1:3;A=[1 2 3 4];subplot(4,2,1)stem(n,A)xlabel('n')ylabel('A')B=[3,4,5,6];subplot(4,2,2)stem(n,B)xlabel('n')ylabel('B')C=A+B;subplot(4,2,3)stem(n,C)xlabel('n')ylabel('C')D=A-BSubplot(4,2,4)stem(n,D)xlabel('n')ylabel('D')E=A.*Bsubplot(4,2,5)stem(n,E)xlabel('n')ylabel('E')F=A./Bsubplot(4,2,6)stem(n,F)xlabel('n')ylabel('F')G=A.^Bsubplot(4,2, 7) stem(n,G) xlabel('n') ylabel('G')nAnBnCnDnEnFnG(2) 用MATLAB 实现下列序列: a) 08(). 0n 15nx n =≤≤ n=0:1:15; x1=0.8.^n; stem(n,x1) xlabel('n') ylabel('x(n)')title('2(a)')nx (n )b) 023(.)() 0n 15j nx n e+=≤≤ n=0:1:15;i=sqrt(-1); a = 0.2+3*i; x2=exp(a*n); figuresubplot(1,2,1) stem(n,real(x2)) xlabel('n')ylabel('x(n)实部') subplot(1,2,2) stem(n,imag(x2)) xlabel('n')ylabel('x(n)虚部')nx (n )实部nx (n )虚部2(b)c) 3012502202501()cos(..)sin(..)x n n n ππππ=+++ 0n 15≤≤ n=0:1:15;x3=3*cos(0.125*pi*n+0.2*pi) + 2*sin(0.25*pi*n+0.1*pi); stem(n,x3) xlabel('n') ylabel('x(n)') title('2(c)')nx (n )2(c)(4) 绘出下列时间函数的图形,对x 轴、y 轴以及图形上方均须加上适当的标注: a)2()sin() 0t 10s x t t π=≤≤t=0:0.001:10; x=sin(2*pi*t); plot(t,x,'r-')xlabel('t'),ylabel('x(t)'),title('sin(2\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )sin(2πt)b) 100()cos()sin() 0t 4s x t t t ππ=≤≤t=0:0.001:4;x=cos(100*pi*t).*sin(pi*t); plot(t,x,'b-')xlabel('t'),ylabel('x(t)'),title('cos(100\pit)*sin(\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )cos(100πt)*sin(πt)(6)给定一因果系统12121106709()()/(..)H z z z z ----=++-+,求出并绘制H (z )的幅频响应和相频响应。
实验一 熟悉MATLAB 环境一、实验目的1. 熟悉MATLAB 环境的主要操作命令。
2. 掌握简单的绘图命令。
3. 用MATLAB 编程并学会创建函数。
二、实验仪器装有MATLAB 语言的计算机 三、实验原理MATLAB 的基本命令和函数 四、实验内容和要求1. 序列的产生1)编写MATLAB 程序,产生并绘制一个单位样本(单位冲激或单位阶跃)序列2)编写MATLAB 程序,生成一个实数值的指数序列(例:1508.0)(≤≤=n n x n 或150)()32.0(≤≤=+n e n x nj );3)编写MATLAB 程序,产生一个正弦信号;(例:150)1.025.0sin(2)2.0125.0cos(3)(≤≤+++=n n n n x ππππ)实验二离散序列的基本运算一、实验目的(1)进一步了解离散时间序列时域的基本运算。
(2)了解MATLAB语言进行离散序列运算的常用函数,掌握离散序列运算程序的编写方法。
二、实验原理离散序列的时域运算包括信号的相加、相乘,信号的时域变换包括信号的移位、反折、倒相及信号的尺度变换等。
三、实验内容1、x(n)=u(n-2)+u(n+2),(-5<n<5)。
MATLAB程序如下:n1=-5;n2=5;n01=2,n02=-2;n=n1:n2;x1=[(n-n01)>=0];x2=[(n-n02)>=0];x3=x1+x2;subplot(3,1,1);stem(n,x1,'filled');axis([n1,n2,1.1*min(x1),1.1*max(x1)]);ylabel('u(n-2)');subplot(3,1,2);stem(n,x2,'filled');axis([n1,n2,1.1*min(x2),1.1*max(x2)]);ylabel('u(n+2)');subplot(3,1,3);stem(n,x3,'filled');axis([n1,n2,1.1*min(x3),1.1*max(x3)]);ylabel('u(n-2)+u(n+2)');2、已知x(n)=3cos(2πn/10),试显示x(n-3)和x(n+3)在0<n<20区间的波形。
实验六 IIR 数字滤波器的设计
一、实验目的
从理论上讲,任何的线性是不变(LTI )离散时间系统都可以看做一个数字滤波器,因此设计数字滤波器实际就是设计离散时间系统。
数字滤波器你包括IIR (无限冲激响应)和FIR (有限冲激响应)型,在设计时通常采用不同的方法。
本实验通过使用MATLAB 函数对数字滤波器进行设计和和实现,要求掌握IIR 数字巴特沃斯滤波器、数字切比雪夫滤波器的设计原理、设计方法和设计步骤;能根据给定的滤波器指标进行滤波器设计;同时也加深学生对数字滤波器的常用指标和设计过程的理解。
二、实验原理
在IIR 滤波器的设计中,常用的方法是:先根据设计要求寻找一个合适的模拟原型滤波器,然后根据一定的准则将此模拟原型滤波器转换为数字滤波器。
IIR 滤波器的阶数就等于所选的模拟原型滤波器的阶数,所以其阶数确定主要是在模拟原型滤波器中进行的。
IIR 数字滤波器的设计方法如下:
(1)冲激响应不变法。
(2)双线性变化法。
一般来说,在要求时域冲激响应能模仿模拟滤波器的场合,一般使用冲激响应不变法。
冲激响应不变法一个重要特点是频率坐标的变化是线性的,因此如果模拟滤波器的频率响应带限于折叠频率的话,则通过变换后滤波器的频率响应可不失真地反映原响应与频率的关系。
与冲激响应不变法比较,双线性变化的主要优点是靠频率的非线性关系得到s 平面与z 平面的单值一一对应关系,整个值对应于单位圆一周。
所以从模拟传递函数可直接通过代数置换得到数字滤波器的传递函数。
MATLAB 提供了一组标准的数字滤波器设计函数,大大简化了滤波器的设计工程。
(1)butter 。
(2)cheby1、cheby2。
三、实验内容及分析
利用MATLAB 编程方法或利用MATLAB 中fdatool 工具设计不同功能的IIR 数字滤波器。
1、基于chebyshev I 型模拟滤波器原型使用冲激不变转换方法设计数字滤波器,要求参数为通带截止频率π4.0=Ωp ;通带最大衰减dB A p 1=;阻带截止频率π4.0=Ωs ;阻带最小衰减dB A s 35=。
程序:
wp=0.2*pi; %通带边界频率
ws=0.4*pi; %阻带截止频率
rp=1; %通带最大衰减
rs=35; %阻带最小衰减
Fs=1000; %¼ÙÉè³éÑùÂö³å1000hz [N,Wn]=cheb1ord(wp,ws,rp,rs,'s');
[Z,P,K]=cheby1(N,rp,Wn,'s');
[H,W]=zp2tf(Z,P,K);
figure(1); freqs(H,W); [P,Q]=freqs(H,W); figure(2); plot(Q*Fs/(2*pi),abs(P)); grid on;
xlabel('频率/Hz');
ylabel('幅度');
2、基于Butterworth 型模拟滤波器原型使用双线性变换方法设计数字滤波器的,要求参数为截止频率π4.0=Ωp ;通带最大衰减dB A p 1=;阻带截止频率π25.0=Ωs ;阻带最小衰减dB A S 40=。
程序:
wp=0.4*pi;
ws=0.25*pi;
rp=1;
rs=40;
fs=500;
ts=1/fs;
wp1=wp*ts;
ws1=ws*ts;
wp2=2*fs*tan(wp1/2);
ws2=2*fs*tan(ws1/2);
[N,Wn]=buttord(wp2,ws2,rp,rs,'s');
[Z,P,K]=buttap(N);
[Bap,Aap]=zp2tf(Z,P,K);
[b,a]=lp2lp(Bap,Aap,Wn);
[bz,az]=bilinear(b,a,fs);
[H,W]=freqz(bz,az);
subplot(2,1,1);
plot(W/pi,abs(H));
grid on ;
xlabel('频率')
ylabel('幅度')
subplot(2,1,2);
plot(W/pi,20*log10(abs(H))); grid on;
xlabel('频率');
ylabel('幅度(dB)');。