《概率论》课程大纲

线性代数与概率论课程教学大纲5篇第一篇：线性代数与概率论课程教学大纲线性代数与概率论课程教学大纲一、课程说明（一）课程名称、所属专业、课程性质、学分；课程名称：线性代数与概率论所属专业：材料物理与材料化学课程属性：必修学分：4（二）课程简介、目标与任务；本课程将对线性代数和概率论里的一些常见概念和基础知识进行讲解。

线性代数里所涉及到的对向量和矩阵的分析和操作，在科学研究和工程技术中均有着广泛的应用。

从向量和矩阵中抽象出来的线性空间和线性变换的概念，将为学生以后更深入的学习和实践提供必要的背景和知识准备。

概率论是统计方向的理论基础，对于将来实际工作中的数据分析和处理有着指导性作用。

这门72学时的课把线性代数和概率论放在一起讲实际上强度是比较大的。

线性代数部分先从行列式讲起，接着介绍关于向量组和矩阵的一些基本概念和运算。

有了这些知识储备后，在第三章对于线性方程组问题给出了一个完整的解答。

第四章对向量和矩阵的数学抽象引入了线性空间与线性变换，并对空间的代数结构和变换性质作了讨论。

最后两章是关于矩阵的比较实用部分，包括特征值与特征向量，矩阵对角化与二次型。

概率论部分先定义了样本空间与随机事件，接着引入概率的概念，列举了一些计算简单概率的方法和例子。

随后对随机事件的量化导致了随机变量的引入。

从第四章到第七章均是关于随机变量和随机变量函数的内容，我们讨论了一些常见分布及其数字特征，包括期望值，方差和关联函数（协方差）等。

对于独立的随机变量序列，我们运用切比雪夫不等式证明了大数律，最后介绍了中心极限定理。

希望学生通过本课程的学习，能够熟悉线性代数里的一些基本概念和思考问题的方法，培养数学抽象思维的能力，理解和熟练掌握向量和矩阵的一些性质和相关运算，对于随机过程和随机变量亦有一个初步的具体认识。

（三）先修课程要求，与先修课与后续相关课程之间的逻辑关系和内容衔接；所需要的先修知识储备为基本的微积分，代数方程和一些矢量分析。

《概率论与数理统计》课程教学大纲一、基本信息英文课名：Probability Theory and Mathematical Statistics A课程代码：课程类别：（理论课：核心必修）学时：96学分：6适用专业：数学与应用数学二、教学目标与要求：（课程任务和基本要求）教学目标：概率论与数理统计是数学与应用数学、信息与计算科学专业的一门专业必修课程，是大学数学课程的重要组成部分，它是在开设数学分析、高等代数等专业基础课之后的一门重要专业课，以微积分和代数理论为基础，学习概率统计的基本理论和方法，研究和揭示随机现象中统计规律，为后继课程的学习和实际应用打下必需的基础。

教学要求：通过本课程的学习，使学生掌握研究随机现象的基本思想与理论方法，初步具备分析解决具有随机因素的实际问题的能力，学会在随机性数据中找出统计规律，为从事中学教学、数学应用，或者继续学习和研究该方向的理论及应用打下基础。

三、教学内容及学时数分配：（一）教学内容第一章随机事件与概率内容：1、随机试验，样本空间，随机事件等基本概念2、古典概型3、概率的公理化定义及概率的性质4、条件概率、全概率公式和贝叶斯公式5、独立性6、贝努利概型第二章随机变量及其分布内容：1、随机变量及其分布2、数学期望的定义和性质3、方差的定义和性质4、随机变量函数的分布列5、常用分布第三章多维随机变量及其分布内容：1、多维随机变量及联合分布2、边际分布与随机变量的独立性3、多维随机变量函数的分布4、多维随机变量的数字特征5、条件分布与条件期望、回归与第二类回归第四章大数定律与中心极限定理内容：1、特征函数2、大数定律3、中心极限定理第五章统计量及其分布内容：1、总体与样本2、统计量及其分布3、三大抽样分布4、充分统计量第六章参数估计内容：1、点估计2、点估计的评价标准3、最小方差无偏估计4、区间估计第七章假设检验内容：1、假设检验的基本思想和概念2、正态总体参数假设检验3、其他分布参数的假设检验4、分布拟合检验第八章方差分析与回归分析内容：1、方差分析2、多重比较3、方差齐性检验4、一元线性回归5、一元非线性回归（二）学时分配四、相关说明（一）、考核方式及成绩评定办法：（考试/考查，成绩评定方式，有实验的要注明实验成绩占课程成绩比例及实验成绩评定方式）：本课程属考试课程，考试方式：笔试，闭卷，成绩评定：平时成绩30%+期末考试70%。

《概率论》课程教学大纲一．课程基本信息开课单位：数理学院课程编号：05040010a英文名称：Probability Theory学时：总计64学时，其中理论授课64学时学分：4.0学分面向对象：数理学院统计学专业学生先修课程：数学分析高等代数后续课程：数理统计随机过程计量经济学教材：《概率论基础》，李贤平编著，高等教育出版社，2010年4月第3版主要教学参考书目或资料：1.《概率论及数理统计（上）》，中山大学统计科学系梁之舜等编著，高等教育出版社2009年7月第4版2. 《概率论与数理统计教程》，茆诗松等编著，高等教育出版社，2004年8月3. 《概率论与数理统计教程》，魏宗舒等编著，高等教育出版社，2003年6月4. 《概率论与数理统计》，陈希孺编著，中国科学技术大学出版社，1992年5月5. 《概率论基础及其应用》，王梓坤编著，北京师范大学出版社，2007年3月第3版6. 《概率论引论》，汪仁官编著，北京大学出版社二．教学目的和任务概率论是研究和揭示随机现象中统计规律性的数学分支，是我校统计学专业的专业基础课程，是继续学习数理统计、随机过程，以及与概率理论相关的课程的基础。

概率论是一门应用性很强的数学学科，广泛地应用于金融、保险，证券，工程技术和自然学科中，是各学科中分析与解决问题的基本工具，概率论与不同的问题结合形成许多分支。

通过本课程的学习，使学生比较系统地获得概率论的基础知识，使学生初步掌握处理随机现象的基本思想与方法，具备分析和处理带有随机性数据的理论基础，为后续课程的学习打下必要的基础。

三．教学目标与要求通过本课程的教学实践，一方面要求学生理解概率论的基本理论和基本计算方法；另一方面要求学生能够运用基本的概率模型、理论和方法解决实际应用中的简单概率问题。

在本课程的执行过程中，内容的选取和讲解都考虑到了学生以后的发展，使学生主要掌握随机事件、随机变量的概念；掌握随机变量的分布及数字特征的计算，掌握大数定律及中心极限定理的实际应用等内容。

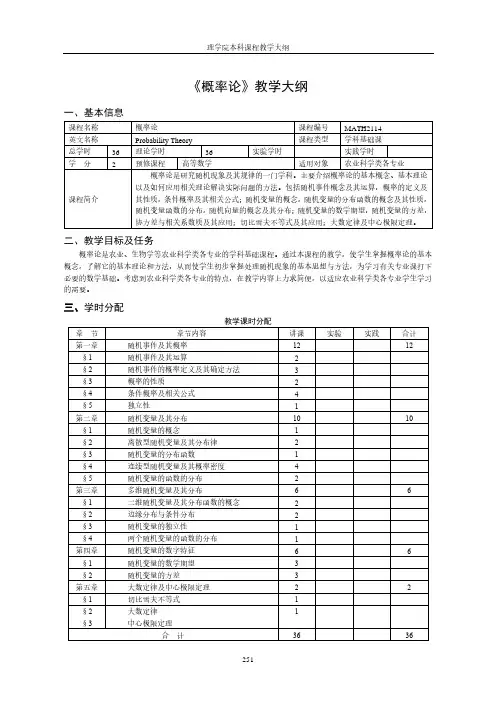
《概率论》教学大纲一、基本信息二、教学目标及任务概率论是农业、生物学等农业科学类各专业的学科基础课程。

通过本课程的教学，使学生掌握概率论的基本概念，了解它的基本理论和方法，从而使学生初步掌握处理随机现象的基本思想与方法，为学习有关专业课打下必要的数学基础。

考虑到农业科学类各专业的特点，在教学内容上力求简便，以适应农业科学类各专业学生学习的需要。

三、学时分配四、教学内容及教学要求第一章随机事件及其概率（12学时）第一节随机事件及其概率1．随机现象和必然现象2．样本空间和随机事件3．事件间的关系与事件的运算习题要点：能写出随机试验的样本点、样本空间、能用判断事件之间的关系、能运用事件运算符来表示一些复杂的事件。

第二节随机事件概率定义及其确定方法1．概率的公理化定义2．随机事件的频率及确定概率的统计方法3．确定概率的古典方法4．确定概率的几何方法习题要点：掌握概率的定义及确定概率的几种方法，能用概率的古典定义和几何定义计算相应时间的概率。

第三节概率的性质1．概率的可加性2．概率的单调性3．概率的加法公式习题要点：掌握概率的基本性质，利用概率的性质来计算事件的概率。

第四节条件概率1．条件概率2．乘法定理3．全概率公式和贝叶斯公式习题要点：能计算相关事件的条件概率，能利用乘法公式、全概率公式以及贝叶斯公式来计算复杂事件的概率，解决实践中的相应问题。

第五节独立性1．事件的独立性2．试验的独立性习题要点：能判断事件的独立性、利用事件的独立性来计算一些事件的概率。

能利用试验的独立性计算相应事件的概率，并解决一些实际问题。

本章重点：1．随机事件的概念；2．古典概率；3．条件概率；4．全概率公式与贝叶斯公式；5．独立试验序列。

本章难点：1．古典概率；2．条件概率；3．全概率公式与贝叶斯公式；4．独立试验序列。

本章教学要求：1．了解随机事件、频率的概念、概率的统计定义；2．理解样本空间和样本点的概念；3．掌握随机事件的运算法则；4．掌握概率的古典定义，并能计算基本的古典概型问题；5．掌握概率的几何定义，并能计算基本的几何概型问题；6．了解概率的公里化体系的知识；7．理解并掌握概率的基本性质，并能正确地运用概率的基本性质解决实际问题；8．理解条件概率的含义，掌握条件概率的计算公式；9．能利用乘法公式和事件的独立性计算积（交）事件的概率；10．能利用全概率公式和贝叶斯公式计算有关的概率问题；11．理解n重独立试验及n重贝努里（Bernoulli）试验的含义，并会利用二项概率公式计算在n重贝努里试验中，事件A恰好出现k次的概率。

《概率论与数理统计》课程教学大纲一、课程基本信息二、课程目标（一）总体目标：概率论与数理统计是研究随机现象客观规律性的数学学科，在高等工科学校教学计划中是一门基础理论课。

通过本课程的学习，使学生掌握概率论与数理统计的基本概念，基本理论和方法，从而使学生初步掌握处理随机现象的基本思想和方法，培养学生运用概率统计方法分析和解决实际问题的能力。

（二）课程目标：课程目标1：知识目标通过本课程的学习，学生系统掌握随机变量及其分布、参数估计与假设检验等重要知识。

课程目标2：技能目标通过本课程的基本概念、基本理论和基本方法的讲授及学生的练习，培养学生的数学推理，数理逻辑，演绎归纳，数据分析，假设论证能力。

课程目标3：素质培养(1) 通过本课程的教学，培养和提高学生对所学知识进行整理、概括、消化吸收能力，以及围绕教学内容阅读参考资料，自我扩充知识领域的能力。

(2) 通过作业和课堂讨论，培养学生口头表达能力，做到思路清晰，层次分明。

(3)通过作业，培养学生独立思考，深入钻研问题的习惯以及一题多解，举一反三的能力，应用数学的意识以及运用数学知识分析问题的良好品质。

(4)具有自主学习和终身学习的意识，有不断学习和适应发展的能力。

（三）课程目标与毕业要求、课程内容的对应关系三、教学内容第一章随机事件及其概率1.教学目标理解随机事件和样本空间的概念；熟练掌握事件之间的关系与基本运算。

理解事件频率的概念；了解随机现象的统计规律性。

知道概率的公理化定义；理解古典概率的概念；了解几何概率；掌握概率的基本性质；会应用这些性质进行概率计算。

理解条件概率的概念；掌握乘法定理、全概率公式和贝叶斯公式，并会应用这些公式进行概率计算。

理解事件独立性的概念；会应用事件的独立性进行概率计算。

2.教学重难点本节是基础知识，在高中阶段大部分已经学过，都是重点内容。

教学的重难点在于事件的三种关系：互斥，独立和包含，事件概率的两个公式：加法公式和乘法公式，以及全概率和贝叶斯公式的应用。

《概率论基础》教学大纲山西财经大学本科生应用数学系课程教学大纲课程名称：概率论基础课程英文名称：Probability Theory base学时数：64 学时(课堂讲授54学时，习题课10学时)学分数：4学分适用专业：应用数学专业开课学期：第Ⅲ或第IV学期第一部分大纲说明一、课程的性质与任务《概率论基础》是研究大量随机现象客观规律性的一门数学课程。

随着现代科学技术的迅速发展，概率论也得到了蓬勃的发展。

它不仅形成了结构宏大的理论体系，而且在很多科学研究、工程技术和经济管理等领域里有愈来愈多的应用。

同时概率论基础也是数理统计和统计学的学习前提。

由于其应用的广泛性和理论的重要性，《概率论基础》被列为我校应用数学系的一门重要的必修课。

概率论有其独特的思维方式，通过各个教学环节，逐步培养学生处理随机现象的能力和综合运用所学思维方法和知识分析问题、解决有关实际问题的能力。

为学生学习后续课程和进一步获得近代科学技术和管理技术知识奠定必要的数学基础。

二、课程的教学基本要求1、概率论是研究随机现象客观规律的一门科学。

通过本课程的学习，使学生对概率的概念和方法有全面、深入的理解，掌握概率常用方法的基本思想；使学生建立随机的思想，认识到随机现象存在的普遍性、概率应用的广泛性和学好这门课的重要性。

2、通过概率论的学习，使学生掌握概率论的基础知识，了解概率论公理化体系，为后续课程---数理统计的学习打下必要的基础。

3、通过概率论的学习，使学生初步掌握概率方法在实际中的应用，并能用一些方法处理较简单的实际问题。

三、学时分配：因本课程涉及数学分析等预备知识，故建议放在第三学期或第四学期。

本课程共64学时（讲授54课时，习题课10课时），4学分。

教材建议选用复旦大学李贤平编著的《概率论论基础》。

序号内容学时1第一章随机事件与概率8+22第二章条件概率与统计独立性6+23第三章随机变量及其分布10+24第四章随机向量及其分布10+25第五章数字特征及特征函数12+26第六章极限定理8四、参考书目：1、《概率论与数理统计》（第三版）浙江大学盛骤等编，高等教育出版社。

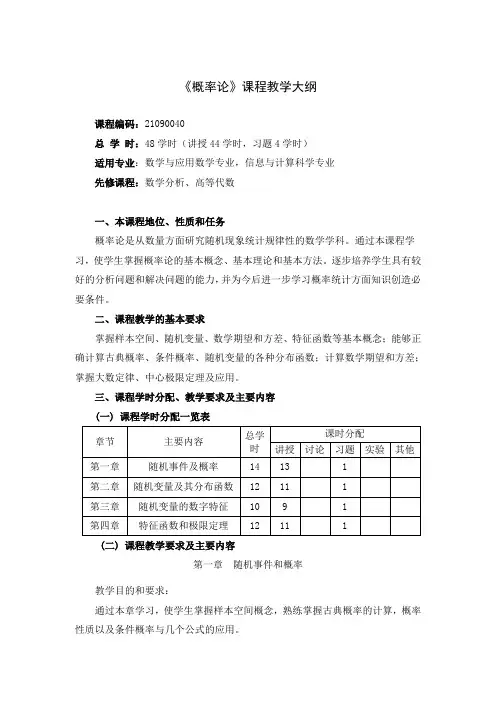
《概率论》课程教学大纲课程编码：21090040总学时：48学时（讲授44学时，习题4学时）适用专业：数学与应用数学专业，信息与计算科学专业先修课程：数学分析、高等代数一、本课程地位、性质和任务概率论是从数量方面研究随机现象统计规律性的数学学科。

通过本课程学习，使学生掌握概率论的基本概念、基本理论和基本方法。

逐步培养学生具有较好的分析问题和解决问题的能力，并为今后进一步学习概率统计方面知识创造必要条件。

二、课程教学的基本要求掌握样本空间、随机变量、数学期望和方差、特征函数等基本概念；能够正确计算古典概率、条件概率、随机变量的各种分布函数；计算数学期望和方差；掌握大数定律、中心极限定理及应用。

三、课程学时分配、教学要求及主要内容(一) 课程学时分配一览表(二) 课程教学要求及主要内容第一章随机事件和概率教学目的和要求：通过本章学习，使学生掌握样本空间概念，熟练掌握古典概率的计算，概率性质以及条件概率与几个公式的应用。

教学重点和难点:重点是概率性质和条件概率，难点在于古典概率的计算。

教学内容：1、随机事件的直观意义及其运算，样本空间；2、古典概率；3、几何概率；4、概率的公理化定义及其性质；5、条件概率、全概率公式和贝叶斯公式；6、随机事件独立性与独立试验概型。

第二章随机变量及其分布函数教学目的和要求：通过本章学习，使学生掌握随机变量概念及其分布，边沿分布，条件分布以及随机变量函数的分布。

理解各种分布计算中积分限的确定。

教学重点和难点:重点是随机变量的分布；难点是随机变量函数的分布及其性质。

教学内容：1、一维随机变量及其分布；2、多维随机变量及其分布；3、随机变量独立性；4、随机变量函数及其分布。

第三章随机变量的数字特征教学目的和要求：通过本章学习使学生熟练掌握随机变量的数学期望、方差的计算及其性质；掌握矩及协方差等概念、计算及其性质的应用。

教学重点和难点：重点随机变量的数学期望，方差的计算；难点随机变量函数的数学期望及方差。

概率论教学大纲版本号2019 适用专业：全校理工科各专业总学时:32 讲课:32 实验:0 上机:0 学分:4大纲使用说明（一）课程地位及教学目标概率论是对随机现象的统计规律进行演绎和归纳的科学。

随着社会的发展，它在经济、管理、社会生活和科学研究等方面的应用越来越广泛，它在解决实际问题，培养和提高数学素质方面发挥着特有的作用。

《概率论》课程的教学目标是通过本课程的学习，使学生初步掌握处理随机现象的基础理论和基本方法，训练学生严密的科学思维及分析问题、解决问题的能力，为学生学习后续课打下良好的基础。

（二）知识、能力及技能方面的基本要求1、学好基础知识,深刻理解和掌握课程中的定义、定理、定律、性质、法则和公式。

不仅要记住以上概念和规律的条件和结论，而且要知道它的基本思想和概率统计意义，以及它与其它概念、规律之间的联系和用途。

2、掌握基本技能，能够根据法则、公式正确地进行运算。

3、培养思维能力，能够对研究的对象进行观察、比较、抽象和概括。

4、提高解决实际问题的能力能够自觉地用所学的知识去观察生活，建立简单的数学模型，解决生活中有关的数学问题。

（三）教学大纲的实施说明教学大纲的具体实施主要是通过采取启发式、讨论式等教学方法在课堂的理论教学、习题课教学过程中来完成，也可以引入多媒体教学课件作为辅助的教学手段来完成教学内容。

（四）对习题、实验环节的要求习题的选取应体现相应的教学内容的基本概念、基本结论、基本计算方法及应用。

（五）对先修课的要求高等数学（六）考核方式及成绩评定方式1.考核方式：考试。

2.考试方法：闭卷。

3.课程总成绩：最终理论考试与中期考试的总和。

教学大纲内容第01部分总学时10学时讲课 10学时实验0学时上机0学时标题：概率论的基本概念具体内容：随机试验样本空间与事件（2学时）频率与概率（2学时）古典概型（2学时）条件概率（2学时）独立性（2学时）重点：掌握古典概型中某事件发生的概率计算方法掌握条件概率公式、全概率公式、贝叶斯公式理解事件独立性的概念难点：全概率公式、贝叶斯公式及应用习题内容：求随机试验的样本空间求古典概型中某事件发生的概率利用乘法公式、全概率公式、贝叶斯公式求概率利用事件的独立性求概率第02部分总学时8学时讲课 8学时实验0学时上机0学时标题：随机变量及其分布具体内容：随机变量及其分布函数（2学时）离散型随机变量的概率分布（2学时）连续型随机变量的概率密度（2学时）随机变量的函数的分布（2学时）重点：理解随机变量的分布函数、离散型随机变量的分布律、连续型随机变量的概率密度等概念，掌握随机变量的分布函数、离散型随机变量的分布律、连续型随机变量的概率密度的基本性质掌握常见离散型随机变量及其分布律和常见连续型随机变量及其概率密度掌握随机变量函数分布难点：随机变量函数的分布习题内容：求离散型随机变量的分布律求随机变量的分布函数求随机变量的函数的分布第03部分总学时8学时讲课 8学时实验0学时上机0学时标题：多维随机变量及其分布具体内容：二维随机变量（2学时）边缘分布（2学时）相互独立的随机变量（2学时）两个随机变量的函数的分布（2学时）重点：理解二维随机变量及其分布掌握二维随机变量联合分布及边缘分布掌握随机变量的相互独立性难点：两个随机变量的函数的分布习题内容：求二维离散型随机变量的联合分布及边缘分布求相互独立的随机变量所构成的二维随机变量的联合分布求两个随机变量的函数的分布第04部分总学时6学时讲课 6学时实验0学时上机0学时标题：随机变量的数字特征具体内容：数学期望（2学时）方差（2学时）几种重要随机变量的数学期望及方差协方差及相关系数（2学时）重点：理解随机变量的数学期望及方差概念，掌握随机变量及其函数的数学期望及方差的求法难点：随机变量函数的数学期望和方差习题内容：求随机变量的数学期望及方差求随机变量函数的数学期望和方差。

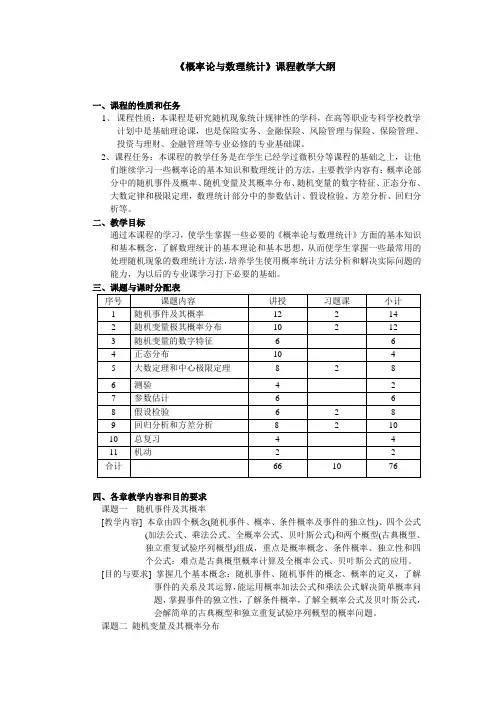
《概率论与数理统计》课程教学大纲一、课程的性质和任务1、课程性质：本课程是研究随机现象统计规律性的学科，在高等职业专科学校教学计划中是基础理论课，也是保险实务、金融保险、风险管理与保险、保险管理、投资与理财、金融管理等专业必修的专业基础课。

2、课程任务：本课程的教学任务是在学生已经学过微积分等课程的基础之上，让他们继续学习一些概率论的基本知识和数理统计的方法，主要教学内容有：概率论部分中的随机事件及概率、随机变量及其概率分布、随机变量的数字特征、正态分布、大数定律和极限定理，数理统计部分中的参数估计、假设检验、方差分析、回归分析等。

二、教学目标通过本课程的学习，使学生掌握一些必要的《概率论与数理统计》方面的基本知识和基本概念，了解数理统计的基本理论和基本思想，从而使学生掌握一些最常用的处理随机现象的数理统计方法，培养学生使用概率统计方法分析和解决实际问题的能力，为以后的专业课学习打下必要的基础。

四、各章教学内容和目的要求课题一随机事件及其概率[教学内容] 本章由四个概念(随机事件、概率、条件概率及事件的独立性)、四个公式(加法公式、乘法公式、全概率公式、贝叶斯公式)和两个概型(古典概型、独立重复试验序列概型)组成，重点是概率概念、条件概率、独立性和四个公式：难点是古典概型概率计算及全概率公式、贝叶斯公式的应用。

[目的与要求] 掌握几个基本概念：随机事件、随机事件的概念、概率的定义，了解事件的关系及其运算，能运用概率加法公式和乘法公式解决简单概率问题，掌握事件的独立性，了解条件概率，了解全概率公式及贝叶斯公式，会解简单的古典概型和独立重复试验序列概型的概率问题。

课题二随机变量及其概率分布[教学内容] 本章由两个概念(随机变量、概率分布)、两种类型(离散型随机变量，连续型随机变量)、五种分布(两点分布、二项分布、泊松分布、均匀分布、指数分布)等组成。

重点是随机变量的概念及两种类型随机变量的表示方法，二项分布、泊松分布和指数分布，难点是分布函数的概念及求法。

《高等概率论课程》教学大纲课程编号：Math1092课程名称：高等概率论英文名称：Advanced Probability Theory开课单位：数学科学学院开课学期：秋课内学时： 34教学方式：讲授适用专业及层次：统计学学术型硕士考核方式：考试预修课程：概率论、实变函数、分析学、代数学一、教学目标与要求《高等概率论》课程是统计学专业研究生的必修专业课程，也是应用性很强的一门数学课程．它是研究随机现象的数量规律的数学学科，以研究生课程分析学与代数学，本科生课程初等概率论与实变函数等为前期课程准备。

高等概率论课程重点给出集合、空间、测度、可测函数与积分的定义，以适合于概率需要的形式讲述了测度论的知识；给出概率、随机变量、随机向量、随机函数的概念，以及概率论研究中的所需的重要工具—常用的矩不等式和基本不等式；空间及其完备性；积分表现定理—Riesz定理；独立性的概念，独立扩张定理，复合定理和乘法定理。

重点是独立随机变量序列的零壹律，独立随机变量和的收敛性与稳定性，利用Borel-Cantelli引理、等价性引理等得到独立随机变量序列的二级数定理、三级数定理以及强大数定理。

通过本课程的教学，应使学生掌握高等概率论的基本概念，了解它的基本理论和方法，从而使学生掌握以测度论为基础的高等概率论的基础知识，为后续课程的学习、开展科学研究打下坚实的理论基础。

二、课程内容与学时分配导论（5学时）0．1 简单随机变量 0.2 Borel强大数律1．3 经验分布函数与格里定理第一章集合、空间与测度（12学时）1．1 序列的极限 1．2 域与-域1．3 单调类 1．4 乘机集合与截口1．5 函数与反函数 1．6 可测函数与可测函数第二章可测函数与积分（12学时）2．1 可测函数 2．2 测度的各种收敛性2．3 依测度收敛 2．4 积分与性质2．5 积分的收敛性定理 2．6 不定积分与累次积分2．7 Radon-Nikodym定理 2．6 无穷乘积概率空间第三章概率（12学时）3．1 概率空间与随机变量 3．2 随机向量、随机序列和随机函数3．3 矩不等式和各种收敛性 3．4 空间及其完备性3．5 积分表现定理—Riesz定理第四章独立随机变量和（13学时）4．1 独立性概念 4．2 独立扩张定理与复合定理4．3 乘法定理与等价性定理 4．4 Borel-Cantelli引理，Kolmogorov 0-1律4．5 独立随机变量和的收敛性与稳定性 4．6 二级数定理与三级数定理三、教材M. Loeve，《Probability Theory I》，4th edition, Springer-Verlag．主要参考书1．缪柏其, 概率论教程, 中国科学技术大学出版社, 1998．2．Y. S. Chow, H. Teicher, Probability Theory, 2nd edition, Springer-Verlag, New York, 1988. 3．Shiryayev A.N, Probability, Springer-Verlag, 1984．4．汪嘉冈, 现代概率论基础, 复旦大学出版社, 1988．5．严加安, 测度与积分, 陕西师范大学出版社, 1988.6．李贤平, 概率论基础, 第三版, 北京:高等教育出版社, 2011.。