下载文档原格式
遗传算法详解（含MATLAB代码）Python遗传算法框架使用实例（一）使用Geatpy实现句子匹配在前面几篇文章中，我们已经介绍了高性能Python遗传和进化算法框架——Geatpy的使用。
本篇就一个案例进行展开讲述：pip install geatpy更新至Geatpy2的方法：pip install --upgrade --user geatpy查看版本号，在Python中执行：import geatpyprint(geatpy.__version__)我们都听过“无限猴子定理”，说的是有无限只猴子用无限的时间会产生特定的文章。
在无限猴子定理中，我们“假定”猴子们是没有像人类那样“智能”的，而且“假定”猴子不会自我学习。
因此，这些猴子需要“无限的时间"。
而在遗传算法中，由于采用的是启发式的进化搜索，因此不需要”无限的时间“就可以完成类似的工作。
当然，需要产生的文章篇幅越长，那么就需要越久的时间才能完成。
下面以产生"T om is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much."的句子为例，讲述如何利用Geatpy实现句子的搜索。
之前的文章中我们已经讲述过如何使用Geatpy的进化算法框架实现遗传算法编程。
这里就直接用框架。
把自定义问题类和执行脚本编写在下面的"main.py”文件中：# -*- coding: utf-8 -*-import numpy as npimport geatpy as eaclass MyProblem(ea.Problem): # 继承Problem父类def __init__(self):name = 'MyProblem' # 初始化name（函数名称，可以随意设置） # 定义需要匹配的句子strs = 'Tom is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much.'self.words = []for c in strs:self.words.append(ord(c)) # 把字符串转成ASCII码M = 1 # 初始化M（目标维数）maxormins = [1] # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）Dim = len(self.words) # 初始化Dim（决策变量维数）varTypes = [1] * Dim # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）lb = [32] * Dim # 决策变量下界ub = [122] * Dim # 决策变量上界lbin = [1] * Dim # 决策变量下边界ubin = [1] * Dim # 决策变量上边界# 调用父类构造方法完成实例化ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)def aimFunc(self, pop): # 目标函数Vars = pop.Phen # 得到决策变量矩阵diff = np.sum((Vars - self.words)**2, 1)pop.ObjV = np.array([diff]).T # 把求得的目标函数值赋值给种群pop的ObjV执行脚本if __name__ == "__main__":"""================================实例化问题对象============================="""problem = MyProblem() # 生成问题对象"""==================================种群设置================================"""Encoding = 'RI' # 编码方式NIND = 50 # 种群规模Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器population = ea.Population(Encoding, Field, NIND) # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）"""================================算法参数设置=============================="""myAlgorithm = ea.soea_DE_rand_1_L_templet(problem, population) # 实例化一个算法模板对象myAlgorithm.MAXGEN = 2000 # 最大进化代数"""===========================调用算法模板进行种群进化========================="""[population, obj_trace, var_trace] = myAlgorithm.run() # 执行算法模板population.save() # 把最后一代种群的信息保存到文件中# 输出结果best_gen = np.argmin(obj_trace[:, 1]) # 记录最优种群是在哪一代best_ObjV = obj_trace[best_gen, 1]print('最优的目标函数值为：%s'%(best_ObjV))print('有效进化代数：%s'%(obj_trace.shape[0]))print('最优的一代是第 %s 代'%(best_gen + 1))print('评价次数：%s'%(myAlgorithm.evalsNum))print('时间已过 %s 秒'%(myAlgorithm.passTime))for num in var_trace[best_gen, :]:print(chr(int(num)), end = '')上述代码中首先定义了一个问题类MyProblem，然后调用Geatpy内置的soea_DE_rand_1_L_templet算法模板，它实现的是差分进化算法DE-rand-1-L，详见源码：运行结果如下：种群信息导出完毕。
实验六：遗传算法求解TSP问题实验3篇以下是关于遗传算法求解TSP问题的实验报告，分为三个部分，总计超过3000字。
一、实验背景与原理1.1 实验背景旅行商问题（Traveling Salesman Problem，TSP）是组合优化中的经典问题。
给定一组城市和每两个城市之间的距离，求解访问每个城市一次并返回出发城市的最短路径。
TSP 问题具有很高的研究价值，广泛应用于物流、交通运输、路径规划等领域。
1.2 遗传算法原理遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传机制的搜索算法。
它通过选择、交叉和变异操作生成新一代解，逐步优化问题的解。
遗传算法具有全局搜索能力强、适用于多种优化问题等优点。
二、实验设计与实现2.1 实验设计本实验使用遗传算法求解TSP问题，主要包括以下步骤：（1）初始化种群：随机生成一定数量的个体（路径），每个个体代表一条访问城市的路径。
（2）计算适应度：根据路径长度计算每个个体的适应度，适应度越高，路径越短。
（3）选择操作：根据适应度选择优秀的个体进入下一代。
（4）交叉操作：随机选择两个个体进行交叉，生成新的个体。
（5）变异操作：对交叉后的个体进行变异，增加解的多样性。
（6）更新种群：将新生成的个体替换掉上一代适应度较低的个体。
（7）迭代：重复步骤（2）至（6），直至满足终止条件。
2.2 实验实现本实验使用Python语言实现遗传算法求解TSP问题。
以下为实现过程中的关键代码：（1）初始化种群```pythondef initialize_population(city_num, population_size): population = []for _ in range(population_size):individual = list(range(city_num))random.shuffle(individual)population.append(individual)return population```（2）计算适应度```pythondef calculate_fitness(population, distance_matrix): fitness = []for individual in population:path_length =sum([distance_matrix[individual[i]][individual[i+1]] for i in range(len(individual) 1)])fitness.append(1 / path_length)return fitness```（3）选择操作```pythondef selection(population, fitness, population_size): selected_population = []fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]for _ in range(population_size):individual = random.choices(population, fitness_probability)[0]selected_population.append(individual)return selected_population```（4）交叉操作```pythondef crossover(parent1, parent2):index1 = random.randint(0, len(parent1) 2)index2 = random.randint(index1 + 1, len(parent1) 1)child1 = parent1[:index1] +parent2[index1:index2] + parent1[index2:]child2 = parent2[:index1] +parent1[index1:index2] + parent2[index2:]return child1, child2```（5）变异操作```pythondef mutation(individual, mutation_rate):for i in range(len(individual)):if random.random() < mutation_rate:j = random.randint(0, len(individual) 1) individual[i], individual[j] = individual[j], individual[i]return individual```（6）更新种群```pythondef update_population(parent_population, child_population, fitness):fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]new_population =random.choices(parent_population + child_population, fitness_probability, k=len(parent_population)) return new_population```（7）迭代```pythondef genetic_algorithm(city_num, population_size, crossover_rate, mutation_rate, max_iterations): distance_matrix =create_distance_matrix(city_num)population = initialize_population(city_num, population_size)for _ in range(max_iterations):fitness = calculate_fitness(population, distance_matrix)selected_population = selection(population, fitness, population_size)parent_population = []child_population = []for i in range(0, population_size, 2):parent1, parent2 = selected_population[i], selected_population[i+1]child1, child2 = crossover(parent1, parent2)child1 = mutation(child1, mutation_rate)child2 = mutation(child2, mutation_rate)parent_population.extend([parent1, parent2]) child_population.extend([child1, child2])population =update_population(parent_population, child_population, fitness)best_individual =population[fitness.index(max(fitness))]best_path_length =sum([distance_matrix[best_individual[i]][best_individual[i +1]] for i in range(len(best_individual) 1)])return best_individual, best_path_length```三、实验结果与分析3.1 实验结果本实验选取了10个城市进行测试，遗传算法参数设置如下：种群大小：50交叉率：0.8变异率：0.1最大迭代次数：100实验得到的最佳路径长度为：1953.53.2 实验分析（1）参数设置对算法性能的影响种群大小：种群大小会影响算法的搜索能力和收敛速度。
Matlab 中可以使用遗传算法工具箱（Genetic Algorithm Toolbox）来实现遗传算法。
该工具箱提供了许多参数可以用于调整算法的行为。
以下是一些常用的参数：1. `PopulationSize`：种群大小，即染色体数量。
通常设置为一个相对较大的数值，以保证算法的搜索能力和多样性。
2. `MaxGenerations`：最大迭代次数。
算法将根据指定的迭代次数进行搜索，直到达到最大迭代次数或找到满足条件的解。
3. `CrossoverFraction`：交叉概率。
在每一代中，根据交叉概率对染色体进行交叉操作，以产生新的染色体。
4. `MutationFcn`：变异函数。
该函数将应用于染色体上的基因，以增加种群的多样性。
5. `Elitism`：精英策略。
该参数决定是否保留最佳个体，以避免算法陷入局部最优解。
6. `PopulationType`：种群类型。
可以选择二进制、实数或整数类型。
7. `ObjectiveFunction`：目标函数。
该函数将用于评估染色体的适应度，以确定哪些染色体更有可能产生优秀的后代。
8. `Variableargin`：变量参数。
可以将需要优化的变量作为参数传递给目标函数和变异函数。
9. `Display`：显示设置。
可以选择在算法运行过程中显示哪些信息，例如每个迭代的最佳个体、平均适应度等等。
以上是一些常用的参数，可以根据具体问题进行调整。
在Matlab 中使用遗传算法时，建议仔细阅读相关文档和示例代码，以便更好地理解算法的实现细节和如何调整参数来获得更好的结果。
1 遗传算法的原理1.1 遗传算法的基本思想遗传算法（genetic algorithms，GA）是一种基于自然选择和基因遗传学原理，借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。
遗传算法是从一组随机产生的初始解（种群）开始，这个种群由经过基因编码的一定数量的个体组成，每个个体实际上是染色体带有特征的实体。
染色体作为遗传物质的主要载体，其内部表现（即基因型）是某种基因组合，它决定了个体的外部表现。
因此，从一开始就需要实现从表现型到基因型的映射，即编码工作。
初始种群产生后，按照优胜劣汰的原理，逐代演化产生出越来越好的近似解。
在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样，后代种群比前代更加适应环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。
计算开始时，将实际问题的变量进行编码形成染色体，随机产生一定数目的个体，即种群，并计算每个个体的适应度值，然后通过终止条件判断该初始解是否是最优解，若是则停止计算输出结果，若不是则通过遗传算子操作产生新的一代种群，回到计算群体中每个个体的适应度值的部分，然后转到终止条件判断。
这一过程循环执行，直到满足优化准则，最终产生问题的最优解。
图1-1给出了遗传算法的基本过程。
1.2 遗传算法的特点1.2.1 遗传算法的优点遗传算法具有十分强的鲁棒性，比起传统优化方法，遗传算法有如下优点：1. 遗传算法以控制变量的编码作为运算对象。
传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算，但遗传算法不是直接以控制变量的值，而是以控制变量的特定形式的编码为运算对象。
这种对控制变量的编码处理方式，可以模仿自然界中生物的遗传和进化等机理，也使得我们可以方便地处理各种变量和应用遗传操作算子。
2. 遗传算法具有内在的本质并行性。
应用MATLAB+yalmip+Gurobi求解TSP问题环境：MATLAB;附加环境：请确认已安装yalmip和Gurobi;说明：如果只安装了yalmip也可以，只是需要将程序中的ops = sdpsettings('solver','gurobi');sol=solvesdp(F,g,ops);两句，直接改为sol=solvesdp(F,g);这样就是默认求解solver为yalmip。
另外：这个简单的程序里面有三个例子，1--随机例子，2--31个省会城市，3--北京高校联合采购与配送--的配送部分例子。
这里默认的是第三个例子，因为是自己博士论文的一小部分。
15所高校之间的距离是应用百度地图的直线距离。
本里的数据可以搜索下载’北京15所高校的路程数据.xlsx’,(/view/ab8c20c1bb68a98270fefa39 )，北京15所高校的路程数据记得放在与本程序相同的路径下，简单地说，同一个文件夹下就行。
%清空环境clcclearN=16;%问题规模X=binvar(N,N,'full'); %最终路径决定矩阵U=intvar(N-1,1,'full');%用于子回路约束%% 例子1：下面是一个随机产生的例子% a = rand(N,N);% b = tril(a,-1)+triu(a',0);% for i=1:N% for j=1:N% if i==j% b(i,j)=0;% end% end% end% b=100*b;%% 例子2：31个省会城市的坐标% A=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;41961004;% 4312 790;4386 570;3007 1970;2562 1756;2788 1491;2381 1676;1332 695;3715 1678;% 3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2367; % 3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975];% for i=1:N% for j=1:N% if i==j% D(i,j)=0;% else% D(i,j)=sqrt((A(i,1)-A(j,1))^2+(A(i,2)-A(j,2))^2);% end% end% end%% 例子3：北京15所高校食堂物资采购配送C=xlsread('北京15所高校的路程数据.xlsx','B3:R18');F1=[sum(X)==1];%节点进入一次F2=[sum(X')==1];%节点离开一次F3=[];%节点去除自循环for i=1:NF3=[F3;X(i,i)==0];endF4=[];for i=2:Nfor j=2:Nif i~=jF4=[F4;U(i-1)-U(j-1)+1<=N*(1-X(i,j))];endendendF=[F1;F2;F3;F4];g=sum(sum(C.*X));ops = sdpsettings('solver','gurobi');sol=solvesdp(F,g,ops);X=double(X);U=double(U);disp('X');disp(X);disp('目标函数');disp(sum(sum(C.*X)))i=1;NUM=0;PATH=1;while NUM<N-1for j=1:Nif X(i,j)==1i=j;NUM=NUM+1;PATH(NUM+1)=j;endendend%% 完整路径disp(' ');disp(' ');disp(' ');disp(' ')disp('最终路径:')disp(PATH);disp('其中1--北京大学,2--清华大学, 3--北京师范大学, 4--北京科技大学, 5--北京理工大学'); disp('6--北京航空航天大学, 7--北京交通大学, 8--北京工业大学, 9--中国矿业大学（北京）,10--北京林业大学, ')disp('11--北方工业大学,12--首都师范大学, 13--华北电力大学, 14--中国人民大学,15--北京化工大学, 16--北京新发地仓储中心')disp(' ');disp(' ');316 Laboratory, School of management, HUST2016/1/4。
用遗传算法求解TSP问题遗传算法（Genetic Algorithm——GA），是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，它是由美国Michigan大学的J。
Holland教授于1975年首先提出的。
J.Holland 教授和它的研究小组围绕遗传算法进行研究的宗旨有两个：抽取和解释自然系统的自适应过程以及设计具有自然系统机理的人工系统。
遗传算法的大致过程是这样的:将每个可能的解看作是群体中的一个个体或染色体，并将每个个体编码成字符串的形式，根据预定的目标函数对每个个体进行评价,即给出一个适应度值。
开始时,总是随机的产生一些个体，根据这些个体的适应度，利用遗传算子-—选择（Selection）、交叉（Crossover)、变异（Mutation)对它们重新组合，得到一群新的个体.这一群新的个体由于继承了上一代的一些优良特性，明显优于上一代，以逐步向着更优解的方向进化.遗传算法主要的特点在于：简单、通用、鲁棒性强。
经过二十多年的发展，遗传算法已经在旅行商问题、生产调度、函数优化、机器学习等领域得到成功的应用。
遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法，与传统的优化算法相比,主要有以下特点：1、遗传算法以决策变量的编码作为运算对象.传统的优化算法往往直接决策变量的实际植本身,而遗传算法处理决策变量的某种编码形式，使得我们可以借鉴生物学中的染色体和基因的概念，可以模仿自然界生物的遗传和进化机理，也使得我们能够方便的应用遗传操作算子.2、遗传算法直接以适应度作为搜索信息，无需导数等其它辅助信息。
3、遗传算法使用多个点的搜索信息,具有隐含并行性。
4、遗传算法使用概率搜索技术，而非确定性规则。
遗传算法是基于生物学的,理解或编程都不太难。
下面是遗传算法的一般算法步骤:1、创建一个随机的初始状态初始种群是从解中随机选择出来的，将这些解比喻为染色体或基因，该种群被称为第一代，这和符号人工智能系统的情况不一样;在那里,问题的初始状态已经给定了。
matlab实用教程实验十遗传算法与优化问题matlab实用教程实验十遗传算法与优化问题一、问题背景与实验目的二、相关函数（命令）及简介三、实验内容四、自己动手一、问题背景与实验目的遗传算法（Genetic Algorithm—GA），是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，它是由美国Michigan大学的J.Holland教授于1975年首先提出的．遗传算法作为一种新的全局优化搜索算法，以其简单通用、鲁棒性强、适于并行处理及应用范围广等显著特点，奠定了它作为21世纪关键智能计算之一的地位．本实验将首先介绍一下遗传算法的基本理论，然后用其解决几个简单的函数最值问题，使读者能够学会利用遗传算法进行初步的优化计算．1．遗传算法的基本原理遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程．它把问题的参数用基因代表，把问题的解用染色体代表（在计算机里用二进制码表示），从而得到一个由具有不同染色体的个体组成的群体．这个群体在问题特定的环境里生存竞争，适者有最好的机会生存和产生后代．后代随机化地继承了父代的最好特征，并也在生存环境的控制支配下继续这一过程．群体的染色体都将逐渐适应环境，不断进化，最后收敛到一族最适应环境的类似个体，即得到问题最优的解．值得注意的一点是，现在的遗传算法是受生物进化论学说的启发提出的，这种学说对我们用计算机解决复杂问题很有用，而它本身是否完全正确并不重要（目前生物界对此学说尚有争议）．（1）遗传算法中的生物遗传学概念由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法；故而在这个算法中要用到各种进化和遗传学的概念．首先给出遗传学概念、遗传算法概念和相应的数学概念三者之间的对应关系．这些概念如下：序号遗传学概念遗传算法概念数学概念1个体要处理的基本对象、结构也就是可行解2群体个体的集合被选定的一组可行解3染色体个体的表现形式可行解的编码4基因染色体中的元素编码中的元素5基因位某一基因在染色体中的位置元素在编码中的位置6适应值个体对于环境的适应程度，或在环境压力下的生存能力可行解所对应的适应函数值7种群被选定的一组染色体或个体根据入选概率定出的一组可行解8选择从群体中选择优胜的个体，淘汰劣质个体的操作保留或复制适应值大的可行解，去掉小的可行解9交叉一组染色体上对应基因段的交换根据交叉原则产生的一组新解10交叉概率染色体对应基因段交换的概率（可能性大小）闭区间[0,1]上的一个值，一般为0.65~0.9011变异染色体水平上基因变化编码的某些元素被改变12变异概率染色体上基因变化的概率（可能性大小）开区间(0,1)内的一个值, 一般为0.001~0.0113进化、适者生存个体进行优胜劣汰的进化，一代又一代地优化目标函数取到最大值，最优的可行解（2）遗传算法的步骤遗传算法计算优化的操作过程就如同生物学上生物遗传进化的过程，主要有三个基本操作（或称为算子）：选择（Selection）、交叉（Crossover）、变异（Mutation）．遗传算法基本步骤主要是：先把问题的解表示成“染色体”，在算法中也就是以二进制编码的串，在执行遗传算法之前，给出一群“染色体”，也就是假设的可行解．然后，把这些假设的可行解置于问题的“环境”中，并按适者生存的原则，从中选择出较适应环境的“染色体”进行复制，再通过交叉、变异过程产生更适应环境的新一代“染色体”群．经过这样的一代一代地进化，最后就会收敛到最适应环境的一个“染色体”上，它就是问题的最优解．下面给出遗传算法的具体步骤，流程图参见图1：第一步：选择编码策略，把参数集合（可行解集合）转换染色体结构空间；第二步：定义适应函数，便于计算适应值；第三步：确定遗传策略，包括选择群体大小，选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数；第四步：随机产生初始化群体；第五步：计算群体中的个体或染色体解码后的适应值；第六步：按照遗传策略，运用选择、交叉和变异算子作用于群体，形成下一代群体；第七步：判断群体性能是否满足某一指标、或者是否已完成预定的迭代次数，不满足则返回第五步、或者修改遗传策略再返回第六步．图1 一个遗传算法的具体步骤遗传算法有很多种具体的不同实现过程，以上介绍的是标准遗传算法的主要步骤，此算法会一直运行直到找到满足条件的最优解为止．2．遗传算法的实际应用例1：设，求．注：这是一个非常简单的二次函数求极值的问题，相信大家都会做．在此我们要研究的不是问题本身，而是借此来说明如何通过遗传算法分析和解决问题．在此将细化地给出遗传算法的整个过程．（1）编码和产生初始群体首先第一步要确定编码的策略，也就是说如何把到2这个区间内的数用计算机语言表示出来．编码就是表现型到基因型的映射，编码时要注意以下三个原则：完备性：问题空间中所有点（潜在解）都能成为GA编码空间中的点（染色体位串）的表现型；健全性：GA编码空间中的染色体位串必须对应问题空间中的某一潜在解；非冗余性：染色体和潜在解必须一一对应．这里我们通过采用二进制的形式来解决编码问题，将某个变量值代表的个体表示为一个{0，1}二进制串．当然，串长取决于求解的精度．如果要设定求解精度到六位小数，由于区间长度为，则必须将闭区间分为等分．因为所以编码的二进制串至少需要22位．将一个二进制串（b21b20b19…b1b0）转化为区间内对应的实数值很简单，只需采取以下两步（Matlab程序参见附录4）：1）将一个二进制串（b21b20b19…b1b0）代表的二进制数化为10进制数：2）对应的区间内的实数：例如，一个二进制串a=<1000101110110101000111>表示实数0.637197．=(1000101110110101000111)2=2288967二进制串<0000000000000000000000>，<1111111111111111111111>，则分别表示区间的两个端点值-1和2．利用这种方法我们就完成了遗传算法的第一步——编码，这种二进制编码的方法完全符合上述的编码的三个原则．首先我们来随机的产生一个个体数为4个的初始群体如下：pop(1)={<1101011101001100011110>，%% a1<1000011001010001000010>，%% a2<0001100111010110000000>，%% a3<0110101001101110010101>} %% a4（Matlab程序参见附录2）化成十进制的数分别为：pop(1)={ 1.523032，0.574022 ，-0.697235 ，0.247238 }接下来我们就要解决每个染色体个体的适应值问题了．（2）定义适应函数和适应值由于给定的目标函数在内的值有正有负，所以必须通过建立适应函数与目标函数的映射关系，保证映射后的适应值非负，而且目标函数的优化方向应对应于适应值增大的方向，也为以后计算各个体的入选概率打下基础．对于本题中的最大化问题，定义适应函数，采用下述方法：式中既可以是特定的输入值，也可以是当前所有代或最近K代中的最小值，这里为了便于计算，将采用了一个特定的输入值．若取，则当时适应函数；当时适应函数．由上述所随机产生的初始群体，我们可以先计算出目标函数值分别如下（Matlab程序参见附录3）：f [pop(1)]={ 1.226437 , 1.318543 , -1.380607 , 0.933350 }然后通过适应函数计算出适应值分别如下（Matlab程序参见附录5、附录6）：取，g[pop(1)]= { 2.226437 , 2.318543 , 0 , 1.933350 }（3）确定选择标准这里我们用到了适应值的比例来作为选择的标准，得到的每个个体的适应值比例叫作入选概率．其计算公式如下：对于给定的规模为n的群体pop={}，个体的适应值为，则其入选概率为由上述给出的群体，我们可以计算出各个个体的入选概率．首先可得，然后分别用四个个体的适应值去除以，得：P(a1)=2.226437 / 6.478330 = 0.343675 %% a1P(a2)=2.318543 / 6.478330 = 0.357892 %% a2P(a3)= 0 / 6.478330 = 0 %% a3P(a4)=1.933350 / 6.478330 = 0.298433 %% a4（Matlab程序参见附录7）（4）产生种群计算完了入选概率后，就将入选概率大的个体选入种群，淘汰概率小的个体，并用入选概率最大的个体补入种群，得到与原群体大小同样的种群（Matlab程序参见附录8、附录11）．要说明的是：附录11的算法与这里不完全相同．为保证收敛性，附录11的算法作了修正，采用了最佳个体保存方法（elitist model），具体内容将在后面给出介绍．由初始群体的入选概率我们淘汰掉a3，再加入a2补足成与群体同样大小的种群得到newpop(1)如下：newpop(1)={<1101011101001100011110>，%% a1<1000011001010001000010>，%% a2<1000011001010001000010>，%% a2<0110101001101110010101>} %% a4（5）交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体，然后得到新的染色体组，组成新的群体（Matlab程序参见附录9）．我们把之前得到的newpop(1)的四个个体两两组成一对，重复的不配对，进行交叉．（可以在任一位进行交叉）<110101110 1001100011110>，<1101011101010001000010>交叉得：<100001100 1010001000010>，<1000011001001100011110><10000110010100 01000010>，<1000011001010010010101>交叉得：<01101010011011 10010101>，<0110101001101101000010>通过交叉得到了四个新个体，得到新的群体jchpop (1)如下：jchpop(1)={<1101011101010001000010>，<1000011001001100011110>，<1000011001010010010101>，<0110101001101101000010>}这里采用的是单点交叉的方法，当然还有多点交叉的方法，不过有些烦琐，这里就不着重介绍了．（6）变异变异也就是通过一个小概率改变染色体位串上的某个基因（Matlab程序参见附录10）．现把刚得到的jchpop(1)中第3个个体中的第9位改变，就产生了变异，得到了新的群体pop(2)如下：pop(2)= {<1101011101010001000010>，<1000011001001100011110>，<1000011011010010010101>，<0110101001101101000010> }然后重复上述的选择、交叉、变异直到满足终止条件为止．（7）终止条件遗传算法的终止条件有两类常见条件：（1）采用设定最大（遗传）代数的方法，一般可设定为50代，此时就可能得出最优解．此种方法简单易行，但可能不是很精确（Matlab程序参见附录1）；（2）根据个体的差异来判断，通过计算种群中基因多样性测度，即所有基因位相似程度来进行控制．3．遗传算法的收敛性前面我们已经就遗传算法中的编码、适应度函数、选择、交叉和变异等主要操作的基本内容及设计进行了详细的介绍．作为一种搜索算法，遗传算法通过对这些操作的适当设计和运行，可以实现兼顾全局搜索和局部搜索的所谓均衡搜索，具体实现见下图2所示．图2 均衡搜索的具体实现图示应该指出的是，遗传算法虽然可以实现均衡的搜索，并且在许多复杂问题的求解中往往能得到满意的结果，但是该算法的全局优化收敛性的理论分析尚待解决．目前普遍认为，标准遗传算法并不保证全局最优收敛．但是，在一定的约束条件下，遗传算法可以实现这一点．下面我们不加证明地罗列几个定理或定义，供读者参考（在这些定理的证明中，要用到许多概率论知识，特别是有关马尔可夫链的理论，读者可参阅有关文献）．定理1 如果变异概率为，交叉概率为，同时采用比例选择法（按个体适应度占群体适应度的比例进行复制），则标准遗传算法的变换矩阵P是基本的．定理2 标准遗传算法（参数如定理1）不能收敛至全局最优解．由定理2可以知道，具有变异概率，交叉概率为以及按比例选择的标准遗传算法是不能收敛至全局最最优解．我们在前面求解例1时所用的方法就是满足定理1的条件的方法．这无疑是一个令人沮丧的结论．然而，庆幸的是，只要对标准遗传算法作一些改进，就能够保证其收敛性．具体如下：我们对标准遗传算法作一定改进，即不按比例进行选择，而是保留当前所得的最优解（称作超个体）．该超个体不参与遗传．最佳个体保存方法（elitist model）的思想是把群体中适应度最高的个体不进行配对交叉而直接复制到下一代中．此种选择操作又称复制（copy）．De Jong对此方法作了如下定义：定义设到时刻t（第t代）时，群体中a*（t）为最佳个体．又设A（t＋1）为新一代群体，若A（t＋1）中不存在a*（t），则把a*(t)作为A（t＋1）中的第n+1个个体（其中，n为群体大小）（Matlab程序参见附录11）．采用此选择方法的优点是，进化过程中某一代的最优解可不被交叉和变异操作所破坏．但是，这也隐含了一种危机，即局部最优个体的遗传基因会急速增加而使进化有可能限于局部解．也就是说，该方法的全局搜索能力差，它更适合单峰性质的搜索空间搜索，而不是多峰性质的空间搜索．所以此方法一般都与其他选择方法结合使用．定理3 具有定理1所示参数，且在选择后保留当前最优值的遗传算法最终能收敛到全局最优解．当然，在选择算子作用后保留当前最优解是一项比较复杂的工作，因为该解在选择算子作用后可能丢失．但是定理3至少表明了这种改进的遗传算法能够收敛至全局最优解．有意思的是，实际上只要在选择前保留当前最优解，就可以保证收敛，定理4描述了这种情况．定理4 具有定理1参数的，且在选择前保留当前最优解的遗传算法可收敛于全局最优解．例2：设，求，编码长度为5，采用上述定理4所述的“在选择前保留当前最优解的遗传算法”进行二、相关函数（命令）及简介本实验的程序中用到如下一些基本的Matlab函数：ones, zeros, sum, size, length, subs, double 等，以及for, while 等基本程序结构语句，读者可参考前面专门关于Matlab的介绍，也可参考其他数学实验章节中的“相关函数（命令）及简介”内容，此略．三、实验内容上述例1的求解过程为：群体中包含六个染色体，每个染色体用22位0—1码，变异概率为0.01，变量区间为，取Fmin=，遗传代数为50代，则运用第一种终止条件（指定遗传代数）的Matlab程序为：[Count,Result,BestMember]=Genetic1(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,50)执行结果为：Count =50Result =1.0316 1.0316 1.0316 1.0316 1.0316 1.03161.4990 1.4990 1.4990 1.4990 1.4990 1.4990BestMember =1.03161.4990图2 例1的计算结果（注：上图为遗传进化过程中每一代的个体最大适应度；而下图为目前为止的个体最大适应度——单调递增）我们通过Matlab软件实现了遗传算法，得到了这题在第一种终止条件下的最优解：当取1.0316时，．当然这个解和实际情况还有一点出入（应该是取1时，），但对于一个计算机算法来说已经很不错了．我们也可以编制Matlab程序求在第二种终止条件下的最优解．此略，留作练习．实践表明，此时的遗传算法只要经过10代左右就可完成收敛，得到另一个“最优解”，与前面的最优解相差无几．四、自己动手1．用Matlab编制另一个主程序Genetic2.m，求例1的在第二种终止条件下的最优解．提示：一个可能的函数调用形式以及相应的结果为：[Count,Result,BestMember]=Genetic2(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,0.00001)Count =13Result =1.0392 1.0392 1.0392 1.0392 1.0392 1.03921.4985 1.4985 1.4985 1.4985 1.4985 1.4985BestMember =1.03921.4985可以看到：两组解都已经很接近实际结果，对于两种方法所产生的最优解差异很小．可见这两种终止算法都是可行的，而且可以知道对于例1的问题，遗传算法只要经过10代左右就可以完成收敛，达到一个最优解．2．按照例2的具体要求，用遗传算法求上述例2的最优解．3．附录9子程序Crossing.m中的第3行到第7行为注解语句．若去掉前面的%号，则程序的算法思想有什么变化？4．附录9子程序Crossing.m中的第8行至第13行的程序表明，当Dim(1)>=3时，将交换数组Population的最后两行，即交换最后面的两个个体．其目的是什么？5．仿照附录10子程序Mutation.m，修改附录9子程序Crossing.m，使得交叉过程也有一个概率值（一般取0.65~0.90）；同时适当修改主程序Genetic1.m或主程序Genetic2.m，以便代入交叉概率．6．设，求，要设定求解精度到15位小数．。
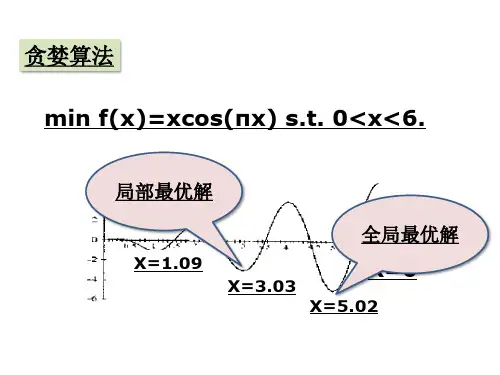
1、遗传算法介绍遗传算法，模拟达尔文进化论的自然选择和遗产学机理的生物进化构成的计算模型，一种不断选择优良个体的算法。
谈到遗传，想想自然界动物遗传是怎么来的，自然主要过程包括染色体的选择，交叉，变异（不明白这个的可以去看看生物学），这些操作后，保证了以后的个基本上是最优的，那么以后再继续这样下去，就可以一直最优了。
2、解决的问题先说说自己要解决的问题吧，遗传算法很有名，自然能解决的问题很多了，在原理上不变的情况下，只要改变模型的应用环境和形式，基本上都可以。
但是遗传算法主要还是解决优化类问题，尤其是那种不能直接解出来的很复杂的问题，而实际情况通常也是这样的。
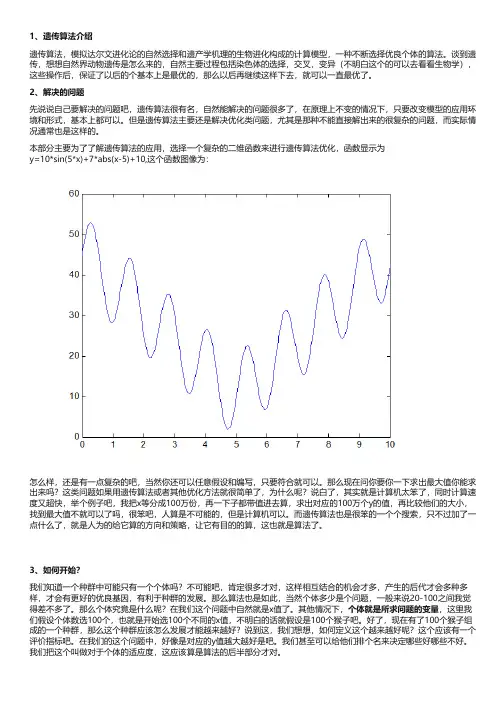
本部分主要为了了解遗传算法的应用，选择一个复杂的二维函数来进行遗传算法优化，函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为：怎么样，还是有一点复杂的吧，当然你还可以任意假设和编写，只要符合就可以。
那么现在问你要你一下求出最大值你能求出来吗？这类问题如果用遗传算法或者其他优化方法就很简单了，为什么呢？说白了，其实就是计算机太笨了，同时计算速度又超快，举个例子吧，我把x等分成100万份，再一下子都带值进去算，求出对应的100万个y的值，再比较他们的大小，找到最大值不就可以了吗，很笨吧，人算是不可能的，但是计算机可以。
而遗传算法也是很笨的一个个搜索，只不过加了一点什么了，就是人为的给它算的方向和策略，让它有目的的算，这也就是算法了。
3、如何开始？我们知道一个种群中可能只有一个个体吗？不可能吧，肯定很多才对，这样相互结合的机会才多，产生的后代才会多种多样，才会有更好的优良基因，有利于种群的发展。
那么算法也是如此，当然个体多少是个问题，一般来说20-100之间我觉得差不多了。
那么个体究竟是什么呢？在我们这个问题中自然就是x值了。
其他情况下，个体就是所求问题的变量，这里我们假设个体数选100个，也就是开始选100个不同的x值，不明白的话就假设是100个猴子吧。
1.遗传算法解决TSP 问题（附matlab源程序）2.知n个城市之间的相互距离，现有一个推销员必须遍访这n个城市，并且每个城市3.只能访问一次，最后又必须返回出发城市。
如何安排他对这些城市的访问次序，可使其4.旅行路线的总长度最短？5.用图论的术语来说，假设有一个图g=(v,e)，其中v是顶点集，e是边集，设d=(dij)6.是由顶点i和顶点j之间的距离所组成的距离矩阵，旅行商问题就是求出一条通过所有顶7.点且每个顶点只通过一次的具有最短距离的回路。
8.这个问题可分为对称旅行商问题(dij=dji,,任意i,j=1,2,3，…,n)和非对称旅行商9.问题(dij≠dji,,任意i,j=1,2,3，…,n)。
10.若对于城市v={v1,v2,v3,…,vn}的一个访问顺序为t=(t1,t2,t3,…,ti,…,tn),其中11.ti∈v(i=1,2,3,…,n)，且记tn+1= t1，则旅行商问题的数学模型为：12.min l=σd(t(i),t(i+1)) （i=1,…,n）13.旅行商问题是一个典型的组合优化问题，并且是一个np难问题，其可能的路径数目14.与城市数目n是成指数型增长的，所以一般很难精确地求出其最优解，本文采用遗传算法15.求其近似解。
16.遗传算法：17.初始化过程：用v1,v2,v3,…,vn代表所选n个城市。
定义整数pop-size作为染色体的个数18.，并且随机产生pop-size个初始染色体，每个染色体为1到18的整数组成的随机序列。
19.适应度f的计算：对种群中的每个染色体vi，计算其适应度，f=σd(t(i),t(i+1)).20.评价函数eval(vi)：用来对种群中的每个染色体vi设定一个概率，以使该染色体被选中21.的可能性与其种群中其它染色体的适应性成比例，既通过轮盘赌，适应性强的染色体被22.选择产生后台的机会要大，设alpha∈(0,1)，本文定义基于序的评价函数为eval(vi)=al23.pha*(1-alpha).^(i-1) 。
[随机规划与模糊规划]24.选择过程：选择过程是以旋转赌轮pop-size次为基础，每次旋转都为新的种群选择一个25.染色体。
赌轮是按每个染色体的适应度进行选择染色体的。
26.step1 、对每个染色体vi,计算累计概率qi，q0=0;qi=σeval(vj) j=1,…,i;i=1,27.…pop-size.28.step2、从区间(0,pop-size)中产生一个随机数r；29.step3、若qi-1 step4、重复step2和step3共pop-size次，这样可以得到pop-size个复制的染色体。
30.grefenstette编码：由于常规的交叉运算和变异运算会使种群中产生一些无实际意义的31.染色体，本文采用grefenstette编码《遗传算法原理及应用》可以避免这种情况的出现32.。
所谓的grefenstette编码就是用所选队员在未选（不含淘汰）队员中的位置，如：33.8 15 2 16 10 7 4 3 11 14 6 12 9 5 18 13 17 134.对应：35.8 14 2 13 8 6 3 2 5 7 3 4 3 2 4 2 2 1。
36.交叉过程：本文采用常规单点交叉。
为确定交叉操作的父代，从到pop-size重复以下过37.程：从[0，1]中产生一个随机数r，如果r 将所选的父代两两组队，随机产生一个位置进行交叉，如：38.8 14 2 13 8 6 3 2 5 7 3 4 3 2 4 2 2 139. 6 12 3 5 6 8 5 6 3 1 8 5 6 3 3 2 1 140.交叉后为：41.8 14 2 13 8 6 3 2 5 1 8 5 6 3 3 2 1 142. 6 12 3 5 6 8 5 6 3 7 3 4 3 2 4 2 2 143.变异过程：本文采用均匀多点变异。
类似交叉操作中选择父代的过程，在r 选择多个染色体vi作为父代。
对每一个选择的父代，随机选择多个位置，使其在每位置44.按均匀变异（该变异点xk的取值范围为[ukmin,ukmax],产生一个[0，1]中随机数r，该点45.变异为x'k=ukmin+r(ukmax-ukmin)）操作。
如：46.8 14 2 13 8 6 3 2 5 7 3 4 3 2 4 2 2 147.变异后：48.8 14 2 13 10 6 3 2 2 7 3 4 5 2 4 1 2 149.反grefenstette编码：交叉和变异都是在grefenstette编码之后进行的，为了循环操作50.和返回最终结果，必须逆grefenstette编码过程，将编码恢复到自然编码。
51.循环操作：判断是否满足设定的带数xzome，否，则跳入适应度f的计算；是，结束遗传52.操作，跳出。
53.54.55.56.matlab 代码57.58.59.60.distTSP.txt61.0 6 18 4 862.7 0 17 3 763. 4 4 0 4 564.20 19 24 0 2265.8 8 16 6 066.%GATSP.m67.function gatsp1()68.clear;69.load distTSP.txt;70.distance=distTSP;71.N=5;72.ngen=100;73.ngpool=10;74.%ngen=input('# of generations to evolve = ');75.%ngpool=input('# of chromosoms in the gene pool = '); % size of genepool76.gpool=zeros(ngpool,N+1); % gene pool77.for i=1:ngpool, % intialize gene pool78.gpool(i,:)=[1 randomize([2:N]')' 1];79.for j=1:i-180.while gpool(i,:)==gpool(j,:)81.gpool(i,:)=[1 randomize([2:N]')' 1];82.end83.end84.end85.86.costmin=100000;87.tourmin=zeros(1,N);88.cost=zeros(1,ngpool);89.increase=1;resultincrease=1;90.for i=1:ngpool,91.cost(i)=sum(diag(distance(gpool(i,:)',rshift(gpool(i,:))')));92.end93.% record current best solution94.[costmin,idx]=min(cost);95.tourmin=gpool(idx,:);96.disp([num2str(increase) 'minmum trip length = ' num2str(costmin)])97.98.costminold2=200000;costminold1=150000;resultcost=100000;99.tourminold2=zeros(1,N);100.tourminold1=zeros(1,N);101.resulttour=zeros(1,N);102.while (abs(costminold2-costminold1) ;100)&(abs(costminold1-costmin) ;100)&(increase ;500) 103.104.costminold2=costminold1; tourminold2=tourminold1;105.costminold1=costmin;tourminold1=tourmin;106.increase=increase+1;107.if resultcost>costmin108.resultcost=costmin;109.resulttour=tourmin;110.resultincrease=increase-1;111.end112.for i=1:ngpool,113.cost(i)=sum(diag(distance(gpool(i,:)',rshift(gpool(i,:))')));114.end115.% record current best solution116.[costmin,idx]=min(cost);117.tourmin=gpool(idx,:);118.%==============119.% copy gens in th gpool according to the probility ratio120.% >1.1 copy twice121.% >=0.9 copy once122.% ;0.9 remove123.[csort,ridx]=sort(cost);124.% sort from small to big.125.csum=sum(csort);126.caverage=csum/ngpool;127.cprobilities=caverage./csort;128.copynumbers=0;removenumbers=0;129.for i=1:ngpool,130.if cprobilities(i) >1.1131.copynumbers=copynumbers+1;132.end133.if cprobilities(i) <0.9134.removenumbers=removenumbers+1;135.end136.end137.copygpool=min(copynumbers,removenumbers);138.for i=1:copygpool139.for j=ngpool:-1:2*i+2 gpool(j,:)=gpool(j-1,:);140.end141.gpool(2*i+1,:)=gpool(i,:);142.end143.if copygpool==0144.gpool(ngpool,:)=gpool(1,:);145.end146.%=========147.%when genaration is more than 50,or the patterns in a couple are too close,do mutation 148.for i=1:ngpool/2149.%150.sameidx=[gpool(2*i-1,:)==gpool(2*i,:)];151.diffidx=find(sameidx==0);152.if length(diffidx)<=2153.gpool(2*i,:)=[1 randomize([2:12]')' 1];154.end155.end156.%===========157.%cross gens in couples158.for i=1:ngpool/2159.[gpool(2*i-1,:),gpool(2*i,:)]=crossgens(gpool(2*i-1,:),gpool(2*i,:));160.end161.162.for i=1:ngpool,163.cost(i)=sum(diag(distance(gpool(i,:)',rshift(gpool(i,:))')));164.end165.% record current best solution166.[costmin,idx]=min(cost);167.tourmin=gpool(idx,:);168.disp([num2str(increase) 'minmum trip length = ' num2str(costmin)])169.end170.171.disp(['cost function evaluation: ' int2str(increase) ' times!'])172.disp(['n:' int2str(resultincrease)])173.disp(['minmum trip length = ' num2str(resultcost)])174.disp('optimum tour = ')175.disp(num2str(resulttour))176.%====================================================177.function B=randomize(A,rowcol)178.% Usage: B=randomize(A,rowcol)179.% randomize row orders or column orders of A matrix180.% rowcol: if =0 or omitted, row order (default)181.% if = 1, column order182.183.rand('state',sum(100*clock))184.if nargin == 1,185.rowcol=0;186.end187.if rowcol==0,188.[m,n]=size(A);189.p=rand(m,1);190.[p1,I]=sort(p);191.B=A(I,:);192.elseif rowcol==1,193.Ap=A';194.[m,n]=size(Ap);195.p=rand(m,1);196.[p1,I]=sort(p);197.B=Ap(I,:)';198.end199.%===================================================== 200.function y=rshift(x,dir)201.% Usage: y=rshift(x,dir)202.% rotate x vector to right (down) by 1 if dir = 0 (default) 203.% or rotate x to left (up) by 1 if dir = 1204.if nargin ;2, dir=0; end205.[m,n]=size(x);206.if m>1,207.if n == 1,208.col=1;209.elseif n>1,210.error('x must be a vector! break');211.end % x is a column vectorelseif m == 1,212.if n == 1, y=x;213.return214.elseif n>1,215.col=0; % x is a row vector endend216.if dir==1, % rotate left or up217.if col==0, % row vector, rotate left218.y = [x(2:n) x(1)];219.elseif col==1,220.y = [x(2:n); x(1)]; % rotate up221.end222.elseif dir==0, % default rotate right or down223.if col==0,224.y = [x(n) x(1:n-1)];225.elseif col==1 % column vector226.y = [x(n); x(1:n-1)];227.end228.end229.%==================================================230.function [L1,L2]=crossgens(X1,X2)231.% Usage:[L1,L2]=crossgens(X1,X2)232.s=randomize([2:12]')';233.n1=min(s(1),s(11));n2=max(s(1),s(11));234.X3=X1;X4=X2;235.for i=n1:n2,236.for j=1:13,237.if X2(i)==X3(j),238.X3(j)=0;239.end240.if X1(i)==X4(j), X4(j)=0;241.end242.end243.end244.j=13;k=13;245.for i=12:-1:2,246.if X3(i)~=0,247.j=j-1;248.t=X3(j);X3(j)=X3(i);X3(i)=t;249.end250.if X4(i)~=0,251.k=k-1;252.t=X4(k);X4(k)=X4(i);X4(i)=t;253.end254.end255.for i=n1:n2256.X3(2+i-n1)=X2(i);257.X4(2+i-n1)=X1(i);258.end259.L1=X3;L2=X4;遗传算法程序 matlab1.遗传算法程序:2.说明: fga.m 为遗传算法的主程序; 采用二进制Gray编码,采用基于轮盘赌法的非线性排名选择, 均匀交叉,变异操作,而且还引入了倒位操作!3.4.function [BestPop,Trace]=fga(FUN,LB,UB,eranum,popsize,pCross,pMutation,pInversion,options)5.% [BestPop,Trace]=fmaxga(FUN,LB,UB,eranum,popsize,pcross,pmutation)6.% Finds a maximum of a function of several variables.7.% fmaxga solves problems of the form:8.% max F(X) subject to: LB <= X <= UB9.% BestPop - 最优的群体即为最优的染色体群10.% Trace - 最佳染色体所对应的目标函数值11.% FUN - 目标函数12.% LB - 自变量下限13.% UB - 自变量上限14.% eranum - 种群的代数,取100--1000(默认200)15.% popsize - 每一代种群的规模；此可取50--200(默认100)16.% pcross - 交叉概率,一般取0.5--0.85之间较好(默认0.8)17.% pmutation - 初始变异概率,一般取0.05-0.2之间较好(默认0.1)18.% pInversion - 倒位概率,一般取0.05－0.3之间较好(默认0.2)19.% options - 1*2矩阵,options(1)=0二进制编码(默认0),option(1)~=0十进制编20.%码,option(2)设定求解精度(默认1e-4)21.%22.% ------------------------------------------------------------------------23.24.T1=clock;25.if nargin<3, error('FMAXGA requires at least three input arguments'); end26.if nargin==3, eranum=200;popsize=100;pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];end27.if nargin==4, popsize=100;pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];end28.if nargin==5, pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];end29.if nargin==6, pMutation=0.1;pInversion=0.15;options=[0 1e-4];end30.if nargin==7, pInversion=0.15;options=[0 1e-4];end31.if find((LB-UB)>0)32.error('数据输入错误,请重新输入(LB<UB):');33.</UB):');34.end35.s=sprintf('程序运行需要约%.4f 秒钟时间,请稍等......',(eranum*popsize/1000));36.disp(s);37.38.global m n NewPop children1 children2 VarNum39.40.bounds=[LB;UB]';bits=[];VarNum=size(bounds,1);41.precision=options(2);%由求解精度确定二进制编码长度42.bits=ceil(log2((bounds(:,2)-bounds(:,1))' ./ precision));%由设定精度划分区间43.[Pop]=InitPopGray(popsize,bits);%初始化种群44.[m,n]=size(Pop);45.NewPop=zeros(m,n);46.children1=zeros(1,n);47.children2=zeros(1,n);48.pm0=pMutation;49.BestPop=zeros(eranum,n);%分配初始解空间BestPop,Trace50.Trace=zeros(eranum,length(bits)+1);51.i=1;52.while i<=eranum53.for j=1:m54.value(j)=feval(FUN(1,:),(b2f(Pop(j,:),bounds,bits)));%计算适应度55.end56.[MaxValue,Index]=max(value);57.BestPop(i,:)=Pop(Index,:);58.Trace(i,1)=MaxValue;59.Trace(i,(2:length(bits)+1))=b2f(BestPop(i,:),bounds,bits);60.[selectpop]=NonlinearRankSelect(FUN,Pop,bounds,bits);%非线性排名选择61.[CrossOverPop]=CrossOver(selectpop,pCross,round(unidrnd(eranum-i)/eranum));62.%采用多点交叉和均匀交叉，且逐步增大均匀交叉的概率63.%round(unidrnd(eranum-i)/eranum)64.[MutationPop]=Mutation(CrossOverPop,pMutation,VarNum);%变异65.[InversionPop]=Inversion(MutationPop,pInversion);%倒位66.Pop=InversionPop;%更新67.pMutation=pm0+(i^4)*(pCross/3-pm0)/(eranum^4);68.%随着种群向前进化，逐步增大变异率至1/2交叉率69.p(i)=pMutation;70.i=i+1;71.end72.t=1:eranum;73.plot(t,Trace(:,1)');74.title('函数优化的遗传算法');xlabel('进化世代数(eranum)');ylabel('每一代最优适应度(maxfitness)');75.[MaxFval,I]=max(Trace(:,1));76.X=Trace(I,(2:length(bits)+1));77.hold on; plot(I,MaxFval,'*');78.text(I+5,MaxFval,['FMAX=' num2str(MaxFval)]);79.str1=sprintf('进化到 %d 代 ,自变量为 %s 时,得本次求解的最优值 %f\n对应染色体是：%s',I,num2str(X),MaxFval,num2str(BestPop(I,:)));80.disp(str1);81.%figure(2);plot(t,p);%绘制变异值增大过程82.T2=clock;83.elapsed_time=T2-T1;84.if elapsed_time(6)<085.elapsed_time(6)=elapsed_time(6)+60; elapsed_time(5)=elapsed_time(5)-1;86.end87.if elapsed_time(5)<088.elapsed_time(5)=elapsed_time(5)+60;elapsed_time(4)=elapsed_time(4)-1;89.end %像这种程序当然不考虑运行上小时啦90.str2=sprintf('程序运行耗时 %d 小时 %d 分钟 %.4f 秒',elapsed_time(4),elapsed_time(5),elapsed_time(6));91.disp(str2);92.93.94.95.%初始化种群96.%采用二进制Gray编码,其目的是为了克服二进制编码的Hamming悬崖缺点97.function [initpop]=InitPopGray(popsize,bits)98.len=sum(bits);99.initpop=zeros(popsize,len);%The whole zero encoding individual100.for i=2:popsize-1101.pop=round(rand(1,len));102.pop=mod(([0 pop]+[pop 0]),2);103.%i=1时,b(1)=a(1);i>1时,b(i)=mod(a(i-1)+a(i),2)104.%其中原二进制串:a(1)a(2)...a(n),Gray串:b(1)b(2)...b(n)105.initpop(i,:)=pop(1:end-1);106.end107.initpop(popsize,:)=ones(1,len);%The whole one encoding individual108.109.110.111.112.%解码113.114.function [fval] = b2f(bval,bounds,bits)115.% fval - 表征各变量的十进制数116.% bval - 表征各变量的二进制编码串117.% bounds - 各变量的取值范围118.% bits - 各变量的二进制编码长度119.scale=(bounds(:,2)-bounds(:,1))'./(2.^bits-1); %The range of the variables120.numV=size(bounds,1);121.cs=[0 cumsum(bits)];122.for i=1:numV123.a=bval((cs(i)+1):cs(i+1));124.fval(i)=sum(2.^(size(a,2)-1:-1:0).*a)*scale(i)+bounds(i,1);125.end126.127.128.129.130.%选择操作131.%采用基于轮盘赌法的非线性排名选择132.%各个体成员按适应值从大到小分配选择概率：133.%P(i)=(q/1-(1-q)^n)*(1-q)^i, 其中 P(0)>P(1)>...>P(n), sum(P(i))=1134.135.function [selectpop]=NonlinearRankSelect(FUN,pop,bounds,bits)136.global m n137.selectpop=zeros(m,n);138.fit=zeros(m,1);139.for i=1:m140.fit(i)=feval(FUN(1,:),(b2f(pop(i,:),bounds,bits)));%以函数值为适应值做排名依据141.end142.selectprob=fit/sum(fit);%计算各个体相对适应度(0,1)143.q=max(selectprob);%选择最优的概率144.x=zeros(m,2);145.x(:,1)=[m:-1:1]';146.[y x(:,2)]=sort(selectprob);147.r=q/(1-(1-q)^m);%标准分布基值148.newfit(x(:,2))=r*(1-q).^(x(:,1)-1);%生成选择概率149.newfit=cumsum(newfit);%计算各选择概率之和150.rNums=sort(rand(m,1));151.fitIn=1;newIn=1;152.while newIn<=m153.if rNums(newIn)<NEWFIT(FITIN)154.selectpop(newIn,:)=pop(fitIn,:);155.newIn=newIn+1;156.else157.fitIn=fitIn+1;158.end159.end160.161.162.163.164.%交叉操作165.function [NewPop]=CrossOver(OldPop,pCross,opts)166.%OldPop为父代种群，pcross为交叉概率167.global m n NewPop168.r=rand(1,m);169.y1=find(r<PCROSS);170.y2=find(r>=pCross);171.len=length(y1);172.if len>2&mod(len,2)==1%如果用来进行交叉的染色体的条数为奇数，将其调整为偶数173.y2(length(y2)+1)=y1(len);174.y1(len)=[];175.end176.if length(y1)>=2177.for i=0:2:length(y1)-2178.if opts==0179.[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=EqualCrossOver(OldPop(y1(i+1),:),OldPop(y1(i+2),:)); 180.else181.[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=MultiPointCross(OldPop(y1(i+1),:),OldPop(y1(i+2),:)); 182.end183.end184.end185.NewPop(y2,:)=OldPop(y2,:);186.187.%采用均匀交叉188.function [children1,children2]=EqualCrossOver(parent1,parent2)189.190.global n children1 children2191.hidecode=round(rand(1,n));%随机生成掩码192.crossposition=find(hidecode==1);193.holdposition=find(hidecode==0);194.children1(crossposition)=parent1(crossposition);%掩码为1，父1为子1提供基因195.children1(holdposition)=parent2(holdposition);%掩码为0，父2为子1提供基因196.children2(crossposition)=parent2(crossposition);%掩码为1，父2为子2提供基因197.children2(holdposition)=parent1(holdposition);%掩码为0，父1为子2提供基因198.199.%采用多点交叉，交叉点数由变量数决定200.201.function [Children1,Children2]=MultiPointCross(Parent1,Parent2)202.203.global n Children1 Children2 VarNum204.Children1=Parent1;205.Children2=Parent2;206.Points=sort(unidrnd(n,1,2*VarNum));207.for i=1:VarNum208.Children1(Points(2*i-1):Points(2*i))=Parent2(Points(2*i-1):Points(2*i));209.Children2(Points(2*i-1):Points(2*i))=Parent1(Points(2*i-1):Points(2*i));210.end211.212.213.214.215.%变异操作216.function [NewPop]=Mutation(OldPop,pMutation,VarNum)217.218.global m n NewPop219.r=rand(1,m);220.position=find(r<=pMutation);221.len=length(position);222.if len>=1223.for i=1:len224.k=unidrnd(n,1,VarNum); %设置变异点数，一般设置1点225.for j=1:length(k)226.if OldPop(position(i),k(j))==1227.OldPop(position(i),k(j))=0;228.else229.OldPop(position(i),k(j))=1;230.end231.end232.end233.end234.NewPop=OldPop;235.236.237.238.239.%倒位操作240.241.function [NewPop]=Inversion(OldPop,pInversion)242.243.global m n NewPop244.NewPop=OldPop;245.r=rand(1,m);246.PopIn=find(r<=pInversion);247.len=length(PopIn);248.if len>=1249.for i=1:len250.d=sort(unidrnd(n,1,2));251.if d(1)~=1&d(2)~=n252.NewPop(PopIn(i),1:d(1)-1)=OldPop(PopIn(i),1:d(1)-1);253.NewPop(PopIn(i),d(1):d(2))=OldPop(PopIn(i),d(2):-1:d(1));254.NewPop(PopIn(i),d(2)+1:n)=OldPop(PopIn(i),d(2)+1:n);255.end256.end257.endTSP问题（又名：旅行商问题，货郎担问题）遗传算法通用matlab程序%D是距离矩阵，n为种群个数,建议取为城市个数的1~2倍，%C为停止代数，遗传到第C代时程序停止,C的具体取值视问题的规模和耗费的时间而定%m为适应值归一化淘汰加速指数,最好取为1,2,3,4 ,不宜太大%alpha为淘汰保护指数,可取为0~1之间任意小数,取1时关闭保护功能,最好取为0.8~1.0 %R为最短路径,Rlength为路径长度function [R,Rlength]=geneticTSP(D,n,C,m,alpha)[N,NN]=size(D);farm=zeros(n,N);%用于存储种群for i=1:nfarm(i,:)=randperm(N);%随机生成初始种群endR=farm(1,:);%存储最优种群len=zeros(n,1);%存储路径长度fitness=zeros(n,1);%存储归一化适应值counter=0;while counter<cfor i=1:nlen(i,1)=myLength(D,farm(i,:));%计算路径长度endmaxlen=max(len);minlen=min(len);fitness=fit(len,m,maxlen,minlen);%计算归一化适应值rr=find(len==minlen);R=farm(rr(1,1),:);%更新最短路径FARM=farm;%优胜劣汰，nn记录了复制的个数nn=0;for i=1:nif fitness(i,1)>=alpha*randnn=nn+1;FARM(nn,:)=farm(i,:);endendFARM=FARM(1:nn,:);[aa,bb]=size(FARM);%交叉和变异while aa<nif nn<=2nnper=randperm(2);elsennper=randperm(nn);endA=FARM(nnper(1),:);B=FARM(nnper(2),:);[A,B]=intercross(A,B);FARM=[FARM;A;B];[aa,bb]=size(FARM);endif aa>nFARM=FARM(1:n,:);%保持种群规模为nendfarm=FARM;clear FARMcounter=counter+1endRlength=myLength(D,R);function [a,b]=intercross(a,b)L=length(a);if L<=10%确定交叉宽度W=1;elseif ((L/10)-floor(L/10))>=rand&&L>10W=ceil(L/10);elseW=floor(L/10);endp=unidrnd(L-W+1);%随机选择交叉范围，从p到p+W for i=1:W%交叉x=find(a==b(1,p+i-1));y=find(b==a(1,p+i-1));[a(1,p+i-1),b(1,p+i-1)]=exchange(a(1,p+i-1),b(1,p+i-1)); [a(1,x),b(1,y)]=exchange(a(1,x),b(1,y));endfunction [x,y]=exchange(x,y)temp=x;x=y;y=temp;% 计算路径的子程序function len=myLength(D,p)[N,NN]=size(D);len=D(p(1,N),p(1,1));for i=1:(N-1)len=len+D(p(1,i),p(1,i+1));end%计算归一化适应值子程序function fitness=fit(len,m,maxlen,minlen)fitness=len;for i=1:length(len)fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.000001))).^m;end已知n个城市之间的相互距离，现有一个推销员必须遍访这n个城市，并且每个城市只能访问一次，最后又必须返回出发城市。
