利用simulink对自适应控制系统模型进行仿真分析

simulink轨迹跟踪方法Simulink是一种基于模型的设计和仿真工具，广泛应用于自动控制系统的开发和测试中。

轨迹跟踪是自动控制系统中的一个重要问题，通过控制对象在给定轨迹上的运动，实现对系统的精确控制。

Simulink提供了多种方法来实现轨迹跟踪，本文将介绍其中几种常用的方法。

1. 基于PID控制器的轨迹跟踪方法：PID控制器是一种常见的控制器，通过比较实际输出与期望输出的偏差，调整控制信号来实现对系统的控制。

在Simulink中，可以使用PID控制器模块来实现轨迹跟踪。

通过调整PID控制器的参数，可以实现对系统的精确控制。

例如，可以调整比例系数来增强系统的响应速度，调整积分系数来消除系统的稳态误差，调整微分系数来抑制系统的震荡。

2. 基于模型预测控制（MPC）的轨迹跟踪方法：模型预测控制是一种基于系统数学模型的控制方法，通过预测系统的未来状态，优化控制信号来实现对系统的控制。

Simulink提供了MPC工具箱，可以方便地进行模型预测控制。

在轨迹跟踪问题中，可以使用MPC来预测系统在给定轨迹上的运动，并根据预测结果来调整控制信号，使系统实现轨迹跟踪。

MPC可以考虑系统的约束条件，例如输入和输出的限制，从而实现对系统的更加精确的控制。

3. 基于模糊控制的轨迹跟踪方法：模糊控制是一种通过模糊推理来实现对系统的控制的方法。

在Simulink中，可以使用模糊控制器模块来实现模糊控制。

在轨迹跟踪问题中，可以使用模糊控制器来根据系统的当前状态和轨迹的要求，输出相应的控制信号，使系统实现轨迹跟踪。

模糊控制器可以考虑系统的非线性和不确定性，适用于复杂系统的控制。

4. 基于神经网络的轨迹跟踪方法：神经网络是一种模拟人脑神经网络结构和工作原理的计算模型。

在Simulink中，可以使用神经网络模块来实现神经网络控制。

在轨迹跟踪问题中，可以使用神经网络来学习系统的输入和输出之间的映射关系，并根据学习到的映射关系来生成控制信号，使系统实现轨迹跟踪。

基于simulink的模糊PID控制例⼦1模糊PID⽤命令Fuzzy打开模糊控制⼯具箱。

Anfisedit打开⾃适应神经模糊控制器，它⽤给定的输⼊输出数据建个⼀个模糊推理系统，并⽤⼀个反向传播或者与最⼩⼆乘法结合的来完成⾪属函数的调节。

Surfview(newfis)可以打开表⾯视图窗⼝8.1 模糊PID 串联型新建⼀个simulink模型同时拖⼊⼀个fuzzy logic controller 模块，双击输⼊已经保存的fis模糊控制器的名字。

由于这个控制模块只有⼀个输⼊端⼝，需要⽤到mux模块。

模糊结合PID,当输出误差较⼤时，⽤模糊校正，当较⼩时，⽤PID校正。

8.2 模糊⾃适应PID（1）PID 参数模糊⾃整定的原则PID 调节器的控制规律为: u( k) = Kp e( k) + Ki Σe( i) + Kd ec( k)其中: Kp 为⽐例系数; Ki 为积分系数; Kd为微分系数; e( k) 、ec( k) 分别为偏差和偏差变化率.模糊⾃整定PID 参数的⽬的是使参数Kp 、Ki 、Kd随着e 和ec 的变化⽽⾃⾏调整,故应⾸先建⽴它们间的关系. 根据实际经验,参数Kp 、Ki 、Kd在不同的e 和ec下的⾃调整要满⾜如下调整原则:(1) 当e 较⼤时,为加快系统的响应速度,防⽌因开始时e 的瞬间变⼤可能会引起的微分溢出,应取较⼤的Kp 和较⼩的Kd ,同时由于积分作⽤太强会使系统超调加⼤,因⽽要对积分作⽤加以限制,通常取较⼩的Ki值;(2) 当 e 中等⼤⼩时,为减⼩系统的超调量, 保证⼀定的响应速度, Kp 应适当减⼩;同时Kd 和Ki的取值⼤⼩要适中;(3) 当e 较⼩时,为了减⼩稳态误差, Kp 与Ki 应取得⼤些,为了避免输出响应在设定值附近振荡,同时考虑系统的抗⼲扰性能,Kd 值的选择根据|ec|值较⼤时，Kd 取较⼩值，通常Kd 为中等⼤⼩。

同时按照需要,将输⼊语⾔变量E 和EC 分为7 个模糊⼦集,分别⽤语⾔值正⼤( PB) 、正中( PM) 、正⼩( PS) 、零(Z) 、负⼩(NS) 、负中(NM) 、负⼤(NB) 来表⽰,它们的⾪属函数为⾼斯型(gaussmf) ,输出语⾔变量Kp′、Ki′、Kd′⽤语⾔值⼩正⼤( PB) 、正中( PM) 、正⼩( PS) 、零(Z) 、负⼩(NS) 、负中(NM) 、负⼤(NB) 来表⽰⾪属函数为三⾓型(t rimf) ,⽅法⼆：图-1模糊⾃适应simulink模型根据各模糊⼦集的⾪属度赋值表和各参数模糊控制模型，应⽤模糊合成推理设计分数阶PID参数的模糊矩阵表，算出参数代⼊下式计算：Kp=Kp0+(E，EC)p;Ki=Ki0+(E，EC)I;Kd=Kd0+(E，EC)d式中：Kp0、Ki0、Kd0为PID参数的初始设计值，由传统的PID控制器的参数整定⽅法设计。

控制系统仿真控制系统仿真是使用计算机模拟现实世界中的控制系统的行为和性能。

它通常涉及建立数学模型来描述实际系统的行为，然后使用计算机来模拟和分析这些模型的响应。

控制系统仿真可以用于多种目的，例如：1. 分析系统的稳定性和性能：通过模拟控制系统的动态响应，可以评估系统的稳定性和性能特性，如超调量、响应时间、稳态误差等。

2. 验证控制算法：在仿真环境中，可以测试和优化控制算法，以确保其在实际系统中的有效性和可靠性。

3. 优化系统设计：通过调整系统参数和控制策略，可以在仿真环境中评估不同设计方案的性能，并选择最佳方案。

4. 教学和学习：仿真可以作为控制系统教学的有力工具，学生可以通过实验和观察仿真结果来深入理解控制系统的原理和设计方法。

要进行控制系统仿真，需要以下步骤：1. 建立数学模型：根据实际系统的物理特性和控制需求，建立数学方程来描述系统的行为。

这可能涉及到使用物理原理和方程、系统辨识技术、统计建模等方法。

2. 确定仿真环境：选择适当的仿真软件或编程语言来实现控制系统仿真。

常用的仿真软件包括MATLAB/Simulink、LabVIEW、Python等。

3. 实现控制算法：根据数学模型和控制需求，实现相应的控制算法。

这可以包括经典的PID控制、优化控制、自适应控制等。

4. 运行仿真：在仿真环境中运行控制系统模型和控制算法，观察和分析系统的响应。

可以根据需要进行参数调整和算法改进。

5. 分析仿真结果：使用仿真结果评估系统的性能，并根据需要进行分析和优化。

6. 验证和应用：将仿真结果与实际系统进行比较和验证，确保仿真结果的准确性和可靠性。

根据需求，将仿真结果应用于实际控制系统的设计和实施。

总之，控制系统仿真是一种有效的工程工具，可以用于评估和优化控制系统的性能、验证和改进控制算法，并为控制系统设计和实施提供支持。

simulink 步长概念-回复Simulink是一种用于建模、仿真和分析动态系统的工具。

在Simulink中，步长是模拟或仿真模型时使用的一个重要概念。

步长定义了模型在每个模拟时间步长上进行计算的精度，影响着仿真的准确性和效率。

本文将逐步回答关于Simulink步长的一些常见问题，并探讨步长对模型仿真的影响。

第一步：什么是Simulink步长？步长是Simulink模型在仿真期间使用的时间间隔，用于获取系统的当前状态并计算下一个时刻的状态。

在仿真中，模型将时间分成一系列小的离散步长，每个步长模型计算一遍模型的状态，并将结果用作下一个时间点的初始条件。

步长的选择是一个重要的决策，因为它直接影响着模型分析的准确性和计算效率。

第二步：如何选择适当的步长？选择适当的步长是确保模型仿真准确性的关键一步。

步长的选择需要考虑到系统动态的特性以及仿真的可接受误差。

一般而言，步长应足够小，以捕捉到系统动态的细节，但又不应过小，以至于使仿真时间过长或导致不稳定的计算。

以下是一些考虑步长选择的重要原则：1. 系统的动态特性：不同类型的系统具有不同的动态响应特征，如快速响应、慢速响应、高频振荡等。

快速响应系统的仿真步长应该相对较小，以捕捉高频率的变化。

而慢速响应系统可以使用较大的步长，以提高仿真效率。

2. 模型的非线性特性：如果模型具有非线性特性，例如非线性函数或激活函数，那么较小的步长可能更合适，以捕捉non-linearity的行为特征。

3. 仿真误差：在某些应用中，需要控制仿真结果与实际结果之间的误差。

较小的步长可以减小仿真误差，但也会增加仿真时间和计算负载。

因此，需要在精度和效率之间进行权衡。

第三步：在Simulink中如何设置步长？在Simulink中，可以通过多种方式来指定仿真步长。

以下是一些常见的设置选项：1. 固定步长：使用固定步长时，仿真将在每个模拟时间步长上进行计算。

可以通过在模型参数对话框中设置固定步长的值来指定步长。

第1篇一、项目背景随着我国经济的快速发展，自动化和智能化技术在各个领域的应用越来越广泛。

控制工程作为自动化和智能化技术的重要组成部分，其研究与应用对于提高生产效率、降低能耗、保障生产安全等方面具有重要意义。

本方案旨在通过实践，验证控制工程理论在实际工程项目中的应用效果，提高学生的实践能力和创新能力。

二、项目目标1. 掌握控制工程的基本原理和方法；2. 熟悉控制系统的设计、调试与优化；3. 提高学生的实践能力和创新能力；4. 为企业培养具备实际操作能力的控制工程人才。

三、实践内容1. 控制系统原理学习（1）了解控制系统的基本概念、分类和特点；（2）掌握控制系统设计的基本方法，如PID控制、模糊控制、自适应控制等；（3）熟悉控制系统的性能指标，如稳态误差、超调量、上升时间等。

2. 控制系统仿真与实践（1）使用MATLAB/Simulink等仿真软件进行控制系统建模与仿真；（2）分析仿真结果，验证控制系统的性能指标；（3）优化控制系统参数，提高控制效果。

3. 控制系统设计与实现（1）选择合适的控制算法，设计控制系统；（2）根据实际需求，选择合适的控制器硬件和软件平台；（3）进行控制器编程与调试，实现控制系统的功能。

4. 实际工程项目应用（1）选择具有实际应用背景的工程项目；（2）分析项目需求，确定控制系统的设计方案；（3）进行控制系统设计与实现，确保项目顺利进行。

四、实践步骤1. 准备阶段（1）收集相关资料，了解控制工程的基本原理和方法；（2）熟悉仿真软件和控制器硬件平台；（3）组建实践团队，明确分工。

2. 学习阶段（1）学习控制系统原理，掌握基本设计方法；（2）学习仿真软件和控制器硬件平台的使用方法；（3）进行仿真实验，验证控制系统的性能。

3. 设计阶段（1）根据实际需求，确定控制系统的设计方案；（2）进行控制器编程与调试；（3）对控制系统进行优化，提高控制效果。

4. 实施阶段（1）根据设计方案，进行控制系统设计与实现；（2）将控制系统应用于实际工程项目，解决实际问题；（3）对控制系统进行测试与评估，确保项目顺利进行。

64 | 电子制作 2021年02月热能，当电流流过电阻材料时，电能转换成热能，产生热量，再通过热的传导、对流、辐射，能有效地用来加热特定的试验件，并保持高的效率，此种加热方式称为辐射加温。

辐射加热具有热转换率高、加热温度高等优点，因此是试验车台上使用最广泛的一种加热方式。

温度是试验任务中一项很重要的监控指标，很多试验任务要求在特定的温度下才能进行，实际温度值和控制的精度、准确度决定了试验能否进行下去，因此研究温度控制工作原理，寻找合适的控制算法具有重要意义。

辐射加温控制系统是典型的一阶纯滞后环节，可用一阶惯性环节加滞后环节表示，具有升温单向性、大惯性、纯滞后、非线性和时变性等特点，用传统控制方式易导致超调大、调节时间长、控制精度低。

其升温、保温是依靠电阻丝加热，当其温度一旦超调就无法用控制手段使其降温。

理论和经验表明，传统的PID 控制对温度控制系统无法达到理想效果[1-2]。

模糊控制是目前十分成熟的一种智能控制方法，其采用模糊逻辑把人的控制经验归纳为定性描述的一组条件语言，利用模糊集理论，将其定量化，使控制器模仿人的操作策略，模糊控制具有很强的鲁棒性和稳定性，大量的理论研究和实践也充分证明了用模糊控制理论控制电阻炉温度是一种非常好的方法策略[3]。

PLC 具有通用性好、性能可靠、编程灵活、扩展方便等优点，在工业控制中广泛使用，PLC 指令越来越强大，能够实现许多复杂的控制算法，利用PLC 实现模糊控制，结合二者的长处，在工业控制中大有前景。

基于上述，本文提出在PLC 平台上将模糊控制方法和常规PID 控制结合的控制策略。

1 控制策略当实际温度值和给定温度值偏差较大时，采用模糊控制合式控制策略，既可以保证系统动态响应效果，又能改善稳态控制精度，系统控制框图如图1所示。

其中S 为转换开关，其设定值一般取最大误差的10%，本文取20，即给定值和实际值偏差在20℃以内采用PID 控制，超过20℃采用模糊[4]模糊控制器能在线对PID 参数进行修改，进一步完善了传统PID 控制器的性能，更好的适应控制系统参数变化和工作条件，如图1所示，模糊控制器由模糊化，模糊推理和解模糊三个环节构成，将工程上的精确量转换为模糊输入信息，利用模糊规则进行模糊推理，经解模糊后转换为精确值，送到被控对象。

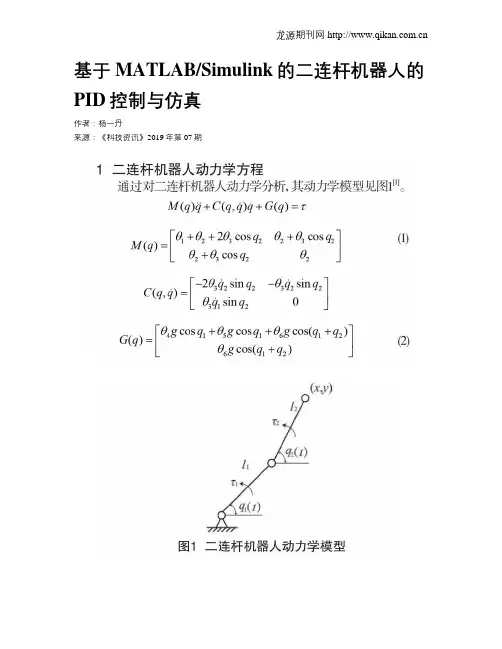
基于MATLAB/Simulink的二连杆机器人的PID控制与仿真作者：***来源：《科技资讯》2019年第07期摘; 要：主要研究了一类二连杆机器人应用PID控制理论进行轨迹追踪的控制方法。

该文首先给出二连杆机器人进行动力学模型，进而利用MATLAB/Simulink仿真环境，构造出PID 控制模型框图，使用Interpreted MATLAB Function嵌入代码。

通过改变PID参数进行仿真，该文分析了不同PID参数对二连杆机器人关节转角误差的影响，使机器人末端实际轨迹实现了很好的跟踪效果。

关键词：二连杆机器人; Simulink; PID控制中图分类号：G64; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 文献标识码：A; ; ; ; ; ; ; ; ; ; ; ; ; 文章编号：1672-3791（2019）03（a）-0030-02二连杆机器人是可自由改变关节转角而完成不同作业的装置，对二连杆机器人的关节转角的准确控制关乎产品的质量和生产的效率，是工业生产关键的一环，因此应用PID控制算法对其转角的控制显得尤为重要。

为减小二连杆机器人转角误差，于具有数值计算分析与数学建模功能的MATLAB/Simulink环境中应用PID控制理论模拟控制的全过程。

该文主要研究PID参数对二连杆机器人关节转角误差的影响，应用MATLAB中精确的矩阵等的运算和清晰的绘图功能，Simulink中简洁的模块联系和动态仿真曲线，得到了不同PID 参数下的误差曲线。

该文依托PID控制理论，以二连杆机器人运动轨迹为研究对象，通过MATLAB编程和Simulink仿真，构造出合理的理论模型，通过分析得到不同PID參数对误差的影响，进而能够使二连杆机器人运动轨迹基本与期望值相同，转角误差降至最低，达到了控制的目的。

1; 二连杆机器人动力学方程通过对二连杆机器人动力学分析，其动力学模型见图1[1]。

如何使用Matlab进行控制系统仿真概述控制系统在工程领域中扮演着重要角色，它用于控制和管理各种工程过程和设备。

而控制系统仿真则是设计、开发和测试控制系统的关键环节之一。

Matlab作为一种功能强大的工程计算软件，提供了丰富的工具和功能，可以帮助工程师进行控制系统仿真。

本文将简要介绍如何使用Matlab进行控制系统仿真，以及一些实用的技巧和建议。

1. Matlab的基础知识在开始控制系统仿真之前，有一些Matlab的基础知识是必要的。

首先，了解Matlab的基本语法和命令，熟悉Matlab的工作环境和编辑器。

其次，学会使用Matlab的集成开发环境（IDE）进行编程和数学建模。

熟悉Matlab的常用函数和工具箱，并了解如何在Matlab中导入和导出数据。

2. 定义系统模型在进行控制系统仿真之前，需要定义系统的数学模型。

根据具体情况选择合适的建模方法，如传递函数、状态空间或差分方程等。

在Matlab中，可以使用tf、ss 或zpk等函数来创建系统模型，并指定系统的参数和输入信号。

此外，Matlab还提供了Simulink这一强大的图形化建模环境，方便用户以图形化界面设计系统模型。

3. 设计控制器控制系统仿真的关键是设计合适的控制器，以实现所需的控制目标。

Matlab提供了各种控制器设计方法和工具，如PID控制器、根轨迹法、频域方法等。

用户可以使用Matlab的Control System Toolbox来设计和分析控制器，并在仿真中进行验证。

此外，Matlab还支持自适应控制和模糊控制等高级控制方法，可根据具体需求选择合适的方法。

4. 进行仿真实验在完成系统模型和控制器设计后，可以开始进行控制系统仿真实验。

首先，确定仿真实验的输入信号，如阶跃信号、正弦信号或随机信号等。

然后，使用Matlab中的sim函数将输入信号应用到系统模型中，并观察系统的输出响应。

通过调整控制器参数或设计不同的控制器，分析系统的性能和稳定性，并优化控制器的设计。

基于MatlabSimulink的电动汽车仿真模型设计与应用一、本文概述随着全球能源危机和环境污染问题的日益严重，电动汽车作为一种清洁、高效的交通工具，受到了越来越多的关注和推广。

在电动汽车的研发过程中，仿真模型的建立与应用发挥着至关重要的作用。

本文旨在探讨基于Matlab/Simulink的电动汽车仿真模型设计与应用，旨在为电动汽车的设计、优化和控制提供理论支持和实践指导。

本文将对电动汽车仿真模型的重要性进行阐述，指出其在电动汽车研发过程中的地位和作用。

接着，将详细介绍Matlab/Simulink在电动汽车仿真模型设计中的应用，包括其强大的建模功能、灵活的仿真能力以及高效的算法处理能力等。

在此基础上，本文将重点讨论电动汽车仿真模型的设计方法。

包括电动汽车动力系统的建模、控制系统的建模以及整车模型的集成等。

将结合具体案例，对电动汽车仿真模型在实际应用中的效果进行展示和分析，以验证其有效性和可靠性。

本文还将对电动汽车仿真模型的发展趋势进行展望，探讨其在未来电动汽车研发中的潜在应用前景。

通过本文的研究，希望能够为电动汽车仿真模型的设计与应用提供有益的参考和启示，推动电动汽车技术的不断发展和进步。

二、电动汽车仿真模型设计基础电动汽车（EV）仿真模型的设计是一个涉及多个学科领域的复杂过程，其中包括电力电子、控制理论、车辆动力学以及计算机建模等。

在Matlab/Simulink环境中，电动汽车仿真模型的设计基础主要包括对车辆各子系统的理解和建模，以及如何利用Simulink提供的各种模块和工具箱进行模型的构建和仿真。

电动汽车的主要子系统包括电池管理系统（BMS）、电机控制系统（MCS）、车辆控制系统（VCS）以及车辆动力学模型。

这些子系统都需要根据实际的电动汽车设计和性能参数进行精确的建模。

电池管理系统（BMS）建模：电池是电动汽车的能源来源，因此，BMS建模对于电动汽车的整体性能至关重要。

BMS模型需要包括电池的荷电状态（SOC）估计、电池健康状况（SOH）监测、电池热管理以及电池能量管理等功能。

doi：10.3969/j.issn.1005-2550.2013.02.012车辆自适应巡航控制系统（Adaptive Cruise Control system，下简称ACC）是一种被广泛研究且具有广阔前景的车辆主动安全装置。

一般认为ACC是一种增强驾乘舒适性的电控装置，其原理是利用激光/毫米波雷达、摄像头等传感器对相同车道内前方目标进行检测，通过电控系统自主地对发动机及制动系统的联合控制实现安全车距保持功能［1，2］。

ACC 有助于缓解驾驶员的驾驶疲劳感，现已经越来越多被应用于国内外中高档轿车上。

在ACC系统开发过程中，涉及的关键技术主要包括：①车辆状态测量（轮速、质心加速度、横摆角速度等）；②目标检测与跟踪（基于雷达或摄像头的目标检测与跟踪）；③ACC核心控制算法的开发；④发动机、制动系统的通讯与控制等。

利用CAE软件辅助开发与设计能显著提高ACC装置开发效率，尤其在ACC核心控制算法开发过程中，CAE软件辅助开发具有结果直观、开发周期短、成本低廉等显著优势。

CarSim是一种专业的车辆动力学仿真软件，能准确模拟车辆对驾驶员操作行为、空气动力学以及路面激励的响应。

在车辆操纵稳定性、平顺性、燃料经济性、动力性等领域有广泛应用［3］。

其优势体现在能方便的模拟各种复杂路面几何形式及峰值附着特性、模拟复杂的驾驶员操作行为和试验工况、通过简单的系统定义输出复杂的多刚体机械结构动力学模型等。

其强大的可扩展性及丰富的接口使其能方便的与Matlab/Simulink、dSpace、Labview等软件进行联合仿真，用于各种高级功能开发，尤其在车辆电控系统的开发模拟方面具有显著优势。

同时CarSim软件存在一定局限性，主要体现在：某些部件具有显著几何非线性特性及材料非线性特性，需要借FEM方法进行刚柔耦合计算才能获得较理想的计算值，CarSim在处理此类部件上显得手段较单一。

结合现有条件，拟采用CarSim与Simulink联合仿真的方式进行ACC控制器开发，并将成功开发的ACC控制器移植到试验样车，以完成原理样机的试验。

Simulink Response OptimizationSimulink Response Optimization——用于优化Simulink模型中的参数Simulink Response Optimization是一个在Simulink模型中调节设计参数的工具，它与Simulink模型结合在一起，根据用户定义的时域内的性能指标约束，自动优化系统参数。

利用该工具，可以对标量形式、矢量形式以及矩阵形式的变量进行优化，并可对任意层次的模型进行变量约束。

Simulink Response Optimization支持连续、离散以及多速率的模型，并可以通过蒙特卡罗仿真处理模型中的某些不确定量。

通过Simulink Response Optimization可以处理一系列优化问题，比如调节多入多出系统参数，对非线性系统设计自适应控制器，优化模型中的物理参数以降低系统能耗、调节滤波器参数等等。

Simulink Response Optimization还可以用于查表调节以及增益的调整等方面。

特点为优化问题的建立和管理提供了图形用户界面提供优化程序用于调节标量、矢量或矩阵参数支持用户自定义的信号约束和期望输出用于指定系统的响应支持蒙特卡罗仿真，对具有模型不确定性的问题提供了更强的鲁棒调节能力强大功能Simulink Response Optimization提供了一个图形用户界面用于在Simulink模型中调节参数。

用户可以随时停止仿真以找回中间结果，调整优化问题，改善收敛性。

可以利用图形用户界面调节所有的参数并可以在仿真中断处重新开始参数调节过程。

利用GUI，可以实现：选择模型中的信号选择和调节参数选择要调节的变量确定模型的不确定量设置仿真和优化选项选择信号可以在模型的任意信号处加入Signal Constraint模块进行信号的选择。

Signal Constraint模块可以通过图形化约束的方式描述期望的系统响应或者也可以通过确定参考信号的输出来描述优化约束。

《智能控制》考试试题试题1：针对某工业过程被控对象：0.520()(101)(21)s G s e s s -=++，试分别设计常规PID 算法控制器、模糊控制器、模糊自适应PID 控制器，计算模糊控制的决策表，并进行如下仿真研究及分析：1. 比较当被控对象参数变化、结构变化时，四者的性能；2. 研究改善Fuzzy 控制器动、静态性能的方法。

解：常规PID 、模糊控制、Fuzzy 自适应PID 控制、混合型FuzzyPID 控制器设计 错误!未找到引用源。

. 常规PID 调节器PID 控制器也就是比例、积分、微分控制器，是一种最基本的控制方式。

它是根据给定值()r t 与实际输出值()y t 构成控制偏差()e t ，从而针对控制偏差进行比例、积分、微分调节的一种方法，其连续形式为：01()()[()()]t p d i de t u t K e t e t dt T T dt=++⎰ （1.1） 式中，p K 为比例系数，i T 为积分时间常数，d T 为微分时间常数。

PID 控制器三个校正环节中p K ，i T 和d T 这三个参数直接影响控制效果的好坏，所以要取得较好的控制效果，就必须合理地选择控制器的参数。

Ziegler 和Nichols 提出的临界比例度法是一种非常著名的工程整定方法。

通过实验由经验公式得到控制器的近似最优整定参数，用来确定被控对象的动态特性的两个参数：临界增益u K 和临界振荡周期u T 。

用临界比例度法整定PID 参数如下：表1.1 临界比例度法参数整定公式51015202530354000.20.40.60.811.21.41.61.8Time(s)y (t )051015202530354000.511.5Time(s)y (t )PID 0.6u K 0.5u T 0.125u T据以上分析，通过多次整定，当 1.168p K =时系统出现等幅振荡，从而临界增益 1.168u K =，再从等幅振荡曲线中近似的测量出临界振荡周期 5.384u T =，最后再根据表1.1中的PID 参数整定公式求出：0.701, 2.692,0.673p i d K T T ===，从而求得：比例系数0.701p K =，积分系数/0.260i p i K K T ==，微分系数0.472d p d K K T ==。

招聘自动控制技术员面试题与参考回答面试问答题（总共10个问题）第一题题目：请简要描述一下PID控制器的工作原理，并说明在自动控制系统中，为什么PID 控制器被广泛使用？参考回答：PID控制器，即比例（Proportional）-积分（Integral）-微分（Derivative）控制器，是自动控制系统中常用的一种反馈回路组件。

其工作原理基于控制系统的输入（设定值）与实际输出（被控量）之间的误差信号来工作，通过调整控制器的输出以最小化这个误差。

1.比例（P）项：它直接根据误差的比例来调整控制量。

当误差增大时，控制作用也相应增强，但仅使用比例项会导致系统稳态误差。

2.积分（I）项：用于消除系统的稳态误差。

积分项是误差随时间累积的结果，它使得控制作用随着时间的推移而逐渐增强，直到误差完全消除。

但积分项也可能导致系统响应速度变慢，甚至引起系统振荡。

3.微分（D）项：它基于误差的变化率来调整控制量，能预测误差变化的趋势，从而提前引入一个修正信号，以加快系统的响应速度，减小超调量，提高稳定性。

为什么PID控制器被广泛使用？PID控制器之所以在自动控制系统中被广泛使用，主要有以下几个原因：•结构简单，易于实现：PID控制算法相对简单，易于在硬件和软件上实现，且对控制器硬件要求不高。

•适用性强：PID控制器适用于大多数线性、非线性和时变系统，以及许多无法精确建模的复杂系统。

•调节方便：通过调整PID的三个参数（比例增益Kp、积分时间Ti、微分时间Td），可以灵活地改变控制器的性能，满足不同的控制需求。

•性能稳定：在适当的参数设置下，PID控制器能够提供良好的稳定性和动态性能，如较快的响应速度、较小的超调量和稳态误差等。

解析：本题主要考察面试者对PID控制器工作原理及其重要性的理解。

PID控制器是自动控制领域中最基本、最重要的控制器之一，其工作原理简单易懂，但应用广泛且效果显著。

通过本题，面试官可以评估面试者的基础知识掌握程度以及对自动控制系统的理解深度。