第6章 Simulink仿真串级控制系统

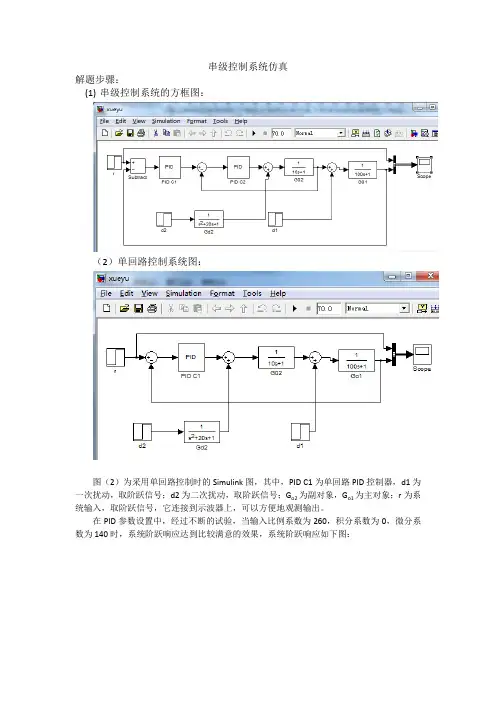
串级控制系统仿真解题步骤：(1)串级控制系统的方框图：（2）单回路控制系统图：图（2）为采用单回路控制时的Simulink图，其中，PID C1为单回路PID控制器，d1为一次扰动，取阶跃信号；d2为二次扰动，取阶跃信号；G o2为副对象，G o1为主对象；r为系统输入，取阶跃信号，它连接到示波器上，可以方便地观测输出。

在PID参数设置中，经过不断的试验，当输入比例系数为260，积分系数为0，微分系数为140时，系统阶跃响应达到比较满意的效果，系统阶跃响应如下图：采用这套PID参数时，二次扰动作用下，置输入为0，系统框图如下。

系统的输出响应如下图：采用这套PID参数时，一次扰动作用下，置输入为0，系统框图如下：系统的输出响应如下从综合以上各图可以看出，采用单回路控制，系统的阶跃响应达到要求时，系统对一次扰动，二次扰动的抑制效果不是很好。

图（1）是采用串级控制时的情况，d1为一次扰动，取阶跃信号；d2为二次扰动，取阶跃信号；PID C1为主控制器，采用PD控制，PID C2为副控制器，采用PID控制；Go2为副对象，Go1为主对象；r为系统输入，取阶跃信号；scope为系统输出，它连接到示波器上，可以方便地观测输出。

经过不断试验，当PID C1为主控制器输入比例系数为550，积分系数为0，微分系数为80时；当PID C2为主控制器输入比例系数为3，积分系数为0，微分系数为0时；系统阶跃响应达到比较满意的效果，系统阶跃响应如下图所示：采用这套PID参数时，二次扰动作用下，置输入为0，系统的框图如下:系统的输出响应如下图:采用这套PID参数时，一次扰动作用下，置输入为0，系统的框图如下:系统的输出响应如下图:从表中可以看出系统的动态过程改善更为明显，可见对二次扰动的最大动态偏差可以减小约6倍，对一次扰动的最大动态偏差也可以减小约2.4倍，系统的调节时间提高了2.5倍。

单回路控制系统在副扰动下的单位阶跃响应曲线如下：串级控制系统在副扰动作用下的节约响应曲线如下：通过对比两曲线可以看出，串级控制系统中因为副回路的存在，当副扰动作用时，副控制器会立即动作，削弱干扰的影响，使被副回路抑制过的干扰再进入主回路，对主回路的影响。

目录1.串级控制的基本概念 (1)2.串级控制系统的原理 (1)3.串级控制系统的特点 (1)4.串级控制主、副控制器的设计 (4)5.Simulink仿真 (6)6.串级控制的改进 (8)附录 (10)参考文献 (11)1.串级控制的基本概念串级控制系统为双闭环或多闭环控制系统，控制系统内环为副控对象，外环为主控对象。

内环的作用是将外部扰动的影响在内环进行处理，而尽可能不使其波动到外环，这就加快了系统的快速性并提高个系统的品质，因此串级控制系统中选择内环时应考虑其响应速度要比外环快得多。

2.串级控制系统的原理串级控制在结构上形成的两个闭环，一个在闭环里面，成为内环、副环或副控回路，其控制器为副控制器，在控制中起“粗调”的作用；一个闭环在外面，成为外环、主环或主控回路，其控制器称为主控制器，在控制中起“细调”作用，最终被控量满足控制要求。

主控制器的输出作为副控制器的给定值，而副控制器的输出则去控制被控对象。

图1为串级控制系统的结构图。

图1 串级控制系统的结构图 3.串级控制系统的特点（1） 副控制回路具有快速性，能够有效的克服进入副控回路的二次干扰。

图2为简化串级控制系统的结构图，其中)(2S G v 为二次干扰通道传递函数。

图2 串级控制系统简化结构图当二次干扰经扰动通道)(2S G v 进入副控回路后，首先影响副参数)(2S Y ，于是副控制器立即动作，力图削弱干扰对)(2S Y 的影响。

显然，干扰经副控回路的抑制后再进主控回路，对)(S Y 的影响将有较大的减弱。

按图2所示的串级系统，二次干扰)(2S V 到主参数)(S Y 的传递函数是)()()()()()(1)()()()(221122122S G S D S G S D S G S D S G S G S V S Y v ++= （3.1） 为了与一个简单单环控制系统相比，由图3可以得到单回路控制下干扰)(2S V 至主参数)(S Y 的传递函数是)()()(1)()()()(21122S G S G S D S G S G S V S Y v += （3.2）图3 单回路控制系统结构图比较（3.1）和（3.2），假定)()(1S D S D =,可以看到串级系统中的)()(2S V S Y 的分母中多了一项，即)()(22S G S D 。

第六章Simulink系统仿真原理本书第二部分对使用Simulink进行动态系统模型建立、系统仿真及分析进行了详细的介绍。

对于一般的用户，使用这些知识便能够对大部分的动态系统进行减免、仿真与分析。

但是对于高级系统设计人员来说，熟悉Simulink对动态系统进行仿真的工作原理必定会对系统的设计、仿真与分析起到很好的作用。

前面所介绍的仅仅是Simulink仿真平台的使用方法，用户完全可以在较短的时间内熟练掌握。

本章将对Simulink系统仿真原理作简单的介绍，以使用户对Simulink进行系统仿真的核心有一个简单的了解。

这对系统分析与设计的作用不言而喻。

&6.1 Simulink求解器概念Simulink求解器是Simulink进行动态系统仿真的核心所在，因此欲掌握Simulink系统仿真原理，必须对Simulink的求解器有所了解。

在第5章中讲述动态系统的Simulink仿真技术时曾简单提及Simulink求解器的选择与使用，本节将对其作深入的介绍。

6.6.1 离散求解器第3章中简单介绍了动态系统的模型及其描述，其中指出，离散系统的动态行为一般可以由差分方程描述。

众所周知，离散系统的输入与输出仅在离散的时刻上取值，系统状态每隔固定的时间才更新一次；而Simulink 对离散系统的仿真核心是对离散系统差分方程的求解。

因此, Simulink 可以做到对离散系统的绝对精确（除去有限的数据截断误差）。

在对纯粹的离散系统进行仿真时，需要选择离散求解器对其进行求解。

用户只需选择Simulink 仿真参数设置对话框中的求解器选项卡中的discrete（no continuous states）选项，即没有连续状态的离散求解器，便可以对离散系统进行精确的求解与仿真。

读者可以参考第5章中相关内容了解离散系统求解器的其它设置，这里不再赘述。

6.1.2 连续求解器与离散系统不同，连续系统具有连续的输入与输出，并且系统中一般都存在着连续的状态设置。

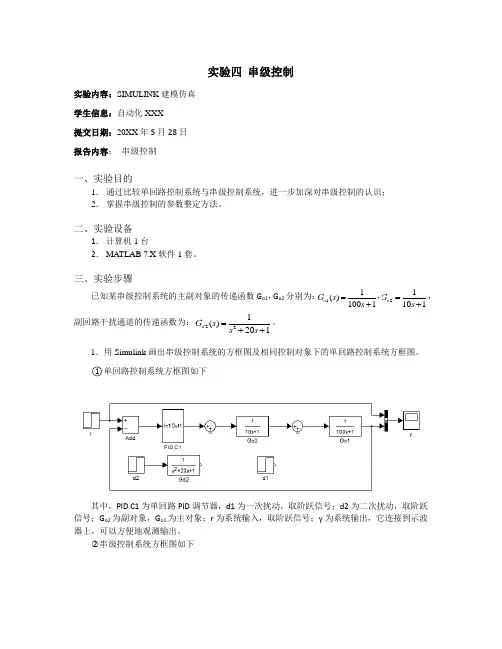
实验四 串级控制实验内容：SIMULINK 建模仿真 学生信息：自动化XXX 提交日期：20XX 年5月28日 报告内容： 串级控制一、实验目的1． 通过比较单回路控制系统与串级控制系统，进一步加深对串级控制的认识； 2． 掌握串级控制的参数整定方法。

二、实验设备1． 计算机1台2． MATLAB 7.X 软件1套。

三、实验步骤已知某串级控制系统的主副对象的传递函数G o1，G o2分别为：211,1001101o G s s ==++，121()101o o G s s =+，副回路干扰通道的传递函数为：221()201d G s s s =++。

1．用Simulink 画出串级控制系统的方框图及相同控制对象下的单回路控制系统方框图。

○1单回路控制系统方框图如下其中，PID C1为单回路PID 调节器，d1为一次扰动，取阶跃信号；d2为二次扰动，取阶跃信号；G o2为副对象，G o1为主对象；r 为系统输入，取阶跃信号；y 为系统输出，它连接到示波器上，可以方便地观测输出。

○2串级控制系统方框图如下其中，PID C1为主调节器，采用PD调节，PID C2为副调节器，采用P调节；q1为一次扰动，取阶跃信号；q2为二次扰动，取阶跃信号；G o2为副对象，G o1为主对象；r为系统输入，取阶跃信号；y为系统输出，它连接到示波器上，可以方便地观测输出。

2．选用PID调节器，整定调节器的参数，并绘制相应的单位阶跃响应曲线。

进行调节器的参数整定，当输入比例系数为260，积分系数为0，微分系数为140时，系统阶跃响应达到比较满意的效果，记录系统阶跃响应图。

采用这套PID参数时，二次扰动作用下，置输入为0，系统框图如下，记录系统的输出响应图。

采用这套PID参数时，一次扰动作用下，置输入为0，系统框图如下，记录系统的输出响应图。

综合以上各图可以看出采用单回路控制，系统的阶跃响应达到要求时，系统对一次和二次扰动的抑制效果不是很好。

某串级系统的方框图如图所示，已知各环节的传递函数如下： 对象特性：，)13)(130(1)(1++=s s s G o ，)110()1(1)(22++=s s s G o 调节器：， )11()(11sT K s G i c c +=，22)(c c K s G = 调节阀： 1)(==v v K s G 变送器： 121==m m G G（1）先用稳定边界法对副调节器进行整定，求出2c K ；然后对主调节器整定，求出主调节器的参数1c K 、i T 。

（2）如果主调也用比例作用，求二类扰动D 2和一类扰动D 1在单位阶跃时主被控量的静差，并进行分析。

（3）若采用简单控制系统，已得调节器的比例增益4.5=c K ，再分别求出二类扰动D 2和一类扰动D 1在单位阶跃时的静差，且与（2）比较分析。

过程控制系统设计仿真实验报告实验名称：串级控制系统仿真实验姓名：学号：班级：一、实验目的1. 掌握串级控制系统的组成和原理2. 掌握串级控制系统两步法PID 参数整定过程。

3. 理解掌握串级控制系统的动态特性和克服扰动能力。

二、实验步骤（1）a:先用稳定边界法对副调节器进行整定，求出2c K =1/P2=12.1①使系统处于串级运行状态，主，副调节器均为比例作用的条件下，先将主调节器的比例度 P1置于100%刻度上，然后有大到小逐渐降低副调节器的比例度P2，直到系统对输入的阶跃 响应出现临界振荡，记下这时的比例放大系数Pm=0.0412;②根据所记录的Pm ，用195页的经验公式计算调节器的整定参数:P2=2Pm=0.0824。

b:然后对主调节器整定，求出主调节器的参数1c K =1/P1=9.9、iT =9.86。

①在副调节器的比例度等于2Pm 的条件下，逐步降低主调节器的比例度P1,直到同样得到临 界振荡，记下这时的比例放大系数Pm=0.0459和临界振荡周期Tm=11.6。

②根据所记录的Pm 和Tm ，用195页的经验公式计算调节器的整定参数： P1=2.2Pm=0.10098,iT =0.85Tm=9.86。