电路基础课后习题答案(专科教材)汇总

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

课后习题参考答案1.元器件实验基础1．通过色环分别求出一下电阻的阻值R1R2R3R1R2R3根据表格可以得出：R1：23×101 ±5%R1的阻值应该在218Ω 到241Ω之间.R2：33×102 ±5%R2的阻值应该在3.2 kΩ 到3.4 kΩ之间.R3：68×103 ±5%R3的阻值应该在64.6 kΩ 到71.4 kΩ之间.如下图左, 将数字万用表(Digital Multimeter, 简称DMM) 设置为[Ω]的测量模式, 并测量出电阻阻值.要注意的是, 任何工程测量都存在误差, 因此DMM所得出的测量误差可以通过仪表参数进行计算, 本章实验中我们不对此做出详细阐述。

2.如上图右，仔细观察图中的信息，已知滑动变阻器是0-10k，那么绿线端和蓝线端的电阻为多少？你是怎么知道的？答：滑动变阻器的总阻值为10kΩ即绿线端到黄线端的电阻大小。

因为蓝线到黄线端的电阻为5.8kΩ，所以绿线端到蓝线端的电阻为4.2k欧姆。

2. 欧姆定律1.如果电压为24 V应用在2.2 kΩ的电阻上，则电流是多少？答：由欧姆定律公式可知：I=V R代入数值：V=24V R=2.2KΩ可以得出电流I=10.9mA2.如果电阻上的电压为12 V，需要多大的电阻来可以得出电流为1.2 mA？答：由欧姆定律公式可以知道：R=V I代入数值：V=12V I=1.2mA可以得出电阻R=10KΩ3.根据下图电路的的连接以及仪器显示，不要在直接测量电阻的方法或者读色环的方法下，能否计算出，所用电阻的阻值？答：从图片可知MEGO提供的电压大小为5V，VEGO测得电流大小为22.72mA。

由欧姆定律公式可以知道：R=V I代入数值：V=5V I=22.72mA可以得出电阻R=220Ω4.表格1中, 第三列电流是根据计算得出, 第四列电流是根据测量得出.两者之间是否足够接近? 两者之间的实验误差是否可以验证欧姆定律以及本实验的正确性.答：略5.绘制欧姆定律关系图. 根据表格1的数据, 在本章结尾处的方格纸中绘制伏安特性图,也就是I-V曲线.答：略6.画出电阻的I-V曲线后, 我们可以根据该曲线得出在不同条件下的电流或电压值.比如: 当I = 5.6 mA, 我们可以在曲线上找出对应的V R值.根据这个特点, 将表格2完成.表格 2(a)通过I-V曲线的斜率可以计算阻值, 其方法如下:斜率(slope)=m=∆y∆x=∆I R∆V R=1R提问: 如果某电阻的I-V曲线斜率为0.001 Ω-1 (单位是: 西门子) , 其阻值是多少?答：略(b)计算:根据(a)中的公式, 假设I-V曲线的斜率为m.如果阻值增长, 那么对应m应当增加或是减少？假设某器件的I-V曲线函数的图像几乎是平坦的, 那么这是一个导体还是绝缘体?答：略绘制电阻的I-V曲线:流电电压3.串联和并联电路1.在表1和表2中, 对比三种方法(计算, 测量, 欧姆定律)所得到的等效阻值是否足够接近？答：略2.仔细观察下图的电路，根据电源以及万用表的读数，连接下图万用表的正端（红色线的部分）使得下图的电路连接以及读数都是合理的。

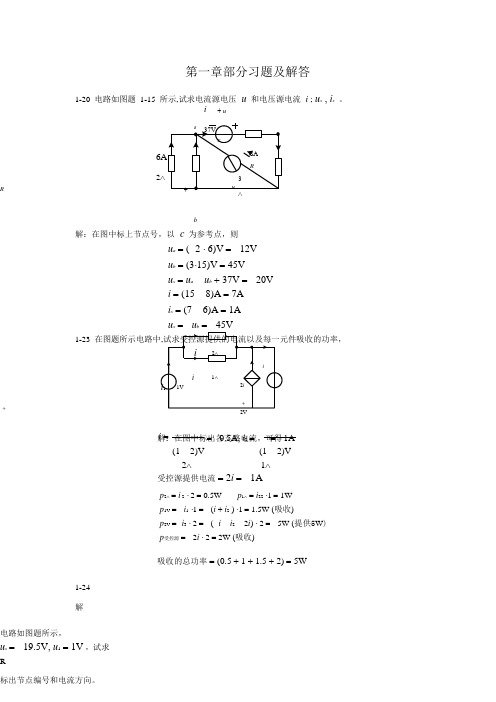
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。

i+ u2Rb解：在图中标上节点号，以 c 为参考点，则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解：在图中标出各支路电流，可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示，u s = 19.5V, u 1 = 1V ，试求R标出节点编号和电流方向。

ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R，需计算i4，u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。

a 1∧ci+6Vb解求解三个未知量需要三个独立方程。

由KCL可得其中之一，即i1 + i2 + i3 = 5对不含电流源的两个网孔，列写KVL方程，得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得： ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。

答案8.1解：)/1()(T t A t f -= T t <<0⎰⎰-==T T dt T t A T dt t f T A 000)/1(1)(1A T t t T A T5.0]2[02=-=⎰-=Tk dtt k T t A T a 0)cos()/1(2ω0)sin(2)]sin()/1(2[020=+⨯-=⎰T T dt t k T k A t k Tk T t A ωωωω ⎰-=Tk dtt k T t A T b 0)sin()/1(2ωπωωωωωk A kT A dt t k T k A t k Tk T t A T T==-⨯--=⎰2)cos(2)]cos()/1(2[020 所以∑∞=+=1sin 5.0)(k t k k AA t f ωπ频谱图如图(b)所示。

.0答案8.2解：电流i 的有效值57.1)2/13.0()2/67.0()2/57.1(12222≈+++=I A只有基波电流与正弦电压形成平均功率，故二端电路输入的平均功率为：95.73)]90(90cos[257.122.94=︒--︒-⨯=P W 注释：非正弦周期量分解成傅里叶级数后，其有效值等于直流分量和不同频率交流分量有效值平方和的平方根。

答案8.3解：对基波︒∠=0100m(1)U V , A 010m(1)︒∠=I 由Ω==-+=10)1(j )1(m )1(m )1(I U C L R Z ωω求得Ω=10R , 01=-CL ωω (1)对三次谐波︒-∠=3050m(3)U V , A 755.1im(3)ψ-∠=I又由Ω+︒-∠==-+=)30(5.28)313(j m(3)m(3))3(i I U C L R Z ψωω (2)所以2225.28)313(=-+CL R ωω (3)将式(1)代入式(3)， 解得mH 9.31=L将mH 9.31=L 代入式（ 1 ），求得F 3.318μ=C再将C L R 、、值代入式(2)，有Ω︒-∠=Ω+=3028.5j26.7)10(i )3(ψZ 解得︒=45.99i ψ答案8.4解: (1) 电压有效值：V 01.80)225()250()2100(222=++=U电流有效值58.74mA )210()220()280(222=++=I (2) 平均功率 kW 42.345cos 210250cos 22050)45cos(280100=︒⨯+︒⨯+︒-⨯=PΩ︒∠=︒∠︒∠=Ω=︒∠︒∠=Ω︒-∠=︒∠︒-∠=k 455.2mA010V 4525k 5.2mA 020V 050k 4525.1mA 080V45100)3()3()2()1(Z Z Z 注释：非正弦周期量分解成傅里叶级数后，某端口的平均功率等于直流分量和不同频率交流分量单独作用产生的平均功率之和。

电路分析基础习题第三章答案（史健芳）电路分析基础习题第三章答案（史健芳）第3章3.1 选择题1．必须设立电路参考点后才能求解电路的方法是( C )。

A ?支路电流法B ?回路电流法C ?节点电压法D?2b法2．对于一个具有n 个结点、 b 条支路的电路，他的KVL 独立方程数为( B )个。

A．n-1 B ．b-n+1 C．b-nD ．b-n-13．对于一个具有n 个结点、 b 条支路的电路列写结点电压方程，需要列写( C )。

A. (n-1)个KVL 方程B．( b-n+1 )个KCL 方程C. (n-1)个KCL 方程D．( b-n-1 )个KCL 方程4．对于结点电压法中的无伴电压源，下列叙述中，( A )是错误的。

A ．可利用电源等效变换转化为电流源后，再列写结点电压方程B ?可选择该无伴电压源的负极性端为参考结点，则该无伴电压源正极性端对应的结点电压为已知，可少列一个方程C ?可添加流过该无伴电压源电流这一新的未知量，只需多列一个该无伴电压源电压与结点电压之间关系的辅助方程即可D ?无伴受控电压源可先当作独立电压源处理，列写结点电压方程，再添加用结点电压表示控制量的补充方程5 ?对于回路电流法中的电流源，下列叙述中，(D )是错误的。

A ?对于有伴电流源，可利用电源等效变换转化为电压源后，再列写回路电流方程B ?对于无伴电流源，可选择合适的回路，使只有一个回路电流流过该无伴电流源，则该回路电流为已知，可少列一个方程C ?对于无伴电流源，可添加该无伴电流源两端电压这一新的未知量，只需多列一个无伴电流源电流与回路电流之间关系的辅助方程即可D ?电流源两端的电压通常为零6 ?对于含有受控源的电路，下列叙述中，(D )是错误的。

A ?受控源可先当作独立电源处理，列写电路方程B ?在结点电压法中，当受控源的控制量不是结点电压时，需要添加用结点电压表示控制量的补充方程C ?在回路电流法中，当受控源的控制量不是回路电流时，需要添加用回路电流表示控制量的补充方程D ?若采用回路电流法，对列写的方程进行化简，在最终的表达式中互阻始终是相等的，即：R ij=R ji3.2填空题1. _ 对于具有n个结点b条支路的电路，可列出n-1 _ 个独立的KCL方程，可列出b-n+1个独立的KVL 方程。

/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。

a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。

20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。

如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。

设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。

问实际的电压应为多少？ 解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。

已知：12315,5,10,R R R =Ω=Ω=Ω。

10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。

教材习题3答案部分（P73）答案略 答案解：（a ） 本题考虑到电桥平衡，再利用叠加定理，计算非常简单。

（1）3V 电压源单独作用,如图(a-1)、(a-2)所示。

(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得：''182A 483I I Ω=-⨯=-Ω+Ω（2）1A 电流源单独作用，如图(a-3)所示。

(a-3)考虑到电桥平衡，"0I =，在由分流公式得："1131A A 134I =-⨯=-+ （3）叠加：'"1A I I I =+= '"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=（b ）（1）4V 电压源单独作用，如图(b-1)所示。

'I '由图(b-1)可得，'24V2V (2+2)U Ω⨯==Ω'136A I U =-=- ''21'5A I I I =+=-（2）2A 电流源单独作用，如图(b-2)所示。

(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯= 对节点②列KCL 方程得，"""1132A 4A I U I +==对节点③列KCL 方程得，"""230I I U ++=解得"5A I =（3） 叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=答案略答案略答案解 ：利用叠加定理，含源电阻网络中的电源分为一组，其作用为'I ，如图(b)所示。

S I 为一组，其单独作用的结果I '' 与S I 成比例，即："S I kI =，如图(c)所示。

答案10.1解：0<t 时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t 时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A 3)363685(V45)0(=Ω+⨯++=-i ，A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得：V 24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i 由KVL 得开关电压：V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解：0<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为 A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

电路分析基础第三版课后答案俎云霄第一章1.1题解答：根据题目给出的电压和电流值，我们可以使用基尔霍夫定律进行求解。

根据基尔霍夫定律，我们可以得到以下两个方程：方程1: V1 = i1 * R1方程2: V1 + V2 + V3 = 0将方程1代入方程2中，我们可以得到以下方程：i1 * R1 + V2 + V3 = 0根据题目给出的电压和电流值，带入以上方程中可以得到：10 * 5 + V2 + V3 = 0解方程得到：V2 + V3 = -50所以，电压V2 + V3的值为-50V。

1.2题解答：根据题目给出的电压和电流值，我们可以使用欧姆定律进行求解。

根据欧姆定律，我们可以得到以下方程：V1 = i1 * R1将题目给出的电压和电流值代入以上方程中，可以得到：5 = i1 * 100解方程得到：i1 = 0.05A所以，电流i1的值为0.05A。

1.3题解答：根据题目给出的电阻值和电流值，我们可以使用欧姆定律进行求解。

根据欧姆定律，我们可以得到以下方程：V1 = I * R将题目给出的电阻值和电流值代入以上方程中，可以得到：12 = I * 6解方程得到：I = 2A所以，电流I的值为2A。

1.4题解答：根据题目给出的电压和电流值，我们可以使用欧姆定律进行求解。

根据欧姆定律，我们可以得到以下方程：V = I * R将题目给出的电压和电流值代入以上方程中，可以得到：20 = I * 4解方程得到：I = 5A所以，电流I的值为5A。

第二章2.1题解答：根据题目给出的电压和电流值，我们可以使用基尔霍夫定律进行求解。

根据基尔霍夫定律，我们可以得到以下两个方程：方程1: V1 + V2 - V3 = 0方程2: I1 + I2 - I3 = 0根据题目给出的电压和电流值，带入以上方程中可以得到：10 + V2 - V3 = 0I1 + 4 - I3 = 0解方程得到：V2 = V3 - 10I1 = I3 - 4所以，电压V2可表示为V3 - 10，电流I1可表示为I3 - 4。