粒子滤波算法研究现状与发展趋势

粒子滤波综述
吕德潮;范江涛;韩刚瓮;马冠一
【期刊名称】《天文研究与技术－国家天文台台刊》
【年(卷),期】2013(010)004
【摘要】主要对粒子滤波算法进行综述.首先详细描述了递归贝叶斯估计的基本原理和基于蒙特卡罗方法的重要性采样/重采样技术,在此基础上引出了粒子滤波标准算法——序贯重要性采样算法和序贯重要性重采样算法.针对这两个算法在应用中存在的问题,从提高算法的有效性和实时性两个方面,对近年来国内外在粒子滤波理论及应用研究方面开展的工作进行了介绍、分析归纳了改进粒子滤波算法及其主要改进思想.最后,对粒子滤波算法的研究方向进行了展望.
【总页数】13页(P397-409)
【作者】吕德潮;范江涛;韩刚瓮;马冠一
【作者单位】中国科学院国家天文台,北京100012;中国科学院大学物理科学学院,北京100049;中国科学院国家天文台,北京100012;中国科学院大学物理科学学院,北京100049;北京航天飞行控制中心,北京100094;中国科学院国家天文台,北京100012
【正文语种】中文
【中图分类】TN911.72
【相关文献】
1.智能优化粒子滤波算法综述研究 [J], 刘淑波;张园;龚丽
2.基于卡尔曼滤波与粒子滤波的SLAM研究综述 [J], 孙海波;童紫原;唐守锋;童敏明;纪玉明
3.Mean Shift和粒子滤波实现红外人体跟踪算法综述 [J], 耿建平; 雷梦英
4.基于卡尔曼滤波与粒子滤波的SLAM研究综述 [J], 孙海波[1];童紫原[2];唐守锋[1];童敏明[1];纪玉明[3]
5.智能优化粒子滤波算法综述研究 [J], 刘淑波[1];张园[1];龚丽[2]
因版权原因，仅展示原文概要，查看原文内容请购买。

文章编号:1671-637Ú(2005)06-0001-04粒子滤波的关键技术及应用夏克寒1,许化龙1,张朴睿2(1.第二炮兵工程学院,陕西西安710025;2.清华大学计算机学院,北京100083)摘要:粒子滤波算法及应用的研究在近几年来取得了很大进展,相继出现了一些新算法、新应用。

首先介绍了粒子滤波的特征及算法分类,然后对其关键技术进行了归纳分析,并给出了粒子滤波的一些典型应用成果,最后指出了粒子滤波技术亟待解决的一些热点和难点问题。

关键词:粒子滤波;稳定性;重要性采样中图分类号:V271.4;TN713文献标识码:ACritical technologies and applications of particle filterXI A Ke-han1,XU Hua-long1,ZHANG Pu-rui2(1.Second Artille ry Engineering Colle ge,Xi.an710025,China; p uter I nstitute,Tsinghua Unive rsity,Beijing100083,China)Abstract:In recent years,great progresses have been made in the research on algorithms and application of particle filter,and some new algorithms and applications were put forward.In this paper,the characteristics and classification of particle filter are introduced first.Then some critical technologies of particle filter are sum marized and analyzed,and some typical application results are given.Finally,some issues are pointed out which should be the focus of future study.Key Words:particle filter;stability;sampling importance0引言在处理非线性滤波问题时最常用的方法是推广卡尔曼滤波[1]。

粒子滤波算法经典粒子滤波算法的一般描述：1.初始化：取k ＝0，按0()p x 抽取N 个样本点()0i x ，i ＝1,…,N 。

2.重要性采样： ()()0:11:(|,)i i k k k kx q x x z -~，令 ()()()0:0:1(,)i i i k k k x x x -=，其中i ＝1,…,N 。

3.计算权值： ()()()()()11()()0:11:(|)(|)(|,)i i i i i k k k k kk i i kk k p z x p x x q xxz ---ω=ω若采用一步转移后验状态分布，该式可简化为()()()1(|)i i i k k k k p z x -ω=ω。

4.归一化权值： ()j j i i kk Nk()()=1ωω=ω∑5.重采样：根据各自归一化权值 ()i k ω的大小复制/舍弃样本 ()0:i k x ，得到N 个近似服从()0:1:(|)i k k p x z 分布的样本()0:i k x 。

令()i k ω＝ ()i k ω＝1/N ，i ＝1,…,N 。

6.输出结果：算法的输出是粒子集()0:{: 1...}i k x i N =，用它可以近似表示后验概率和函数0:()k k g x 的期望0:0:1:0:11(|)()i kNk k k x i p x z dx N()==δ∑0:0:11(())()Nik k k k i E g x g x N==∑7.K=K+1,重复2步至6步。

其它粒子滤波 正则粒子滤波正则粒子滤波(Regularized Particle Filter ，RPF)是为了解决由重采样引入的新问题而提出的一种改进的粒子滤波。

当通过序贯重要性采样后引起粒子退化问题时，前面提到可以用重采样的方法来减小退化的影响，但是引入重采样策略同时也引入了新的问题，即粒子匮乏问题，经过若干次迭代之后，所有粒子都趋向于同一个粒子，导致粒子的多样性丧失。

粒子滤波及mat I ab实现粒子滤波就是指：通过寻找一组在状态空间中传播的随机样本来近似的表示概率密度函数，用样本均值代替积分运算，进而获得系统状态的最小方差估计的过程，这些样本被形象的称为“粒子”,故而叫粒子滤波。

粒子滤波通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波，适用于任何能用状态空间模型描述的非线性系统，精度可以逼近最优估计。

粒子滤波器具有简单、易于实现等特点，它为分析非线性动态系统提供了一种有效的解决方法，从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。

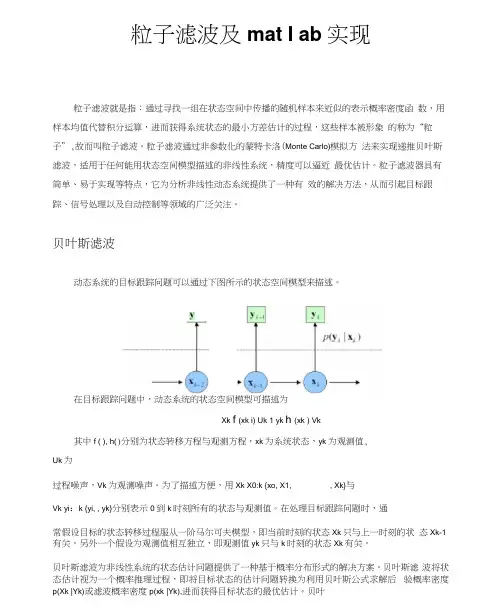
贝叶斯滤波动态系统的目标跟踪问题可以通过下图所示的状态空间模型来描述。

在目标跟踪问题中，动态系统的状态空间模型可描述为Xk f (xk i) Uk 1 yk h (xk ) Vk其中f ( ), h()分别为状态转移方程与观测方程，xk为系统状态，yk为观测值,Uk为过程噪声，Vk为观测噪声。

为了描述方便，用Xk X0:k {xo, X1, , Xk}与Vk yi：k {yi, , yk}分别表示0到k时刻所有的状态与观测值。

在处理目标跟踪问题时，通常假设目标的状态转移过程服从一阶马尔可夫模型，即当前时刻的状态Xk只与上一时刻的状态Xk-1有关。

另外一个假设为观测值相互独立，即观测值yk只与k时刻的状态Xk有关。

贝叶斯滤波为非线性系统的状态估计问题提供了一种基于概率分布形式的解决方案。

贝叶斯滤波将状态估计视为一个概率推理过程，即将目标状态的估计问题转换为利用贝叶斯公式求解后验概率密度p(Xk |Yk)或滤波概率密度p(xk |Yk),进而获得目标状态的最优估计。

贝叶斯滤波包含预测和更新两个阶段，预测过程利用系统模型预测状态的先验概率密度，新过程则 利用最新的测量值对先验概率密度进行修正，得到后验概率密度。

假设已知k 1时刻的概率密度函数为p(x k1| Y-),贝叶斯滤波的具体过程如下：(1) 预测过程，由 p (xk 11 Yk 1)神 p(xk | Yk i)p ( Xk, Xk 11 Yk i) p (xk | Xk 1, Yk i) p (xk 11 Yk i)当给定Xk 1时，状态Xk 与Yk 1相互独立，因此p (xk, Xk 11 Yk i) p (xk | Xk i) p (xki | Yk i)上式冷Xk 1积分，可得Chapman-Komo I gorov 方程p (xk| Yk i) p (xk| Xk i) p (xk 11 Yk i) dxk 1⑵更新过程，由p(xk | Yk i)得到p(xk | Yk)：获取k 时刻的测量yk 后，利用贝叶斯公式对先验概率密度进行更新，得到后验概率p (yk | Xk, Yk i) p (xk | Yk i)P ( yk | Yk i) P (yk | xk)p (yk | Xk) p (xk | Yk i)P (yk| Yk i)其中，p(yk |Yk i)为归一化常数p (yk | Yk i) p (yk | xk) p (xk | Yk 1) dxk贝叶斯滤波以递推的形式给出后验(或滤波)概率密度函数的最优解。

粒子滤波算法
粒子滤波算法（Particle Filtering Algorithm）是一种在最近几年被广泛应用于机器人视觉定位和机器人轨迹跟踪领域的定位技术。

这种算法具有快速、精确、实时等优点，可以帮助机器人及时准确地定位自身位置。

粒子滤波算法的基本原理是建立一个概率分布模型，该模型用于跟踪机器人的位置，它基于一系列计算步骤，主要包括：
1）状态预测步骤：将机器人的上一个位置作为输入，利用状态估计算法（如Kalman滤波）预测机器人的下一个位置，以便在系统中实现实时定位。

2）更新步骤：通过使用环境感知技术（如视觉定位）获取机器人位置的实时反馈信息，进行状态更新，以便更准确地定位机器人的位置。

3）变量步骤：将位置反馈信息转换为概率分布模型，根据模型和其他环境信息，推断出机器人当前位置的变量信息。

4）计算步骤：根据变量信息，计算出机器人当前位置，以及当前位置的置信度，以便决定准确度。

粒子滤波算法具有计算量小、操作简单等优点，可以高效准确地定
位机器人位置，有效提高机器人自主定位能力。

该算法已被广泛应用于机器人定位、轨迹跟踪、室内建图、机器人视觉、导航系统等领域，为机器人智能系统发展做出了重要贡献。

gru粒子滤波算法"GRU粒子滤波算法"这句话指的是使用门控循环单元（GRU）与粒子滤波算法相结合的方法。

首先，我们来了解一下相关的概念：1.GRU：门控循环单元（GRU）是一种循环神经网络（RNN）的变体，用于处理序列数据。

与传统的RNN相比，GRU具有更少的参数和更简单的结构，能够更好地捕捉序列中的长期依赖关系。

2.粒子滤波算法：粒子滤波是一种基于蒙特卡罗方法的递归贝叶斯滤波算法，用于估计一个动态系统的状态。

它通过随机采样和重采样技术，从一组代表系统状态的粒子中估计状态变量的后验概率分布。

将GRU与粒子滤波算法相结合，可以利用GRU对序列数据的处理能力，以及粒子滤波算法在非线性、非高斯系统中的估计性能。

这种结合的方法可以应用于各种领域，如目标跟踪、语音识别、自然语言处理等。

以下是一些使用GRU与粒子滤波算法结合的示例：1.目标跟踪：在目标跟踪问题中，可以使用GRU来捕捉目标的运动模式，并使用粒子滤波算法估计目标的轨迹和状态。

通过结合GRU和粒子滤波算法，可以更好地处理目标的非线性运动和动态变化。

2.语音识别：在语音识别任务中，可以使用GRU来捕捉语音信号的时间依赖性，并使用粒子滤波算法对语音特征进行跟踪和识别。

这种方法可以处理语音信号的非线性特性和噪声干扰。

总结来说，"GRU粒子滤波算法"是指将门控循环单元（GRU）与粒子滤波算法相结合的方法。

这种结合可以利用GRU对序列数据的处理能力，以及粒子滤波算法在非线性、非高斯系统中的估计性能。

通过结合这两种算法，可以应用于各种领域，如目标跟踪、语音识别、自然语言处理等。

粒子滤波通俗讲解粒子滤波（Particle Filter）是一种基于蒙特卡洛方法的非线性滤波算法，常用于目标跟踪、定位和SLAM（同步定位与地图构建）等领域。

它的核心思想是通过一系列粒子（也称为样本或假设）来近似表示系统的后验概率分布，从而实现对系统状态的估计和预测。

粒子滤波的基本原理是利用一组随机生成的粒子来表示系统的潜在状态。

每个粒子都有一个权重，反映了它与真实状态的拟合程度。

粒子滤波通过对粒子的重采样和更新，逐步减小粒子权重的方差，从而逼近真实状态的后验概率分布。

在粒子滤波中，首先需要初始化一组随机粒子，这些粒子在状态空间中均匀或按某种分布进行采样。

然后，根据系统的状态转移方程，将粒子进行预测，得到下一时刻的状态估计。

预测过程中，可以考虑系统的动力学模型和外部扰动等因素。

接下来，需要利用观测数据对粒子进行更新。

观测数据可以是传感器采集到的现实数据，如图像、激光雷达或GPS测量值等。

通过比较观测数据和预测状态之间的差异，可以计算粒子的权重，即粒子与真实状态的拟合程度。

在更新过程中，通常会使用重要性采样（Importance Sampling）来调整粒子的权重。

重要性采样的基本思想是根据观测数据的条件概率分布，对粒子的权重进行重新分配。

权重较高的粒子将被保留，而权重较低的粒子将被淘汰。

为了避免粒子权重的退化（degeneracy），即只有少数粒子具有较高权重，大多数粒子权重趋近于0，需要进行重采样（Resampling）。

重采样过程中，根据粒子的权重对粒子进行有放回或无放回的随机抽样，使得权重较高的粒子被重复选择，而权重较低的粒子被剔除。

通过重采样，粒子滤波可以实现对系统状态的精确估计。

重采样后，可以利用重采样后的粒子集合进行下一时刻的预测和更新，循环迭代直到获得最终的状态估计。

粒子滤波作为一种基于蒙特卡洛方法的非线性滤波算法，具有一定的优势。

与传统的卡尔曼滤波相比，粒子滤波可以处理非线性系统和非高斯噪声，并且不需要对系统进行线性化。

卫星姿态确定及敏感器误差修正的滤波算法研究一、内容综述近年来，随着空间技术的迅速发展，卫星在通信、导航、气象、国防等方面都发挥着越来越重要的作用。

为了准确而稳定地获取卫星的各种信息，精确的卫星姿态确定与敏感器误差修正显得尤为重要。

针对这一问题，研究者们对卫星姿态确定与敏感器误差修正方法开展了广泛而深入的研究。

本文将对这些方法进行综述，从基本原理到算法实现，全面展现当前该领域的进展。

卫星姿态确定主要涉及到卫星位置和角度的确定，是卫星自主导航、控制与管理的基础。

卫星上通常设置有三轴陀螺仪和三轴加速度计等敏感器来测量卫星姿态变化，并通过滤波算法实现对姿态的精确估计。

在实际运行过程中，由于各种因素的影响，如敏感器的制造误差、环境条件变化等，会导致敏感器输出数据存在偏差，从而影响卫星姿态确定的精度和稳定性。

为了提高姿态确定的准确性，需要采用有效的误差修正方法对敏感器数据进行校正。

现有的误差修正方法可分为两类：基于统计的方法和基于模型的方法。

统计方法主要依赖于大量的历史数据，通过对数据进行拟合和预测来实现误差修正，但难以处理非线性关系和复杂动态环境。

而基于模型的方法则是利用系统内部的先验知识，建立误差模型进行误差修正，具有较强的实时性和适应性。

滤波算法作为一种高效的数值计算方法，已被广泛应用于卫星姿态确定与敏感器误差修正中。

通过对观测数据进行处理，滤波算法能够估计出卫星的实际姿态，并通过反馈控制进一步优化姿态估计精度，实现卫星的高精度、高稳定性的运行。

1. 卫星在现代通信、导航及遥感中的重要性近年来，随着空间技术的迅猛发展，卫星在现代通信、导航及遥感领域的应用越来越广泛，其重要性也日益凸显。

卫星通信技术的发展使得全球范围内的信息交流变得更加迅速和便捷，为全球信息化社会的建设提供了有力支持。

导航技术在军事、交通、消防、救援等领域发挥着越来越重要的作用，极大地提高了人们的出行效率和安全性。

卫星遥感技术在农业、林业、海洋、环境监测等领域的应用也为我们认识和改造世界提供了强大的手段。

粒子滤波原理及应用matlab仿真一、引言粒子滤波（Particle Filter）是贝叶斯滤波（Bayesian Filter）的一种扩展，用于解决非线性和非高斯问题。

它是一种基于蒙特卡罗方法的状态估计算法，可以用于目标跟踪、机器人定位、信号处理等领域。

本文将详细介绍粒子滤波的原理及其在matlab中的应用。

二、贝叶斯滤波贝叶斯滤波是一种基于贝叶斯定理的概率推断方法，用于估计状态变量在给定观测值下的后验概率分布。

其核心思想是将先验概率分布和观测数据结合起来，得到后验概率分布。

具体地，在时间步k时刻，假设状态变量为x(k)，观测变量为y(k)，则根据贝叶斯定理：P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中，P(x(k)|y(1:k))表示在已知前k个观测值下x(k)的后验概率分布；P(y(k)|x(k))表示在已知x(k)时y(k)的条件概率分布，也称为似然函数；P(x(k)|y(1:k-1))表示在已知前k-1个观测值下x(k)的先验概率分布；P(y(k)|y(1:k-1))表示前k-1个观测值的边缘概率分布。

三、粒子滤波基本原理粒子滤波是一种基于贝叶斯滤波的蒙特卡罗方法，它通过在状态空间中随机采样一组粒子来近似表示后验概率分布。

每个粒子都代表一个可能的状态变量，其权重反映了该状态变量与观测值之间的匹配程度。

具体地，在时间步k时刻，假设有N个粒子{ x(1), x(2), ..., x(N) }，则每个粒子都有一个对应的权重w(i)，且满足：∑ w(i) = 1根据贝叶斯定理可得：P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中，P(y(k)|x(k))和P(x(k)|y(1:k-1))可以通过系统模型和观测模型计算得到。

粒子滤波算法原理
粒子滤波属于一种非参数（无给定参数）的有效滤波算法，它通过模拟某一随机变量的一系列取值可能性统计特征，来实现滤波的功能。

粒子滤波算法的基本思想是：采用一致采样方法，观察上面相应的传感器检测器读数综合，估计系统状态。

利用随机性（根据目前状态、测量噪声及控制输入）预测模型，并采用卡尔曼滤波算法进行实际状态估计。

粒子滤波的重点是从采样点统计特征，确定最有可能的状态来应对变幻的环境参数，有别于卡尔曼滤波的估计过程。

其主要步骤为：滤波引入采样点；选择根据当前状态预测新状态；观察新状态和新观测结果并且计算根据当前观测结果的后验概率来更新分布；根据观测结果更新后的后验概率控制采样点来估计。

粒子滤波算法精确可靠，是一种有效的滤波算法，适用于各种状态估计过程。