可液化土层中地下车站的地震反应分析_王刚

地震对地下铁路与隧道的影响及应急修复地震是自然灾害中的一种，它对地下铁路与隧道造成的影响通常是灾难性的。

地下铁路与隧道是城市重要的交通设施，如何及时做好地震应急修复工作对于恢复城市正常交通运行至关重要。

本文将重点探讨地震对地下铁路与隧道的影响及应急修复措施。

1、地震对地下铁路与隧道的影响
地震通常会导致地下结构物受到水平和垂直方向的振动，从而对地下铁路与隧道产生一系列直接或间接的影响。

首先，地震可能导致地下铁路与隧道结构的损坏，例如墙体开裂、管道破裂等；其次，地震可能导致地下设备的损坏，如电力系统、通信系统等；再次，地震可能导致土体液化，进而影响地下铁路与隧道的稳定性。

总之，地震对地下铁路与隧道的影响主要表现为结构破坏、设备损坏和土体液化等方面。

2、地震应急修复措施
地震一旦发生，地下铁路与隧道可能会受到不同程度的影响，因此需要及时采取应急修复措施。

首先，第一时间需要确定地下铁路与隧道受损情况，进行紧急评估；其次，要组织专业队伍进行抢险救援，清理垮塌物、疏通通道；再次，要开展维修工作，修复受损结构和设备；最后，要进行必要的防范措施，加固地下铁路与隧道的结构，提高其地震抗震性能。

综上所述，地震对地下铁路与隧道造成的影响是不可忽视的，而应
急修复工作又至关重要。

只有在地震发生后，能够迅速做好应急修复，才能最大限度地减少地下铁路与隧道的损失，保障城市交通的畅通。

希望相关部门能够重视地下铁路与隧道的地震风险，加强防范和准备
工作，做好地震应急修复准备，确保城市的安全和稳定。

地下车站抗震案例分析发表时间：2017-06-26T15:25:19.910Z 来源：《基层建设》2017年5期作者：谢特赐[导读] 地铁作为百年工程，关系国计民生，地铁结构必须满足抗震的要求。

本文以某地下车站为例，采用非线性时程分析法对地下车站抗震有限元计算。

广州地铁设计研究院有限公司 510010摘要：目前是我国轨道交通行业快速发展的时期，地铁建设如火如荼。

地铁作为百年工程，关系国计民生，地铁结构必须满足抗震的要求。

本文以某地下车站为例，采用非线性时程分析法对地下车站抗震有限元计算。

关键词：轨道交通；车站；抗震；非线性时程法1、案例概况本文以某沿海城市地铁1号线某车站为例。

该车站采用明挖法施工，为地下两层12m岛式站台车站，采用地下两层双柱三跨钢筋混凝土框架结构。

本工程抗震设防分类为乙类，抗震等级为三级，按7度抗震设防烈度要求进行抗震计算。

2、抗震分析抗震设计中地震效应的计算方法有反应位移法，地震系数法，弹性时程方法，非线性时程方法等。

根据规范要求，采用反应位移法和时程分析法进行抗震效应计算。

本文仅介绍采用非线性时程分析法对车站进行有限元抗震计算。

由于本站分布均匀、规则且纵向较长，结构分析采用平面应变分析模型。

2.1计算模型建模时取1延米平面框架，柱按抗弯刚度等效原则转化为墙，根据抗弯刚度等效原则计算等效墙厚。

岩土采用平面应变单元、结构采用梁单元进行有限元建模。

岩土采用摩尔-库伦理想弹塑性模型，结构采用线弹性模型。

岩土单元的尺寸约为1m×1m，以满足动力分析的要求。

计算模型底面采用固定边界，侧面采用粘性人工边界。

模型底面取至<17-2>号散体状强风化花岗岩层面，顶面取地表面，侧面边界到结构的距离取结构水平宽度的3倍。

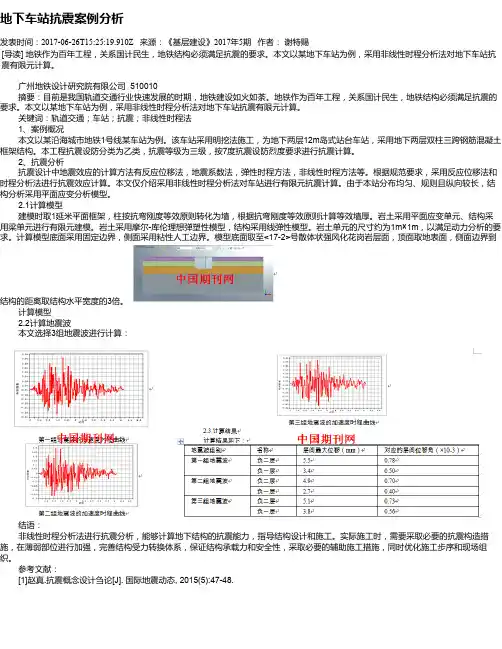
计算模型2.2计算地震波本文选择3组地震波进行计算：结语：非线性时程分析法进行抗震分析，能够计算地下结构的抗震能力，指导结构设计和施工。

实际施工时，需要采取必要的抗震构造措施，在薄弱部位进行加强，完善结构受力转换体系，保证结构承载力和安全性，采取必要的辅助施工措施，同时优化施工步序和现场组织。

0引言随着我国轨道交通工程建设的不断发展，地铁交通也成为公共交通中越来越重要的组成部分，作为百年工程，无论是从公众人身安全角度，或者城市建设经济效益方面，都需要保证地铁车站在各种工况下的安全。

而作为地铁相交线路的网络节点—换乘站，结构受力等方面更加复杂，人员更加集中，一旦遭受破坏将带来更大的社会影响及损失[1]。

近年来，地震灾害较为频繁，带来较大的损失，而根据地铁设计计算，针对地震荷载作用下的车站受力进行分析，从而指导车站设计及建设，对于保证车站安全具有很重要的意义。

根据《城市轨道交通抗震设计规范》（GB50909-2014），车站地震验算推荐使用反应位移法和时程分析法。

其中反应位移法因为计算简单而受到广泛使用，但对于换乘车站，尤其在交叉换乘节点处，车站受力特性复杂，仅采用二维的反应位移法计算不能得到较准确的结果。

因此需采用三维时程分析方法针对换乘车站进一步分析。

目前关于车站的抗震计算分析，国内针对不同的城市、地层条件、车站形式做了具体的研究。

黄伟[1]根据郑州地铁6号线龙湖北路T型换乘站位例进行计算分析，结果表明，车站结构的开口断面和标准断面内主要部位的受力规律基本一致，但断面内两种分析方法计算结果之间表现出一定差异性。

吕娇娇等[2]针对处于软土地区的天津地铁10号线典型车站的抗震进行的分析，考虑使用过程中可能出现的各种荷载组合，分别用反应位移法和时程分析法进行了计算，得出车站在不同工况下的受力特性，在水平地震作用下的换乘车站结构型式变化处，抗震工况将起控制作用。

朱雯蕾等[3]以青岛地铁某明挖车站为例，通过建立二维数值模型，并对复杂节点建立三维模型，经计算对比，结果表明地震工况对车站结构配筋不起控制作用。

龚易洁[4]采用大型通用有限元计算软件ADINA，对合肥地铁某换乘车站地震动力响应进行数值模拟计算与分析，研究车站地震工况下的内力及配筋、构造措施。

本文结合南京软土地区5号线与9号线换乘的下关站抗震受力进行分析，分别采用反应位移法和时程分析法进行验算，分析其受力特性。

地下地铁车站抗震浅析发布时间：2022-04-29T10:00:13.086Z 来源：《工程建设标准化》2022年37卷第1月1期作者：姬仁楠何锋[导读] 本文以某地区城市轨道交通地下地铁车站为背景姬仁楠何锋（中交铁道（武汉）建设科技有限公司湖北武汉 430056）摘要: 本文以某地区城市轨道交通地下地铁车站为背景，利用反应位移法对其地震作用下的部分指标进行抗震分析。

结果表明，在设防地震和罕遇地震下，车站结构的地震作用响应均能满足规范要求。

计算结果已为该车站的抗震设计提供依据，且分析方法可为同类型地下站提供参考。

关键词: 地下地铁车站；反应位移法；设防地震；罕遇地震1·工程概况某轨道交通工程地铁车站为地下二层岛式站台车站，站台宽度12m。

车站外包总长218m，标准段宽21.7m，高13.24m，结构标准段采用地下两层双柱双三跨钢筋混凝土框架箱型结构，地下一层为站厅层，站台层布置在地下二层。

车站顶板覆土3m左右，底板埋深约16.44~18.32m。

本工程抗震设防分类为乙类，抗震设防烈度为6度。

场地类别为Ⅲ类。

地震动峰值加速度为0.05g，场地地震动峰值加速度调整系数为1.3，故本场区基本地震动峰值加速度αmax为0.065g，场地基本地震加速度反应谱特征周期为0.45s。

框架抗震等级为二级。

图1.1 车站断面布置图2·抗震设防目标结合《地铁设计规范》（GB50157-2013）及《城市轨道交通结构抗震设计规范》(GB 50909-2014)中对不同类型地铁结构抗震的相关设防目标的要求，本工程抗震设防目标设定如下：1）Ⅰ级目标：结构在重现期为100年的地震作用下不破坏，完全保证其正常使用功能，结构处于弹性工作状态，完全不影响运营及行车安全。

（50年设计基准期超越概率40%，多遇地震）2）Ⅱ级目标：结构在重现期为475年的地震作用下，不破坏或轻微破坏，应能够保持其正常使用功能；结构处于弹性工作阶段，不应因结构的变形影响正常运营，不因结构变形导致轨道的过大变形而影响行车安全。

混凝土动弹模对地铁车站结构地震响应影响的分析摘要:建立了地铁车站结构的三维计算模型,研究了混凝土动弹性模量对地铁车站结构三维地震响应的影响,确定了在进行地铁车站结构抗震分析时混凝土动弹性模量的合理取值。

该结论可为地铁车站结构的抗震设计提供参考。

关键词:地铁车站结构;三维计算模型;动弹模;地震响应0引言地铁工程是生命线工程的重要组成部分,其抗震问题已经成为城市工程抗震和防灾减灾研究的重要组成部分。

1995年日本阪神地震清楚地表明:在地层可能发生较大变形和位移的部位,地铁等地下结构可能会出现严重的震害,因此对其抗震问题应给予高度重视。

影响地铁车站结构等地下结构动力响应的因素颇多,材料参数的选取如混凝土动弹性模量的取值就是其中之一。

在地震等冲击荷载作用下,材料的强度会有提高,提高的幅度与冲击荷载的幅值及频率等因素有关。

郑永来[1]对混凝土材料进行动力试验表明,混凝土的动弹模比静弹模量高出30~50%。

杨林德[5]、杨超[3]、刘齐建[4]、王国波[5]等在研究上海市典型软土地铁车站结构地震响应时均根据文献[1]的研究成果取平均值(动弹模提高40%)。

本文拟在上述研究成果的基础上,研究混凝土动弹模对地铁车站结构地震响应的影响,得到在对地铁车站结构进行抗震分析时,混凝土动弹模的合理取值,为地铁车站结构抗震设计提供参考。

1地铁车站结构的三维计算模型[4]1.1计算范围图1为典型地铁车站剖面图,由图可见,地铁车站结构是一两层三跨的框架结构,水平横向宽21.24m,高12.39m,水平纵向长112m(纵向柱距8m,共13根柱子)。

土柱状图见图2所示,物理力学性质参数见表1。

根据文献[5]提出的三维计算方法,水平横向的计算宽度取车站结构5倍的横向宽度(结构左右两侧土体均取2倍的车站结构横向宽度),水平纵向计算长度取车站结构纵向长与4倍的车站结构横向宽度之和(即车站结构前后土体的长度各取2倍车站结构横向的宽度),深度取70m。

地震对地下地铁隧道工程的影响地震是地球上常见的自然灾害之一，它不仅对人类生活和建筑物产生严重影响，也会对地下地铁隧道工程的安全性和稳定性带来挑战。

本文将探讨地震对地下地铁隧道工程的影响和相关的防护措施。

1. 地震对地下地铁隧道工程地基的影响地震会导致地下地铁隧道工程所在地地基的动态变化，包括土壤的液化、沉降和侧移等。

液化是指土壤由于地震引起的振动而失去履力，变为类似液体的状态。

这种现象会导致地下隧道的沉降和变形，进而威胁到隧道工程的安全性。

2. 地震对地下地铁隧道工程结构的影响地铁隧道工程的结构包括地下隧道本身以及相关的支撑结构。

地震会对这些结构产生巨大的振动力和位移力，进而损害隧道的结构完整性。

地震可能导致地下隧道的坍塌、裂缝和变形等，对乘客和设备安全构成潜在威胁。

3. 地震对地下地铁隧道运行的影响地震发生时，地下地铁隧道可能会受到震动的冲击，从而影响其正常运行。

隧道内的轨道、信号系统和相关设备可能会受到破坏，导致列车停运或运行受阻。

此外，如果地震造成地面道路塌陷或地面塌方，地铁进出口可能被阻断，使运营受到极大影响。

4. 地震对地下地铁隧道工程的防护措施为了减缓地震对地下地铁隧道工程的影响，一系列防护措施应当采取。

首先，隧道的设计和建设应考虑到地震的因素，采取可靠的结构设计，以提高地震抗力。

其次，隧道的施工过程中应加强地质勘察和土壤处理，以避免地震引起的液化现象。

此外，隧道的支撑结构应具备一定的弹性和抗震性能，能够承受地震所带来的振动力。

5. 地震对地下地铁隧道工程的监测和维护为了及时了解地下地铁隧道工程的变化情况，应进行地震监测和结构维护工作。

地震监测系统可以实时检测地震活动和隧道结构的变化情况，提前采取措施以防止灾害事故的发生。

同时，定期的结构维护和检查可以确保隧道的稳定性和安全性。

总结起来，地震对地下地铁隧道工程造成的影响是不可忽视的。

为了减轻地震带来的风险，隧道的设计和建设需充分考虑地震因素，采取相应的防护措施。

轨道交通工程地下车站结构抗震设计摘要：随着我国城市化进程的不断加快，人们生活质量和周边环境也发生了翻天覆地变化。

随着城市人口数量的增长，城市腰痛压力越来越大，轨道交通工程地下车站的出现有助于环节交通压力。

但轨道交通不仅要满足运输功能，还要有一定安全性和抗震能力。

本文以A市B地下车站为例，展开地下车站抗震设计分析，分析结果可作为后续地下车站抗震设计相关参考。

关键词：轨道交通工程；地下车站；结构；抗震设计引言现代化城市建设过程中，城市轨道交通不仅要具备良好的运输能力，还要在设计方面充分考虑其抗震性能和安全性。

地下车站结构施工要严格按照国家规定相关抗震设计标准进行设计，如此不仅能提升地下车站抗震性能，还能为日后城市的健康、可持续发展奠定良好基础。

一、抗震设防目标（一）抗震设防类别、烈度与等级根据《城市轨道交通结构抗震设计规范》的相关要求，城市轨道交通结构应划分为：标准设防类；重点设防类；特殊设防类，三个抗震设防类别。

标准设防类：抗震措施应按本地区抗震设防烈度确定；地震作用应按现行国家标准《中国地震动参数区划图》GB 18306规定的本地区抗震设防要求确定；重点设防类：抗震措施应按本地区抗震设防烈度提高一度的要求确定；地震作用应按现行国家标准《中国地震动参数区划图》GB18306规定的本地区抗震设防要求确定；对进行过工程场地地震安全性评价的。

应采用经国务院地震工作主管部门批准的建设工程的抗震设防要求确定，但不应低于本地区抗震设防要求确定的地震作用；特殊设防类：抗震措施应按本地区抗震设防烈度提高一度的要求确定；地震作用应按国务院地震工作主管部门批准的建设工程的抗震设防要求且高于本地区抗震设防要求确定[1]。

抗震设防地震动峰值加速度与抗震设防地震动分档和抗震设防烈度之间对应关系如表1所示。

表1：抗震设防地震动峰值加速度与抗震设防地震动分档和抗震设防烈度之间对应关系（二）论证对象的判定根据住房和城乡建设部印发的《市政公用设施抗震设防专项论证技术要点（地下工程篇）》的相关规定，轨道交通地下车站建筑面积超过10000㎡的可以判定该地下车站工程可以作为单体工程进行抗震专项论证分析。

可液化的灵敏性土对地基处理设计方案的影响分析发布时间：2021-08-05T10:27:49.870Z 来源：《建筑实践》2021年9期作者：闫秀英[导读] 避免因此类特殊地层导致桩基施工质量不理想而产生经济损失。

闫秀英山西冶金岩土工程勘察有限公司，山西太原 030002 摘要:本文以某地区可液化的灵敏性土层对地基处理的影响为例；结合工程实例得出在该地层桩基施工中存在的问题，为今后类似地层的地基处理过程中提供一些经验参考。

避免因此类特殊地层导致桩基施工质量不理想而产生经济损失。

关键词:液化土;灵敏性土;地基处理;桩基0 引言土的灵敏度是指在不排水条件下，原状土的无侧限抗压强度（本质上是抗剪强度）与重塑土（完全扰动即土的原结构完全破坏但土体含水量不变）的无侧限抗压强度之比。

当土体受到扰动时，如开挖、震动、打桩等，结构强度很容易受到破坏，而使土的强度显著降低，压缩性大大增加，这种变化用土的灵敏度表示。

根据灵敏度可以将黏性土分为低灵敏度、中灵敏度、高灵敏度。

灵敏度越高结构性越强，受扰动后强度降低越多。

对于中、高灵敏性土，要特别注意避免扰动否则，土的物理、力学性质指标变化极大，对工程不利【1】。

液化是指饱和的粉、细砂在时间短、强度大的地震荷载作用下，体积受到压缩，孔隙水压力急剧上升，同时由于振动内摩擦角?值也大为降低，这些作用可使抗剪强度τf=0，整个地层就像液体一样振荡，这就称为饱和粉、细松砂的振动液化，粉土也有这种特征。

液化区很高的水压力产生自下而上的渗流，当动水压力大于土的浮重度时，又会造成上部土层新的液化，这种类型的液化称为间接液化。

如果地下孔隙水压力极大，甚至大于远大于上覆地层的自重压力，此时就会产生严重的喷水冒砂现象及大面积的地层塌陷【1】。

在太原南部小店区、综改区、清徐县区域存在可液化灵敏性土层，多为中等到严重液化，中-高灵敏性土。

对该地层进行地基处理时出现很多问题，如采用碎石桩处理时，处理后的复合地基承载力特征值提高不明显有的甚至比天然地基承载力特征值还小；CFG桩施工时出现窜孔、缩径等，桩基施工后单桩极限承载力标准值达不到设计值等问题。

地铁车站结构抗震分析摘要：随着城市化的进程，各个城市的规模日益扩大，进几年来各个城市对城市轨道交通建设的投入也不断加大。

过去人们普遍认为，地下建筑结构具有良好的抗震性能。

然而近年来世界各地已发生的地震灾害中，发现很多地下结构也遭受了不同程度的破坏，甚至部分出现了很严重的破坏。

目前地铁抗震设计主要参考《城市轨道交通结构抗震设计规范》(GB 50909-2014)进行抗震计算。

本文将以浙江金华地铁工程的某个地下车站为例，采用“I反应位移法”分析地震作用的工况，并提出一些抗震方面的意见和建议。

关键词：城市轨道交通；抗震性能；反应位移法；地震作用工况1 车站抗震设计概况1.1工程概况地铁车站为金华-义乌-东阳市域轨道交通工程一个站。

车站为地下一层侧式车站，主体结构为地下一层单柱双跨钢筋混凝土框架结构，标准段宽度为17.6m，顶板覆土厚度2.8-3.2m，底板埋深12.1m，车站总长291.1m。

车站结构采用明挖法施工。

图一：车站标准横断面1.2抗震设防目标依据住房和城乡建设部下发的《市政公用设施抗震设防专项论证技术要点（地下工程篇）》及《城市轨道交通结构抗震设计规范》（GB50909-2014），并考虑到轨道交通地下车站的重要性和震后修复难度，抗震设防目标如下：（1）结构在遭受相当于本工程抗震设防烈度的地震影响时，即475年一遇地震动作用下，不破坏或轻微破坏，应能够保持其正常使用功能，结构处于弹性工作阶段，不应因结构的变形导致轨道的过大变形而影响行车安全；（2）结构在遭受高于本工程抗震设防烈度的罕遇地震（高于设防烈度1度）影响时，即2450年一遇地震动作用下可能破坏，经修补，短期内应能恢复其正常功能，结构局部进入弹塑性工作阶段。

475年一遇地震作用，对应50年超越概率10%地震作用，即《城市轨道交通结构抗震设计规范》（GB50909-2014）中E2地震作用。

2450年一遇地震作用，对应50年超越概率2%地震作用，即《城市轨道交通结构抗震设计规范》（GB50909-2014）中E3地震作用。

软土地铁车站地震响应数值计算方法的研究摘要:对饱和软粘土采用粘弹塑性动力本构模型,利用拉格朗日差分法对典型软土地铁车站结构建立地铁车站地震响应的数值计算方法。

并进一步利用该方法对软土地铁车站结构振动台模型试验进行数值拟合分析,结果表明土体和结构模型的加速度响应、结构模型表面的动土压力以及结构构件的应变规律的计算结果与试验结果基本吻合。

关键词:软土;地铁车站结构;振动台试验;数值计算方法1引言神户地震和历史上发生的大震一再表明,对软土地基中的地铁车站等地下结构的抗震设计开展研究有重要的意义。

对地下结构地震响应的计算,迄今已提出多种算法[1],然而由于对其涉及的各类复杂因素的影响尚认识不足,不同的计算方法或模型得出的结果存在很大的差异,且很难鉴别各自的合理性。

本文建立软土地铁车站地震响应的分析理论与计算方法,并通过对模型试验进行拟合分析验证了所建立的车站结构动力响应的计算方法的正确性和合理性,以便工程设计实践参考。

2软土地铁车站结构的振动台试验软土地铁车站结构的振动台模型试验分自由场振动台模型试验、典型地铁车站结构振动台模型试验和地铁车站接头结构振动台模型试验等三种。

试验开展过程中遇到的技术难题包括对地铁车站纵向长度的模拟,场地土的动力特性与地震响应的模拟,模型箱的构造与边界效应的模拟,以及量测元件设置位置的优选等。

笔者对这些技术难题逐一进行了研究,并都提出了行之有效的解决方法,使试验取得了可靠的数据[2][3]。

试验过程中,首先进行了自由场振动台模型试验,用以模拟自由场地土层的地震反应,据以获得模型箱内不同位置处的土的加速度响应,确定“边界效应”的影响程度和鉴别模型箱构造的合理性;然后通过典型地铁车站结构振动台模型试验了解地铁车站结构与土共同作用时地震动反应的规律与特征,为建立地铁车站地震响应的分析理论和计算方法提供试验数据。

振动台模型试验记录了在不同荷载级别的ｅｉ-ｃｅｎｔｒｏ波、上海人工波和正弦波激振下,加速度测点传感器的反应;由动土压力传感器,得到了各测点在不同加载工况下的动土压力反应时程;根据结构模型构件上布置的应变片,测得了构件应变的变化。

液化场地桩基侧向响应分析中p_y曲线模型研究进展第40卷第3期力学进展Vol.40No.3 2010年5月25日ADVANCES IN MECHANICS May25,2010液化场地桩基侧向响应分析中p-y曲线模型研究进展*凌贤长唐亮?哈尔滨工业大学土木工程学院,哈尔滨150090摘要采用非线性Winkler地基梁模型分析侧向液化土-桩相互作用所面临的首要难题是液化土p-y曲线的确定.因此较全面地阐述了液化土p-y曲线模型的国内外研究历史、现状与重要成果,对获得液化土p-y曲线不同试验手段的典型试验作一简明分析,并概括了桩基侧向响应分析中常用的液化土p-y曲线.液化土p-y曲线的模型研究国外已取得不少很有价值的科研成果并开始用于桩基设计中,而国内才刚刚起步且以试验研究为主,基于这个事实,提出了对曲线模型研究的若干建议与认识,为曲线模型研究提供一些技术思路.液化土p-y曲线模型研究水平的提升将推动我国发展基于变形的液化场地桩基桥梁抗震设计方法.关键词p-y曲线,液化,侧向液化土-桩相互作用,地震1引言桩基广泛应用于桥梁工程中[1].桥梁地基多数为可液化砂土层,极易发生地震液化而丧失强度和承载力,桩周土强度与刚度对桩基分析与设计影响极其明显[2,3].如今,非液化土强度与刚度的定量研究已较深入,但是针对液化土强度与刚度的研究稍显不足[3,4].因此,液化土强度与刚度、液化土-桩相互作用问题成为当前岩土地震工程与工程抗震研究的热点[2,4～6].地震振动、场地失效引起桩基震害主要表现为桩基受到附加侧向载荷作用[3,7～9].因此,液化场地桩基侧向响应分析也受到工程界的重视.事实上,不同的桩基设计方法主要通过模拟桩-土相互作用实现[10],应用最广泛的桩-土相互作用分析模型为非线性Winkler地基梁模型;该模型可避开液化土的本构关系选取问题,具有概念清晰、模型简单、易于数值实现、计算耗时少等优点,且易将土的非线性特征很好地嵌入到相互作用体系中,因而广泛用于实际工程中[11].侧向桩-土相互作用通过非线性的p-y曲线模拟来获取,p为单位桩长受到的侧向土反力,y为桩的侧向位移.本文将针对液化场地桩基侧向响应分析中的p-y曲线模型研究进展作一较系统的阐述.2研究历史沿革与现状过去30年,国际上桩-土相互作用p-y曲线已有较长研究历史且在桥梁工程、海洋工程中一度获得较多应用[11,12].1958年,MClelland 和Focht 首次引入且实测土的p-y曲线[13].1970年,Mat-lock等最早提出非线性Winkler地基梁模型法(p-y 曲线法)[14].之后,国内外对常规土的静力p-y曲线进行了较多研究[12～16],并获得黏土和砂土的p-y 曲线.Matlock和Reese理论奠定了非液化土p-y曲线的分析基础,并被多国规范采纳,以美国石油学会(American Petroleum Institute,API)规范最具代收稿日期:2008-12-08,修回日期:2010-04-25国家自然科学基金重大研究计划项目(90815009),西部交通建设科技项目(2009318000100),教育部留学回国人员科研启动基金和国家自然科学基金(50378031,50178027)项目资助E-mail:*************第3期凌贤长等:液化场地桩基侧向响应分析中p-y曲线模型研究进展251表性[17].关于桩-土相互作用的动力p-y曲线,早期针对非液化场地条件,通过水平动载试验进行实测,一般为桩头加载方式,只能反映地震中上部结构对桩的惯性力效应,不能刻画桩-土运动相互作用.目前,针对液化场地条件,国际上一直尝试建立并发展液化土p-y曲线模型,并逐步进行不少尝试性工作且取得一些有益的成果.简述如下.桩-土相互作用分析中,非线性Winkler地基梁模型曾获得较多应用,如Matlock模型[18]、Novak模型[19]、Nogami模型[20],以及Otani[21], Naggar等[22]和Rojas等[23]改进的非线性Win-kler地基梁模型.研究者真正开始关注液化场地桩基侧向响应分析中p-y曲线模型问题始于日本道路协会(Japan Road Association,JRA)、和日本建筑学会设计(Architectural Institute of Japan,AIJ)规范中采用静力安全系数折减法,评价液化场地桩的侧向承载力[24,25].Ting等[26]为了统一静力与循环载荷作用下土的p-y曲线的不一致性,首次完成了可液化场地足尺单桩水平循环动力载荷试验(桩头加载),得到的沿桩身的p-y曲线形状显示了砂土的应变软化、滞回属性及桩土之间裂缝效应,且随着埋深曲线逐渐呈现线性关系,见图1;然而,Ting未用孔压定量分析液化对砂土p-y曲线的潜在影响.Miura等[27]用双线性力-位移关系表示桩-土相互作用,并假定表层非液化土位移为常数、液化土位移呈线性递减,基于有限元法模拟地面液化侧向位移对桩的影响.T okida[28]通过冲击砂土液化方法,研究动荷速率对土反力折减系数的影响.Liu和Dobry[29]首次报道了在伦斯勒工业学院完成的离心机模型试验成果,并据此评估液化扩展作用对桩的影响,提出将砂土的静力p-y曲线中p折减0.9倍描述液化砂土的p-y关系,并获得折减系数随孔压比呈线性变化以及侧向土反力衰减取决于超孔压而孔压比达到1时土反力最小的认识.随后,Abdoun[30]在伦斯勒工业学院完成了8个液化场地离心机模型试验,地基均倾斜4.8?且受到频率为2Hz的正弦波激励,得出桩的最大弯矩均出现在液化土与非液化土分界处.基于上述离心机试验结果,Abdoun[31]提出了一种与不排水强度法相似的极限平衡法预测液化侧扩作用下桩的弯矩,假定峰值为9.25kN/m2的分布液化土压力施加到单桩有效宽度之上.应该注意到,Abdoun建议9.25kN/m2的峰值液化土压力可能是率相关的.Dobry和Abdoun(1998)修订Abdoun[31]提出的极限平衡法,建议液化土压力为三角形分布以及自由桩端处土压力峰值为17.7kN/m2,对桩上最大弯矩与沿桩长弯矩分布的预测较建议的液化土压峰值为9.25kN/m2条件下预测值要好,并被离心机试验证实;试验中观察到液化侧扩条件下上部结构的刚度和质量对桩的属性影响也被随后的研究证实[32,33].据推测, 17.7kN/m2的峰值土压力可能是液化土层厚度的函数.然而,Dobry和Abdoun[32]未给出不同液化砂土厚度条件下峰值土压力的可能值.Wilson[34]为了研究地震作用过程中液化砂土中桩的动力响应问题,在加州大学戴维斯分校完成了不同相对密度液化场地桩承结构离心机试验.Boulanger 等[35]和Wilson等[34]先后对试验结果及分析进行报道.Wilson等[34]首次获得液化砂土的动力p-y曲线,曲线与不排水剪切作用下饱和砂土的应力-应变特征相似;注意到曲线取决于砂土初始相对密度,建议依据API 规范中砂土的静力p-y曲线,构造不同相对密度液化砂土的弱化动力p-y曲线的折减系数值,具体值为松散砂(相对密度为35%)约0.1～0.2,中密砂(相对密度为55%)约0.25～0.35. Wang和Reese[10]建议采用由Matlock(1970)和Reese(1984)的软黏土p-y曲线构造液化砂土的弱化p-y曲线.Yasuda等[36]通过室内实验研究了液化后砂土的应力-应变关系,其形状与非液化土明显不同,这与Yasuda等[37]的扭剪试验得到液化砂土的属性一致.Goh和O’Rourke[38]基于二维有限差分法推求液化土中圆形桩的p-y曲线并预测桩的极限侧向土反力.Boulanger等[39]结合离心机试验与理论分析,并基于有限元平台GeoFEAP,评估动力非线性Winkler地基梁模型法.Tokimatsu[40]报道了日本1995年Kobe 地震中液化侧扩作用下桩的性能研究成果,根据日本设计规范采用p-乘因子法确定了液化侧扩土体施加在桩上的最大水平载荷,反分析了由于液化作用向濒临滨水区运动的两个桩承建筑结构变形,确定了在0.05～0.2之间变化的适当p-乘因子以解释桩的变位,这与日本设计规范中液化土压力侧向系数在0.25～1之间变化保持一致.T okimatsu等[41]完成液化场地桩基振动台试验,发现液化前土应力主要由上部结构惯性力引起,液化后土应力主要由桩土相对运动控制;液化前土的p-y曲线呈线性关系,液化后随着孔压累积及循环载荷作用土抗力逐渐降低并表现出强非线性.Curras等[42]通过离心机试验,采用动力非线性252力学进展2010年第40卷Winkler 地基梁模型法对桩群支承结构进行评估分析.Goh 等[43]在伦斯勒工业学院实施完成了离心机试验,验证了液化砂土中土-结构相互作用非线性Winkler 地基梁分析模型,并发展了无量纲液化砂土的p -y 曲线.Takahashi 等[44]完成一组管桩牵引试验,研究速率对液化侧向土反力的影响,表明桩的侧向土反力对侧向位移速率具有很大依存性.Gerber [45]通过爆炸诱发场地液化,实施液化前、液化后桩水平循环加载试验(TILT 工程),研究桩周土载荷-位移反应,获得单桩与群桩条件下液化砂土的p -y 曲线,给出了液化土p -y 曲线近似经验公式.Ashour 和Norris [46]将自由近场孔压发展与应变楔形模型结合,提出了新的场地液化中单桩侧向响应分析方法,可预测动力p -y 曲线.Tokimatsu 等[47]通过振动台试验研究了液化场地中桩基反应及桩的材性、土层液化对反应的影响,获得了动力p -y 曲线中p 可能较真实的相互作用力偏大的认识.Tokimatsu 等[48]通过振动台试验,结合Abdoun 等[31]和Dobry 等[32]的离心机试验,得到液化砂土的动力p -y 曲线.Malhotra 等[49]首次将桩-土地震相互作用过程分为远场效应、近场效应、惯性力效应,近场效应涵盖桩-土之间滑移效应和裂缝效应.Brandenberg 等[50]通过离心机试验研究了液化场地桩基屈服破坏特性,并提出了新的防止桩基破坏的规范.Weaver 等[51]由场地爆炸液化钻孔桩现场测试,获得动力p -y 曲线与主要因素的影响,发现通过砂土的静力p -y 曲线的折减系数法构造液化砂土的拟静力p -y 曲线并不能准确表述液化砂土的p -y 特性.Rollins 等[52,53]在上述场地爆炸液化足尺桩水平加载试验基础上,研究表明液化后群桩效应可以忽略,液化砂土p -y 曲线的斜率随着挠度的增大而增加且呈上“凹”型,可采用桩径因子修正因桩径增大而引起土反力增大.Knappett 和Madabhushi [54]基于Abaqus 软件平台建立数值模型并嵌入p -y 曲线的方法,研究了液化条件群桩不稳定失效问题,对倒塌载荷进行合理预测.Zheng 和Luna [55]采用非线性Winkler 地基梁模型法且引入退化乘子考虑液化对桩-土相互作用的影响,建立液化场地桩-土-结构地震相互作用耦合分析方法,研究液化对桥梁桩基侧向性能的影响.Taka-hashi 和Sugita 等[56]基于非线性Winkler 地基梁模型并选用双曲线型的p -y 曲线,建立了液化侧扩土中桩基分析方法.Ashford 和Juirnarongrit 等[57]为了评估液化侧扩对单桩、4根群桩及9根群桩的影响,通过控制爆炸,在日本北海道Tokachi 人工岛完成2个足尺液化场地桩基试验.Juirnarongrit 和Ashford [58]通过将液化土p -y 弹簧刚度假定为零,在桩头附一旋转弹簧,以替代桩头限制效应的等价单桩来模拟群桩,并采用离散土弹簧刚度的p -乘因子法考虑群桩效应,基于非线性Winkler 地基梁模型法分析液化侧扩条件下单桩与群桩的性能.图1循环动载荷作用下可液化场地桩的p -y 曲线[26]相比之下,我国在液化土p -y 曲线方面研究起步较晚.过去更多关心饱和砂土是否发生地震液化[4～6],而对于场地液化是否对桩基桥梁造成危害和危害程度则重视不够[3,9],尽管近十年来逐步关注这一问题,但是研究尚显不足[59～63].特别是在液化土p -y 曲线方面,只有几位学者在国内率先开展工作.刘惠珊、乔太平和陈克景是国内最早完成桩基振动台试验的学者,研究液化土层中桩基破坏机理,但是没有涉及到上部结构.凌贤长等[59]率先在国内成功完成液化场地桩-土-桥梁结构地震相互作用振动台试验,很好再现自然地震触发砂土液化及桩基破坏等各种宏观震害现象.黄雨等[60,61]很好总结国内外液化场地桩基抗震设计现状,主要的模型有文克尔地基梁模型、有限元模型和集中参数模型,指出各种设计方法存在的问题,并基于Biot 两相饱和多孔介质动力耦合理论且采用有效应力原理对液化场地桩基地震反应进行有限元分析.凌贤长等[62]开展1:10模型的自由场地基液化振动台模型试验研究,再现自然地震触发地基砂土液化的各种宏观现象,尤其是模型地基的试验破坏与其原型实际震害情况比较吻合.张建民等[63]采用能准确描述场地液化前、后(尤其是液化后)土体大变形的本构模型,基于Pen-zien 简化法建立桩-土地震相互作用计算模型,对第3期凌贤长等:液化场地桩基侧向响应分析中p-y曲线模型研究进展253阪神地震中受到液化侧向扩流的桩基进行计算分析.凌贤长等[64]基于目前广泛应用的Bockingham π定理,主要采用量纲分析方法并考虑模型与原型之间材料变形应力-应变本构关系及桩-土接触边界动力响应相似性,求解液化场地桩-土-桥梁结构动力相互作用下,振动台试验模型设计的相似关系,同时提出人工质量问题的解决办法.冯士伦等[65]通过振动台试验研究饱和砂土中桩基振动特性,对桩-土动力相互作用有初步的认识.王建华和冯士伦[66,67]基于振动台试验,研究场地液化中弱化动力p-y曲线随孔压比变化规律,并提出依据孔压比和静力p-y曲线构造动力p-y曲线方法,利用API规范中p-y关系得到静力初始p-y 曲线,通过对其中p乘以合适的衰减系数反映液化砂土侧向承载力p-y曲线.李雨润等[68]通过振动台试验获得液化场地桩-土地震相互作用动力p-y曲线,据此提出液化场地动力p-y曲线修正方法与计算公式.冯士伦[69]通过饱和砂土中桩基振动台试验,获得不同相对密度砂层液化时桩的弯矩和桩顶重物加速度,并提出利用静力p-y曲线折减法得到液化砂土中桩的水平承载特性方法.凌贤长等[70]基于数值模拟手段,运用有效应力原理以及振动孔隙水压力增长经验模式,采用应力循环孔压增量计算方法,直接针对液化场地桩-土-桥梁结构动力相互作用的振动台试验,建立数值分析模型,据此进行液化场地桩基、地基动力响应和砂层孔压动力增长的数值模拟研究.王成雷等[71,72]依据加权余量法原理,提出通过振动台试验建立动力p-y曲线的方法,分析不同初始相对密度土层液化中动力p-y曲线的弱化,并对动力p-y曲线和拟静力弱化p-y曲线做比较.戚春香等[73]论述液化场地振动载荷作用下桩-土相互作用的有关理论研究和试验成果.王建华等[74]为了研究p-y关系与水平极限抗力随饱和砂土中残余孔压增加时的变化规律,采用给土层施加反压的方法控制饱和砂层孔压,模拟饱和砂层液化过程中具有一定残余孔压时的弱化状态,进而针对不同弱化状态饱和砂土与桩的相互作用进行模型试验.袁晓铭等[75]通过非液化和液化土层中桩基础宏观震害现象以及等幅波与真实地震波振动台模型实验中桩和土层的加速度、位移、桩土相互作用力、桩动力p-y曲线、桩身弯矩与孔压发展过程对比,研究地震引起的地面横向往返运动下可液化土层中桩基响应机理.凌贤长等[76]直接针对大型振动台模型试验,建立液化场地桩-土-桥梁结构地震相互作用数值模拟的二维分析模型和计算方法.李雨润等[77]借助液化场地桩-土动力相互作用振动台试验,以API规范为基础,提出可液化土层中桩基动力p-y曲线双参数修正方法及修正计算公式,解决目前API规范折减系数法计算可液化土层中桩基动力p-y曲线不符合实际、工程设计上难以接受的问题.为了深入研究液化场地低桩承台-群基础、高承台群桩基地震响应规律,凌贤长等[70]在同济大学土木工程防灾国家重点实验室,以钢筋混凝土桩基-独柱式桥墩为研究对象,完成4个模型的液化场地和1个模型的非液化场地的桩-土-桥梁结构地震相互作用振动台试验; 3种桩基:单桩基,低承台2×2群桩基,高承台2×2群桩基;3种地基:上部和下部均为黏土层、中间为砂土层地基,上部为黏土层、下部为砂土层地基,全部为黏土层地基;上部桥梁结构配以质量块,试验输入的地震波均为El Centro波.唐亮等[78]针对两种土层结构的可液化场地条件,采用2×2低承台群桩-独柱墩结构形式,完成了两个试验体的群桩-独柱墩结构地震反应振动台试验,很好地再现了自然地震触发场地液化及结构反应的各种宏观现象.唐亮等[79]基于相同土层结构地基条件下,分别采用低承台群桩-独柱墩与高承台群桩-独柱墩结构,完成了两次可液化场地群桩-土-桥梁结构地震反应振动台试验,据此研究了承台型式对桥梁桩-柱墩地震反应的影响.目前,我国海洋平台桩基设计中,仍将液化土水平承载力取为零而作为一种保守估计,显然与实际出入较大.综上所述,目前液化场地桩基侧向分析的液化土p-y曲线模型研究成果主要基于离心机试验、振动台试验与室内试验,结合少量的现场足尺试验并辅于数值技术外推考虑基本参数(如桩径、间距)变化对液化土p-y曲线的影响而获得.液化土p-y曲线模型研究国外已取得了不少很有价值的科研成果,开始用于桩基设计中,国内则刚刚起步且以试验研究为主.3获得液化土p-y曲线的典型试验为了研究液化土的p-y曲线特性,一些学者完成了不同类型桩基试验.试验表明了液化土p-y曲线的形状和幅度与当前实际工程中采用的p-y曲线有所不同.事实上,p-y曲线可通过土的指标特性和桩的尺寸刻画.土的指标特性基本上可采用应力-应变属性表示.p-y曲线的几何形状与土的254力学进展2010年第40卷应力-应变曲线很相似.以下结合典型试验对液化土p-y曲线的特性进行初步探讨.(1)室内试验Yasuda等[36]通过一系列室内试验研究了液化后砂土的应力-应变关系,结果表明液化砂土与常规土的应力-应变曲线在形状上有很大不同. 液化土p-y曲线的形状几乎为“凹”形,在低于某一应变时液化土p-y曲线的初始刚度很小,超过这一应变后土将获得很大的刚度,且曲线的刚度与初始界限应变主要由砂土的相对密度控制,见图2 所示.相反,土的典型非线性应力-应变关系曲线具有初始刚度很大的凸曲线.在Yasuda等[37]完成的不同类型的砂土扭转剪切试验中观察到液化砂土具有相似属性.图2液化后砂土(a)剪应力-应变与(b)孔压-剪应变关系[36]图中,σ为上覆有效应力,F L为液化安全率,u为超孔压,D r为砂土相对密度.(2)离心机模型试验为了研究地震作用下液化砂土中桩的动力响应,Wilson等[80]完成了一系列离心机模型试验.通过试验获得了液化砂土的p-y曲线,见图3所示,这些曲线显示了与Yasuda等[36]室内试验获得的液化砂土的应力-应变曲线形状相似,且有别于常规土的应力-应变曲线,同时试验也表明甚至在砂土完全液化的状态下,仍然有显著的土反力抵抗桩的侧向位移.尽管真实的液化土p-y曲线与实际工程中采用的p-y曲线不同,但是能够完全刻画液化砂土的p-y曲线尚不多见,Z为埋深,D为桩径.图3典型的液化后中密砂p-y曲线[80](3)振动台模型试验Takahashi等[44]采用防水砂箱完成一组圆柱体管桩牵引试验,研究速率对液化侧向土反力的影响,表明桩的侧向土反力对侧向位移速率具有很大依存性,见图4所示,V为加载速率,p0为初始上覆应力.图4不同速率条件圆柱体归一化位移与归一化侧向土反力关系[44](4)足尺现场试验Rollins等[52]采用爆炸方法引起场地液化并实施了足尺现场群桩试验,研究了液化场地中桩-土-桩相互作用效应.试验反算的p-y曲线显示了完全液化砂土具有相似的凹面特性,见图5.通常认为完全液化的砂土有效应力为零且随着埋深不发生改变,事实上,p-y曲线的刚度与埋深具有相关性.图5爆炸触发场地液化后桩的变位与土反力的关系[51]第3期凌贤长等:液化场地桩基侧向响应分析中p-y曲线模型研究进展2554液化土p-y曲线模型目前,静力与循环载荷作用下黏性土和砂性土的p-y曲线研究较成熟,但是关于液化土p-y曲线的可用信息还很少.通常,液化常伴随强震发生;震动开始出现,松散砂土趋于密实,由于砂层不能迅速排水,超孔压上升导致了土的有效应力逐渐减小,进而减弱了土体承受侧向载荷的能力.液化过程中土的状态从固态渐变为液态,土性的改变使得液化土-桩相互作用尤为复杂.实际工程中,采用非线性Winkler地基梁模型,并对土反力乘以一个衰减p-乘因子以考虑土的液化效应等手段,简单地处理上述问题.衰减因子取决于场地条件,如液化程度、液化与非液化土层厚度比等因素.事实上,讨论液化土-桩之间的关系,需要区分两种可能的载荷情况.第1种载荷:液化土为主动体,桩承受完成液化的土体引起的被动土压力,此时桩为被动体.一般这种情况发生在场地液化引起土体发生侧向扩展的条件下,这时液化土将沿着斜坡向着临空面运动.第2种载荷:桩为主动体,通过作用桩正面的被动土压与桩背面上的主动土压力之差抵抗着桩的运动.由于两种液化土反力类型不同,判别其适用条件显得尤为重要.从设计角度上讲,将桩考虑为被动桩似乎更趋于高估了峰值液化土反力,避免了桩上受到过大的载荷.相反,将桩处理为主动桩,似乎低估了总的土反力峰值或循环残余土反力,由于不适当地避免了抵抗桩运动的土反力,桩出现过大的变位或弯矩.换言之,由于桩的角色不同,用于主动或被动桩中液化砂土的载荷-位移响应及土压力控制量应该是不同的.诸多震害表明,由于两种载荷引起桩的失效特别是在桥梁工程中经常发生,这些破坏使得工程设计指导文件考虑了液化土对结构的抗震设计的影响.然而,却很少有详细的说明如何考虑液化对结构抗震设计的影响,造成这种模糊局面的原因主要源于对液化土-桩相互作用机理的理解不够深入与量化不够精确.以下简述将基于p-y曲线模型的液化场地桩基侧向承载力设计方法.由于这些表示液化土p-y曲线的方法只是极其复杂现象的近似,其可靠性可能仍具有较大的局限性.。