固定床反应器的数学模型
- 格式:doc
- 大小:335.00 KB
- 文档页数:9

第六早 气-固相催化反应器设计本章核心内容:本章讨论的气固相催化反应反应器包括固定床反应器和流化床反应器。
在固定床反应器部分,介绍了气固相催化反应器的各种类型和固定床层的流动特性, 给出了固定床反应器的两种设计方法:经验或半经验法和数学模型法。
在流化床反应器部分,在对固体颗粒流态化现象和流态化特征参数介绍的基础上, 讨论了流化床反应器的分类和工业应用。
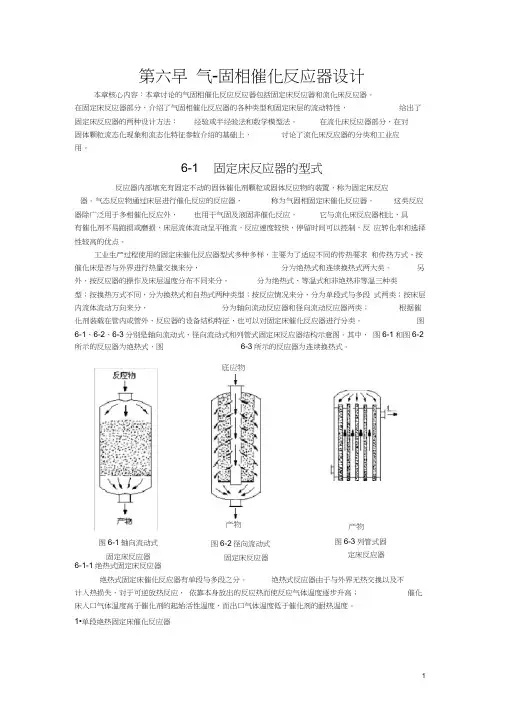
6-1 固定床反应器的型式反应器内部填充有固定不动的固体催化剂颗粒或固体反应物的装置,称为固定床反应器。
气态反应物通过床层进行催化反应的反应器, 称为气固相固定床催化反应器。
这类反应器除广泛用于多相催化反应外,也用于气固及液固非催化反应, 它与流化床反应器相比,具有催化剂不易跑损或磨损,床层流体流动呈平推流,反应速度较快,停留时间可以控制,反 应转化率和选择性较高的优点。
工业生产过程使用的固定床催化反应器型式多种多样,主要为了适应不同的传热要求 和传热方式,按催化床是否与外界进行热量交换来分, 分为绝热式和连续换热式两大类。
另外,按反应器的操作及床层温度分布不同来分,分为绝热式、等温式和非绝热非等温三种类型;按换热方式不同,分为换热式和自热式两种类型;按反应情况来分,分为单段式与多段 式两类;按床层内流体流动方向来分,分为轴向流动反应器和径向流动反应器两类;根据催化剂装载在管内或管外、反应器的设备结构特征,也可以对固定床催化反应器进行分类。
图6-1、6-2、6-3分别是轴向流动式、径向流动式和列管式固定床反应器结构示意图。
其中, 图6-1和图6-2所示的反应器为绝热式,图6-3所示的反应器为连续换热式。
6-1-1绝热式固定床反应器绝热式固定床催化反应器有单段与多段之分。
绝热式反应器由于与外界无热交换以及不计入热损失,对于可逆放热反应, 依靠本身放出的反应热而使反应气体温度逐步升高; 催化床入口气体温度高于催化剂的起始活性温度,而出口气体温度低于催化剂的耐热温度。


固定床反应器的设计计算固定床反应器是一种广泛应用于化工工业中的反应器。
它由一个固定的反应床和气体或液体通过床体流动的装置组成。
固定床反应器通常用于进行催化反应,例如催化剂的制备、氢气的生成以及石油炼制过程中的裂化反应等。
在设计固定床反应器时,需要考虑反应床的尺寸、催化剂的选择、反应温度和压力等因素。
下面将介绍固定床反应器的设计计算流程。
首先,设计固定床反应器时需要确定反应物的种类和摩尔比。
通过摩尔比可以计算出反应物的总流量以及各个组分的摩尔流量。
接下来,需要考虑反应床的尺寸和形状。
反应床通常为一根或多根管子,可以是圆柱形、方形或其他形状。
根据反应床的形状和尺寸,可以计算出反应床的体积。
在确定了反应床的尺寸后,需要选择合适的催化剂。
催化剂的选择应考虑反应的速率和选择性。
常见的催化剂有金属催化剂、氧化物催化剂和酸碱催化剂等。
选择催化剂后,需要计算催化剂的质量和体积。
在反应过程中,需要控制反应温度和压力。
反应温度对于反应速率和选择性具有重要影响。
根据反应的热力学数据和催化剂的性质,可以计算出反应的热效应和放热量。
根据反应的放热量和反应床的热传导性能,可以计算出反应床的冷却要求。
在设计固定床反应器时,还需要考虑反应物和产物的流动情况。
根据流动特性可以计算出反应床的压降和流速。
压降对于反应过程有重要影响,它影响着反应物在床体中的停留时间和反应速率。
最后,需要考虑反应物的进料方式和产物的排放方式。
进料和排放方式应选择合适的装置,以保证反应物的均匀分布和产物的高效排放。
在设计固定床反应器时,需要综合考虑以上因素,并进行相应的计算。
通过计算可以确定反应床的尺寸和形状、催化剂的选择、反应温度和压力以及进料和排放方式。
这些计算可以保证固定床反应器的高效运行和最佳性能。
总结起来,设计固定床反应器需要考虑反应物的种类和摩尔比、反应床的尺寸和形状、催化剂的选择、反应温度和压力、反应床的冷却要求、反应物和产物的流动情况以及进料和排放方式等因素。

固定床:当气体以较小的速度流过固定床时,流动气体的上升阻力不致使颗粒的运动状态发生变化,床高维持不变;床层压降随流速对数增大而增大。
流化床:固体颗粒可以像水等液体一样在设备内有明显的界面,即使设备倾斜,界面仍会保持水平;床层压降不随流速变化(基本不变)。
输送床:固体颗粒在设备内无明显界面;床层压力随流速增大而减小。
流化床和沸腾床可能只是叫法上不同。
流化床,也就是沸腾床,接触面大,传热传质效率高,时空产率高,但返混严重。
需要注意的是不能堵塞气体分布器,堵了很麻烦的。
固定床和移动床比较适合气-气、气-液和液-液反应,床层本身作为[wiki]催化剂[/wiki],优点是返混小,固相带出少,分离简单。
流化床的床型是设计中很重要的,与反应体系的匹配要求比较高。
此外,操作中的气速、带出量、与配套的旋风等分离设备设计比较严格。
流化床的传热和破汽泡、沟流措施也是研究比较多的。
固定床反应器是一种被广泛采用的多相催化反应器,反应器内填充有固定不动的固体颗粒,可以是固体催化剂也可以是固体反应物.例如管式固定床反应器,管内装催化剂,管内装催化剂,反应物料自上而下通过床层,管间为载热体与管内反应物进行换热,以维持所需的温度条件.此外,固定床反应器也可用于气固及液固非催化反应.沸腾床是流化床的一种,固体在流化床反应器内流动,流体和固体颗粒所构成的床层犹如沸腾的液体. 沸腾床反应器下部设有分布板,板上放固体颗粒,流体自分布板下送入,当流体速度达到一定数值后,固体颗粒开始松动,再增大流速就进入流化状态.反应器内一般设有挡板,换热器,及流体与固体分离装置等内部部件.移动床与固定床相似,不同的是固体颗粒自顶部连续加入,由底部卸出.沸腾床因为固体处于运动状态,反应或传热效果好,但动力消耗大,而且在煤调湿中粉尘携带量大.固定床:固定床反应器又称填充床反应器,装填有固体催化剂或固体反应物用以实现多相反应过程的一种反应器。
固体物通常呈颗粒状,粒径2~15mm左右,堆积成一定高度(或厚度)的床层。




催化重整固定床反应器传递及反应过程的数值模拟催化重整固定床反应器的传递及反应过程的数值模拟可以通过以下步骤进行:
1. 建立反应器的数学模型:根据反应机理和物理性质,建立反应器的数学模型,包括传递过程和反应过程的方程。
传递过程方程通常包括质量传递、能量传递和动量传递方程,反应过程方程通常包括反应速率方程。
2. 离散化反应器:将反应器分为若干小段,分别进行离散化处理。
可以选择均匀离散或非均匀离散的方法,根据实际情况选取最合适的离散化方法。
3. 运用数值方法求解方程:根据离散化后的方程,运用数值方法(如有限差分法、有限体积法、有限元法等)求解方程组,得到各个离散段上的物理量分布。
4. 确定边界条件:根据反应器的实际情况,确定反应器的边界条件。
边界条件通常包括流体的入口温度、压力、物质浓度等。
5. 进行数值模拟和计算:根据离散化后的方程和边界条件,进行数值模拟和计算。
可以采用迭代方法,不断更新每个离散段上的物理量,直至达到收敛条件。
6. 分析和评估模拟结果:根据模拟结果,分析反应器的性能、效率等指标,评估反应器的优化方案和潜在问题。
需要注意的是,在进行数值模拟时,需要考虑反应器内部的催化剂颗粒的分布和反应速率方程的影响。
这可以通过引入催化剂颗粒床层的物理结构参数和反应速率方程来进行模拟。
同时,还需要考虑传递和反应过程之间的相互作用,以及其他因素(如温度、压力)对反应过程的影响。

固定床反应器设计计算固定床反应器是化工领域中常见的一种反应器类型,特点是固定催化剂床,反应物通过固定床的床层进行反应,反应产物从固定床的出口处得到。
固定床反应器设计是化工生产中的重要环节,涉及反应器的尺寸、催化剂的选择、操作条件的确定等方面。
下面将介绍固定床反应器设计的基本原理和计算方法。
1.催化剂床的选择:催化剂床的选择应根据反应物的性质和反应条件来确定。
常见的固定床催化剂床有球形、多孔材料和填料等,催化剂床的选择应考虑到活性、稳定性和成本等因素。
2.反应器尺寸的确定:反应器尺寸的确定与催化剂床的选择等因素有关。
反应器的长度、直径、催化剂床的高度等参数需要根据反应物的流量、反应速率和传质传热等条件进行计算。
3.操作条件的确定:反应器的操作条件包括温度、压力和流量等参数,这些参数的确定与反应物的性质、反应速率和反应体系等因素有关。
操作条件的设计需要尽可能提高反应速率和产物的选择性。
1.传质和传热计算:传质和传热是固定床反应器中重要的过程,需要考虑到传质和传热的速率以及催化剂床的吸附和扩散等因素。
传质和传热计算可以通过质量传递和能量传递方程进行,根据质量传递和能量传递方程可以计算出反应器中流体的温度和浓度分布。
2.反应动力学计算:反应动力学是固定床反应器设计中的关键环节,可以通过实验和理论模型来确定反应物的反应速率和产物的选择性。
反应物的反应速率可以通过实验测定得到,也可以通过理论模型进行计算。
反应物的选择性可以通过反应速率常数和转化率来计算。
3.负载平衡计算:固定床反应器的负载平衡是指催化剂床的催化剂负载均匀性和催化剂的失活过程。
负载平衡计算需要考虑到催化剂床的催化剂负载情况和催化剂的失活速率。
催化剂的负载均匀性可以通过实验和模拟计算得到,催化剂的失活过程可以根据反应动力学和传质传热过程进行计算。
以上是固定床反应器设计的基本原理和计算方法的介绍,固定床反应器设计是化工生产中的一个重要环节,需要充分考虑到传质和传热、反应动力学和负载平衡等方面的因素来确定反应器的尺寸和操作条件。

化学反应工程复习题这些化学反应工程试题对于学习很有帮助,多练习,更容易懂的。
第一章1.化学反应工程是一门研究“化学反应的工程问题”的科学。
2.所谓数学模型是指:用数学式来表达各参数间的关系。
3.化学反应器的数学模型包括:动力学方程式、物料恒算式、热量恒算式、动量恒算式和参数计算式。
4.所谓控制体积是指:能把反应速率视作定值的最大空间。
5.模型参数随空间而变化的数学模型称为“分布参数模型”。
6.模型参数随时间而变化的数学模型称为“动态模型”。
7.建立物料、热量和动量衡算方程的一般式为:累积量=输入量-输出量。
第二章1.均相反应是指:在均一的气相或液相中进行的反应。
2.对于反应aA+bB→pP+S,则rP=_______rA。
3.着眼反应物A的转化率的定义式为:反应的量/反应开始的量。
4.产物P的收率ΦP与得率ХP和转化率某A间的关系为_________________________________________________。
5.化学反应速率式为rA=kCCAαCBβ,用浓度表示的速率常数为kC,假定符合理想气体状态方程,如用压力表示的速率常数kP,则kC=_______kP。
6.对反应aA+bB→pP+S的膨胀因子的定义式为___________________。
7.膨胀率的物理意义为:反应物全部转化后系统体积的变化分率。
这些化学反应工程试题对于学习很有帮助,多练习,更容易懂的。
8.活化能的大小直接反映了“反应速率”对温度变化的敏感程度。
9.反应级数的大小直接反映了“反应速率”对浓度变化的敏感程度。
10.对复合反应,生成主产物的反应称为:主反应,其它的均为:副反应。
11.平行反应A→P、A→S均为一级不可逆反应,若E1>E2,选择性Sp与“活化能”无关,仅是“温度”的函数。
12.如果平行反应A→P、A→S均为一级不可逆反应,若E1>E2,提高选择性SP应增加温度。
13.一级连串反应A→P→S在平推流反应器中,为提高目的产物P的收率,应______k2/k1。
列管式固定床反应器的模拟与设计摘要:列管式固定床反应器是化工行业和石化行业中一种非常重要的反应器,对一些强放热反应优势明显。
传统的模拟和设计列管式反应器的方法是基于单管实验,假定工业反应器内各反应管的操作条件与单管实验条件相同,也就是说忽视了工业反应器内冷却条件和流动的不均匀性,这个假定会引起很大的误差。
邻二甲苯氧化制苯配是工业生产苯配的主要工艺,其工业生产主要在列管式固定床反应器内进行。
要设计合理的列管式反应器,最重要的就是确定壳程空间的最优解。
本文提出了一个关于壳程的二维小池模型,将壳程空间分成若干个二维小池,在所有小池内,冷却剂的流动只有平行于管束和垂直于管束两个分量。
关键词:列管式反应器,固定床,结构设计目录列管式固定床反应器的模拟与设计 (1)第1章前言 (3)第2章文献综述 (4)2.1苯配生产 (4)2.2列管式固定床反应器的结构 (5)2.3列管式固定床反应器的设计进展 (7)2.4反应器的分析方法 (18)2.5反应器结构的优化 (19)第3章列管式固定床反应器中邻二甲苯氧化反应的研究 (20)3.1邻二甲苯氧化制苯配工艺 (20)3.2一维拟均相模型求解管侧 (22)3.3二维拟均相模型求解管侧 (24)3.4操作参数对邻二甲苯氧化反应的影响 (26)3.5结果与讨论 (28)第6章全文总结 (29)参考文献 (31)第1章前言固定床催化反应器是化学工业和石油化学工业中应用多、用面广泛的反应设备,根据其换热方式可分为绝热和非绝热(列管式)两种。
对于反应热效应很大,收率对温度敏感而又要求高转化率和高选择性的反应,为维持适宜的温度,必须用换热介质来移走或供给热量,采用列管式固定床反应器是非常合适的。
如丙烯胺氧化制备丙烯睛、蔡或邻二甲苯氧化制备苯配、乙烯氧化制环氧乙烷、苯或正丁烷氧化制顺配、异丁烯氧化制备甲基丙烯酸等[1][5]。
如今,相当一部分气固相催化反应在列管式固定床反应器中进行,而该反应器的设计开发技术大都是从国外引进,国内的装置普遍存在温差较大的问题,主要是壳程冷却剂流动分布不均的问题。
反应过程与技术固定床反应器的计算固定床反应器是一种广泛应用于化学工业中的反应装置。
它的设计和计算涉及到多种因素,包括反应过程的动力学、传质过程、热力学等等。
下面将详细介绍固定床反应器的计算方法。
固定床反应器是通过固体催化剂催化气体或液体相中的化学反应进行的。
在固定床反应器中,催化剂被放置在反应器中,反应物经过催化剂层与之接触,催化剂可以提供活性位点,从而促进反应的进行。
反应物在通过催化剂层时与催化剂发生反应,生成产物。
固定床反应器的设计和计算就是为了达到最佳的反应效果和产物质量。
固定床反应器的计算主要涉及到以下几个方面:反应动力学、传质过程、热力学和传递过程。
首先,反应动力学是固定床反应器设计和计算的基础。
反应动力学研究反应速率与反应条件之间的关系。
在固定床反应器中,反应速率与反应物浓度、反应温度等因素有关。
通过实验方法或者数学模型可以获得反应动力学的参数,进而计算出在不同反应条件下的反应速率。
其次,传质过程也很重要。
在固定床反应器中,反应物通过催化剂层时会发生质量传递过程,包括物质的传递和能量的传递。
传质过程的研究可以帮助优化反应物在催化剂层中的传递效率,提高反应速率和产物质量。
然后,热力学也是固定床反应器设计和计算的重要一环。
在反应过程中,热量的产生或吸收会影响反应物的浓度、速率和产物的选择性。
通过热力学计算可以确保反应器内部的温度控制在一定范围内,提高反应的稳定性和效果。
最后,传递过程也需要考虑。
固定床反应器中,反应物通过催化剂层时会发生动量传递和能量传递。
传递过程的计算可以帮助优化反应物在催化剂层中的分布和流动状态,进一步提高反应的效率。
综上所述,固定床反应器的计算主要包括反应动力学、传质过程、热力学和传递过程等方面。
通过合理的设计和计算,可以提高固定床反应器的反应效率和产物质量,实现化学工业过程的优化和提升。
固定床列管式反应器的设计◆乙烯法合成乙酸乙烯的原理 (2)一、催化剂 (2)1. 催化剂的组成 (2)2. 催化剂的制备 (2)3. 催化剂物性 (2)二、反应方程 (2)三、工艺条件的确定 (3)1、反应温度 (3)2、反应压力 (3)3、原料配比 (3)◆乙烯法合成乙酸乙烯反应器的设计计算 (4)一、设计选材 (4)二、设计数据和工作参数 (4)三、反应器进出物料组成 (4)四、基本物性数据 (5)1、相对分子质量 (5)2、密度 (5)3、黏度 (5)4、比热容 (6)五、反应器的数学模型 (6)1、床层对外的径向换热项 (6)2、动力学方程 (6)3、浓度分布方程 (7)4、温度分布方程 (7)5、数学模型方程参数 (7)6、数学模型计算及其结果 (8)六、反应管排布 (9)七、气体分布板设计 (9)1、气体分布板的形式 (9)2、分布板的压降 (9)3、板厚 (11)4、孔数和孔径的确定 (11)八、壳程换热 (12)1) 换热介质进出口结构 (12)2) 换热介质 (12)3) 折流板型式 (12)九、管口设计 (12)1、反应物进口 (12)2、产物出口 (13)3、换热介质进口 (13)4、换热介质出口 (13)十、预热器 (13)十一、封头 (13)十二、支座 (13)◆附录一 (14)◆参考文献 (16)◆乙烯法合成乙酸乙烯的原理一、催化剂[6]选用Bayer-I型催化剂1.催化剂的组成:●活性组分——钯、金:组分金的作用是防止活性组分钯产生氧化凝聚,使钯在载体上维持良好的分散状态。
●助催化剂——乙酸钾:乙酸钾的存在有助于反应组分乙酸在钯金属上缔合,促进物理吸附的乙酸的离解和释放氢离子,使钯-氧间的键结合力减弱,促使乙酸钯的分解;此外,还可抑制深度氧化反应,从而提高了反应的选择性。
●载体——硅胶:承载活性组分及助催化剂,使其在载体表面上呈高度分散状态。
2.催化剂的制备:●结构:μ;中间的第二层是一层黑Bayer-I型催化剂为球星颗粒,最外面的第一层是灰色的表皮层,厚度约为100mμ;最里面的第三层是载体硅胶,呈浅土黄色。
第六章 固定床反应器1.凡是流体通过不动的固体物料所形成的床层而进行反应的装置都称作_______。
(固定床反应器)2.固定床中催化剂不易磨损是一大优点,但更主要的是床层内流体的流动接近于_______,因此与返混式的反应器相比,可用较少量的催化剂和较小的反应器容积来获得较大的生产能力。
(平推流)3.固定床中催化剂不易磨损是一大优点,但更主要的是床层内流体的流动接近于平推流,因此与返混式的反应器相比,可用_______的催化剂和_______的反应器容积来获得较大的生产能力。
(较少量、较小)4.目前描述固定床反应器的数学模型可分为_______和_______的两大类。
(拟均相、非均相)5.描述固定床反应器的拟均相模型忽略了粒子与流体之间_______与_______的差别。
(温度、浓度)6.描述固定床反应器的数学模型,忽略了粒子与流体之间温度与浓度的差别的模型称之为_______。
(拟均相模型)7.描述固定床反应器的数学模型,考虑了粒子与流体之间温度与浓度的差别的模型称之为_______。
(非均相模型)8.描述固定床反应器的拟均相模型,根据流动模式与温差的情况它又可分为平推流与有轴向返混的_______模型,和同时考虑径向混合和径向温差的_______模型。
(一维、二维)9.固定床中颗粒的体积相当直径定义为具有相同体积P V 的球粒子直径,表达式V d =_______。
(3/1)/6(πP V )10.固定床中颗粒的面积相当直径是以外表面P a 相同的球形粒子的直径,表达式a d =_______。
(π/P a ) 11.固定床中颗粒的比表面相当直径是以相同的比表面V S 的球形粒子直径来表示,表达式S d =_______。
(V S /6) 12.对于非球形粒子,其外表面积P a 必大于同体积球形粒子的外表面积S a ,故可定义颗粒的形状系数=S ϕ_______。
(P Sa a /) 13.颗粒的形状系数S ϕ对于球体而言,=S ϕ_______,对于其他形状的颗粒S ϕ_______。
固定床:当气体以较小的速度流过固定床时,流动气体的上升阻力不致使颗粒的运动状态发生变化,床高维持不变;床层压降随流速对数增大而增大。
流化床:固体颗粒可以像水等液体一样在设备内有明显的界面,即使设备倾斜,界面仍会保持水平;床层压降不随流速变化(基本不变)。
输送床:固体颗粒在设备内无明显界面;床层压力随流速增大而减小。
流化床和沸腾床可能只是叫法上不同。
流化床,也就是沸腾床,接触面大,传热传质效率高,时空产率高,但返混严重。
需要注意的是不能堵塞气体分布器,堵了很麻烦的。
固定床和移动床比较适合气-气、气-液和液-液反应,床层本身作为[wiki]催化剂[/wiki],优点是返混小,固相带出少,分离简单。
流化床的床型是设计中很重要的,与反应体系的匹配要求比较高。
此外,操作中的气速、带出量、与配套的旋风等分离设备设计比较严格。
流化床的传热和破汽泡、沟流措施也是研究比较多的。
固定床反应器是一种被广泛采用的多相催化反应器,反应器内填充有固定不动的固体颗粒,可以是固体催化剂也可以是固体反应物.例如管式固定床反应器,管内装催化剂,管内装催化剂,反应物料自上而下通过床层,管间为载热体与管内反应物进行换热,以维持所需的温度条件.此外,固定床反应器也可用于气固及液固非催化反应.沸腾床是流化床的一种,固体在流化床反应器内流动,流体和固体颗粒所构成的床层犹如沸腾的液体. 沸腾床反应器下部设有分布板,板上放固体颗粒,流体自分布板下送入,当流体速度达到一定数值后,固体颗粒开始松动,再增大流速就进入流化状态.反应器内一般设有挡板,换热器,及流体与固体分离装置等内部部件.移动床与固定床相似,不同的是固体颗粒自顶部连续加入,由底部卸出.沸腾床因为固体处于运动状态,反应或传热效果好,但动力消耗大,而且在煤调湿中粉尘携带量大.固定床:固定床反应器又称填充床反应器,装填有固体催化剂或固体反应物用以实现多相反应过程的一种反应器。
固体物通常呈颗粒状,粒径2~15mm左右,堆积成一定高度(或厚度)的床层。
固定床反应器的数学模型1、概述凡是流体通过不动的固体物料所形成的床层而进行反应的装置都称作固定床反应器,其中尤以用气态的反应物料通过由固体催化剂所构成的床层进行反应的气-固相催化反应器占最主要的地位。
如炼油工业中的催化重整,异构化,基本化学工业中的氨合成、天然气转化,油化工中的乙烯氧化制环氧乙烷、乙苯脱氢制苯乙烯等等。
此外还有不少非催化的气-固相反应,如水煤气的生产,氮与电反应生成灰氮(CaCN2)以及多矿物的焙烧等,也都采用固定床反应器。
固定床反应器之所以成为气固催化反应器的主要形式,是由于具有床的流体轴向流动可看作为平推流,在完成同样的生产任务时,所需的催化剂用量(或反应器体积)最小;床流体的停留时间可格控制,温度分布可适当调节,因而有利于提高化学反应的转化率和选择性;床催化剂不易磨损,可以在高温高压下操作等优点,但固定床中传热较差,对于热效应大的反应过程,传热与控温问题就成为固定床技术中的难点和关键,为解决这一问题而提出了多种形式的床层结构。
2、固定床反应器的结构形式固定床反应器类型很多.按换热式不同可分为:绝热式反应器和换热式反应器。
2.1绝热式反应器在反应器中的反应区(催化剂层)不与外界换热的称为绝热式反应器。
一般来说,反应热效应小;调节进A反应器的物料温度,就可使反应温度不致超出反应允的温度围的反应过程等可采用绝热式反应器。
绝热式反应器具有结构简单,反应空间利用率高,造价便宜等优点。
图1是绝热床反应器的示意图。
如果反应热效应较大,为了减小反应区轴间温度分布不均,可将绝热反应器改成多段绝热式反应器,在各段之间进行加热或冷却,它可使各段反应区接近适宜温度。
图2是多段绝热床反应器的示意图。
总之,不论是吸热或放热的反应,绝热床的应用相当广泛。
特别对大型的,高温的或高压的反应器,希望结构简单,同样大小的装置能容纳尽可能多的催化剂以增加生产能力(少加换热空间),而绝热床正好能符合这种要求。
不过绝热床的温度变化总是比较大的,而温度对反应结果的影响也是举足轻重的,因此如取舍,要综合分析并根据实际情况来决定。
此外还应注意到绝热床的高/径比不宜过大,床层填充务必均匀,并注意气流的预分布,以保证气流在床层的均匀分布。
物料气催化剂产物图1 绝热式反应器图2 多段绝热床反应器的示意图2.2换热式反应器为了改善热效应大的反应过程反应区的温度条件,可在反应区进行热交换,这种反应器称为换热式反应器。
换热式反应器又有自热式和外热式两种。
自热式是以原料气体来加热或冷却反应区(图3),外热式则是用载热体加热或冷却反应区换热式反应器以列管式为多,通常在管放催化剂,管外走热载体(图4)。
列管的管径一般取25~50mm为宜,催化剂的粒径应小于管径的8倍,以防管壁处出现沟流。
图3换热式反应器(乙炔法合成氯乙烯反应器)图4 自热式反应器示意图3、固定床反应器的数学模型反应器是整个化工生产过程的核心装置,其中固定床反应器是应用较为广泛的反应设备,建立能准确描述其特性的数学模型,不但可以给反应器设计和最优化操作提供理论依据,更减少了工作量。
实现其优化操作,具有重要意义。
描述固定床反应器的数学模型按其传递过程的不同可分为拟均相模型和非均相模型两大类。
拟均相模型不考虑流体与催化剂间的传热、传质阻力,把流体和催化剂看成均相物系,催化剂粒子和流体之间没有温度和浓度上的差别。
拟均相模型又可分为拟均相一维模型和拟均相二维模型(表1)。
非均相模型则考虑了流体与催化剂外表面间的温度梯度和浓度梯度,须对流体和催化剂分别列出物料衡算式。
表1 固定床反应器的数学模型拟均相模型非均相模型一维 基本模型 (A-Ⅰ) +相间梯度 (B-Ⅰ) +轴向混合 (A-Ⅱ) +颗粒梯度(B-Ⅱ) 二维 +径向混合 (A-Ⅲ)+径向梯度 (B-Ⅲ)3.1拟均相基本模型(A-I)(拟均相一维活塞流模型)将实际非均相反应系统简化为均相系统处理。
适用于:(1)化学反应为控制步骤;(2)流固相间或固相部存在传递阻力;“拟均相”是只指将实际上为非均相的反应系统简化为均相系统处理,即认为流体相和固体相之间不存在浓度差和温度差。
“一维”的含义是只在流动向上存在浓度梯度和温度梯度,而垂直于流动向的同一截面上各点的浓度和温度均相等。
“活塞流”的含义则是在流动向上不存在任形式的返混。
物料衡算程:当为等摩尔反应时,能量衡算程: 管: 管外:流动阻力程:()()()d d d d A A A B A AB A N N N r V N r Vρρ=++--=-()()d d d d AB A A B A uA c r A z u c r z ρρ-=--=-()()()d 4d g pR B A c tT Uu c H r T T z d ρ∆ρ=----()d 4d c c c pcc tT Uu c T T z d ρ=-2d d g k pu pf z d ρ-=边界条件:对于绝热反应器:对反应物流和载热体并流的列管式反应器:求解法用龙格库塔法。
对反应物流和载热体逆流的列管式反应器:求解式:打靶法。
3.2拟均相轴向分散模型(A-Ⅱ)反应物流通过固体颗粒床层是不断分流和汇合,并作绕流流动,造成一定程度的轴向混合(返混),用分散模型描述。
管物料衡算程:管能量衡算程::管外EB 和流动阻力程同拟均相基本模型。
边界条件:与拟均相基本模型相比,引入轴向混合项的作用主要在于:(1)降低转化率;(2)当轴向混合足够大时,反应器可能存在多重定态。
对于反应速率随床层轴向距离单调减小的情形,如果进口条件满足下面两式,可忽略轴向混合影响的判据:0000, , , , A A c c z c c T T p p z L T T ======处处0000, , , A A z c c T T p p ====处00000, , , , A A c c z c c T T T T p p =====处()22d d d d A Aea B A c u c D r z zρ-=-()()()22d d 4d d ea g p R B A c tT T Uu c H r T T z z d λρ∆ρ-+=----()()000d 0, d d d d d ,0d d AA A ea g p eaA c z u c c D z Tu c T T zp p c Tz L z zρλ=-=--=-====处处()()ma PB A Pe d r <<-0ρ3.3拟均相二维模型(A-Ⅲ)对于管径较粗或反应热较大,造成径向位置处反应速率和反应物浓度的差别, 需采用二维模型,同时考虑轴向及径向分布。
在列管反应器的某反应管中,以反应管轴线为中心线,取以半径为r ,径向厚度为dr ,轴向高度为dz 的环状微元体,如图5所示图5 拟均相二维模型对微元体作组分A 的物料衡算:气相主体流动自z 面进入微元体的组分A 的量为: 气相主体流动自(z+dz )面流出微元体的组分A 的量为:从r 面扩散进入微元体的组分A 的量:从r +dr 面扩散出微元体的组分A 的量:()()()()ha Pg W PB A Pe c u T T d r H <<--∆-ρρ00Ardruc π2⎪⎭⎫⎝⎛∂∂+dz z c c rdru A A π2rc rdzD A er∂∂-π2组分A 在微元体的反应量:在定态条件下:进入微元体的量-出微元体的量=微元体反应的量3.4考虑颗粒界面梯度的活塞流非均相模型(B-I)对于热效应很大而且速率极快的反应,可能需要考虑流体相和固体相之间的浓度差和温度差。
气相衡算程:固相衡算程:边界条件:求解式:先通过迭代求解固相式后再代入气相式进行数值解微分程。
)()(222dr rc r c dzD dr r AA er ∂∂+∂∂+-π()A B r rdrdz -ρπ2()()()H r r T r r T z Tc u r r c r rc D z c u A B er p g A B A A er A∆--+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂--⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂ρλρρ112222能量守恒方程:物料衡算方程:000,000=∂∂=∂∂=∂∂====rT r T rcz r T T c c r z sA A A 为任意值处,,为任意值处,,边界条件:()()()d d d 4d Ag A As g p s c t c uk a c c z T U u c ha T T T T z d ρ-=-=---()()()()(),,g A As A As s B s A As s B k a c c r c T ha T T r c T H ρρ∆-=-⎡⎤⎣⎦-=--⎡⎤⎣⎦000, , A A z c c T T ===处3.4考虑颗粒界面梯度和颗粒梯度的活塞流非均相模型(B-Ⅱ)当催化剂颗粒的传热、传质阻力很大时,颗粒不同位置的反应速率是不均匀的。
气相衡算程:固相衡算程:气相程的边值条件:固相程的边值条件:3.4非均相二维模型(B-Ⅲ)迄今结构最复杂的固定床反应器数学模型,既考虑了沿反应器轴向和径向的浓度分布和温度分布,也考虑了气固相间和固相部的浓度差和温度差。
该模型在考虑床层部和床层与器壁的传热时,都对气相和固相的贡献作了区分。
气相衡算程:)(dzd As A g Ac c a k c u-=-)(4)(dz dT C tS pg T T D UT T ha c u ---=ρ0)),(()d dc (d d D As22e =--s s As A T c r ρξξξξ0)),()(()d dT (d d s22e =-∆-+s s As A T c r H ρξξξξλ00,0T T c c z A A ===处,)(d dc -2As A Asec c a k Dd g p -==ξξ处,0d dT d dc 0sAs ===ξξξ处,)T T (d dT s se-=-ha ξλ()As A g A A er Ac c a k r c r rc D z c u -=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-122固相衡算程: 边值条件:()()As A g B A c c a k r -=-ρη()()()T T ha r T r r T H r s serB A -=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∆--122λρη()()rT T T h rT T T h rcz d t r T r T rcz r T T c c r z s s er s w s wer w wA t sA A A ∂∂=-∂∂=-=∂∂==∂∂=∂∂=∂∂====λλf f000,200,0,,0为任意值处,为任意值处,为任意值处,。