郧县城关一中七年级下垂线导学案

P O A BCCBA新人教版七年级数学下册第五章《垂线（第2课时）》导学案学习目标：1. 理解垂线段的概念、点到直线的距离的概念，并会度量点到直线的距离。

2. 掌握垂线的性质，并会利用所学知识进行简单的推理应用。

学习重点：垂线段的性质。

学习难点：垂线性质的应用点，到直线的距离的理解。

学前准备：经过直线l 外一点P 画l 的垂线，并说明这样的垂线能画出几条？【导入】【自主学习，合作交流】阅读教材第五至六四页练习前面部分，解决下列问题：1.如图，连接直线l 外一点P 与直线l 上各点O ，A,B,C,……,其中l PO （我们称PO 为点P 到直线l 的垂线段）。

比较线段PO 、PA 、PB 、PC ……的长短，这些线段中，哪一条最短？2．性质2 连接直线外一点与直线上各点的所有线段中， 最短。

简单说成： 最短。

3. 点到直线的距离：直线外一点到这条直线的______________的长度叫做点到直线的距离。

4.完成课本5页的思考中的问题【师生互动，精讲点拔】例.如图，AC ⊥BC, AC=3, BC=4, AB=5, 则B 到AC 的距离是___________, 点A 到BC 的距离是__________, 点C 到AB 的距离是__________。

如图，CD ⊥AB,则有CD CB (填＞或 ＜ )，根据是_______________ 小试牛刀:如图,AC⊥BC,C 为垂足,CD⊥AB,D 为垂足,BC=8,CD=4.8, BD=6.4,AD=3.6,AC= 6,那么点C 到AB 的距离是_______, 点A 到BC 的距离是________,点B 到CD 的距离是_____, A 、B 两点的距离是_________. 【精讲点拔】：学生出现问题教师精讲点拔【课后小结】今天你有什么收获？还有什么困惑？【当堂测试】 一、选择题:1.如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段DCBAO DCA(1) (2) (3)2.如图1所示,能表示点到直线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条3.如图2所示,AD ⊥B D,BC ⊥CD,AB=acm,BC=bcm,则BD 的范围是( ) A.大于acm B.小于bcmC.大于acm 或小于bcmD.大于bcm 且小于acm 4.到直线L 的距离等于2cm 的点有( )A.0个B.1个;C.无数个D.无法确定5.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到 直线m的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cm【课后作业】 必做题E D BAO FE DC BA 11.已知钝角∠AOB,点D 在射线OB 上. (1)画直线DE⊥OB;(2)画直线DF⊥OA,垂足为F.2. 如图，直线AB,CD 相交于点O,的度数。

垂线一、温故知新 1．如下图，若∠∠3=____、∠2．改变上图中∠1请画出这3=____、∠二、设问导读阅读课本P 3-P 6仿照课本3型，生活中垂直的例子如图 与 垂直，记作 ，垂足为 ，AB CD 是_____几何语言：（1）因为AB ⊥CD 所以______（（2）因为∠1=90所以________（2、垂线的画法⑴如图1直线l 的垂线，__________条；⑵如图2，点⑶如图3直线与已知直线种判定两条直线的垂直的方）两条直线lO mn1B3、如图，已知直线AB、CD都经过O点，OE为射线，若∠1＝35°，∠2＝55°，则OE与AB的位置关系是。

4、作图题：直线AB，CD相交于点O，Q为CD上一点，（1）过点Q画AB的垂线，E为垂足。

（2）过点O画CD的垂线。

互动学习、问题解决导入新课二、交流展示学用结合、提高能力一、巩固训练1、如图，画AE⊥BC，CF⊥AD，垂足分别为E，F。

2、两条直线相交所成的四个角中，下列条件中能判定两条直线垂直的是( )（A）有两个角相等（B）有两对角相等（C）有三个角相等（D）有四对邻补角3、如图，BO⊥AO，∠BOC与∠COA的度数之比为1:5，那么∠COA＝_____,∠BOC的补角为______度。

6、如图，AB与CD交于点O，OA平分∠EOC, ∠EOC=100°，则∠B OC的度数是（）A.120°B.40C.130D.80 °7.如图∠2是∠1的3倍, 则∠3=__ ，若∠2－∠1=40。

,则∠4=__二、拓展延伸、如图,直线AB、CD相交于点O.(1)若∠AOC+∠BOD=100°,求各角的度数。

(2)若∠BOC比∠AOC的2倍多33°,求各角的度数。

ODCBA课堂小结、形成网络________________________________ba432112 34BC。

课题：5.1.2 垂线（2）课型：新授课 总第3节 时间：星期三【学习目标】1、经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念培养学生用几何语言准确表达的能力。

2、了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离。

【学习重点】垂线的性质。

【学习难点】垂线的性质的应用。

预 习 篇1、上学期我们学习过“什么什么最短”的几何知识,还记得吗? 。

2、思考P5图5.1-8中提出问题:要把河中的水引到农田P 处, 如何挖渠能使渠道最短?3、自学课本内容后，你能解决2中提出的问题吗？若不能，有哪方面的困惑？学 习 篇知识点一、垂线段的性质 探究一、 1、问题转化如果把小河看成是直线L ，把要挖的渠道看成是一条线段，则该线段的一个端点自然是农田P ，另一个端点就是直线L 上的某个点。

那么最短渠道问题会变成是怎样的数学问题？（提示：用数学眼光思考:在连接直线L 外一点P 与直线L 上各点的线段中,哪一条最短?）3、画图验证(1)画直线L,在L 外取一点P;(2)过P 点出PO ⊥L,垂足为O;(3)点A1,A2,A3……在L 上,连接PA 、PA2、PA3……;(4)用度量法比较线段PO 、PA1、PA2、PA3……的大小，.得出线段______ 最小。

归纳结论.1、 连接直线外一点与直线上各点的所有线段中，_______________ .简单说成: ____________________________2、从直线外一点到已知直线的的垂线段的长度叫_______________如图，点A 到直线l 的距离就是垂线段＿＿＿＿的长度。

精练、1、 (1)垂线段与垂线有何区别联系？(2)垂线段与线段有何区别与联系？ lA D C BED C B A2、此时你会解决课本P5图5.1-8中提出的问题吗？在图形中画出“最短渠道”的位置。

.探究“点到直线的距离”？定义:(1) 回答什么叫“点到直线的距离”？默写一遍：____________________________ 叫做点到直线的距离。

七年级数学下册导学案1．两条直线互相垂直，•其中的一条直线叫做另一条直线的_______，•交点叫做________．2．过一点有且只有_______与已知直线_______．3．连结直线外一点与直线上各点的所有线段中，________最短．4．直线外一点到这条直线的________的长度，叫做点到直线的距离．5. 垂直用符号“⊥”来表示，若“直线AB垂直于直线CD，垂足为O”，则记为___________，6．如图，若∠1=60°，那么∠2=_______、∠3=_______、∠4=_______7.改变上图中∠1的大小，若∠1=90°，请画出这种图形，并求出此时∠2、∠3、∠4的大小。

例1.（1）同一平面内，点与直线的位置关系：和（2）已知直线a有条垂线（3）作图：①过直线l上一点A,作直线AB l 垂足为A②过直线AB外一点C,作CD AB,垂足为D.（4）垂线的性质：例2.垂直的推理应用：（1）∵∠AOD=90°（）∴AB⊥CD （）（2）∵ AB⊥CD （）∴∠AOD=90°（）3．如图1直线AB，CD与EF相交，构成_______个角，其中∠1与∠5是_______，∠3与∠5是______，∠4与∠5是_______．图1 图2 图34．如图2所示，CD⊥AB，则点D是_____，∠ADC=∠CDB=________．5．如图3所示，l1⊥l2，垂足为_____，∠1与∠2是一组_____的邻补角，∠1•与______是一对_______的对顶角．6.如图(1),OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD=________.7.如图(2),AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=________.8.如图(3),直线AB、CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB的位置关系是_________.1.如图所示，l1⊥l2，图中与直线L1垂直的直线是（）A．直线a B．直线L2C．直线a，b D．直线a，b，c2．如图所示，下列说法不正确的是（）A．∠1与∠B是同位角B．∠1与∠4是内错角C．∠3与∠B是同旁内角D．∠C与∠A不是同旁内角3.过点P向线段AB所在直线引垂线，正确的是（）4.已知点A，与点A的距离是5cm的直线可画（）A.1条B.2条C.3条D.无数条5.如图，∠ACB=90°CD⊥AB，线段AC、BC、CD中最短的是（）A.ACB.BCC.CDD.不能6.如图：直线AB、CD相交于点O, OE AB于点O,,则7.已知如图，BC ⊥AC，BC= 8，AC= 6，AB= 10,则点B到AC的距离是 , 点A到BC的距离是 ,点A、点B之间的的距离是8.如图，= 90°，,=3，= 4，= 5 (1)点A到BC的距离是, 点B到AC的距离是 ,(2)求线段CD的长9.已知直线AB、CD交于O, OE CD，OF AB，且，求和的度数10.我国“十一五”规划其中一重要目标是，建设社会主义新农村，国家对农村公路建设投资近1000亿人民币．西部的某落后山村准备在河流M上架上一座桥梁，如图所示，桥建在何处才能使A，B两个村庄的之间修建路面最短？。

课题：5、1、2 垂线（1）课型：新授课总第2节时间：星期二【学习目标】1、理解垂线、垂线段的概念，会用三角尺或量角器过一点画已知直线的垂线。

2、掌握点到直线的距离的概念，并会度量点到直线的距离。

3、掌握垂线的性质，并会利用所学知识进行简单的推理。

【学习重点】垂线的定义及性质。

【学习难点】垂线的画法预习篇1、如图，若∠1=60°，那么∠2=_______、∠3=_______、∠4=_______2、改变上图中∠1的大小，若∠1=90°，请画出这种图形，并求出此时∠2、∠3、∠4的大小。

学习篇探究一:1、当两条直线相交所成的四个角中有一个角是90°时，这两条直线互相＿＿＿＿，其中一条直线叫做另一条直线的＿＿＿＿，两条直线的交点叫＿＿＿＿，垂直用符号＿＿＿＿来表示，读作＿＿＿＿，如直线AB垂直CD，就记作＿＿＿＿。

回答上面所画图形中两条直线的关系是__________，知道两条直线互相________是两条直线相交的特殊情况。

总结：用语言概括垂直定义1、两条直线相交，所成四个角中有一个角是_____时，我们称这两条直线__________其中一条直线是另一条的_____，他们的交点叫做_____。

2、垂直的表示方法：垂直用符号“⊥”来表示，若“直线AB垂直于直线CD，垂足为O”，则记为__________________，并在图中任意一个角处作上直角记号,如下图。

3、垂直的推理应用：（1）∵∠AOD=90°（）∴AB⊥CD （）（2）∵ AB⊥CD （）∴∠AOD=90°（）探究二:1、用三角尺或量角器画出已知直线l的垂线，这样的垂线能画出几条？(1)ODC BA(2)ODCBA E(3)O D CBA 2、经过直线l 上一点A 画出l 的垂线，能画出几条？ 3、经过直线l 外一点B 画出l 的垂线，能画出几条？总结： 由此我们得出如下结论：1、一条直线的垂线有＿＿＿＿条。

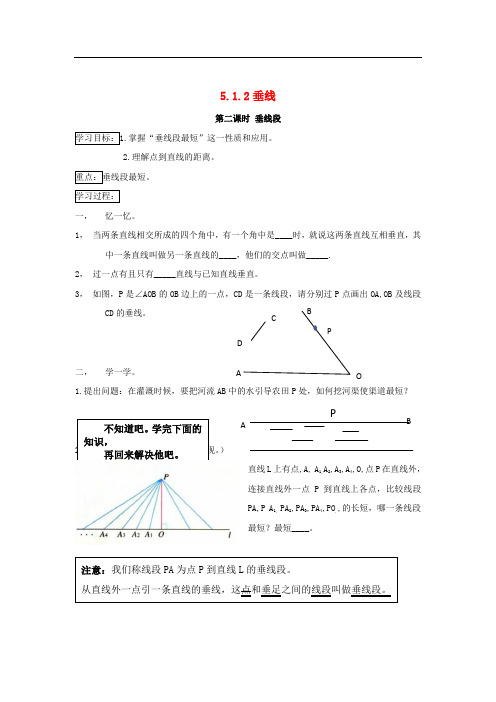
5.1.2垂线第二课时 垂线段掌握“垂线段最短”这一性质和应用。

2.理解点到直线的距离。

一， 忆一忆。

1， 当两条直线相交所成的四个角中，有一个角中是____时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的____，他们的交点叫做_____.2， 过一点有且只有_____直线与已知直线垂直。

3， 如图，P 是∠AOB 的OB 边上的一点，CD 是一条线段，请分别过P 点画出OA,OB 及线段CD 的垂线。

二， 学一学。

1.提出问题：在灌溉时候，要把河流AB） 直线L 上有点,A, A 1,A 2,A 3,A 4,O,点P 在直线外，连接直线外一点P 到直线上各点，比较线段PA,P A 1, PA 2,PA 3,PA 4,PO ,,的长短，哪一条线段最短？最短____。

再回来解决他吧。

结论：连接直线外一点与直线上各点的所有直线中，垂线段最短。

简而言之：垂线段最短。

3.现在能完成1的问题了吧？动手画起来。

4.直线外一点到这条直线的垂线段的距离的长度，叫做点到直线的距离。

上图中，线段PA 的长度就是点P 到直线L 的距离。

5.垂线段的画法（师生共同完成）。

已知：如图，三角形ABC ，∠BAC 是钝角。

（1） 画出点C 到AB 的距离。

（2） 过点A 画BC 的垂线。

（3） 量出点B 到AC 的距离。

三．试一试。

1.课本6页练习。

2.如图。

BC ⊥AC,CB=8cm.AC=6cm,AB=10cm, 那么点B 到AC 的距离是_____.点A 到BC 的距离是_____.A,B 两点之间的距离是_____. 1. 如图所示。

一辆汽车在直线形的公路AB 上由A 向B 行驶，M,N 分别是位于公路两侧的村庄。

（1）、假设车子行驶在公路AB 上点P 位置时，距离村庄M 最近，行驶在点Q 位置时，距离村庄N 最近，请在图中的公路AB 上分别画出点P 和Q 的位置（保留作图痕迹）。

（2）、当汽车从A 出发向B 行驶时，在公路AB 的那一段路上距离M,N 两村都越来越近？在那一段路上距离村庄N 越来越近，而离村庄M 越来越远？（分别用文字表示你的结论）。

一、预习导学（甲）（乙）这是两幅草坪的图案。

在绿色的草坪上，画着两条交叉的道路。

你觉得甲图、乙图那幅更漂亮、更匀称。

这是什么原因？演示自制教具，这两条相交线有没有特殊位置？什么情况下它们的位置特殊？图甲是两条直线相交的一种特殊情况，它在生活、生产实际中应用比较广，你有没有见过？例如：书本相邻的两条边、窗户框相邻的两边、红十字等，因此今天我们就来研究这种特殊情况二、新课探究（一）垂线的定义直线a不动，当直线b转到什么位置时，两条直线互相垂直？转动木条b时，它和不动的木条a互相垂直的位置有几个？当a、b相交有一个角是直角时，其他三个角呢？垂线的定义：当两条直线相交所成的四个角，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫垂足。

建筑工人在砌墙时，常用铅垂线来检查所砌的墙面是否和地面（水平面）垂直。

（二）符号表示“⊥”读作“垂直于”如AB⊥CD垂足为O，含义：直线AB与直线CD垂直，垂足是O你能说出由什么条件能知道AB与CD互相垂直吗？∵∠BOC=90º(已知)∴AB⊥CD (垂直的定义)其它三个角中的一个角等于90º,能不能得到AB⊥CD 呢?反过来,如果AB⊥CD,那么可得到什么结论?(填空)∵AB⊥CD于O (已知)∴________________(垂直的定义)（三）垂线的画法（1）已知直线l，有多少条直线与已知直线l垂直？（2）点与直线的位置关系有几种？如图2中，过点A画直线BD的垂线B ·A DAD 图1 B在学生画出垂线的基础上，教师总结出用三角板画垂线的基本方法强调用两条直角边“一贴”：贴住已知直线，“一靠”：靠住已知点再画线并引导学生思考：这样画出的为何是已知直线的垂线?（四）发现垂线的性质在学生熟练地画出各条垂线之后，1、过A点作BD的垂线有没有？2、过A点作BD的垂线有几条？在此基础上，又引导学生概括出：垂线的第一个性质公理：过一点有且只有一条直线与注：①“有且只有”中，“有”指“存在”，“只有”指（五）垂线的第二个性质1、量跳远的成绩时有人想多量点，都采取了什么手段？为什麽？2、用刻度尺量一量下列垂线段OP与线段PA、PB、PC的大小PA B O C（1）什么是垂线段？直线外一点与直线上各点连结的所有的线段中，垂线段最短六、点到直线的距离要把水渠的水引到水池C，为了节省人力物力财力，请你十分钟小测1、下列说法是否正确：两条直线相交，有一条角是直角，则两条直线互相垂直。

人教版七年级数学下册导学案 第五章 相交线与平行线 5.1.2 垂线（第一课时）【学习目标】1．理解垂线的概念，会用三角尺或量角器过一点画已知直线的垂线.2．掌握垂线的性质，并会利用所学知识进行简单的推理.【课前预习】1．点P 是直线l 外一点，A 为垂足，PA ⊥l ，且PA=5cm ，则点P 到直线l 的距离（ ）A ．小于PA=5cmB ．等于PA=5cmC ．大于PA=5cmD ．不确定2．下列说法中，正确的是（ ）A ．在同一平面内，过一点有无数条直线与已知直线垂直B ．两直线相交，对顶角互补C ．垂线段最短D ．直线外一点到这条直线的垂线段叫做点到直线的距离3．下列四个说法：①两点之间，线段最短；②连接两点之间的线段叫做这两点间的距离；③经过直线外一点，有且只有一条直线与这条直线平行；④直线外一点与这条直线上各点连接的所有线段中，垂线段最短.其中正确的个数有（ ） A ．1个 B ．2个 C ．3个 D ．4个4．下列说法中，不正确的是（ ）A ．两直线相交所成的四个角中有两个角相等，则这两条直线互相垂直B ．在同一平面内，经过一已知点能画一条直线和已知直线垂直C ．一条直线可以有无数条垂线D ．在同一平面内，过射线的端点与射线垂直的直线只有一条5．点P 为直线m 外一点,点A ,B ,C 为直线m 上三点,PA =4cm ,PB =5cm ,PC =2cm ,则点P 到直线m 的距离为( ) A ．4cm B ．2cm ; C ．小于2cm D ．不大于2cm6．如图所示，直线AB ，CD 相交于点O ，OE AB ⊥于点O ，OF 平分AOE ∠，11530'∠=︒，则下列结论中不正确的是（ ）A ．245∠=︒B ．13∠=∠C ．AOD ∠与1∠互为补角 D ．1∠的余角等于7530'︒7．如图，直线AB 与CD 相交于点O ，∠BOD=40°，OE∠AB ，则∠COE 的度数为（ ）A ．140B ．130C ．120D ．1108．如图，A 是直线l 外一点，过点A 作AB l ⊥于点B ，在直线l 上取一点C ，连接AC ，使2AC AB =，P 在线段BC 上，连接AP ．若3AB =，则线段AP 的长不可能是（ ）A ．4B ．5C ．2D ．5.59．甲，乙两位同学用尺规作“过直线l 外一点C 作直线l 的垂线”时，第一步两位同学都以C 为圆心，适当长度为半径画弧，交直线l 于D ，E 两点（如图）；第二步甲同学作∠DCE 的平分线所在的直线，乙同学作DE 的中垂线．则下列说法正确的是（ ）A ．只有甲的画法正确B ．只有乙的画法正确OD C B AC ．甲，乙的画法都正确D ．甲，乙的画法都不正确10．如图，∠1＝20º，AO ⊥CO ，点B 、O 、D 在同一条直线上，则∠2的度数为（ ）A ．70ºB ．20ºC ．110ºD ．160º【学习探究】自主学习 阅读课本，完成下列问题1．观察教室里的课桌面、黑板面相邻的两条边，方格纸的横线与竖线。

5.1。

2 垂线第一课时 垂线（预习）学习目标：1，了解垂线的定义，2,掌握垂线的性质，回过一点作已知直线的垂线.重点：垂线的概念 学习过程；一， 忆一忆。

1，若两角有一条公共边，他们的另一边互为____________.具有这种关系的两个角互为领补角.2，若两个角有一个公共____。

且他们的每个角的两边都互为_____________________。

具有这两种关系的两个角，互为对顶角，对顶角_____.3，如图，直线a ，b 相交。

若∠1=350，则∠2=__，∠3=__,∠4=__. 若∠1=900. 则∠2=__,∠3=__,∠4=__。

若∠1=m 0。

则∠2=__，∠3=__,∠4=__。

二， 学一学。

1. 垂线的定义.【阅读课本第三页,思考完成下列问题】（1） 垂线是两条直线____时的一种特殊情况,特殊在两条直线所形成的四个角一个是____（或是等于___）。

因此，垂直是反映两条直线的______关系.（2）.如图，直线AB ，CD ，互相垂直，记作______，垂足为P.直线AB 叫做直线CD 的_____.直线CD 叫做直线AB 的_______. (3），利用垂直的定义，可进行 如下的推理:a2 1 34bP∵AB ⊥ CD(已知） 或∵AB ⊥ CD(已知) ∴∠A PC=900（垂直定义） 2，如图∠BAC=900, AD ⊥BC ， 垂足为D 。

则以下结论 (1)AB 与AC 互相垂直。

(2）AD 和AC 互相垂直。

（3)∠ADB=∠ADC=900其中准确的是______（写序号）。

3举出生活中反映两条互相垂直的线条的一些例子.1. 垂线的画法：经过点A 画L 的垂线,（根据下列方法，动手试试）让直角三角板的一条直角边与L重合。

沿着L 移动三角板，使其另一条直角边经过点A.沿着此直角边画直线，就得到L 的垂线.5，探究垂线的性质（动手画图，并回答问题）（1） 用三角尺画出已知直线的垂线，这样的垂线能画多少？能画____条（2能画____条（3）。

5.1.2 垂线中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。

一、教材分析：本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握，让学生开始对书法的入门学习有一定了解。

书法作为中国特有的一门线条艺术，在书写中与笔、墨、纸、砚相得益彰，是中国人民勤劳智慧的结晶，是举世公认的艺术奇葩。

早在5000年以前的甲骨文就初露端倪，书法从文字产生到形成文字的书写体系，几经变革创造了多种体式的书写艺术。

1、教学目标：使学生了解书法的发展史概况和特点及书法的总体情况，通过分析代表作品，获得如何欣赏书法作品的知识，并能作简单的书法练习。

2、教学重点与难点：（一）教学重点了解中国书法的基础知识，掌握其基本特点，进行大量的书法练习。

（二）教学难点：如何感受、认识书法作品中的线条美、结构美、气韵美。

3、教具准备：粉笔，钢笔，书写纸等。

4、课时：一课时二、教学方法：要让学生在教学过程中有所收获，并达到一定的教学目标，在本节课的教学中，我将采用欣赏法、讲授法、练习法来设计本节课。

（1）欣赏法：通过幻灯片让学生欣赏大量优秀的书法作品，使学生对书法产生浓厚的兴趣。

（2）讲授法：讲解书法文字的发展简史，和形式特征，让学生对书法作进一步的了解和认识，通过对书法理论的了解，更深刻的认识书法，从而为以后的书法练习作重要铺垫！（3）练习法：为了使学生充分了解、认识书法名家名作的书法功底和技巧，请学生进行局部临摹练习。

三、教学过程：（一）组织教学让学生准备好上课用的工具，如钢笔，书与纸等;做好上课准备，以便在以下的教学过程中有一个良好的学习气氛。

（二）引入新课，通过对上节课所学知识的总结，让学生认识到学习书法的意义和重要性！（三）讲授新课1、在讲授新课之前，通过大量幻灯片让学生欣赏一些优秀的书法作品，使学生对书法产生浓厚的兴趣。

2、讲解书法文字的发展简史和形式特征，让学生对书法作品进一步的了解和认识通过对书法理论的了解，更深刻的认识书法，从而为以后的书法练习作重要铺垫！A书法文字发展简史：①古文字系统甲古文——钟鼎文——篆书早在5000年以前我们中华民族的祖先就在龟甲、兽骨上刻出了许多用于记载占卜、天文历法、医术的原始文字“甲骨文”；到了夏商周时期，由于生产力的发展，人们掌握了金属的治炼技术，便在金属器皿上铸上当时的一些天文，历法等情况，这就是“钟鼎文”（又名金文）；秦统一全国以后为了方便政治、经济、文化的交流，便将各国纷杂的文字统一为“秦篆”，为了有别于以前的大篆又称小篆。