贝叶斯网络 (2)

贝叶斯网络与因果推理贝叶斯网络是一种常用的概率图模型，被广泛应用于因果推理领域。

它以概率分布和有向无环图为基础，能够帮助我们理解和分析变量之间的因果关系。

本文将详细介绍贝叶斯网络的原理与应用，以及它在因果推理中的重要作用。

一、贝叶斯网络的原理贝叶斯网络基于贝叶斯定理和条件独立性假设，通过节点、边和概率表达式构成有向无环图，从而建立变量之间的因果关系模型。

在贝叶斯网络中，节点代表随机变量，边表示变量之间的依赖关系，而概率表达式则描述了变量之间的条件概率分布。

贝叶斯网络的核心是贝叶斯定理，其形式为P(A|B) = (P(B|A) * P(A)) / P(B)。

其中，P(A|B)表示在已知B发生的条件下，A发生的概率；P(B|A)表示在已知A发生的条件下，B发生的概率；P(A)和P(B)分别表示A和B独立发生的概率。

二、贝叶斯网络的应用1. 分类和预测：贝叶斯网络可以通过学习已知数据的概率关系，进行分类和预测任务。

通过给定一些观测变量，可以计算出其他未观测变量的概率分布，从而进行分类或预测。

2. 诊断和故障检测：贝叶斯网络可以用于诊断系统故障或进行故障检测。

通过观测系统中的一些变量，可以推断其他未观测变量的概率分布，从而确定系统的故障原因。

3. 原因分析和决策支持：贝叶斯网络可以用于原因分析和决策支持。

通过构建概率模型，可以确定某个事件发生的原因，从而辅助决策制定。

三、贝叶斯网络与因果推理1. 因果关系建模：贝叶斯网络可以帮助我们理解和建模变量之间的因果关系。

通过有向无环图，我们可以确定变量之间的依赖关系和因果关系。

贝叶斯网络的条件概率表达式则描述了变量之间的因果关系。

2. 因果推理：贝叶斯网络可以用于因果推理，即通过观测到的一些变量，来推断其他未观测变量的概率分布。

这种推理方式能够帮助我们分析和预测因果关系，并进行有效的决策。

3. 因果关系判定：贝叶斯网络可以用于判定变量之间的因果关系。

通过条件独立性和概率计算，我们可以判断出某个变量对另一个变量的影响程度，从而确定因果关系。

贝叶斯网络及其应用贝叶斯网络是一种基于概率数学的图形模型，可以表示多个变量之间的关系，包括因果关系和依赖关系。

贝叶斯网络常用于分类、预测和诊断等领域，具有广泛的应用价值。

一、贝叶斯网络的原理贝叶斯网络的核心思想是贝叶斯定理，即在观测变量的前提下，推断未观测变量的概率分布。

具体而言，贝叶斯网络由节点（变量）和边（关系）构成，其中节点表示变量，边表示变量之间的关系。

例如，一个人的身高和体重之间存在一定的关系。

如果用贝叶斯网络表示，身高和体重分别是两个节点，它们之间存在一条边。

因为身高可以影响体重，但是体重不能影响身高。

贝叶斯网络可以表示更为复杂的关系，例如，多个变量之间的依赖关系或因果关系。

应用贝叶斯网络可以对复杂的现象进行建模，并进行推理和预测。

二、贝叶斯网络的应用1. 分类贝叶斯网络在分类问题中有广泛的应用。

例如，在医学诊断中，病人的症状和疾病之间存在复杂的关系，使用贝叶斯网络可以对病情进行分类。

另外，在垃圾邮件分类中，使用贝叶斯网络可以对邮件进行分类，以便过滤垃圾邮件。

2. 预测贝叶斯网络在预测问题中也有广泛的应用。

例如，在金融领域，使用贝叶斯网络可以对股票价格进行预测。

另外，在环境研究中，使用贝叶斯网络可以对气候变化等问题进行预测。

3. 诊断贝叶斯网络在诊断领域中也有广泛的应用。

例如，在医学诊断中，使用贝叶斯网络可以根据病人的症状和疾病之间的关系，进行病情诊断。

另外，在工业控制中，使用贝叶斯网络可以对机器故障进行诊断。

三、贝叶斯网络的局限性贝叶斯网络虽然具有广泛的应用价值，但也存在一些局限性。

其中最主要的局限性是数据要求较高。

因为贝叶斯网络需要大量的数据来进行建模和训练，如果数据量太少，可能会影响预测的准确性。

另外，贝叶斯网络对于较为复杂的现象建模能力有限，可能无法完全反映真实的现象。

四、结论贝叶斯网络是一种基于概率数学的图形模型，可以表示多个变量之间的关系。

它具有广泛的应用价值，包括分类、预测和诊断等领域。

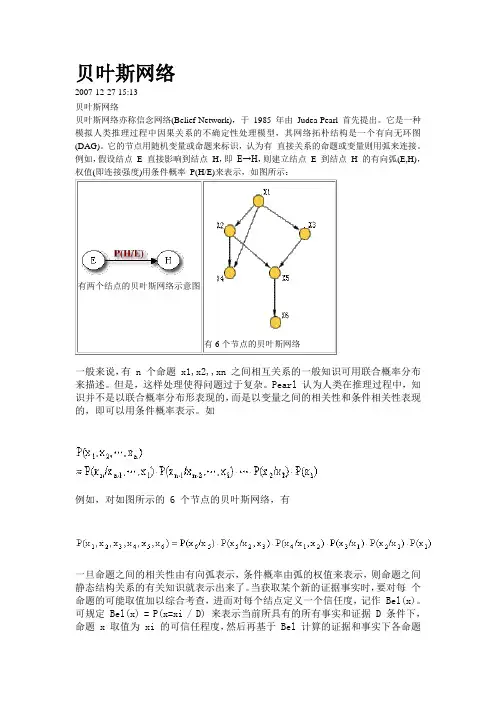
贝叶斯网络2007-12-27 15:13贝叶斯网络贝叶斯网络亦称信念网络(Belief Network)，于1985 年由Judea Pearl 首先提出。

它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

它的节点用随机变量或命题来标识，认为有直接关系的命题或变量则用弧来连接。

例如，假设结点E 直接影响到结点H，即E→H，则建立结点E 到结点H 的有向弧(E,H)，权值(即连接强度)用条件概率P(H/E)来表示，如图所示：一般来说，有 n 个命题 x1,x2,,xn 之间相互关系的一般知识可用联合概率分布来描述。

但是，这样处理使得问题过于复杂。

Pearl 认为人类在推理过程中，知识并不是以联合概率分布形表现的，而是以变量之间的相关性和条件相关性表现的，即可以用条件概率表示。

如例如，对如图所示的 6 个节点的贝叶斯网络，有一旦命题之间的相关性由有向弧表示，条件概率由弧的权值来表示，则命题之间静态结构关系的有关知识就表示出来了。

当获取某个新的证据事实时，要对每个命题的可能取值加以综合考查，进而对每个结点定义一个信任度，记作 Bel(x)。

可规定 Bel(x) = P(x=xi / D) 来表示当前所具有的所有事实和证据 D 条件下，命题 x 取值为 xi 的可信任程度，然后再基于 Bel 计算的证据和事实下各命题的可信任程度。

团队作战目标选择在 Robocode 中，特别在团队作战中。

战场上同时存在很多机器人，在你附近的机器人有可能是队友，也有可能是敌人。

如何从这些复杂的信息中选择目标机器人，是团队作战的一大问题，当然我们可以人工做一些简单的判断，但是战场的信息是变化的，人工假定的条件并不是都能成立，所以让机器人能自我选择，自我推理出最优目标才是可行之首。

而贝叶斯网络在处理概率问题上面有很大的优势。

首先，贝叶斯网络在联合概率方面有一个紧凑的表示法，这样比较容易根据一些事例搜索到可能的目标。

贝叶斯网络的原理及应用贝叶斯网络是一种用于建立概率模型的图论工具，它的核心思想是利用已知变量之间的依赖关系，推断出未知变量的概率分布。

它能够在复杂的环境中推断因果关系，并且在实际应用中，贝叶斯网络已经被广泛应用于分类、预测、诊断、决策等领域。

一、贝叶斯网络的基本原理贝叶斯网络是通过将变量之间的关系表示为一个有向无环图（Directed Acyclic Graph, DAG），来表示因果关系的一种方法。

每个节点代表一个变量，每条有向边表示这两个变量之间存在的因果关系。

在贝叶斯网络中，每个节点的状态是随机的，因此我们需要知道每个节点的先验概率分布，也就是在不考虑其他节点的情况下，该节点的概率分布。

比如，在预测肺癌的成功率时，我们需要知道不吸烟的人得肺癌的概率以及吸烟的人得肺癌的概率，这样可以作为我们推断整个网络的先验概率分布的基础。

同时，每个节点之间的关系也需要知道，也就是我们需要知道条件概率分布。

比如，在上述预测肺癌的例子中，假设我们知道吸烟的人得肺癌的概率是普通人的两倍，那么我们就可以得到一个条件概率分布，即在知道吸烟与否之后得到肺癌的概率。

在具体使用中，我们可以通过向网络中添加已知信息来进行推断，例如，在预测成功率时，我们可以通过添加是否吸烟或不吸烟这样的信息，来得到成功率的后验概率分布。

二、贝叶斯网络的应用贝叶斯网络的应用非常广泛，其中最常见的就是在医疗诊断和健康预测中。

它可以通过收集大量的病例数据，并通过建立基于这些数据的贝叶斯网络，来进行诊断和预测。

例如，在对肾结石病人进行诊断时，可以构建一个基于病人病史、身体特征等变量的贝叶斯网络，从而准确地确定病人是否患有肾结石。

除了医疗应用外，贝叶斯网络还广泛使用于金融风险评估、机器人导航、图像识别、自然语言处理等领域。

在金融风险评估方面，贝叶斯网络可以用来预测股票市场的走势，从而帮助投资者做出正确的投资决策。

在机器人导航方面，贝叶斯网络可以模拟机器人在不同环境下的行动路径，从而进行路线规划和控制。

贝叶斯网络在数据挖掘中的应用研究1.引言贝叶斯网络是一种概率图模型，其能够处理复杂的数据关系，并具有强大的预测能力。

在数据挖掘领域，贝叶斯网络得到了广泛应用，尤其是在分类、聚类、回归等问题上具有良好的效果。

本文将探讨贝叶斯网络在数据挖掘中的应用研究。

2.贝叶斯网络基础2.1 贝叶斯定理贝叶斯网络是基于贝叶斯定理的概率图模型。

贝叶斯定理的公式为P(A|B)=P(B|A)P(A)/P(B)其中，P(A|B)表示在已知B的条件下A发生的概率，P(B|A)表示在已知A的条件下B发生的概率，P(A)和P(B)分别表示A和B 的先验概率。

2.2 贝叶斯网络的基本概念贝叶斯网络是由变量集和有向边集组成的有向无环图(DAG)，其中，变量表示随机变量，有向边表示变量之间的因果关系。

贝叶斯网络中的节点表示变量，边表示变量之间的条件概率关系。

一个节点的父节点表示该节点的条件概率。

3.贝叶斯网络在分类问题中的应用3.1 贝叶斯网络分类器基础贝叶斯网络分类器是基于贝叶斯网络模型实现的分类器，其主要思想是在已知类别的情况下，对新样本进行分类。

贝叶斯网络分类器的公式为P(C|X)=P(X|C)P(C)/P(X)其中，C表示类别，X表示样本，P(C|X)表示在已知样本X的条件下C类别的概率，P(X|C)表示在已知C的条件下X样本的概率，P(C)表示类别C的先验概率，P(X)表示样本X的先验概率。

3.2 贝叶斯网络在文本分类中的应用文本分类是数据挖掘中一个重要的任务，其在信息检索、情感分析、垃圾邮件识别等领域有着广泛的应用。

贝叶斯网络在文本分类中的应用主要涉及到文本切分、特征提取和模型训练三个方面。

其中，文本切分可以通过自然语言处理技术实现，特征提取需要选择合适的特征表示方法，模型训练可以通过最大似然估计方法实现。

4.贝叶斯网络在聚类问题中的应用聚类是数据挖掘中另一个重要的任务，其主要目的是将数据集划分为若干个簇，簇内的数据点具有较高的相似性，而簇间的数据点具有较小的相似性。

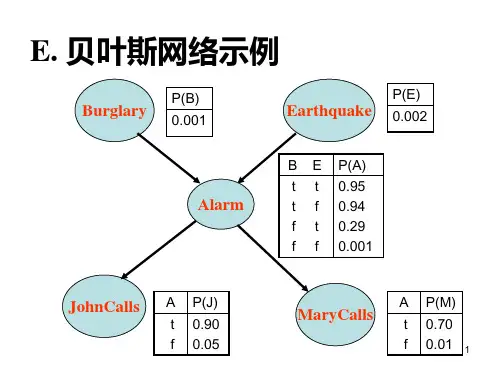
探索贝叶斯网络算法贝叶斯网络算法的探索贝叶斯网络（Bayesian Network）是一种用于建模概率关系的有向无环图结构，其应用包括遗传学、医学诊断、自然语言处理、数据挖掘等领域。

基于概率模型和图论的理论基础，贝叶斯网络算法已成为机器学习和人工智能领域的重要研究方向。

本文将探索贝叶斯网络算法的基本概念、核心理论和实际应用。

一、贝叶斯网络的基本概念贝叶斯网络是基于贝叶斯定理（Bayes’ Theorem）的一种概率模型。

在贝叶斯网络中，节点表示随机变量，有向边表示变量之间的条件依赖关系。

节点的概率分布可以通过给定父节点的概率分布计算得出。

贝叶斯网络通常包括两种节点类型：随机变量节点和参数节点。

其中随机变量节点表示真实变量的取值，该类型节点的概率分布可以通过其他节点推理得到；参数节点则表示分布的参数，该类型节点的取值可以从先验分布中获得。

二、贝叶斯网络的核心理论贝叶斯网络模型的训练和推理需要依赖贝叶斯网络的理论基础。

常用的贝叶斯网络推理算法包括贝叶斯定理、变量消元、采样和MCMC等算法。

其中，贝叶斯定理是基于全概率公式和条件概率公式推导出的概率推理公式，用于在给定观测数据和模型结构的前提下计算后验概率分布。

变量消元算法则是一种基于高斯消元的推理算法，可以通过消去未被观测的变量来简化计算。

采样算法则是利用Markov Chain Monte Carlo（MCMC）方法生成随机样本，从而估计概率分布。

MCMC算法则是一种随机游走算法，通过对参数空间进行随机游走，以获得参数的后验分布。

三、贝叶斯网络的实际应用贝叶斯网络算法可以应用于各种实际问题的建模和推理过程。

例如，贝叶斯网络可以用来构建遗传病的筛查模型，根据家族病史和疾病表现预测个体的发病风险。

同时，贝叶斯网络在医学诊断中也有广泛的应用，可以根据临床数据和病因知识推导出疾病的概率分布。

贝叶斯网络还可以应用于自然语言处理中的问题建模和推理，例如语音识别和机器翻译。

统计学中的贝叶斯网络推断算法统计学中的贝叶斯网络推断算法是一种基于贝叶斯定理的概率推断方法，用于描述变量之间的依赖关系。

本文将介绍贝叶斯网络的基本概念和原理，以及贝叶斯网络推断算法的应用和相关领域的研究进展。

一、贝叶斯网络的基本概念和原理1.1 贝叶斯网络的定义贝叶斯网络是一种统计模型，用于描述一组变量之间的条件依赖关系。

它由有向无环图表示，其中节点表示变量，边表示条件依赖关系。

贝叶斯网络利用条件概率表来表示变量之间的依赖关系。

1.2 贝叶斯网络的基本原理贝叶斯网络基于贝叶斯定理进行推断。

给定一些观察到的变量的取值，我们可以通过贝叶斯网络计算未观察到的变量的后验概率分布。

贝叶斯网络的推断可以分为两个步骤：先学习贝叶斯网络的结构和参数，然后利用学到的模型进行推断。

二、贝叶斯网络推断算法的应用2.1 贝叶斯网络推断算法的基本步骤贝叶斯网络推断算法的基本步骤包括：（1）根据给定的数据学习贝叶斯网络的结构；（2）学习贝叶斯网络的参数；（3）根据学习到的贝叶斯网络进行推断。

2.2 贝叶斯网络推断算法的应用领域贝叶斯网络推断算法在许多领域中都有广泛的应用。

例如，在医学诊断中，可以利用贝叶斯网络推断算法对患者的病情进行准确的诊断。

在金融风险评估中，可以利用贝叶斯网络推断算法对市场风险进行评估和预测。

此外，贝叶斯网络推断算法还可以应用于自然语言处理、图像识别等领域。

三、贝叶斯网络推断算法的研究进展3.1 贝叶斯网络结构学习算法贝叶斯网络的结构学习算法是贝叶斯网络推断算法中的重要部分。

研究者们提出了许多用于学习贝叶斯网络结构的算法，如贪婪算法、约束-based算法等。

这些算法在结构学习的准确性和效率方面都有显著的提升。

3.2 贝叶斯网络参数学习算法贝叶斯网络参数的学习是贝叶斯网络推断算法中的另一个重要方面。

研究者们提出了许多用于学习贝叶斯网络参数的算法，如EM算法、最大似然估计等。

这些算法在参数学习的准确性和效率方面都有显著的提高。

贝叶斯网络的结构与推断贝叶斯网络是一种以概率论为基础的图模型，用于表示和推断变量之间的依赖关系。

它由节点和有向边组成，节点代表变量，有向边表示变量之间的依赖关系。

在这篇文章中，我们将介绍贝叶斯网络的结构和推断算法。

一、贝叶斯网络的结构贝叶斯网络的结构以有向无环图（DAG）的形式呈现。

节点表示变量，有向边表示变量之间的依赖关系。

一个节点的父节点是其直接的依赖节点。

通过这种结构，我们可以很直观地表示变量之间的因果关系。

在贝叶斯网络中，节点的概率分布是条件概率分布。

每个节点根据其父节点的取值情况来计算其概率分布。

这种条件概率的建模方式使得贝叶斯网络能够灵活地处理不同节点之间的依赖关系。

二、贝叶斯网络的推断贝叶斯网络可以用于推断未观测到的节点的概率分布。

在推断过程中，我们可以利用已观测到的节点的取值来推断未观测到的节点的取值。

贝叶斯网络通过贝叶斯定理来进行推断，即根据观测到的证据来更新后验概率。

推断的常用算法有变量消除和近似推断算法。

变量消除算法通过对贝叶斯网络进行剪枝和重组，来减少计算量。

近似推断算法则采用一些近似方法来简化推断过程，以提高计算效率。

三、贝叶斯网络的应用贝叶斯网络在许多领域都有广泛的应用。

其中，最常见的应用是决策分析和风险评估。

例如，在医学诊断中，贝叶斯网络可以用于推断患者的疾病概率，从而辅助医生做出诊断和治疗决策。

此外，贝叶斯网络还可以应用于自然语言处理、图像处理和机器学习等领域。

在自然语言处理中，贝叶斯网络可以用于词义消歧和信息抽取。

在图像处理中，贝叶斯网络可以用于目标识别和图像分割。

在机器学习中，贝叶斯网络可以用于模式分类和数据挖掘。

四、贝叶斯网络的优势和局限性贝叶斯网络具有许多优势，例如其能够处理不确定性、灵活性和解释性。

贝叶斯网络能够通过概率分布来描述不确定性，允许对不完全观测到的现象进行建模。

同时，贝叶斯网络的灵活性使其适用于各种领域和问题。

此外，贝叶斯网络还具有解释性，可以帮助我们理解变量之间的因果关系。

贝叶斯网络在金融风险管理中的应用作为一种基于概率推断的图模型，贝叶斯网络在不确定性领域中有着广泛的应用。

特别是在金融风险管理中，利用贝叶斯网络可以对各种各样的金融风险进行量化和管理。

一、贝叶斯网络的概念贝叶斯网络（Bayesian network）是一种概率图模型，通常被用于处理不确定性和因果关系。

它建立在贝叶斯定理的基础上，能够对某个事件的概率进行推断和估计，同时也能够作为一种决策支持工具来帮助人们制定决策。

贝叶斯网络由节点和有向边组成，节点表示变量，有向边表示变量之间的依赖关系和因果关系。

二、2.1 风险评估和预测通过构建贝叶斯网络模型，可以对金融风险进行评估和预测。

比如，可以利用贝叶斯网络对股票市场的波动性进行预测，也可以对信贷违约情况进行评估和风险控制。

同时，通过对每个因素的概率进行估计，可以用来制定决策和调整风险管理策略。

2.2 投资组合优化在资产组合管理中，利用贝叶斯网络可以将各种潜在因素转化为概率指标，为投资组合提供量化的评估和优化。

例如，可以利用股票收益率、市场指数、国家经济指标等因素构建一个贝叶斯网络模型，来对某个投资组合的表现进行预测和评估。

2.3 风险监测和控制贝叶斯网络可以通过对各种影响因素之间的依赖关系进行建模，帮助金融机构监测和控制风险。

例如，在市场波动性高、系统性风险大的情况下，基金公司可以利用贝叶斯网络对基金的净值波动情况进行监测和控制，以便及时进行调整和决策。

三、贝叶斯网络应用中的挑战和未来尽管贝叶斯网络在金融风险管理中有广泛的应用和潜力，在实际应用中也存在一些挑战。

首先，贝叶斯网络需要大量的数据和先验知识来训练和构建模型，而这些数据和知识有时候并不容易获取。

其次，贝叶斯网络在建模的过程中需要面临复杂、高维的数据结构，这也需要一定的技术和算法能力。

不过，随着技术和数据科学的不断发展，贝叶斯网络在金融风险管理中的应用前景非常广阔。

未来，可以通过深度学习、自然语言处理等技术手段，进一步加强贝叶斯网络在金融风险管理中的应用，为机构和投资者提供更加精确和可靠的决策支持。