利用EXCE的规划求解进行求解威布尔分布参数共49页文档

用Excel求解数学规划武汉大学水利水电学院万飚Excel是Microsoft Office办公软件中的一个组件，以其强大的电子表格处理功能备受广大用户的青睐。

由于Excel支持丰富的公式和函数，因而在一般财务计算、高级财务管理、财务分析、信息管理、管理决策、市场营销、工程管理，以及管理科学、经济学和统计学等领域都得到了广泛的应用。

一、关于规划求解“规划求解”是Microsoft Excel中的一个加载宏，借助它可以求解许多运筹学中的数学规划问题。

Excel的“规划求解”工具来自德克萨斯大学奥斯汀分校的Leon Lasdon和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码；线性规划和整数规划算法来自Frontline Systems公司的John Watson和Dan Fylstra 提供的有界变量单纯形法和分支定界法。

安装Office的时候，系统默认的安装方式不会安装该宏程序，需要用户自己选择安装。

安装方法为：从Excel菜单中选择“工具”→“加载宏”，打开如下对话框：选择其中的“规划求解”后单击“确定”按钮，会出现提示：“这项功能目前尚未安装，是否现在安装?”，选择“是”，系统要你插入Office的安装光盘，准备好后单击确定，很快就会安装完毕。

于是，你会发现在“工具”菜单下多出一个名为“规划求解”的子菜单，说明“规划求解”功能已经成功安装。

二、第一个线性规划问题例：求解以下线性规划问题：⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,124 16 48232 21212121x x x x x x x x z max 步骤：1．将模型中的目标函数和约束条件的系数输入到单元格中；为了使我们在操作过程中看得更清楚，可以附带输入相应的标识符，并给表格加上边框。

如下图所示：2．在E4单元格（目标值）输入“=SUMPRODUCT($C$3:$D$3,C4:D4)”；其中，SUMPRODUCT 函数的功能是将数组间对应的元素相乘，并返回乘积之和，即SUMPRODUCT($C$3:$D$3,C4:D4)＝C3×C4＋D3×D4；$C$3:$D$3表示这几个单元格为绝对引用。

例1. 工厂生产计划优化问题
某工厂生产4种小型工具，由于该四种工具有 不同的大小、形状、重量和风格，所以它们所需要 的主要原料（钢材和橡胶）、制作时间、最大销售 量与利润均不相同。该厂每天可提供的钢材、橡胶 和工人劳动时间分别为600单位、1000单位与400小 时，详细的数据资料见下表。
应如何安排这四种工具的日产量，使得该厂的日利 润最大？
，求x2+3y的最大值。
完整的模型描述：
第二步 在“工具”菜单中选择“规划求解”。 第三步 在“规划求解参数”对话框进行选择如下图。
第四步 点击“选项”按钮，弹出“规划求解选项”对话框
第五步 单击“求解”，即可解决此题。
最后结果如下页图所示。
例2. 整数求解问题
完成下题的求解：
一般数值求解问题： 已知x,y取值满足
工具类型
表1 生产基本数据
12 3
4 可提供两
劳动时间（小时/件） 2 1 3 2 400小时
钢材（单位/件）
4 2 1 2 600单位
橡胶（单位/件）
6 2 1 2 1000单位
单位利润（元/件） 60 20 40 30
最大销售量（件） 100 200 50 100
解：依题意，设置四种工具的日产量分别为决策变量
2.如何加载“规划求解”
1) 在“工具”菜单上,单击“加载宏”
2) 在弹出的对话框中的“可用加载宏”列表框 中,选定待添加的加载宏“规划求解”选项旁 的复选框,然后单击“确定”.单击“确定” 后,“工具”菜单下就会出现一项“规划求解”
3. “规划求解”各参数设置
单击“规划求解”按钮,将会出现以下规划求Fra bibliotek解参数设置对话框

利用线性回归方法求解生产计划方法一：1、建立数学模型:①设变量：设生产拉盖式书桌x台，普通式书桌y台，可得最大利润②确定目标函数及约束条件目标函数：y=max+115P90x约束条件：200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220yx ..........................⑷,≥2、在Excel中求解线性规划①首先，如图1所示，在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项：图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT（B6:C6,F6:F7)；F3=MMULT（B3:C3,F6:F7)；F2=MMULT（B4:C4,F6:F7)；F2=MMULT（B5:C5,F6:F7)；出现图2样式：图2线性规划问题的电子表格模型建好后，即可利用“线性规划”功能进行求解。

选择“工具”→“规划求解”出现“规划求解参数”窗口，如图3所示:图3在该对话框中，目标单元格选择F2，问题类型选择“最大值”，可变单元格选择F6：F7，点击“添加”按钮，弹出“添加约束条件”窗口，如图4所示:图4根据所建模型，共有4个约束条件，针对约束（1）：2002010≤+y x ，左端“单元格所引用位置”选择F3，右端“约束值”选择D3，符号类 型选择“<=”，同理继续添加约束（2）（3）（4），完成后选择“确定”，回到“规划求解参数”对话框，如5图所示：图5④点击“选项”按钮，弹出“规划求解选项”对话框，选择“采用线性模型”和“假定非负”两项，如图6所示：图6⑤点击“确定”→“求解”，选择“运算结果报告”“敏感性报告”“极限值报告”三项，最后点击“确定”，输出结果： 运算结果报告：敏感性报告：极限报告：方法二：1、建立数学模型设生产拉盖式书桌x 台，普通式书桌y 台，总利润为Z 元 确定目标函数及约束条件 目标函数：y x Z 90115max += 约束条件：⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型，如图1所示：图11)在E2中输入“=B2*B6+C2*C6”如图2所示，同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”，在弹出的“规划求解参数”对话框输入各项参数：✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0；E2:E4≤D2:D4参数设置完毕，如图3：图33）点击“选项”，弹出“规划求解选项”对话框，选择“采用线性模型”、“假定非负”和“显示迭代结果”，说明要求求解的问题是线性模型且所求的变量必须为非负，如图4所示：图44）点击“确定”→“求解”，选择“运算结果报告”“敏感性报告”“极限值报告”三项，最后点击“确定”，输出结果：运算结果报告：敏感性报告：极限值报告：。

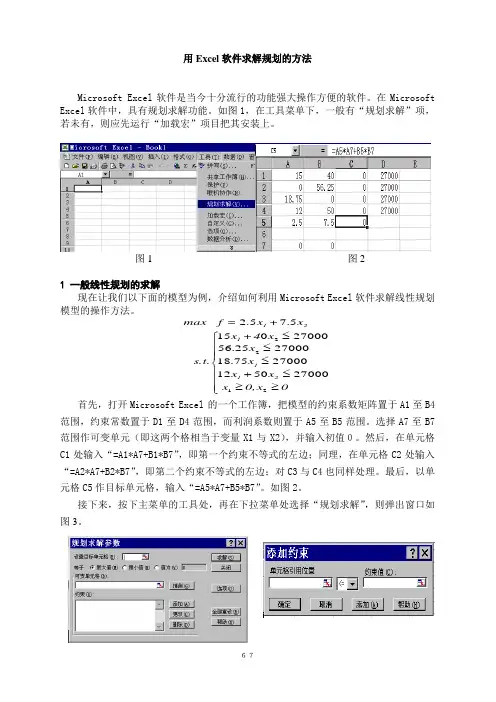
用Excel 软件求解规划的方法Microsoft Excel 软件是当今十分流行的功能强大操作方便的软件。

在Microsoft Excel 软件中，具有规划求解功能。

如图1，在工具菜单下，一般有“规划求解”项，若未有，则应先运行“加载宏”项目把其安装上。

图1 图21 一般线性规划的求解现在让我们以下面的模型为例，介绍如何利用Microsoft Excel 软件求解线性规划模型的操作方法。

首先，打开Microsoft Excel 的一个工作簿，把模型的约束系数矩阵置于A1至B4范围，约束常数置于D1至D4范围，而利润系数则置于A5至B5范围。

选择A7至B7范围作可变单元（即这两个格相当于变量X1与X2），并输入初值０。

然后，在单元格C1处输入“=A1*A7+B1*B7”，即第一个约束不等式的左边；同理，在单元格C2处输入“=A2*A7+B2*B7”，即第二个约束不等式的左边；对C3与C4也同样处理。

最后，以单元格C5作目标单元格，输入“=A5*A7+B5*B7”。

如图2。

接下来，按下主菜单的工具处，再在下拉菜单处选择“规划求解”，则弹出窗口如图3。

⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤≤≤0x 0,x x x x x x 4+x s.t. x +x =f max 21112121222700050122700075.182700025.56270000155.75.2图3 图4在“设置目标单元格”处输入“C5”,然后选“最大值”，再在“可变单元格”处输入“A7:B7”,在“约束”处按一下“添加”按钮，又弹出如图4的窗口。

在此，我们要添加5个约束：“C1 <= D1”、“C2 <= D2”、“C3 <= D3”、“C4 <= D4”、“A7：B7 >= 0”。

对第一个约束，在“单元格引用位置”处输入“C1”,在中间下拉框选择“<=”, 再在“约束值”处输入“D1”。

然后按“添加”按钮，再类似地添加其它约束。

− i + i − 3 + 3 − 2 + 2
− 1
+ 1


3、规划求解一般步骤 1.加载宏 1.加载宏 2.在excel中将模型表示出来 2.在excel中将模型表示出来 3.设置单元格及目标值的确定 3.设置单元格及目标值的确定 4.选定可变单元格 4.选定可变单元格 5.添加约束条件 5.添加约束条件 6.求解 6.求解

5、规划求解结果

2、利用“规划求解”解整数规划问题 利用“规划求解”
仍然以上述线性规划问题为例，假定变量全为整数，则只 需添加一个约束条件即可：

此时的参数设定

计算结果： 计算结果：

整数规划问题的特例0 整数规划问题的特例0—1型问题 不难发现，在刚才的例子中，假定变量的取值非 不难发现，在刚才的例子中，假定变量的取值非0 型问题， 即1，则整数规划问题就转化为 ，则整数规划问题就转化为0—1型问题，在 型问题 excel规划求解中只需在约束条件中添加两个约束条 规划求解中只需在约束条件中添加两个约束条 件即可： 件即可：
Excel的规划求解 Excel的规划求解
一、Excel规划求解预备知识 Excel规划求解预备知识
1.加载“规划求解” 1.加载“规划求解”宏 加载
注：宏加载的越多，excel启动越慢，请根据实际情况酌情考虑 宏加载的越多， 启动越慢， 启动越慢

2、“规划求解”各参数解释和设置 、 规划求解”

2、“规划求解”各参数解释和设置 、 规划求解”

二、Excel规划求解 Excel规划求解 利用“规划求解” 利用“规划求解”解线性规划问题 利用“规划求解” 利用“规划求解”解整数规划问题 利用“规划求解”解运输问题 利用“规划求解” 利用“规划求解” 利用“规划求解”解目标规划问题 利用“规划求解” 利用“规划求解”解最短路问题 利用“规划求解” 利用“规划求解”解最大流问题 利用“规划求解”解数据包络分析(DEA)问 利用“规划求解”解数据包络分析 问 题 • 利用“规划求解”解其他运筹学问题（精确重 利用“规划求解” • • • • • • •

解答Excel之规划求解
2006-09-30 23:38
一个工厂接了一批鼠标,键盘的订单,用现在的设备来生产,鼠标每个\1分钟,键盘第个\1.5分钟,1个鼠标的毛利是50元,1个键盘的毛利是75元,成本价鼠标为15元,键盘为20元,鼠标每日要生产最少200个,一天成本控制在10000元以下,每天10小时,这个工厂每天生产多少个鼠标?多少个键盘才能赚到最大的利润?
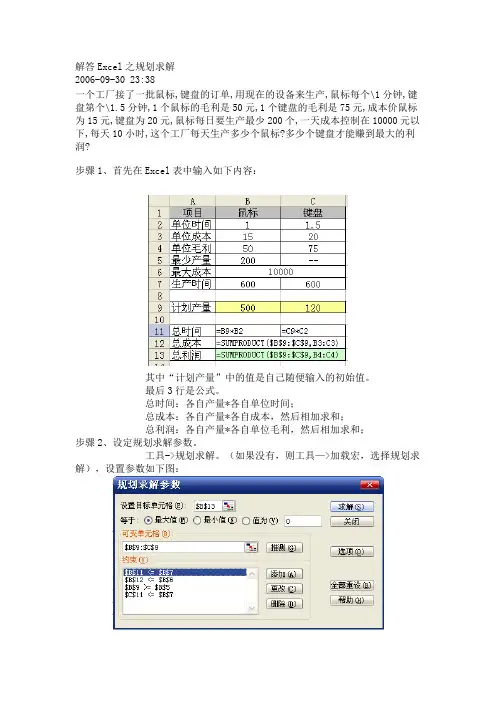
步骤1、首先在Excel表中输入如下内容：
其中“计划产量”中的值是自己随便输入的初始值。

最后3行是公式。

总时间：各自产量*各自单位时间；
总成本：各自产量*各自成本，然后相加求和；
总利润：各自产量*各自单位毛利，然后相加求和；
步骤2、设定规划求解参数。

工具->规划求解。

（如果没有，则工具—>加载宏，选择规划求解），设置参数如下图：
其中：“设置目标单元格”是所求的最大利润；
可变单元格是鼠标键盘的各自计划产量，即通过改变产量搭配，以实现在满足约束条件情况下得到最大利润；
几个约束条件的解释：
1)、鼠标、键盘的各自生产总时间不超过10小时（600分钟）；
2)、总成本不超过最大成本10000；
3)、鼠标产量不小于200；
点击“选项”，在弹出窗口中勾选“采用线性模型”和“假定非负”，然后单击“确定”。

步骤3、设置完成后，点击“求解”，规划求解将计算出一个最佳解决方案（如果有）。

本题中，我求得的结果是：
计划产量：鼠标200，键盘350；
最大利润：36250。

3.4 规划求解
6）约束条件将出现在“约束”列表区：$C$4=6和 $D$4=3。若约束条件设置有误，可通过“更改” 或“删除”对约束条件进行改变。 7）所有参数设置好后，按“求解”，得到相应结果：
3.4 规划求解

3.4.2 解非线性方程组
多元一次线性方程比较容易，对初始值设定无严 格要求。若方程为非线性，则必须设置不同初始 值，才能保证解的可信性。
例：在Cd(ClO4)2和NaCN的水溶液中有如下平衡：
CdCNi2-i Cd 2 iCN H + +CN HCN H + +OH H 2 O
2-i CdCN i i 2 i Cd CN + H CN Ka HCN + KW H OH
3.4 规划求解
Excel步骤：
4）“设置目标单元格”输 入方程F1所在位置： $B$4，“等于”栏设置 目标值为0。“可变单元 格”编辑框输入未知数所 在单元格：$B$2:$D$2。
3.4 规划求解
Excel步骤：
5）单击“约束”选项区的“添加”按钮，出现添加 约束对话框，在“单元格引用位置”处输入方程 F2的位“添加”， 给出新的添加约束对话框，继续增“单元格引用 位置”处输入F3的位置：$D$4，选“＝”，约束 值为3。单击“确定”，回到“规划求解参数”对 话框。
3.4 规划求解
CL是加入的NaCN总浓度，CM是加入的Cd(ClO4)2总 浓度，KW是水的离子积（＝10-14）。 三个方程均为未知浓度的高次函数，用“规划求解” 步骤如下： 1）在B1:B3单元格输入Cd2＋总浓度CM ，CN－的总 浓度CL，HCN的酸解离常数Ka。 2）D2:F2是要求解的未知浓度[CN]、[Cd2+]和[H+]所 在位置。

威布尔分布表达式
威布尔分布是一种概率分布，通常用于描述一些物理、化学或生物现象的寿命或失效时间。

其概率密度函数表示为：f(x) = (α/λ)×(x/λ)^(α-1)×exp(-(x/λ)^α)，其中α和λ为分布的形状参数和尺度参数。

威布尔分布表达式的推导可以使用最大似然估计方法，通过样本数据对参数进行估计。

对于给定的n个样本数据x1,x2,...,xn，威布尔分布的似然函数为：L(α,λ) = ∏(i=1 to n)[(α/λ)×(xi/λ)^(α-1)×exp(-(xi/λ)^α)]。

通过对似然函数进行求导，并令其等于0，可以求得最大似然估计值：α = (n/Σ(xi/λ)^2)^(1/α)，λ = (Σ(xi/λ)^α/n)^(1/α)。

这个估计方法可以通过计算机程序实现，方便地得到威布尔分布的参数估计值。

威布尔分布表达式的应用十分广泛，包括风力场和振动信号的分析、设备寿命的预测、信号传输的可靠性评估等。

其具有良好的数学性质，可以方便地进行推导和计算，因此被广泛应用于工程和科学领域。

- 1 -。

excel韦伯分布拟合韦伯分布（Weibull distribution）是一种常见的概率分布函数，经常在工程学、风险分析和可靠性工程等领域中使用。

它的概率密度函数为：f(x) = (k/λ) * (x/λ)^(k-1) * exp(-(x/λ)^k)其中，x是一个随机变量，k是形状参数（shape parameter），λ是尺度参数（scale parameter）。

韦伯分布可以表示正向偏移（k>1）、反向偏移（k<1）以及无偏移（k=1）的情况。

对于给定的样本数据，我们可以使用Excel做出韦伯分布的拟合。

下面将介绍具体的步骤。

步骤一：准备数据首先，在Excel的一个工作表中准备你要进行拟合的样本数据。

这些数据可以是连续的，也可以是离散的，但要确保数据的数量足够大，这样可以确保拟合结果的准确性。

步骤二：计算分布参数的初值然后，我们需要计算分布参数k和λ的初值。

可以使用Excel的相关函数来完成这一步骤。

具体的函数如下：-形状参数k的估计值可以使用Excel的GAMMA.INV函数来计算。

函数的参数为：样本数据的平均值，样本数据的标准差，以及一个概率值（推荐选择0.5）。

-尺度参数λ的估计值可以使用Excel的AVERAGE函数计算样本数据的平均值。

步骤三：计算拟合函数值接下来，使用Excel的韦伯分布函数（WEIBULL.DIST）来计算拟合函数的值。

该函数的参数为：输入数据，形状参数k，尺度参数λ，以及一个布尔值（若为TRUE，则返回累积分布函数值）。

步骤四：绘制拟合曲线在完成拟合函数值的计算后，我们可以使用Excel的绘图功能来绘制拟合曲线。

具体的步骤如下：1.在Excel中选择一个空白的单元格，输入一个x值序列，用于绘制横轴。

这里可以选择的x值区间可以根据数据的范围来确定。

2.在相邻的单元格中，使用韦伯分布函数计算对应的y值序列。

函数的参数为：x值序列，形状参数k，尺度参数λ。

excel2020规划求解的方法
excel2007规划求解的方法：
规划求解步骤1：首先要在Excel中调出规划求解工具。

规划求解步骤2：点击开始——Excel选项
规划求解步骤3：在选项的【加载项】下，看到了【规划求解加
载项】，处于【非活动应用】状态。

规划求解步骤4：点击【转到】，开始激活它
规划求解步骤5：弹出的对话框中，勾选【规划求解加载项】，
点击【确定】
规划求解步骤6：发现，在【数据】选项卡下出现了【规划求解】工具。

点击【规划求解】
弹出一个对话框
规划求解步骤7：【目标单元格】设为E8，即合计的总价。

规划求解步骤8：将目标值设成10000
规划求解步骤9：【可变单元格】设成购买数量
规划求解步骤10：再点击【添加】，添加约束条件。

规划求解步骤11：【引用位置】选择购买量，
约束条件为>=1，表示最小购买量为1。

规划求解步骤12：再点击【添加】，添加另外的约束条件
规划求解步骤13：新的约束条件中，引用位置依旧是购买量，
但约束值选择为【int】【整数】。

表示购买量一定是整数。

规划求解步骤14：点击【确定】
规划求解参数就设置好了。

规划求解步骤15：点击【求解】
结果出来了，购买量都规划出来了，土豪的10000元，我帮他花个精光。

规划求解步骤17：如果还需要试试约束条件，就先【保存方案】，再调整约束条件。

这是运算结果报告。

8. 单击“求解”按钮开始运算，并显示运算结果，如图所示。 然后单击“确定”按钮保存此结果，结果如图所示。
5.3 求解任务分配
1. 问题描述 某医院新建一个病房，需要配备护士，周一到周日分别最少需
要16、12、12、15、14、16、14人，按规定一个护士一周要连续 上班5天，医院病房给配备了20名护士，是否够用？
单击“文件”选项卡下的“选项”，在弹出的 “Excel选项”对话框中单击左侧列表中的“加载项” 选项卡，然后在右下方“管理”组合框中选择 “Excel加载项”，并单击“转到”按钮，如图所示。
5.1 规划求解基础
在弹出的“加载宏”的对话框中勾选“规划求解加载项”复选 框，并单击“确定”按钮完成操作，如图所示。在Excel主界面点击 “数据”选项卡，在“分析”选项组中，显示“规划求解”，如图 所示。
5.1 规划求解基础
规划求解的特点： 1. 有多个可以调整的单元格。 2. 可以通过更改其他单元格来确定某个单元格的最大值或最小值。 3. 可以指定可调整单元格可能的数值约束。 4. 一个问题可以有多个解。
5.1 规划求解基础
1. 规划求解问题的特点 规划求解是一组命令的组成部分，这些命令有时也称作假设分析
ቤተ መጻሕፍቲ ባይዱ
5.3 求解任务分配
6. 显示如图所示，单击“确定”按钮。显示如图所示，给出求解结 果。
再见！
5.2 求解取料问题
4. B12单元格实际丁原料的使用量，输入公式： “B12=SUM(D5:E5)”。
5. B13单元格为总成本，设定为目标单元格输入公式： “B13= SUMPRODUCT(C2:C5,D2:D5+E2:E5)”
5.2 求解取料问题
6.选中B13单元格，打开“规划求解参数”对 话框，在“设置目标单元格”文本框中选择 B13单元格，选中“最小值”单选按钮，在可 变单元格文本框中选择D2:E5单元格区域。

Weibull 分布
常用于为失效时间数据建模。

例如，一个制造商希望计算某个部件在一年、两年或更多年后失效的概率。

此分布广泛地应用于工程、医学研究、金融和气候学。

Weibull 分布由形状、尺度和阈值等参数描述。

阈值参数为零的情况称为 2 参数 Weibull 分布。

只为非负变量定义此分布。

取决于参数的值，Weibull 分布可以具有各种形状。

这种分布的主要优点之一在于它可以具有其他类型分布的特征，从而在拟合不同类型的数据时极其灵活。

例如，
·指数分布是 Weibull 分布的一种特殊情况，常用于研究辐射或风速的散布。

·Weibull 分布是存在偏斜数据时正态分布的备择。

·如果 X 服从 Weibull 分布，则 Ln(X) 服从极值分布。

此分布用于描述极端情况，如极端阵风、地震期间的极端能量或极端压力。

当形状参数为 2 时，可从 Weibull 分布派生 Rayleigh 分布。

风能资源统计与计算——威布尔（Weibull）分布
来源：作者：佚名发布时间： 2008-8-27 13:29:15
关于风速的分布，国外有过不少的研究，近年来国内也有探讨。

风速分布一般均为正偏态分布，一般说，风力愈大的地区，分布曲线愈平缓，峰值降低右移。

这说明风力大的地区，一般大风速所占比例也多。

如前所述，由于地理、气候特点的不同，各种风速所占的比例有所不同。

通常用于拟合风速分布的线型很多，有瑞利分布、对数正态分布、 分布、双参数威布尔分布、三参数威布尔分布等，也可用皮尔逊曲线进行拟合。

但威布尔分布双参数曲线，普遍认为适用于风速统计描述的概率密度函数。

图13：威布尔分布双参数曲线。

绝对引用是指被引用的单元与引用的公式单元的位置 关系是绝对的，无论将这个公式复制到任何单元，公式所 引用的还是原来单元格的数据。
（4）混合引用
格式： $A3 B$ 3
列是绝对的，行是相对的 列是相对的，行是绝对的
..........
6
使用Excel进行求解
1.关于“规划求解” 2.如何加载“规划求解” 3. “规划求解”各参数设置 4. “规划求解”步骤 5. 利用“规划求解”解线性规划问题
第五章 利用EXCEL求解线性规划问题
目的：
➢建立线性规划问题的模型 ➢利用EXCEL求解线性规划问题 ➢分析运算结果（敏感性分析）
..........
1
一、EXCEL 基本知识
功能： 存储信息、进行计算、排序数据、用图或表的形 式显示数据、规划求解、财会分析、概率与统计分析等 等
1、命名工作表
（1）激活工作表1，单击sheet 1 标签
目标函数值的增加仍然为影子价格的大小。因此，右端项在
一定范围内变化时，影子价格不变，目标函数值的变动等于
右端项变动值乘以影子价格..........
29
极限值报告解释
列出目标单元格和可变单元格以及它们的数值、上下限和目标
值。含有整数约束条件的模型不能生成本报告。其中，下限是
在满足约束条件和保持其它可变单元格数值不变的情况下，某
1E+30 3.4 1.5
允许增加值 允许减少值
$E$4 $E$5 $E$6
第一资源约束 58 第二资源约束 37 第三资源约束 60
0
70
1E+30
12
2ቤተ መጻሕፍቲ ባይዱ8
37
15
31

附录4 Excel“规划求解”1. 在系统中安装“规划求解”1、启动EXCEL。

打开“工具”菜单。

如果没有“规划求解”，单击“加载宏”。

弹出以下窗口：2、在复选框中选中“规划求解”，单击“确定”后返回Excel。

这时在“工具”菜单中出现“规划求解”。

关闭“工具”菜单2. 在Excel中创建线性规划模型1、输入线性规划模型的约束条件系数、右边常数和目标函数系数。

定义线性规划的变量单元格、约束条件左边单元格和目标函数单元格。

2、定义“设备能力占用”（即约束条件左边）以及“总利润”的计算公式。

首先定义设备A的“能力占用”单元格（G3）的计算公式，界面如下：其次定义设备B的“能力占用”单元格（G4）的计算公式，界面如下：再次定义设备C的“能力占用”单元格（G5）的计算公式，界面如下：最后定义“总利润”单元格（C8）的计算公式，界面如下：3、将光标停留在“总利润”值的单元格（C8）中，打开“工具/规划求解”，弹出以下窗口：4、设置目标函数单元格：检查“设置目标函数单元格”是否在“$C$8”，如不是，单击文本框右侧的图标，重新选定目标函数单元格，也可以直接单击Excel表中的“C8”。

5、设置变量：单击“规划求解窗口”中“可变单元格”文本框，然后在Excel工作表中选定变量单元格（C7、D7、E7和F7），在文本框中出现“$C$7:$F$7”，如下图所示。

6、设置约束单击“添加”，弹出以下窗口：单击“单元格引用位置”文本框空白处，然后单击工作表G3单元格，“单元格引用位置”文本框中出现“$G$3”；打开“单元格引用位置”和“约束值”之间的下拉文本框，选定“<=”；单击“约束值”文本框空白处，然后单击工作表H3单元格。

结果如下图所示。

单击“添加”，完成第一个约束设置。

继续设置第二、第三个约束，最后设置所有变量非负。

约束设置完成以后，单击“确定”，返回“规划求解参数”窗口，如下图所示。

7、设置叠代参数。

单击“选项”，弹出以下窗口：输入“最长运行时间”、“叠代次数”、“精度”、“允许误差”、“收敛度”等叠代参数。

指数威布尔分布指数威布尔分布是一种常见的概率分布，它在可靠性工程、生物学、医学、金融等领域中得到广泛应用。

本文将介绍指数威布尔分布的定义、特点、应用以及如何进行参数估计。

指数威布尔分布是由指数分布和威布尔分布组合而成的一种概率分布。

它的概率密度函数为：$$f(x)=\frac{\beta}{\alpha}(\frac{x}{\alpha})^{\beta-1}e^{-(\frac{x}{\alpha})^{\beta}}$$其中，$\alpha$和$\beta$是分布的参数，$\alpha>0$，$\beta>0$。

指数威布尔分布的累积分布函数为：$$F(x)=1-e^{-(\frac{x}{\alpha})^{\beta}}$$指数威布尔分布具有以下特点：1. 分布形状：指数威布尔分布的形状由参数$\beta$决定，当$\beta=1$时，分布退化为指数分布；当$\beta>1$时，分布呈现出右偏的形态；当$\beta<1$时，分布呈现出左偏的形态。

2. 可靠性：指数威布尔分布在可靠性工程中得到广泛应用，它可以用来描述产品的寿命分布。

当$\beta=1$时，分布具有无记忆性，即寿命的分布不受之前的使用情况影响；当$\beta>1$时，分布具有加速寿命特性，即寿命随时间的增加而逐渐减少；当$\beta<1$时，分布具有减速寿命特性，即寿命随时间的增加而逐渐增加。

3. 参数估计：指数威布尔分布的参数估计可以使用最大似然估计法或贝叶斯估计法。

最大似然估计法是一种常用的参数估计方法，它通过最大化样本的似然函数来估计参数值。

贝叶斯估计法则是一种基于贝叶斯定理的参数估计方法，它将参数看作是随机变量，通过先验分布和样本数据来计算后验分布，从而得到参数的估计值。

4. 应用：指数威布尔分布在生物学、医学、金融等领域中也有广泛应用。

例如，在医学领域中，可以使用指数威布尔分布来描述疾病的潜伏期分布；在金融领域中，可以使用指数威布尔分布来描述股票价格的波动分布。

威布尔分布：在可靠性工程中被广泛应用，尤其适用于机电类产品的磨损累计失效的分布形式。

由于它可以利用概率纸很容易地推断出它的分布参数，被广泛应用与各种寿命试验的数据处理。

瑞典工程师威布尔从30年代开始研究轴承寿命，以的又研究结构强度和疲劳等问题。

他采用了“链式”模型来解释结构强度和寿命问题。

这个模型假设一个结构是由若干小元件(设为n个)串联而成，于是可以形象地将结构看成是由n个环构成的一条链条，其强度(或寿命)取决于最薄弱环的强度(或寿命)。

单个链的强度(或寿命)为一随机变量，设各环强度(或寿命)相互独立，分布相同，则求链强度(或寿命)的概率分布就变成求极小值分布问题，由此给出威布尔分布函数。

由于零件或结构的疲劳强度(或寿命)也应取决于其最弱环的强度(或寿命)，也应能用威布尔分布描述。

根据1943年苏联格涅坚科的研究结果，不管随机变量的原始分布如何，它的极小值的渐近分布只能有三种，而威布尔分布就是第Ⅲ种极小值分布。

由于威布尔分布是根据最弱环节模型或串联模型得到的，能充分反映材料缺陷和应力集中源对材料疲劳寿命的影响，而且具有递增的失效率，所以，将它作为材料或零件的寿命分布模型或给定寿命下的疲劳强度模型是合适的。

目前，二参数的威布尔分布主要用于滚动轴承的寿命试验以及高应力水平下的材料疲劳试验，三参数的威布尔分布用于低应力水平的材料及某些零件的寿命试验，一般而言，它具有比对数正态分布更大的适用性。

但是，威布尔分布参数的分析法估计较复杂，区间估计值过长，实践中常采用概率纸估计法，从而降低了参数的估计精度．这是威布尔分布目前存在的主要缺点，也限制了它的应用。