Dijkstra算法的流程图及算法代码
- 格式:doc
- 大小:134.00 KB
- 文档页数:7

dijkstra算法代码pythonDijkstra算法是一种贪心算法,用于计算图中单源最短路径。
该算法基于贪心算法的原则,每次选择一个距离源点最近的顶点,然后更新这个顶点的邻元素的距离。
算法步骤:1. 初始化距离数组,设置源点的距离为0,其余点的距离为无穷大(表示没有到达该点的路径)。
2. 创建一个空的集合S,用于存放已经求出的最短路径的结点。
3. 循环执行以下步骤,直到所有点都被添加到集合S中:- 在未确定最短路径的结点中,选择距离源点最近的结点,并将该结点添加到S集合中。
- 更新该结点的邻元素的距离,如果新路径的距离小于目前已知的最短路径,则更新最短路径。
在实现Dijkstra算法时,需要使用图的邻接矩阵或邻接表来表示图。
下面是使用邻接矩阵实现Dijkstra算法的Python代码:def dijkstra(graph, src):# 初始化距离数组dist = [float('inf')] * len(graph)# 设置源点的距离为0dist[src] = 0# 用于存放最短路径的结点s = []# 循环执行直到所有点都被添加到集合S中while len(s) < len(graph):# 在未确定最短路径的结点中,选择距离源点最近的结点,并将该结点添加到集合S 中min_dist = float('inf')min_index = -1for i in range(len(graph)):if i not in s and dist[i] < min_dist:min_dist = dist[i]min_index = is.append(min_index)return dist# 示例graph = [[0, 2, 4, 0, 0],[2, 0, 1, 3, 0],[4, 1, 0, 5, 6],[0, 3, 5, 0, 2],[0, 0, 6, 2, 0]]上述代码通过邻接矩阵表示图,其中0表示两点之间没有边,其他数字表示该边的边权。

最短路径dijkstra算法一、介绍Dijkstra算法是一种用于解决带有非负边权的加权图中单源最短路径问题的算法。
它被广泛应用于路由算法和其他网络应用中。
二、算法原理1. 算法流程Dijkstra算法的基本思想是从起点开始,逐步扩展到距离它最近的节点,然后再逐步扩展到距离起点第二近的节点,以此类推,直到扩展到终点为止。
具体实现过程如下:(1)初始化:将起点s加入集合S,其他节点加入集合U,并赋初值dist数组表示从起点s到其他节点的距离,初始值为无穷大。
(2)找到当前距离起点最短的节点v,并将其加入集合S中。
(3)更新dist数组:对于所有与v相邻接的未被访问过的节点w,如果通过v可以使得从s到w的距离更短,则更新dist[w]为新的更短距离,并记录前驱节点prev[w]=v。
(4)重复执行步骤(2)和(3),直至终点t被加入集合S中或者所有可达节点都已经被访问过。
2. 算法优化Dijkstra算法可以通过以下两种方式进行优化:(1)使用优先队列:每次从未访问节点中选择距离起点最近的节点时,可以使用优先队列来维护未访问节点的距离,这样可以避免每次都要遍历整个dist数组来找到最小值。
(2)使用堆优化的Dijkstra算法:在稠密图中,使用堆优化的Dijkstra算法可以进一步减少时间复杂度。
三、算法应用Dijkstra算法被广泛应用于路由算法和其他网络应用中。
例如,在互联网中,路由器需要根据网络拓扑和链路质量等信息计算出最短路径,以便将数据包传输到目标地址。
四、算法复杂度Dijkstra算法的时间复杂度取决于实现方式和图的结构。
在稠密图中,堆优化的Dijkstra算法的时间复杂度为O(|V|^2),其中|V|表示节点数;在稀疏图中,使用优先队列实现Dijkstra算法的时间复杂度为O((|E|+|V|)log|V|),其中|E|表示边数。
五、总结Dijkstra算法是一种经典的单源最短路径算法,在网络应用和其他领域有广泛应用。
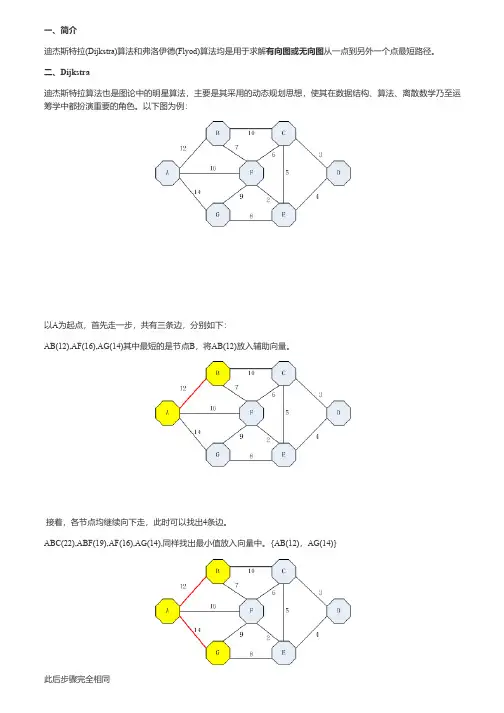
一、简介迪杰斯特拉(Dijkstra)算法和弗洛伊德(Flyod)算法均是用于求解有向图或无向图从一点到另外一个点最短路径。
二、Dijkstra迪杰斯特拉算法也是图论中的明星算法,主要是其采用的动态规划思想,使其在数据结构、算法、离散数学乃至运筹学中都扮演重要的角色。
以下图为例:以A为起点,首先走一步,共有三条边,分别如下:AB(12),AF(16),AG(14)其中最短的是节点B,将AB(12)放入辅助向量。
接着,各节点均继续向下走,此时可以找出4条边。
ABC(22),ABF(19),AF(16),AG(14),同样找出最小值放入向量中。
{AB(12),AG(14)}此后步骤完全相同A B C D A 0426B 50∞12C∞∞3ABC(22),ABF(19),AF(16),AGF(23),AGE(22),选中AF(16)。
同样,接下来的步骤有:ABC(22),AFC(22),AFE(18),AGE(22),选中AFE(18);ABC(22),AFC(22),AFEC(23),AFED(22),这种情况随便选取一个最小值,以ABC(22)为例;ABCD(25),AFED(22)选中后者,至此,已经完全找到A 和所有节点之间的最短路径及最短路径的长度。
最短路径向量为{AB(12),AG(14),AF(16),AFE(18),ABC(22),AFED(22)}三、Floyd弗洛伊德是另外一种求最短路径的方式,与迪杰斯特拉算法不同,弗洛伊德偏重于多源最短路径的求解,即能迪杰斯特拉能够求一个节点到其余所有节点的最短路径,但是弗洛伊德能够求出任意两个节点的最短路径,当然迪杰斯特拉重复N 次也能达到目标。
两种方式的时间复杂度均为O(n^3),但弗洛伊德形式上会更简易一些。
以下面的有向有权图为例:老版visio 不知道为啥这么糊?首先写出图的邻接矩阵AdjA B C DD71∞0若想缩短两点间的距离,仅有一种方式,那就是通过第三节点绕行,如果我们假设仅能通过A点绕行,那么仅需判断是否现有的距离Adj[i][j]小于Adj[i][1]+Adj[1][j]的距离,如果有更短的选择,那么进行更新就好了。

dijkstra算法代码实现Dijkstra算法是用来求解单源最短路径问题的一种贪心算法。
下面是Dijkstra算法的代码实现:```import sys# 定义一个类来保存图的节点和边的信息class Node:def __init__(self, name): = nameself.visited = Falseself.distance = sys.maxsizeself.adjacent_nodes = []self.previous_node = None# Dijkstra算法的实现函数def dijkstra(start_node):start_node.distance = 0unvisited_nodes = [start_node]while unvisited_nodes:current_node = unvisited_nodes[0]for neighbor in current_node.adjacent_nodes:if not neighbor.visited:new_distance = current_node.distance +neighbor.distanceif new_distance < neighbor.distance:neighbor.distance = new_distanceneighbor.previous_node = current_nodecurrent_node.visited = Trueunvisited_nodes.remove(current_node)unvisited_nodes.sort(key=lambda node: node.distance)# 测试nodeA = Node("A")nodeB = Node("B")nodeC = Node("C")nodeD = Node("D")nodeE = Node("E")nodeF = Node("F")nodeA.adjacent_nodes = [(nodeB, 10), (nodeC, 15)]nodeB.adjacent_nodes = [(nodeD, 12), (nodeF, 15)]nodeC.adjacent_nodes = [(nodeE, 10)]nodeD.adjacent_nodes = [(nodeE, 2), (nodeF, 1)]nodeF.adjacent_nodes = [(nodeE, 5)]dijkstra(nodeA)print(nodeE.distance)```在上面的代码中,我们定义了一个`Node`类用来保存节点的信息,包括节点的名称、是否已访问、距离起始节点的距离、相邻节点和前置节点等。

Dijkstra算法是一种用于计算图中从一个顶点到其他所有顶点的最短路径的算法。
它由荷兰计算机科学家艾兹赫尔·戴克斯特拉于1956年提出。
Dijkstra算法的基本思想是通过不断更新起始顶点到其他顶点的最短路径长度,逐步找到最短路径。
以下将详细介绍Dijkstra算法的步骤,并给出一个例题和表格供读者参考。
一、算法步骤1. 初始化- 设置起始顶点的最短路径为0,其余顶点的最短路径为无穷大。
- 将起始顶点加入已访问的顶点集合。
2. 更新- 从未访问的顶点中选择离起始顶点最近的顶点,将其加入已访问的顶点集合。
- 更新起始顶点到其他顶点的最短路径长度,如果经过新加入的顶点到其他顶点的路径长度小于当前已知的最短路径长度,则更新最短路径长度。
3. 重复更新直到所有顶点都被访问过。
二、算法实例为了更好地理解Dijkstra算法的具体应用步骤,我们通过一个实际的例题来演示算法的执行过程。
假设有以下带权重的图,起始顶点为A:顶点 A B C D EA 0 3 4 ∞ ∞B ∞ 0 ∞ 1 7C ∞ 4 0 2 ∞D ∞ ∞ ∞ 0 5E ∞ ∞ ∞ ∞ 0表中每个元素表示从对应顶点到其它顶点的边的权重,"∞"表示没有直接相连的边。
我们按照Dijkstra算法的步骤来计算从顶点A到其他顶点的最短路径长度。
1. 初始化起始顶点为A,初始化A到各顶点的最短路径长度为0,其余顶点的最短路径长度为∞。
将A加入已访问的顶点集合。
2. 更新选择A到B的路径长度最短,将B加入已访问的顶点集合。
更新A到C和A到D的最短路径长度。
3. 重复更新依次选择离起始顶点最近的顶点,并更新最短路径长度,直到所有顶点被访问。
通过不断的更新,最终得到从顶点A到其他顶点的最短路径长度表格如下:顶点 A B C D E最短路径长度 0 3 4 5 9三、总结通过以上Dijkstra算法的步骤和实例计算,我们可以清晰地了解该算法的执行过程和原理。

最短路径dijkstra算法过程
Dijkstra算法是一种用于解决最短路径问题的经典算法,其过
程如下:
1. 创建一个距离表,记录从起始节点到每个节点的距离。
初始时,除了起始节点,其他节点的距离被设置为无穷大,起始节点的距离被设置为0。
2. 创建一个集合Q,用于存放还未被访问的节点。
3. 在集合Q中找到距离最小的节点v并将其从集合Q中移除。
如果没有找到,则说明所有节点已被访问完毕,算法结束。
4. 遍历节点v的所有邻居节点u,对于每个邻居节点u,更新
其距离表中的距离。
如果通过节点v可以获得比原先距离更短的路径,则更新距离。
5. 重复步骤3和步骤4,直到集合Q为空。
6. 返回距离表,其中记录了从起始节点到其他节点的最短距离。
需要注意的是,在实现过程中,需要使用一个优先队列来快速找到集合Q中距离最小的节点v,以提高算法的效率。
以上就是Dijkstra算法的基本过程。
通过不断更新距离表,算
法可以找到从起始节点到其他节点的最短路径。

Dijkstra算法详解今天给⼤家讲解dijkstra图论最短路算法在讲解dijkstra算法之前,先来给⼤家讲解⼀下图论中的松弛操作。
松弛,即relaxtion,是⼀种编程学术语。
举例说明,例如我们可以从某个机场坐飞机达到若⼲个机场,然后从这些机场出发,我们⼜需做⽕车前往若⼲个城镇。
现在假设我们⼿⾥有飞⾏时间表(list或者dict),⽽A u表⽰的是从当前位置出发,我们到达u机场所需的时间。
类似地,我们⽤b uv来表⽰坐⽕车从 u 机场到达 v 城镇所需的时间(B ⾃然为list of lists或dict)。
下⾯我们从到达各镇的路径中随机选择⼀条,它所需的时间为C v:C[v] = float('inf')for u in A:C[v] = min(C[v], A[u]+B[u][v]) //松弛法(relaxation)是⼀数学术语,描述的是⼀些求解⽅法,这些⽅法会通过逐步接近的⽅式获得相关问题的最佳解法。
每运⽤⼀次松弛法就好像我们“移动”了⼀次,⽽我们要做的就是在尽可能少的移动次数内找到最佳解决⽅案。
理论上来说,我们可以在整个空间上运⽤相关的松弛法,但关键在于找到⼀个正确的执⾏次序。
讲完了松弛法,接下来就给⼤家讲解dijkstra算法(1).dijkstra算法解决问题范围dijkstra算法主要解决的是单源点的最短路和最短路径问题,且路径的权值不为负权。
(2).dijkstra算法思想及原理dijkstra算法思想是基于贪⼼算法思想的。
所谓贪⼼算法即始终保持当前迭代解为当前最优解。
意思就是在已知的条件下或是当前拥有的全部条件下保证最优解,若在此后的迭代中由于加⼊了新的条件使得产⽣了更优解则替代此前的最优解。
通过不断的迭代不断保证每次迭代的结果都是当前最优解,那么当迭代到最后⼀轮时得到的就会是全局最优解。
由于下⼀轮迭代会参考上⼀轮的最优解,因此每⼀轮的迭代的⼯作量基本⼀致,降低了整体⼯作的复杂性。

dijkstra最短路径算法详解
Dijkstra最短路径算法是一种常用的图算法,用于求解带权图中的单源最短路径问题,即从一个固定的源节点到图中的其他节点的最
短路径。
以下是详细的算法步骤:
1. 初始化
一开始,将源节点的距离设为0,其余节点的距离设置为正无穷,在未访问的节点集合中把源节点压入堆中。
2. 确定最短路径
从堆中取出未访问节点集合中距离源节点最近的节点v,标记其
为已访问。
之后,对于v的邻居节点w,计算从源节点到v再到w的距离,如果经过v的路径比已经计算得到的路径短,则更新路径。
更新
后的距离先暂时放入堆中,如果后边有更短的路径,则更新。
3. 重复第2步
重复第2步,直到取出的节点为终点节点,或者堆为空。
4. 算法结束
算法结束后,各节点的距离就是从源节点到它们的最短距离。
Dijkstra算法的复杂度是O(NlogN),其中N是节点个数。
其优
势在于只需要算一次即可得到所有最短路径,但是要求所有边的权值
必须非负,否则会导致算法不准确。
总之,Dijkstra算法是一种简单有效的最短路径算法,其实现也比较直观。
在处理如飞机和火车等交通路径规划问题中有较好的应用。


Dijkstra算法步骤详述Dijkstra算法是一种经典的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
本文将详细介绍Dijkstra算法的步骤和实现。
1. 初始化首先,我们需要将算法的输入进行初始化。
假设我们有一个带权重的有向图,其中节点集合为V,边的集合为E。
对于每个节点v ∈ V,我们设置初始距离d[v]为正无穷大(INF),表示从起点到节点v的距离为无穷大;同时,我们设置起点s的初始距离d[s]为0,表示从起点到自身的距离为0。
2. 确定最短路径接下来,我们将在图中逐步确定起点到其他节点的最短路径。
首先,我们从起点s开始,将s标记为当前节点。
然后,对于s的所有邻居节点v,我们更新其当前最短路径,并标记v为下一个当前节点。
这一步骤可以通过以下过程实现:a. 对于节点s的所有邻居节点v,计算通过s到达v的距离。
如果该距离小于d[v],则将d[v]更新为该距离,并将s作为节点v的前驱节点(即最短路径上v的前一个节点)。
b. 从剩余的未标记节点中选择一个距离最短的节点作为下一个当前节点。
具体而言,从未标记节点中选择一个节点u,使得d[u]最小,并将其标记为当前节点。
3. 更新最短路径在上一步中,我们确定了起点到一个节点的最短路径。
现在,我们将以已选择的当前节点继续执行第2步,直到所有节点都被标记为止。
具体而言,重复进行以下步骤:a. 在当前节点的所有邻居节点中,更新其最短路径并选择下一个当前节点,过程与第2步相同。
b. 如果不存在未标记节点,则算法终止。
4. 输出最短路径当算法终止时,我们可以得到从起点到达所有节点的最短路径。
对于每个节点v,最短路径可以通过回溯每个节点的前驱节点得到。
具体而言,从目标节点开始,通过前驱节点一直回溯到起点,即可得到最短路径。
总结:Dijkstra算法通过逐步确定起点到其他节点的最短路径,从而找到整个图中的最短路径。
它的步骤包括初始化、确定最短路径和更新最短路径。

Dijkstra算法Dijkstra算法是一种用于解决单源最短路径问题的经典算法。
它能够找到从一个顶点到其他所有顶点的最短路径。
算法原理Dijkstra算法的基本原理是利用贪心策略,逐步确定从起始顶点到其他顶点的最短路径。
该算法通过维护一个距离数组,记录起始顶点到每个顶点的当前最短距离,并逐步更新这些距离值。
具体来说,Dijkstra算法包含以下步骤:1.创建一个长度与图中顶点数量相同的距离数组dist[],用于记录起始顶点到每个顶点的当前最短距离。
2.初始化dist[]数组,将起始顶点的距离设为0,其他顶点的距离设为无穷大。
3.创建一个集合visited[],用于记录已经找到最短路径的顶点。
4.循环执行以下步骤直到visited[]包含所有顶点:–从未访问过的顶点中选择dist[]值最小的顶点u,并将其标记为visited[u]。
–更新与u相邻且未访问过的顶点v的距离。
如果通过u可以获得更小的距离,则更新dist[v]的值。
5.循环结束后,dist[]数组中存储的就是起始顶点到其他所有顶点的最短路径。
算法实现下面是Dijkstra算法的C语言代码实现:#include <stdio.h>#include <stdbool.h>#define INF 9999#define V 6void dijkstra(int graph[V][V], int src) {int dist[V];bool visited[V];for (int i = 0; i < V; i++) {dist[i] = INF;visited[i] = false;}dist[src] = 0;for (int count = 0; count < V - 1; count++) {int minDist = INF, minIndex;for (int v = 0; v < V; v++) {if (!visited[v] && dist[v] <= minDist) {minDist = dist[v];minIndex = v;}}int u = minIndex;visited[u] = true;for (int v = 0; v < V; v++) {if (!visited[v] && graph[u][v] && dist[u] != INF && dist[u] + grap h[u][v] < dist[v]) {dist[v] = dist[u] + graph[u][v];}}}printf("顶点\t\t距离\n");for (int i = 0; i < V; i++) {printf("%d\t\t%d\n", i, dist[i]);}}int main() {int graph[V][V] ={{0, 4, 0, 0, 0, 0},{4, 0, 8, 0, 0, 0},{0, 8, 0, 7, 9, 0},{0, 0, 7, 0, 10, 2},{0, 0, 9, 10, 0, 1},{0, 0 ,4 ,2 ,1 ,INF}};dijkstra(graph, 0);return 0;}算法分析Dijkstra算法的时间复杂度为O(V^2),其中V是图中顶点的数量。
图论算法(四)Dijkstra算法最短路算法(三)Dijkstra算法PS:因为这两天忙着写GTMD segment_tree,所以博客可能是seg+图论混搭着来,另外segment_tree的基本知识就懒得整理了……Part 1:Dijkstra算法基本信息以下,我们⽤dis[n]表⽰1->n的最短路径长度,vis[n]表⽰n号节点有没有被访问过Dijkstra算法基于贪⼼的思想,每次从dis[ ]数组中取出⼀个dis[ ]值最⼩的节点x,把vis[x]标记为true,同时⽤这个点的所有连边去更新与x相连的点y的dis[ ]值其中,更新的条件是这样的:(dis[y]=min(dis[y],dis[x]+x->y)),也就是y的更新后最短路值=min(当前y的最短路值,x的最短路值+x->y 的边权)每次松弛操作,使得1->x,1->y,x->y这三条边满⾜三⾓形不等式,扫完x点的所有边之后,此时,没有被访问过且dis值最⼩的点的最短路就已经被确定了重复取出dis[ ]值最⼩节点的操作,更新y的值,直到vis[ ]全部为true,也就是所有节点都被访问过。
此时,dis数组中dis[i]就是1->i的最短路下⾯给出dijkstra的证明⽅法(拓展内容):证明可以仅做了解,毕竟OI不是证明能⼒⼤赛另外,出现负边权的时候,dijkstra算法不能正常⼯作Part 2:优化Dijkstra算法还记得吗?前⾯我们提到了在松弛之前,有⼀个取出dis数组中最⼩值的操作,对吧?这个操作的复杂度是O(n)的,再加上⽤来更新的for循环,整体复杂度就变成了O(n2)的显然,O(n2)的复杂度还不够快,那么考虑怎么优化?很容易想到数据结构对吧?这⾥我们可以使⽤⼀个⼩根堆来实时维护dis中的最⼩值和这个最⼩值所对应的编号,取得最⼩值所在节点编号的复杂度降低到了O(logn)这样做,使得整体复杂度降低到了O((m+n)logn)(其中m是边数,n是点数)问题⼜来了,⼿写⼩根堆优化会导致码量的暴增,⽽且容易出错,我们迫切的需要⼀种简洁,易实现的代码当然不,STL中queue头⽂件为我们提供了priority_queue这样⼀个⼤根堆,我们想想,可不可以利⽤这个⼤根堆呢?想要利⽤priority_queue,⾸先要解决两个问题:1、我们需要存下两个变量,⼀个是dis数组中的值,当做第⼀关键字⼊堆,还有这个dis值对应的节点编号,这需要开⼀个结构体开结构体⼜导致另⼀个问题——priority-queue不知道以谁为关键字⼊堆排序2、把优先队列的⼤根堆形式变成⼩根堆“做到这些,需要⼀些奇技淫巧” ——By ⼀扶苏⼀ 2020.6.28解决⽅法⼀:重载‘<’运算符我们重载‘<’号运算符,让priority_queue⼀dis值为第⼀关键字的同时,把原来的⼤根堆变成⼩根堆代码如下:struct node{int sp,num;bool friend operator < (node a,node b){return a.sp>b.sp;priority_queue<node>q;}}这⾥我们重载了‘<’运算符(PS:对于所有C++STL,需要⽐较⼤⼩的,只要求我们重载‘<’运算符,因为通过‘<’号的定义,可以推⾄所有别的符号的定义,⽐如,这⾥我把‘<’重载为返回sp⼤的,那么‘>’⾃然就是返回sp⼩的),⼀次性解决了上⾯的两个问题解决⽅法⼆:C++内置pair⼆元组我们可以使⽤C++内置的⼆元组pair来解决关键字的问题,因为pair默认以第⼀维为第⼀关键字(PS:pair以第⼆维为第⼆关键字,但是这⾥第⼆关键字我们并不关⼼,因为不会影响到dijkstra的结果)C++内置pair基本⽤法如下代码:#include<cstdio>#include<iostream>using namespace std;int main(){pair<int,int>x;//声明⼆元组的第⼀维,第⼆维的数据类型和⼆元组名字x=make_pair(1,2);//给⼆元组赋值,先把“1,2”⽤make_pair()打包,然后分别赋值给第⼀维和第⼆维int a=x.first,b=x.second;//分别返回⼆元组x的第⼀维,第⼆维printf("%d %d",a,b);}另外,把⼤根堆变成⼩根堆,我们可以在⼊堆的时候把dis值取反(只是在堆中是相反数,dis值保持原样),这样我们就⽤pair解决了这两个问题仅供参考Part 3:Dijkstra 模板代码Part 3:Dijkstra 模板代码 仅供参考#include<cstring>#include<cstdio>#include<queue>using namespace std;const int N=100010,M=500010;int head[N],ver[M],edge[M],Next[M],d[N];bool v[N];int n,m,tot,s;priority_queue< pair< int,int > >q;//包含pair的优先队列void add(int x,int y,int z){//链式前向星存图ver[++tot]=y;edge[tot]=z;Next[tot]=head[x];head[x]=tot;}void dijkstra(int x){memset(d,0x3f,sizeof(d));//把距离初始化⽆限⼤memset(v,0,sizeof(v));//初始化没有访问过d[x]=0;//初始节点距离为0q.push((make_pair(0,x)));//初始节点⼊堆while(q.size()!=0){int x=q.top().second;//访问第⼆维,也就是节点编号q.pop();//弹出if(v[x]==1) continue;//如果⾛过了,直接进⾏下⼀次v[x]=1;//标记访问过for(int i=head[x];i;i=Next[i]){//链式前向星访问连边int y=ver[i],z=edge[i];if(d[y]>d[x]+z){//松弛d[y]=d[x]+z;//更新最短路q.push(make_pair(-d[y],y));//把d[y]的相反数⼊堆,⼤根堆变⼩根堆}}}}int main(){scanf("%d%d%d",&n,&m,&s);//n点m边,s出发点for(int i=1,x,y,z;i<=m;i++){scanf("%d%d%d",&x,&y,&z);//读边add(x,y,z);}dijkstra(s);//求单元最短路for(int i=1;i<=n;i++)printf("%d ",d[i]);//输出到每⼀个节点的距离,如果到不了该节点,输出0x3f3f3f3freturn 0;}板⼦题:洛⾕P4779、洛⾕P3371PS:P4779板⼦粘上去就过,P3371板⼦粘上去再加个231的特判⼜AC了……P4779传送门:P3371传送门:“不要光刷题意相同的题,不要光刷板⼦题!”——By ⼀扶苏⼀ 2020.7.2所以,建议做完板⼦题之后,多找找最短路的题⽬,斟酌⼀下SPFA、Dijkstra,Floyd⽤哪个,具体怎么实现,快速完成代码,最好做到不要出错到此,图论最短路算法,终于完结。
题目:Dijkstra 算法的实现 一、问题分析和任务定义1.1题 目:对任意图,选择合适的数据结构表示图,在此基础上实现求解最短路径的Dijkstra 算法。
1.2 要 求:对所设计的图的数据结构,提供必要的基本功能。
1.3具体任务:建立图的表示模块,顶点的插入和删除操作模块;在建立图之后从单源点开始求最短路径,并显示出最短路径长度及路径途径! 2、实现功能:2.1建立有向图2.2在建立好的有向图中,显示出来从源点到其他各个顶点的最短路径长度及路径途径。
3、测试用例:3.1正确数据:a )顶点:3;边值信息:0 1 2;1 0 3;1 2 5;2 1 6;0 0 0; b )顶点:0;边值信息:0 0 0; 3.2错误数据:a )顶点:#;b )顶点:3;边值信息:0 1 #; 3.3参考用图:图1图1. 有向图问题分析: 题目要求选择合适的数据结构表示图,本程序邻接矩阵存储结点和弧等图的有关信息对用邻接矩阵表示的有向图,从某一顶点出发(称为源点)到该图其他各顶点(称为终点)有无路径?最短路径是什么?路径长为多少?问题要求写一个程序从有向网中的某一顶点出发找出该顶点到其余各顶点的最短路径。
对邻接矩阵arsc[n][n]中的每一个元素只能有三种情况:①当顶点i 到j 无边时,distance[j]= MAX;② 当顶点i 到j 有边且权值为edges[i][j]时,distance[j]= edges[i][j];2③当顶点i 到就经过t 有最短路径时,distance[j]=distance[t]+edges[t][j]; 由于题目中没有规定输出格式,本程序以顶点序号的形式将最短路径输出到终端上去,并输出该最短路径的长度及路径途径。
二、数据结构的选择和概要设计 1) 数据存储结构以邻接矩阵存储有向图,如图2中有向图G 所示,其邻接矩阵为图 3 edges 。
图2. 有向图 图3.矩阵edges有向图的邻接矩阵arcs[i][j]定义为int edges[MAX_VERTEX_NUM][ MAX_VERTEX_NUM]; 2)概要设计对用邻接矩阵表示的有向图,从某一顶点出发(称为源点)到该图其他各顶点(称为终点)有无路径?最短路径是什么?路径长为多少?问题要求写一个程序从有向网中的某一顶点出发找出该顶点到其余各顶点的最短路径。
dijkstra算法代码c语言Dijkstra算法代码C语言简介Dijkstra算法是一种用于寻找带权有向图中最短路径的经典算法。
它由荷兰计算机科学家Edsger Dijkstra于1956年发明。
本文将介绍Dijkstra算法的基本原理和用C语言实现的代码。
算法原理1.初始化:设定一个起始点,将起始点到其他所有点的距离初始为无穷大,将起始点到自身的距离设为0,创建一个空的集合用于存放已找到最短路径的点。
2.选取最短路径:从未找到最短路径的点中选择一个距离起始点最近的点,将其加入到已找到最短路径的点的集合中。
3.更新距离:对于新加入的点,更新它周围点到起始点的最短距离。
如果通过新加入的点到达某个点的距离比当前已知最短距离小,则更新该点的最短距离。
4.重复步骤2和步骤3,直到所有点都找到最短路径。
C语言实现下面是用C语言实现Dijkstra算法的代码:#include <>#include <>#define SIZE 10#define INFINITY 9999void dijkstra(int graph[SIZE][SIZE], int startNode) {int distance[SIZE];bool visited[SIZE];for (int i = 0; i < SIZE; i++) {distance[i] = INFINITY;visited[i] = false;}distance[startNode] = 0;for (int count = 0; count < SIZE - 1; count++) {int minDistance = INFINITY;int minIndex;for (int i = 0; i < SIZE; i++) {if (!visited[i] && distance[i] <= minDistanc e) {minDistance = distance[i];minIndex = i;}}visited[minIndex] = true;for (int i = 0; i < SIZE; i++) {if (!visited[i] && graph[minIndex][i] && dis tance[minIndex] != INFINITY &&distance[minIndex] + graph[minIndex][i] < distance[i]) {distance[i] = distance[minIndex] + graph [minIndex][i];}}}printf("最短路径为:\n");for (int i = 0; i < SIZE; i++) {printf("%d 到 %d 的距离: %d\n", startNode, i, di stance[i]);}}int main() {int graph[SIZE][SIZE] = {{0, 6, 0, 1, 0},{6, 0, 5, 2, 2},{0, 5, 0, 0, 5},{1, 2, 0, 0, 1},{0, 2, 5, 1, 0}};int startNode = 0; // 起始点的索引dijkstra(graph, startNode);return 0;}总结Dijkstra算法是解决最短路径问题的一种有效方法。
dijskra算法代码Dijkstra算法是一种用于寻找图中两点之间最短路径的算法。
它是一种贪心算法,通过不断地选择距离目标点最近的节点,逐步缩小搜索范围,最终找到最短路径。
下面是一个简单的Dijkstra算法的Python代码实现:```pythonimportheapqdefdijskra(graph,start,end):#初始化距离数组和访问状态数组distances=[float('inf')]*len(graph)visited=[False]*len(graph)queue=[(0,start)]whilequeue:#从队列中取出距离最小的节点current_distance,current_node=heapq.heappop(queue)#如果当前节点已经被访问过,跳过ifvisited[current_node]:continue#标记当前节点为已访问visited[current_node]=True#遍历当前节点的邻居节点forneighbor,weightingraph[current_node].items():distance=current_distance+weight#如果找到了更短的路径,更新距离数组和访问状态数组ifdistance<distances[neighbor]:distances[neighbor]=distanceheapq.heappush(queue,(distance,neighbor))#返回最短路径长度和最短路径上的节点returndistances[end],[nodefornode,distanceinenumerate(dis tances)ifdistance==distances[end]]```这个代码实现的基本思路是使用一个堆队列来存储待访问的节点,每次从队列中取出距离目标点最近的节点,遍历它的邻居节点,如果找到了更短的路径,就更新距离数组和访问状态数组。
最短路径算法——Dijkstra算法一、最短路径问题最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
在带权图(即网络)G=(V,E)中,若顶点v i,v j是图G的两个顶点,从顶点v i到v j 的路径长度定义为路径上各条边的权值之和。
从顶点v i到v j可能有多条路径,其中路径长度最小的一条路径称为顶点v i到v j的最短路径。
求最短路径具有很高的实用价值,在各类竞赛中经常遇到。
一般有两类最短路径问题:一类是求从某个顶点(即源点)到其他顶点(即终点)的最短路径;另一类是求图中每一对顶点间的最短路径。
本讲主要讲述一种单源最短路径(Single source shortest path)算法——Dijkstra 算法,用于解决非负权有向图的单源最短路径问题。
二、Dijkstra算法2.1 Dijkstra算法Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率偏低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
2.2 Dijkstra算法思想对于图G=(V,E),假设(u,v)是E中的边,c u,v是边的长度(即边权)。
如果把顶点集合V划分为两个集合S和T:S中所包含的顶点,他们到u的距离已经确定;T中所包含的顶点,他们到u的距离尚未确定。
Dijkstra算法是一种用于求解带权有向图中单源最短路径问题的算法。
以下是Dijkstra 算法的步骤:
1. 创建一个数组dist[],用于存储起始节点到其他节点的最短距离。
初始时,将起始节点到自身的距离设置为0,其余节点的距离设置为正无穷大(或者一个足够大的值)。
2. 创建一个集合visited[],用于记录已经求得最短路径的节点。
3. 重复下述步骤,直到所有节点都被访问:
a. 在未访问的节点中选择距离起始节点最近的节点,标记为当前节点。
b. 更新当前节点的邻居节点的最短距离。
对于每个邻居节点,如果从起始节点经过当前节点到达该邻居节点的距离小于当前记录的最短距离,则更新最短距离。
4. 完成上述步骤后,dist[]数组中存储的就是起始节点到各个节点的最短距离。
注意:在步骤3b中,可以通过比较当前节点的最短距离加上当前节点到邻居节点的边的权重与邻居节点的当前最短距离的大小来更新最短距离。
Dijkstra算法的时间复杂度取决于实现方式,一般为O(V^2),其中V表示图中节点的数量。
优化的实现方式可以将时间复杂度降低至O((V+E)logV),其中E表示图中边的数量。
开始
定义全局变量
dist[N],
v0,cost[N][N]
初始化变量
final[N],i,v,w,
min,k
K=0
K Dijkstra算法的流程图 s为源,w[u,v] 为点u 和v 之间的边的长度,结果保存在 dist[] 循环n-1次: 2. 对于每个与u相邻的点v,如果dist[u] + w[u,v] < dist[v], 结束:此时对于任意的u,dist[u]就是s到u的距离。 int main()
V
需求和规格说明:
Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节
点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展
到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍
历计算的节点很多,所以效率低。
算法本身并不是按照我们的思维习惯——求解从原点到第一个点的
最短路径,再到第二个点的最短路径,直至最后求解完成到第n个点
的最短路径,而是求解从原点出发的各有向路径的从小到大的排列,
但是算法最终确实得到了从原点到图中其余各点的最短路径,可以说
这是个副产品,对于算法的终结条件也应该以求得了原点到图中其余
各点的最短路径为宜。清楚了算法的这种巧妙构思后,理解算法本身
就不是难题了。
实现注释:
想要实现的功能
Dijkstra算法是用来求任意两个顶点之间的最短路径。在该实验中,
我们用邻接矩阵来存储图。在该程序中设置一个二维数组来存储任意
两个顶点之间的边的权值。用户可以将任意一个图的信息通过键盘输
入,让后在输入要查找的两个顶点,程序可以自动求出这两个顶点之
间的最短路径。
已经实现的功能:
在该实验中,我们用邻接矩阵来存储图。在该程序中设置一个全局变
量的二维数组,用它来存储任意两个顶点之间的边的权值。然后通过
最短路径的计算,输入从任意两个顶点之间的最短路径的大小。
用户手册:
对于改程序,不需要客户进行什么复杂的输入,关键是用来存放图的
任意两个顶点之间的边的权值的二维数组的初始化,即将要通过
Dijkstra算法求最短路径的图各条边的权值放入二维数组中。这样
程序就可以自动的计算出任意两个顶点之间的最短路径并且进行输
出。
设计思想:
初始化:源的距离dist[s]设为0,其他的点距离设为无穷大,同时
把所有的点状态设为没有扩展过。
1. 在没有扩展过的点中取一距离最小的点u,并将其状态设为已扩
展。
那么把dist[v]更新成更短的距离dist[u] + w[u,v]。此时到点v
的最短路径上,前一个节点即为u。
#include
#include "Conio.h"
#define true 1
#define false 0
#define I 9999 // 无穷大
#define N 5 // 城市顶点的
数目
int cost[N][N] = {
{0,3,I,8,I},
{3,0,5,I,4},
{I,5,0,4,7},
{8,I,4,0,2},
{I,4,7,2,0}};
int dist[N]; // 存
储当前最短路径长度
int v0 = 'A' - 65; // 初
始点是 A
{
int final[N],i,v,w,min,k;
printf("\n任意两个定点之间的最短路径如下:\n\n");
for(k=0;k
// 初始化最短路径长度数据,所有数据都不是最终数据
for (v = 0; v < N; v++)
{
final[v] = false;
dist[v] = cost[v0][v];
}
// 首先选v0到v0的距离一定最短,最终数据
final[v0] = true;
final[v] = true;
// 寻找另外 N-1 个结点
for (i = 0; i < N-1; i++)
{
min = I; // 初始最短长度无穷大
// 寻找最短的边
for (w = 0; w < N; w++)
{
if (!final[w] && dist[w] < min)
{
min = dist[w];
v = w;
}
}
final[v] = true; // 加入新边
for (w = 0; w < N; w++)
{ // 更新 dist[] 数据
if (!final[w] && dist[v] + cost[v][w] <
dist[w])
{
dist[w] = dist[v] + cost[v][w];
}
}
}
for (i = 0; i < N; i++)
{
printf("%c->%c: %2d\t", v0 + 65, i + 65, dist[i]);
}
printf("\n");
v0++;
}
return 0;
}
运行结果: