耦合摆小振动问题研究
- 格式:doc
- 大小:975.50 KB
- 文档页数:7

解决多物理场耦合振动问题的简洁计算模型*摘要:复杂系统的振动产生来源于多物理场的耦合,通过高性能计算机直接从多物理场的耦合入手解决问题往往计算效率较低。
以机电耦合振动问题为例,提出一种简洁计算模型,从而把实际中复杂的多物理场耦合问题转化为单物理场振动问题,并使用有限元仿真的方法讨论了多种振动控制方案的性能,最终得到优化的振动控制方案。
关键词:数值仿真,多物理场耦合,振动控制A Concise Computation Model for the Analysis ofMulti-physics field Coupling Vibration ProblemAbstract:The cause of vibration in complex system is usually from multi-physics field coupling,the analysis of which is usually inef-ficient.Based on the electro-mechanical coupling system,a concise computation model is introduced to solve the multi-physics field coupling problem via single physics field vibration problem.Different vibration control schemes are examined through the simulation re-sults from the proposed concise computation model,and an optimized vibration control scheme is obtained.Keywords:Numerical Simulation,Multi-physics field coupling,Vibration Control0引言复杂系统的振动源往往非常复杂,甚至包括多物理场的耦合问题[1,2]。


失谐耦合摆运动规律的研究陈伟;刘明;葛帅良;刘芬;王爱芳【摘要】We theoretically studied the motion of the detuning coupled pendulums using Lagrange method,and experimentally measured the influence of slope factors ε on the pendulums’ angular frequencies. The results prove that the pendulums’ frequencies have the larger variationasε <0 thanε >0 and their vibrations can be controlled continuously through changing the slope of spring. Base on these results,we discussed the law of mo-tion of detuning coupled pendulums under two inclined springs actions,and found the detuning coupled pendu-lums can be backto resonance again as two slope factors meet the appropriate conditions. These results in this paper are helpful for designing new resonance devices and meanwhile afford a new way to control resonance.%本文利用拉格朗日方法,理论上分析了失谐耦合摆的运动规律,并从实验上观测了弹簧的倾斜因子ε对双摆振动角频率的不同影响,确定了弹簧向下偏离平衡位置时较向上偏离时对两摆角频率的影响大,通过改变弹簧的倾斜因子可以连续调节摆的振动规律。

耦合摆学号 20100601050125密级 ______________ 兰州城市学院本科毕业论⽂耦合摆运动⾮线性现象仿真研究学院名称:培黎⼯程技术学院专业名称:物理学学⽣姓名:杨亚军指导教师:陈建宏讲师⼆○⼀四年五⽉BACHELOR'S DEGREE THESISOF LANZHOU CITY UNIVERSITYSimulation study on nonlinear phenomena in the motion of coupled pendulumCollege :School of Bailie engineering & technolog ySubject :PhysicsName :Yang YajunDirected by :Chen Jianhong lecturerMay 2014郑重申明本⼈呈交的学位论⽂,是在导师的指导下,独⽴进⾏研究⼯作所取得的成果,所有数据、图⽚资料真实可靠。
尽我所知,除⽂中已经注明引⽤的内容外,本学位论⽂的研究成果不包含他⼈享有著作权的内容。
对本论⽂所涉及的研究⼯作做出贡献的其他个⼈和集体,均已在⽂中以明确的⽅式标明。
本学位论⽂的知识产权归属于培养单位。
本⼈签名:⽇期:摘要本论⽂⾸先从耦合摆的理论分析⼊⼿,应⽤⼒学的知识,推导得出串联耦合摆和并联耦合摆的运动⽅程。
然后,利⽤计算⼯具Mathematica对微分⽅程进⾏数值求解,做出串联耦合摆和并联耦合摆的相图和庞加莱截⾯图。
相图是分析⾮线性现象的主要⽅法;庞加莱截⾯是区分周期、准周期与混沌的判据,是分析⾮线性现象的最好⼯具。
所以本⽂主要运⽤这两种⽅法对串联耦合摆和并联耦合摆的进⾏定性分析,最后得出串联耦合摆和并联耦合摆运动中的⾮线性特点。
关键字:耦合摆;⾮线性;相图;庞加莱截⾯。
ABSTRACTFirst, this thesis analyzed the theory of coupled pendulum, with the application of mechanical knowledge, we can obtain the equation of motion about coupled pendulum in series and coupled pendulum in multiple. Then, using computational tools of Mathematica, we can get numerical solution of the differential equation. Meanwhile, we can draw the phase diagram and Poincare cross section of the coupled pendulum in series and coupled pendulum in multiple. As Phase diagram is the main approach for the analysis of nonlinear phenomena; Poincare cross section is distinguishing between period, quasi periodic and chaotic, is the best tool for the analysis of n nonlinear phenomena. we use these two methods for qualitative analysis. In the end , we draw the conclusion of the nonlinear phenomenon of coupled pendulum in series and coupled pendulum in multiple.Key words:coupled pendulum; nonlinearity; phase diagram; Poincare cross section;⽬录第1章绪论1.1 引⾔---------------------------------------------------------------------------------------- 11.1.1耦合振动 -------------------------------------------------------------------------- 21.1.2 ⾮线性动⼒学基础 ------------------------------------------------------------- 21.1.3 数值计算和计算物理 ---------------------------------------------------------- 31.1.4 平⾯相图与庞加莱截⾯ ------------------------------------------------------- 41.2 本⽂主要内容 --------------------------------------------------------------------------- 4第2章串联耦合摆运动的仿真研究2.1串联耦合摆的理论推导 ---------------------------------------------------------------- 52.2 串联耦合摆的⾮线性现象分析 ------------------------------------------------------ 6L对运动的影响-------------------------------------------------- 102.2.1 摆线长度12.2.2 摆球质量对运动的影响 ----------------------------------------------------- 132.2.3 弹簧劲度系数对运动的影响 ----------------------------------------------- 162.3 本章⼩结-------------------------------------------------------------------------------- 19第3章并联耦合摆运动的仿真研究3.1 并联耦合摆的理论推导 ------------------------------------------------------------- 203.2 并联耦合摆的⾮线性现象分析 ---------------------------------------------------- 213.2.1 摆长对并联耦合摆运动的影响 -------------------------------------------- 233.2.2 摆球质量对并联耦合摆运动的影响-------------------------------------- 243.2.3 劲度系数对并联耦合摆运动的影响-------------------------------------- 263.3 本章⼩结-------------------------------------------------------------------------------- 28第4章总结分析参考⽂献----------------------------------------------------------------------------------------- 30致谢 -------------------------------------------------------------------------------------------- 31附录 -------------------------------------------------------------------------------------------- 32第1章绪论1.1 引⾔20世纪50年代以后,⾮线性[1]学科逐步成型并慢慢地发展成为⼀门综合性的学科。

分子振动耦合是一种广泛存在于分子内和分子间的分子振动耦合和能量转移现象。
分子内的费米共振现象由某个基团的基频和另一个基团的组频或某两个基团的和频发生耦合而产生。
分子振动耦合在分子振动态、电子态相互耦合、分子结构与性能等研究中具有重要的理论意义,在材料、生物和化学等领域应用广泛,如酶分子构型的确定、抗癌药物疗效的考证、地质学中包裹体的压力分析、晶体中杂质检测和声子及光子器件的研制等,已引起人们广泛关注。
机械振动学中的振动与润滑耦合分析机械振动学是研究机械系统在运动过程中发生的振动现象的学科。
在机械系统中,振动与润滑是两个密切相关的问题。
振动会对机械系统的运行产生不利影响,而润滑则可以减少机械系统在运行过程中的摩擦与磨损,从而提高机械系统的运行效率和寿命。
振动与润滑之间存在着一定的耦合关系,正确分析振动与润滑的耦合问题对于提高机械系统的运行性能具有重要意义。
一、振动与润滑的基本概念振动是指物体在平衡位置附近做小幅度周期性的运动。
在机械系统中,振动可以引起机械零部件之间的碰撞与撞击,导致机械系统的损坏与故障。
润滑是指在机械系统中使用油脂、润滑油等润滑介质来减少摩擦与磨损,以达到减少能量损失、降低运行温度、延长寿命的目的。
二、振动对润滑的影响振动会改变机械系统中润滑膜的形态与分布,影响润滑膜的厚度与质量分布,从而影响摩擦副之间的滑动摩擦性能。
振动会导致机械系统中的润滑油或润滑脂在摩擦表面上形成不均匀的润滑膜,增加摩擦副之间的摩擦力与磨损,降低机械系统的运行效率与寿命。
三、润滑对振动的影响润滑可以减少机械系统中零部件之间的直接接触,减少摩擦与磨损,从而减小振动的幅度与频率。
良好的润滑可以减少机械系统中的摩擦损失,提高系统的运行效率,减少振动对机械系统的影响。
在机械系统中,适当的润滑可以减小机械零部件之间的振动幅度,减少机械系统的振动噪声。
四、振动与润滑的耦合分析振动与润滑是机械系统中密切相关的问题,二者之间存在着一定的耦合关系。
在机械系统中,振动会改变润滑膜的形态与性能,影响润滑副之间的摩擦性能。
润滑膜的形态与性能又会对振动的幅度与频率产生一定的影响。
因此,在机械振动学中,必须对振动与润滑的耦合问题进行深入分析,以确保机械系统的安全稳定运行。
在振动与润滑的耦合分析中,需要考虑机械系统的结构特性、工作条件、润滑方式、摩擦特性等因素。
通过理论分析、计算模拟与实验测试相结合的方法,可以准确评估机械系统中振动与润滑的耦合问题,并提出相应的改进措施。
学号 20100601050125密级 ______________ 兰州城市学院本科毕业论文耦合摆运动非线性现象仿真研究学院名称:培黎工程技术学院专业名称:物理学学生姓名:杨亚军指导教师:陈建宏讲师二○一四年五月BACHELOR'S DEGREE THESISOF LANZHOU CITY UNIVERSITYSimulation study on nonlinear phenomena in the motion of coupled pendulumCollege :School of Bailie engineering & technolog ySubject :PhysicsName :Yang YajunDirected by :Chen Jianhong lecturerMay 2014郑重申明本人呈交的学位论文,是在导师的指导下,独立进行研究工作所取得的成果,所有数据、图片资料真实可靠。
尽我所知,除文中已经注明引用的内容外,本学位论文的研究成果不包含他人享有著作权的内容。
对本论文所涉及的研究工作做出贡献的其他个人和集体,均已在文中以明确的方式标明。
本学位论文的知识产权归属于培养单位。
本人签名:日期:摘要本论文首先从耦合摆的理论分析入手,应用力学的知识,推导得出串联耦合摆和并联耦合摆的运动方程。
然后,利用计算工具Mathematica对微分方程进行数值求解,做出串联耦合摆和并联耦合摆的相图和庞加莱截面图。
相图是分析非线性现象的主要方法;庞加莱截面是区分周期、准周期与混沌的判据,是分析非线性现象的最好工具。
所以本文主要运用这两种方法对串联耦合摆和并联耦合摆的进行定性分析,最后得出串联耦合摆和并联耦合摆运动中的非线性特点。
关键字:耦合摆;非线性;相图;庞加莱截面。
ABSTRACTFirst, this thesis analyzed the theory of coupled pendulum, with the application of mechanical knowledge, we can obtain the equation of motion about coupled pendulum in series and coupled pendulum in multiple. Then, using computational tools of Mathematica, we can get numerical solution of the differential equation. Meanwhile, we can draw the phase diagram and Poincare cross section of the coupled pendulum in series and coupled pendulum in multiple. As Phase diagram is the main approach for the analysis of nonlinear phenomena; Poincare cross section is distinguishing between period, quasi periodic and chaotic, is the best tool for the analysis of n nonlinear phenomena. we use these two methods for qualitative analysis. In the end , we draw the conclusion of the nonlinear phenomenon of coupled pendulum in series and coupled pendulum in multiple.Key words:coupled pendulum; nonlinearity; phase diagram; Poincare cross section;目录第1章绪论1.1 引言---------------------------------------------------------------------------------------- 11.1.1耦合振动 -------------------------------------------------------------------------- 21.1.2 非线性动力学基础 ------------------------------------------------------------- 21.1.3 数值计算和计算物理 ---------------------------------------------------------- 31.1.4 平面相图与庞加莱截面 ------------------------------------------------------- 41.2 本文主要内容 --------------------------------------------------------------------------- 4第2章串联耦合摆运动的仿真研究2.1串联耦合摆的理论推导 ---------------------------------------------------------------- 52.2 串联耦合摆的非线性现象分析 ------------------------------------------------------ 6L对运动的影响-------------------------------------------------- 102.2.1 摆线长度12.2.2 摆球质量对运动的影响 ----------------------------------------------------- 132.2.3 弹簧劲度系数对运动的影响 ----------------------------------------------- 162.3 本章小结-------------------------------------------------------------------------------- 19第3章并联耦合摆运动的仿真研究3.1 并联耦合摆的理论推导 ------------------------------------------------------------- 203.2 并联耦合摆的非线性现象分析 ---------------------------------------------------- 213.2.1 摆长对并联耦合摆运动的影响 -------------------------------------------- 233.2.2 摆球质量对并联耦合摆运动的影响-------------------------------------- 243.2.3 劲度系数对并联耦合摆运动的影响-------------------------------------- 263.3 本章小结-------------------------------------------------------------------------------- 28第4章总结分析参考文献----------------------------------------------------------------------------------------- 30致谢 -------------------------------------------------------------------------------------------- 31附录 -------------------------------------------------------------------------------------------- 32第1章绪论1.1 引言20世纪50年代以后,非线性[1]学科逐步成型并慢慢地发展成为一门综合性的学科。
科技馆的耦合摆的原理
嘿,朋友们!今天咱来说说科技馆里超有意思的耦合摆!你知道吗,这耦合摆就像是一场神奇的舞蹈!
想象一下,有两个小摆锤,就好像是两个亲密无间的小伙伴。
它们挂在那里,你动一下这个,那个也会跟着动起来,是不是特别神奇?这就好像是你和你的好朋友,一个人笑了,另一个也会忍不住跟着笑,它们之间有着奇妙的联系呢!
我那次去科技馆,亲眼看到工作人员摆弄那些耦合摆。
哇塞,就看到一个摆锤晃起来,然后另一个也像是得到了某种信号一样,跟着有节奏地摆动起来。
这感觉就像一场默契十足的表演!旁边的小朋友们都看得目瞪口呆的,一个劲儿地喊着:“哇,好厉害呀!”你说这多有意思呀!
而且哦,耦合摆的原理其实也不难理解。
就好比是两个志同道合的人,一个人的行动会影响到另一个人。
它们相互呼应,相互作用,共同演绎出这精彩的场面。
你看,生活中不也常常有这样的情况吗?你的情绪会感染身边的人,你的行动也可能带动别人一起行动。
这耦合摆真的是让我大开眼界呀!它让我看到了事物之间那种微妙而又神奇的联系。
它不只是一些机械的摆动,更是一种对我们生活中各种关系的隐喻。
所以呀,大家有机会一定要去科技馆看看这神奇的耦合摆,亲自感受一下它的魅力!我觉得每个人都能从中学到点什么,感受到一些特别的东西。
你难道不想去体验一下吗?。
耦合摆小振动问题研究
唐志根
(华南师范大学物理与电信工程学院 08物理学专业3班 20082301053)
摘要:利用拉格朗日方程,给出了耦合摆在平衡位置附近的动力学方程,求解出
耦合摆在平衡位置附近作小振动时的本征频率。并对耦合摆的振动坐标作适当的线性
组合,得出了简正坐标和简正振动频率。
关键词:拉格朗日方程;小振动;耦合摆;简正坐标;
Key words:Lagrange equation;small oscillation;couple pendulum;normal coordinate
Abstract:The dynamic equations of the couple pendulum near the balance location were
given by using Lagrange equation.The eigenfrequency of small oscillation of the couple
pendulum near the balanced location was also solved.The normal coordinates and normal
oscillation frequency were gained by making adaptablely linear combination with
oscillation coordinates of couple pendulum.
前言:力学系统大多是较为复杂的非线性系统,不太可能对其运动得出完整的一
般解。但对某些小振动下的非线性系统能通过某些过程给出解析解。耦合摆由两个单
摆通过一弹簧相连构成,关于耦合摆的小振动在大学力学教材中曾求解过,而且简正
坐标的求法不少文献作了讨论,但求解过程较繁。本文利用分析力学的拉格朗日方程,
求解了耦合摆在平衡位置附近作小振动时的情况,给出了处理耦合摆小振动的一种较
简单适用的方法。虽然只是两个自由度的力学体系,但它包含了处理非线性力学系在
平衡位置,附近作小振动的主要过程。
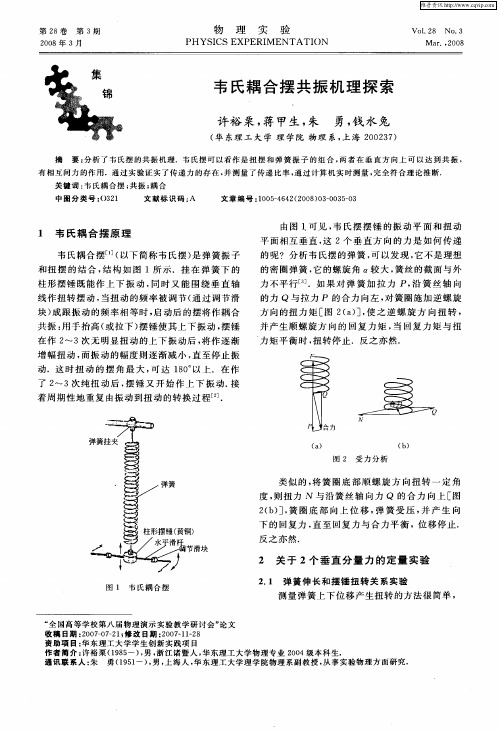
1、耦合摆
如上图所示,耦合摆由两个相同的单摆平行悬挂,两个摆锤之间用一轻质弹
簧相连构成。两球摆锤的质量同为m:摆长为l;弹簧劲度系数为k;弹簧的质量忽
略不计。
2、耦合摆的小振动
如上图,设耦合摆在自身的铅直平面内作微小摆动,两个摆锤摆动的角度分
别为θ和,这两个独立变量确定了系统的位形,可作为系统的广义坐标。显然二
摆都竖直下垂时,系统处于能量最小的平衡状态,即θ及等于零时的状态。这是
两个自由度的较为简单的力学系。
2.1 系统的动能和势能
由上图几何关系,设平衡位置为零势能点,可得系统动能与势能公式如下:
动能
(1)
势能
(2)
在小振动的情形下,和以及初始角速度都是很小的量(在实际操作中,摆
角应小于5度,可以对势能
在系统平衡位置附近展开,保留到的二次项,且
在平衡位置附近处
==0,则
=
小振动时系统的势能函数近似为
=
(3)
2.2 耦合摆的动力学方程
系统作小振动时的拉格朗日函数
(4)
将L代入拉格朗日方程得动力学方程
得
(5)
2.3 方程的解
本问题的解法有两种,本文采用第二种,下面先介绍第一种。
第一种解法:
假设方程(5)具有振动类型的解
将其代入(5)式,可得关于、的齐次代数方程组
(6)
要使、有非零解的必要条件是他们系数行列式为零。于是求得
:
令 ,=;
当为;
即可得通解
(7)
(7)式中、、可由边界条件决定(由于本次解法并不
采用上述方法,固在这里不分析各常数如何确定,在第二种方法中有详细分析)。
第二种解法(简正坐标):
这两个独立简谐运动分别代表以不同的本征频率振动的两个独立振动模式。
这些独立的简谐振动模式称为体系的简正振动,简正振动的频率是体系的本征频
率,称为简正频率,与简正振动相对应的广义坐标,称为简正坐标。
耦合摆的摆动相互关联着,不是独立的。原因是势能表达式(3)中存在θ及的
乘积项。进一步探讨则发现,只要对两个摆的振动坐标(θ,)作适当的线性组合
成为新的广义坐标参量,就可以使动能表达式仍保持为广义速度平方和的形式,
同时又能使势能函数中也不出现广义坐标的交叉(乘积)项。对上面所讨论的耦合
摆来说,这种坐标变换不难得到。若令
将此坐标(参量)变换关系代入式(4),得出拉氏函数
这样,拉氏函数都只包含广义速度及广义坐标的平方项,不再存在交叉乘积
项。这是两个独立振子的拉格朗日函数。相应的动力学方程为
下列讨论,,,如何由边界得出:
设摆角初始位置,初角速度为。
则有
则有
3、计算机模拟耦合摆小振动
在不破坏小振动的条件下设定,,,,可得到不同的耦合摆小振
动公式,利用科学计算与模拟平台进行计算,可以模拟出耦合摆振动图象。
下面图象为一组符合小振动条件的参数下的模拟耦合摆振动,图象下部为弹簧弹
力的动态显示。
注意:本程序设计了多条滚动条可以改变系统的各参数以及边界条件(即初
始条件),请读者必须在小振动的条件下调节。因为前面公式是在小振动情况下
作了近似得出的,如果超出小振动范围将有不符合实际的情况出现。
下面为模拟图象:
4、结论
通过对耦合摆在平衡位置附近的小振动问题的研究及求解耦合摆小振动的过
程,利用拉格朗日函数来处理原来的问题,再解得出的微分方程。明确了耦合摆
的小振动既可以从两个摆的振动和(t)去研究,也可以分解成两种独立简谐
振动模式来计算,再进行反演,本次操作中使用第二种方法,强调了各种函数可
利用其他本证函数展开的思想,十分巧妙地解决了问题。
5、参考文献:
1、韩萍 耦合摆小振动问题的研究 2008年4月
2、包兴明,向必纯,袁玉全 对称四弹性振子的二维非线性振动 2008年
3、周衍柏 理论力学教程 2004年