统计学第四章

第四章 假设检验填空（5题/章），选择（5题/章），判断（5题/章），计算（3题/章） 一、填空1、在做假设检验时容易犯的两类错误是 和2、如果提出的原假设是总体参数等于某一数值，这种假设检验称为 ，若提出的原假设是总体参数大于或小于某一数值，这种假设检验称为3、假设检验有两类错误，分别是 也叫第一类错误，它是指原假设H0是 的，却由于样本缘故做出了 H0的错误；和 叫第二类错误，它是指原假设H0是 的, 却由于样本缘故做出 H0的错误。

4、在统计假设检验中，控制犯第一类错误的概率不超过某个规定值α,则α称为 。

5、 假设检验的统计思想是小概率事件在一次试验中可以认为基本上是不会发生的，该原理称为 。

6、从一批零件中抽取100个测其直径，测得平均直径为5.2cm ，标准差为1.6cm ，想知道这批零件的直径是否服从标准直径5cm ，在显著性水平α下，否定域为7、有一批电子零件，质量检查员必须判断是否合格，假设此电子零件的使用时间大于或等于1000，则为合格，小于1000小时，则为不合格，那么可以提出的假设为 。

（用H 0，H 1表示）8、一般在样本的容量被确定后，犯第一类错误的概率为α，犯第二类错误的概率为β，若减少α，则β9、某厂家想要调查职工的工作效率，用方差衡量工作效率差异，工厂预计的工作效率为至少制作零件20个/小时，随机抽样30位职工进行调查，得到样本方差为5，试在显著水平为0.05的要求下，问该工厂的职工的工作效率 （有，没有）达到该标准。

KEY: 1、弃真错误，纳伪错误 2、双边检验，单边检验3、拒真错误，真实的，拒绝，取伪错误，不真实的，接受4、显著性水平5、小概率事件6、1.25>21α-z7、H 0：t≥1000 H 1：t ＜1000 8、增大 9、有二、 选择1、假设检验中，犯了原假设H 0实际是不真实的，却由于样本的缘故而做出的接受H 0的错误，此类错误是（ ）A 、α类错误B 、第一类错误C 、取伪错误D 、弃真错误 2、一种零件的标准长度5cm ，要检验某天生产的零件是否符合标准要求，建立的原假设和备选假设就为（ ）A 、0:5H μ=，1:5H μ≠B 、0:5H μ≠，1:5H μ>C 、0:5H μ≤，1:5H μ>D 、0:5H μ≥，1:5H μ< 3、一个95%的置信区间是指（ ） A 、总体参数有95%的概率落在这一区间内 B 、总体参数有5%的概率未落在这一区间内C 、在用同样方法构造的总体参数的多个区间中，有95%的区间包含该总体参数D 、在用同样方法构造的总体参数的多个区间中，有95%的区间不包含该总体参数4、假设检验中，如果增大样本容量，则犯两类错误的概率（ ） A 、都增大 B 、都减小 C 、都不变 D 、一个增大一个减小5、一家汽车生产企业在广告中宣称“该公司的汽车可以保证在2年或24000公里内无事故”，但该汽车的一个经销商认为保证“2年”这一项是不必要的，因为汽车车主在2年内行驶的平均里程超过24000公里。

第四章一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是（）A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数（）A．比例相对数B．比较相对数C．结构相对数D．动态相对数3.某企业工人劳动生产率计划提高5%，实际提高了10%，则提高劳动生产率的计划完成程度为（）A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%，则产品成本计划完成程度（）A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量，但可以同时存在多个标志总量B.可以存在多个单位总量，但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是（）A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求（）A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是（）A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分，最高分是96分，最低分是62分，根据这些信息，可以计算的测度离散程度的统计量是（）A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时，其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额，要求计算4个商店苹果的平均单价，应采用（）A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。

《统计学原理》第四章习题及答案一．判断题部分题目1：同一个总体，时期指标值的大小与时期长短成正比，时点指标值的大小与时点间隔成反比。

（）题目2：全国粮食总产量与全国人口对比计算的人均粮食产量是平均指标。

（）题目3：根据分组资料计算算术平均数，当各组单位数出现的次数均相等时，按加权算数平均数计算的结果与按简单算数平均数计算的结果相同。

（）题目4：同一总体的一部分数值与另一部分数值对比得到的相对指标是比较相对指标。

（）题目5：某年甲、乙两地社会商品零售额之比为1：3，这是一个比例相对指标。

（）题目6：某企业生产某种产品的单位成本，计划在上年的基础上降低2%，实际降低了3%，则该企业差一个百分点，没有完成计划任务。

（）题目7：标准差系数是标准差与平均数之比，它说明了单位标准差下的平均水平。

（）题目8：1999年与1998年相比，甲企业工人劳动生产率是乙企业的一倍，这是比较相对指标。

（）题目9：中位数与众数都是位置平均数，因此用这两个指标反映现象的一般水平缺乏代表性。

（）题目10：对两个性质相同的变量数列比较其平均数的代表性，都可以采用标准差指标。

（）题目11：利用变异指标比较两总体平均数的代表性时，标准差越小，说明平均数的代表性越大；标准差系数越小，则说明平均数的代表性越小。

（）题目12：标志变异指标数值越大，说明总体中各单位标志值的变异程度越大，则平均指标的代表性越小。

（）题目13：权数对算数平均数的影响作用只表现为各组出现次数的多少，与各组次数占总次数的比重无关。

（）题目14；能计算总量指标的总体必须是有限总体。

（）二．单项选择题题目1：反映社会经济现象发展总规模、总水平的综合指标是（）。

A、质量指标B、总量指标C、相对指标D、平均指标题目2：总量指标按反映时间状况的不同，分为（）。

A、数量指标和质量指标B、时期指标和时点指标C、总体单位总量和总体标志总量D、实物指标和价值指标题目3：总量指标是用（）表示的。

第四章动态数列一、填空题1.绝对数动态数列可以分为数列和数列。

2.测定季节变动的方法有和。

3.增长速度与发展速度之间的关系是：增长速度= 。

4.测定长期趋势的方法有、和。

5.某企业1996年至2000年的产品产量（公斤）为550、570、600、630、700。

则该企业1996年至2000年平均产量为。

6.逐期增长量与累计增长量之间的关系是：累计增长量= 。

二、判断题1.各时期环比增长速度的连乘积等于相应时期的定基增长速度。

（）2.各时期环比发展速度的连乘积等于相应时期的定基发展速度。

（）3.某产品产量2003年是1998年的135%，则1999年——2003年的平均发展速度135。

（）为6%4.在用按月平均法计算季节指数时，各月季节指数之和应等于1200%。

（）5.某企业生产某种产品，产量2002年比2000年增长了8%，2003年比2000年增长了12%，则2003年比2002年增长了8%×12%。

（）6.某高校学生人数2001年比2000年增长2%，2002年比2001年增长5%，2003年比2002年8%，则2000年到2003年该校学生总的增长了15.67%。

（）7.在用按季平均法计算季节比率时，各季季节比率之和应等于1200%。

（）8.增长1%的绝对值=基期水平∕100。

（）9.相邻两个累计增长量之和等于相应时期的逐期增长量。

（）10.相邻两个定基发展速度相除等于相应时期的环比发展速度。

（）11.相邻两个定基增长速度相除等于相应时期的环比增长速度。

（）12.平均增长速度等于平均发展速度-1。

（）13.如果现象发展没有季节变动，则季节比率等于0。

（）14.各时期逐期增长量之和等于相应时期的累计增长量。

（）15.增长速度=增长量∕基期水平。

（）三、单项选择题1.累计增长量等于（）。

A.相应的各个逐期增长量之和B.报告期水平减去前一期水平C.相邻两个逐期增长量之差D.最末水平比最初水平2.环比增长速度等于（）。

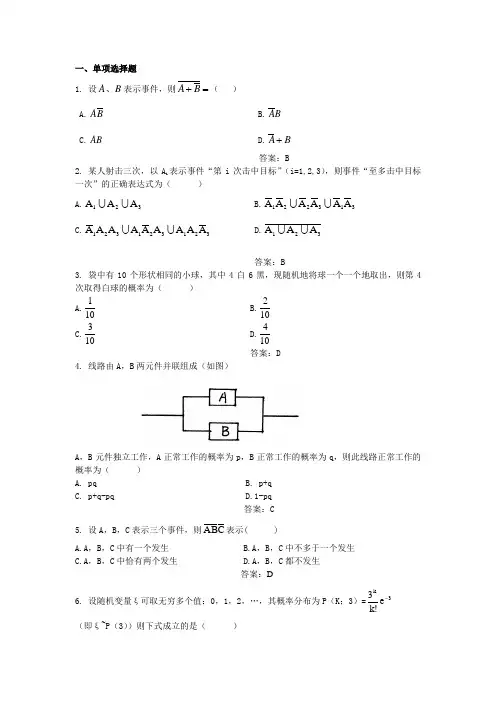
一、单项选择题1. 设B A 、表示事件，则=+B A （ ）A.B AB.B AC.ABD.B A +答案：B2. 某人射击三次，以A i 表示事件“第i 次击中目标”（i=1,2,3），则事件“至多击中目标一次”的正确表达式为（ ）A.321A A AB.313221A A A A A AC.321321321A A A A A A A A AD.321A A A答案：B3. 袋中有10个形状相同的小球，其中4白6黑，现随机地将球一个一个地取出，则第4次取得白球的概率为（ ）A.101 B.102C.103D.104 答案：D 4. 线路由A ，B 两元件并联组成（如图）A ，B 元件独立工作，A 正常工作的概率为p ，B 正常工作的概率为q ，则此线路正常工作的概率为（ ）A. pqB. p+qC. p+q-pqD.1-pq答案：C 5. 设A ，B ，C 表示三个事件，则C B A 表示( )A.A ，B ，C 中有一个发生B.A ，B ，C 中不多于一个发生C.A ，B ，C 中恰有两个发生D.A ，B ，C 都不发生答案：D6. 设随机变量ξ可取无穷多个值：0，1，2，…，其概率分布为P （K ；3）=3k e !k 3- （即ξ~P （3））则下式成立的是（ ）A.E ξ=D ξ=3B.E ξ=D ξ=31 C.E ξ=3，D ξ=31D.E ξ=31，D ξ=3 答案：A7. 设随机变量ξ的分布列为P{ξ=k}=Ak,k=1,2,3,4,5，则常数A=（ ） A.5 B.10C.15D.20答案：C 8. 设ξ的分布为则常数α=（ ） A.0.1B.0.2C.0.3D.0.4答案：A9. 设ζ的分布列为则E ζ2=( ) A.-0.2 B.0.2 C.2.76 D.2.8答案：D10. 设随机变量ξ的密度函数p(x)=⎪⎩⎪⎨⎧∈ 其它 ,x ,Cx 0[0,1]4,则常数C ＝（ ）A ．51B ．41 C ．4D ．5答案：D11．设随机变量ζ的概率密度为p(x)=⎪⎩⎪⎨⎧<<-其他,0,21a x a a，其中A>0，要使P{ζ>1}=31，则A=（ ） A.1B.2C.3D.4答案：C12．设ζ的分布函数为F(x)=A++∞<<∞-πx x arctan 1，则常数A=（ ）A.21B.1C.2D.π答案：A13. 独立随机变量ξ，η，若ξ～N （1，4），η～N （3，16），下式中不成立．．．的是（ ） A ．E （ξ＋η）＝4B ．E （ξη）＝3C ．D （ξ－η）＝12D ．D （η＋2）＝16答案：C14．将一枚均匀硬币反复抛掷10次，已知前三次抛掷中恰出现了一次正面，则第二次出现正面的概率为（ ）A.31B.21C.41D.103 答案：A15. 13．设随机变量ζ的密度函数p(x)=⎩⎨⎧π∈其他,0],0[x ,ASinx ，则常数A=（ ）A.41B.21 C.1D.2答案：B16.设试验成功概率是p(0<p<1)，则在三次重复独立试验中至少失败一次的概率是( ) A. (1-p)3 B. 1-p 3C. 3(1-p)D. (1-p)3+p(1-p)2+p 2(1-p)答案：B 17.设随机变量X 在[A ，B]上服从均匀分布，则其标准差)(X D 为 A.12/)(2a b -B. 6/)(2a b -C. 32/)(a b -D. 6/)(a b -答案：C18.设),(~2σμN X ，则=)(2X E A.22σμ+B. 2σμ+C.σμ+2D. σμ+答案：A19.若,2)(=X D 则=-)14(X D A.32B.8C. 2D. 31答案：A20.若,2)(,1)(==Y E X E 则=-)2(Y X E A.0B.-1C. 1D. 2答案：A二、多项选择题（略） 三、名词解释1.古典概型2.随机事件的独立性3.分布函数4.依概率收敛[参考答案]1.古典概型：古典概型是指满足下面两个特征的随机试验模型：1）样本空间是有限的，{}n ωωω,,,21 =Ω其中),,2,1(n i i =ω是样本点（基本随机事件）；2）各基本事件的出现是等可能的，即它们发生的概率相同； 3）各基本事件互不相容，即);,,2,1,(j i n j i j i ≠=Φ= ωω2.随机事件的独立性：若事件A 、B 满足)()()(B P A P AB P =，称A 、B 相互独立。

第4章练习题1、一组数据中出现频数最多的变量值称为（）A.众数B.中位数C.四分位数D.平均数2、下列关于众数的叙述，不正确的是（）A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为（）A.众数B.中位数C.四分位数D.平均数4、一组数据排序后处于25%和75%位置上的值称为（）A.众数B.中位数C.四分位数D.平均数5、非众数组的频数占总频数的比例称为（）A.异众比率B.离散系数C.平均差D.标准差6、四分位差是（）A.上四分位数减下四分位数的结果B.下四分位数减上四分位数的结果C.下四分位数加上四分位数D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为（）A.平均差B.标准差C.极差D.四分位差8、各变量值与其平均数离差平方的平均数称为（）A.极差B.平均差C.方差D.标准差9、变量值与其平均数的离差除以标准差后的值称为（）A.标准分数B.离散系数C.方差D.标准差10、如果一个数据的标准分数-2，表明该数据（）A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差11、经验法则表明，当一组数据对称分布时，在平均数加减2个标准差的范围之内大约有（）A.68%的数据B.95%的数据C.99%的数据D.100%的数据12、如果一组数据不是对称分布的，根据切比雪夫不等式，对于k=4，其意义是（）A.至少有75%的数据落在平均数加减4个标准差的范围之内B. 至少有89%的数据落在平均数加减4个标准差的范围之内C. 至少有94%的数据落在平均数加减4个标准差的范围之内D. 至少有99%的数据落在平均数加减4个标准差的范围之内13、离散系数的主要用途是（）A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平14、比较两组数据离散程度最适合的统计量是（）A.极差B.平均差C.标准差D.离散系数15、偏态系数测度了数据分布的非对称性程度。

第四章 推断统计概述第一部分 概率论基本知识← 一、概率的定义；二、概率的性质；三、概率的加法定理和乘法定理← 四、概率分布类型四、概率分布类型← 概率分布（probability distribution ）是指对随机变量取不同值时的概率的描述，一般用概率分布函数进行描述。

← 依不同的标准，对概率分布可作不同的分类。

１、离散型分布与连续型分布← 依随机变量的类型，可将概率分布分为离散型概率分布与连续型概率分布。

← 教育统计学中最常用的离散型分布是二项分布，最常用的连续型分布是正态分布。

２、经验分布与理论分布← 依分布函数的来源，可将概率分布分为经验分布与理论分布。

← 经验分布（empirical distribution ）是指根据观察或实验所获得的数据而编制的次数分布或相对频率分布。

← 理论分布（theoretical distribution ）是按某种数学模型计算出的概率分布。

３、基本随机变量分布与抽样分布← 依所描述的数据的样本特性，可将概率分布分为基本随机变量分布与抽样分布（sampling distribution ）。

← 基本随机变量分布是随机变量各种不同取值情况的概率分布，← 抽样分布是从同一总体内抽取的不同样本的统计量的概率分布。

第二部分 几种常见的概率分布← 一、二项分布← 二项分布（binomial distribution ）是一种具有广泛用途的离散型随机变量的概率分布，它是由贝努里创始的，因此又称为贝努里分布。

← 2．二项分布函数← 二项分布是一种离散型随机变量的概率分布。

← 用 n 次方的二项展开式来表达在 n 次二项试验中成功事件出现的不同次数（X ＝0，1…，n ）的概率分布，叫做二项分布函数。

← 二项展开式的通式（即二项分布函数）：← ←← ← ←← 成功概率 p ；样本容量 n← 在成功概率为p 的总体中随机抽样，抽取样本容量为n 的样本中，有X 次为成()011111100q p C q p C q p C q p C q p n n n n n n n n n n n ++++=+---Λ()Xn X X n X q p C P -⋅⋅=()X n X q p X n X n -⋅-=!!!功的概率： ←（X ＝0，1…，n ） ←称X 服从参数为n ，p 的二项分布，记为： ←X ～B(n ,p ) 其中，0<p<1 ←二项分布的性质 ←二项分布有如下性质： ←①当p=q 时，图形是对称的。

第四章抽样估计一、判断题1.抽样估计的目的是用以说明总体特征。

2.抽样分布就是样本分布。

3.既定总体在当抽样方法、抽样组织形式和样本容量确定时，样本均值的分布惟一确定。

4.样本容量就是样本个数。

5.在抽样中，样本容量是越大越好。

6.抽样的目的是判断样本估计值是否处于以总体指标为中心的某规定区域范围内。

7.当估计量有偏时，人们应该弃之不用。

8.对于一个确定的抽样分布，其方差是确定的，因而抽样标准误也是确定的。

9.抽样极限误差越大，用以包含总体参数的区间就越大，估计的把握程度也就越大，因此极限误差越大越好。

10.非抽样误差会随着样本容量的扩大而下降。

二、单项选择题1.想了解学生的眼睛视力状况，准备抽取若干学校、若干班级的学生进行测试，则（）。

A.观测单位是学校B.观测单位是班级C.观测单位是学生D.观测单位可以是学校、也可班级或学生2.下列误差中属于非一致性的有（）。

A.估计量偏差B.偶然性误差C.抽样标准误D.非抽样误差3.抽样估计中最常用的分布理论是（）。

A.t分布理论B.二项分布理论C.正态分布理论D.超几何分布理论4.抽样标准误大小与下列哪个因素无关？（）A.样本容量B.抽样方式、方法C.概率保证程度D.估计量5.下列关于抽样标准误的叙述哪个是错误的？（）A.抽样标准误是抽样分布的标准差B.抽样标准误的理论值是惟一的，与所抽样本无关C.抽样标准误比抽样极限误差小D.抽样标准误只能衡量抽样中的偶然性误差的大小三、计算分析题1. 某小组5个工人的每周工资分别为520、540、560、580、600元，现从中用简单随机抽样形式（不重复抽样）随机抽取2个工人周工资构成样本。

要求：（1）计算总体平均工资的标准差；（2）列出全部可能的样本平均工资；（3）计算样本平均工资的平均数，并检验其是否等于总体平均工资；（4）计算样本平均工资的标准差；（5）用抽样平均误差的公式计算并验证是否等于（4）的结果。

2.从某大型企业中随机抽取100名职工，调查他们的工资。

统计学第四章1.动态数列的构成要素是（）。

[单选题] *A)变量和次数B)时间和指标数值(正确答案)C)时间和次数D)主词和宾词2.动态数列中,每个指标数值可以相加的是（）。

[单选题] *A)相对数动态数列B)时期数列(正确答案)C)间断时点数列D)平均数动态数列4.定基增长速度与环比增长速度的关系为（）。

[单选题] *A)定基增长速度等于相应的各个环比增长速度的算术和B)定基增长速度等于相应的各个环比增长速度的连乘积C)定基增长速度等于相应的各个环比增长速度加1后的连乘积再减1(正确答案)D)定基增长速度等于相应的各个环比增长速度连乘积加1(或100%)5.按季平均法测定季节比率时,各季的季节比率之和应等于（） [单选题] *A)100%B)400%(正确答案)C)120%D)1200%9.某城市2016年末有人口750万人，有零售商业网点3万个，则该市的商业网点密度指标是（）。

[单选题] *A)2.5千人/个B)250人/个(正确答案)C)0.25个/千人D)250个/人10.按水平法计算的平均发展速度推算可以使（） [单选题] *A)推算的各期水平之和等于各期实际水平之和B)推算的期末水平等于实际期末水平(正确答案)C)推算的各期定基发展速度等于实际的各期定基发展速度D)推算的各期增长量等于实际的逐期增长量11.增长1%的绝对值是（）。

[单选题] *A)水平指标B)速度指标C)水平与速度相结合的指标(正确答案)D)什么也不是12.评比城市间的社会发展状况,将各城市每人分摊的绿化面积按年排列的动态数列是属于（）。

[单选题] *A)总量指标的时期数列B)总量指标的时点数列C)相对指标动态数列(正确答案)D)平均指标动态数列13.年距增长速度的计算公式是（）。

[单选题] *A)年距增长量÷最初水平B)逐期增长量÷最初水平C)逐期增长量÷前期水平D)年距增长量÷上年同期发展水平(正确答案)14.动态数列中的发展水平（）。