基于SPSS的多元回归分析模型选取的应用

多因素logistic回归分析spssLogistic回归分析是一种用来研究影响离散变量的因素的方法，该方法的输出是一个logistic模型，这一模型可以用于预测变量的值，即预测该变量的值有多高的概率会取各种可能的取值。

简言之，logistic回归分析的主要目的是把客观的结果（例如，是否改变某个政策，是否感染某种疾病等）变成可预测的离散变量，以便分析影响客观结果的各种因素。

Spss可以提供多因素logistic回归分析，这种分析可用于识别影响离散变量（例如，是否改变某个政策，是否感染某种疾病等）的多个因素之间的关联。

该分析需要有一个组合变量作为自变量，以及一个离散变量作为因变量。

例如，如果您要研究性别和年龄两个因素如何影响某种疾病的发生率，那么性别和年龄两个因素就是组合变量，而疾病的发生率则是因变量。

1.建立变量和分类（上述示例中需要建立性别和年龄两个变量，以及分类变量的可能的取值）。

2.执行logistic回归分析。

打开spss，并在“分析”菜单中打开多元分析，然后点击“逻辑回归”，并选择您要研究的变量和分类。

3.生成回归模型和检验其统计学意义。

在spss中，您可以使用类似“回归系数”之类的描述性统计学方法来估算回归模型，并可以使用“p-值”来判断回归模型中各变量的统计学意义。

4.Interpret模型。

根据p值判断各变量的统计学意义，进而分析影响离散变量的多个因素之间的关联。

四、总结Logistic回归分析是一种用来研究影响离散变量的因素的方法，spss可以提供多因素logistic回归分析，这种分析可用于识别影响离散变量的多个因素之间的关联，spss中步骤：建立变量和分类，执行logistic回归分析，生成回归模型和检验其统计学意义，Interpret模型。

SPSS数据分析—多元线性模型多元线性模型是一种广泛应用于数据分析领域的统计方法，可以帮助研究者研究多个自变量对一个因变量的影响。

本文档将介绍使用SPSS软件进行多元线性模型分析的基本步骤。

步骤一：准备数据在进行多元线性模型分析之前，首先需要准备好所需的数据。

确保数据集中包含了自变量和因变量，并且数据是完整和准确的。

可以使用SPSS软件打开数据文件。

步骤二：选择分析方法在SPSS软件中，选择“Analyze”菜单，然后选择“Regression”子菜单。

在弹出的窗口中，选择“Linear”选项，然后将所需的自变量和因变量添加到相应的列表中。

步骤三：设置模型选项在设置模型选项时，可以选择是否需要常数项、是否需要标准化因子等。

根据研究的需求和背景，进行相应的设置。

步骤四：运行分析设置好模型选项后，点击“OK”按钮，SPSS软件会开始进行多元线性模型分析。

请耐心等待分析结果的生成。

步骤五：解读结果分析完成后，SPSS软件会生成分析结果的汇总表和详细报告。

通过查看汇总表，可以了解自变量和因变量之间的相关性以及回归系数的显著性。

详细报告将提供更深入的分析结果和解读。

步骤六：结果验证在解读结果之前，需要验证多元线性模型是否符合分析的假设。

可以通过检查残差的正态分布、方差齐性和线性关系来验证模型的适应度。

结论通过SPSS软件进行多元线性模型分析可以帮助研究者了解自变量对因变量的影响，并且提供了统计上的支持。

然而，在进行分析和解读结果时，需要注意模型的假设和验证步骤，以确保分析结果的有效性。

以上是关于SPSS数据分析中多元线性模型的简要介绍和步骤。

希望本文档对您的研究能有所帮助。

多元线性回归模型spss
多元线性回归，简称回归，是一种常用的统计分析方法，是一种用来研究两种或两种以上变量之间关系的技术。

当变量之间相互联系时，多重线性回归分析就显得尤为重要。

SPSS是一款用于统计分析的软件。

它轻松让人类处理巨大的数据，
分析挖掘结果，并运用各种模型分析统计数据，如多元线性回归模型。

多元线性回归模型应用于多因素变量分析。

举个例子，假设有三种因素可以影响学生的成绩：自学的时间，自学的方法和家庭的社会经济程度。

使用SPSS可以分析这三个变量之间的关系，即它们同时受不同因素的影响，共同影响学生的成绩，从而帮助我们更好地了解和解释这三种变量之间的相互关系。

使用这款软件时，不仅要熟悉数据的直观感受，还要搞清楚变量之间的关系，这要求SPSS用户具有统计学的基础知识，帮助用户进行解释建模，识别可能的隐藏模式，并进行正确的变量分析。

SPSS的多元线性回归模型提供了许多有用的统计工具和统计方法，可以有效
地处理复杂的变量间关系，为政府和企业提供可靠的数据。

它可以用于市场调研，查明消费者购买某种产品和服务的最佳价格；生产管理，以降低生产成本和提高效率；以及科学研究，以探究物理现象的联系和机制。

总的来说，多元线性回归模型是一种强有力的统计技术，可有效分析多变量间的关系，为政府和企业提供可靠的数据支持。

有了SPSS，多重线性回归变得更加
简单，更有效。

哈尔滨商业大学数学实验报告实验题目：___用SPSS软件实现多元线性回归分析___ 姓名：____张彦琛____ 学号：_201214390009__ 专业：________数学与应用数学_______________ 日期：________2014-10-27___________________一、实验目的用SPSS软件来实现多元线性回归分析及其应用。

二、实验内容水泥凝固时放出的热量Y与水泥中的四种化学成分x1,x2,x3,x4有关，今测得一组数据如下，试用多元回归分析的方法建立模型。

三、实验步骤及结论（一）实验步骤把实验所用数据从Word文档复制到Excel，并进一步导入到SPSS数据文件中进行回归分析。

选择菜单“分析—>回归—>线性”，为了解决多重共线性问题，采用逐步回归法。

（二）实验结论表一：表一显示了用逐步回归法得到了两个回归模型的拟合情况。

由表可知，引入x4得到模型1，模型1的R方为0.675，调整R方为0.645，x4对y影响显著。

同时又引入x1得到模型2，模型2的R方为0.972，调整R 方为0.967，x4，x1对y影响最为显著。

由0.675<0.972，0.645<0.967，且接近1，说明模型的拟合效果很好。

表二：表二给出了两个回归模型的方差分析及检验结果。

模型1的F 值为22.799，Sig.值为0.001<0.05。

模型2的F值为176.627，Sig.值为000<0.05。

模型1,2都通过F检验，可见模型1与模型2在整体上都是显著的。

表三:表三给出了回归模型的非标准化估计系数、标准化估计系数、系数的显著性检验结果以及共线性统计量的方差膨胀因子VIF。

在模型1，2中，对应t统计量的Sig.的值均小于0.05，则说明每个系数对y 的影响是显著的。

共线性统计量中VIF<10，则克服了共线性的影响。

模型1,2都通过了统计显著性检验，由表可得两个回归模型。

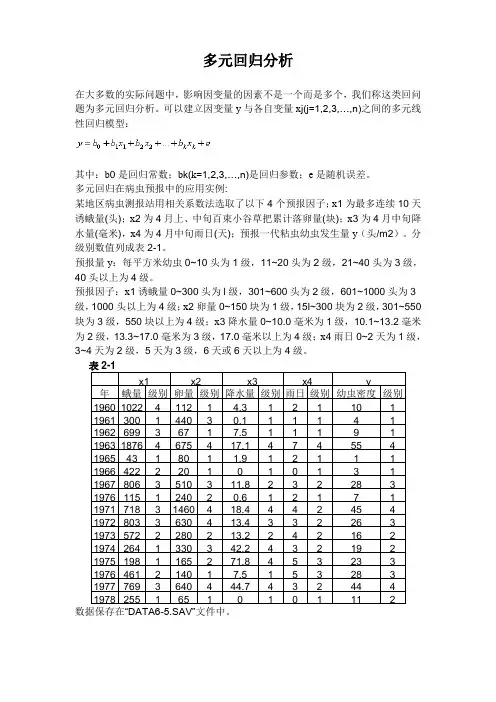
1）准备分析数据在SPSS数据编辑窗口中，创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量，并输入数据。

再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”，它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。

编辑后的数据显示如图2-1。

图2-1或者打开已存在的数据文件“DATA6-5.SAV”。

2）启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项，将打开如图2-2所示的线性回归过程窗口。

图2-2 线性回归对话窗口3) 设置分析变量设置因变量：用鼠标选中左边变量列表中的“幼虫密度[y]”变量，然后点击“Dependent”栏左边的向右拉按钮，该变量就移到“Dependent”因变量显示栏里。

设置自变量：将左边变量列表中的“蛾量[x1]”、“卵量[x2]”、“降水量[x3]”、“雨日[x4]”变量，选移到“Independent(S)”自变量显示栏里。

设置控制变量: 本例子中不使用控制变量，所以不选择任何变量。

选择标签变量: 选择“年份”为标签变量。

选择加权变量: 本例子没有加权变量，因此不作任何设置。

4）回归方式本例子中的4个预报因子变量是经过相关系数法选取出来的，在回归分析时不做筛选。

因此在“Method”框中选中“Enter”选项，建立全回归模型。

5）设置输出统计量单击“Statistics”按钮，将打开如图2-3所示的对话框。

该对话框用于设置相关参数。

其中各项的意义分别为：图2-3 “Statistics”对话框①“Regression Coefficients”回归系数选项：“Estimates”输出回归系数和相关统计量。

“Confidence interval”回归系数的95%置信区间。

“Covariance matrix”回归系数的方差-协方差矩阵。

本例子选择“Estimates”输出回归系数和相关统计量。

多元线性回归模型及其应用摘要本文介绍了多元线性回归模型，其过程分为模型构建、模型参数估计、模型检验和模型预测等几个方面。

通过对与我国物价指数CPI相关的几个因素建立初始多元线性回归模型，分析CPI的影响因素，之后对该模型进行各种统计检验，在模型检验中发现初始模型中有部分变量的系数不能通过检验，可能存在多重共线性的问题，最后采用逐步回归分析法来进行去除显著性不高的变量，并且建立新的模型，最终找出了影响CPI的关键要素是农业生产资料价格和人均GDP，通过最终确定的CPI与其影响因素之间的线性回归方程可以清晰地得到各个指标对CPI的影响大小，进而为我国控制CPI提供方向性的建议指导。

关键词多元线性回归 CPI影响因素逐步回归Multiple linear regression model and its applicationAbstract This article introduces the multiple linear regression model, and its process is divided into several aspects: model construction, model parameter estimation, model testing and model prediction. By establishing an initial multiple linear regression model on several factors related to China's price index CPI, analyzing the influencing factors of CPI, and then carrying out various statistical tests on the model, it is found in the model test that the coefficients of some variables in the initial model cannot pass Test, there may be a problem of multicollinearity, and finally use a stepwise regression analysis method to remove less significant variables, and establish a new model, and finally find out that the key factors affecting CPI are agricultural production materials prices and GDP per capita, Through the final linear regression equation between the CPI and its influencing factors, we can clearly get the impact of various indicators on the CPI, and then provide directional recommendations for the control of CPI in China.Key words Multiple linear regression CPI influencing factors stepwise regression目录引言 (1)1. 多元线性回归分析基本理论 (2)1.1 多元线性回归模型的一般形式 (2)1.2 多元线性回归模型的基本假设 (2)1.3 参数估计 (2)1.3.1 回归系数的估计 (2)1.3.2 样本方差的估计 (3)1.4 模型检验 (3)1.4.1 回归方程的显著性检验 (4)1.4.2 回归系数的显著性检验 (4)1.4.3 回归方程的拟合优度检验 (4)1.5 模型预测 (5)1.6 自变量的筛选方法 (5)2. 多元线性回归在CPI影响因素中的应用 (6)2.1 数据筛选 (6)2.1.1 指标选取 (6)2.1.2 数据收集 (6)2.2实证分析 (7)2.1.3 建立模型 (7)2.1.4 参数估计 (8)2.1.5 模型检验 (8)2.1.6 模型优化 (9)2.1.7 残差检验 (11)结论与建议 (13)参考文献 (14)致谢................................................................ 错误!未定义书签。

用SPSS做回归分析回归分析是一种统计方法，用于研究两个或多个变量之间的关系，并预测一个或多个因变量如何随着一个或多个自变量的变化而变化。

SPSS（统计软件包的统计产品与服务）是一种流行的统计分析软件，广泛应用于研究、教育和业务领域。

要进行回归分析，首先需要确定研究中的因变量和自变量。

因变量是被研究者感兴趣的目标变量，而自变量是可能影响因变量的变量。

例如，在研究投资回报率时，投资回报率可能是因变量，而投资额、行业类型和利率可能是自变量。

在SPSS中进行回归分析的步骤如下：1.打开SPSS软件，并导入数据：首先打开SPSS软件，然后点击“打开文件”按钮导入数据文件。

确保数据文件包含因变量和自变量的值。

2.选择回归分析方法：在SPSS中，有多种类型的回归分析可供选择。

最常见的是简单线性回归和多元回归。

简单线性回归适用于只有一个自变量的情况，而多元回归适用于有多个自变量的情况。

3.设置因变量和自变量：SPSS中的回归分析工具要求用户指定因变量和自变量。

选择适当的变量，并将其移动到正确的框中。

4.运行回归分析：点击“运行”按钮开始进行回归分析。

SPSS将计算适当的统计结果，包括回归方程、相关系数、误差项等。

这些结果可以帮助解释自变量如何影响因变量。

5.解释结果：在完成回归分析后，需要解释得到的统计结果。

回归方程表示因变量与自变量之间的关系。

相关系数表示自变量和因变量之间的相关性。

误差项表示回归方程无法解释的变异。

6.进行模型诊断：完成回归分析后，还应进行模型诊断。

模型诊断包括检查模型的假设、残差的正态性、残差的方差齐性等。

SPSS提供了多种图形和统计工具，可用于评估回归模型的质量。

回归分析是一种强大的统计分析方法，可用于解释变量之间的关系，并预测因变量的值。

SPSS作为一种广泛使用的统计软件，可用于执行回归分析，并提供了丰富的功能和工具，可帮助研究者更好地理解和解释数据。

通过了解回归分析的步骤和SPSS的基本操作，可以更好地利用这种方法来分析数据。

spss用多元线性回归分析GDP的结论通过建立多元线性回归模型对国内生产总值的影响因素作实证分析，以其拟合出较为优良的GDP模型：
根据奥肯定律我们认为，就业人数和GDP应当是相互促进的的增长的，但在文中模型它的增长反而会使GDP下降。

这主要是因为20世纪90年代以来，我国的经济迅速增长，但大多是靠投资和进出口带动，并没有真正的带动就业同步增长。

产业结构和人才结构不匹配，资本和技术密集程度提高，而且，人口的增长也抵消了很多就业岗位的增加，这就使得劳动力人数和GDP之间呈现出了负向的变化。

当然，GDP只是反应经济增长的一个指标，不能单纯的注重它在数量方面的增长，更要注重一个合理且优良的结构，比如这几年十分受到关注的绿色GDP 等。

要全面协调的经济发展才是不断提升综合国力和提高人民生活水平的正确方法。

SPSS多元线性回归结果分析输出下⾯三张表第⼀张R⽅是拟合优度对总回归⽅程进⾏F检验。

显著性是sig。

结果的统计学意义，是结果真实程度（能够代表总体）的⼀种估计⽅法。

专业上，p 值为结果可信程度的⼀个递减指标，p 值越⼤，我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。

p 值是将观察结果认为有效即具有总体代表性的犯错概率。

如 p=0.05 提⽰样本中变量关联有 5% 的可能是由于偶然性造成的。

即假设总体中任意变量间均⽆关联，我们重复类似实验，会发现约 20 个实验中有⼀个实验，我们所研究的变量关联将等于或强于我们的实验结果。

（这并不是说如变量间存在关联，我们可得到 5% 或 95% 次数的相同结果，当总体中的变量存在关联，重复研究和发现关联的可能性与设计的统计学效⼒有关。

）在许多研究领域，0.05 的 p 值通常被认为是可接受错误的边界⽔平。

F检验：对于多元线性回归模型，在对每个回归系数进⾏显著性检验之前，应该对回归模型的整体做显著性检验。

这就是F检验。

当检验被解释变量y t与⼀组解释变量x1, x2 , ... , x k -1是否存在回归关系时，给出的零假设与备择假设分别是H0：b1 = b2 = ... = b k-1 = 0 ,H1：b i, i = 1, ..., k -1不全为零。

⾸先要构造F统计量。

由（3.36）式知总平⽅和（SST）可分解为回归平⽅和（SSR）与残差平⽅和（SSE）两部分。

与这种分解相对应，相应⾃由度也可以被分解为两部分。

SST具有T - 1个⾃由度。

这是因为在T个变差 ( y t -), t = 1, ..., T，中存在⼀个约束条件，即 = 0。

由于回归函数中含有k个参数，⽽这k个参数受⼀个约束条件制约，所以SSR具有k -1个⾃由度。

因为SSE中含有T个残差，= y t -, t = 1, 2, ..., T，这些残差值被k个参数所约束，所以SSE具有T - k个⾃由度。

相关性分析spss2篇篇一：多元线性回归分析在SPSS中的应用一、前言多元线性回归是一种统计分析方法，它可以用来解决多个自变量与一个因变量之间的关系。

在实际应用中，多元线性回归分析被广泛用于预测和模拟。

本文主要介绍多元线性回归在SPSS中的应用。

二、数据导入在分析多元线性回归之前，需要先将数据导入SPSS软件。

SPSS软件支持多种数据文件格式，如Excel、CSV等。

下面以Excel数据格式为例进行说明。

打开SPSS软件，选择File -> Open -> Data，再选择Excel文件格式。

在弹出的窗口中选择数据所在的工作表和范围，然后点击OK。

三、模型建立在SPSS软件中，可以通过菜单栏选择Analyze -> Regression -> Linear来建立多元线性回归模型。

在Linear Regression窗口中，将Y变量和X变量分别添加到Dependent 和Independent栏中，并点击OK按钮。

如果需要进行对各个特征变量的系数进行统计学显著性检验，可以在Linear Regression窗口中点击Statistics按钮，然后勾选Model fit和Coefficients即可。

四、模型评估为了评估多元线性回归模型的拟合程度，可以使用R²（R Square）和调整后的R²（Adjusted R Square）这两个指标。

R²表示模型解释因变量变异程度的比例，值越接近1表示模型拟合程度越好；Adjusted R²则考虑了独立变量的数量，是更具有实际意义的指标。

在SPSS中，可以在Linear Regression窗口的Model Summary表格中查看R²和Adjusted R²指标的值。

五、模型预测在模型建立完成后，可以使用该模型进行预测。

在SPSS软件中，可以通过菜单栏选择Analyze -> Regression -> Predict来进行预测。

模型的预测能力评估
预测残差图
通过观察预测残差是否随机分布，判断模型是否具有预测能力。
预测值与实际值散点图
观察预测值与实际值之间的接近程度，越接近表示模型预测能力越 好。
预测置信区间
通过计算预测值的置信区间，判断模型预测的准确性。
CHAPTER 05
多元线性回归的实例分析
实例数据来源与处理
实例数据
02
自变量之间不存在多重 共线性，即它们是独立 的。
03
自变量与因变量之间的 误差项是独立的，且具 有零均值和同方差。
04
误差项与自变量之间无 相关性。
CHAPTER 02
SPSS软件介绍
SPSS软件的特点
01
02
03
04
界面友好
SPSS采用图形界面，操作简 单直观，用户可以轻松上手。
功能强大
SPSS提供了丰富的统计分析 方法，包括回归分析、方差分
本案例将使用某地区的房价数据作为 实例，数据来源于房地产市场调查。
数据处理
对数据进行清洗和整理，包括缺失值 处理、异常值处理、数据转换等，以 确保数据质量。
执行多元线性回归分析
变量选择
选择自变量（如房屋面积、房龄、卧室数量等）和因变量（房价），建立多元线 性回归模型。
模型拟合
使用SPSS软件进行多元线性回归分析，对模型进行拟合，并评估模型的拟合优度 。
互效应。
ቤተ መጻሕፍቲ ባይዱ
THANKS FOR WATCHING
感谢您的观看
特点
能够同时考虑多个影响因素，揭 示它们之间的关系，并给出预测 模型。
多元线性回归的应用场景
01
02
03
经济学

SPSS多元线性回归分析报告实例操作步骤步骤1：导入数据首先，打开SPSS软件，并导入准备进行多元线性回归分析的数据集。

在菜单栏中选择"File"，然后选择"Open"，在弹出的窗口中选择数据集的位置并点击"Open"按钮。

步骤2：选择变量在SPSS的数据视图中，选择需要用于分析的相关自变量和因变量。

选中的变量将会显示在变量视图中。

确保选择的变量是数值型的，因为多元线性回归只适用于数值型变量。

步骤3：进行多元线性回归分析在菜单栏中选择"Analyze"，然后选择"Regression"，再选择"Linear"。

这将打开多元线性回归的对话框。

将因变量移动到"Dependent"框中，将自变量移动到"Independent(s)"框中，并点击"OK"按钮。

步骤4：检查多元线性回归的假设在多元线性回归的结果中，需要检查多元线性回归的基本假设。

这些假设包括线性关系、多重共线性、正态分布、独立性和等方差性。

可以通过多元线性回归的结果来进行检查。

步骤5：解读多元线性回归结果多元线性回归的结果会显示在输出窗口的回归系数表中。

可以检查各个自变量的回归系数、标准误差、显著性水平和置信区间。

同时，还可以检查回归模型的显著性和解释力。

步骤6：完成多元线性回归分析报告根据多元线性回归的结果，可以编写一份完整的多元线性回归分析报告。

报告应包括简要介绍、研究问题、分析方法、回归模型的假设、回归结果的解释以及进一步分析的建议等。

下面是一个多元线性回归分析报告的示例：标题：多元线性回归分析报告介绍：本报告基于一份数据集，旨在探究x1、x2和x3对y的影响。

通过多元线性回归分析，我们可以确定各个自变量对因变量的贡献程度，并检验模型的显著性和准确性。

研究问题：本研究旨在探究x1、x2和x3对y的影响。

基于SPSS的数据分析及模型应用研究随着科技的不断进步和社会发展需求的不断变化，数据分析作为一项重要的技术在我国的各行各业都受到了广泛的关注和运用。

数据分析的目的在于通过收集数据、分类整理、统计分析，找出数据之间的关系，为决策提供依据。

而SPSS作为专门用于数据统计分析软件，被广泛应用于科学研究、市场调查、政府管理、金融分析等领域中。

本文旨在从两个层面展开探讨，一是对SPSS的功能和应用做一个简要介绍，二是基于SPSS的数据分析及模型应用做具体的案例研究。

一、SPSS功能和应用介绍1、SPSS的基本概念和功能SPSS（Statistical Package for Social Sciences）是针对社会科学领域而设计的一套数据分析软件。

其主要功能是实现数据的收集、分析、统计和展示等。

SPSS提供了一个友好的交互式界面，简单易学，能够帮助用户快速完成各种类型的研究设计和分析任务。

此外，SPSS还支持多种数据文件格式导入，可以将数据从更多的数据来源获得，如数据库、Excel、文本文件等。

2、SPSS的应用领域SPSS可以广泛应用于以下领域：（1）典型研究- SPSS支持各种数据类型，如整数、浮点数、日期和字符串等，能够快速、准确地完成各种计算和统计分析操作，包括描述性统计、推论统计、因子分析、聚类分析等。

（2）市场调查 - SPSS可以进行市场调查问卷调查数据分析，可以解决许多重要商业问题，如扩张与收缩、定价策略、产品定位、品牌知名度和广告效果等。

（3）社会学研究 - SPSS能够帮助社会科学家分析各类社会现象和变化，如就业率、婚姻率、失业率等，并且能够做出更加准确的预测和预测。

（4）金融分析 - SPSS可用于分析和预测金融市场中的风险和收益，如曲线回归、分类树、时间序列分析、迭代式训练方法和人工神经网络等。

（5）医学研究 - SPSS提供许多工具和技术，以支持医学研究，如卡方检验、托管、逐步线性回归、存活分析和病例控制研究等。

gi

ln(
p(y i) ) p(y J)

bi0
bi1x1
bi2 x2

bip xp
•而对于参考类别, 其模型中的所有系数均为0。
•最后，求得第i类的概率值：
p( yi )
exp( gi )
J
exp( gk )
k 1
•另：参数估计表(Parameter Estimates) 中的Exp(B) 表示某 因素(自变量) 内该类别是其相应参考类别具有某种倾向性的 倍数。
分析的一般步骤
• 变量的编码 • 哑变量的设置和引入(设置参照类) • 各个自变量的单因素分析 • 变量的筛选 • 交互作用的引入 • 建立多个模型 • 选择较优的模型 • 模型应用条件的评价 • 输出结果的解释
Logistic回归的分类
• 二项Logistic回归 (Binary Regression)
•
log it( p)

ln( p ) 1 p

b0
b1x1

bpxp
ez
eb0 b1x1 bp x p
p 1 e z 1 eb0 b1x1 bp x p
建立回归模型：
ln( p 1
p
)

b0

b1x
其中，p=p(y=1)
1 拥有住房 y=
0 其它情况
5
4.909
4
5.548
5
4.281
6
4.406
2
1.816
0
1.313
1
1.011
1
.537
0
.179
住房Y = 1

spss多元回归分析实验报告
本实验旨在探究以不同特征预测车辆燃油效率的SPSS多元回归分析。

为此，随机抽取了训练集和测试集数据集，其中训练集包括2000条记录，测试集包括301条记录。

该数据集中包括独立变量，包括：车辆排量（单位：升），车辆总重量（单位：公斤），气缸（单位：个），驱动方式（单位：RWD或FWD）和变速箱（单位：自动或手动）。

这些独立变量与响应变量（车辆燃油效率）形成了一个回归模型，并用SPSS分析软件进行多元回归计算。

结果显示，排量、总重量和气缸之间存在显著正相关，而驱动方式与变速箱对燃油效率无显著影响。

回归分析 R2为0.45,表明45%的燃油经济性是由车辆的排量、总重量和气缸决定的。

根据回归方程，可以计算出燃油效率的具体值。

从实验结果来看，回归模型能够有效地预测车辆燃油效率。

实验发现，排量，总重量和气缸对燃油效率影响最大，其中排量对燃油效率影响最大，总重量次之，气缸最小。

在改变车辆排量、总重量和气缸时，都可以影响车辆燃油效率。

虽然实验结果清晰，但也有改进的空间。

首先，研究蒙特卡罗技术可能会更好地提高模型效果。

其次，在实际应用中，还可以研究其他因素如车辆使用时间，路况等，对车辆燃油效率的影响，以及车辆燃油一般的效率等因素，最终优化车辆燃油效率。

总之，SPSS多元回归分析有助于我们更好地了解影响车辆燃油效率的因素，从而实现车辆燃油效率优化。

SPSS多元线性回归分析实例操作步骤SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学研究领域。

其中，多元线性回归分析是SPSS中常用的一种统计方法，用于探讨多个自变量与一个因变量之间的关系。

本文将演示SPSS中进行多元线性回归分析的操作步骤，帮助读者了解和掌握该方法。

一、数据准备在进行多元线性回归分析之前，首先需要准备好数据。

数据应包含一个或多个因变量和多个自变量，以及相应的观测值。

这些数据可以通过调查问卷、实验设计、观察等方式获得。

确保数据的准确性和完整性对于获得可靠的分析结果至关重要。

二、打开SPSS软件并导入数据1. 启动SPSS软件，点击菜单栏中的“文件（File）”选项；2. 在下拉菜单中选择“打开（Open）”选项；3. 导航到保存数据的文件位置，并选择要导入的数据文件；4. 确保所选的文件类型与数据文件的格式相匹配，点击“打开”按钮；5. 数据文件将被导入到SPSS软件中，显示在数据编辑器窗口中。

三、创建多元线性回归模型1. 点击菜单栏中的“分析（Analyse）”选项；2. 在下拉菜单中选择“回归（Regression）”选项；3. 在弹出的子菜单中选择“线性（Linear）”选项；4. 在“因变量”框中，选中要作为因变量的变量；5. 在“自变量”框中，选中要作为自变量的变量；6. 点击“添加（Add）”按钮，将自变量添加到回归模型中；7. 可以通过“移除（Remove）”按钮来删除已添加的自变量；8. 点击“确定（OK）”按钮，创建多元线性回归模型。

四、进行多元线性回归分析1. 多元线性回归模型创建完成后，SPSS将自动进行回归分析并生成结果；2. 回归结果将显示在“回归系数”、“模型总结”和“模型拟合优度”等不同的输出表中；3. “回归系数”表显示各个自变量的回归系数、标准误差、显著性水平等信息；4. “模型总结”表提供模型中方程的相关统计信息，包括R方值、F 统计量等；5. “模型拟合优度”表显示模型的拟合优度指标，如调整后R方、残差平方和等；6. 可以通过菜单栏中的“图形（Graphs）”选项，绘制回归模型的拟合曲线图、残差图等。

SPSS多元线性回归分析实例操作步骤在数据分析的领域中，多元线性回归分析是一种强大且常用的工具，它能够帮助我们理解多个自变量与一个因变量之间的线性关系。

下面，我们将通过一个具体的实例来详细介绍 SPSS 中多元线性回归分析的操作步骤。

假设我们正在研究一个人的体重与身高、年龄和每日运动量之间的关系。

首先，打开 SPSS 软件，并将我们收集到的数据输入或导入到软件中。

数据准备阶段是至关重要的。

确保每个变量的数据格式正确，没有缺失值或异常值。

如果存在缺失值，可以根据具体情况选择合适的处理方法，比如删除包含缺失值的样本，或者使用均值、中位数等进行填充。

对于异常值，需要仔细判断其是否为真实的数据错误，如果是，则需要进行修正或删除。

接下来，点击“分析”菜单，选择“回归”，然后再选择“线性”。

在弹出的“线性回归”对话框中，将我们的因变量（体重）选入“因变量”框中，将自变量（身高、年龄、每日运动量）选入“自变量”框中。

然后，我们可以在“方法”选项中选择合适的回归方法。

SPSS 提供了几种常见的方法，如“进入”“逐步”“向后”“向前”等。

“进入”方法会将所有自变量一次性纳入模型；“逐步”方法则会根据一定的准则，逐步选择对因变量有显著影响的自变量进入模型；“向后”和“向前”方法则是基于特定的规则，逐步剔除或纳入自变量。

在这个例子中，我们先选择“进入”方法，以便直观地看到所有自变量对因变量的影响。

接下来，点击“统计”按钮。

在弹出的“线性回归：统计”对话框中，我们通常会勾选“描述性”，以获取自变量和因变量的基本统计信息，如均值、标准差等；勾选“共线性诊断”，用于检查自变量之间是否存在严重的多重共线性问题；勾选“模型拟合度”，以评估回归模型的拟合效果。

然后，点击“绘制”按钮。

在“线性回归：图”对话框中，我们可以选择绘制一些有助于分析的图形，比如“正态概率图”，用于检验残差是否服从正态分布；“残差图”，用于观察残差的分布情况，判断模型是否满足线性回归的假设。