2019四川中考数学考前专题训练几何图形的相关计算(12道)

中考数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1．下列各图经过折叠后不能围成一个正方体的是（）A．B．C．D．【答案】C【分析】根据平面图形的折叠、正方体的展开图的特点即可得出答案．【详解】解：A．是正方体的展开图，经过折叠后能围成一个正方体，故A不符合题意；B．是正方体的展开图，经过折叠后能围成一个正方体，故B不符合题意；C．不是正方体的展开图，经过折叠后不能围成一个正方体，故C符合题意；D．是正方体的展开图，经过折叠后能围成一个正方体，故D不符合题意．故选：C．【点睛】本题主要考查了展开图折叠成几何体，属于基础题，要充分展开想象，注意培养自己的立体感．2．一副三角板按如图所示的方式摆放，则∠1补角的度数为（）A．45︒B．135︒C．75︒D．165︒【答案】D【分析】根据题意得出∠1=15°，再求∠1补角即可．∠=︒-︒=︒【详解】由图形可得1453015∠∠1补角的度数为18015165︒-︒=︒故选：D．【点睛】本题考查利用三角板求度数和补角的定义，熟记各个三角板的角的度数是解题的关键．3．用一个放大10倍的放大镜看一个10°的角，这个角是（）A ．100°B ．10°C ．110°D ．170° 【答案】B 【分析】根据放大镜看一个角只会改变边的长度，不会改变角本身的度数即可求解．【详解】解：用放大镜看一个角，不会改变角本身的度数，故选：B ．【点睛】本题考查角的大小比较，放大镜看到的角不会改变角本身的度数． 4．如果点C 在线段AB 所在直线上，则下列各式中AC AB =，AC CB =，2AB AC =，AC CB AB +=，能说明C 是线段AB 中点的有（ ）A ．1个B ．2个C ．3个D ．4个 【答案】A【分析】根据线段中点的定义，能判断AC=CB 的条件都能说明C 是线段AB 中点．【详解】根据分析得：若AC=AB ，则不能判断C 是线段AB 中点；若AC=CB ，则可判断C 是线段AB 中点；若AB=2AC ，则不能判断C 是线段AB 中点；若AC+CB=AB ，则不能判断C 是线段AB 中点；综上可得共有1个正确.故选A.【点睛】本题考查线段中点的定义，解题的关键是掌握线段中点的定义.5．如图，已知BD CF =，B F ∠=∠，//AC DE 下列结论不正确的是（ ）A ．FD BC =B ．EF CB =C ．//EF ABD ．AE ∠=∠【答案】B 【分析】根据全等三角形的判定和性质、平行线的判定和性质以及线段的和差进行判断即可得解．【详解】解：∠//AC DE∠ACB EDF ∠=∠∠BD CF =∠BD CD CF CD +=+∠BC DF =∠在ABC 和EFD △中B F BC FDACB EDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∠()ABC EFD ASA ≌∠A E ∠=∠故说法D 正确；∠B F ∠=∠∠//EF AB故说法C 正确；∠BD CF =∠BD CD CF CD +=+∠BC DF =故说A 正确，说法B 错误．故选：B【点睛】本题考查了全等三角形的判定和性质、平行线的判定和性质以及线段的和差，熟悉各知识点是解题的关键．6．如图，OC 平分AOD ∠，30DOC AOB ∠-∠=︒，有下列结论：∠30BOC ∠=︒；∠BOC ∠的度数无法确定；∠若20AOB ∠=︒，则100AOD ∠=︒；∠若60AOB ∠=︒，则A ，O ，D 三点在同一条直线上．其中，正确的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】根据角平分线定义得出DOC AOC ∠=∠，根据30DOC AOB ∠-∠=︒，即可求出30BOC ∠=︒，判断出∠正确，∠错误；根据30BOC ∠=︒，20AOB ∠=︒，求出50AOC AOB BOC ∠=∠+∠=︒，根据角平分线定义求出100AOD ∠=︒，即可判断∠正确；求出180AOD ∠=︒，即可判断∠正确．【详解】解：∠OC 平分AOD ∠，∠DOC AOC ∠=∠，∠30DOC AOB AOC AOB BOC ∠-∠=∠-∠=∠=︒，故∠正确，∠错误．由∠知，30BOC ∠=︒，∠50AOC AOB BOC ∠=∠+∠=︒，∠2100AOD AOC ∠=∠=︒，故∠正确．∠30BOC ∠=︒，60AOB ∠=︒，∠90AOC BOC AOB ∠=∠+∠=︒，∠2180AOD AOC ∠=∠=︒，∠A 、O 、D 三点在一条直线上，故∠正确．综上，正确的为∠∠∠，共3个，故C 正确．故选：C ．【点睛】本题主要考查了角平分线的定义，几何图形中角的计算，解题的关键是根据角平分线的定义和已知条件，求出30BOC ∠=︒．7．如图，120AOB ∠=︒，13AOC BOC ∠=∠，OM 平分BOC ∠，则AOM ∠的度数为（ ）A ．45︒B ．65︒C ．75︒D ．80︒故选C．【点睛】本题考查了角平分线定义，角的有关计算的应用，解此题的关键是求出∠AOC和∠COM的大小．8．如图，这是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的表面上，与汉字“爱”相对的面上的汉字是（）A．西B．电C．附D．中【答案】C【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“我”与“电”是相对面，“爱”与“附”是相对面，“西”与“中”是相对面．故选：C．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．9．如果A、B、C三点在同一直线上，线段AB=3cm，BC=2cm，那么A、C两点之间的距离为（）A．1cmB．5cmC．1cm或5cmD．无法确定【答案】C【详解】试题解析：由题意可知，C点分两种情况，∠C点在线段AB延长线上，如图1，AC=AB+BC=3+2=5cm；∠C点在线段AB上，如图2，AC=AB-BC=3-2=1cm．综合∠∠A、C两点之间的距离为1cm或5cm．故选C．【点睛】由题意可知，点C分两种情况，画出线段图，结合已知数据即可求出结论．本题考查了两点间的距离，解题的关键是根据题意画出线段图，找准线段间的关系．10．如图，AD平分∠BAC，点E在AB上，EF∥AC交AD于点G，若∠DGF＝40°，则∠BEF的度数为（）A．20°B．40°C．50°D．80°【答案】D【分析】由EF∥AC，∠DGF＝40°，得出∠DAC=∠DGF＝40°，∠BEF=∠BAC，又AD 平分∠BAC，则∠BEF=∠BAC=2∠DAC=80°．【详解】解：∠EF∥AC，∠DGF＝40°，∠∠DAC=∠DGF＝40°，∠BEF=∠BAC，∠AD平分∠BAC，∠∠BEF=∠BAC=2∠DAC=80°．故选：D．【点睛】本题主要考查平行线的性质以及角平分线的定义，熟练掌握平行线的性质以及角平分线的定义是解决本题的关键．11．若钟表分针走30分钟，则钟表的时针转（）A．5︒B．15︒C．30︒D．120︒【答案】B【分析】根据“整个钟面12小时，时针每小时转30︒”即可得．．将一副直角三角尺按如图所示的不同方式摆放，则图中与不一定．．．相等的是（ ）A ．B ．C ．D ．【答案】B 【分析】A 选项由图形即直角三角形的性质即可判断；B 选项由两角互余即可的判断；C 选项由对顶角相等即可判断；D 选项由同角的余角相等即可判断．【详解】A 选项中，90,45αβα∠+∠=︒∠=︒，45βα∴∠=∠=︒，故不符合题意；B 选项中，90αβ∠+∠=︒，则α∠与∠β不一定相等，故符合题意；C 选项中，,αβ∠∠是对顶角，αβ∴∠=∠，故不符合题意；D 选项如图，190,190αβ∠+∠=︒∠+∠=︒，αβ∴∠=∠，故不符合题意；故选：B ．【点睛】本题考查了对顶角相等，余角，同角的余角相等等知识点，熟练掌握这些知识是解题的关键．13．如下图的正方体，选项中哪一个图形是它的展开图（ ）A ．B ．C ．D ．【答案】A【分析】根据正方体相邻面及其表面展开图的特点解答即可．【详解】解：A 、展开图中，其三个相邻面上的线段位置，符合题意，B 、展开图中，其中有两个有线段的两个面相对，不符合题意；C 、展开图中，其中有两个面上的线段平行，不符合题意；D 、展开图中，其中有两个有线段的两个面相对，不符合题意，故选：A ．【点睛】本题考查正方体的展开图，弄清正方体展开图中哪些面相邻，哪些面相对是解答的关键．14．把立方体的六个面分别涂上六种不同的颜色，并画出朵数不等的花，各面上的颜色与花朵的朵数情况列表如下：现将上述大小相同，颜色、花朵分布完全样的四个立方体拼成一个水平放置的长方体，如图所示，那么长方体的下底面共有花朵数是（ ）A ．11B ．13C ．15D ．17 【答案】D【分析】由图中显示的规律，可分别求出，右边正方体的下边为白色，左边为绿色，后面为紫色，按此规律，可依次得出右二的立方体的下侧为绿色，右三的为黄色，左一的为紫色，即可求出下底面的花朵数．【详解】解：由题意可得，右一的立方体的下侧为白色，右二的立方体的下侧为绿色，右三的为黄色，左一的为紫色，那么长方体的下底面共有花数4＋6＋2＋5＝17朵．故长方体的下底面共有17朵花．故选D ．【点睛】本题考查生活中的立体图形与平面图形，同时考查了学生的空间思维能力．注意正方体的空间图形，从相对面入手，分析及解答问题．15．如图，在四边形ABCD 中，90A BCD ∠=∠=︒，BC DC =，CE AD ⊥，垂足为E ，若3AE CE ==．则四边形ABCD 的面积为（ ）A ．9B ．12C ．272D ．无法求出 【答案】A 【分析】过点C 作CF 垂直AB 的延长线于点F ，先证明四边形AFCE 是矩形，再证明FCB ECD △≌△，进而将四边形ABCD 的面积转化为矩形AFCE 的面积求解即可．【详解】解：如图，过点C 作CF 垂直AB 的延长线于点F ，∠90A BCD ∠=∠=︒， CE AD ⊥，CF AF ⊥，∠四边形AFCE 是矩形，90==︒CED F ∠∠，∠90FCE FCB BCE ∠=∠+∠=︒，3CF AE CE === ，∠90BCD BCE DCE ∠=∠+∠=︒，∠FCB ECD ∠=∠，在FCB 和ECD 中，CED F FCB ECD BC DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠FCB ECD △≌△，∠==339ABCD AFCE AE CE S S ⋅=⨯=四边形矩形，故选：A ．【点睛】本题主要考查了全等三角形的判定及性质、同角的余角相等，垂直定义以及矩形的判定及性质，熟练掌握全等三角形的判定及性质是解题的关键．16．如图，在ABC 中，以A 为圆心，适当长为半径作弧，分别交AB 、AC 于点D 、E ，再分别以D 、E 为圆心，相同长为半径作弧，分别交DB、EC 于点F 、G ，连接EF 、DG ，交于点H ，连接AH 并延长交BC 于点I ，则线段AI 是( )A ．ABC 的高B ．ABC 的中线 C ．ABC 的角平分线D ．以上都不对【答案】C 【分析】根据题意利用SAS 可证AFE AGD △≌△，即可得EG DF =，再利用AAS 可证EHG DHF ≌△△，即可得EH DH =，用SSS 可证明AHE AHD △≌△，即可得EAH DAH ∠=∠，即可得．【详解】解：由作图可知，AE AD =，EG DF =，∠AE EG AD DF +=+，即AG AF =，在AFE △和AGD △中，AE AD EAF DAG AF AG =⎧⎪∠=∠⎨⎪=⎩，∠AFE AGD △≌△（SAS ），∠AFE AGD ∠=∠，在EHG 和DHF △中，EHG DHF EGH DFH EG DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠EHG DHF ≌△△（AAS ），∠EH DH =在AHE 和AHD 中，AE AD AH AH EH DH =⎧⎪=⎨⎪=⎩，∠AHE AHD △≌△（SSS ），∠EAH DAH ∠=∠，∠AI 是ABC 的角平分线．故选：C ．【点睛】本题考查了全等三角形的判定与性质，角平分线的判定，解题的关键是掌握全等三角形的判定与性质．17．如图：∠AOB ：∠BOC ：∠COD ＝2：3：4，射线OM 、ON ，分别平分∠AOB 与∠COD ，又∠MON ＝84°，则∠AOB 为（ ）A ．28°B ．30°C ．32°D ．38°【答案】A 【分析】首先设∠AOB ＝2x °，则∠BOC ＝3x °，∠COD ＝4x °，然后利用角的和差关系和角平分线的定义列出方程，即可求出∠AOB 的度数．【详解】解：设∠AOB ＝2x °，则∠BOC ＝3x °，∠COD ＝4x °，∠射线OM 、ON 分别平分∠AOB 与∠COD ，18．如图，在ABCD 中，DAB ∠的平分线AE 交CD 于E ，6AB =，4BC =，则EC的长为（ ）A ．2B ．2.5C ．3D ．3.5【答案】A 【分析】根据平行四边形的性质及AE 为角平分线可知：BC=AD=DE=4，又有CD=AB=6，可求EC 的长．【详解】解：根据平行四边形的对边相等，得：CD=AB=6，AD=BC=4．根据平行四边形的对边平行，得：CD∠AB ，∠∠AED=∠BAE ，又∠DAE=∠BAE ，∠∠DAE=∠AED ．∠ED=AD=4，∠EC=CD-ED=6-4=2．故选：A ．【点睛】本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．19．如图，直线EO∠CD ，垂足为点O ，AB 平分∠EOD ，则∠BOD 的度数为（ ）A．120°B．130°C．135°D．140°【答案】C【详解】试题分析：根据直线EO∠CD，可知∠EOD=90°，根据AB平分∠EOD，可知∠AOD=45°，再根据邻补角的定义即可求出∠∠BOD=180°-45°=135°考点：垂线、角平分线的性质、邻补角定义．二、填空题20．已知：∠AOC=146°，OD为∠AOC的平分线，∠AOB=90°，∠BOD的度数_____．21．2022年10月16日，党的第二十次全国代表大会在北京召开，这是一次在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的十分重要的大会．如图是一个正方体的展开图，请你判断，正方体上与“荣”字相对的面上的汉字是_______．【答案】祖【分析】根据正方体展开图中相对的面总是隔着一个面的特征解题即可．【详解】解：根据正方体展开图中相对的面总是隔着一个面的特征可得荣字相对的面上的汉字为“祖”，故答案为：祖．【点睛】本题主要考查正方体展开图的特征，能够根据特征得出结论是解题关键．22．用一个平面截圆锥，可以得到________、________及类似拱形形状．如图：【答案】圆等腰三角形【解析】略23．如图，要用一张长方形的纸片折成一个纸袋，两条折痕的夹角为80°（即∠POQ＝80°），就可以做成一个纸袋，那么粘胶水部分所构成的这个角∠A'OB'＝_____．【答案】20°【分析】根据折叠性质得出∠POA=∠POA′，∠QOB=∠QOB′，根据∠AOB为平角，∠POA+∠QOB=180°-∠POQ=100°，再利用∠A′OB′=∠POA′+∠QOB′-∠POQ=20°即可．【详解】解：∠OP为折痕，OQ为折痕，∠∠POA=∠POA′，∠QOB=∠QOB′，∠∠AOB为平角∠∠POA+∠QOB=180°-∠POQ=100°，∠∠A′OB′=∠POA′+∠QOB′-∠POQ=∠POA+∠QOB-∠POQ=100°-80°=20°．故答案为：20°．【点睛】本题考查折叠性质，平角，角的和差，掌握折叠性质，平角，角的和差是解题关键．24．下午三点半时，时针与分针所夹的锐角的大小为________．【答案】75︒##75度【分析】先求出时钟上，每一个大格的度数为30︒，再根据下午三点半时，时针与分针所夹的锐角为2.5个大格即可得．︒÷=︒，【详解】解：时钟上，共有12个大格，每一个大格的度数为3601230因为下午三点半时，时针与分针所夹的锐角为2.5个大格，⨯︒=︒，所以下午三点半时，时针与分针所夹的锐角的大小为2.53075故答案为：75︒．【点睛】本题考查了钟面角，熟练掌握时钟上，每一个大格的度数为30︒是解题关键．25．点C是线段AB上的一点，2=，点M、N分别是线段AC、BC的中点，BC ACMN BC等于_________．那么:26．已知∠a=50°18′，则∠a的余角是________°________′.【答案】3942【分析】互余的概念：和为90度的两个角互为余角．用90°减去一个角的余角就等于这个角的度数．【详解】根据余角的定义，知∠A的余角是90°﹣50°18'=39°42'．故答案为39，42．【点睛】本题考查了余角和角度的计算，关键是记住互为余角的两个角的和为90度．27．在一个圆形时钟的表面，OA 表示秒针，OB 表示分针（O 为两针的旋转中心）若现在时间恰好是12点整，则经过__________秒钟后，∠OAB 的面积第一次达到最大． 【答案】151559##9005928．如图，直线AB 、CD 相交于点O ，OE 平分BOD ∠，COB ∠为100︒，则AOE ∠=___________度识是解题的关键．29．小王从家出发向南偏东30°的方向走了100米到达小军家，此时小王家在小军家的_________方向． 【答案】北偏西30︒【分析】根据方向角的定义作出示意图，根据图形即可解答．【详解】解：如图所示，由题意知∠BAC ＝30°，则在∠ABC 中，∠BAC ＋∠ACB ＝90°，∠∠ACB ＝60°．又∠∠ACB ＋∠ACD ＝90°，∠∠ACD ＝30°，即小王家在小军家北偏西30°方向．故答案是：北偏西30°．【点睛】本题考查了方向角的定义，理解定义作出示意图是关键．30．如图所示，已知ABC 的周长为12，5BC =，在边AC 、AB 上有两个动点P 、Q ，它们同时从点A 分别向点C 、B 运动，速度分别为m 和n ，运动时间t 后，PC CB BQ ++=__________．【答案】()12m n t -+【分析】根据PC AC AP BQ AB AQ =-=-，，可得PC BQ AC AB AP AQ +=+--，进一步得到PC CB BQ ++，依此即可求解．【详解】解：PC AC AP BQ AB AQ =-=-，，()1257PC BQ AC AB AP AQ mt nt m n t ∴+=+--=---=-+，()()7512PC CB BQ m n t m n t ∴++=-++=-+．故答案为：()12m n t -+．【点睛】本题考查了列代数式，线段的和差关系，整式的加减运算，关键是得到PC BQ +的表达式．31．已知∠α＝60°，则∠α的补角等于_______． 【答案】120°【分析】利用互为补角的两个角之和为180°，解题即可【详解】因为∠α＝60°，所以∠α的补角是180°-60°=120°故填120°32．将三角尺按右图所示的方式放置在一张长方形纸片上，90EGF ∠=︒，30FEG ∠=︒，1130∠=︒，则BFG ∠的度数为___________．【答案】110°【分析】由长方形AD 与BC 平行，求出∠EFB ，由直角三角形求∠EFG ，再求两角的和即可．【详解】∠AD ∠BC ，∠∠1+∠EFB =180゜∠∠1=130゜∠∠EFB =180゜-130゜=50゜，∠∠EGF =90°，∠FEG =30°，∠∠EFG =180°-∠EGF -∠FEG =60°∠∠BFG =∠EFB +∠EFG =50°+60゜=110゜．故答案为：110゜．【点睛】本题考查角的度数问题，关键抓住平行线，同旁内角互补，三角形两锐角互余．33．若船A 在灯塔B 的北偏东30°方向上，则灯塔B 在船A 的_________方向上．【答案】南偏西30°【分析】本题画出A 、B 的位置，即分别以A 、B 为为原点，分别画出A 、B 的正北、正南、正西、正东方向，标出A 与B 的关系即可求解.【详解】从图中可以看出，B 在A 的南偏西30°.故答案为南偏西30°.【点睛】本题考查一个物体相对于另一物体的位置，注意这类题中“北偏东30°”的含义，是从正北方向开始，向东方向偏，偏角为30°.34．18°33′25″×3=_________．【答案】55°40′15″【分析】将度分秒分别乘以3后进位化简即可.【详解】1833253549975'''︒'"⨯==55°40′15″，故答案为：55°40′15″.【点睛】此题考查角度的计算，根据乘法法则进行计算，计算后每个单位满60向前一单位进一.35．如图，将一副三角板()90CAB DAE ∠=∠=︒按如图放置，则下列结论：∠13∠=∠；∠如果230∠=︒，则有//AC DE ；∠如果230∠=︒，则有//BC AD ；∠如果230∠=︒，必有4C ∠=∠．其中正确的有________．（填序号）【答案】∠∠∠【分析】根据两种三角板的各角的度数，利用平行线的判定与性质结合已知条件对各个结论逐一验证，即可得出答案．【详解】解：∠∠∠CAB=∠EAD=90°，∠∠1=∠CAB-∠2，∠3=∠EAD-∠2，∠∠1=∠3．∠∠正确．∠∠∠2=30°，∠∠1=90°-30°=60°，∠∠E=60°，∠∠1=∠E，∠AC∠DE．∠∠正确．∠∠∠2=30°，∠∠3=90°-30°=60°，∠∠B=45°，∠BC不平行于A D．∠∠错误．∠由∠得AC∠DE．∠∠4=∠C．∠∠正确．故答案为：∠∠∠．【点睛】此题主要考查学生对平行线判定与性质、余角和补角的理解和掌握，解答此题时要明确两种三角板各角的度数．36．如图，OC是∠AOB的平分线，如果∠AOB=130°,∠BOD=24°48＇，那么∠COD=_____.【答案】40.2°【分析】由角平分线定义，求出∠BOC的度数，然后利用角的和差关系，即可得到答案.【详解】解：∠OC是∠AOB的平分线，∠AOB=130°，37．如图，,AC BD 在AB 的同侧，2,8,8AC BD AB ===，点M 为AB 的中点，若120CMD ∠=，则CD 的最大值是_____．【答案】14 【分析】如图，作点A 关于CM 的对称点A ′，点B 关于DM 的对称点B ′，证明△A ′MB ′为等边三角形，即可解决问题．【详解】解：如图，作点A 关于CM 的对称点'A ，点B 关于DM 的对称点B'． 120CMD ∠=，60AMC DMB ∴∠+∠=，∴''60CMA DMB ∠+∠=，''60A MB ∴∠=，''MA MB =，''A MB ∴∆为等边三角形''''14CD CA A B B D CA AM BD ≤++=++=，CD ∴的最大值为14，故答案为14．【点睛】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题38．如图，在四边形ABCD 中，DAB ∠的角平分线与ABC ∠的外角平分线相交于点P ，且240D C ∠+∠=°，则P ∠=______．【答案】30︒##30度39．如图，在边长为2的菱形ABCD 中，60ABC ∠=︒，将BCD △沿直线BD 平移得到B C D '''，连接AC '、AD '，则AC AD ''+的最小值为________．ABC∠=由对称性可得：三、解答题∠，40．按要求补全图形并证明．如图，150∠=︒，OC垂直OB，OD平分AOCAOB∠．OE平分BOC(1)利用三角板依题意补全图形(2)求DOE∠的度数75【分析】（190，根据150，得出60，根据∠∠，即可得出EOC BOC30AOC=，4575．）解：补全图形，如图所示：90，150，60，AOC ，30AOC ∠， 45， 75．【点睛】本题主要考查了角平分线的定义，垂线的定义，解题的关键是数形结合，熟练掌握角平分线的定义．41．已知,,,AE GF BC GF EF DC EF AB ∥∥∥∥，猜想A ∠与C ∠的关系如何？并说明理由．解：因为,AE GF BC GF ∥∥（已知）所以AE BC ∥（______）所以______180(______)A ∠+=︒；同理，______180C ∠+=︒；所以______（______）．【答案】平行于同一条直线的两直线平行；∠B ；两直线平行，同旁内角互补；∠A ＝∠C ；同角的补角相等或等式性质【分析】根据平行线的判定和性质以及同角的补角相等求解即可．【详解】解：因为AE GF ∥，BC GF ∥（已知）所以AE BC ∥（平行于同一条直线的两直线平行）；所以∠A＋∠B＝180°（两直线平行，同旁内角互补）；同理，∠C＋∠B＝180°；∠∠A＝∠C（同角的补角相等或等式的性质）．故答案为：平行于同一条直线的两直线平行；∠B；两直线平行，同旁内角互补；∠A ＝∠C；同角的补角相等或等式的性质．【点睛】本题主要考查了平行线的性质与判定，同角的补角相等，熟知平行线的性质与判定是解题的关键．42．如图，点B在线段AC上，点E在线段DF上，EC，AF，DB∠EC，下面写出了说明“∠C＝∠D”的过程．说明：∠∠A＝∠F（已知），∠DF∠．根据：∠∠DEC+∠C＝180°．根据：∠DB∠EC（已知），∠∠DEC+∠＝180°．根据：∠∠C＝∠D．根据：．【答案】AC；内错角相等，两直线平行；两直线平行，同旁内角互补；D；两直线平行，同旁内角互补；同角的补角相等．【分析】根据平行线的性质与判定进行求解即可．【详解】说明：∠∠A＝∠F（已知），∠DF∥AC．根据：内错角相等，两直线平行；∠∠DEC+∠C＝180°．根据：两直线平行，同旁内角互补；∠DB∥EC（已知），∠∠DEC+∠D＝180°．根据：两直线平行，同旁内角互补；∠∠C＝∠D．根据：同角的补角相等．故答案为：AC；内错角相等，两直线平行；两直线平行，同旁内角互补；D；两直线平行，同旁内角互补；同角的补角相等．【点睛】本题主要考查了平行线的性质与判定，同角的补角相等，解题的关键在于能够熟练掌握相关知识进行求解．43．如图，O为直线AB上一点，∠BOC=α．(1)若α=40°，OD平分∠AOC，∠DOE=90°，如图（a）所示，求∠AOE的度数；(2)若∠AOD=13∠AOC，∠DOE=60°，如图（b）所示，请用α表示∠AOE的度数；(3)若∠AOD=1n∠AOC，∠DOE=180n︒（n≥2，且n为正整数），如图（c）所示，请用α和n表示∠AOE的度数（直接写出结果）．44．如图，在△ABC中，AB∠BC，BE∠AC于E，AF平分∠BAC交BE于点F，DF∠BC．（1）试说明：BF＝DF；（2）延长AF交BC于点G，试说明：BG＝DF．【答案】（1）说明见解析；（2）说明见解析．【分析】（1）由角平分线的性质可得FE=FH，由“ASA”可证∠DEF∠∠BHF，可得BF=DF；（2）由等角的余角相等可得∠AFE=∠AGB=∠BFG，可得BF=BG=DF．【详解】解：（1）如图，延长DF交AB于H，延长AF交BC于G，∠AB∠BC，DF∠BC，∠DH∠AB，∠AF平分∠BAC，BE∠AC，DH∠AB，∠FE＝FH，又∠∠DFE＝∠BFH，∠DEF＝∠BHF＝90°，∠∠DEF∠∠BHF（ASA），∠BF＝DF；（2）∠AF平分∠BAC，∠∠EAF＝∠BAG，∠∠EAF+∠AFE＝90°，∠BAG+∠AGB＝90°，∠∠AFE＝∠AGB，∠∠BFG＝∠AGB，∠BF＝BG，∠BG＝DF．【点睛】本题考查了全等三角形的判定和性质，角平分线的性质，直角三角形的性质，灵活运用全等三角形的性质是本题的关键．45．如图，在Rt∠ABC中，∠ACB＝90°，∠A＝40°，∠ABC的外角∠CBD的平分线BE 交AC的延长线于点E．(1)求∠CBE的度数；(2)过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．(3)若把直线FD绕点F旋转，直线DF和直线BE相交于点M，当DF和三角形ABC的一边平行时，请直接写出∠FME的度数．【答案】(1)65°(2)25°(3)65°或115°．【分析】（1）根据三角形外角的性质得出∠CBD的度数，再根据角平分线定义即可求得∠CBE的度数；（2）先根据三角形外角的性质得出∠CEB的度数，再根据平行线的性质求出∠F的度数；（3）根据题意分别画出图形，再利用平行线的性质解决．（1）解：∠Rt∠ABC中，∠ACB＝90°，∠A＝40°，∠∠CBD=∠ACB+∠A=130°，∠BE是∠CBD的角平分线，46．已知a＝﹣（﹣2）2×3，b＝|﹣9|+7，c＝1115 53⎛⎫-⨯⎪⎝⎭．（1）求3[a﹣（b+c）]﹣2[b﹣（a﹣2c）]的值．（2）若A＝2212119272⎛⎫⎛⎫⎛⎫-÷-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭×（1﹣3）2，B＝|a|﹣b+c，试比较A和B的大小．（3）如图，已知点D是线段AC的中点，点B是线段DC上的一点，且CB：BD＝2：3，若AB＝ab12ccm，求BC的长．∠BC ＝2cm ．【点睛】本题主要考查了有理数的混合运算以及与线段的中点有关的计算，熟练掌握运算法则是解答本题的关键．47．如图1，已知直线EF 与直线AB 交于点E ，直线EF 与直线CD 交于点F ，EM 平分AEF ∠交直线CD 于点M ，且FEM FME ∠=∠，点G 是射线MD 上的一个动点(不与点M F 、重合)，EH 平分FEG ∠交直线CD 于点H ，过点H 作HN EM ∥交直线AB 于点N ，设EHN a ∠=，EGF β∠=．(1)求证：AB CD ∥；(2)当点G 在点F 的右侧时，∠依据题意在图1中补全图形;∠若70β=︒，则α=________°；(3)当点G 在运动过程中，α和β之间有怎样的数量关系？直接写出你的结论． AB CD ；根据题目要求画出图形即可；110︒=，再根据，再根据ME ）分两种情况进行讨论：当点G 在点F2248．如图，上面的图形分别是下面哪个立体图形展开的形状，请你把有对应关系的平面图形与立体图形连接起来．【答案】见解析．【分析】根据常见的各种立体几何图形的展开图的特征即可得答案．【详解】∠三个长方形和两个三角形如图摆放是三棱柱的展开图，一个扇形和一个圆是圆锥如图摆放的展开图，六个长方形如图摆放是长方体的展开图，一个长方形和两个圆如图摆放是圆柱的展开图，∠连接如图：【点睛】本题考查常见立体几何图形的展开图，熟记各立体几何图形的展开图是解题关键．49．如图，把一个棱长8厘米的正方体的六个面都涂上红色，再将它的棱四等分，然后从等分点把正方体锯开．(1)能得到多少个棱长为2厘米的小正方体？(2)三个面有红色的小正方体有多少个？(3)两个面有红色的小正方体有多少个？(4)一个面有红色的小正方体有多少个？(5)有没有各面都没有红色的小正方体？如果有，那么有多少个？【答案】(1)64个(2)8个(3)24个(4)24个(5)有，8个【分析】（1）棱长是8cm的立方体体积512cm3，棱长为2cm的小正方体体积为8cm3，由此能求出共得到多少个棱长为2cm的小正方体；（2）三面涂色的小正方体是位于棱长是8cm的立方体的顶点处的小正方体，由此能求出三面涂色的小正方体有多少个；（3）二面涂色的小正方体是位于棱长是8cm的立方体的各边上的正方体，由此能求出二面涂色的小正方体有多少个；（4）一个面有红色的小正方体位于棱长是8cm的立方体的表面上既不是顶点又不是各边上的正方体，由此能求出二面涂色的小正方体有多少个；（5）六个面均没涂色的小正方体为棱长是8cm的立方体中心的正方体，由此能求出六个面均没有涂色的小正方体有多少个．【详解】（1）棱长是8cm的立方体体积为：8×8×8=512（cm3），棱长为2cm的小正方体体积为8cm3，∠共得到512÷8=64个小正方体．（2）三面涂色的小正方体是位于棱长是8cm的立方体的顶点处的小正方体，∠立方体共有8个顶点，∠三面涂色的小正方体有8个，（3）二面涂色的小正方体是位于棱长是8cm的立方体的各边上的正方体，∠立方体共有12条边，每边有2个正方体，∠二面涂色的小正方体有24个，（4）一面涂色的小正方体在棱长是8cm的立方体的表面上既不是顶点又不是各边上的正方体，∠立方体共有6个面，每个面有4个正方体，∠一面涂色的小正方体有24个，（5）六个面均没涂色的小正方体为棱长是8cm的立方体中心的正方体，共有64-8-24-24=8个，【点睛】本题考查大正方体分割成小正方体的计算，是中档题，解题时要认真审题，要熟练掌握正方体的结构特征．。

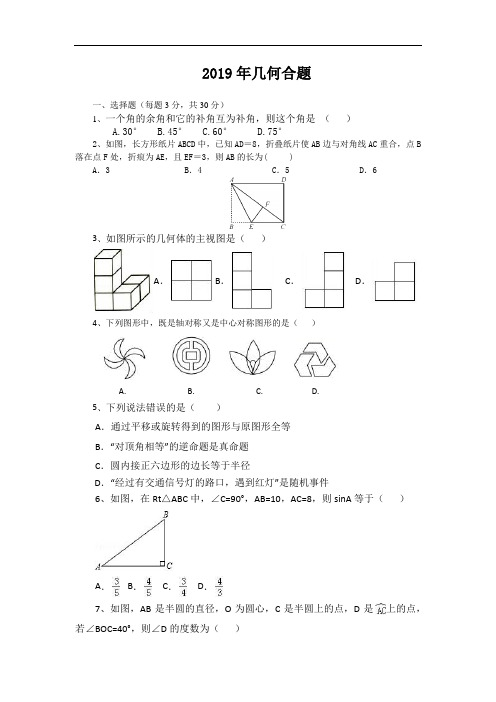
2019年几何合题一、选择题（每题3分，共30分）1、一个角的余角和它的补角互为补角，则这个角是（）A.30°B.45°C.60°D.75°2、如图，长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B 落在点F处，折痕为AE，且EF＝3，则AB的长为( )A．3 B．4 C．5 D．63、如图所示的几何体的主视图是（）A． B．C．D．4、下列图形中，既是轴对称又是中心对称图形的是（）A. B. C. D.5、下列说法错误的是（）A．通过平移或旋转得到的图形与原图形全等B．“对顶角相等”的逆命题是真命题C．圆内接正六边形的边长等于半径D．“经过有交通信号灯的路口，遇到红灯”是随机事件6、如图，在Rt△ABC中，∠C=90°，AB=10，AC=8，则sinA等于（）A．B．C．D．7、如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC=40°，则∠D的度数为（）A．100°B．110°C．120° D．130°8、如图，若△ABC内接于半径为R的⊙O，且∠A=60°，连接OB、OC，则边BC的长为（）A．B．C．D．9、如图，某海监船以20海里/小时的速度在某海域执行巡航任务，当海监船由西向东航行至A处时，测得岛屿P恰好在其正北方向，继续向东航行1小时到达B处，测得岛屿P在其北偏西30°方向，保持航向不变又航行2小时到达C 处，此时海监船与岛屿P之间的距离（即PC的长）为（）A．40海里B．60海里C．20海里D．40海里10、如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（）A．1 B．C． 1 D．二、填空题（每题4分，共24分）11、如图，直线a∥b，∠l=60°，∠2=40°，则∠3=．12、用半径为，圆心角为的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为________ ．13、如图，平行四边形ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为_______.14、如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为____。

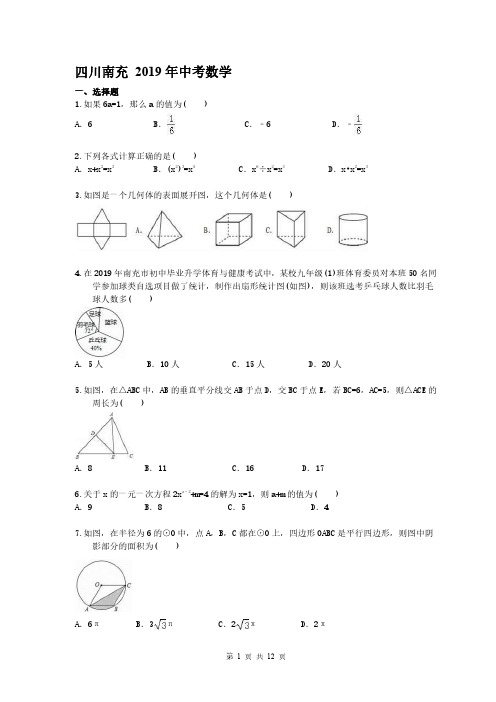
题库：几何图形操作变化型问题类型一 折叠问题★1. 将一个矩形纸片ABCD 放置到平面直角坐标系中，点A 、B 恰好落在x 轴的正、负半轴上，若将该纸片沿AF 折叠，点B 恰好落在y 轴上的点E 处，设OA ＝1.(1)如图①，若OB ＝1，则点F 的坐标为________； (2)如图②，若OB ＝2，求点F 的坐标； (3)若OB ＝n ，请直接写出点F 的坐标．第1题图解：(1)(1，233)【解法提示】由折叠的性质可知AE ＝AB ＝2, ∠EAF ＝∠BAF ，∵OA ＝1，AE ＝2，∠AOE ＝90°，∴∠AEO ＝30°，∴∠EAO ＝60°，∴∠F AB ＝30°，∴BF ＝AB ·tan ∠F AB ＝233，则点F 的坐标为(1，233)．(2)如解图，作FM ⊥y 轴于点M ， ∴∠AEF ＝∠ABF ＝90°，FM ⊥y 轴，∴∠AEO ＋∠FEM ＝90°，∠FEM ＋∠EFM ＝90°，∴∠AEO ＝∠EFM ， ∵sin ∠AEO ＝AO AE ＝13，第1题解图∴sin ∠EFM ＝13. 设EM ＝x ，则EF ＝3x ，由勾股定理得MF ＝22x ，OE ＝22， ∵OB ＝2， ∴22x ＝2， 解得x ＝22，∴OM ＝OE －EM ＝322， ∴点F 的坐标为(2，322)； (3)(n ，n 2＋nn 2＋2n)． 【解法提示】如解图，作FM ⊥y 轴于点M ， 同理∠AEO ＝∠EFM ，∵sin ∠AEO ＝AO AE ＝1n ＋1，∴sin ∠EFM ＝1n ＋1，设EM ＝x ，则EF ＝(n ＋1)x ， 由勾股定理得MF ＝n 2＋2n x ，OE ＝n 2＋2n ，∵OB ＝n ， ∴n 2＋2n x ＝n .解得x ＝n n 2＋2n，∴OM ＝OE －EM ＝n 2＋2n －nn 2＋2n＝n 2＋nn 2＋2n， ∴点F 的坐标为(n ，n 2＋nn 2＋2n)． ★2. 如图，将一个正方形纸片AOCD 放置在平面直角坐标系中，点A (0，4)，点O (0，0)，点D 在第一象限，点P 为正方形AD 边上的一点(不与点A 、点D 重合)，将正方形纸片折叠，使点O 落在点P 处，点C 落在点G 处，PG 交DC 于点H ，折痕为EF ，连接OP ，OH .设P 点的横坐标为m .(1)若∠APO ＝60°，求∠OPG 的大小；(2)当点P 在边AD 上移动时，△PDH 的周长l 是否发生变化？若变化，用含m 的式子表示l ；若不变化，求出周长l ；(3)设四边形EFGP 的面积为S ，当S 取得最小值时，求点P 的坐标(直接写出结果即可)．第2题图解：(1)∵折叠正方形纸片，使点O落在点P处，点C落在点G 处，∴∠POC＝∠OPG，∵四边形AOCD是正方形，∴AD∥OC，∴∠APO＝∠POC，∴∠APO＝∠OPG，∵∠APO＝60°，∴∠OPG＝60°；(2)△PDH的周长不发生变化，理由：如解图①，过点O作OQ⊥PG，垂足为点Q，则∠DAO ＝∠PQO＝90°.第2题解图①由(3)知∠APO＝∠OPG，又∵OP＝OP，∴△AOP≌△QOP，∴AP＝QP，AO＝QO，∵AO＝OC，∴OC＝OQ，∵∠OCD＝∠OQH＝90°，OH＝OH，∴Rt△OCH≌Rt△OQH，∴CH＝QH，∴△PDH的周长l＝PD＋DH＋PH＝PD＋DH＋PQ＋QH＝PD＋PQ＋DH＋QH＝PD＋AP＋DH＋CH＝AD＋CD＝8，∴△PDH的周长l不发生变化，周长l为定值8；(3)当S取得最小值时，点P的坐标为(2，4)．【解法提示】如解图②，过点F作FM⊥OA于点M，设EF与OP交于点N，第2题解图②由折叠的性质知△EON与△EPN关于直线EF对称，∴△EON≌△EPN，∴ON＝PN，EP＝EO，EN⊥PO，∵∠OAP＝∠ENO，∠AOP＝∠NOE，∴△POA∽△EON，∴PO EO ＝P AEN＝OAON①，设P A＝x，∵点A(0，4)，∴OA＝4，∴OP＝OA2＋P A2＝16＋x2，∴ON＝12OP＝1216＋x2，将OP，ON代入①式得，OE＝PE＝18(16＋x2)，∵∠EFM＋∠OEN＝90°，∠AOP＋∠OEN＝90°，∴∠EFM＝∠AOP，在△EFM和△POA中，⎩⎪⎨⎪⎧∠EFM ＝∠AOP FM ＝OA∠OAP ＝∠EMF ， ∴△EFM ≌△POA (ASA)， ∴EM ＝P A ＝x ，∴FG ＝CF ＝OM ＝OE －EM ＝ 18(16＋x 2)－x ＝18x 2－x ＋2，∴S ＝S 梯形EFGP ＝S 梯形OCFE ＝12(FC ＋OE )·OC ＝12；18x 2－x ＋2＋18(16＋x 2)]×4＝12(x －2)2＋6，∴当x ＝2时，S 最小， 即AP ＝2，∴点P 的坐标是(2，4)．★3. 已知：如图所示的一张矩形纸片ABCD (AD ＞AB )，将纸片折叠一次，使点A 与点C 重合，再展开，折痕EF 交AD 边于点E ，交BC 边于点F ，分别连接AF 和CE .(1)求证：四边形AFCE 是菱形；(2)若AE ＝10cm ，△ABF 的面积为24cm 2，求△ABF 的周长； (3)在线段AC 上是否存在一点P ，使得2AE 2＝AC ·AP ？若存在，请说明点P 的位置，并予以证明；若不存在，请说明理由．第3题图(1)证明：由题意可知OA＝OC，EF⊥AO，∵AD∥BC，∴∠AEO＝∠CFO，∠EAO＝∠FCO，∴△AOE≌△COF(AAS)，∴AE＝CF，又∵AE∥CF，∴四边形AECF是平行四边形，由图形折叠的性质可知，AC⊥EF，∴四边形AECF是菱形；(2)解：∵四边形AECF是菱形，∴AF＝AE＝10cm，设AB＝a，BF＝b，∵△ABF的面积为24cm2，∴a2＋b2＝100，ab＝48，∴(a＋b)2＝196，∴a＋b＝14或a＋b＝﹣14(不合题意，舍去)，∴△ABF的周长为14＋10＝24cm；(3)解：存在，如解图，过点E作BC的垂线，交AC于点P，点P就是符合条件的点；证明：∵∠AEP＝∠AOE＝90°，∠EAO＝∠EAO，∴△AOE∽△AEP，∴AE AP ＝AO AE，∴AE2＝AO·AP，∵四边形AECF是菱形，∴AO＝12AC，∴AE2＝12AC·AP，∴2AE2＝AC·AP.第3题解图★4. 如图①，已知△ABC中，∠C＝90°，AC＝6，BC＝8，点E，F分别在AC，BC上，将△ABC沿EF折叠，点C落在点D处，设△EDF 与四边形ABFE重叠部分面积为y，CF长为x.第4题图(1)如图②，当EF ∥AB ，CF ＝4时，试求y 的值；(2)当EF ∥AB 时，试求y 与x 的函数关系式，并求x 为何值时y 的值最大；(3)如图③，当CF ＝4，DF ⊥BC 时，求y 的值． 解：(1)如解图①，连接CD ，交EF 于点H第4题解图①∵CF ＝4，BC ＝8，∴BF ＝4，CD ＝AC ×BCAB ＝4.8， ∵EF ∥AB ，∴EF ＝12AB ＝5，CH ＝DH ＝12CD ＝2.4， ∴y ＝12×EF ×DH ＝12×5×2.4＝6；(2)①当0＜x ≤4时，如解图②，作CM ⊥AB 交AB 于点M ，则CM 必过点D ，第4题解图②由(1)知CM ＝4.8， ∵EF ∥AB ，∴CN CM ＝CF BC ＝EF AB ，即CN 4.8＝x 8＝EF 10，∴CN ＝0.6x ，EF ＝54x ，∴y ＝S △DEF ＝S △CEF ＝12×EF ×CN ＝12×54x ×0.6x ＝38x 2，∴当x ＝4时，y max ＝38×42＝6；②当4＜x ≤8时，如解图③，第4题解图③过点C 作CM ⊥AB 交AB 于点M ，过点F 作FN ⊥AB 交AB 于点N ，连接ED ，FD ，分别交AB 于点G ，I ，∴BF BC ＝FN CM ，∵CF ＝x ，∴BF ＝8－x ，由(1)有，CM ＝4.8，∴8－x 8＝FN 4.8，∴FN ＝0.6(8－x )，∵DH ＝CH ＝CM －HM ＝CM －FN ＝4.8－0.6(8－x )＝0.6x ， DM ＝DH －MH ＝DH －FN ＝0.6x －0.6(8－x )＝1.2x －4.8， ∵EF ∥AB ，∴EF AB ＝CH CM ，即EF 10＝0.6x 4.8∴EF ＝54x ，∵EF ∥AB ，∴DM DH ＝GI EF ，∴1.2x －4.80.6x ＝GI 54x，∴GI ＝52(x －4)，∴y ＝12(GI ＋EF )×FN ＝12×；52(x －4)＋54x ]×0.6(8－x )＝－98(x －163)2＋8，∴当x ＝163时，y max ＝645.(3)如解图④，在CB 上取一点H 使CH ＝DM ，作∠CHG ＝∠DMN ，第4题解图④在Rt △ABC 中，AC ＝6，BC ＝8，∴tan ∠B ＝AC BC ＝68＝34，在△BFM 中，DF ⊥BC ，BF ＝BC －CF ＝4，∠B ＋∠BMF ＝90°，∴tan ∠B ＝FM BF ＝FM 4＝34，∴FM ＝3，∴CH ＝DM ＝1，∵∠CHG ＝∠DMN ，∠BMF ＝∠DMN ，∴∠CHG ＝∠BMF ，∵∠B ＋∠BMF ＝90°，∵∠B ＋∠CHG ＝90°，∠CHG ＋∠CGH ＝90°，∴∠B ＝∠CGH ，在Rt △HCG 中，tan ∠CGH ＝CH CG ＝tan ∠B ＝34，∴CG ＝43×CH ＝43，∵∠BFD ＝90°，由折叠有∠CFE ＝∠DFE ＝45°，∴CE ＝CF ，∴y ＝S 四边形EFMN ＝S △DEF －S △DMN ＝S △CEF －S △CHG ＝12CE ×CF －12×CH ×CG ＝12×4×4－12×1×43＝223.★5. 将边长为8cm 的正方形纸片ABCD 沿EG 折叠(折痕EG 分别与AB 、DC 交于点E 、G )，使点B 落在AD 边上的点F 处，FN 与DC 交于点M ，连接BF 与EG 交于点P .第5题图(1)当点F与AD的中点重合时(如图①)；①△AEF的边AE＝________cm，EF＝________cm，线段EG与BF的大小关系是EG________BF；(填“>”、“＝”或“<”)②求△FDM的周长．(2)当点F在AD边上除点A，D外的任意位置时(如图②)；①试问第(1)题中线段EG与BF的大小关系是否发生变化？请证明你的结论；②当点P在何位置时，四边形AEGD的面积S最大？最大值是多少？解：(1)①AE＝3cm，EF＝5cm；EG＝BF，设AE＝x，则EF＝8－x，AF＝4，∠A＝90°，42＋x2＝(8－x)2，解得x＝3.∴AE＝3cm，EF＝5cm，EG＝BF；②如解图①，∵∠MFE＝90°，∴∠DFM＋∠AFE＝90°，又∵∠A＝∠D＝90°，∠AFE＝∠DMF，∴△AEF∽△DFM，∴EF FM ＝AE DF ＝AF DM ，又∵AE ＝3，AF ＝DF ＝4，EF ＝5，∴5FM ＝34，解得FM ＝203，34＝4DM ，解得DM ＝163，∴△FMD 的周长＝4＋203＋163＝16；第5题解图(2)①FG ＝BF 不会发生变化，证明：如解图②，∵B 、F 关于GE 对称，∴BF ⊥EG 于点P ，过G 作GK ⊥AB 于点K ，∴∠FBE ＝∠KGE ，在正方形ABCD 中，GK ＝BC ＝AB ，∠A ＝∠EKG ＝90°， ∴△AFB ≌△KEG (AAS)，∴EG ＝BF ；②如解图②，设AF ＝x ，EF ＝8－AE ，则x 2＋AE 2＝(8－AE )2， ∵△AFB ≌△KEG ，∴AF ＝EK ＝x ，AK ＝AE ＋EK ＝AF ＋AE ＝4－116x 2＋x ，S ＝AE ＋DG 2×8＝12×8(AE ＋AK )＝4×(4－116x 2＋4－116x 2＋x )＝－12x 2＋4x ＋32，S ＝－12(x －4)2＋40，(0<x <8)当x ＝4，即F 与AD 的中点重合时，S 最大＝40.类型二 旋转问题★1. 在Rt △ABC 中，AB ＝BC ＝5，∠B ＝90°，将一块等腰直角三角板的直角顶点放在斜边AC 的中点O 处，三角板的两直角边分别交AB 、BC 的延长线于E 、F 两点，如图①.(1)求证：△EOB ≌△FOC ；(2)将等腰直角三角板绕直角顶点O 顺时针旋转，三角板的两直角边分别交AB 、BC 于E 、F 两点，如图②，则△OFC 能否成为等腰直角三角形？若能，直接写出△OFC 是等腰直角三角形时BF 的长；若不能，请说明理由；(3)若将三角板的直角顶点移动到点P 处，两直角边分别交AB 、BC 于E 、F 两点，如图③，若PE PF ＝13，请求出P A 的长．第1题图(1)证明：由题知，△ABC 和△OEF 均为等腰直角三角形，O 为AC 中点，∴∠BOC ＝∠EOF ＝90°，OB ＝OC ，OE ＝OF ，∵∠EOB ＋∠COE ＝90°，∠FOC ＋∠COE ＝90°，∴∠EOB ＝∠FOC .在△EOB 和△FOC 中，⎩⎪⎨⎪⎧OB ＝OC ∠EOB ＝∠FOC OE ＝OF，∴△EOB ≌△FOC (SAS)；(2)解：△OFC 能成为等腰直角三角形，此时BF ＝52或0；【解法提示】∵△ABC 为等腰直角三角形，∴∠ACB ＝45°.①当OF ＝CF ，∠OFC ＝90°，时∵∠ABC ＝90°，∴OF ∥AB ，又∵O 为AC 的中点，∴OF 为△ABC 的中位线，∴F 为BC 的中点，∴△OFC 是等腰直角三角形，∵AB ＝BC ＝5，∴BF ＝52；②当OF ＝OC 时，点F 与点B 重合，此时△OFC 为等腰直角三角形，∴BF ＝0.(3)解：如解图，过点P 作PM ⊥AB ，垂足为M ，作PN ⊥BC ，垂足为N ，∵∠EPM ＋∠EPN ＝∠EPN ＋∠FPN ＝90°，∴∠EPM ＝∠FPN ，又∵∠EMP ＝∠FNP ＝90°，∴△PME ∽△PNF ，∴PM PN ＝PE PF ，∵△ABC 为等腰直角三角形，∴△APM 和△PCN 均为等腰直角三角形，∴△APM ∽△PCN ，∴AM PN ＝AP PC ，第4题解图∵AM ＝PM ，∴PM PN ＝AP PC ，∴P A PC ＝PE PF ，∵PE PF ＝1 3，∴P A PC ＝1 3，∴P A＝14AC，∵AB＝BC＝5，∴AC＝52，∴P A＝14AC＝52 4.★2. 已知Rt△ABC中，∠ACB＝90°，CA＝CB，有一个圆心角为45°，半径长等于CA的扇形CEF绕点C旋转，直线CE、CF分别与直线AB交于点M、N.(1)当扇形CEF绕点C在∠ACB的内部旋转时，如图①，求证：MN2＝AM2＋BN2；思路点拨：考虑MN2＝AM2＋BN2符合勾股定理的形式，需转化为在直角三角形中解决．可将△ACM沿直线CE对折，得△DCM，连DN，只需证DN＝BN，∠MDN＝90°就可以了．请你完成证明过程；(2)当扇形CEF绕点C旋转至图②的位置时，关系式MN2＝AM2＋BN2是否仍然成立？若成立，请证明；若不成立，请说明理由．第2题图(1)证明：将△ACM沿直线CE对折，得△DCM，连接DN，如解图①，第2题解图①则△DCM≌△ACM.有CD＝CA，DM＝AM，∠DCM＝∠ACM，∠CDM＝∠A.∵CA＝CB，∴CD＝CB，∵∠DCN＝∠ECF－∠DCM＝45°－∠ACM，∠BCN＝∠ACB－∠ECF－∠ACM＝90°－45°－∠ACM＝45°－∠ACM，∴∠DCN＝∠BCN.又∵CN＝CN，∴△CDN≌△CBN.∴DN＝BN，∠CDN＝∠B.∴∠MDN＝∠CDM＋∠CDN＝∠A＋∠B＝90°.∴在Rt△MDN中，由勾股定理，得MN2＝DM2＋DN2，即MN2＝AM2＋BN2；(2)关系式MN2＝AM2＋BN2仍然成立．证明：将△ACM沿直线CE对折，得△GCM，连接GN，如解图②，第2题解图②则△GCM≌△ACM.∴CG＝CA，GM＝AM，∠GCM＝∠ACM，∠CGM＝∠CAM.∵CA＝CB，∴CG＝CB.∵∠GCN＝∠GCM＋∠ECF＝∠GCM＋45°，∠BCN＝∠ACB－∠ACN＝90°－(∠ECF－∠ACM)＝45°＋∠ACM，∴∠GCN＝∠BCN.又∵CN＝CN，∴△CGN≌△CBN.∴GN＝BN，∠CGN＝∠B＝45°，∠CGM＝∠CAM＝180°－∠CAB ＝135°，∴∠MGN ＝∠CGM －∠CGN ＝135°－45°＝90°.∴在Rt △MGN 中，由勾股定理，得MN 2＝GM 2＋GN 2，即MN 2＝AM 2＋BN 2.★3. 如图，在△ABC 中，AB ＝BC ＝10，tan ∠ABC ＝43，点P 是边BC 上的一点，M 是线段AP 上一点，线段PM 绕点P 顺时针旋转90°得线段PN ，设BP ＝t .(1)如图①，当点P 在点B ，点M 是AP 中点时，试求AN 的长；(2)如图②，当PM MA ＝13时，①求点N 到BC 边的距离(用含t 的代数式表示)；②当点P 从点B 运动至点C 时，试求点N 运动路径的长．第3题图解：(1)∵在Rt △ABN 中，∠ABN ＝90°，AB ＝10，∴BN ＝BM ＝12AB ＝5，∴AN ＝102＋52＝55；(2)①(Ⅰ)当0≤t ≤6时(如图①)，第3题解图①如解图：过点A 作AE ⊥BC 于点E ，过点N 作NF ⊥BC 于点F ，∵tan ∠ABC ＝AE BE ＝43，设AE ＝4x ，则BE ＝3x ，在Rt △ABE 中，∠AEB ＝90°，∴AB 2＝AE 2＋BE 2，102＝(3x )2＋(4x )2，解得：x ＝2，∴AE ＝8，BE ＝6当0 ≤t ≤6时．∵∠AEP ＝∠PFN ＝90°，∠APE ＋∠FPN ＝90°，∠APF ＋∠P AE ＝90°，∴∠P AE ＝∠FPN ，∴△APE ∽△PNF ，∵PM MA ＝13，∴PF AE ＝FN PE ＝PN AP ＝14，∴FN ＝14(6－t )＝32－14t ；(Ⅱ)当6≤t ≤10时，同理可得：FN ＝14(t －6)＝14t －32；②如图2点N 的运动路径是一条线段，第4题解图②当P 与O 重合时，FN ＝32，PF ＝2，当P 与C 重合时，F ′N ′＝1，CF ′＝2，∴点N 的路径长NN ′＝102＋（1＋32）2＝51720. ★4. 已知△ABC 是边长为4的等边三角形，边AB 在射线OM 上，且OA ＝6，点D 是射线OM 上的动点，当点D 不与点A 重合时，将△ACD 绕点C 逆时针方向旋转60°得到△BCE ，连接DE .(1)如图①，猜想：△CDE 的形状是____三角形．(2)设OD ＝m .①当6<m <10时，△BDE 周长是否存在最小值？若存在，求出△BDE 周长的最小值；若不存在，请说明理由．②是否存在m 的值，使△DEB 是直角三角形，若存在，请直接写出m 的值；若不存在，请说明理由．第4题图解：(1)等边；[解法提示]：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；(2)①存在，当6<m<10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE＋DB＋DE＝AB＋DE＝4＋DE，由(1)知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD＋4，由点到直线垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝23，∴△BDE的最小周长＝CD＋4＝23＋4；②存在，当m＝2或14时，以O、E、B为顶点的三角形是直角三解形，；【解法提示】：Ⅰ∵当点D与点B重合时，D、B、E不能构成三角形，∴当点D与点B重合时，不符合题意，Ⅱ当0≤m<6时，由旋转可知∠CBE＝120°，∴∠ABE＝60°，∠BDE<60°，∴若∠BED＝90°，由(1)可知，△CDE是等边三角形，∴∠DEC＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA－DA＝6－4＝2，∴m＝2；Ⅲ当6<m<10时，由∠DBE＝120°>90°∴此时不存在；Ⅳ当m>10时，由旋转性质可知∠CBE＝60°，∴∠DBE＝60°，又由(1)知∠CDE＝60°，∴∠BDE＝∠CDE＋∠BDC＝60°＋∠BDC，∵∠BDC>0°，∴∠BDE>60°，∴若∠BDE＝90°，∴∠BCD＝∠BDC＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．★5. 如图①，在▱ABCD中，AB＝10cm，BC＝4cm，∠BCD＝120°，CE平分∠BCD交AB于点E.点P从A点出发，沿AB方向以1cm/s的速度运动，连接CP，将△PCE绕点C逆时针旋转60°，使CE与CB重合，得到△QCB，连接PQ.(1)求证：△PCQ是等边三角形；(2)如图②，当点P在线段EB上运动时，△PBQ的周长是否存在最小值？若存在，求出△PBQ周长的最小值；若不存在，请说明理由；(3)如图③，当点P在射线AM上运动时，是否存在以点P、B、Q为顶点的直角三角形？若存在，求出此时t的值；若不存在，请说明理由．第5题图∴CP＝CQ∵∠PCQ＝60°，∴△PCQ为等边三角形；(2)解：存在．∵CE平分∠BCD，∴∠BCE＝60°，∵在▱ABCD中，∴AB∥CD，∴∠ABC＝180°－120°＝60°，∴△BCE为等边三角形，∴BE＝CB＝4，∵△PCE旋转得到△QCB，∴△PCE≌△QCB，∴EP＝BQ，∴C△PBQ＝PB＋BQ＋PQ＝PB＋EP＋PQ＝BE＋PQ＝4＋CP.∵CP⊥AB时，△PBQ周长最小，当CP⊥AB时，CP＝BC sin60°＝23，∴△PBQ周长最小为4＋23；(3)存在①当点B与点P重合时，P，B，Q不能构成三角形．②当0≤t＜6时，由旋转可知，∠CPE＝∠CQB，∠CPQ＝∠CPB＋∠BPQ＝60°，则：∠BPQ＋∠CQB＝60°，又∵∠QPB＋∠PQC＋∠CQB＋∠PBQ＝180°，∴∠PQC＝180°－60°－60°＝60°，∴∠QBP＝60°，∠BPQ＜60°，∴∠PQB可能为直角，若∠PQB＝90°，由(1)知，△PCQ为等边三角形，∴∠PBQ＝60°，∠CQB＝30°，∵∠CQB＝∠CPB，∴∠CPB＝30°，∵∠CEB＝60°，∴∠PCE＝∠CPB＝30°，∴PE＝CE＝4，∴AP＝AB－BE－EP＝10－4－4＝2，∴t＝2÷1＝2s③当6＜t＜10时，由∠PBQ＝120°＞90°，所以不存在；④当t＞10时，由旋转得：∠PBQ＝60°，由(1)得∠CPQ＝60°，∴∠BPQ＝∠CPQ＋∠BPC＝60°＋∠BPC，∵∠BPC＞0°，∴∠BPQ＞60°，若∠BPQ＝90°，∴∠BPC＝30°，∵∠CBE＝60°，∴∠BPC＝∠BCP，∴BP＝BC＝4，∴AP＝14cm∴t＝14s，综上所述：t为2s或者14s时，以点P、B、Q为顶点的三角形为直角三角形．。

专题08投影、视图与几何变换投影与视图部分一、选择题1．（2019四川巴中）如图是由一些小立方体与圆锥组合成的立体图形，它的主视图是（）A．B．C．D．【答案】C．【解析】解：如图所示，它的主视图是：．故选：C．2．（2019四川遂宁）如图为正方体的一种平面展开图，各面都标有数字，则数字为﹣2的面与其对面上的数字之积是（）A．﹣12B．0C．﹣8D．﹣10【答案】A．【解析】解：数字为﹣2的面的对面上的数字是6，其积为﹣2×6＝﹣12．故选：A．3．（2019四川成都）如图所示的几何体是由6个大小相同的小立方块搭成，它的左视图是（）A．B．C．D．【答案】B．【解析】解：从左面看易得第一层有2个正方形，第二层左边有1个正方形，如图所示：故选：B．4．（2019四川达州）如图是由7个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，这个几何体的左视图是（）A．B．C．D．【答案】B．【解析】解：从左面看可得到从左到右分别是3，1个正方形．故选：B．5．（2019四川眉山）如图是由6个完全相同的小正方体组成的立体图形，它的左视图是（）A．B．C．D．【答案】D ．【解析】解：左视图有2层3列，第一层有3个正方形，第二层有一个正方形；每列上正方形的分布从左到右分别是2，1，1个．故选：D ．6.（2019四川绵阳）下列几何体中，主视图是三角形的是（）A. B. C. D.【答案】C.【解析】A 、正方体的主视图是正方形，故此选项错误；B 、圆柱的主视图是长方形，故此选项错误；C 、圆锥的主视图是三角形，故此选项正确；D 、六棱柱的主视图是长方形，中间还有两条竖线，故此选项错误；故选：C ．7．（2019四川广安）如图所示的几何体是由一个圆锥和一个长方体组成的，则它的俯视图是（）A ．B ．C ．D ．【答案】A ．【解析】解：该组合体的俯视图为故选：A ．8．（2019四川南充）如图是一个几何体的表面展开图，这个几何体是（）A．B．C．D．【答案】C．【解析】解：由平面图形的折叠及三棱柱的展开图的特征可知，这个几何体是三棱柱．故选：C．9．（2019四川自贡）如图是一个水平放置的全封闭物体，则它的俯视图是（）A．B．C．D．【答案】根据俯视图是从物体上面看，从而得到出物体的形状．【解析】解：从上面观察可得到：．故选：C．几何变换部分一、选择题1．（2019四川达州）剪纸是我国传统的民间艺术，下列剪纸作品中，轴对称图形是（）A．B．C．D．【答案】D．【解析】解：A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；C、不是轴对称图形，故此选项不合题意；D、是轴对称图形，故此选项符合题意；故选：D．2.（2019四川乐山）下列四个图形中，可以由图通过平移得到的是A B C D图1【答案】D【解析】平移前后的图像的大小、形状、方向是不变的，故选D.3．（2019四川凉山州）如图，在△AOC中，OA＝3cm，OC＝1cm，将△AOC绕点O顺时针旋转90°后得到△BOD，则AC边在旋转过程中所扫过的图形的面积为（）cm2．A．B．2πC．πD．π【答案】B．【解析】解：∵△AOC≌△BOD，∴阴影部分的面积＝扇形OAB的面积﹣扇形OCD的面积＝＝2π，故选：B．二、填空题4．（2019四川眉山）如图，在Rt△ABC中，∠B＝90°，AB＝5，BC＝12，将△ABC绕点A逆时针旋转得到△ADE，使得点D落在AC上，则tan∠ECD的值为．【答案】．【解析】解：在Rt△ABC中，由勾股定理可得AC＝13．根据旋转性质可得AE＝13，AD＝5，DE＝12，∴CD＝8．在Rt△CED中，tan∠ECD＝．故答案为．5．（2019四川资阳）如图，在△ABC中，已知AC＝3，BC＝4，点D为边AB的中点，连结CD，过点A作AE⊥CD于点E，将△ACE沿直线AC翻折到△ACE′的位置．若CE′∥AB，则CE′＝．【答案】．【解析】解：如图，作CH⊥AB于H．由翻折可知：∠AE′C＝∠AEC＝90°，∠ACE＝∠ACE′，∵CE′∥AB，∴∠ACE′＝∠CAD，∴∠ACD＝∠CAD，∴DC＝DA，∵AD＝DB，∴DC＝DA＝DB，∴∠ACB＝90°，∴AB＝＝5，∵•AB•CH＝•AC•BC，∴CH＝，∴AH＝，∵CE∥AB，∴∠E′CH+∠AHC＝180°，∵∠AHC＝90°，∴∠E′CH＝90°，∴四边形AHCE′是矩形，∴CE′＝AH＝，故答案为．6.（2019四川绵阳）如图，△ABC、△BDE都是等腰直角三角形，BA=BC，BD=BE，AC=4，DE=2．将△BDE绕点B逆时针方向旋转后得△BD′E′，当点E′恰好落在线段AD′上时，则CE′=．【答案】.【解析】解：如图，连接CE′，∵△ABC、△BDE都是等腰直角三角形，BA=BC，BD=BE，AC=4，DE=2，∴AB=BC=2，BD=BE=2，∵将△BDE绕点B逆时针方向旋转后得△BD′E′，∴D′B=BE′=BD=2，∠D′BE′=90°，∠D′BD=∠ABE′，∴∠ABD′=∠CBE′，∴△ABD′≌△CBE′（SAS），∴∠D′=∠CE′B=45°，过B作BH⊥CE′于H，在Rt△BHE′中，BH=E′H=BE′=，在Rt△BCH中，CH=，∴CE′=，故答案为：．三、解答题7．（2019四川巴中）△ABC在边长为l的正方形网格中如图所示．①以点C为位似中心，作出△ABC的位似图形△A1B1C，使其位似比为1：2．且△A1B1C位于点C的异侧，并表示出A1的坐标．②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C．③在②的条件下求出点B经过的路径长．【答案】①作图见解析，点A1的坐标为（3，﹣3）；②见解析；③π．【解析】解：①如图，△A1B1C为所作，点A1的坐标为（3，﹣3）；②如图，△A2B2C为所作；③OB＝，点B经过的路径长＝＝π．8．（2019四川广安）在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）【答案】见解析．【解析】解：如图所示9．（2019四川自贡）（1）如图1，E是正方形ABCD边AB上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转90°，旋转后角的两边分别与射线BC交于点F和点G．①线段DB和DG的数量关系是；②写出线段BE，BF和DB之间的数量关系．（2）当四边形ABCD为菱形，∠ADC＝60°，点E是菱形ABCD边AB所在直线上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转120°，旋转后角的两边分别与射线BC交于点F和点G．①如图2，点E在线段AB上时，请探究线段BE、BF和BD之间的数量关系，写出结论并给出证明；②如图3，点E在线段AB的延长线上时，DE交射线BC于点M，若BE＝1，AB＝2，直接写出线段GM的长度．【答案】（1）①DB＝DG，理由见解析；②BF+BE＝BD，理由见解析；（2）①BF+BE＝BD，理由见解析；②．【解答】解：（1）①DB＝DG，理由是：∵∠DBE绕点B逆时针旋转90°，如图1，由旋转可知，∠BDE＝∠FDG，∠BDG＝90°，∵四边形ABCD是正方形，∴∠CBD＝45°，∴∠G＝45°，∴∠G＝∠CBD＝45°，∴DB＝DG；故答案为：DB＝DG；②BF+BE＝BD，理由如下：由①知：∠FDG＝∠EDB，∠G＝∠DBE＝45°，BD＝DG，∴△FDG≌△EDB（ASA），∴BE＝FG，∴BF+FG＝BF+BE＝BC+CG，Rt△DCG中，∵∠G＝∠CDG＝45°，∴CD＝CG＝CB，∵DG＝BD＝BC，即BF+BE＝2BC＝BD；（2）①如图2，BF+BE＝BD，理由如下：在菱形ABCD中，∠ADB＝∠CDB＝∠ADC＝×60°＝30°，由旋转120°得∠EDF＝∠BDG＝120°，∠EDB＝∠FDG，在△DBG中，∠G＝180°﹣120°﹣30°＝30°，∴∠DBG＝∠G＝30°，∴DB＝DG，∴△EDB≌△FDG（ASA），∴BE＝FG，∴BF+BE＝BF+FG＝BG，过点D作DM⊥BG于点M，如图2，∵BD＝DG，∴BG＝2BM，在Rt△BMD中，∠DBM＝30°，∴BD＝2DM．设DM＝a，则BD＝2a，DM＝a，∴BG＝2a，∴，∴BG＝BD，∴BF+BE＝BG＝BD；②过点A作AN⊥BD于N，过D作DP⊥BG于P，如图3，Rt△ABN中，∠ABN＝30°，AB＝2，∴AN＝1，BN＝，∴BD＝2BN＝2，∵DC∥BE，∴，∵CM+BM＝2，∴BM＝，Rt△BDP中，∠DBP＝30°，BD＝2，∴BP＝3，由旋转得：BD＝BF，∴BF＝2BP＝6，∴GM＝BG﹣BM＝6+1﹣＝．。

题型二 几何图形的相关计算类型一 与旋转有关1.如图,在等边△ABC 中, AB =10,点D 是BC 的中点,将△ABD 绕点A 旋转后得到△ACE ,则线段DE 的长度为（ ）A .34B .35C .36D .37第1题图B 【解析】∵△ABC 为等边三角形,∴AB =BC =10, ∠B = ∠BAC =60°,∵D 是BC 的中点,即BD =DC =12BC =5, AD ⊥BC , ∠BAD =30°,∴AD =3BD =35,∵△ABD 绕点A 旋转后得到△ACE , ∴∠DAE =∠BAC =60°, AD =AE ,∴△ADE 为等边三角形,∴DE =AD =35.2.如图,在Rt△ABC 中,∠ACB = 90°,∠A = 30°,BC =２,将△ABC 绕点C 顺时针旋转得到△EDC ,此时点B 的对应点D 恰好落在边AB 上,斜边DE 交AC 边于点F ,则重叠部分的面积为 .第2题图23 【解析】∵△ABC 是直角三角形,∠ACB =90°,∠A = 30°,BC = 2,∴∠B = 60°,AC=BC ·tan∠B =2×3=32,AB = 2BC = 4,∵△EDC 是由△ABC 旋转而成,∴BC = DC = 2, ∵∠B =60°,∴△B C D 是等边三角形,∴∠B C D =60°, ∴∠DCF =∠BCA -∠BCD = 30°,∵∠EDC =∠B =60°,∴∠DFC = 90°, 即DE ⊥AC ,∴DE ∥BC ,∵221==AB BD ,∴DF 是△ABC 的中位线, ∴DF=BC 211221=⨯=, ==AC CF 21 33221=⨯, ∴S △CDF =CF DF ·21233121=⨯⨯=.3．如图,线段AB = 4,O 为AB 的中点,动点P 到点O 的距离是1,连接PB ,将线段PB 绕点P 逆时针旋转90°得到线段PC ,连接AC ,则线段AC 长度的最大值是 ．第3题图23 【解析】如解图,以点O 为原点,AB 为x 轴建立平面直角坐标系,过点C 作CD ⊥y 轴, 垂足为D ,过点P 作PE ⊥DC ,垂足为E ,延长EP 交 x 轴于点F ．∵AB = 4,O 为AB 的中点,∴A （-2,0）, B （2,0）．设点P 的坐标为（x , y ）,则122=+y x ．∵∠EPC+∠BPF = 90°,∠EPC+∠ECP =90°, ∴∠ECP =∠FPB ．由旋转的性质可知,PC =PB .在△ECP 和△FPB中,,⎪⎩⎪⎨⎧=∠=∠∠=∠PB PC PFB PEC FPB ECP ∴△ECP ≌△FPB .∴EC =PF =y , FB =EP =2-x .∴C （x +y , y+2-x ）.∵A B =4,O 为A B 的中点, ∴()()2222x y y x AC -++++==882222+++y y x .∵122=+y x ,∴y AC 810+=．∵-1≤y ≤1,∴当y =1时,AC 有最大值, AC 的最大值为2318=．第3题解图类型二 与折叠有关（含最值）4.如图,在平行四边形ABCD 中,点P 为边AB 上一点,将△CBP 沿CP 翻折,点B 的对应点B ′恰好落在DA 的延长线上,且PB ′⊥AD ,若CD =3,BC =4,则BP 的长度为（ ）A .34B .35C .43D .45第4题图A 【解析】由折叠的性质可得：PB′=PB ,∠PB′C =∠B ,∵四边形ABCD 是平行四边形,PB′⊥AD ,∴∠B=∠D ,∠PB′A=90°,∴∠D+∠CB′D=90°,∴∠DCB′=90°,∵CD =3,BC =4,∴AD =B′C =BC =4,∴DB′=22B C CD '+=5,∴AB′=DB′-AD =1,设BP =x ,则PB′=x ,PA =3-x ,在Rt△AB′P 中,PA 2=AB ′ 2+P B ′ 2,∴x 2+12= （3-x ）2 ,解得x=34,∴BP =34. 5. 如图,在Rt△ABC 中,∠ACB =90°,∠A <∠B ,CM 是斜边AB 上的中线,将△ACM 沿直线CM 折叠,点A 落在点D 处,若AB 恰好平分CD ,AB =25,则△ABC 的面积为（）A . 52B . 5 3C . 532D . 10第5题图C 【解析】在Rt△ABC 中,∵CM 是斜边AB 的中线,∴CM =AM =BM =12AB ,由折叠的性质可知∠MCA = ∠MCD ,AM =DM ,∴∠A =∠MCD ,CM =DM ,又∵AB 恰好平分CD ,∴DC ⊥MB ,∴∠MCD ＋∠BMC =90°,又∵ ∠B M C =∠A ＋∠M C A =∠M C D ＋∠M C A =2∠M C D , ∴∠B M C =60°,∴∠B =60°,∴B C =A B ·c o s 60°=25×12=5,A C =A B ·s i n 60°=25× 32=15,∴S △ABC =12BC ·AC =12×5×15=532. 6.如图,矩形纸片ABCD 中,AB =1,BC =2,点M ,N 分别在边BC ,AD 上,将矩形纸片ABCD 沿直线MN 对折,使点A 落在CD 边上,则线段BM 的取值范围是________．第6题图 34≤BM ≤1 【解析】如解图,连接A ′M ,AM ,由折叠的性质可知, AM =A ′M ,设BM =x ,A ′C =t ,则CM =2－x ,∵∠B =∠C =90°, ∴AB 2＋BM 2=CM 2＋A ′C 2,即12＋x 2=(2－x )2＋t 2,解得：x =t 2＋34(0≤t ≤1),当t =0时,BM =x 的值最小,即BM =34,当t =1时,BM =x 的值最大,即BM =1,∴线段BM 的取值范围是：34≤BM ≤1.第6题解图类型三 与动点有关（含最值）7.如图,菱形ABCD 的边长为2,∠ABC =60°,点E 是AD 边中点,点P 是对角线BD 上的动点,当AP ＋PE 的值最小时,PC 的长是（ ）A . 3B . 2 3C . 233D . 33第7题图C 【解析】如解图,连接AC ,作点E 关于直线BD 的对称点E ′,连接AE ′,则线段AE ′的长即为AP ＋PE 的最小值,∵菱形ABCD的边长为2,E 是AD 的中点, ∴DE =DE ′=12AD =1 , ∵∠ABC =60°, ∴∠ADC =60°,又∵AD=CD,∴△ACD为等边三角形,∴AE′ ⊥ CD,∴△AE′D是直角三角形,∵∠PDE′=1 2∠A D C=30°,∴PE′=DE′·tan30°=33,∴PC=PD=2PE′=233.第7题解图8.如图,矩形ABCD中, AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ＋QP的最小值是（）A. 3 2B. 3 3C. 3D. 12第8题图B 【解析】如解图,作点A关于直线CD的对称点E,过点E作EP⊥AC于点P,交CD于点Q.∵四边形ABCD是矩形,∴∠ADC=90°,∴DQ⊥AE,∵DE=AD,∴QE=QA,∴QA＋QP=QE＋QP=EP,∴此时Q A＋Q P最短(垂线段最短),∵∠CAB=30°,∴∠DAC=60°,在Rt△APE中,∵∠APE=90°,AE=2AD=6,∴EP=AE·sin 60°=6×32=33.第8题解图9.如图,△ABC中,AB=AC=2,BC=23,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是.第9题图A . 3 3B . 3C . 3D . 2 3A 【解析】如解图,过点A 作A E ⊥BC 于点E ,过点D 作D F ⊥B C 于点F ,∵A B =A C =2,B C =23,∴AE =1,∠B A C =120°,D 点是 △ABC 所在平面上的一个动点,且∠BDC =60°, ∴2∠BDC =∠BAC , ∴点D 在以点A 为圆心,AB 长为半径的圆上,BC 一定,要使△DBC 的面积取最大值,即DF 过圆心A ,此时DF =2＋1=3.∴S △DBC 最大=12·BC ·DF =12×23×3=33.第9题解图类型四 非动态几何图形的相关计算10.如图,菱形ABCD 的对角线AC 与BD 交于点O ,过点C 作AB 的垂线交AB 延长线于点E ,连接OE ,若52=AB ,BD =4,则OE 的长为( )第10题图A ．6B ．5C ．5D ．4D 【解析】∵四边形A B C D 是菱形, ∴O A =O C , B D ⊥A C , ∵CE ⊥A B ,∴O E =O A =O C ,∵B D =4,∴221==BD OB ,在 R t △A O B 中,52=AB ,O B =2, ∴O A =22OB AB -=4,∴O E=OA =4. 11.如图,以等边三角形ABC 的BC 边为直径画半圆,分别交 AB 、AC 于点E 、D , DF 是圆的切线,过点F作BC的垂线交BC于点G．若AF的长为2,则FG的长为（）第11题图A．4 B．23 C．6 D．33D 【解析】如解图,连接OD,∵DF为⊙O的切线, ∴OD⊥DF, ∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°,∵OD=OC,∴△OCD为等边三角形,∴∠C D O=∠A=60°,∠A B C=∠D O C=60°,∴O D∥A B,∴D F⊥AB,在Rt△AFD中,∠ADF=30°,AF=2,∴AD=4,即AC=8,∴FB=AB-AF=8-2=6,在Rt△BFG 中,∠B F G=30°, ∴BG=3,则根据勾股定理得FG=33．第11题解图12.如图,△ABC是等边三角形,点D、E分别是BC、AC上一点,且AE=CD,连接 AD、BE,AD与BE相交于点P,过点B作BQ⊥AD于点Q,PQ=3,PE=1,则AD的长为.第12题图7 【解析】∵△ABC是等边三角形, ∴AB=BC=CA, ∠BAE =∠ACD=60°,又∵AE=CD,在△A B E 和△C A D 中, ,⎪⎩⎪⎨⎧=∠=∠=CD AE ACD BAE CA AB △A B E ≌△C A D （S A S ）, ∴B E =A D ,∠A B E =∠C A D ,∴∠B P Q =∠A B E +∠B A D =∠B A D +∠C A D = ∠BAE =60°,∵BQ ⊥AD ,∴∠AQB =90°,则∠PBQ =90°- 60°=30°, ∵PQ =3,∴BP = 2PQ = 6,又∵PE = 1,∴AD = BE = BP + PE =7．。

四川各2019年中考数学分类解析-专项9：三角形专题9：三角形选择题1. 〔2018四川乐山3分〕如图，在Rt△ABC中，∠C=90°，AB=2BC，那么sinB的值为【】A、B、C、D、1【答案】C。

【考点】锐角三角函数定义，特殊角的三角函数值。

【分析】∵Rt△ABC中，∠C=90°，AB=2BC，∴sinA=BC BC1==AB2BC2∴∠A=30°。

∴∠B=60°。

∴sinB=。

应选C。

2sin602. 〔2018四川乐山3分〕如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动〔点E不与点A、C重合〕，且保持AE=CF，连接DE、DF、EF、在此运动变化的过程中，有以下结论：①△DFE是等腰直角三角形；②四边形CEDF不可能为正方形；③四边形CEDF的面积随点E位置的改变而发生变化；④点C到线段EF的最大距离为、其中正确结论的个数是【】A、1个B、2个C、3个D、4个【答案】B。

【考点】全等三角形的判定和性质，等腰直角三角形，三角形中位线定理，勾股定理。

【分析】①连接CD〔如图1〕。

∵△ABC是等腰直角三角形，∴∠DCB=∠A=45°，CD=AD=DB。

∵AE=CF，∴△ADE≌△CDF〔SAS〕。

∴ED=DF，∠CDF=∠EDA。

∵∠ADE+∠EDC=90°，∴∠EDC+∠CDF=∠EDF=90°。

∴△DFE是等腰直角三角形。

故此结论正确。

BC。

②当E、F分别为AC、BC中点时，∵由三角形中位线定理，DE平行且等于12∴四边形CEDF是平行四边形。

又∵E、F分别为AC、BC中点，AC=BC，∴四边形CEDF是菱形。

又∵∠C=90°，∴四边形CEDF是正方形。

故此结论错误。

③如图2，分别过点D，作DM⊥AC，DN⊥BC，于点M，N，由②，知四边形CMDN是正方形，∴DM=DN。

四川各2019年中考数学分类解析-专项8：平面几何基础 专题8：平面几何基础选择题①等边三角形是中心对称图形；②在同圆或等圆中，相等的弦所对的圆周角相等；③三角形有且只有一个外接圆；④垂直于弦的直径平分弦所对的两条弧、其中真命题的个数有【】A 、 1个B 、 2个C 、 3个D 、 4个【答案】B 。

【考点】命题与定理，中心对称图形，圆周角定理，三角形的外接圆与外心，垂径定理。

【分析】∵等边三角形是轴对称图形，但不是中心对称图形，∴①是假命题； 如图，∠C 和∠D 不相等，即②是假命题；三角形有且只有一个外接圆，外接圆的圆心是三角形三边垂直平分线的交点，即③是真命题。

垂直于弦的直径平分弦，且平分弦所对的两条弧，即④是真命题。

故②④是真命题。

应选B 。

2.〔2018四川内江3分〕以下图形中，既是轴对称图形又是中心对称图形的有【】A.4个B.3个C.2个D.1个【答案】C 。

【考点】轴对称和中心对称图形。

【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。

因此，四个图形都是轴对称图形，同时第【二】四个又是中心对称图形。

应选C 。

3.〔2018四川内江3分〕如图，=∠=∠=∠3,1402,651,//00则b a 【】0100 B.0105C.0110 D.0115【答案】B 。

【考点】平行的性质，三角形外角性质。

【分析】如图，反向延长b，形成∠4。

∵//a b，∴∠3＝1800－∠4。

又∵∠2＝∠1＋∠4，即∠4＝∠2—∠1。

∴()()00000 31802118014065105∠=-∠-∠=--=。

应选B。

4.〔2018四川达州3分〕以下几何图形中，对称性与其它图形不同的是【】【答案】A。

【考点】轴对称图形，中心对称图形。

【分析】根据轴对称及中心对称的定义，分别判断各选项，然后即可得出答案：A、是轴对称图形，不是中心对称图形；B、既是轴对称图形也是中心对称图形；C、既是轴对称图形也是中心对称图形；D、既是轴对称图形也是中心对称图形。

2019年全国各地中考数学真题汇编（四川专版）三角形一．选择题（共6小题）1．（2019•凉山州）如图，在△ABC中，CA＝CB＝4，cos C＝，则sin B的值为（）A．B．C．D．2．（2019•广元）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，且AB ＝10，AC＝8，则BD的长为（）A．2B．4C．2D．4.83．（2019•遂宁）如图，▱ABCD中，对角线AC、BD相交于点O，OE⊥BD交AD于点E，连接BE，若▱ABCD的周长为28，则△ABE的周长为（）A．28B．24C．21D．144．（2019•乐山）把边长分别为1和2的两个正方形按如图的方式放置．则图中阴影部分的面积为（）A．B．C．D．5．（2019•巴中）如图▱ABCD，F为BC中点，延长AD至E，使DE：AD＝1：3，连结EF交DC 于点G，则S△DEG：S△CFG＝（）A．2：3B．3：2C．9：4D．4：96．（2019•宜宾）如图，∠EOF的顶点O是边长为2的等边△ABC的重心，∠EOF的两边与△ABC 的边交于E，F，∠EOF＝120°，则∠EOF与△ABC的边所围成阴影部分的面积是（）A．B．C．D．二．填空题（共10小题）7．（2019•自贡）如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD交AC于点E，DE＝．8．（2019•成都）如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A'B'D'，分别连接A'C，A'D，B'C，则A'C+B'C的最小值为．9．（2019•广元）如图，△ABC中，∠ABC＝90°，BA＝BC＝2，将△ABC绕点C逆时针旋转60°得到△DEC，连接BD，则BD2的值是．10．（2019•乐山）如图，在△ABC中，∠B＝30°，AC＝2，cos C＝．则AB边的长为．11．（2019•眉山）如图，在Rt△ABC中，∠B＝90°，AB＝5，BC＝12，将△ABC绕点A逆时针旋转得到△ADE，使得点D落在AC上，则tan∠ECD的值为．12．（2019•广安）等腰三角形的两边长分别为6cm，13cm，其周长为cm．13．（2019•宜宾）如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则AD＝．14．（2019•凉山州）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2，则⊙O 的半径是．15．（2019•达州）如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为．16．（2019•凉山州）如图，正方形ABCD中，AB＝12，AE＝AB，点P在BC上运动（不与B、C 重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为．三．解答题（共18小题）17．（2019•攀枝花）如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．求证：（1）点D在BE的垂直平分线上；（2）∠BEC＝3∠ABE．18．（2019•成都）2019年，成都马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅提升了成都市的国际影响力，如图，在一场马拉松比赛中，某人在大楼A处，测得起点拱门CD的顶部C的（结俯角为35°，底部D的俯角为45°，如果A处离地面的高度AB＝20米，求起点拱门CD的高度．果精确到1米；参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）19．（2019•广元）如图，已知：在△ABC中，∠BAC＝90°，延长BA到点D，使AD＝AB，点E，F分别是边BC，AC的中点．求证：DF＝BE．20．（2019•绵阳）如图，AB是⊙O的直径，点C为的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．（1）求证：△BFG≌△CDG；（2）若AD＝BE＝2，求BF的长．21．（2019•泸州）如图，海中有两个小岛C，D，某渔船在海中的A处测得小岛位于东北方向上，且相距20nmile，该渔船自西向东航行一段时间到达点B处，此时测得小岛C恰好在点B的正北方向上，且相距50nmile，又测得点B与小岛D相距20nmile．（1）求sin∠ABD的值；（2）求小岛C，D之间的距离（计算过程中的数据不取近似值）．22．（2019•遂宁）如图，在四边形ABCD中，AD∥BC，延长BC到E，使CE＝BC，连接AE交CD 于点F，点F是CD的中点．求证：（1）△ADF≌△ECF．（2）四边形ABCD是平行四边形．23．（2019•广元）如图，某海监船以60海里/时的速度从A处出发沿正西方向巡逻，一可疑船只在A的西北方向的C处，海监船航行1.5小时到达B处时接到报警，需巡査此可疑船只，此时可疑船只仍在B的北偏西30°方向的C处，然后，可疑船只以一定速度向正西方向逃离，海监船立刻加速以90海里/时的速度追击，在D处海监船追到可疑船只，D在B的北偏西60°方同．（以下结果保留根号）（1）求B，C两处之间的距离；（2）求海监船追到可疑船只所用的时间．24．（2019•遂宁）汛期即将来临，为保证市民的生命和财产安全，市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固．如图，加固前大坝背水坡坡面从A至B共有30级阶梯，平均每级阶梯高30cm，斜坡AB的坡度i＝1：1；加固后，坝顶宽度增加2米，斜坡EF的坡度i＝1：，问工程完工后，共需土石多少立方米？（计算土石方时忽略阶梯，结果保留根号）25．（2019•南充）如图，点O是线段AB的中点，OD∥BC且OD＝BC．（1）求证：△AOD≌△OBC；（2）若∠ADO＝35°，求∠DOC的度数．26．（2019•眉山）如图，在岷江的右岸边有一高楼AB，左岸边有一坡度i＝1：2的山坡CF，点C 与点B在同一水平面上，CF与AB在同一平面内．某数学兴趣小组为了测量楼AB的高度，在坡底C处测得楼顶A的仰角为45°，然后沿坡面CF上行了20米到达点D处，此时在D处测得楼顶A的仰角为30°，求楼AB的高度．27．（2019•达州）如图，在Rt△ABC中，∠ACB＝90°，AC＝2，BC＝3．（1）尺规作图：不写作法，保留作图痕迹．①作∠ACB的平分线，交斜边AB于点D；②过点D作BC的垂线，垂足为点E．（2）在（1）作出的图形中，求DE的长．28．（2019•宜宾）如图，为了测得某建筑物的高度AB，在C处用高为1米的测角仪CF，测得该建筑物顶端A的仰角为45°，再向建筑物方向前进40米，又测得该建筑物顶端A的仰角为60°．求该建筑物的高度AB．（结果保留根号）29．（2019•巴中）如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE ⊥直线m于点E，BD⊥直线m于点D．①求证：EC＝BD；②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．30．（2019•广安）如图，某数学兴趣小组为测量一颗古树BH和教学楼CG的高，先在A处用高1.5米的测角仪AF测得古树顶端H的仰角∠HFE为45°，此时教学楼顶端G恰好在视线FH上，再向前走10米到达B处，又测得教学楼顶端G的仰角∠GED为60°，点A、B、C三点在同一水平线上．（1）求古树BH的高；（2）求教学楼CG的高．（参考数据：＝1.4，＝1.7）31．（2019•达州）渠县賨人谷是国家AAAA级旅游景区，以“奇山奇水奇石景，古賨古洞古部落”享誉巴渠，被誉为川东“小九寨”．端坐在观音崖旁的一块奇石似一只“啸天犬”，昂首向天，望穿古今．一个周末，某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离．他们把蹲着的“啸天犬”抽象成四边形ABCD，想法测出了尾部C看头顶B的仰角为40°，从前脚落地点D看上嘴尖A的仰角刚好60°，CB＝5m，CD＝2.7m．景区管理员告诉同学们，上嘴尖到地面的距离是3m．于是，他们很快就算出了AB的长．你也算算？（结果精确到0.1m．参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84.≈1.41，≈1.73）32．（2019•巴中）某区域平面示意图如图所示，点D在河的右侧，红军路AB与某桥BC互相垂直．某校“数学兴趣小组”在“研学旅行”活动中，在C处测得点D位于西北方向，又在A处测得点D 位于南偏东65°方向，另测得BC＝414m，AB＝300m，求出点D到AB的距离．（参考数据sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）33．（2019•资阳）如图，南海某海域有两艘外国渔船A、B在小岛C的正南方向同一处捕鱼．一段时间后，渔船B沿北偏东30°的方向航行至小岛C的正东方向20海里处．（1）求渔船B航行的距离；（2）此时，在D处巡逻的中国渔政船同时发现了这两艘渔船，其中B渔船在点D的南偏西60°方向，A渔船在点D的西南方向，我渔政船要求这两艘渔船迅速离开中国海域．请分别求出中国渔政船此时到这两艘外国渔船的距离．（注：结果保留根号）34．（2019•凉山州）如图，正方形ABCD的对角线AC、BD相交于点O，E是OC上一点，连接EB．过点A作AM⊥BE，垂足为M，AM与BD相交于点F．求证：OE＝OF．。

四川省2019年、2020年数学中考试题分类（12）——图形的变换一．选择题（共27小题）1．（2020•德阳）如图是一个几何体的三视图，根据图中所示数据计算这个几何体的表面积是( )A ．20πB ．18πC ．16πD ．14π2．（2020•德阳）如图，Rt ABC ∆中，30A ∠=︒，90ABC ∠=︒．将Rt ABC ∆绕点B 逆时针方向旋转得到△A BC ''．此时恰好点C 在A C ''上，A B '交AC 于点E ，则ABE ∆与ABC ∆的面积之比为( )A ．13B ．12C ．23D ．343．（2020•眉山）如图，正方形ABCD 中，点F 是BC 边上一点，连接AF ，以AF 为对角线作正方形AEFG ，边FG 与正方形ABCD 的对角线AC 相交于点H ，连接DG ．以下四个结论：①EAB GAD ∠=∠；②AFC AGD ∆∆∽；③22AE AH AC =；④DG AC ⊥．其中正确的个数为( )A ．1个B ．2个C ．3个D ．4个4．（2020•眉山）如图所示的几何体的主视图为( )A ．B ．C ．D ．5．（2020•绵阳）如图，在四边形ABCD 中，//AD BC ，90ABC ∠=︒，27AB =，2BB '=，2AD =，将ABC ∆绕点C 顺时针方向旋转后得△A B C ''，当A B ''恰好经过点D 时，△B CD '为等腰三角形，则(AA '= )A ．11B ．23C ．13D ．146．（2020•雅安）一个几何体由若干大小相同的小正方体组成，它的俯视图和左视图如图所示，那么组成该几何体所需小正方体的个数最少为( )A ．4B ．5C ．6D ．77．（2020•宜宾）如图所示，圆柱的主视图是( )A ．B ．C ．D ．8．（2020•内江）如图，矩形ABCD 中，BD 为对角线，将矩形ABCD 沿BE 、BF 所在直线折叠，使点A 落在BD 上的点M 处，点C 落在BD 上的点N 处，连结EF ．已知3AB =，4BC =，则EF 的长为( )A ．3B ．5C ．5136D ．13 9．（2020•乐山）观察下列各方格图中阴影部分所示的图形（每一小方格的边长为1)，如果将它们沿方格边线或对角线剪开重新拼接，不能拼成正方形的是( ) A ． B ．C ．D ．10．（2020•达州）图2是图1中长方体的三视图，用S 表示面积，23S x x =+主，2S x x =+左，则(S =俯 )A ．232x x ++B ．221x x ++ C ．243x x ++ D ．224x x +11．（2020•泸州）古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将一线段MN 分为两线段MG ，GN ，使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项，即满足512MG GN MN MG -==，后人把512-这个数称为“黄金分割”数，把点G 称为线段MN 的“黄金分割”点．如图，在ABC ∆中，已知3AB AC ==，4BC =，若D ，E 是边BC 的两个“黄金分割”点，则ADE ∆的面积为( )A ．1045-B ．355-C ．525- D ．2085- 12．（2020•泸州）下列正多边形中，不是中心对称图形的是( ) A ． B ． C ． D ．13．（2020•凉山州）如图所示，ABC ∆的顶点在正方形网格的格点上，则tan A 的值为( )A ．12B ．22C ．2D ．22 14．（2020•泸州）在平面直角坐标系中，将点(2,3)A -向右平移4个单位长度，得到的对应点A '的坐标为( )A ．(2,7)B ．(6,3)-C ．(2,3)D ．(2,1)-- 15．（2020•成都）如图，直线123////l l l ，直线AC 和DF 被1l ，2l ，3l 所截，5AB =，6BC =，4EF =，则DE 的长为( )A ．2B ．3C ．4D ．10316．（2020•凉山州）点P (2,3)关于x 轴对称的点P '的坐标是( )A ．(2,3)-B ．(2,3)-C ．(2,3)--D ．(3,2)17．（2020•南充）如图，点A ，B ，C 在正方形网格的格点上，则sin (BAC ∠= )A ．2 B ．26 C ．26 D ．13 18．（2020•遂宁）如图，在平行四边形ABCD 中，ABC ∠的平分线交AC 于点E ，交AD 于点F ，交CD 的延长线于点G ，若2AF FD =，则BE EG 的值为( ) A ．12 B ．13 C ．23 D ．3419．（2020•遂宁）如图，在正方形ABCD 中，点E 是边BC 的中点，连接AE 、DE ，分别交BD 、AC 于点P 、Q ，过点P 作PF AE ⊥交CB 的延长线于F ，下列结论：①90AED EAC EDB ∠+∠+∠=︒，②AP FP =，③10AE AO =， ④若四边形OPEQ 的面积为4，则该正方形ABCD 的面积为36，⑤CE EF EQ DE =．其中正确的结论有( )A ．5个B ．4个C ．3个D ．2个20．（2020•自贡）在平面直角坐标系中，将点(2,1)向下平移3个单位长度，所得点的坐标是( )A ．(1,1)-B ．(5,1)C ．(2,4)D ．(2,2)-21．（2020•遂宁）下列图形中，既是轴对称图形，又是中心对称图形的是( ) A ．等边三角形 B ．平行四边形 C ．矩形 D ．正五边形22．（2019•阿坝州）如图，ABC ∆中，//DE BC ，2AD =，1DB =，4AE =，则EC 的长度为( )A ．1B ．2C ．3D ．423．（2019•雅安）如图是下面哪个图形的俯视图( )A ．B ．C ．D ．24．（2019•雅安）如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△111A B C 相似的是( )A ．B ．C ．D ．25．（2019•内江）如图，将ABC ∆沿着过BC 的中点D 的直线折叠，使点B 落在AC 边上的1B 处，称为第一次操作，折痕DE 到AC 的距离为1h ；还原纸片后，再将BDE ∆沿着过BD 的中点1D 的直线折叠，使点B 落在DE 边上的2B 处，称为第二次操作，折痕11D E 到AC 的距离记为2h ；按上述方法不断操作下去⋯⋯经过第n 次操作后得到折痕11n n D E --，到AC 的距离记为n h ．若11h =，则n h 的值为( )A ．1112n -+B ．112n +C ．1122n -- D ．122n- 26．（2019•内江）下列几何体中，主视图为三角形的是( ) A ． B ． C ． D ．27．（2019•内江）如图，在ABC ∆中，//DE BC ，9AD =，3DB =，2CE =，则AC 的长为( )A ．6B ．7C ．8D ．9二．填空题（共11小题）28．（2020•德阳）如图，海中有一小岛A ，它周围10.5海里内有暗礁，渔船跟踪鱼群由西向东航行．在B 点测得小岛A 在北偏东60︒方向上，航行12海里到达D 点，这时测得小岛A 在北偏东30︒方向上．如果渔船不改变航线继续向东航行，那么渔船还需航行 海里就开始有触礁的危险．29．（2020•眉山）如图，在Rt ABC ∆中，90BAC ∠=︒，2AB =．将ABC ∆绕点A 按顺时针方向旋转至△11AB C 的位置，点1B 恰好落在边BC 的中点处，则1CC 的长为 ．30．（2020•宜宾）在Rt ABC ∆中，90ACB ∠=︒，D 是AB 的中点，BE 平分ABC ∠交AC 于点E ，连结CD交BE 于点O ．若8AC =，6BC =，则OE 的长是 ．31．（2020•绵阳）平面直角坐标系中，将点(1,2)A -先向左平移2个单位，再向上平移1个单位后得到的点1A 的坐标为 ．32．（2020•宜宾）如图，四边形ABCD 中，DA AB ⊥，CB AB ⊥，3AD =，5AB =，2BC =，P 是边AB 上的动点，则PC PD +的最小值是 ．33．（2020•攀枝花）如图，在边长为4的正方形ABCD 中，点E 、F 分别是BC 、CD 的中点，DE 、AF 交于点G ，AF 的中点为H ，连接BG 、DH ．给出下列结论：①AF DE ⊥；②85DG =；③//HD BG ；④ABG DHF ∆∆∽． 其中正确的结论有 ．（请填上所有正确结论的序号）34．（2020•凉山州）如图，矩形ABCD 中，12AD =，8AB =，E 是AB 上一点，且3EB =，F 是BC 上一动点，若将EBF ∆沿EF 对折后，点B 落在点P 处，则点P 到点D 的最短距离为 ．35．（2020•泸州）如图，在矩形ABCD 中，E ，F 分别为边AB ，AD 的中点，BF 与EC 、ED 分别交于点M ，N ．已知4AB =，6BC =，则MN 的长为 ．36．（2020•自贡）如图，我市在建高铁的某段路基横断面为梯形ABCD，//DC AB．BC长6米，坡角β为45︒，AD的坡角α为30︒，则AD长为米（结果保留根号）．37．（2020•乐山）如图是某商场营业大厅自动扶梯示意图．自动扶梯AB的倾斜角为30︒，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60︒，A、C之间的距离为4m．则自动扶梯的垂直高度BD=m．（结果保留根号）38．（2020•甘孜州）如图，有一张长方形纸片ABCD，8AB cmBC cm=，点E为CD上一点，将纸片=，10沿AE折叠，BC的对应边B C''恰好经过点D，则线段DE的长为cm．三．解答题（共2小题）39．（2020•内江）为了维护我国海洋权力，海监部门对我国领海实行了常态化巡航管理．如图，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A处测得灯塔P在北偏东60︒方向上，海监船继续向东航行1小时到达B处，此时测得灯塔P在北偏东30︒方向上．（1）求B处到灯塔P的距离；（2）已知灯塔P的周围50海里内有暗礁，若海监船继续向正东方向航行是否安全？40．（2020•达州）如图，在梯形ABCD中，//AB cmCD cm=．P为线段BC上=，2AB CD，90B∠=︒，6的一动点，且和B、C不重合，连接PA，过点P作PE PA⊥交射线CD于点E．聪聪根据学习函数的经验，对这个问题进行了研究：（1）通过推理，他发现ABP PCE∽，请你帮他完成证明．∆∆（2）利用几何画板，他改变BC的长度，运动点P，得到不同位置时，CE、BP的长度的对应值：/ BP cm ⋯12345⋯/ CE cm ⋯0.83 1.33 1.50 1.330.83⋯/ BP cm ⋯1234567⋯/ CE cm ⋯1.172.00 2.50 2.67 2.50 2.00 1.17⋯①填空：根据函数的定义，我们可以确定，在BP和CE的长度这两个变量中，的长度为自变量，的长度为因变量；②设BC mcm=，当点P在线段BC上运动时，点E总在线段CD上，求m的取值范围．四川省2019年、2020年数学中考试题分类（12）——图形的变换一．选择题（共27小题）1．（2020•德阳）如图是一个几何体的三视图，根据图中所示数据计算这个几何体的表面积是( )A ．20πB ．18πC ．16πD ．14π【解答】解：这个几何体的表面积223222218ππππ=++=，故选：B ．2．（2020•德阳）如图，Rt ABC ∆中，30A ∠=︒，90ABC ∠=︒．将Rt ABC ∆绕点B 逆时针方向旋转得到△A BC ''．此时恰好点C 在A C ''上，A B '交AC 于点E ，则ABE ∆与ABC ∆的面积之比为( )A ．13B ．12C ．23D ．34 【解答】解：30A ∠=︒，90ABC ∠=︒，60ACB ∴∠=︒，将Rt ABC ∆绕点B 逆时针方向旋转得到△A BC ''，BC BC '∴=，60ACB A C B ''∠=∠=︒，BCC '∴∆是等边三角形，60CBC '∴∠=︒， 60ABA '∴∠=︒，90BEA ∴∠=︒， 设CE a =，则3BE a =，3AE a =， ∴13CE AE =， ∴34AE AC =， ABE ∴∆与ABC ∆的面积之比为34． 故选：D ．3．（2020•眉山）如图，正方形ABCD 中，点F 是BC 边上一点，连接AF ，以AF 为对角线作正方形AEFG ，边FG 与正方形ABCD 的对角线AC 相交于点H ，连接DG ．以下四个结论：①EAB GAD ∠=∠；②AFC AGD ∆∆∽；③22AE AH AC =；④DG AC ⊥．其中正确的个数为( )A ．1个B ．2个C ．3个D ．4个 【解答】解：四边形ABCD ，四边形AEFG 都是正方形， 90EAG BAD ∴∠=∠=︒，45FAG AFG DAC ACB ∠=∠=∠=∠=︒，2AF AG =，2AC AD =，EAG BAG BAD BAG ∴∠-∠=∠-∠，EAB DAG ∴∠=∠，故①正确；2AF =，2AC AD =，∴2AF AC AG AD==， 45FAG CAD ∠=∠=︒，FAC DAG ∴∠=∠，FAC DAG ∴∆∆∽，故②正确，45ADG ACB ∴∠=∠=︒，延长DG 交AC 于N ，45CAD ∠=︒，45ADG ∠=︒，90AND ∴∠=︒，DG AC ∴⊥，故④正确，FAC FAH ∠=∠，45AFG ACF ∠=∠=︒，AFH ACF ∴∆∆∽，∴AH AF AF AC=， 2AF AH AC ∴=， 22AE AH AC ∴=，故③正确，故选：D ．4．（2020•眉山）如图所示的几何体的主视图为( )A ．B ．C ．D ．【解答】解：从几何体的正面看，是一个矩形，矩形的中间有一条纵向的实线．故选：D ．5．（2020•绵阳）如图，在四边形ABCD 中，//AD BC ，90ABC ∠=︒，27AB =，2BB '=，2AD =，将ABC ∆绕点C 顺时针方向旋转后得△A B C ''，当A B ''恰好经过点D 时，△B CD '为等腰三角形，则(AA '= )A 11B ．23C 13D 14【解答】解：过D 作DE BC ⊥于E ，则90DEC DEB ∠=∠=︒，//AD BC ，90ABC ∠=︒， 90DAB ABC ∴∠=∠=︒，∴四边形ABED 是矩形， 2BE AD ∴==，27DE AB ==将ABC ∆绕点C 顺时针方向旋转后得△A B C ''，90DB C ABC ∴∠'=∠=︒，B C BC '=，AC AC '=，ACA B CB ∠'=∠'， ∴△A CA '∽△B CB '，∴A A AC B B BC'='， △B CD '为等腰三角形，∴△B CD '为等腰直角三角形，2CD B C ∴='，设B C BC x '==，则2CD x =，2CE x =-，222CD CE DE =+，222(2)(2)7)x x ∴=-+，4x ∴=（负值舍去）， 4BC ∴=，22211AC AB BC ∴+，∴21124A A '=， 11A A ∴'=，故选：A ．6．（2020•雅安）一个几何体由若干大小相同的小正方体组成，它的俯视图和左视图如图所示，那么组成该几何体所需小正方体的个数最少为()A．4B．5C．6D．7【解答】解：由俯视图与左视图知，该几何体所需小正方体个数最少分布情况如下图所示：所以组成该几何体所需小正方体的个数最少为5，故选：B．7．（2020•宜宾）如图所示，圆柱的主视图是()A．B．C．D．【解答】解：从正面看，是一个矩形．故选：B．8．（2020•内江）如图，矩形ABCD中，BD为对角线，将矩形ABCD沿BE、BF所在直线折叠，使点A落在BD上的点M处，点C落在BD上的点N处，连结EF．已知3AB=，4BC=，则EF的长为()A．3B．5C 513D13【解答】解：四边形ABCD是矩形，3AB CD ∴==，4AD BC ==，90A C EDF ∠=∠=∠=︒，2222345BD AB AD ∴=+=+=，将矩形ABCD 沿BE 所在直线折叠，使点A 落在BD 上的点M 处，AE EM ∴=，90A BME ∠=∠=︒，90EMD ∴∠=︒，EDM ADB ∠=∠，EDM BDA ∴∆∆∽，∴ED EM BD AB=， 设DE x =，则4AE EM x ==-，∴453x x -=， 解得52x =， 52DE ∴=， 同理DNF DCB ∆∆∽，∴DF NF BD BC=， 设DF y =，则3CF NF y ==-，∴354y y -=， 解得53y =． 53DF ∴=． 222255513()()23EF DE DF ∴=+=+=． 故选：C ．9．（2020•乐山）观察下列各方格图中阴影部分所示的图形（每一小方格的边长为1)，如果将它们沿方格边线或对角线剪开重新拼接，不能拼成正方形的是( )A ．B ．C ．D ．【解答】解：由题意，选项D 阴影部分面积为6，A ，B ，C 的阴影部分的面积为5，如果能拼成正方形，选项D 6，选项A ，B ，C 5，观察图象可知，选项A ，B ，C 阴影部分沿方格边线或对角线剪开均可得图1的5个图形，可以拼成图25的正方形，故选：D ．10．（2020•达州）图2是图1中长方体的三视图，用S 表示面积，23S x x =+主，2S x x =+左，则(S =俯 )A ．232x x ++B ．221x x ++C ．243x x ++D ．224x x +【解答】解：()233S x x x x =+=+主，()21S x x x x =+=+左， ∴俯视图的长为3x +，宽为1x +，则俯视图的面积()()23143S x x x x =++=++俯，故选：C ． 11．（2020•泸州）古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将一线段MN 分为两线段MG ，GN ，使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项，即满足51MG GN MN MG -==，后人把51-这个数称为“黄金分割”数，把点G 称为线段MN 的“黄金分割”点．如图，在ABC ∆中，已知3AB AC ==，4BC =，若D ，E 是边BC 的两个“黄金分割”点，则ADE ∆的面积为( )A ．1045-B ．355C 525-D ．2085-【解答】解：作AH BC ⊥于H ，如图，AB AC =，122BH CH BC ∴===， 在Rt ABH ∆中，22325AH =-，D ，是边BC 的两个“黄金分割”点，512(51)252BE -∴===， 2522254HE BE BH ∴=-=-=，2458DE HE ∴==-1(458)510452ADE S ∆∴=⨯-⨯=-． 故选：A ．12．（2020•泸州）下列正多边形中，不是中心对称图形的是( )A ．B ．C ．D ．【解答】解：A ．正方形是中心对称图形，故本选项不合题意；B ．正五边形不是中心对称图形，故本选项符合题意；C ．正六边形是中心对称图形，故本选项不合题意；D ．正八边形是中心对称图形，故本选项不合题意；故选：B ．13．（2020•凉山州）如图所示，ABC ∆的顶点在正方形网格的格点上，则tan A 的值为( )A ．12B ．2C ．2D ．22【解答】解：如图，连接BD ，由网格的特点可得，BD AC ⊥， 222222AD =+=，22112BD =+=，21tan 222BD A AD ∴===， 故选：A ．14．（2020•泸州）在平面直角坐标系中，将点(2,3)A -向右平移4个单位长度，得到的对应点A '的坐标为()A ．(2,7)B ．(6,3)-C ．(2,3)D ．(2,1)--【解答】解：将点(2,3)A -先向右平移4个单位，∴点A 的对应点A '的坐标是(24,3)-+，即(2,3)．故选：C ．15．（2020•成都）如图，直线123////l l l ，直线AC 和DF 被1l ，2l ，3l 所截，5AB =，6BC =，4EF =，则DE 的长为( )A ．2B ．3C ．4D ．103 【解答】解：直线123////l l l ，∴AB DE BC EF=， 5AB =，6BC =，4EF =，∴564DE =， 103DE ∴=， 故选：D ．16．（2020•凉山州）点P (2,3)关于x 轴对称的点P '的坐标是( )A ．(2,3)-B ．(2,3)-C ．(2,3)--D ．(3,2)【解答】解：点(2,3)P 关于x 轴对称的点P '的坐标是(2,3)-．故选：A ．17．（2020•南充）如图，点A ，B ，C 在正方形网格的格点上，则sin (BAC ∠= )A ．2B ．26C ．26D ．13 【解答】解：如图，过点B 作BD AC ⊥于D ， 由勾股定理得，223213AB =+=，223332AC =+=，1113213222ABC S AC BD BD ∆==⨯=⨯⨯， 2BD ∴=， 2262sin 13BD BAC AB ∴∠===． 故选：B ．18．（2020•遂宁）如图，在平行四边形ABCD 中，ABC ∠的平分线交AC 于点E ，交AD 于点F ，交CD 的延长线于点G ，若2AF FD =，则BE EG的值为( ) A ．12 B ．13 C ．23 D ．34【解答】解：由2AF DF =，可以假设DF k =，则2AF k =，3AD k =，四边形ABCD 是平行四边形，//AD BC ∴，//AB CD ，AB CD =，AFB FBC DFG ∴∠=∠=∠，ABF G ∠=∠，BE 平分ABC ∠，ABF CBG ∴∠=∠，ABF AFB DFG G ∴∠=∠=∠=∠，2AB CD k ∴==，DF DG k ==，3CG CD DG k ∴=+=，//AB DG ，ABE CGE ∴∆∆∽，∴2233BE AB k EG CG k ===， 故选：C ．19．（2020•遂宁）如图，在正方形ABCD 中，点E 是边BC 的中点，连接AE 、DE ，分别交BD 、AC 于点P 、Q ，过点P 作PF AE ⊥交CB 的延长线于F ，下列结论：①90AED EAC EDB ∠+∠+∠=︒，②AP FP =，③10AE AO =， ④若四边形OPEQ 的面积为4，则该正方形ABCD 的面积为36，⑤CE EF EQ DE =．其中正确的结论有( )A ．5个B ．4个C ．3个D ．2个【解答】解：如图，连接OE ．四边形ABCD 是正方形，AC BD ∴⊥，OA OC OB OD ===，90BOC ∴∠=︒，BE EC =，45EOB EOC ∴∠=∠=︒， EOB EDB OED ∠=∠+∠，EOC EAC AEO ∠=∠+∠，90AED EAC EDO EAC AEO OED EDB ∴∠+∠+∠=∠+∠+∠+∠=︒，故①正确，连接AF ．PF AE ⊥，90APF ABF ∴∠=∠=︒，A ∴，P ，B ，F 四点共圆，45AFP ABP ∴∠=∠=︒，45PAF PFA ∴∠=∠=︒，PA PF ∴=，故②正确，设BE EC a ==，则5AE a =，2OA OC OB OD a ====，∴5102AE a AO a ==，即10AE AO =，故③正确，根据对称性可知，OPE OQE ∆≅∆，122OEQ OPEQ S S ∆∴==四边形，OB OD =，BE EC =，2CD OE ∴=，//OE CD ，∴12EQ OE DQ CD ==，OEQ CDQ ∆∆∽，4ODQ S ∆∴=，8CDQ S ∆=，12CDO S ∆∴=，48ABCD S ∴=正方形，故④错误，90EPF DCE ∠=∠=︒，PEF DEC ∠=∠，EPF ECD ∴∆∆∽，∴EF PEED EC =，EQ PE =，CE EF EQ DE ∴=，故⑤正确，故选：B ．20．（2020•自贡）在平面直角坐标系中，将点(2,1)向下平移3个单位长度，所得点的坐标是()A ．(1,1)-B ．(5,1)C ．(2,4)D ．(2,2)-【解答】解：将点(2,1)向下平移3个单位长度所得点的坐标为(2,13)-，即(2,2)-；故选：D ．21．（2020•遂宁）下列图形中，既是轴对称图形，又是中心对称图形的是( )A ．等边三角形B ．平行四边形C ．矩形D ．正五边形【解答】解：A 、等边三角形是轴对称图形，不是中心对称图形．故本选项不合题意； B 、平行四边形是中心对称图形，不是轴对称图形．故本选项不合题意；C 、矩形既是轴对称图形，又是中心对称图形．故本选项符合题意；D 、正五边形是轴对称图形，不是中心对称图形．故本选项不合题意．故选：C ．22．（2019•阿坝州）如图，ABC ∆中，//DE BC ，2AD =，1DB =，4AE =，则EC 的长度为( )A ．1B ．2C ．3D ．4【解答】解：//DE BC ，∴AD AE DB EC =， 又2AD =，1DB =，4AE =，∴241EC=， 2EC ∴=，故选：B ．23．（2019•雅安）如图是下面哪个图形的俯视图( )A ．B ．C ．D ．【解答】解：A ．球的俯视图为一个圆（不含圆心），不合题意；B ．圆柱的俯视图为一个圆（不含圆心），不合题意； C ．圆台的俯视图为两个同心圆，不合题意；D ．圆锥的俯视图为一个圆（含圆心），符合题意； 故选：D ．24．（2019•雅安）如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△111A B C 相似的是( )A ．B ．C ．D ．【解答】解：因为△111A B C 中有一个角是135︒，选项中，有135︒角的三角形只有B ，且满足两边成比例夹角相等，25．（2019•内江）如图，将ABC ∆沿着过BC 的中点D 的直线折叠，使点B 落在AC 边上的1B 处，称为第一次操作，折痕DE 到AC 的距离为1h ；还原纸片后，再将BDE ∆沿着过BD 的中点1D 的直线折叠，使点B 落在DE 边上的2B 处，称为第二次操作，折痕11D E 到AC 的距离记为2h ；按上述方法不断操作下去⋯⋯经过第n 次操作后得到折痕11n n D E --，到AC 的距离记为n h ．若11h =，则n h 的值为( )A ．1112n -+B ．112n +C ．1122n -- D ．122n-【解答】解：D 是BC 的中点，折痕DE 到AC 的距离为1h ∴点B 到DE 的距离11h ==，1D 是BD 的中点，折痕11D E 到AC 的距离记为2h ，11D E ∴到AC 的距离21h h =+点B 到11D E 的距离1111122h =+=+，同理：3211111424h h h =+=++，431111118248h h h =+=+++⋯⋯11111111224822n n n h --=++++⋯+=-故选：C ． 26．（2019•内江）下列几何体中，主视图为三角形的是( )A ．B ．C ．D ． 【解答】解：A 、主视图是三角形，故此选项正确； B 、主视图是矩形，故此选项错误； C 、主视图是圆，故此选项错误； D 、主视图是矩形，故此选项错误； 故选：A ． 27．（2019•内江）如图，在ABC ∆中，//DE BC ，9AD =，3DB =，2CE =，则AC 的长为( )A ．6B ．7C ．8D ．9【解答】解：//DE BC ， ∴AD AE DB EC =，即932AE =， 6AE ∴=，628AC AE EC ∴=+=+=．二．填空题（共11小题） 28．（2020•德阳）如图，海中有一小岛A ，它周围10.5海里内有暗礁，渔船跟踪鱼群由西向东航行．在B 点测得小岛A 在北偏东60︒方向上，航行12海里到达D 点，这时测得小岛A 在北偏东30︒方向上．如果渔船不改变航线继续向东航行，那么渔船还需航行 4.5 海里就开始有触礁的危险．【解答】解：只要求出A 到BD 的最短距离是否在以A 为圆心，以10.5海里的圆内或圆上即可， 如图，过A 作AC BD ⊥于点C ，则AC 的长是A 到BD 的最短距离， 30CAD ∠=︒，60CAB ∠=︒，603030BAD ∴∠=︒-︒=︒，906030ABD ∠=︒-︒=︒， ABD BAD ∴∠=∠， 12BD AD ∴==海里，30CAD ∠=︒，90ACD ∠=︒，162CD AD ∴==海里，由勾股定理得：2212663AC =-=（海里），如图，设渔船还需航行x 海里就开始有触礁的危险，即到达点D '时有触礁的危险， 在直角△AD C '中，由勾股定理得：222(6)(63)10.5x -+=． 解得 4.5x =．渔船还需航行4.5海里就开始有触礁的危险． 故答案是：4.5．29．（2020•眉山）如图，在Rt ABC ∆中，90BAC ∠=︒，2AB =．将ABC ∆绕点A 按顺时针方向旋转至 △11AB C 的位置，点1B 恰好落在边BC 的中点处，则1CC 的长为 23 ．【解答】解：在Rt ABC ∆中，90BAC ∠=︒，将该三角形绕点A 按顺时针方向旋转到△11AB C 的位置，点1B 恰好落在边BC 的中点处，112AB BC ∴=，11BB B C =，1AB AB =，11BB AB AB ∴==，1ABB ∴∆是等边三角形， 160BAB B ∴∠=∠=︒，160CAC ∴∠=︒，将ABC ∆绕点A 按顺时针方向旋转至△11AB C 的位置，1CA C A ∴=，∴△1AC C 是等边三角形，1CC CA ∴=， 2AB =， 23CA ∴=， 123CC ∴=．故答案为：23． 30．（2020•宜宾）在Rt ABC ∆中，90ACB ∠=︒，D 是AB 的中点，BE 平分ABC ∠交AC 于点E ，连结CD交BE 于点O ．若8AC =，6BC =，则OE 的长是 95．【解答】解：在Rt ACB ∆中，90ACB ∠=︒，8AC =，6BC =，由勾股定理得：10AB =， 过A 作//AF BC ，交BE 延长线于F ，//AF BC ， F CBE ∴∠=∠， BE 平分ABC ∠， ABE CBE ∴∠=∠， F ABE ∴∠=∠， 10AB AF ∴==， //AF BC ，AEF CEB ∴∆∆∽， ∴AF AE BC CE =， ∴1068AE AE=-， 解得：5AE =，853CE =-=，在Rt ECB ∆中，由勾股定理得：226335BE =+=， 过D 作//DM AC ，交BC 于M ，交BE 于N ，D为AB的中点，//DM AC，M∴为BC的中点，N为BE的中点，115 2.522DN AE∴==⨯=，1352BN NE BE===，//DM AC，DNO CEO∴∆∆∽，∴DN ONCE EO=，∴352.523OEOE-=，解得：95OE=，故答案为：95．31．（2020•绵阳）平面直角坐标系中，将点(1,2)A-先向左平移2个单位，再向上平移1个单位后得到的点1A的坐标为(3,3)-．【解答】解：将点(1,2)A-先向左平移2个单位，横坐标2-，再向上平移1个单位纵坐标1+，∴平移后得到的点1A的坐标为：(3,3)-．故答案为：(3,3)-．32．（2020•宜宾）如图，四边形ABCD中，DA AB⊥，CB AB⊥，3AD=，5AB=，2BC=，P是边AB 上的动点，则PC PD+的最小值是52．【解答】解：延长CB到C'，使2C B CB'==，连接DC'交AB于P．则DC'就是PC PD+的和的最小值．//AD BC，A PBC∴∠=∠'，ADP C∠=∠'，ADP∴∆∽△BC P'，::3:2AP BP AD BC∴='=，'23PB AP∴=，5AP BP AB+==，3AP∴=，2BP=，22223332PD AD AP∴=+=+22222222PC BP BC'=+'=+，322252DC PD PC∴'=+'==PC PD∴+的最小值是52故答案为52．33．（2020•攀枝花）如图，在边长为4的正方形ABCD 中，点E 、F 分别是BC 、CD 的中点，DE 、AF 交于点G ，AF 的中点为H ，连接BG 、DH ．给出下列结论：①AF DE ⊥；②85DG =；③//HD BG ；④ABG DHF ∆∆∽．其中正确的结论有 ①④ ．（请填上所有正确结论的序号）【解答】解：四边形ABCD 为正方形， 90ADC BCD ∴∠=∠=︒，AD CD =， E 和F 分别为BC 和CD 中点， 2DF EC ∴==，()ADF DCE SAS ∴∆≅∆，AFD DEC ∴∠=∠，FAD EDC ∠=∠， 90EDC DEC ∠+∠=︒， 90EDC AFD ∴∠+∠=︒，90DGF ∴∠=︒，即DE AF ⊥，故①正确；4AD =，122DF CD ==，224225AF ∴=+=，45DG AD DF AF ∴=⨯÷=，故②错误； H 为AF 中点，152HD HF AF ∴==，HDF HFD ∴∠=∠， //AB DC ，HDF HFD BAG ∴∠=∠=∠，2285AG AD DG =-=，4AB =， ∴45AB AB AG DH HF DF===， ~ABG DHF ∴∆∆，故④正确； ABG DHF ∴∠=∠，而AB AG ≠， 则ABG ∠和AGB ∠不相等， 故AGB DHF ∠≠∠，故HD 与BG 不平行，故③错误； 故答案为：①④．34．（2020•凉山州）如图，矩形ABCD 中，12AD =，8AB =，E 是AB 上一点，且3EB =，F 是BC 上一动点，若将EBF ∆沿EF 对折后，点B 落在点P 处，则点P 到点D 的最短距离为 10 ．【解答】解：如图，连接PD ，DE ，四边形ABCD 是矩形， 90A ∴∠=︒，8AB =，3BE =， 5AE ∴=， 12AD =，2251213DE ∴=+=， 由折叠得：3EB EP ==， EP DP ED +，∴当E 、P 、D 共线时，DP 最小， 13310DP DE EP ∴=-=-=； 故答案为：10． 35．（2020•泸州）如图，在矩形ABCD 中，E ，F 分别为边AB ，AD 的中点，BF 与EC 、ED 分别交于点M ，N ．已知4AB =，6BC =，则MN 的长为 43．【解答】解：延长CE 、DA 交于Q ，如图1，四边形ABCD 是矩形，6BC =，90BAD ∴∠=︒，6AD BC ==，//AD BC ， F 为AD 中点， 3AF DF ∴==，在Rt BAF ∆中，由勾股定理得：2222435BF AB AF =+=+=， //AD BC ， Q ECB ∴∠=∠，E 为AB 的中点，4AB =， 2AE BE ∴==， 在QAE ∆和CBE ∆中 QEA BEC Q ECB AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩()QAE CBE AAS ∴∆≅∆， 6AQ BC ∴==， 即639QF =+=， //AD BC ，QMF CMB ∴∆∆∽， ∴96FM QF BM BC ==， 5BF =，2BM ∴=，3FM =，延长BF 和CD ，交于W ，如图2，同理4AB DW ==，8CW =，5BF FW ==， //AB CD ，BNE WND ∴∆∆∽， ∴BN BE NW DW =， ∴2554BN BN =-+，解得：103BN =， 104233MN BN BM ∴=-=-=， 故答案为：43． 36．（2020•自贡）如图，我市在建高铁的某段路基横断面为梯形ABCD ，//DC AB ．BC 长6米，坡角β为45︒，AD 的坡角α为30︒，则AD 长为 62 米（结果保留根号）．【解答】解：过点D 作DE AB ⊥于E ，过点C 作CF AB ⊥于F ．//CD AB ，DE AB ⊥，CF AB ⊥， DE CF ∴=，在Rt CFB ∆中，sin 4532CF BC =︒=（米)，32DE CF ∴==（米)，在Rt ADE ∆中，30A ∠=︒，90AED ∠=︒， 262AD DE ∴==（米)，故答案为：62． 37．（2020•乐山）如图是某商场营业大厅自动扶梯示意图．自动扶梯AB 的倾斜角为30︒，在自动扶梯下方地面C 处测得扶梯顶端B 的仰角为60︒，A 、C 之间的距离为4m ．则自动扶梯的垂直高度BD = 23 m ．（结果保留根号）【解答】解：BCD BAC ABC ∠=∠+∠，30BAC ∠=︒，60BCD ∠=︒， 30ABC BCD BAC ∴∠=∠-∠=︒， BAC ABC ∴∠=∠， 4BC AC ∴==，在Rt BDC ∆中，sin BDBCD BC∠=，3sin 604BD ∴︒==， 23()BD m ∴=， 故答案为：338．（2020•甘孜州）如图，有一张长方形纸片ABCD ，8AB cm =，10BC cm =，点E 为CD 上一点，将纸片沿AE 折叠，BC 的对应边B C ''恰好经过点D ，则线段DE 的长为 5 cm ．【解答】解：将纸片沿AE 折叠，BC 的对应边B C ''恰好经过点D ， 8AB AB cm '∴==，10BC B C cm ''==，CE C E '=，22100646B D AD B A cm ''∴=-=-=， 4C D B C B D cm ''''∴=-=， 222DE C D C E ''=+， 2216(8)DE DE ∴=+-， 5DE cm ∴=， 故答案为：5．三．解答题（共2小题） 39．（2020•内江）为了维护我国海洋权力，海监部门对我国领海实行了常态化巡航管理．如图，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A 处测得灯塔P 在北偏东60︒方向上，海监船继续向东航行1小时到达B 处，此时测得灯塔P 在北偏东30︒方向上． （1）求B 处到灯塔P 的距离；（2）已知灯塔P 的周围50海里内有暗礁，若海监船继续向正东方向航行是否安全？【解答】解：（1）30PAB ∠=︒，120ABP ∠=︒， 18030APB PAB ABP ∴∠=︒-∠-∠=︒， 60PB AB ∴==海里；（2）作PH AB ⊥于H ． 30BAP BPA ∠=∠=︒， 60BA BP ∴==，在Rt PBH ∆中，3sin 6060303PH PB =︒=⨯=，30350>，∴海监船继续向正东方向航行是安全的．40．（2020•达州）如图，在梯形ABCD 中，//AB CD ，90B ∠=︒，6AB cm =，2CD cm =．P 为线段BC 上的一动点，且和B 、C 不重合，连接PA ，过点P 作PE PA ⊥交射线CD 于点E ．聪聪根据学习函数的经验，对这个问题进行了研究：（1）通过推理，他发现ABP PCE ∆∆∽，请你帮他完成证明．（2）利用几何画板，他改变BC 的长度，运动点P ，得到不同位置时，CE 、BP 的长度的对应值： /BP cm⋯ 1 2 3 4 5 ⋯/CE cm⋯ 0.83 1.33 1.50 1.33 0.83 ⋯/BP cm⋯ 1 2 3 4 5 6 7 ⋯/CE cm⋯ 1.17 2.00 2.50 2.67 2.50 2.00 1.17 ⋯①填空：根据函数的定义，我们可以确定，在BP 和CE 的长度这两个变量中， BP 的长度为自变量， 的长度为因变量；②设BC mcm =，当点P 在线段BC 上运动时，点E 总在线段CD 上，求m 的取值范围．【解答】（1）证明：//AB CD ， 180B C ∴∠+∠=︒， 90B ∠=︒，90B C ∴∠=∠=︒， AP PE ⊥， 90APE ∴∠=︒，90APB EPC ∴∠+∠=︒， 90EPC PEC ∠+∠=︒， APB PEC ∴∠=∠， ABP PCE ∴∆∆∽．（2）解：①根据函数的定义，我们可以确定，在BP 和CE 的长度这两个变量中，BP 的长度为自变量，EC 的长度为因变量，故答案为：BP ，EC ．②设BP xcm =，CE ycm =． ABP PCE ∆∆∽， ∴AB BP PC CE =， ∴6x m x y=-， 2221111()666224m y x mx x m ∴=-+=--+， 106-<， 12x m ∴=时，y 有最大值224m ， 点E 在线段CD 上，2CD cm =，∴22 24m，43 m∴，043m∴<．。