第九章杆件的变形及刚度计算

《建筑力学》课程教学大纲一、本课程的地位、作用和任务《建筑力学》是水利水电建筑工程专业的一门重要的专业基础课，在本专业中起着承上启下的作用，为后续课程打基础。

《建筑力学》的任务是：教授学生掌握物体受力分析与静力平衡问题的求解方法；杆件及结构内力与变形的分析方法；关于构件的强度、刚度与稳定性的计算及构件应力、应变的方法。

通过本课程的学习，要求学生具备对常见结构、构件进行受力分析、内力与变形计算的能力，并初步具备对结构的实验分析能力。

二、教学内容和教学要求第一章绪论1、教学内容建筑力学的研究对象、研究方法、主要内容。

2、教学要求了解建筑力学课程的性质、地位和作用，了解建筑力学各部分的内容、了解建筑力学的学习方法。

第一篇、静力学第二章刚体静力分析基础1、教学内容2—1 力与力偶1）力的概念和性质2）力对点之矩3）力偶的概念和性质2—2 约束与约束反力1）约束与约束反力的概念2）工程中常见的约束与约束反力2—3 受力分析与受力图2、教学要求（1）理解力、力对点的矩、平面力偶的概念及静力学的四个公理，合力矩定理、刚体的概念；掌握平面力偶系合成的计算。

（2）了解约束的概念及荷载的分类；了解作用在构件上荷载的计算方法；掌握常见工程中的约束类型及其约束反力的确定；第三章平面力系1、教学内容3—1 平面力系向一点的简化1）力的平移定理2）平面力系向一点的简化3）力在坐标轴上的投影主矢与主矩的计算4）平面力系向一点简化结果的进一步分析3—2 平衡方程及其应用1）平面一般力系的平衡条件和平衡方程2）平面力系的几种特殊情形3）静定与超静定问题4）物体系的平衡问题2、教学要求（1）了解力的平移定理的内容；掌握力在坐标轴上的投影的概念及计算，掌握合力的投影定理；（2）理解平面一般力系的概念；了解平面一般力系向一点简化和简化结果分析。

（3）掌握平面一般力系、平面汇交力系、平面平行力系及平面力偶系的平衡方程及其应用，重点掌握常见物体支座反力的求法。

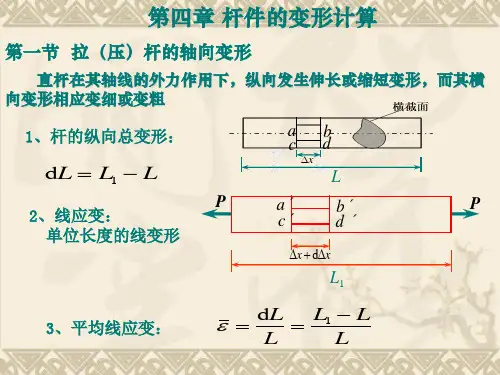
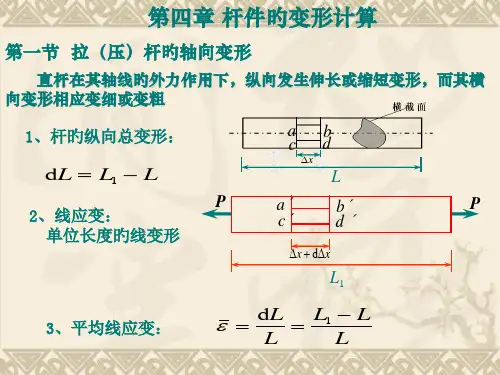
抗弯刚度计算公式ei在结构力学中，抗弯刚度是指杆件或梁的抵抗弯曲变形的能力。

抗弯刚度计算公式EI是计算杆件或梁的抗弯刚度的基本公式，其中E表示杨氏模量，I表示截面惯性矩。

在实际工程中，抗弯刚度是一个非常重要的参数，它直接影响着杆件或梁的承载能力和稳定性。

因此，准确地计算抗弯刚度是非常必要的。

在计算抗弯刚度时，首先需要确定杆件或梁的材料和截面形状，然后根据公式EI进行计算。

材料的选择对于抗弯刚度的计算至关重要。

不同材料的杨氏模量不同，因此使用不同材料的杆件或梁的抗弯刚度也会有所不同。

在实际工程中，常用的材料有钢、混凝土、木材等。

截面形状也是影响抗弯刚度的重要因素。

不同截面形状的杆件或梁的抗弯刚度也会有所不同。

常见的截面形状有矩形、圆形、梯形等。

在计算抗弯刚度时，需要先计算出截面惯性矩。

截面惯性矩是描述杆件或梁抵抗弯曲变形能力的重要参数，它反映了截面形状和材料的特性。

截面惯性矩越大，杆件或梁的抗弯刚度就越大。

计算截面惯性矩时，需要根据截面形状进行计算。

对于矩形截面，截面惯性矩的计算公式为I=bh^3/12，其中b为截面宽度，h为截面高度。

对于圆形截面，截面惯性矩的计算公式为I=πr^4/4，其中r为截面半径。

对于梯形截面，截面惯性矩的计算公式为I=(b1h1^3-b2h2^3)/12，其中b1、b2为上下底宽度，h1、h2为上下底高度。

计算出截面惯性矩后，就可以根据公式EI计算出杆件或梁的抗弯刚度。

公式EI的计算公式为EI=E*I，其中E为杨氏模量，I为截面惯性矩。

需要注意的是，公式EI只适用于杆件或梁在弹性范围内的抗弯刚度计算。

当杆件或梁受到超过弹性极限的载荷时，就会发生塑性变形，此时抗弯刚度就会发生变化。

总之，抗弯刚度计算公式EI是计算杆件或梁抗弯刚度的基本公式，它对于工程设计和结构分析具有重要意义。

在实际工程中，需要根据具体情况选择合适的材料和截面形状，并准确地计算出截面惯性矩和抗弯刚度，以确保结构的承载能力和稳定性。

割线刚度计算公式割线刚度是指杆件抵抗弯曲的能力。

在工程力学中，割线刚度是一个重要的概念，它用于描述杆件在受到外力作用时的变形情况。

割线刚度决定了杆件的弯曲程度和抵抗弯曲的能力，对于工程设计和结构分析具有重要的意义。

割线刚度的计算公式可以通过弯曲力和弯曲矩来表示。

弯曲力是指作用在杆件上的力，弯曲矩是指力对杆件产生的弯曲效应。

割线刚度的计算公式可以表示为割线刚度=弯曲力/弯曲矩。

在实际的工程设计中，割线刚度的计算是非常重要的。

它可以帮助工程师确定杆件的强度和稳定性，并为结构的设计和分析提供依据。

在制定工程设计方案时，工程师需要根据割线刚度的计算结果来选择合适的材料和尺寸，以确保结构的安全性和可靠性。

割线刚度的计算公式是工程力学中的基础知识，它不仅可以应用于静力学的计算，还可以应用于动力学、弹性力学等领域。

通过割线刚度的计算公式，工程师可以对杆件的变形和应力进行准确的分析和计算。

割线刚度的计算公式不仅适用于简单的杆件，还可以扩展到复杂的结构体系中。

在实际的工程应用中，割线刚度的计算公式可以通过数值方法或者解析方法来求解。

数值方法通过离散化杆件，采用有限元法或者其他数值方法来计算割线刚度。

解析方法则通过解析解来计算割线刚度，适用于简单的结构体系或者特定的边界条件。

割线刚度的计算公式还可以应用于杆件的优化设计。

通过改变材料的性质、尺寸的选择或者结构的布局，可以改变割线刚度的数值，从而达到优化设计的目的。

割线刚度的计算公式可以为工程师提供重要的参考和指导，帮助他们在设计过程中做出正确的决策。

割线刚度的计算公式是工程力学中的重要内容，它可以帮助工程师对杆件的弯曲变形和应力分析进行准确的计算。

割线刚度的计算公式不仅适用于静力学，还可以应用于动力学、弹性力学等领域。

通过割线刚度的计算公式，工程师可以对结构的设计和分析提供重要的参考和指导，确保工程的安全性和可靠性。

杆件的强度计算公式资料讲解杆件的强度、刚度和稳定性计算1.构件的承载能⼒，指的是什么？答：构件满⾜强度、刚度和稳定性要求的能⼒称为构件的承载能⼒。

(1)⾜够的强度。

即要求构件应具有⾜够的抵抗破坏的能⼒，在荷载作⽤下不致于发⽣破坏。

(2)⾜够的刚度。

即要求构件应具有⾜够的抵抗变形的能⼒，在荷载作⽤下不致于发⽣过⼤的变形⽽影响使⽤。

(3)⾜够的稳定性。

即要求构件应具有保持原有平衡状态的能⼒，在荷载作⽤下不致于突然丧失稳定。

2.什么是应⼒、正应⼒、切应⼒？应⼒的单位如何表⽰？答：内⼒在⼀点处的集度称为应⼒。

垂直于截⾯的应⼒分量称为正应⼒或法向应⼒，⽤σ表⽰；相切于截⾯的应⼒分量称切应⼒或切向应⼒，⽤τ表⽰。

应⼒的单位为Pa。

1 Pa=1 N／m2⼯程实际中应⼒数值较⼤，常⽤MPa或GPa作单位1 MPa=106Pa1 GPa=109Pa3.应⼒和内⼒的关系是什么？答：内⼒在⼀点处的集度称为应⼒。

4.应变和变形有什么不同？答：单位长度上的变形称为应变。

单位纵向长度上的变形称纵向线应变，简称线应变，以ε表⽰。

单位横向长度上的变形称横向线应变，以ε/表⽰横向应变。

5.什么是线应变？什么是横向应变？什么是泊松⽐？答：（1）线应变单位长度上的变形称纵向线应变，简称线应变，以ε表⽰。

对于轴⼒为常量的等截⾯直杆，其纵向变形在杆内分布均匀，故线应变为l l?=ε（4-2）拉伸时ε为正，压缩时ε为负。

线应变是⽆量纲（⽆单位）的量。

（2）横向应变拉(压)杆产⽣纵向变形时，横向也产⽣变形。

设杆件变形前的横向尺⼨为a，变形后为a1，则横向变形为aaa-=1横向应变ε/为a a=/ε（4-3）杆件伸长时，横向减⼩，ε/为负值；杆件压缩时，横向增⼤，ε/为正值。

因此，拉(压)杆的线应变ε与横向应变ε/的符号总是相反的。

（3）横向变形系数或泊松⽐试验证明，当杆件应⼒不超过某⼀限度时，横向应变ε/与线应变ε的绝对值之⽐为⼀常数。

此⽐值称为横向变形系数或泊松⽐，⽤µ表⽰。

第九章 压杆稳定第一节 压杆稳定的概念对于一般的构件，其满足强度及刚度条件时，就能确保其安全工作。

但对于细长压杆，不仅要满足强度及刚度条件，而且还必须满足稳定条件，才能安全工作。

例如，取两根截面（宽300mm ，厚5mm ）相同；其抗压强度极限40=c σMpa 的松木杆；长度分别为30mm 和1000mm ，进行轴向压缩试验。

试验结果，长为30mm 的短杆，承受的轴向压力可高达6kN （A c σ），属于强度问题；长为1000mm 的细长杆，在承受不足30N 的轴向压力时起就突然发生弯曲，如继续加大压力就会发生折断，而丧失承载能力，属于压杆稳定性问题。

如图9-1(a)所示，下端固定，上端自由的理想细长直杆，在上端施加一轴向压力P 。

试验发现当压力P 小于某一数值cr P 时，若在横向作用一个不大的干扰力，如图9-1b 所示，杆将产生横向弯曲变形。

但是，若横向干扰力消失，其横向弯曲变形也随之消失，如图9-1c 所示，杆仍然保持原直线平衡状态，这种平衡形式称为稳定平衡。

当压力cr P P =时，杆仍然保持直线平衡，但此时再在横向作用一个不大的干扰力，其立刻转为微弯平衡，但此时在，如图9-1d 所示，并且当干扰力消失后，其不能再回到原来的直线平衡状态，这种平衡形式称为不稳定平衡。

压杆由原直线平衡状态转为曲线平衡状态，称为丧失稳定性，简称失稳。

使压杆原直线的平衡由稳定转变为不稳定的轴向压力值cr P ，称为压杆的临界载荷。

在临界载荷作用下，压杆既能在直线状态下保持平衡，也能在微弯状态保持平衡。

所以，当轴向压力达到或超过压杆的临界载荷时，压杆将产生失稳现象。

图9-1在工程实际中，考虑细长压杆的稳定性问题非常重要。

因为这类构件的失稳常发生在其强度破坏之前，而且是瞬间发生的，以至于人们猝不及防，所以更具危险性。

例如：1907年，加拿大魁北克的圣劳伦斯河上一座跨度为548m 的钢桥，在施工过程中，由于两根受压杆件失稳，而导致全桥突然坍塌的严重事故；1912年，德国汉堡一座煤气库由于其一根受压槽钢压杆失稳，而致致使其破坏。