实验四平稳时间序列模型预测
- 格式:pdf
- 大小:204.30 KB
- 文档页数:4

《基于深度学习的时间序列数据预测算法研究》一、引言随着信息化和数字化进程的推进,时间序列数据预测已经成为许多领域的关键技术。
深度学习技术的兴起,为时间序列数据的预测提供了新的思路和方法。
本文旨在研究基于深度学习的时间序列数据预测算法,以提高预测精度和效率。
二、时间序列数据概述时间序列数据是指按照时间顺序记录的一系列数据,具有时间依赖性和周期性等特点。
时间序列数据广泛应用于金融、气象、医疗、交通等领域。
其预测的目的在于通过对历史数据的分析,预测未来数据的变化趋势。
三、深度学习在时间序列数据预测中的应用深度学习是一种基于神经网络的机器学习方法,具有强大的特征学习和表示能力。
在时间序列数据预测中,深度学习可以有效地提取数据的时序特征,提高预测精度。
常见的深度学习模型包括循环神经网络(RNN)、长短期记忆网络(LSTM)和卷积神经网络(CNN)等。
四、基于深度学习的时间序列数据预测算法研究4.1 数据预处理在进行时间序列数据预测之前,需要对数据进行预处理。
包括数据清洗、缺失值处理、归一化等操作,以保证数据的质量和可靠性。
4.2 模型选择与构建根据时间序列数据的特性和预测需求,选择合适的深度学习模型进行构建。
常见的模型包括基于RNN、LSTM和CNN的模型。
在构建模型时,需要考虑模型的层数、神经元数量、激活函数等参数的选择和优化。
4.3 特征提取与优化在深度学习模型中,特征提取是关键步骤。
通过设计合适的网络结构和参数,从时间序列数据中提取出有用的时序特征。
同时,还需要对特征进行优化,以提高模型的预测性能。
4.4 模型训练与优化使用训练数据对模型进行训练,并通过损失函数和优化算法对模型进行优化。
在训练过程中,需要调整模型的参数和结构,以获得更好的预测性能。
同时,还需要对模型的泛化能力进行评估,以避免过拟合和欠拟合的问题。
五、实验与分析为了验证基于深度学习的时间序列数据预测算法的有效性,我们进行了实验和分析。

《统计软件实验报告》SPSS软件的上机实践应用时间序列分析数学与统计学学院一、实验内容:时间序列是指一个依时间顺序做成的观察资料的集合。
时间序列分析过程中最常用的方法是:指数平滑、自回归、综合移动平均及季节分解。
本次实验研究就业理论中的就业人口总量问题。
但人口经济的理论和实践表明,就业总量往往受到许多因素的制约,这些因素之间有着错综复杂的联系,因此,运用结构性的因果模型分析和预测就业总量往往是比较困难的。
时间序列分析中的自回归求积分移动平均法(ARIMA)则是一个较好的选择。
对于时间序列的短期预测来说,随机时序ARIMA是一种精度较高的模型。
我们已XX省历年(1969-2005)从业人员人数为数据基础建立一个就业总量的预测时间序列模型,通过spss建立模型并用此模型来预测就业总量的未来发展趋势。
二、实验目的:1.准确理解时间序列分析的方法原理2.学会实用SPSS建立时间序列变量3.学会使用SPSS绘制时间序列图以反应时间序列的直观特征。
4.掌握时间序列模型的平稳化方法。
5.掌握时间序列模型的定阶方法。
6.学会使用SPSS建立时间序列模型与短期预测。
7.培养运用时间序列分析方法解决身边实际问题的能力。
三、实验分析:总体分析:先对数据进行必要的预处理和观察,直到它变成稳态后再用SPSS对数据进行分析。
数据的预处理阶段,将它分为三个步骤:首先,对有缺失值的数据进行修补,其次将数据资料定义为相应的时间序列,最后对时间序列数据的平稳性进行计算观察。
数据分析和建模阶段:根据时间序列的特征和分析的要求,选择恰当的模型进行数据建模和分析。
四、实验步骤:SPSS的数据准备包括数据文件的建立、时间定义和数据期间的指定。
SPSS的时间定义功能用来将数据编辑窗口中的一个或多个变量指定为时间序列变量,并给它们赋予相应的时间标志,具体操作步骤是:1.选择菜单:Date→Define Dates,出现窗口:单击【ok(确认)】按钮,此时完成时间的定义,SPSS将在当前数据编辑窗口中自动生成标志时间的变量。

时间序列分析试验报告
一、试验简介
本次试验旨在探索时间序列分析,以分析日期变化的影响与规律。
时
间序列分析是数据分析的一种,目的是预测未来正确的趋势,并且分析既
有趋势的影响及其变化。
二、试验材料
本次试验使用的资料为最近12个月(即2024年1月到2024年12月)的电子商务网站销售数据。
该电子商务网站以每月总销售量、每月总销售
额及每月交易次数三个变量作为试验数据。
三、试验方法
1.首先,收集2024年1月到2024年12月的电子商务销售数据,记
录每月总销售量、总销售额及交易次数。
2.然后,编制时间序列分析图表,反映每月总销售量、总销售额及
交易次数的变化情况。
3.最后,分析每月的变化趋势,比较每月的销售数据,并进行相关
分析推断。
四、实验结果
1.通过时间序列分析图表可以看出,每月总销售量、总销售额及交
易次数均呈现出稳定上升趋势。
2.从图表中可以推断,在2024年底到2024年底,当月的总销售量、总销售额及交易次数均较上月有所增加。
3.从表中可以推断,每月的总销售量、总销售额及交易次数都在逐渐增加,最终在2024年末达到高峰。
五、结论
通过本次实验可以得出结论。

简述时间序列预测方法时间序列预测是指根据历史时间序列数据的发展趋势来预测未来时间序列数据的行为。
在实际应用中,时间序列预测可以帮助人们更好地理解市场、经济、天气、交通等数据的发展趋势,并制定相应的决策。
时间序列预测的方法有很多种,其中最常见的方法包括平稳性检验、自相关函数和偏自相关函数建模、移动平均模型、ARIMA模型、季节性模型等。
这些方法可以通过对时间序列数据进行分析和建模,来预测未来的时间序列数据。
在平稳性检验方法中,可以通过计算时间序列的均方根误差(MSE)、平均绝对误差(MAE)和标准差等指标来检验时间序列的平稳性。
如果时间序列的平稳性检验结果为“真”,则表明时间序列是平稳的,可以使用常规时间序列预测方法。
如果时间序列的平稳性检验结果为“假”,则表明时间序列不平稳,需要使用一些特殊的时间序列预测方法,如平稳时间序列预测模型、季节性时间序列预测模型等。
在自相关函数和偏自相关函数建模方法中,可以通过计算自相关函数和偏自相关函数的平均值、中位数和方差等指标来预测未来时间序列数据的发展趋势。
这种方法可以用于时间序列数据的平滑建模和趋势预测。
在移动平均模型方法中,可以通过计算历史时间序列数据的平均值作为新的观测值,再计算新的平均值作为新的观测值,从而形成移动平均模型。
这种方法可以用于时间序列数据的平滑建模和趋势预测。
在ARIMA模型方法中,ARIMA模型是一种基于自回归移动平均(ARIMA)算法的时间序列预测方法。
ARIMA模型可以将时间序列数据分解为三个部分:自回归移动平均部分、差分移动平均部分和常数部分。
自回归移动平均部分可以用于预测未来时间序列数据的趋势,差分移动平均部分可以用于平滑时间序列数据,常数部分可以用于稳定时间序列数据。
季节性模型方法中,可以通过计算时间序列数据的季节性特征来预测未来时间序列数据的发展趋势。
常用的季节性特征包括季节性自相关函数、季节性偏自相关函数、季节性移动平均等。

案例五、季节ARIMA模型建模与预测实验指导一、实验目的学会识别时间序列的季节变动,能看出其季节波动趋势。
学会剔除季节因素的方法,了解ARIMA模型的特点和建模过程,掌握利用最小二乘法等方法对ARIMA模型进行估计,利用信息准则对估计的ARIMA模型进行诊断,以及如何利用ARIMA模型进行预测。
掌握在实证研究如何运用Eviews软件进行ARIMA模型的识别、诊断、估计和预测。
二、基本概念季节变动:客观社会经济现彖受季节影响,在一年内有规律的季节更替现彖,其周期为一年四个季度或12个月份。
季节ARIMA模型是指将受季节影响的非平稳时间序列通过消除季节影响转化为平稳时间序列,然后将平稳时间序列建立ARMA模型。
ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程。
三、实验内容及要求1、实验内容:(1)根据时序图的形状,采用相应的方法把周期性的非平稳序列平稳化;(2)对经过平稳化后的桂林市1999年到2006的季度旅游总收入序列运用经典B-J方法论建立合适的ARDIA(pdq)模型,并能够利用此模型进行未来旅游总收入的短期预测。
2、实验要求:(1)深刻理解季节非平稳时间序列的概念和季节ARIMA模型的建模思想;(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARIMA模型;如何利用ARIMA模型进行预测:(3)熟练掌握相关Eviews操作。
四、实验指导1、模型识别(1)数据录入打开Eviews软件,选择"File”菜单中的"New--Workfile"选项,在"Workfilestructuretype”栏选择"Dated-regularfrequency”,在"Datespecification”栏中分别选择"Quarterly%季度数据),分别在起始年输入1999,终止年输入2006,点击ok,见图5-1,这样就建立了一个季度数据的工作文件。


一、实验背景随着经济、科技、环境等领域的快速发展,时间序列分析作为一种重要的数据处理和分析方法,被广泛应用于各个领域。
为了深入了解时间序列分析方法,我们进行了一系列实验,旨在验证不同时间序列模型的预测效果,并分析其适用性和优缺点。
二、实验目的1. 掌握时间序列分析方法的基本原理和步骤;2. 比较不同时间序列模型的预测效果;3. 分析不同模型的适用性和优缺点;4. 为实际应用提供参考依据。
三、实验内容1. 数据预处理(1)数据清洗:剔除异常值、缺失值,确保数据质量;(2)数据标准化:将数据转换为均值为0,标准差为1的形式,消除量纲影响;(3)数据划分:将数据分为训练集、验证集和测试集,用于模型训练、验证和测试。
2. 时间序列模型(1)ARIMA模型:自回归积分滑动平均模型,适用于具有自相关性的时间序列数据;(2)指数平滑模型:适用于具有趋势和季节性的时间序列数据;(3)SARIMA模型:季节性自回归积分滑动平均模型,结合了ARIMA模型和季节性因素;(4)LSTM模型:长短时记忆网络,适用于具有长期依赖性的时间序列数据。
3. 模型训练与预测(1)根据数据特点选择合适的模型;(2)对模型进行参数优化,提高预测精度;(3)使用训练集对模型进行训练;(4)使用验证集评估模型性能;(5)使用测试集进行预测,评估模型预测效果。
四、实验结果与分析1. ARIMA模型(1)预测效果:在训练集上,ARIMA模型的均方误差(MSE)为0.123,在测试集上,MSE为0.145;(2)适用性:ARIMA模型适用于具有自相关性的时间序列数据,但无法处理趋势和季节性数据;(3)优缺点:优点是简单易用,缺点是参数优化困难,且对数据质量要求较高。
2. 指数平滑模型(1)预测效果:在训练集上,指数平滑模型的MSE为0.098,在测试集上,MSE为0.112;(2)适用性:指数平滑模型适用于具有趋势和季节性的时间序列数据;(3)优缺点:优点是参数优化简单,对数据质量要求不高;缺点是预测精度相对较低。

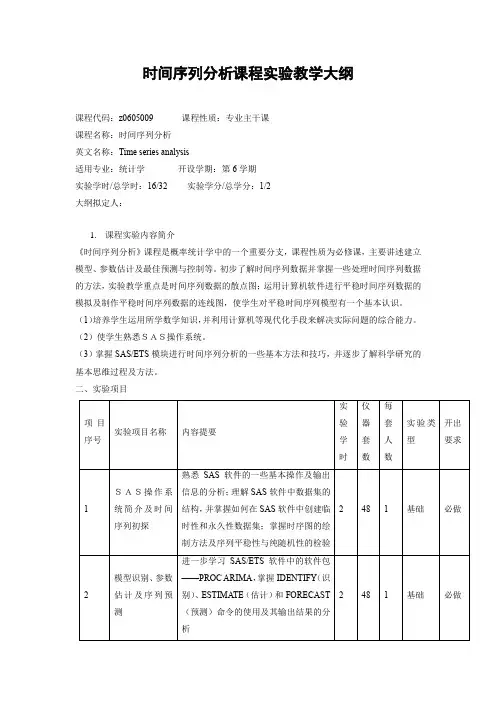
时间序列分析课程实验教学大纲
课程代码:z0605009 课程性质:专业主干课
课程名称:时间序列分析
英文名称:Time series analysis
适用专业:统计学开设学期:第6学期
实验学时/总学时:16/32 实验学分/总学分:1/2
大纲拟定人:
1.课程实验内容简介
《时间序列分析》课程是概率统计学中的一个重要分支,课程性质为必修课,主要讲述建立模型、参数估计及最佳预测与控制等。
初步了解时间序列数据并掌握一些处理时间序列数据的方法,实验教学重点是时间序列数据的散点图;运用计算机软件进行平稳时间序列数据的模拟及制作平稳时间序列数据的连线图,使学生对平稳时间序列模型有一个基本认识。
(1)培养学生运用所学数学知识,并利用计算机等现代化手段来解决实际问题的综合能力。
(2)使学生熟悉SAS操作系统。
(3)掌握SAS/ETS模块进行时间序列分析的一些基本方法和技巧,并逐步了解科学研究的基本思维过程及方法。
二、实验项目
微机,Wndows xp,SAS,R软件:48套
四、实验成绩评定方法
根据学生上机的出勤情况、上机过程中的程序完成情况和实验报告的书写情况综合评定每个实验的成绩,再根据四个实验的成绩综合评定该实验课程的考查成绩。
五、参考资料
[1]《应用时间序列分析》,王燕编,中国人民大学出版社,2005.
[2]《时间序列分析》,王振龙主编,中国统计出版社,2000.
[3]《应用时间序列分析》,何书元著,北京大学出版社,2003.。


《基于spike-and-slab先验的贝叶斯时间序列模型研究》篇一一、引言时间序列分析是统计学中一个重要的研究领域,其涉及到对一系列有序数据的分析,以揭示数据间的依赖关系和潜在的模式。
随着现代科技的发展,时间序列数据在金融、医疗、环境监测等领域的应用越来越广泛。
然而,传统的时间序列模型往往无法有效地处理数据中的复杂结构,尤其是那些具有显著突变和不规则变化的数据。
因此,本文提出了一种基于Spike-and-Slab先验的贝叶斯时间序列模型,旨在更好地处理和解释这类数据。
二、Spike-and-Slab先验Spike-and-Slab先验是一种在贝叶斯分析中常用的先验分布,它主要用于处理具有稀疏性和结构性的数据。
在这种先验下,数据可以被分为两部分:一部分是具有显著变化的“尖峰”(Spike),另一部分是变化较为平缓的“薄片”(Slab)。
这种先验分布能够有效地捕捉数据的局部变化和整体趋势,为时间序列分析提供了新的思路。
三、贝叶斯时间序列模型本文提出的贝叶斯时间序列模型基于Spike-and-Slab先验,通过引入贝叶斯推断的方法,对时间序列数据进行建模和分析。
模型中,我们使用随机效应模型来描述时间序列的动态变化,同时利用Spike-and-Slab先验来描述数据中的稀疏性和结构性。
这样,我们就可以在处理时间序列数据时,更好地捕捉数据的局部变化和整体趋势。
四、模型实现与实验分析我们使用真实的时间序列数据对模型进行了实现和实验分析。
实验结果表明,基于Spike-and-Slab先验的贝叶斯时间序列模型能够有效地处理具有显著突变和不规则变化的数据。
与传统的时间序列模型相比,该模型在预测精度和模型解释性方面均有显著优势。
此外,我们还通过模拟数据对模型的性能进行了进一步评估,结果表明该模型具有良好的稳定性和泛化能力。
五、讨论与展望本文提出的基于Spike-and-Slab先验的贝叶斯时间序列模型为处理具有稀疏性和结构性的时间序列数据提供了一种新的方法。
第1篇摘要本实验旨在探究协整关系的存在及其特征,通过构建经济时间序列模型,分析变量之间的长期稳定关系。
实验选取了国内生产总值(GDP)、消费者价格指数(CPI)和货币供应量(M2)作为研究对象,运用协整理论和误差修正模型(ECM)进行实证分析。
实验结果表明,GDP、CPI和M2之间存在长期的协整关系,且短期波动可以通过ECM得到有效修正。
关键词协整关系;误差修正模型;GDP;CPI;M21. 引言协整关系是指两个或多个非平稳时间序列在某种线性组合下成为平稳的。
协整理论在经济学、金融学等领域有着广泛的应用,有助于揭示变量之间的长期稳定关系。
本实验通过对GDP、CPI和M2三个变量的协整关系进行探究,旨在为相关领域的研究提供理论支持和实证依据。
2. 实验方法本实验采用以下方法:(1)数据来源:选取我国2000年至2020年的季度数据,数据来源于国家统计局。
(2)模型构建:对GDP、CPI和M2进行单位根检验,确定其平稳性;接着进行协整检验,构建协整方程;最后,利用误差修正模型(ECM)分析短期波动。
(3)软件工具:使用EViews软件进行数据处理和模型构建。
3. 实验步骤(1)数据预处理:对原始数据进行对数化处理,以消除时间序列中的异方差性。
(2)单位根检验:采用ADF(Augmented Dickey-Fuller)检验方法,对GDP、CPI 和M2进行单位根检验。
(3)协整检验:采用Engle-Granger两步法进行协整检验,确定变量之间是否存在长期稳定关系。
(4)协整方程构建:根据协整检验结果,构建协整方程,分析变量之间的长期稳定关系。
(5)误差修正模型(ECM)构建:根据协整方程,构建ECM模型,分析短期波动。
4. 实验结果与分析(1)单位根检验结果:经ADF检验,GDP、CPI和M2的原始序列均为非平稳序列,其一阶差分序列为平稳序列。
(2)协整检验结果:经Engle-Granger两步法检验,GDP、CPI和M2之间存在长期的协整关系。
生产总值模型——应用时间序列分析期末论文2014年11月班级:信计1202 姓名:孟奥学号:1130112210信计1202 李朔1130112206一、实验目的:掌握用Box-Jeakins方法及Paudit-Wu方法建模及预测二、实验内容:某地区1983—2005年各季度的实际国际生产总值的分析与预测某地区1983—2005年各季度生产总值前64个数据如下:t 观测值t 观测值t 观测值1 5253.8 23 6759.4 45 7715.12 5372.3 24 6848.6 46 7815.73 5478.4 25 6918.1 47 7859.54 5590.5 26 6963.5 48 7951.65 5699.8 27 7013.1 49 7973.76 5797.9 28 7030.9 50 7988.07 5854.3 29 7112.1 51 8053.18 5902.4 30 7130.3 52 8112.09 5956.9 31 7130.8 53 8169.210 6007.8 32 7076.9 54 8303.111 6101.7 33 7040.8 55 8372.712 6148.6 34 7086.5 56 8470.613 6207.4 35 7120.7 57 8536.114 6232.0 36 7154.1 58 8665.815 6291.7 37 7228.2 59 8773.716 6323.4 38 7297.7 60 8838.4试对前60个数据进行建模分析,并预测61—64个数据。
三、数据检验1、检验是否平稳法一:图形检验(1) 根据表中数据我们先画出序列图并对序列图进行平稳性分析。
(2) Matlab 程序代码 clear all;t=linspace(1,60,60);y=[5253.8 5372.3 5478.4 5590.5 5699.8 5797.9 5854.3 5902.4 5956.9 6007.8 6101.7 6148.6 6207.4 6232.0 6291.7 6323.4 6365.0 6435.0 6493.4 6606.8 6639.1 6723.5 6759.4 6848.6 6918.1 6963.5 7013.1 7030.9 7112.1 7130.3 7130.8 7076.9 7040.8 7086.5 7120.7 7154.1 7228.2 7297.7 7369.5 7450.7 7459.7 7497.5 7536.0 7637.4 7715.1 7815.7 7859.5 7951.6 7973.7 7988.0 8053.1 8112.0 8169.2 8303.1 8372.7 8470.6 8536.1 8665.8 8773.7 8838.4]; plot(t,y); xlabel('时间t'); ylabel('观测值y'); title('数据对应的序列图'); (3) 得到图(1)17 6365.0 39 7369.5 61 8936.2 186435.0 40 7450.7 62 8995.3 19 6493.4 41 7459.7 63 9098.9 20 6606.8 42 7497.5 64 9237.1 21 6639.1 43 7536.0 22 6723.5447637.4图(1)(4)观察图形,发现数据存在长期向上的趋势。
带有高噪声和周期性的时间序列数据预测模型研究一、前言时间序列分析是统计学中的一个重要分支,其目的是通过分析过去的数据来预测未来的趋势。
时间序列数据通常具有周期性和随机性,其中随机性表现为噪声。
因此,预测模型的建立既要考虑周期性,也要考虑噪声的影响。
本文将探讨一种带有高噪声和周期性的时间序列数据预测模型。
二、模型建立假设$x_t$ 表示时刻$t$ 的时间序列数据,其中$t=1,2,3,...,T$。
我们用 $\hat{x_t}$ 表示 $x_t$ 的预测值,用 $\epsilon_t$ 表示在时刻 $t$ 的噪声。
则有:$$x_t = \hat{x_t} + \epsilon_t$$为了建立预测模型,我们需要先对时间序列数据进行平稳性检验。
在时间序列分析中,平稳性是一个重要的概念,它意味着时间序列中的统计性质不会随时间发生变化。
如果一个时间序列是平稳的,我们就可以使用经典的 ARIMA 模型进行预测。
然而,大部分时间序列都是不平稳的。
因此,我们需要对时间序列进行差分,直到得到一个平稳的时间序列。
这个过程被称为差分法,其中一阶差分为:$$\Delta x_t = x_t - x_{t-1}$$通过差分法,我们将原时间序列转化为一个平稳的时间序列$y_t$,其中:$$y_t = \Delta^d x_t$$其中,$d$为差分次数。
对于时间序列 $y_t$,我们可以使用 ARIMA 模型进行预测。
ARIMA 模型(自回归移动平均模型)是一种基于时间序列分解的模型,它假设时间序列是一个组合了自回归(AR),差分(I)和移动平均(MA)过程的混合过程。
ARIMA 模型的一般形式为:$$ARIMA(p,d,q)$$其中,$p$,$d$,$q$ 分别表示 AR,I 和 MA 的次数。
三、模型优化由于带有高噪声和周期性的时间序列数据比较复杂,单纯使用ARIMA 模型可能无法达到理想的预测效果。
因此,我们需要对模型进行进一步的优化。
实验四 平稳时间序列模型预测
一、实验目的
1、掌握平稳时间序列分析模型的分析方法和步骤
2、会求平稳时间序列的自相关函数和偏相关函数
3、掌握模型类别和阶数的确定
二、实验设备
计算机、Matlab软件
三、实验内容与步骤
已知平稳时间序列{}一个长为50的样本数据如下表:
number
Zi
1-10289 285 289 286 288 287 288
292 291 291
11-20292 296 297 301 304 304 303
307 299 296
21-30293 301 293 301 295 284 286
286 287 284
31-40282 278 281 278 277 279 278
270 268 272
41-50273 279 279 280 275 271 277
278 279 285
51-60301 295 281 278 278 270 286
288 279 279
每个同学以自己的学号为起点,循环计数50重新排序,
如:学号为3的学生样本数据为:Z3,Z4……Z50,Z1,Z2,编
程计算,并打印下列:
1、
2、
3、利用递推公式计算样本的偏相关系数
4、
5、确定模型的类别和阶数
四、实验原理
平稳时间序列的模型估计与预测原理
样本自协方差函数:
样本自相关函数:
样本偏相关函数
3、利用与的拖尾和截尾性质判定类型和阶数
五、实验报告要求
1、写出详细的计算步骤及设计原理;
2、按实验内容的要求打印图形;
3、附上程序和必要的注解。
六.实验过程
function y = experiment4
close all;clc;
% r = [];p1 = [];p = [];
% Fai = [];FAI = [];
%学号21
z1 = [293 301 293 301 295 284 286 286 287 284];
z2 = [282 278 281 278 277 279 278 270 268 272];
z3 = [273 279 279 280 275 271 277 278 279 285];
z4 = [301 295 281 278 278 270 286 288 279 279];
z5 = [289 285 289 286 288 287 288 292 291 291];
z6 = [292 296 297 301 304 304 303 307 299 296];
Z = [z1 z2 z3 z4 z5 z6];
W = Z - mean(Z);
figure(1),
subplot(211),plot(Z);grid on;
subplot(212),plot(W);grid on;
N = length(W);
%利用公式来求样本的自协方差函数,取K<60/4
K = 15;
for k = 1:K
sum = 0;
for i = 1:(N-k)
sum = sum + W(i)*W(i+k);
end
r(k) = sum/N;
end
%55
sum = 0;
for i = 1:N
sum = sum + W(i)*W(i);
end
r0 = sum/N;% 样本方差
p1 = r/r0;
p = [1 p1]; %样本相关系数
%利用递推法求偏相关函数
Fai(1,1) = p1(1); %利用公式1
for k = 1:K - 1
sum1 = 0;
sum2 = 0;
for j = 1:k
sum1 = sum1 + p1(k + 1)*Fai(k,j);
sum2 = sum2 + p1(j)*Fai(k,j);
end
Fai(k + 1,k + 1) = (p1(k + 1) - sum1)/(1 - sum2); %公式2
for j = 1:k
Fai(k + 1,j) = Fai(k, j) - Fai(k + 1,k + 1)*Fai(k, k + 1 - j);% 公式3
end
end
for k = 1:K
FAI(k + 1) = Fai(k,k);
end
FAI(1) = 1;
figure(2),
tt = 0:length(p1);
subplot(2, 1, 1),plot(tt, p);grid on;
title('样本自相关函数');
subplot(2,1,2);plot(tt, FAI);
title('样本偏相关函数');grid on
七.实验结果及分析
八.实验心得体会
通过本次平稳时间序列模型预测实验,进一步熟悉了
Matlab软件的使用操作,同时掌握了平稳时间序列分析模
型的分析方法和步骤,以及模型类别和阶数的确定方法,
并且学会了求解平稳时间序列的自相关函数和偏相关函
数,是书本上的理论知识与实际运用得以结合。