2005级物理化学-final-A

合肥工业大学2005年攻读硕士学位研究生入学考试试题 考试科目：物理化学 适用专业：应用化学、化学工艺等专业（各位考试请注意：答题请写在报考点统一发放的答题纸上，写在试卷上一律无效.）一、选择填空题（每题3分，选做20题（多选倒扣分），每题选一个答案，此题在试卷上作答！）1. 非理想气体经绝热可逆压缩过程，则有：A. B. C. 0<ΔU 0<ΔH 0Δ=S D. 0<ΔS2. /)()/(,U H p G n T −=∂∂，−=∂H S U n V ()/(, S /)3. 恒温恒压下，铜锌可逆电池对外做电功2000kJ ，并放热60kJ ，则H Δ为 A. -2060kJ B. -1940kJ C. 1940kJ D. 2060kJ4. 300K 和p θ下，反应3C(s)+O 2(g)+3H 2(g) CH 3COOH(l)的Q p,m -Q v,m 最接近的值为： A. -15000J/mol B. -10000J/mol C. 5000J/mol D. 12500J/mol5. 300K 下，理想气体在10p θ和5p θ化学势分别为μ1和μ2，则μ1和μ2的关系为 A. μ1<μ2 B. μ1=μ2 C. μ1<μ2 D. μ1<μ26. 400K 时液体A 和B 的纯态饱和蒸气分别为100kPa 和150kPa ，气相中A 量分数为0.5时，理想液态混合物中A 的量分数为x ，则接近x 的应为： A. 0.30 B. 0.40 C. 0.50 D. 0.607. 2 mol 重水与8mol 水在300K ， p θ下形成理想液态混合物，则混合过程有100=ΔΔmin min /G H ，=ΔΔ+Δmin min min /)10(S U G 。

8. NH 4HCO 3(s)在真空容器中部分分解并达到平衡：NH 4HCO 3(s)＝NH 3(g)+H 2O(g)+CO 2(g)。

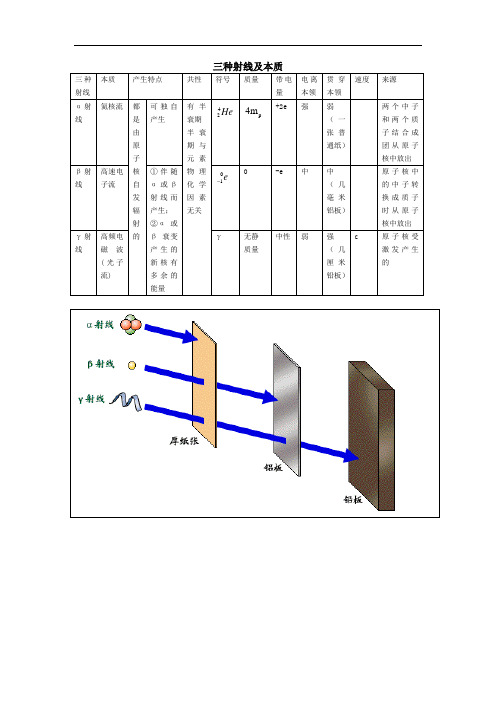
三种射线本质产生特点共性符号质量带电
量
电离
本领
贯穿
本领
速度来源
α射线氦核流都
是
由
原
子
核
自
发
辐
射
的
可独自
产生
有半
衰期
半衰
期与
元素
物理
化学
因素
无关
4
2
He p
4m+2e强弱
（一
张普
通纸）
两个中子
和两个质
子结合成
团从原子
核中放出
β射线高速电
子流
①伴随
α或β
射线而
产生；
②α或
β衰变
产生的
新核有
多余的
能量
1
e
0-e中中
（几
毫米
铝板）
原子核中
的中子转
换成质子
时从原子
核中放出
γ射线高频电
磁波
(光子
流)
γ无静
质量
中性弱强
（几
厘米
铅板）
c原子核受
激发产生
的。

中国药科大学物理化学试卷（函授）一. 选择题:(2分/题，计20分)1.下列公式中,非理想气体同样成立的是RC C S T H G n RT U H V V RT W r r =-∆∆=∆∆+∆=∆=m v,m p,r r r 12)4(-)3()2(ln n )1(2.对下面的热化学方程式,结论正确的是:1r 221m o l kJ 42.112)CO(g (g)O )金C(-⋅-=∆=+H 刚石 (1)1 m c mol kJ 42.112),(-⋅-=∆金刚石C H (2) 1m f mol kJ 42.112)g CO,(-⋅-=∆H (3)1molC(金刚石)和1molO 2(g)混合将放热112.42kJ.(4)以C(金刚石)和O 2(g)混合，当有1molCO(g)生成时，将放热112.42kJ .3.在下图中,Ｂ的化学势可表示为: mm RT p T μμB m B ln ),(*,B += 则标准态),(p T μ*B,m 是图中的哪一点:(1)a (2)b (3)c (4)d (5) e4.如果C p 不随温度而变化,下列说法正确的是:(1).Δr H 不随温度而变化.p B * m B BA p m B(2).Δr G 不随温度而变化.(3).Δr H 和Δr G 都不会随温度而变化.(4).Δr H 和Δr G 都可能随温度而变化.5. 在一定温度压力下，对于一化学反应，能用以判断其反应方向的是。

(1) m r G ∆ (2) K p (3) m r G ∆ (4) Δr H6．现有萘的苯溶液1L ，其化学势为μ1，2L 同溶液的化学势为μ2，下列表达式正确的是：(1) μ1 =2μ2 (2) μ1 =μ2 (3) μ2 =2μ1 (4) μ2 =(2μ1)27．3．298 K ，已知下列化学反应的平衡常数2A 2B + C K 1A B + 1/2C K 2则有： （1）K 2 ＝K 1 ； （2）K 2 ＝（K 1 ）21； （3）K 2 ＝（K 1 ）2；8.对于恒沸混合物，下列说法中错误的是：（1）不具有确定组成 （2） 平衡时气、液相组成相同（3）其沸点随外压而变化9．对于光化学反应的描述，下面何种说法是正确的？（1）其反应速度与反应物浓度呈正比 （2）量子效率φ<1（3）反应速度随反应温度的升高而加快 （4）Δr G m 0 可以大于010．用细玻璃管连接两个大小不等肥皂泡，则可以观察到:（1）大的变大，小的变小，直至小的消失为止（2）小的变大，大的变小，直至两这曲率半径相等为止（3）大的变大，小的变小，直至两这曲率半径相等为止（2）小的变大，大的变小，直至大的消失为止二、填空题：(总计30分)1．（2分）ΔU =Q v 公式的适用条件是 .2．（3分）下列各物理量中,是状态函数的是 . 是强度性质的是 .T; p ; U ;ΔU ; C ; C p,m ; Q r ; W ; μi ; G ; A ; S.3．（5分）Kelvin 得出了曲率对蒸气压的影响的公式ρσRTr M p p r 2ln=，请据此解释液体的暴沸现象，并指出一种最简单的解决办法4. （5分）有物质A 和B 形成下列相图形，请绘出a 和b 点的步冷曲线。

Physica A345(2005)404–410/locate/physaBonaÿde stochastic resonance:a view pointfrom stochastic energeticsDebasis Dan∗,A.M.JayannavarInstitute of Physics,Sachivalaya Marg,Bhubaneswar751005,IndiaReceived28March2003Available online15June2004AbstractWe investigate the resonance type behaviour of an overdamped Brownian particle in a bistable potential driven by external periodic signal.It has been shown previously that the input energy pumpedinto the system by the external d rive shows resonance type behaviour as a function of noise strength.We further extend this idea to study the behaviour as a function of frequency of the external driving force and show the occurrence of similar nonmonotonic behaviour,which can be ascribedas a signature of bonaÿd e stochastic resonance.Both weak andstrong d riving limits have been exploredind icating the occurrence of marginal supra-thresholdstochastic resonance in a bistable potential system.c 2004Publishedby Elsevier B.V.PACS:05.40.−a;02.50.EyKeywords:Stochastic resonance;Bonaÿde resonance;Stochastic energetics1.IntroductionStochastic resonance(SR)is a nonlinear phenomena where the combinede ects of noise andnonlinearity(bistable systems or thresholdsystems)lead s to an enhanced response of a weak periodic signal with an addition of noise of optimal intensity.This counter intuitive phenomenon has been observedexperimentally andin numerical and analog simulations[1].However,there have been a lot of discussions in the recent years regarding the validity of SR as bonaÿde stochastic resonance[2].The archetype∗Corresponding author.Tel.:91-674-581-825;fax:91-674-581-142.E-mail address:dan@iopb.res.in(D.Dan).0378-4371/$-see front matter c 2004Publishedby Elsevier B.V.doi:10.1016/j.physa.2004.05.069D.Dan,A.M.Jayannavar/Physica A345(2005)404–410405 of SR models is represented by a simple symmetric bistable potential driven by a zero mean Gaussian white noise andan external sinusoid al bias.The response of such a system has been mainly characterizedby the response amplitud e(RA)of the periodic component of the process x(t) or the signal-to-noise ratio(SNR).Both these response functions show typical resonance type features with increasing noise amplitude D[1].This resonance has been attributedto the matching of the escape rate across the barrier and the frequency of the external periodic drive.An obvious conclusion is the occurrence of a similar peak with increasing frequency of the bias.But such nonmonotonic behaviour has not been observedin spite of exhaustive numerical and analytical studies on SNR and RA.However,Ref.[3]shows the existence of peak in SNR with increasing frequency for a system with rectangular potential barrier andfor a special type of driving.Other criteria have been proposedto stud y the resonance behaviour as a function of frequency,thus characterizing SR as a bonaÿde resonance.Gammaitoni et al.have shown that residence time distribution N(T)has a resonant behaviour as function of forcing frequency.Marchesoni et al.recently showednumerically that in a Schmitt trigger,N(T)shows a peak with frequency for both weakly andstrongly d riven system. The relationship between SR andsynchronization of passages from one well to another can also be characterizedby a hysteresis loop area[4,5].This loss can be taken as a measure of SR andSR is shown as a bonaÿd e resonance.Recently it is arguedthat input energy is also a goodmeasure of SR[7].This energy is equivalent to the work done by the external agent which drives the potential periodically.The input energy not only shows peaking behaviour with temperature(noise strength)but also takes into account only the interwell behaviour.In the conventional SNR,both intrawell as well as interwell motion is taken into account andhence for small d riving frequency and noise strength,the motion is predominated by the intrawell oscillations[7].Hence the peak in the input energy is a better indicator of the matching of escape rate and the external driving frequency.This assertion has been made by taking into account the detailed comparison between various measures of SR.In this work,we show that input energy not only correctly shows the matching condition for noise-induced escape rate and the external periodic drive,but resonance type behaviour is also obtainedas function of!(frequency of external drive),a signature of bonaÿde SR.Bonaÿde SR is a relatively new term in stochastic dynamics, by which one means the actual matching of the time scales T es(barrier escape time) and T!(periodof external d rive,2 =!).This is manifestedas a peak in the plot of input energy with T!and D.The existence of SR in supra-thresholdregime has also been demonstrated.We make an exhaustive study throughout the parameter regime of our problem andshow the d etailedbehaviour of SR peak as function of D;!and A in our model.2.ModelWe consider an overdamped Brownian particle moving in a bistable potential V(x;t)=−x2=2+x4=4−Ax sin(!t)under the in uence of a zero-mean white Gaussian noise (t)406 D.Dan,A.M.Jayannavar /Physica A 345(2005)404–410with correlations (t ) (t ) =2D (t −t ).The Langevin equation for such a system is˙x (t )=−V (x;t )+ (t )(1)andthe correspond ing Fokker Planck equation (FPE)is 9P (x;t )9t =−99x V (x;t )−D 99x P (x;t );(2)where P (x;t )is the probability density of the particle at position x at time t .The barrier height V =0:25.We consider both weak forcing Ax m ¡ V as well as strong forcing Ax m ¿ V limit.Depending on the parameter regime,the Brownian particle is either dominated by intrawell or interwell oscillations.For small driving force the mo-tion is mostly dominated by intrawell oscillations.At a certain optimal noise strength the interwell motion is enhancedd ue to the combinede ect of noise andweak peri-odic modulation.Such resonant enhancement of interwell motion is termed as SR.In this particular case,the oscillatory driving force keeps the system away from equilib-rium.The energy requiredto d rive the system (E in )can be calculatedfrom Sekimoto’s stochastic energetics formalism [6]andit has been shown that E in depends nonmono-tonically on the noise strength D .Since the mean current in the system is zero,hence no work is done by the system and all the input energy is dissipated into the bath.This suggests that input energy is relatedto d issipative loss or hysteresis loss in the system [4,5].Our e ort is to ÿndthe signatures of SR in the input energy of the system as a function of system parameters !and D .The input energy per period(T !)is deÿned as [6,7]E in = t 0+T !t 0 9V (x;t )9t d t =−A! t 0+T !t 0x (t )cos (!t )d t :(3)The average ··· is done over an ensemble of particles.The asymptotic probability distribution P (x;t )is calculatedby solving the FPE (2).The input energy E in can be rewritten in terms of asymptotic distribution as E in = ∞−∞d x t 0+T !t 0d t x (t )cos(!t )P asy (x;t ):(4)where P asy (x;t )=P asy (x;t +T !).This distribution is obtained after the initial transients have died down and asymptotic probability density assumes a unique limiting periodic distribution in time.The maxima of E in as function of D is taken as a signature of SR.We numerically solve Eq.(2)by the methodof ÿnite d i erence to obtain the asymptotic distribution P asy (x;t ):E in is obtainedby numerically integrating Eq.(4).Throughout this work all the physical quantities are in dimensionless units [1].3.Results and discussionsThe input energy shows a rich structure as a function of A;!and D .We mainly concentrate on the low-amplitude drive,Ax m = ¡1.In this regime,input energy shows a sharp maxima both as function of D and !.In Fig.1we plot E in as a function of D for A =0:1andd i erent values of !.The peak in the input energy can be attributedtoD.Dan,A.M.Jayannavar /Physica A 345(2005)404–410407Fig.1.E in vs.D for A =0:1.The inset shows the plot of E in vs.D for !=0:1;0:2;0:3from top to bottom at A =0:2.the synchronization of escape from the potential well and the external periodic drive as has been extensively discussed in previous literatures [7].With increasing !the temperature at which E in peaks increases are shown in Fig.1.The most favourable condition for hopping to an other potential well is when the barrier height is minimum.When !is increased,the Brownian particle spends less time in the most favourable condition and hence stronger uctuations are needed to cross the barrier.Barrier height also decreases with increase in amplitude of external drive.Hence for reasons similar to the above,the resonance peak shifts towards lower temperature as shown in the inset,where we have plotted E in vs.D for various values of A as mentionedin the caption.However,our main motive is to check whether these resonance features are also observed when the frequency of the external drive is varied.In Fig.2we plot E in as function of !for A =0:1andd i erent values of temperature.Unlike other response function like SNR,RA which characterize SR and has monotonic dependence on !,input energy shows a nonmonotonic anda peaking behaviour with !.For a small amplitude drive and at low temperature the resonant frequency is very close to half the Kramer’s rate for the unperturbedsystem (the resonance cond ition being 1=r k =T !=2→!= =r k ).For D =0:2,the Kramer’s rate (r k =(1=√2 )exp(−0:25=D ))is 0.0645,which is very close to != =0:14= =0:0446.With higher amplitude the resonance peak shifts to higher frequency for a given temperature as shown in the inset.Thus SR as a bona ÿde resonance is established.It is known that for A A max ,where A max is the dynamical threshold above which deterministic switch events take place driven by the periodic signal alone (absence of noise),SR is not observed.The dynamical threshold depends on both the modulation408 D.Dan,A.M.Jayannavar /Physica A 345(2005)404–410Fig.2.E in vs.!for A =0:1.Inset is the plot of E in vs.!at A =0:2for D =0:15,0.2,0.25from top to bottom curve,respectively.Fig.3.E in vs.D at !=1:0for large amplitude A =0:85,0.87,0.90and0.92,respectively.frequency andthe wave form A (t ).For the form given in Eq.(1)A max =A th =1+ÿ( =a ),where ÿ=(2√3= )g 1and g 1is the smallest zero of the Airy function Ai (−x ),is order of unity [8].We investigate the marginal supra-thresholdregime (A ¿A max )andshow that SR is observedwith increasing temperature provid ed A is not very large compared to A max .The occurrence of SR in this regime is relatedto noise-ind ucedstability [5,8].In Fig.3we plot the input energy for four di erent values of A at !=1:0.Fig.4D.Dan,A.M.Jayannavar/Physica A345(2005)404–410409Fig.4.The deterministic trajectories(D=0)for amplitudes A=0:85,0.90and0.92.All these trajectories cross the barrier at x=0.shows the corresponding deterministic trajectories.As shown in Fig.4,A=0:85is the threshold,i.e.,the particle is just able to cross the barrier at x=0.Hence higher values of A is above dynamic threshold.For A¿0:85the input energy shows a resonance peak with increasing temperature.This peak in E in,in supra-thresholdregime is shown for a very small window of A.For the speciÿc parameter values as above,the peak vanishes for A¿0:91.This peak can be ascribedto resonant trapping as d iscussedin the previous literature[5,8].However,in supra-thresholdregime,E in clearly exhibits peaking behaviour as a function of![9]for all values of A.This is more akin to conventional resonance(absence of barrier).In conclusion,we have calculatedthat the input energy pumpedinto the system by an external drive using the method of stochastic energetics.This input energy is shown to be a goodquantitative measure of SR.Moreover SR is shown to be a bonaÿd e resonance.References[1]L.Gammaitoni,P.Hanggi,P.Jung,F.Marchesoni,Rev.Mod.Phys.70(1998)223.[2]L.Gammaitoni,F.Marchesoni,S.Santucci,Phys.Rev.Lett.74(1995)1052;M.H.Choi,R.F.Fox,P.Jung,Phys.Rev.E57(1998)6335;G.Giacomelli,F.Marin,I.Rabbiosi,Phys.Rev.Lett.82(1999)675;F.Marchesoni,L.Gammaitoni,F.Apostolico,S.Santucci,Phys.Rev.E62(2000)146.[3]V.Berdichevsky,M.Gitterman,J.Phys.A29(1996)L447.[4]M.C.Mahato,S.R.Shenoy,Phys.Rev.E50(1994)2503;M.C.Mahato,A.M.Jayannavar,Phys.Rev.E55(1997)6266.410 D.Dan,A.M.Jayannavar/Physica A345(2005)404–410 [5]M.C.Mahato,A.M.Jayannavar,Mod.Phys.Lett.B11(1997)815;M.C.Mahato,A.M.Jayannavar,Physica A248(1998)138.[6]K.Sekimoto,J.Phys.Soc.Jpn.66(1997)6335;F.Takagi,T.Hondou,Phys.Rev.E60(1999)4954.[7]T.Iwai,Physica A300(2001)350;T.Iwai,J.Phys.Soc.Jpn.70(2001)353.[8]F.Apostolico,L.Gammaitoni,F.Marchesoni,S.Santucci,Phys.Rev.E55(1997)36;R.N.Mantegna,B.Spagnolo,Phys.Rev.Lett.76(1996)563.[9]A.L.Pankratov,Phys.Rev.E65(2002)022101.。

2005年全国化学竞赛初赛模拟试卷（21）（时间：3小时满分：100分）题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 满分8 4 8 6 6 5 6 8 7 8 8 8 8 10H** 相对原子质量He **Li ** Be**B**C**N**O**F**Ne**Na ** Mg**Al**Si**P**S**Cl**Ar**K ** Ca**Sc**Ti**V**Cr**Mn**Fe**Co**Ni**Cu**Zn**Ga**Ge**As**Se**Br**Kr**Rb ** Sr**Y**Zr**Nb**Mo** Tc[98]Ru**Rh**Pd**Ag**Cd**In**Sn**Sb**Te**I**Xe**Cs ** Ba** La－LuHf**Ta**W**Re**Os**Ir**Pt**Au**Hg**Tl**Pb**Bi** Po[210]At[210]Rn[222]Fr [223]Ra[226]Ac－La Rf Db Sg Bh Hs Mt Ds第一题（8分）超分子通常是指由两种或两种以上分子依靠分子间作用结合在一起，组装成复杂的、有组织的聚集体，并保持一定的完整性，使其具有明确的微观结构和宏观特征。

超分子体系和其他化学体系一样，由分子形成稳定超分子的因素，在不做有用功（如光、电）时，可从热力学自由焓的降低（ΔG＜0）来理解：ΔG＝ΔH－TΔS；式中ΔH是焓变，代表降低体系的能量因素；ΔS是体系熵增的因素。

1．我们在分析超分子稳定形成的因素时，属于能量降低的因素有；属于熵增的因素有。

A、静电作用B、氢键C、螯合效应D、疏水空腔效应E、M(金属)—L(配位体分子)配位键F、π~π堆叠作用2．尿素[(NH2)2CO]可以与正烷烃（n~C m H2m+ 2，m≥8）形成超分子包合物。

其中尿素分子通过氢键（写出具体形式）有序地组合成具有蜂窝状六角形通道结构的接受体，如(a)所示。

武 汉 大 学2005年攻读硕士学位研究生入学考试试题答案科目名称：物理化学和高分子化学 科目代码：注意：所有的答题内容必须答在答题纸上，凡答在试题或草稿纸上的一律无效。

物理化学部分（75分）k : 1.381×10-23 J·K -1 h : 6.626×10-34 J·s1． （15分）一．有一双原子分子理想气体，T 1=300K ，p 1=5p ，S m (300K,5 p )=191.83J/K.mol ，经历一途径到达末态，已知此始末两态间的ΔG ＝15957 J/mol ，ΔG －ΔF ＝－831.4 J 。

试求：此始末两态间的ΔU 、ΔH 、ΔS 、ΔF ；以及末态的温度和压力? 解： ∵ ΔG=Δ(F+pV) ∴ ΔG －ΔF ＝Δ(F+pV)－ΔF ＝Δ (pV)=RT 2－RT 1= －831.4 J T 2= T 1＋（－831.4/R ）= 300－100＝200 K ΔU ＝C V ΔT ＝2.5R·（200-300）＝－2078.5 J ΔH ＝C p ΔT ＝3.5R·（200-300）＝－2909.9 J ΔF= ΔG+831.4=16788.4 JΔG=ΔH －Δ(TS) =ΔH －(T 2S 2－T 1S 1)S 2= [ΔH －ΔG ＋T 1S 1]/T 2 = [－2909.9－15957＋300×191.83]/200=193.41 J/K.mol ΔS= 193.41－191.83=1.58 J/K.mol ∵ ΔS= C p ln(T 2/T 1)+Rln(p 1/p 2)=3.5Rln(200/300)+Rln(5p /p 2)=1.58Rln(5p /p)=1.58－3.5Rln(2/3)=1.58+11.80=13.38ln(5p /p 2)= 1.609p 2=1p 解得： ΔU=－2078.5 J ΔH=－2910 J ΔF= 16788.4 JΔS= 1.58 J/KT 2=200Kp 2=1p2．（10分）NaCl-H 2O 体系的定压相图如图所示：(1) 分别写出相区A 、B 、C 、D 、E 、F 的相态、相数和自由度； (2) 指明图中自由度为零的地方，并标明相态。